dr inż. Remigiusz Nowak
Wydział Energetyki i Paliw AGH

MODELOWANIE MATEMATYCZE - Równania różniczkowe rzędu I

Zadania problemowe

Zad 1.
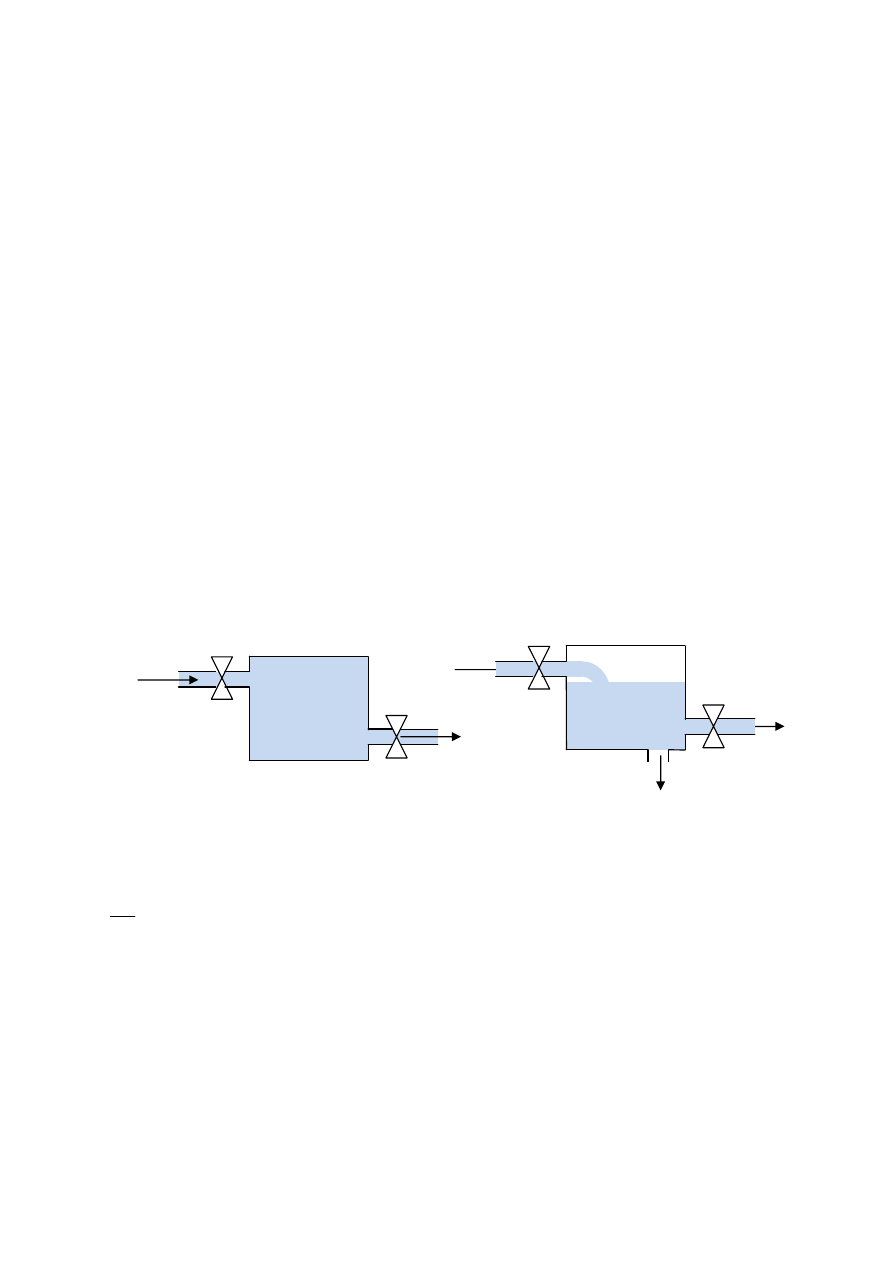
Zbiornik o pojemności 500 litrów wypełniono w całości wodą, zawierającą ok. 5 kg soli. Po
otwarciu zaworu 1, do zbiornika zaczęto doprowadzać roztwór wody z solą. W tym samym
czasie otworzono zawór 2, aby umożliwić swobodny wypływ mieszanki ze zbiornika.

(a) Zakładając, że strumienie doprowadzanego i odprowadzanego roztworu są równe
i wynoszą 5 l/min, oraz, że zawartość soli w doprowadzanym roztworze wynosi
0,2 kg/litr, oblicz jaka będzie koncentracja soli (w kg/litr) w zbiorniku po upływie
10 minut od otwarcia zaworów 1 i 2.

(b) Po 10 minutach w zbiorniku pojawia się niewielka nieszczelność, którą zaczyna wyciekać
roztwór. Oblicz jaka będzie koncentracja soli w zbiorniku (w kg/l) po 20 minutach od
wystąpienia nieszczelności, przy założeniu, że strumień wypływającego w ten sposób
roztworu wynosi 1 l/min.

(b1) Jakie będzie graniczne (maksymalne) stężenie soli (kg/l) w zbiorniku po wystąpieniu
nieszczelności. Kiedy (po jakim czasie zostanie ono osiągnięte). Jaka będzie
maksymalna ilość soli w zbiorniku (w kg). Czy maksymalne stężenie i ilość wystąpią w
tym samym czasie?

(a)

(b)

Pomoc w rozwiązaniu przykładu (b) - rozwiązanie równania
Rozwiązanie równania liniowego w przypadku zmiany wartości współczynnika P(x)

(x) y

x

dy

P

dx

+

=

(1)

1

y

=

1,

0

2

(x)

3,

2

x

P

x

≤ ≤



=



>



- Krok 1: Znajdź rozwiązanie ogólne równania dla przedziału od 0 do 2
- Krok 2: Wyznacz stałą, tak aby spełniała warunek początkowy
- Krok 3: Znajdź rozwiązanie ogólne dla przedziału x>2
- Krok 4: Dobierz stałą dla rozwiązania z kroku 3 w taki sposób, aby rozwiązanie z kroku 2 i
kroku 3 pokrywały się ze sobą w punkcie x = 2.

(1)

(2)

5 l/min
0,2 kg/l

5 l/min

X(t)

X(0) = ?

500 l

(1)

(2)

5 l/min
0,2 kg/l

5 l/min

1 l/min

X(t)

X(10) = ?

? l

dr inż. Remigiusz Nowak
Wydział Energetyki i Paliw AGH

Zad 2.
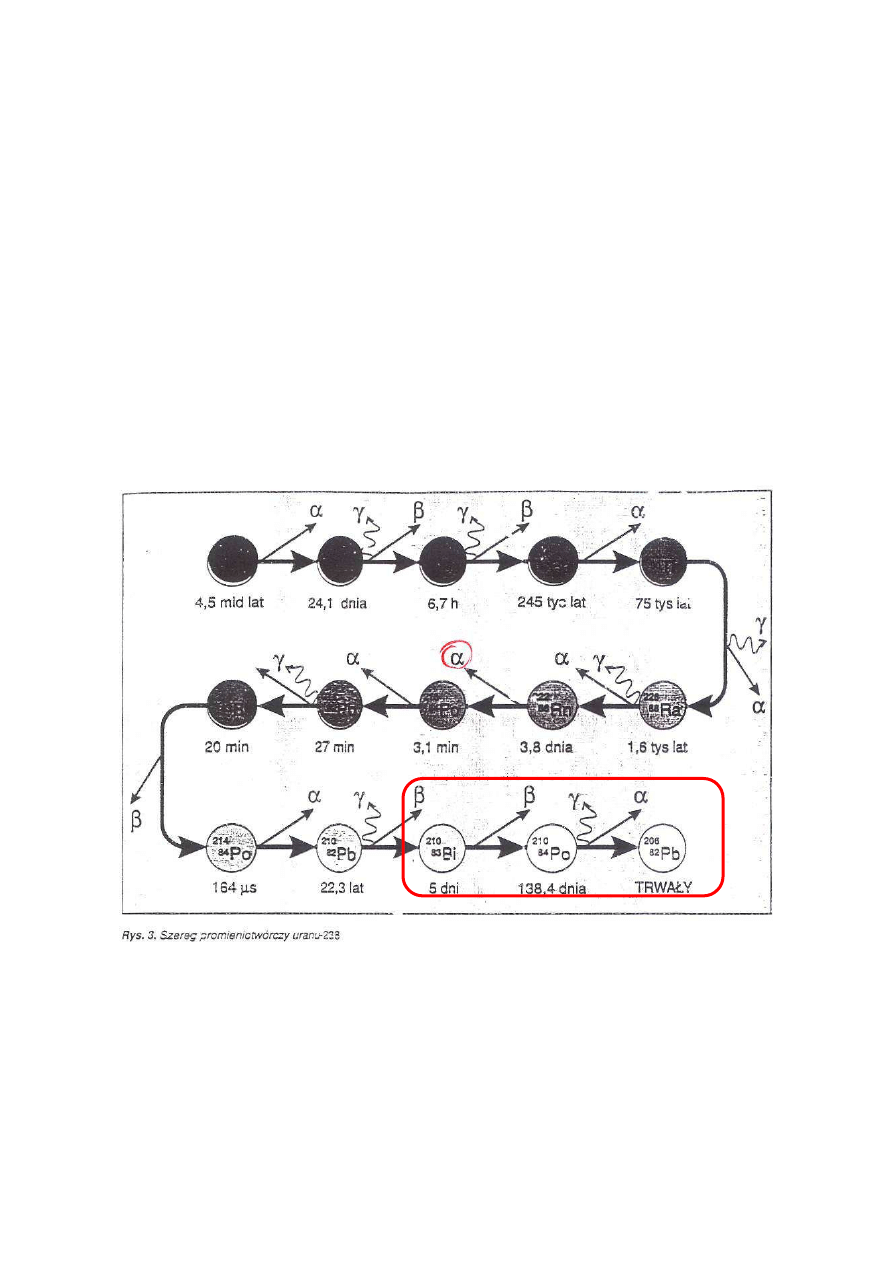
Trzy ostatnie izotopy uranowo-radowego szeregu promieniotwórczego to: Bizmut 210 (Bi
210), Polon 210 (Po 210) oraz Ołów 206 (Pb 206). W łańcuchu tym izotop Pb 206 jest stały i
nie ulega już rozpadowi promieniotwórczemu. Przyjmując stałą rozpadu Bi 210 oraz Po 210
równe odpowiednio k

1

= 0,14 [1/dzień] oraz k

2

= 0,005 [1/dzień] oraz początkową ilość

Bizmutu 210 równą 1 kg.

(a) Oblicz jaka będzie ilość każdego z izotopów po 65 dniach.
(b) Oblicz ile czasu upłynie zanim izotopy Bizmutu oraz Polonu rozpadną się całkowicie do
izotopu trwałego.
(c) Przy pomocy programu Excel sporządź wykresy otrzymanych zależności, ilości danego
izotopu od czasu i na tej podstawie zbadaj poprawność otrzymanego rozwiązania.
(d) Jaka maksymalna ilość (w kg) izotopu Po 210 powstanie w tym układzie z 1 kg Bi 210

Ź

ródło rysunku - www.if.pw.edu.pl/

dr inż. Remigiusz Nowak
Wydział Energetyki i Paliw AGH

Zad 3.
Początkowo, 1000 W żelazko, którego płyta grzewcza wykonana jest ze stopu aluminium o
grubości 0,5 cm (ρ = 2770 kg/m

3

, c

p

= 875 J/kgK, a = 7.3·10

-5

m

2

/s) powierzchni 0.03 m

2

znajduje się w równowadze termodynamicznej z otaczającym powietrzem o temperaturze
22°C. Przyjmując, że współczynnik wnikania ciepła wynosi 12 W/m

2

K oraz zakładając, że

85% ciepła generowanego przez opór przewodu elektrycznego dociera do powierzchni
grzejnej żelazka, oblicz ile czasu upłynie zanim osiągnie ona temperaturę 140 °C.



Zad 4.
W poniedziałkowy poranek, temperatura w sali wykładowej wynosi 4 °C. O godzinie 7:00 w
budynku włączono piec i nastawiono go na temperaturę 21 °C. Zakładając, że ilość ciepła
doprowadzonego prze piec do sali wykładowej jest wyrażona równaniem:

(

)

( )

( )

U

D

U t

K

T

T t

=

−

,gdzie T

D

jest oczekiwaną (pożądaną temperaturą w pomieszczeniu) oraz, że stała czasowa

budynku (nie uwzględniającą zainstalowanych urządzeń grzewczych) 1/K = 2 godz., a także
fakt, iż stała czasowa budynku (z uwzględnieniem systemów grzewczych tj. np. piec) wynosi
1/K

1

= 0,5 godz., gdzie K

1

= K + K

U

, oblicz:

(a) Jaka będzie temperatura w sali wykładowej o godzinie 8:00
(b) Kiedy temperatura w budynku osiągnie wartość 18,5 °C.