UKŁADY
WSPÓŁRZĘDNYCH
STOSOWANE W GEODEZJI
UKŁADY
WSPÓŁRZĘDNYCH
STOSOWANE W GEODEZJI
Wielkościami określającymi połoŜenie punktów na powierzchni odniesienia są ich współrzędne w
przyjętych układach.
KaŜdy układ współrzędnych musi posiadać dokładną charakterystykę geometryczną:
•Początek układu współrzędnych
•Zdefiniowane kierunki osi współrzędnych
Układ współrzędnych -
jest to zespół obiektów geometrycznych, względem których określa się
jednoznacznie połoŜenie punktu:
1.
Układ współrzędnych na elipsoidzie
2.
Prostokątne układy współrzędnych na płaszczyźnie:
•
1965
•
1992
•
2000
3. Układ współrzędny biegunowy
UKŁADY WSPÓŁRZĘDNYCH NA ELIPSOIDZIE
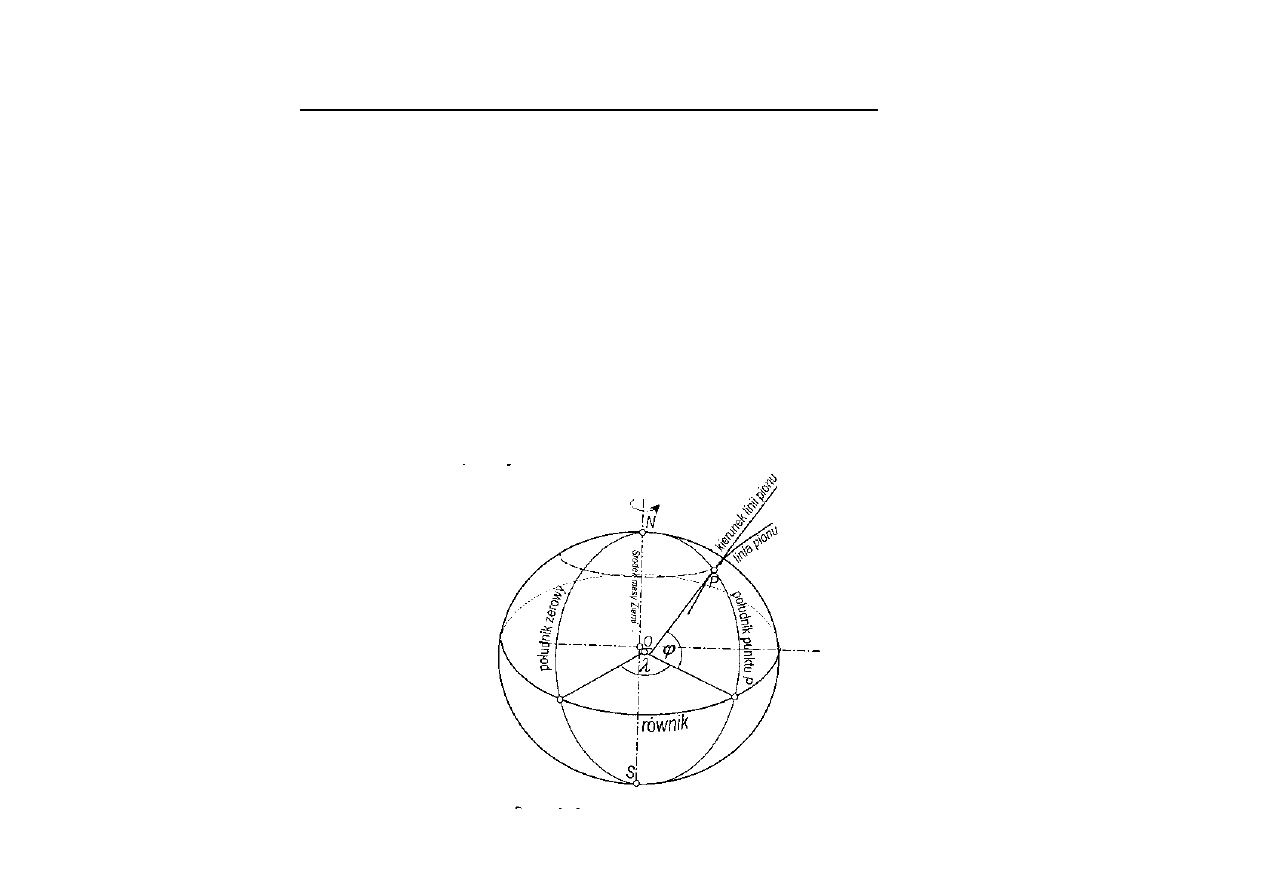
Układ współrzędnych geograficznych - astronomicznych
Szerokość geograficzna – astronomiczna : jest to kąt zawarty pomiędzy kierunkiem linii pionu w
danym punkcie P (miejsce obserwacji) a płaszczyzną równika astronomicznego. Przedział
współrzędnej to od 0
0
do +90
0
na północ od równika i od 0
0
do -90
0
na południe od równika
Długość geograficzna – astronomiczna : jest to kąt dwuścienny zawarty pomiędzy płaszczyznami
południków astronomicznych: Greenwich i danego punktu P. Przedział współrzędnej to od 0
0
do +180
0
na wschód od południka 0
0
i od 0
0
do -180
0
na zachód od południka 0
0
Szerokość
i długość
geograficzna-astronomiczna wyznaczana jest na podstawie pomiarów
wykonanymi metodami astronomii geodezyjnej
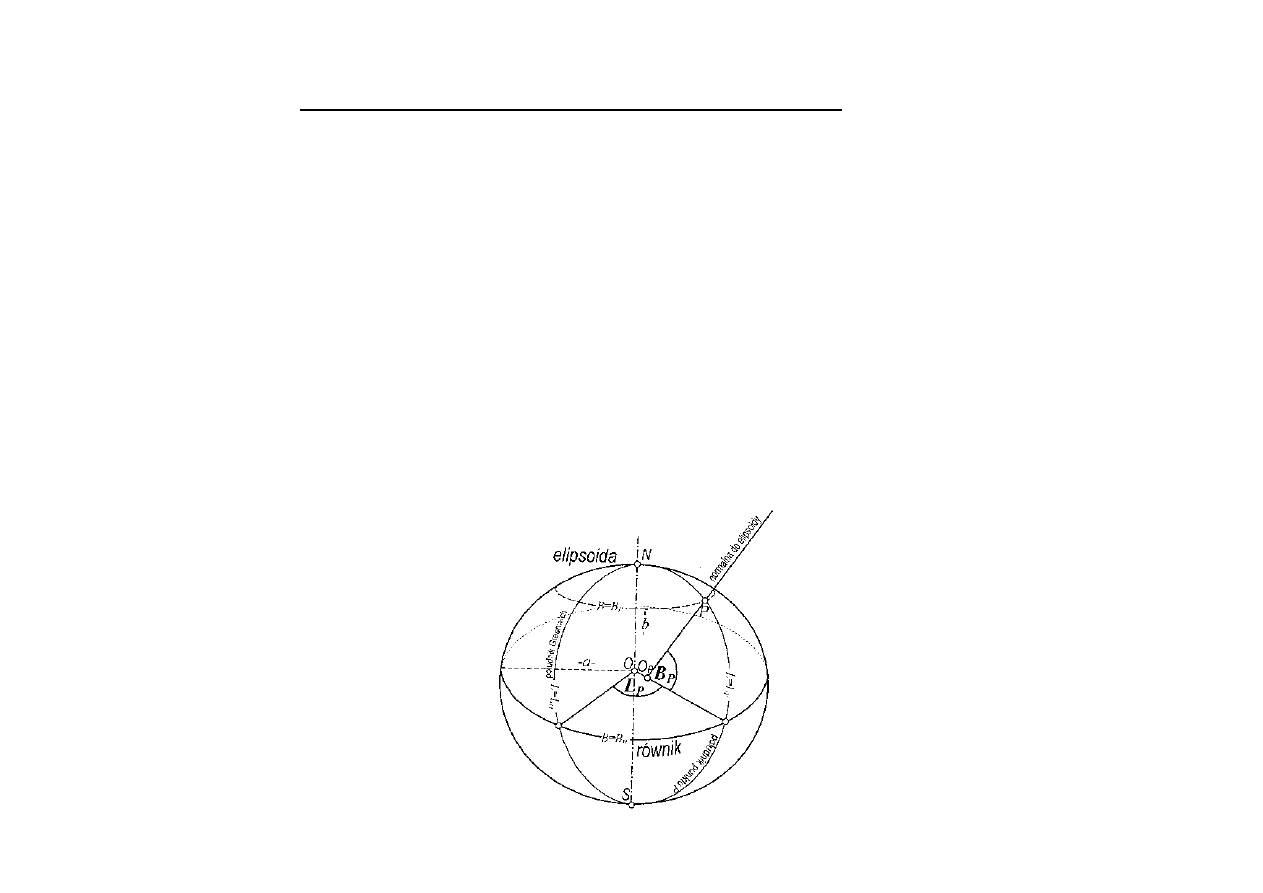
Układ współrzędnych geograficznych - geodezyjnych
Szerokość geograficzna – geodezyjna (elipsoidalna) : jest to kąt zawarty pomiędzy normalną do
elipsoidy w danym punkcie P (miejsce obserwacji) a płaszczyzną równika geodezyjnego. Równik ten
jest kołem utworzonym w wyniku przecięcia elipsoidy płaszczyzną przechodzącą przez jej środek i
prostopadłą do osi obrotu elipsoidy
Długość geograficzna – geodezyjna (elipsoidalna): jest to kąt dwuścienny zawarty pomiędzy
płaszczyzną
geodezyjnego
południka
zerowego
a
płaszczyzną
geodezyjnego
południka
przechodzącego przez dany punkt P. Oś obrotu elipsoidy i normalna do elipsoidy w danym punkcie
wyznaczają płaszczyzny południków. Południki geodezyjne są elipsami powstałymi w wyniku
przecięcia elipsoidy płaszczyznami przechodzącymi przez oś obrotu elipsoidy
Trzecią współrzędną jest wysokość elipsoidalna
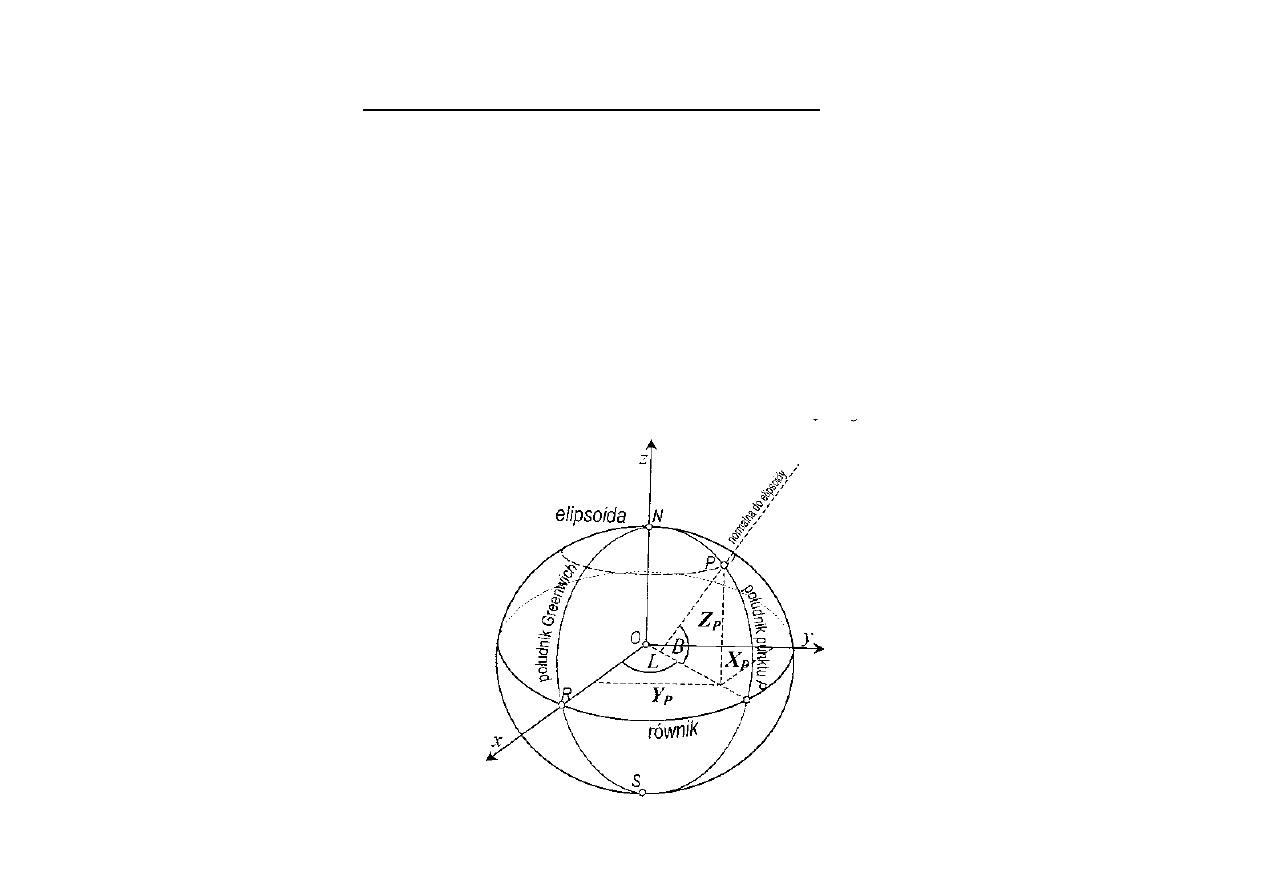
Układ współrzędnych prostokątnych X, Y, Z
Jest to elipsoidalny układ przestrzenny geocentryczny.
Początek układu – znajduje się w płaszczyźnie równika geodezyjnego w środku cięŜkości masy
Ziemi
Oś X – jest śladem przecięcia płaszczyzn równika i południka zerowego
Oś Y – jest śladem przecięcia płaszczyzn równika i południka 90
0
Oś Z – pokrywa się z osią obrotu elipsoidy i jest skierowana na północ
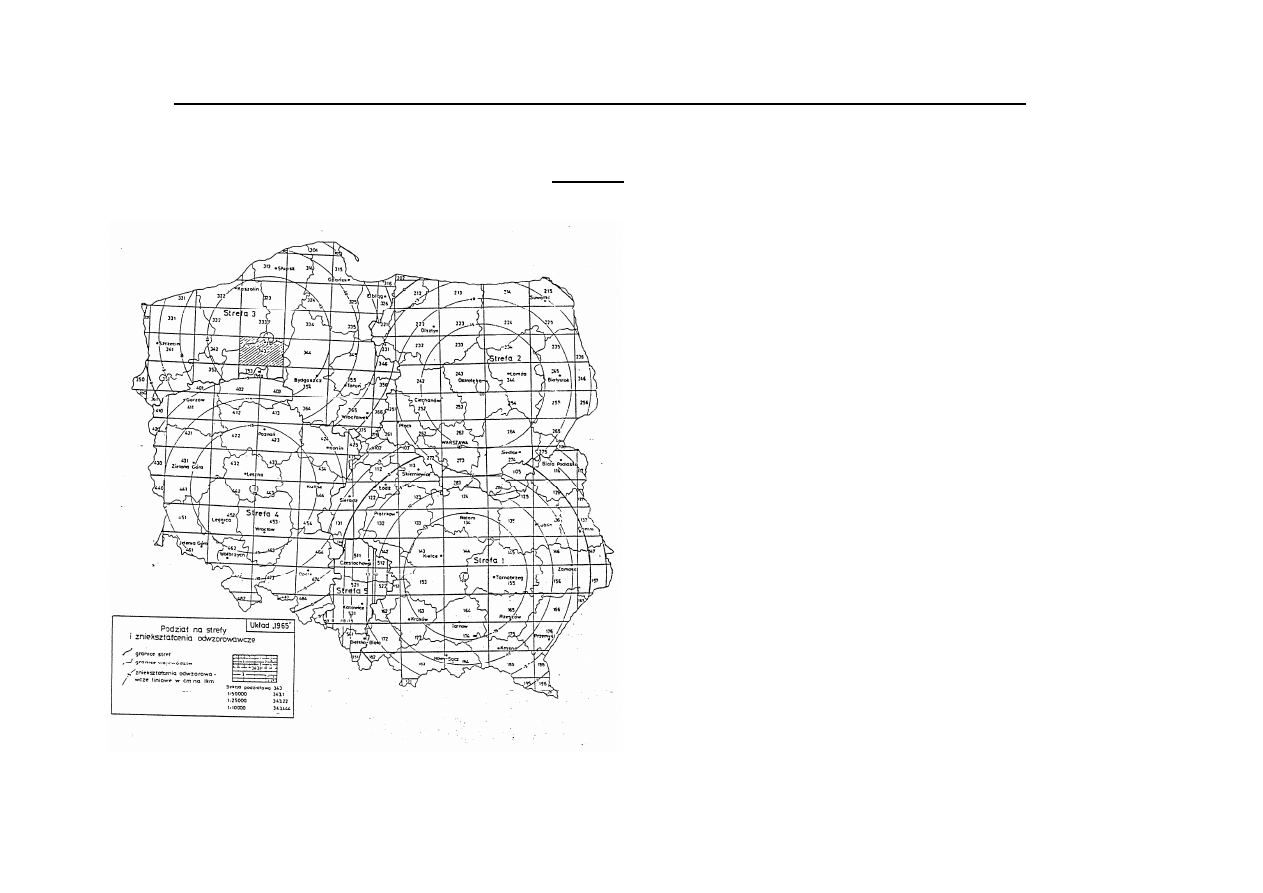
PROSTOKĄTNE UKŁADY WSPÓŁRZĘDNYCH NA PŁASZCZYŹNIE
„1965”
Tworzy go 5 stref odwzorowawczych, z których 4,
o numerach od I do IV, związane są
z
odwzorowaniem quasi – stereograficznym, V zaś
– z odwzorowaniem Gaussa – Krőgera W kaŜdej z
tych
stref
jako
powierzchnię
odniesienia
przyjmuje się elipsoidę Krasowskiego.
Układ stref odwzorowawczych i zniekształceń
liniowych w układzie „1965”
Skalę odwzorowania m
0
w punkcie głównym w
kaŜdej strefie od I do IV przyjęto równą 0,9998,
zaś m
0
w południku osiowym dla strefy V – równą
0,999983. Dla kaŜdej z tych stref przyjęto
niezaleŜny układ współrzędnych prostokątnych o
parametrach podanych w tabeli
Układ współrzędnych
1965
Strefa 1
Strefa 2
Strefa 3
Strefa 4
Strefa 5
Odwzorowanie kartograficzne
Quasi-stereograficzne
Gauss-
Krüger
Punkt przyłoŜenia elipsoidy
Pułkowo „1942”
Jednostka miary
m
m
m
m
m
Rzędna punktu głównego X (na
północ)
5467000,00
5806000,00
5999000,00
5627000,00
-4700000
Odcięta punktu głównego Y (na
wschód)
4637000,00
4603000,00
3501000,00
3703000,00
237000
Azymut dodatniej odciętej Y
(stopnie na wschód od północy)
90
90
90
90
90
Szerokość geograficzna punktu
głównego odwzorowania
(stopnie)
50
°
37
′
30,0
″
53
°
00
′
07,0
″
53
°
35
′
00,0
″
51
°
40
′
15,0
″
Długość geograficzna punktu
głównego odwzorowania
(stopnie)
21
°
05
′
00,0
″
21
°
30
′
10,0
″
17
°
00
′
30,0
″
16
°
40
′
20,0
″
18
°
57
′
30,0
″
Współczynnik redukcji skali na
południku środkowym
0,9998
0,9998
0,9998
0,9998
0,999983
Dane do zdefiniowania odwzorowania stosowanego w poszczególnych strefach odwzorowawczych
państwowego układu współrzędnych prostokątnych płaskich
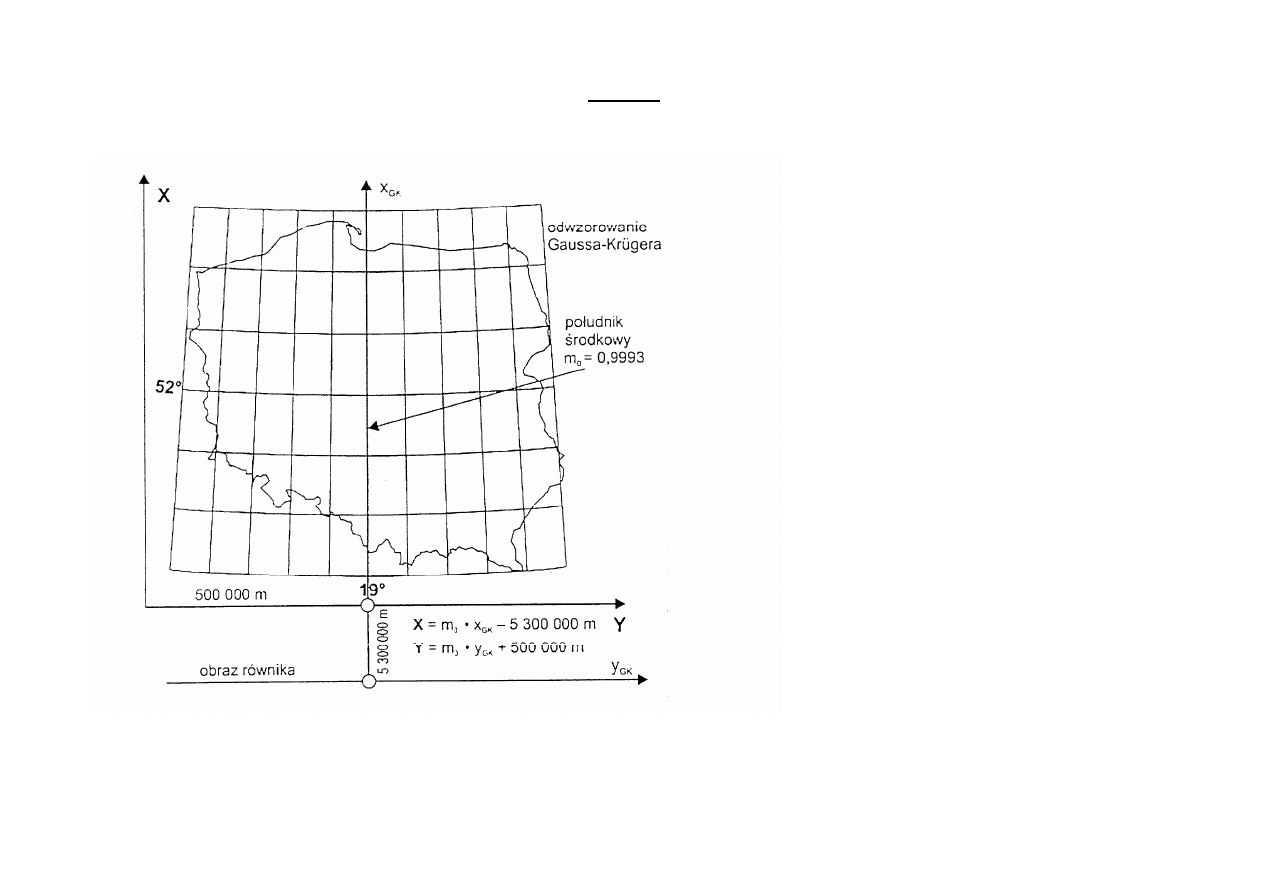
„1992”
Układ
przeznaczony
jest
do
wykorzystania
głównie
przy
opracowywaniu map topograficznych
(małoskalowych). Bazuje on na
współrzędnych
geograficznych
geodezyjnych w tym układzie, które
zgodnie z zasadami i załoŜeniami
odwzorowania Gaussa – Krőgera
zostały dla obszaru całej Polski
przeliczone
na
współrzędne
prostokątne płaskie – w jednej strefie
(pasie) 10 stopniowej szerokości,
przy jej południku osiowym o L
0
=
19º i przy współczynniku skali w tym
południku m
0
= 0,9993. Początkiem
tego układu współrzędnych jest punkt
przecięcia się
obrazu południka
osiowego z obrazem równika, przy
czym
ostateczne
wartości
współrzędnych przeliczanych w tym
układzie punktów pomniejsza się o
wartość 5 300 000 m wzdłuŜ osi x,
oraz zwiększa się o 500 000 m –
wzdłuŜ osi y.
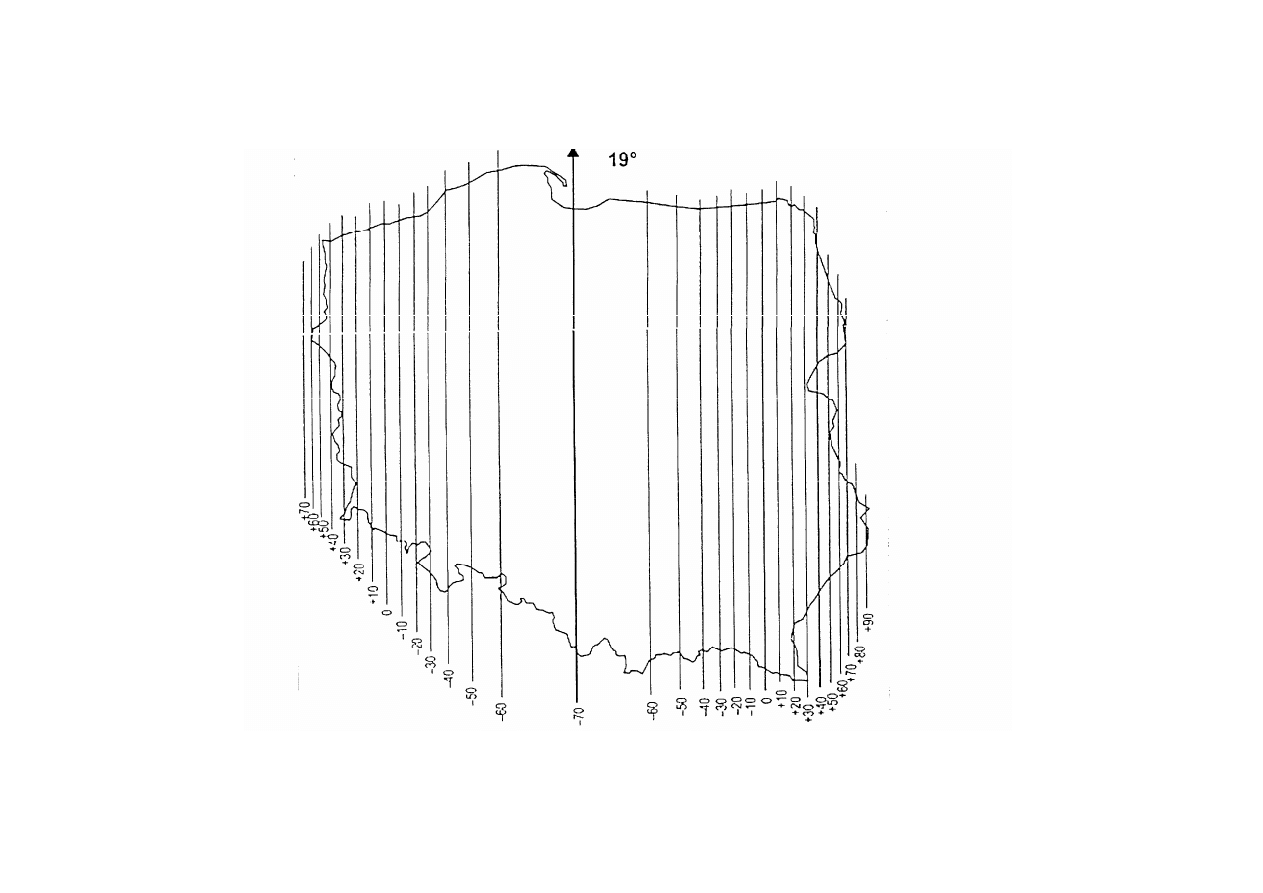
Rozkład zniekształceń długościowych w układzie1992
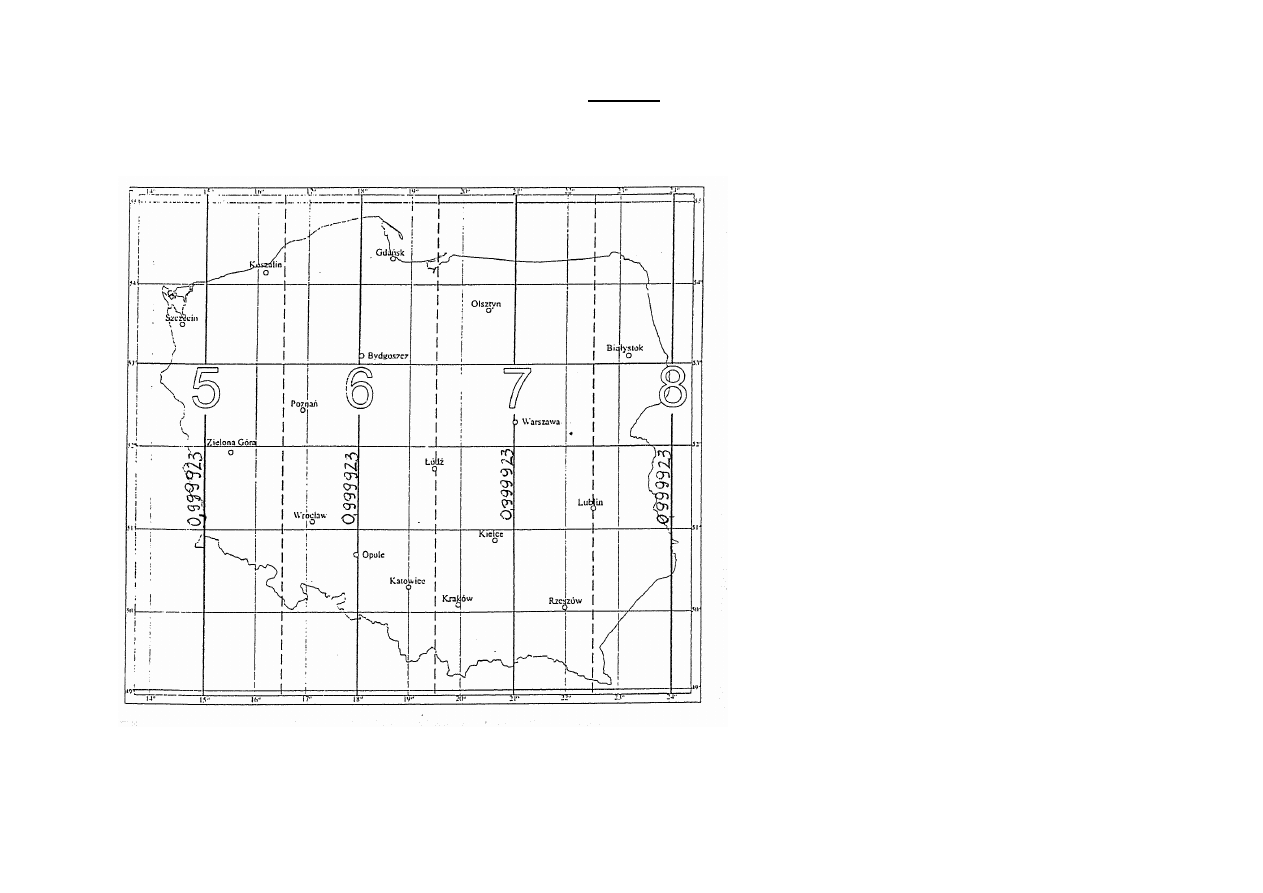
„2000”
Współrzędne płaskie prostokątne x, y
są
obliczane
w
odwzorowaniu
Gaussa – Krőgera w pasach (strefach)
trzystopniowych,
o
południkach
osiowych L
0
równych kolejno: 15º,
18º, 21º i 24º, ponumerowanych
odpowiednio
5,
6,
7
i
8.
Współczynnik
zmiany
skali
w
południku
osiowym
równy
jest
0,999923 taki sam w kaŜdej strefie.
Obraz równika jest linią o równaniu x
= 0, a obraz południa osiowego w
poszczególnych strefach – linią o
równaniu:
– y = 5 500 000 m – przy południku
L
0
= 15º – w strefie 5,
– y = 6 500 000 m – przy południku
L
0
= 18º – w strefie 6,
- y = 7 500 000 m – przy południku
L
0
= 21º – w strefie 7
- y = 8 500 000 m – przy południku
L
0
= 24º – w strefie 8
Rozkład zniekształceń długościowych w układzie 2000
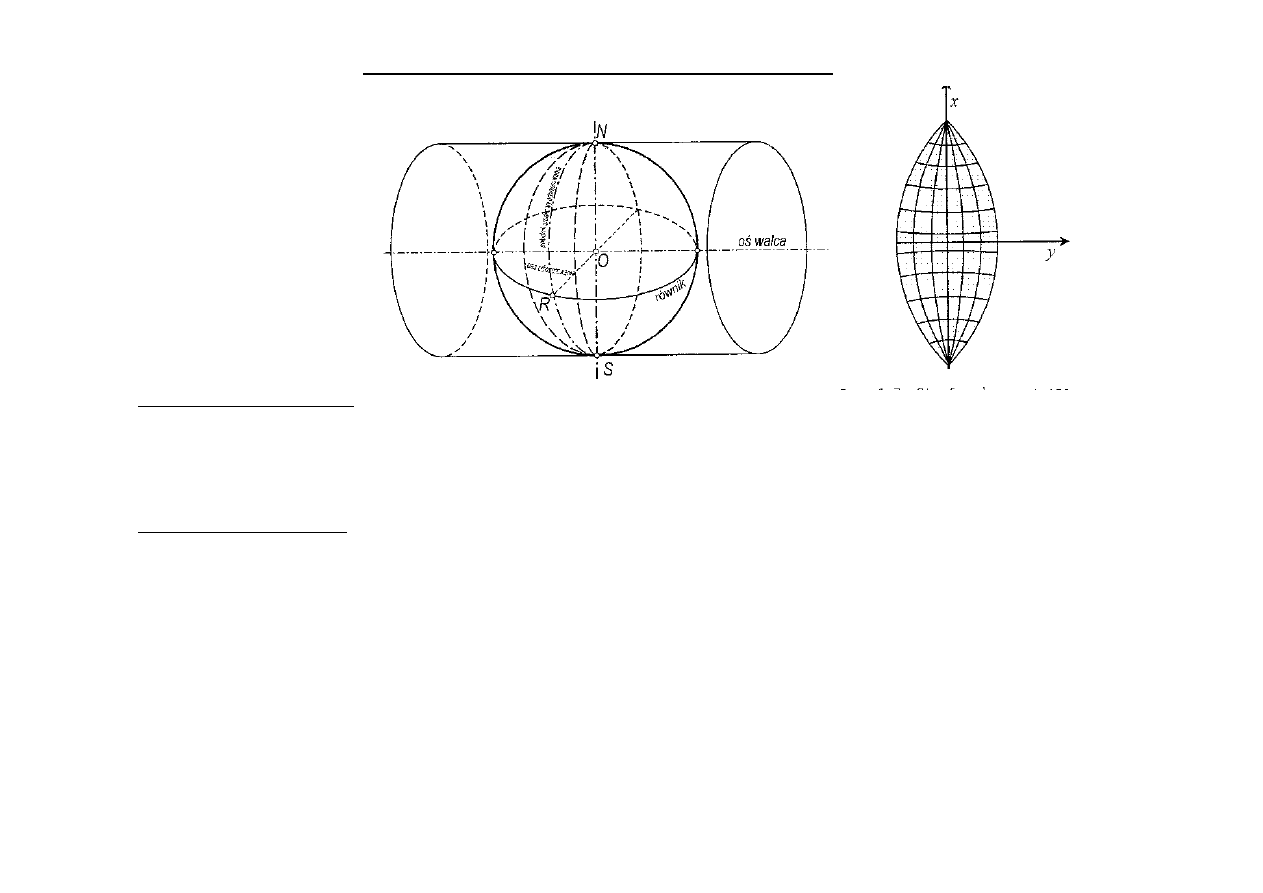
„ODWZOROWANIE GAUSSA KRUGERA”
1.
Odwzorowanie elipsoidy na kulę a potem kulę na pobocznicę walca – Gauss
2.
Odwzorowanie kuli na pobocznicę walca – ulepszenie wersji Gaussa przez Krugera
Zasada odwzorowania
Cechy odwzorowania
1.
Podział na pasy południkowe zwane strefami – w celu ograniczenia zniekształceń – i kaŜdą strefę
odwzorowuje się oddzielnie
2.
Południk środkowy stanowi oś symetrii strefy
3.
KaŜda strefa posiada własny układ, w którym oś x jest południkiem środkowym strefy a oś Y
obrazem równika, zaś punkt ich przecięcia początkiem układu
4.
W celu uniknięcia znaku minus dla wsp. Y – przyjmuje się jej wartość początkową równą 500km
5.
Zniekształcenia długości wzrastają w miarę oddalania się od południka środkowego