1

SYSTEMY ELEKTROENERGETYCZNE 

Rozdział

5

STABILNOŚĆ

NAPIĘCIOWA

Łódź, 2011

rok

Andrzej Kanicki

2

STABILNOŚĆ

NAPIĘCIOWA

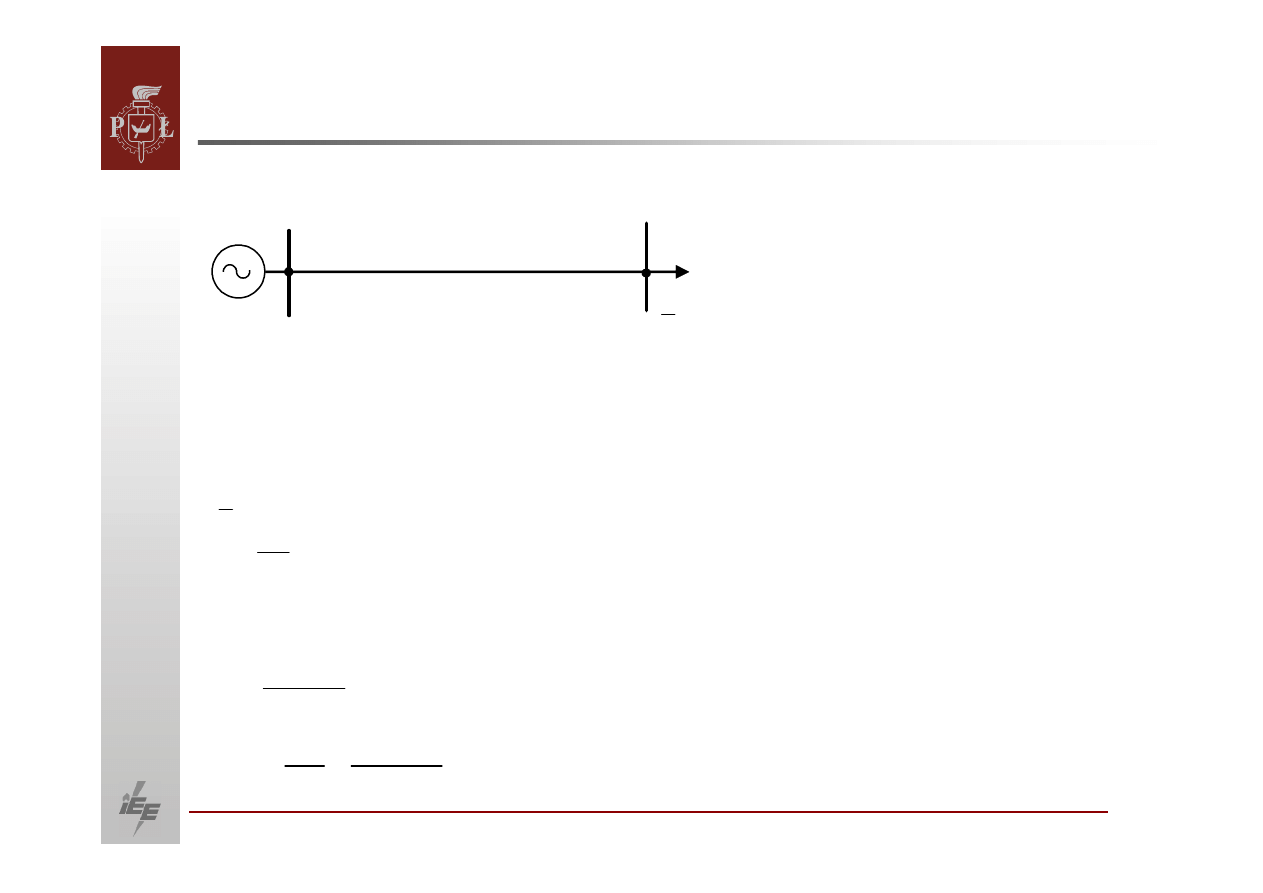
Rozważmy bardzo prosty układ jak na rysunku. 

G

L

A

B

o

o

o

Q

j

P

S

+

=

Celem naszym będzie określenie zależności pomiędzy napięciem na końcu linii 

a jej obciążeniem. 
Założymy, że generator utrzymuje stałe napięcie na szynach A                    . 
Moc odbieraną

z szyn B wynosi: 

Moc czynną

i bierną

odbieraną

z szyn B można wyrazić

w

funkcji

napięć, 

reaktancji linii (przy pominięciu rezystancji) oraz kąta pomiędzy napięciami: 

const.

=

A

U

(

)

β

j

P

Q

j

P

S

o

o

o

o

+

=

+

=

1

ϕ

β

tan

=

=

o

o

P

Q

12

sin

δ

⋅

⋅

=

X

U

U

P

B

A

o

12

2

cos

δ

⋅

⋅

+

−

=

X

U

U

X

U

Q

B

A

B

o

3

STABILNOŚĆ

NAPIĘCIOWA

Wykorzystując 

mamy 

Powyższe równanie jest równaniem dwukwadratowym względem napięcia na 

szynach B można je rozwiązać

analitycznie i na wykresie. 

(

) (

)

1

cos

sin

2

2

=

+

δ

δ

( )

1

2

2

2

=

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

+

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

B

A

B

o

B

A

o

U

U

U

X

Q

U

U

X

P

(

)

( )

(

)

(

)

2

2

2

2

B

A

B

o

o

U

U

U

X

P

X

P

=

+

+

β

( )

(

)

( )

(

)

0

1

2

2

2

2

2

2

4

=

+

+

−

+

X

P

U

U

X

P

U

o

B

A

o

B

β

β

4

STABILNOŚĆ

NAPIĘCIOWA

1.2

0

V2 P

( )

V2a P

( )

V2b P

( )

V2c P

( )

V2d P

( )

V2e P

( )

1.2807

0

P

0

0.2

0.4

0.6

0.8

1

1.2

1.4

0

0.2

0.4

0.6

0.8

1

1.2

1

2

3

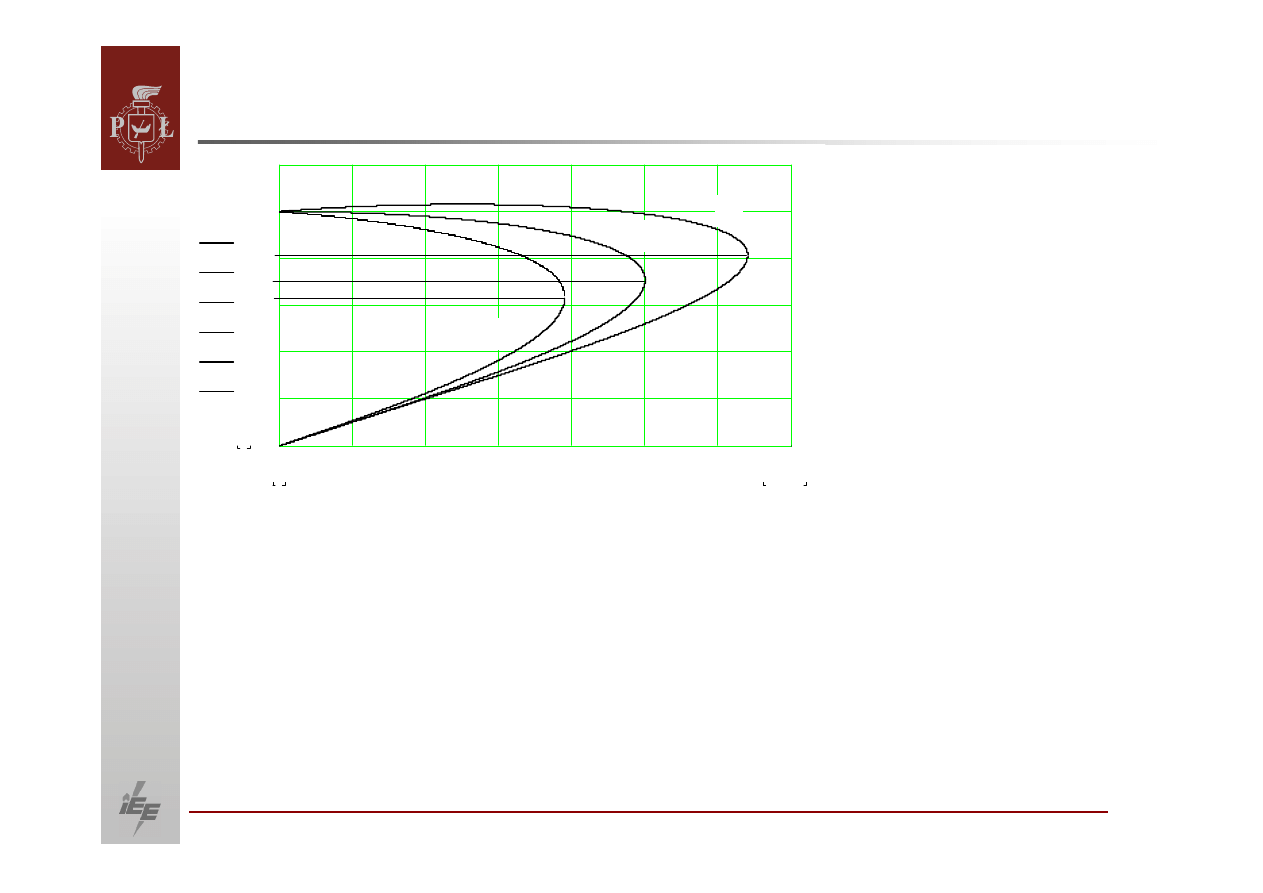
Zależność

napięcia       od mocy        dla:  

1 ‐
2 ‐
3 –
Z rysunków tych wynika, że istnieje pewna moc maksymalna, jaką

możemy 

przesłać, również

w układzie

promieniowym w przypadku gdy nasze odbiory 

mają

charakterystyki różne od kwadratowej. 

B

U

o

P

ind.

97

.

0

cos

=

ϕ

0

.

1

cos

=

ϕ

poj.

97

.

0

cos

=

ϕ

5

STABILNOŚĆ

NAPIĘCIOWA

Napięcia, przy których występuje przepływ mocy maksymalnej to napięcie 

krytyczne. 
W sytuacji gdy moc osiągnie swoją

wartość

maksymalną

to jakiekolwiek 

zakłócenie powoduje całkowite załamanie się

napięcia, w końcu będzie ono 

równe zeru. Zjawisko to nazywamy lawiną

napięcia. 

Zmiana charakterystyk napięciowych odbiorów spowoduje zmianę

tych 

krzywych. Dla odbiorów o kwadratowej charakterystyce (odbiory 

impedancyjne) zjawisko to nie wystąpi. 
W oparciu o powyższe wykresy można sformułować

kryterium stabilności 

napięciowej: 

stabilny

0

⇒

<

U

d

P

d

y

niestabiln

0

⇒

≥

U

d

P

d

STABILNOŚĆ

NAPIĘCIOWA

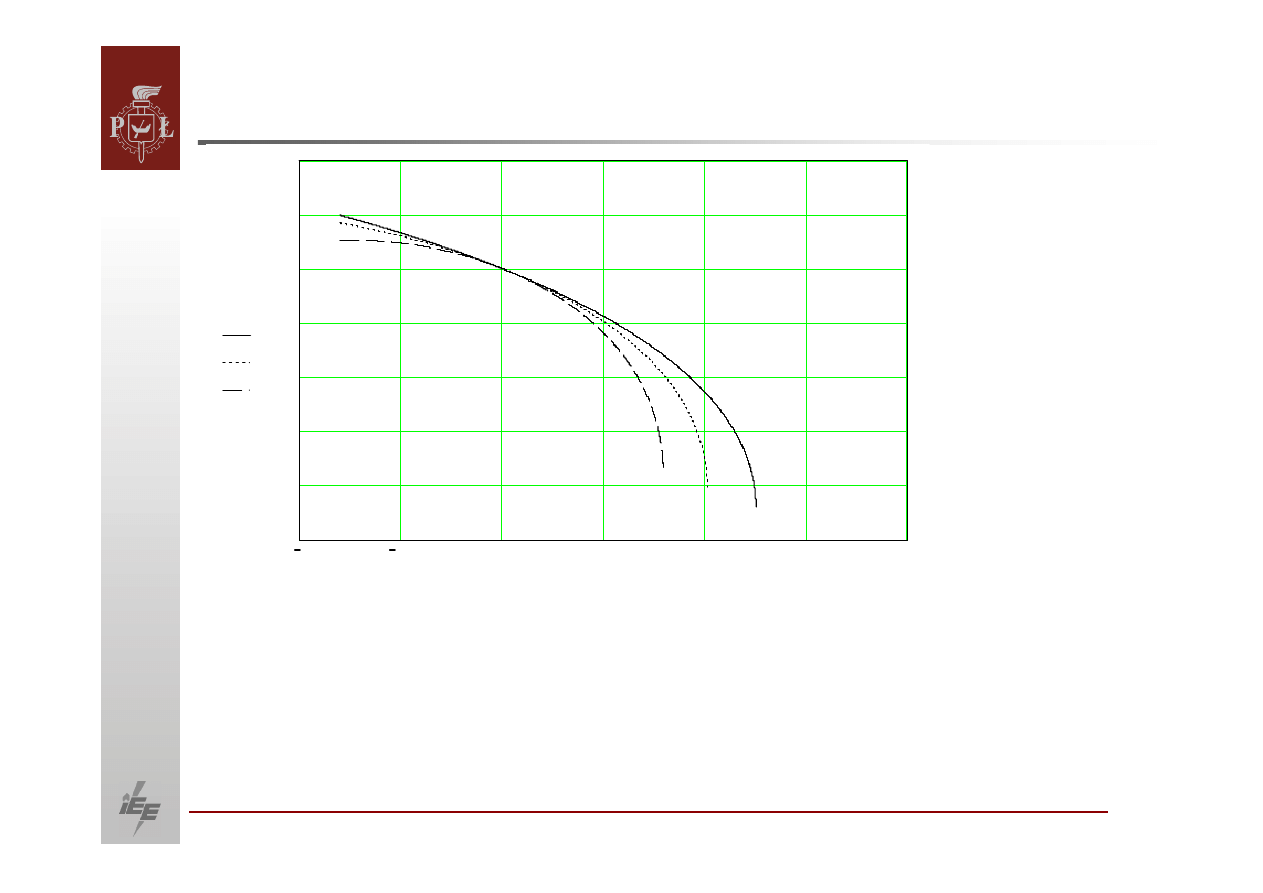
Zależność

napięcia od mocy biernej dla współczynnika mocy: 

„

krzywa ciągła ‐

,

„

krzywa kropkowa ‐

,

„

krzywa kreskowa ‐

6

1

0.5

0

0.5

1

1.5

2

0.5

0.6

0.7

0.8

0.9

1

1.1

1.2

1.2

0.5

V2 Q

( )

V2a Q

( )

V2b Q

( )

2

1

−

Q

ind.

8

,

0

cos

=

ϕ

.

9

,

0

cos

ind

=

ϕ

.

i

95

,

0

cos

nd

=

ϕ

STABILNOŚĆ

NAPIĘCIOWA

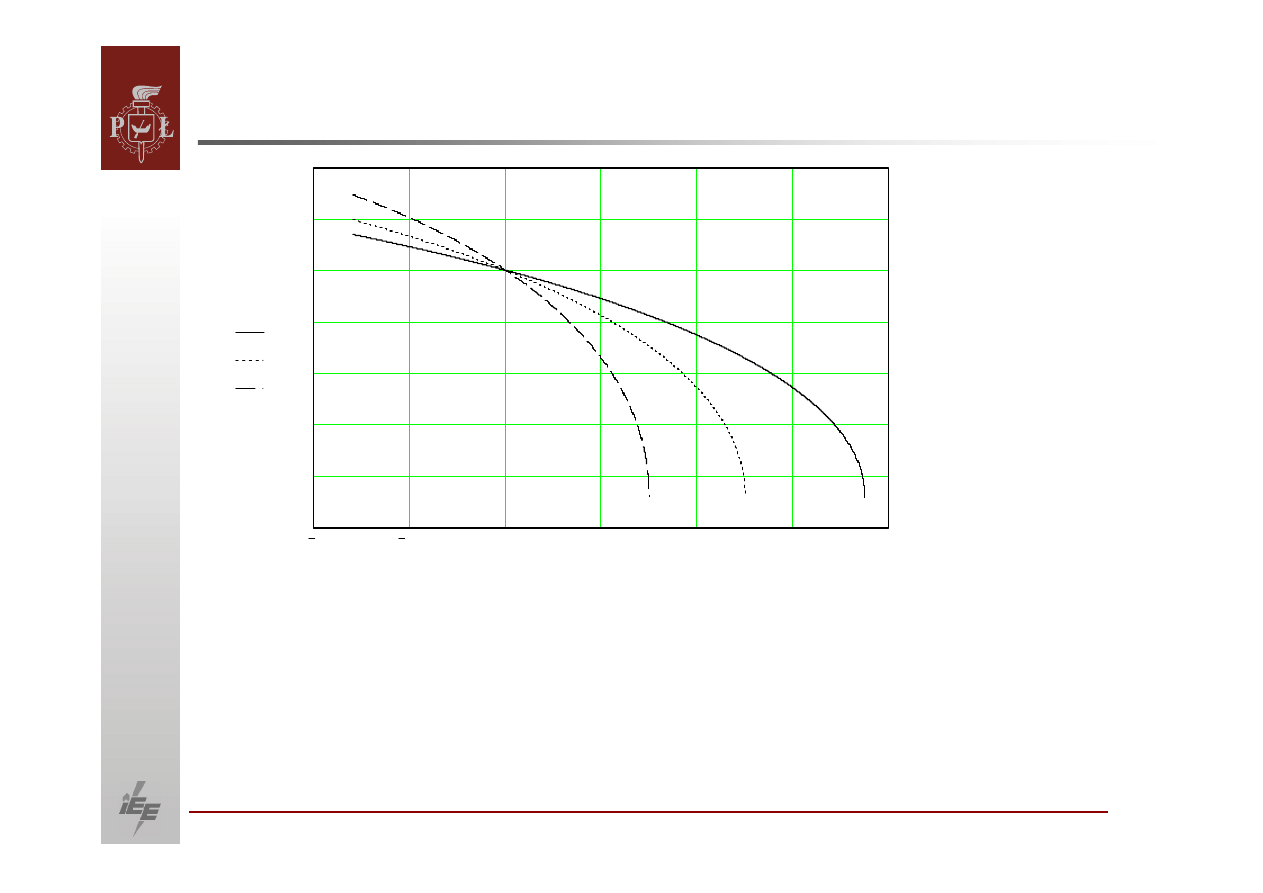
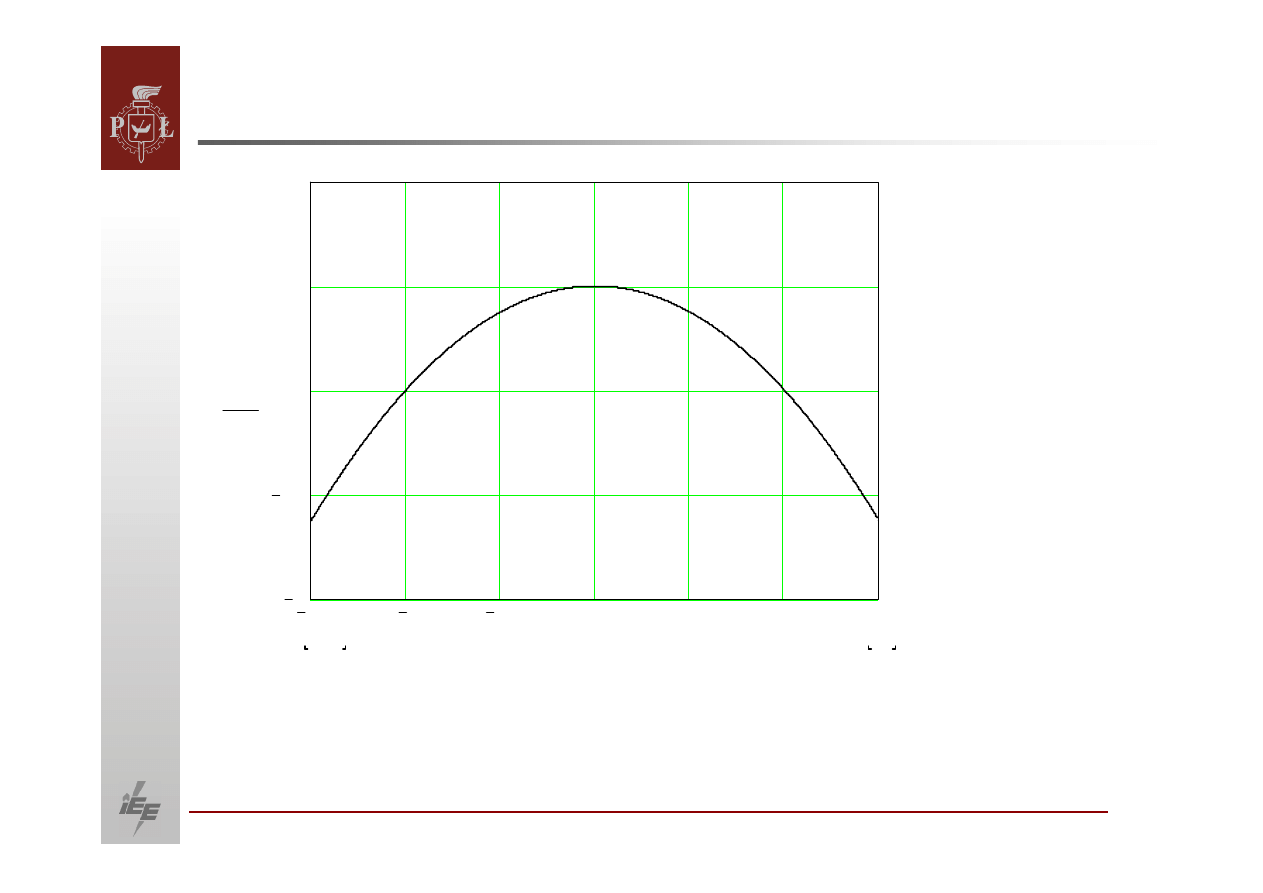
Zależność

napięcia od mocy biernej dla reaktancji sieci : 

„

krzywa ciągła – 0,1,

„

krzywa kropkowa – 0,15,

„

krzywa kreskowa – 0,2.

7

1

0.5

0

0.5

1

1.5

2

0.5

0.6

0.7

0.8

0.9

1

1.1

1.2

1.2

0.5

V2 Q

( )

V2a Q

( )

V2b Q

( )

2

1

−

Q

STABILNOŚĆ

NAPIĘCIOWA

1.5

1

0.5

0

0.5

1

1

0.5

0

0.5

1

1

1

−

Q1 P

( )

1.5

1.5

−

P

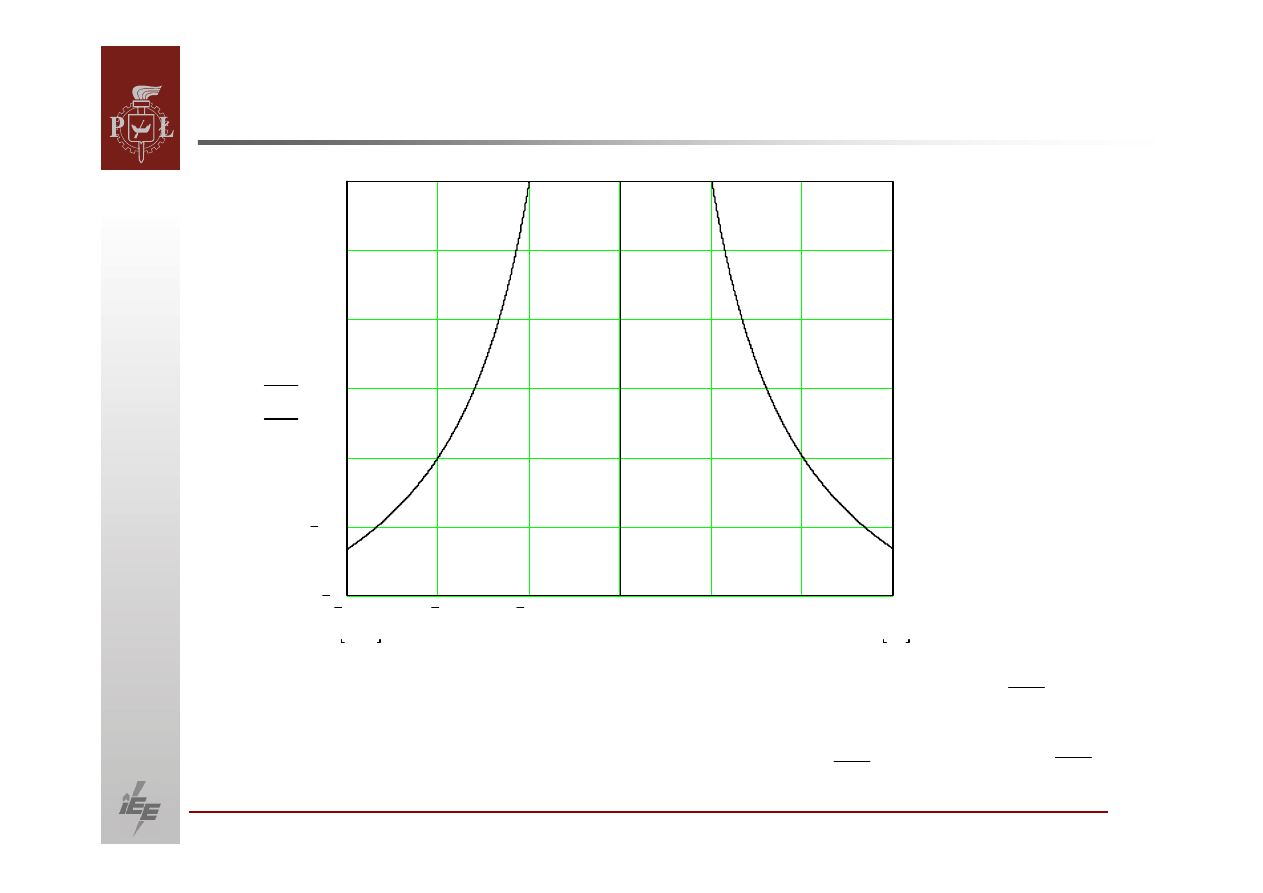
Dopuszczalny obszar pracy generatora przy P=const. i Q=const.

STABILNOŚĆ

NAPIĘCIOWA

1.5

1

0.5

0

0.5

1

1

0.5

0

0.5

1

1.5

2

2

1

−

Q1 P

( )

Q2 P

( )

1.5

1.5

−

P

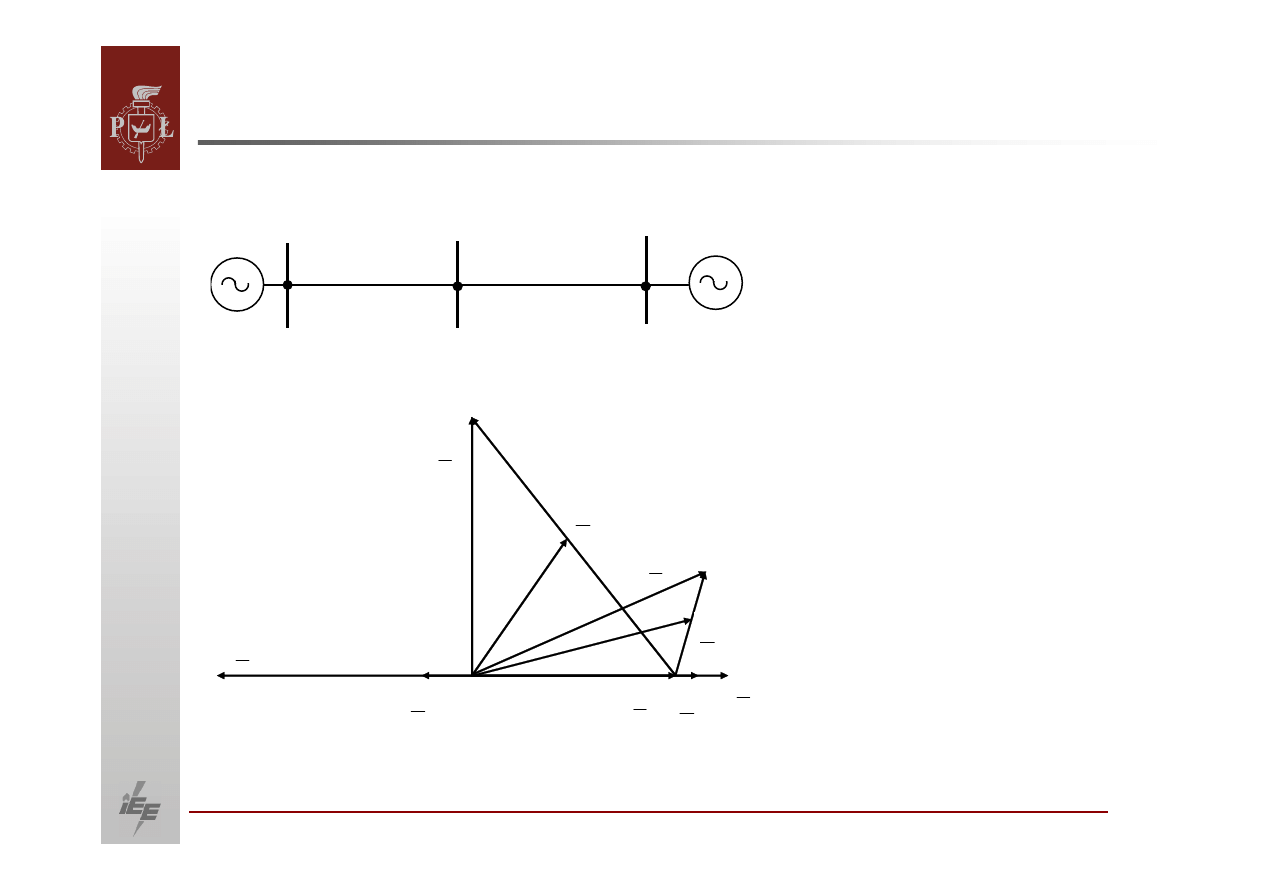
Dopuszczalny obszar pracy generatora przy                      i

.

Dopuszczalny obszar pracy generatora przy                       

i

to cała płaszczyzna PQ.

.

const

P

o

=

2

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

⋅

=

u

n

o

U

U

Q

Q

2

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

⋅

=

u

n

o

U

U

P

P

2

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

⋅

=

u

n

o

U

U

Q

Q

10

STABILNOŚĆ

NAPIĘCIOWA

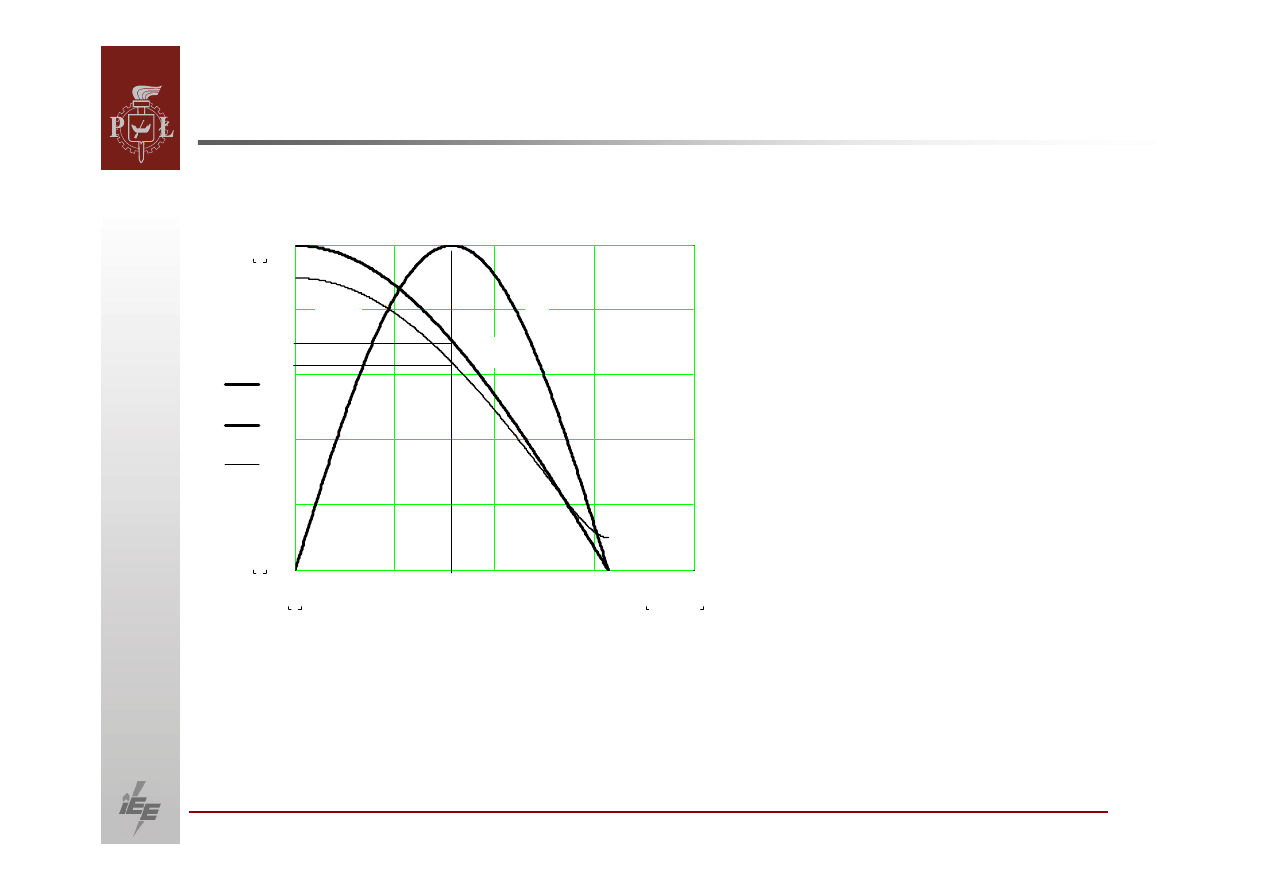
Rozważmy układ dwumaszynowy: 

Wykres wskazowy tego układu przesyłowego: 

G

L

A

B

G

L

C

0

1

E

0

2

E

0

B

U

1

1

E

1

B

U

2

B

U

3

B

U

2

1

E

3

1

E

11

STABILNOŚĆ

NAPIĘCIOWA

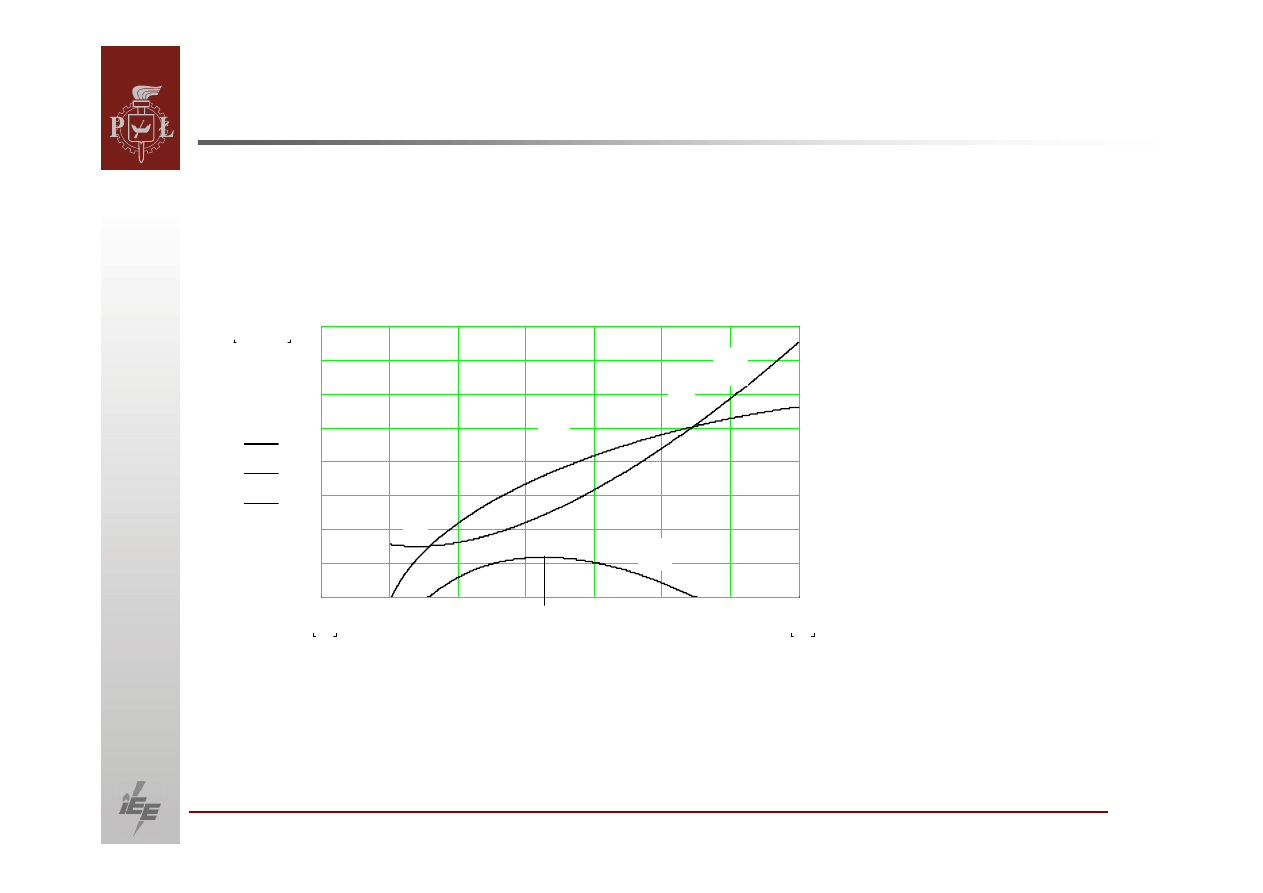
Przebieg mocy i napięcia w funkcji kąta, kiedy obie siły elektromotoryczne są

jednakowe lub różne.

Powyższy wykres potwierdza warunki stabilności napięciowej opisane 

poprzednimi równaniami. 

1

0

P1

i

UB

i

U

i

3.141593

0

δ i.

0

1

2

3

4

0

0.2

0.4

0.6

0.8

1

P

1

B

U

2

B

U

12

STABILNOŚĆ

NAPIĘCIOWA

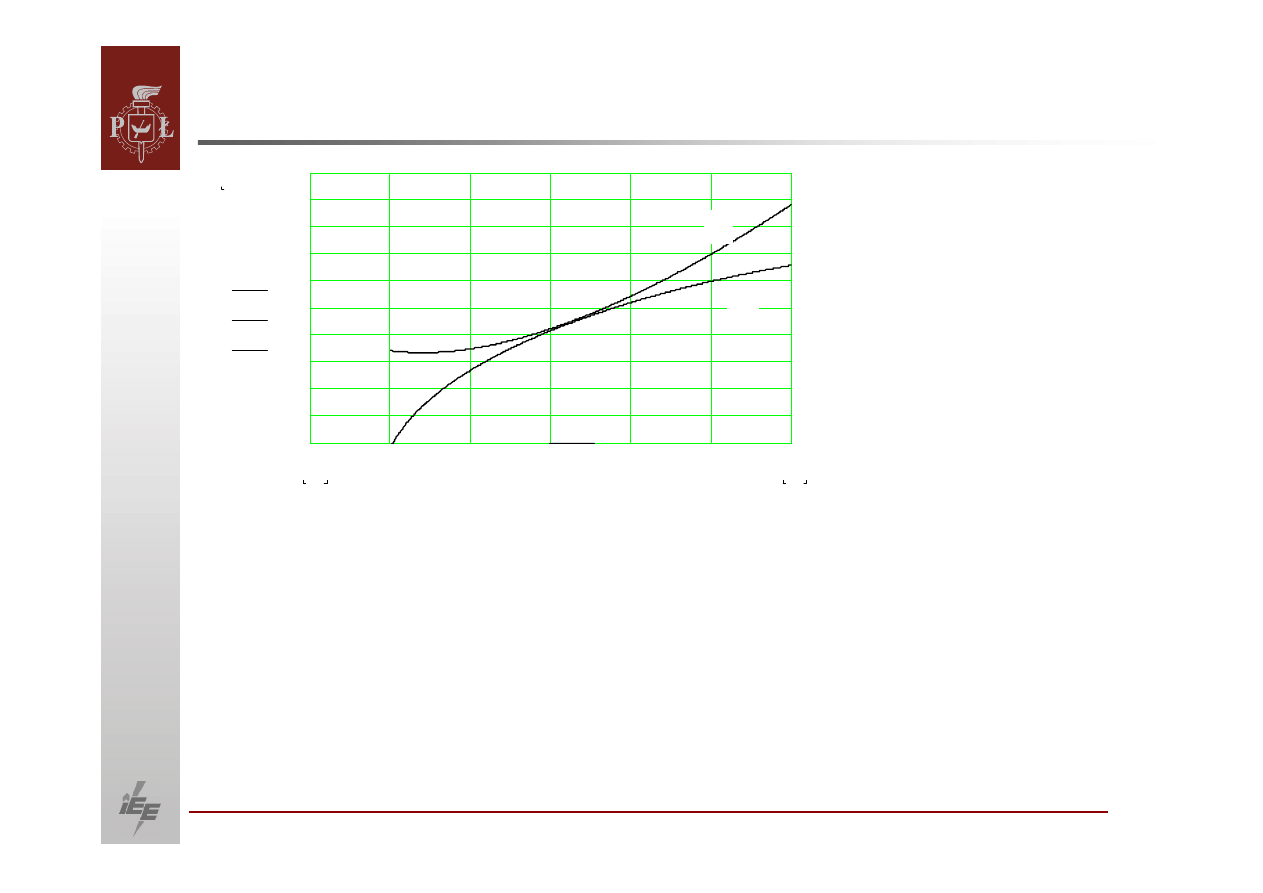
Dotychczasowe rozważania nie uwzględniały charakterystyk napięciowych 

odbioru. Na jednym wykresie porównamy charakterystykę

mocy biernej 

pobieranej przez odbiór i charakterystykę

mocy biernej wytwarzanej przez 

generator w

funkcji

napięcia w węźle. 

0.940889

0

Q U

( )

Q1 U

( )

ΔQ U

( )

1.2

0.6

U

0.5

0.6

0.7

0.8

0.9

1

1.1

1.2

0

0.13

0.25

0.38

0.5

0.63

0.75

0.88

1

o

Q

G

Q

A

B

U

Q

Q

Δ

Rozważmy zachowanie się

układu podczas zakłócenia występującego w jednym 

z dwóch punktów pracy –

punktu A lub B, gdzie moc bierna odbioru jest równa 

mocy biernej źródła. 

13

STABILNOŚĆ

NAPIĘCIOWA

1.

Praca w punkcie A:
Zmniejszenie napięcia o       ,              powoduje, że:  
‐

maleje, 

‐

maleje,

ale                a              to pociągnie wzrost napięcia i powrót do punktu 

równowagi A. 

Zwiększenie napięcia o       ,               powoduje, że: 
‐

rośnie, 

‐

rośnie,

ale               a              to pociągnie zmalenie napięcia i powrót do punktu

równowagi A.

2.

Praca w punkcie B: 
Zwiększenie napięcia o        ,              powoduje, że:  
‐

rośnie, 

‐

rośnie,

ale                a to pociągnie wzrost napięcia i powrót do punktu A.

U

Δ

G

Q

o

Q

o

G

Q

Q

>

U

Δ

G

Q

o

Q

o

G

Q

Q

<

U

Δ

0

>

Q

Δ

0

<

Q

Δ

0

<

U

Δ

0

>

U

Δ

0

>

U

Δ

G

Q

o

Q

o

G

Q

Q

>

14

STABILNOŚĆ

NAPIĘCIOWA

Praca w punkcie B jest pracą

niestabilną. 

Zmniejszenie napięcia o       ,              powoduje, że:  
‐

maleje, 

‐

rośnie,

i                a              to pociągnie spadek napięcia.

Układ oddala się

od punktu równowagi przy stale malejącym napięciu. 

Zjawisko to nazywamy lawiną

napięcia. Zjawisko to jest szczególnie 

niebezpieczne, gdy odbiorami są

silniki asynchroniczne. Lawina napięcia 

spowoduje zatrzymanie się

silników a to gwałtowny wzrost 

zapotrzebowania na moc bierną, co pogłębi spadki napięć

i może 

spowodować

zmianę

(lawinę) napięcia w innym sąsiednim węźle. 

Napięcie, przy którym      

nazywamy napięciem krytycznym. 

U

Δ

0

<

U

Δ

G

Q

o

Q

o

G

Q

Q

<

0

<

Q

Δ

0

=

dU

dQ

15

STABILNOŚĆ

NAPIĘCIOWA

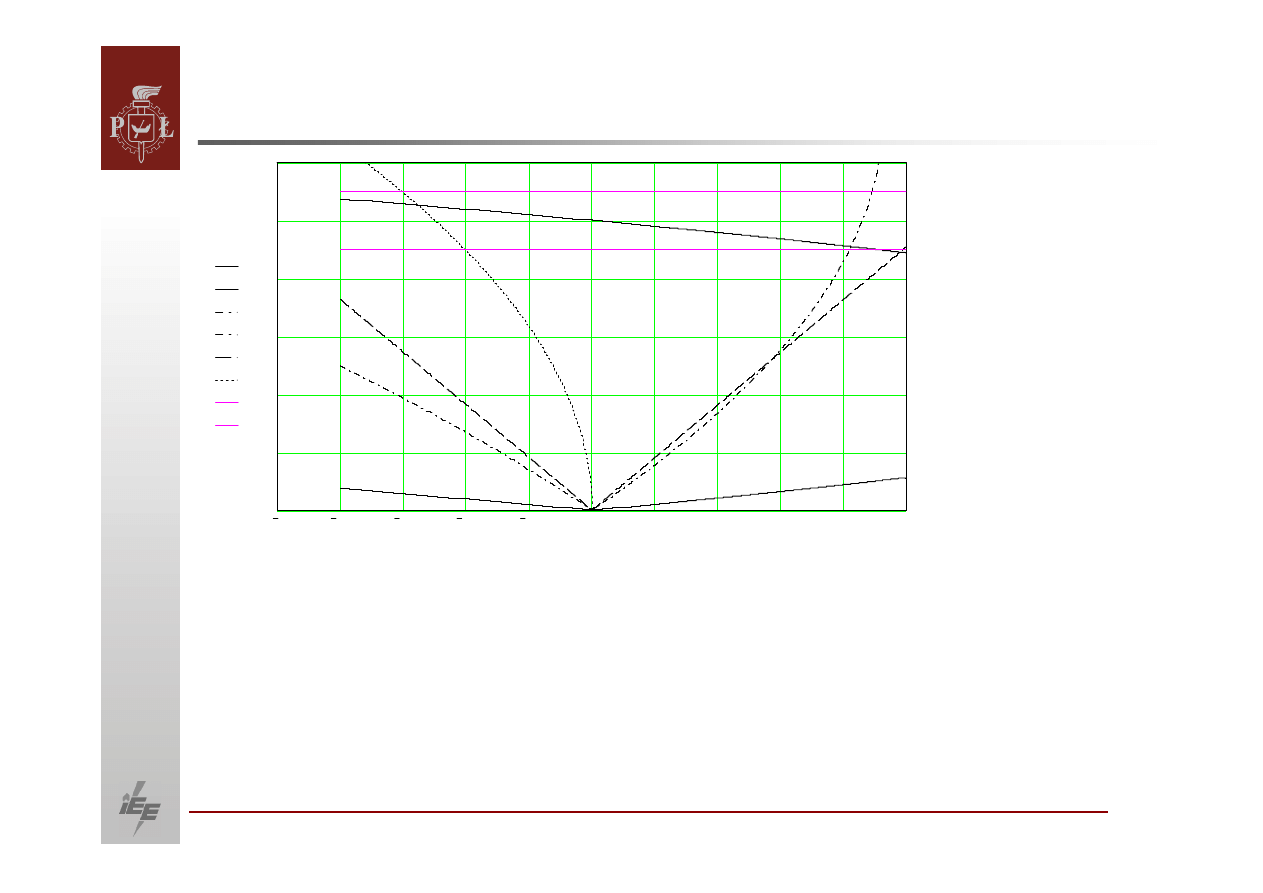
Wniosek:  punkt A jest punktem pracy stabilnej zaś

punkt B jest punktem pracy   

niestabilnej.
Z rozważań

tych wynika: 

Dołączenie nowego odbioru powoduje, że charakterystyka odbioru porusza się

ku górze. W pewnym momencie dochodzimy do sytuacji, że jest tylko jeden 

punkt przecięcia się

obu charakterystyk. Jest to punkt niestabilny a dalsze 

powiększenie mocy biernej odbieranej powoduje trwałą

utratę

stabilności. 

stabilny

0

⇒

<

U

d

Q

d

Δ

Δ

y

niestabiln

0

⇒

>

U

d

Q

d

Δ

Δ

i

stabilnosc

granica

0

⇒

=

U

d

Q

d

Δ

Δ

16

STABILNOŚĆ

NAPIĘCIOWA

0.883289

0

Q U

( )

Q1 U

( )

ΔQ U

( )

1.1

0.6

U

0.5

0.6

0.7

0.8

0.9

1

1.1

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

o

Q

Q

U

G

Q

17

STABILNOŚĆ

NAPIĘCIOWA

1

0.8

0.6

0.4

0.2

0

0.2

0.4

0.6

0.8

1

0

0.2

0.4

0.6

0.8

1

1.2

1.2

0

V2 Q

( )

V2a Q

( )

V3 Q

( )

V3a Q

( )

V4 Q

( )

V5 Q

( )

V6 Q

( )

V7 Q

( )

1

1

−

Q

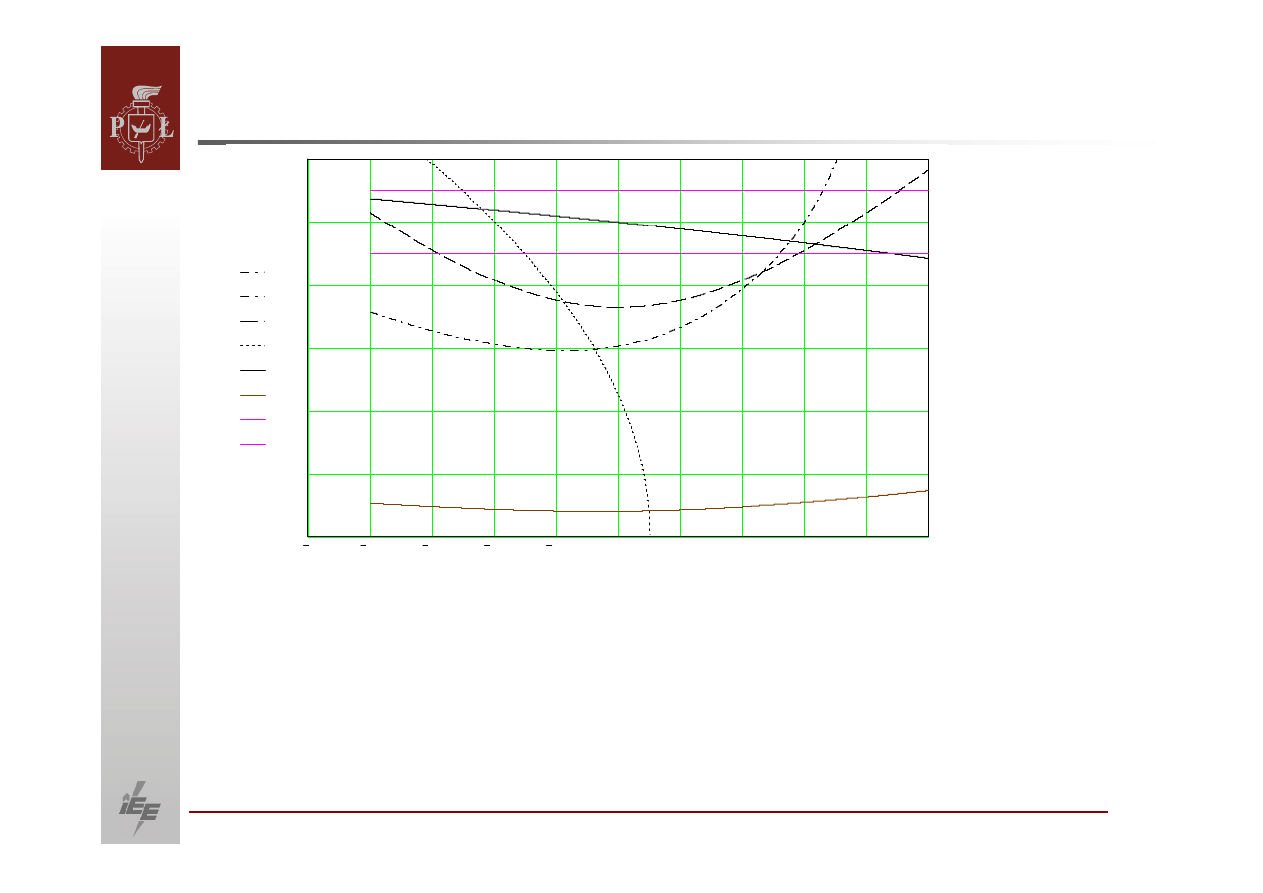
Zależność

napięcia generatora w funkcji mocy biernej podczas biegu jałowego 

z uwzględnieniem

regulatora napięcia generatora i ograniczeń, gdzie

linia:

•

ciągła to charakterystyka napięcia od mocy biernej,

•

kropkowana to charakterystyka przy maksymalnym kącie,

•

kreskowana to charakterystyka

przy maksymalnym prądzie stojana,

•

kreskowano‐

kropkowana

to charakterystyka

przy maksymalnym prądzie

wzbudzenia.

STABILNOŚĆ

NAPIĘCIOWA

Zależność

napięcia generatora w funkcji mocy biernej podczas obciążenia 

znamionowego

z

uwzględnieniem

regulatora napięcia i ograniczeń, gdzie

linia:

•

ciągła to charakterystyka napięcia od mocy biernej,

•

kropkowana to charakterystyka przy maksymalnym kącie,

•

kreskowana to charakterystyka przy maksymalnym prądzie stojana,

•

kreskowano‐

kropkowana przy maksymalnym prądzie wzbudzenia.

18

1

0.8

0.6

0.4

0.2

0

0.2

0.4

0.6

0.8

1

0

0.2

0.4

0.6

0.8

1

1.2

1.2

0

V3a Q

( )

V3 Q

( )

V4 Q

( )

V5 Q

( )

V1 Q

( )

V1a Q

( )

V6 Q

( )

V7 Q

( )

1

1

−

Q