29

6.6. Zagadnienie transportowe – algorytm transportowy

Do problemów decyzyjnych rozwiązywanych przy pomocy metod programowania

liniowego należy klasyczne zagadnienie transportowe. Polega ono na ustaleniu takiego planu
przewozów, aby ponieść jak najmniejsze łączne koszty.
W zagadnieniu transportowym wyróżniamy:
1. Punkty nadania towaru - nazywane dostawcami. Przyjmujemy, że w analizowanym

problemie występuje m dostawców, których oznaczamy symbolami:

m

D

D

D

,

,

,

2

1

K

.

2. Punkty odbioru towaru - nazywane odbiorcami. Przyjmujemy, że w analizowanym

problemie występuje n odbiorców, których oznaczamy symbolami:

n

O

O

O

,

,

,

2

1

K

.

Zakładamy, że każdy z dostawców posiada taki sam towar, takiej samej jakości (bez

braków), odpowiednio w ilościach:

m

a

a

a

,

,

,

2

1

K

(ilości te określają podaż towaru u

dostawców). Na ten sam towar zgłosili zapotrzebowanie odbiorcy odpowiednio w ilościach:

n

b

b

b

,

,

,

2

1

K

(popyt odbiorców). Jednostkowy koszt przewozu towaru od dostawcy „i” do

odbiorcy „j” wynosi

ij

c

dla

m

i

,

,

2

,

1

K

=

oraz

n

j

,

,

2

,

1

K

=

.

Oznaczmy przez

ij

x

(zmienna decyzyjna) ilość towaru przewożoną na od dostawcy „i” do

odbiorcy „j” ( na trasie

)

,

(

j

i

) wówczas plan przewozów zapiszemy jako macierz

























=

mn

m

m

n

n

x

x

x

x

x

x

x

x

x

L

M

M

M

M

M

M

L

L

2

1

2

22

21

1

12

11

X

.

Zakładamy, że macierz X jest macierzą o nieujemnych elementach (dla wszystkich dostaw:

0

≥

ij

x

- towar jest przewożony od dostawcy do odbiorcy a nie odwrotnie).

Model zadania transportowego można zapisać następująco:

Znaleźć najmniejszą wartość funkcji

∑∑

=

=

⋅

=

m

i

n

j

ij

ij

x

c

f

1

1

)

(X

na zbiorze rozwiązań

dopuszczalnych

X

,w którym spełnione są:

a. warunki dla dostawców













≤

+

+

+

≤

+

+

+

≤

+

+

+

m

mn

m

m

n

n

a

x

x

x

a

x

x

x

a

x

x

x

L

L

L

L

L

L

L

L

L

L

L

L

L

2

1

2

2

22

21

1

1

12

11

30

b. warunki dla odbiorców













=

+

+

+

=

+

+

+

=

+

+

+

n

mn

n

n

m

m

b

x

x

x

b

x

x

x

b

x

x

x

L

L

L

L

L

L

L

L

L

L

L

L

L

2

1

2

2

22

12

1

1

21

11

c. warunki brzegowe

0

≥

ij

x

dla

m

i

,

,

2

,

1

K

=

oraz

n

j

,

,

2

,

1

K

=

.

Macierz współczynników przy niewiadomych jest macierzą wymiaru

)

(

)

(

n

m

n

m

⋅

×

+

, której

elementy przyjmują wartości ze zbioru

}

1

,

0

{

.

Zauważmy, że zgodnie z wcześniejszymi założeniami - łączna podaż dostawców

wynosi:

∑

=

m

i

i

a

1

natomiast łączne zapotrzebowanie odbiorców jest równe:

∑

=

n

j

j

b

1

. Mogą zajść

następujące przypadki:

1.

∑

=

m

i

i

a

1

≥

∑

=

n

j

j

b

1

- zadanie transportowe nazywamy zadaniem otwartym;

2.

∑

=

m

i

i

a

1

=

∑

=

n

j

j

b

1

- zadanie transportowe nazywamy zadaniem zamkniętym;

3.

∑

=

m

i

i

a

1

≤

∑

=

n

j

j

b

1

- zadanie transportowe jest wówczas zadaniem sprzecznym.

Zadania transportowe otwarte (1.) można przekształcić na zadania zamknięte

zwiększając liczbę dostawców. Przyjmujemy, że w problemie występuje dostawca dodatkowy
(fikcyjny, traktowany jako magazyn dostawców) oznaczamy go symbolem

1

+

n

O

, którego

zapotrzebowanie jest równe różnicy między podażą i popytem;

∑

∑

=

=

+

−

=

n

j

j

m

i

i

n

b

a

b

1

1

1

.

Przyjmujemy, że jednostkowe koszty przewozu towaru od dostawcy „

i” do odbiorcy „n+1”

wynoszą

0

1

,

=

+

n

i

c

dla

m

i

,

,

2

,

1

K

=

.

Klasyczne zadanie transportowe jest więc zadaniem programowania liniowego i do

jego rozwiązania można zastosować algorytm simpleks. Jest on jednak mało efektywny ze

względu na dużą liczbę niewiadomych występujących w modelu. Stąd też dla zadań

transportowych opracowano nowy, efektywniejszy sposób wyznaczania rozwiązania

optymalnego nazywany algorytmem transportowym (zostanie on zaprezentowany w

następnym punkcie). Opis tej metody można znaleźć także, np. w pozycji [3] s.92-111.

Algorytm transportowy

Jest, podobnie jak algorytm simpleks, metodą numeryczną realizowaną w sposób

iteracyjny. Algorytm transportowy stosujemy do wyznaczania rozwiązania optymalnego
zadań transportowych zamkniętych. Jego zastosowanie nie wymaga zapisu modelu
matematycznego zadania (było to konieczne przystosowaniu algorytmu simpleks) lecz

31

jedynie informacji o parametrach zadania. W algorytmie tym wykonuje się dwa powtarzające
się na przemian etapy: wyznaczanie rozwiązania bazowego i sprawdzania czy jest ono
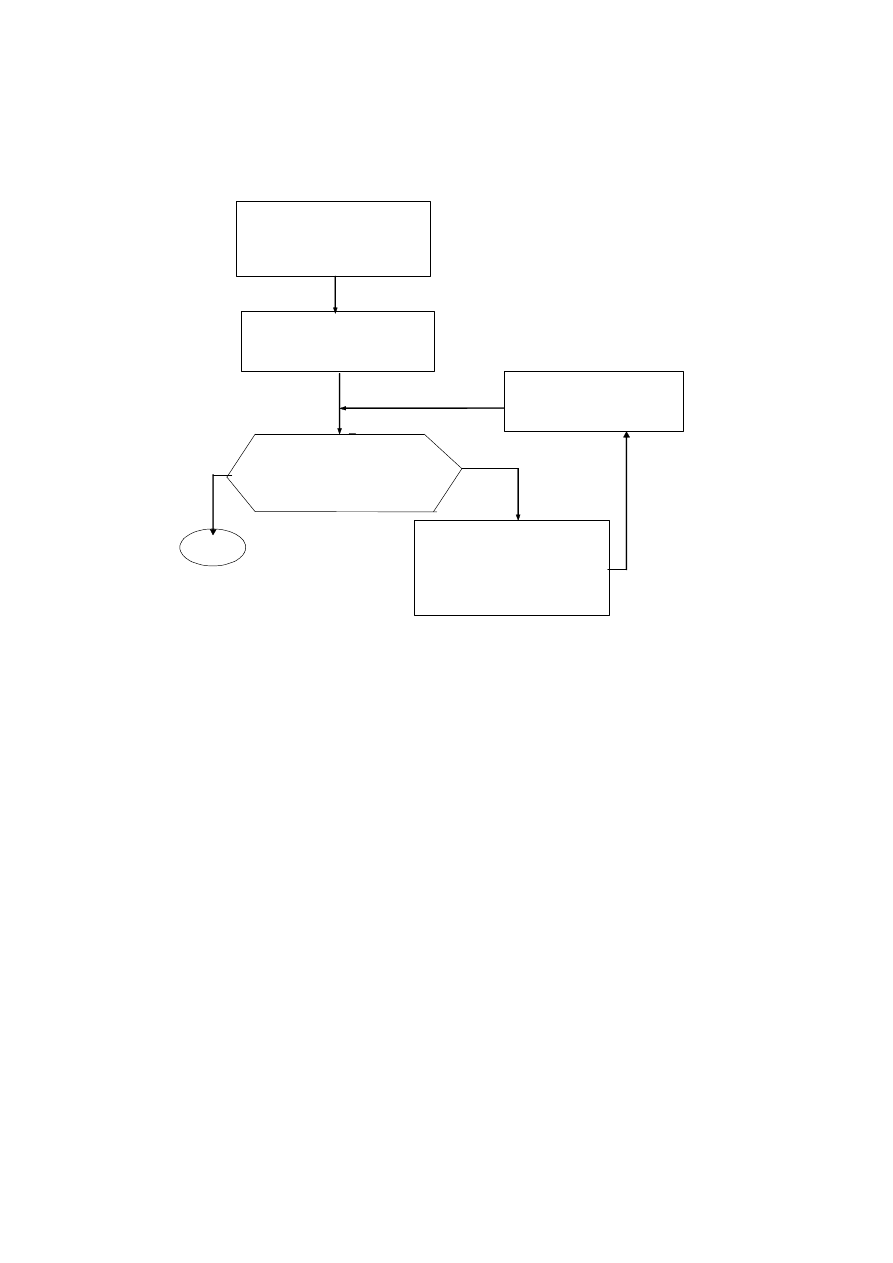
optymalne. Schemat działania tego algorytmu podano na Rys 2.

Poda

ć

parametry zadania

m

a

a

a

,

,

,

2

1

K

;

n

b

b

b

,

,

,

2

1

K

ij

c

dla

m

i

,

,

2

,

1

K

=

oraz

n

j

,

,

2

,

1

K

=

W yznaczy

ć

dowolny

bazowy plan dostaw

i zapisa

ć

go w tablicy

Sprawdzi

ć

, czy wyznaczone

rozwi

ą

zanie bazowe jest

optymalnym planem

przewozów?

Koniec

oblicze

ń

1. W ybra

ć

tras

ę

przewozu

)

,

(

j

i

na której uzyskujemy

najwy

ż

sz

ą

obni

ż

k

ę

kosztów:

2. Ustali

ć

wielko

ść

przewozu

ij

x

na wybranej trasie

TAK

NIE

W yznaczy

ć

nowy poprawiony

(bazowy) plan dostaw

i zapisa

ć

go w tablicy

Rys. 2. Schemat blokowy postępowania w algorytmie transportowym

Omówimy teraz poszczególne fragmenty tego postępowania.

A. Wyznaczanie startowego rozwiązania bazowego i zapis tego rozwiązania w tablicy
transportowej

Postępowanie iteracyjne rozpoczynamy od wyznaczenia dowolnego, ale bazowego

dopuszczalnego planu dostaw (spełniającego warunki dla dostawców, warunki dla odbiorców
oraz warunki brzegowe). Rozwiązanie bazowe (bazowy plan dostaw) zamkniętego zadania
transportowego zawiera (

m+n-1) zmiennych decyzyjnych

ij

x

(co wynika z faktu, że dla

zadania zamkniętego warunki dla dostawców są spełnione jako równości i rzędy: macierzy
współczynników otrzymanego układu (

m+n) równań i układu uzupełnionego o kolumnę

wyrazów wolnych są równe (

m+n-1)). Wobec tego należy zbudować taki plan dostaw aby

liczba dodatnich dostaw (

0

>

ij

x

) była nie większa niż (

m+n-1).

Wśród metod wyznaczania takiego planu wyróżnimy: metodę kąta północno

zachodniego i metodę minimalnego elementu macierzy kosztów. Sposoby te omówimy
dokładnie w przykładzie AT-1.

B. Sprawdzenie, czy wyznaczone rozwiązanie bazowe określa optymalny plan dostaw,

czyli taki w którym łączne koszty transportu są najmniejsze

Polega to na wyznaczeniu wskaźników optymalności

ij

∆

dla każdej z tras

)

,

( j

i

odpowiadających zmiennym niebazowym

ij

x

. Wskaźniki te wyznaczamy jako różnice

32

ij

ij

ij

c

c

~

−

=

∆

,

gdzie

ij

c~

są tzw. kosztami pośrednimi, które obliczamy jako sumy

j

i

ij

v

u

c

+

=

~

.

Liczby

i

u i

j

v

wyznacza się jako dowolne rozwiązanie szczególne nieoznaczonego układu

(

m+n-1) równań postaci:

ij

j

i

c

v

u

=

+

,

otrzymanego dla tych kosztów jednostkowych, które odpowiadają bazowym zmiennym
decyzyjnym

ij

x

.

Jeżeli wskaźniki optymalności spełniają warunek

0

)

,

(

≥

∆

∀

ij

j

i

,

to plan dostaw jest planem optymalnych, czyli takim przy którym łączne koszty
transportu są najmniejsze.

Postępowanie przy sprawdzaniu optymalności planu dostaw będzie omówione szczegółowo
w przykładzie AT-2.

C. Budowa nowego, poprawionego rozwiązania bazowego

Jeśli sprawdzając optymalność planu dostaw otrzymamy ujemne wartości wskaźników

ij

∆

, to plan ten nie jest optymalny i poszukujemy nowego lepszego planu dostaw. W

pierwszej kolejności ustalamy trasę

)

,

( j

i

, na którą należy skierować dostawę tak aby

najbardziej obniżyć łączne koszty transportu. Wybieramy taką trasę

)

,

( l

k

dla której

kl

∆

jest

najmniejsza z ujemnych

ij

∆

:

{ }

ij

kl

ij

∆

=

∆

<

∆

0

min

.

W następnej kolejności szukamy cyklu, który tworzy wybrana trasa

)

,

( l

k

z tymi

trasami (niekoniecznie z wszystkimi), które odpowiadały niewiadomym bazowym

ij

x

,

a następnie ustalamy wielkość dostawy

kl

x na trasie

)

,

( l

k

. Szczegóły tego postępowania

zilustrowane będą w przykładzie AT-3.

Zagadnienia związane z modelowaniem i rozwiązywaniem zadań transportowych

omówione są, np. w pozycjach: [3] , s.91-104, [5] s. 88-111.

Inne problemy takie jak: degeneracja w zadaniu transportowym, zagadnienie częściowej

i całkowitej blokady tras przewozu oraz zagadnienie transportowe z kryterium czasu znaleźć
można w kursie: Ekonometria – studia II stopnia, a także np. [5] s. 112-137.