Ć w i c z e n i e 37

BADANIE DRGAŃ TŁUMIONYCH CEWKI

GALWANOMETRU ZWIERCIADŁOWEGO

37.1. Opis teoretyczny

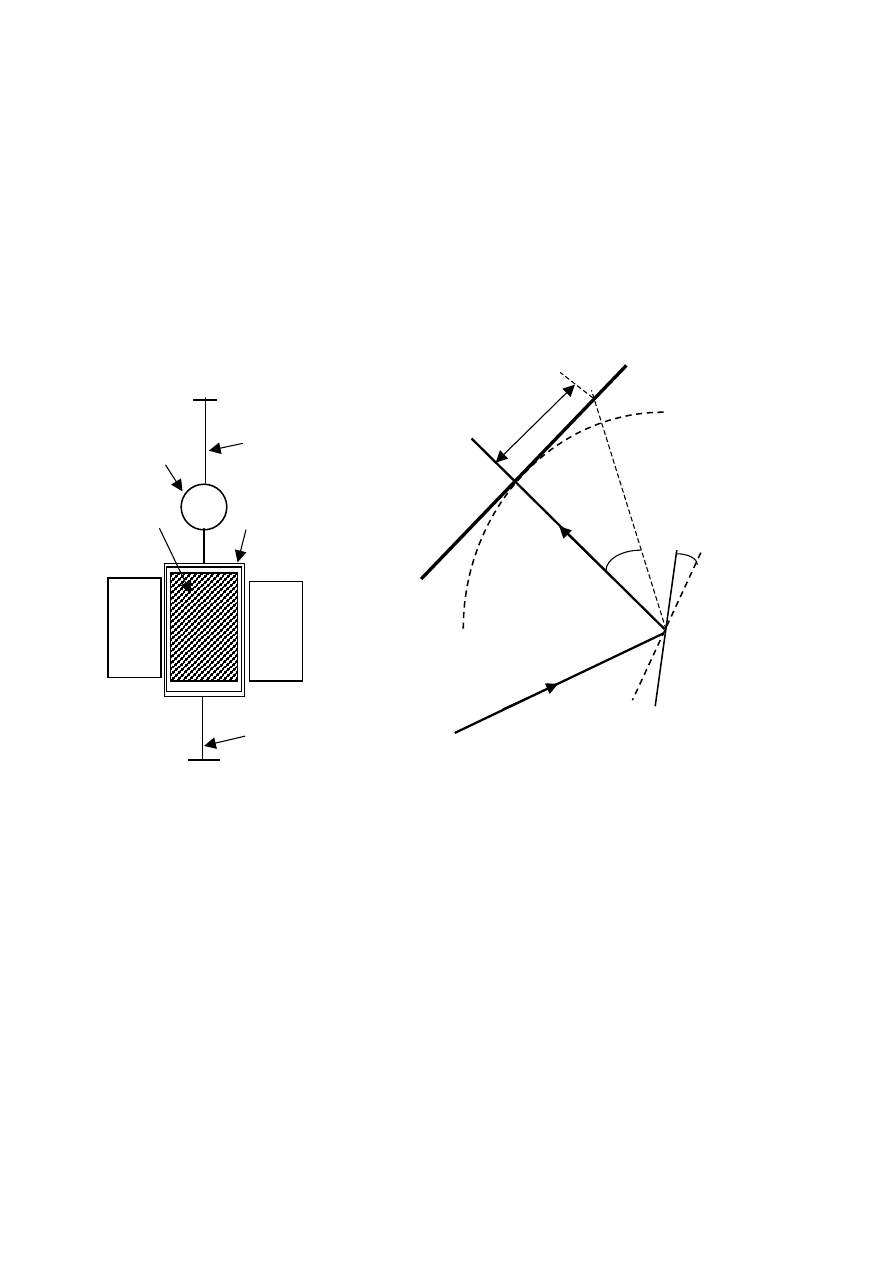
W ćwiczeniu testowany jest układ drgań, jakim jest cewka galwanometru zwierciadłowego. Opis
budowy takiego galwanometru przedstawiony jest w ćwiczeniu 16, a na rys. 37.1 przedstawione
zostały tylko podstawowe elementy potrzebne do zrozumienia powstawania drgań tłumionych.

a)

b)

wychylenie A

nić sprężysta

lusterko

0

rdzeń z żelaza 1 cewka

ekran

l

ϕ

2

ϕ

N

S

lusterko

nić

X wiązka światła

Rys. 37.1. Schemat galwanometru zwierciadłowego (a) i schemat do odczytu wychyleń

ramki galwanometru (b).

Cewka pomiarowa (1) o dużej liczbie zwojów z cienkiego drutu zawieszona jest na sprężystej nici
metalowej (2) i może wykonywać drgania skrętne w szczelinie wytworzonej między nabiegunni-
kami trwałego magnesu a rdzeniem wykonanym z magnetycznie miękkiego żelaza (3). Dzięki
rdzeniowi pole magnetyczne w szczelinie jest radialne i w przybliżeniu ma prawie wszędzie jedna-
kowe natężenie. Do nici przytwierdzone jest lusterko (4). Jeżeli skierujemy na nie wiązkę światła,
to na umocowanym naprzeciw ekranie (skali) można obserwować ruch plamki świetlnej. Zwiększa-
jąc odległość pomiędzy lusterkiem a zwierciadłem można dla małych skręceń sprężystej nici
otrzymać dostatecznie duże wychylenie plamki świetlnej na skali. Schemat działania układu odczy-
towego przedstawia rys. 37.1b. Zgodnie z prawem odbicia światła skręceniu lusterka o kąt

ϕ odpo-

wiada wychylenie plamki o 2

ϕ.

W czasie ruchu obrotowego na cewkę działa moment związany ze skręceniem nici sprężystej (cza-
sem sprężyny spiralnej), jest to tzw. moment siły kierującej. Przyjmując liniowy model zależności
wielkości tego momentu od kąta skręcenia (praktycznie realizowany przy dostatecznie małych ką-
tach) mamy:

M

K

= - D

K

ϕ (37.1)

gdzie D

K

oznacza współczynnik proporcjonalności zwany momentem kierującym, uwzględniający

właściwości sprężyste nici, na której zawieszona jest cewka.
Znak minus w zależności (37.1) uwzględnia fakt, że moment kierujący ma zwrot przeciwny do kąta
wychylenia cewki zależnego od wielkości prądu, który przez nią przepływa. Na przewody cewki
umieszczone w polu magnetycznym działa siła, której moduł jest równy

F = n I a B (37.2)

gdzie: n - liczba zwoi cewki, I - natężenie prądu, a - wysokość cewki, B - indukcja pola magnetycz-
nego.
Siła ta jest prostopadła do płaszczyzny ramki i ze względu na rdzeń, dzięki któremu pole magne-
tyczne jest radialne, niezależna od kąta

ϕ. Moment działający na cewkę, spowodowany przepływem

przez nią prądu, ma więc postać

B

S

I

n

2

b

F

2

M

=

=

(37.3)

gdzie: S = a b oznacza przekrój ramki, b – szerokość ramki.
Z równowagi momentu kierującego (37.1) i momentu skręcającego (37.3) wynika kąt wychylenia
cewki

K

D

B

S

n

I

=

ϕ

(37.4)

Tak więc pod wpływem przepływającego przez cewkę prądu I wychyli się ona o kąt

ϕ proporcjo-

nalny do wielkości tego prądu. Wzór ten opisuje zasadę działania galwanometru.
Jeżeli w pewnej chwili przerwiemy obwód zasilający cewkę galwanometru, zniknie moment
skręcający, a moment kierujący zgodnie z drugą zasadą dynamiki dla ciał w ruchu obrotowym, nada
cewce przyspieszenie

J

M

ε

K

r

r =

(37.5)

gdzie: J – moment bezwładności cewki względem osi obrotu,

2

2

dt

(t)

d

ε

ϕ

=

- przyspieszenie kątowe.

Korzystając z (37.1) otrzymujemy równanie opisujące drgania cewki:

0

(t)

ω

dt

(t)

d

2
0

2

2

=

+

ϕ

ϕ

(37.6)

gdzie

K

0

D

J

ω

=

- częstość kątowa.

Jest to równanie drgań harmonicznych. Jego rozwiązanie ma postać:

)

δ

t

ω

sin(

(t)

0

0

+

=

ϕ

ϕ

gdzie:

0

ϕ

- amplituda drgań,

δ - faza początkowa

W przypadku, gdy obwód cewki po odłączeniu go od źródła prądu zostanie zwarty przez oporność
R

Z

0, powstaje moment, który „tłumi” ruch cewki. Zgodnie z prawem indukcji Faradaya w cewce

poruszający się w polu magnetycznym pod wpływem M

≥

K

wyindukowuje się siła elektromotoryczna

ε równa:

dt

dΦ

ε

−

=

(37.7)

gdzie

Φ oznacza strumień pola magnetycznego przechodzący przez zwoje cewki.

Dla małej wartości wychylenia

ϕ mamy

Φ = n a b ϕ B

skąd

dt

d

B

S

n

dt

d

B

b

a

n

ε

ϕ

ϕ

−

=

−

=

(37.8)

Gdy obwód cewki jest zamknięty oporem R

Z

, popłynie w niej prąd, którego kierunek zgodnie z

regułą Lenza jest taki, że przeciwdziała zmianie strumienia, która go wywołała, czyli hamuje ruch
cewki

Z

g

Z

g

R

R

dt

d

B

S

n

R

R

ε

I

+

−

=

+

=

ϕ

(37.9)

przy tym R

g

jest opornością cewki.

Pod wpływem tego prądu powstaje moment hamujący (wzór 37.3):

dt

d

R

R

B)

S

(n

I

B

S

n

M

Z

g

2

H

ϕ

+

−

=

=

(37.10)

Moment ten jest więc proporcjonalny do

szybkości zmian kąta

ϕ,

a jego zwrot, jak już powiedziano,

jest przeciwny do kierunku ruchu cewki (moment M

H

przeciwdziała zmianom strumienia magne-

tycznego B, która wynika z ruchu cewki). Na cewkę działają teraz dwa momenty M

H

i M

K

Korzy-

stając z drugiej zasady dynamiki

J

M

M

ε

H

K

r

r

r

+

=

otrzymujemy

0

(t)

ω

dt

(t)

d

β

2

dt

(t)

d

2
0

2

2

=

+

+

ϕ

ϕ

ϕ

(37.11)

gdzie

)

R

J(R

2

B)

S

(n

β

Z

g

2

+

=

– współczynnik tłumienia drgań i nadal

K

0

D

J

ω

=

Równanie to jest znanym równaniem różniczkowym ruchu harmonicznego tłumionego. Analo-
giczną postać równania otrzymalibyśmy analizując ruch wahadła lub ciężarka zawieszonego na

sprężynie z tłumikiem. W obwodzie elektrycznym „drgającym” rolę elementu tłumiącego spełnia
oporność R

z

.

Wielkość

β w ćwiczeniu zależy od R

z

, przez którą zwieramy obwód cewki. W przypadku, gdy R

z

→ ∞, to β→ 0, co jest zgodne z tym co powiedzieliśmy o rozwartym obwodzie cewki galwanome-
tru. Częstość kątowa

ω

o

jest częstością drgań własnych, tj. częstością drgań tego samego układu,

gdy nie ma oporów ruchu.
Rozwiązanie równania (37.11) ma postać:

)

δ

t

ω

sin(

(t)

t

β

0

+

=

−

e

ϕ

ϕ

(37.12)

przy czym

2

2
0

β

ω

ω

−

=

Stałe

ϕ

o

,

δ mogą być określone z warunków początkowych. Wyrażenie ϕ

o

e

-

βt

spełnia rolę amplitu-

dy drgań, która w przeciwieństwie do ruchu harmonicznego prostego nietłumionego nie jest stałą w
czasie, lecz maleje wykładniczo, skąd zrozumiałe staje się nazwanie

β współczynnikiem tłumienia.

Ruch jaki wykonuje cewka zależy od tego, jak duży jest współczynnik tłumienia

β:

1. Jeżeli

β < ω

0

, czyli

mamy do czynienia z ruchem harmonicznym o malejącej

amplitudzie

ϕ

0

β

ω

ω

2

2
0

2

〉

−

=

o

e

-

βt

(rys. 37.2a) i okresie drgań

ω

π

2

T

=

(37.13)

Szybkość zmiany amplitudy często przedstawia się za pomocą tzw. logarytmicznego dekrementu
tłumienia. Określa się go z zależności

T

β

e

e

ln

ln

λ

)

T

t

(

β

0

t

β

0

1

n

n

=

=

=

+

−

−

+

ϕ

ϕ

ϕ

ϕ

(37.14)

Logarytmiczny dekrement tłumienia charakteryzuje tłumiony obwód drgający, jest stały w czasie i
określa, jak szybko zmienia się amplituda drgań po czasie równym okresowi drgań tłumionych.

a)

ϕ

10


5

t

-5


-10

ϕ

0

e

-

βt

-

ϕ

0

e

-

βt

ϕ

n

ϕ

n+1

b)

ϕ

t

ϕ

0

0

Rys.37.3. Wykresy drgań: a) drgania słabo tłumione, b) silnie tłumione powodujące brak drgań

2. Jeżeli siły oporu są na tyle duże, że , to ruch ma charakter aperiodyczny, tzn. ciało
wychylone z położenia równowagi wraca do tego położenia zbliżając się doń asymptotycznie, ale
nigdy go nie osiągając (rys. 37.2b).

0

β

ω

2

2
0

≤

−

37.2. Opis układu pomiarowego

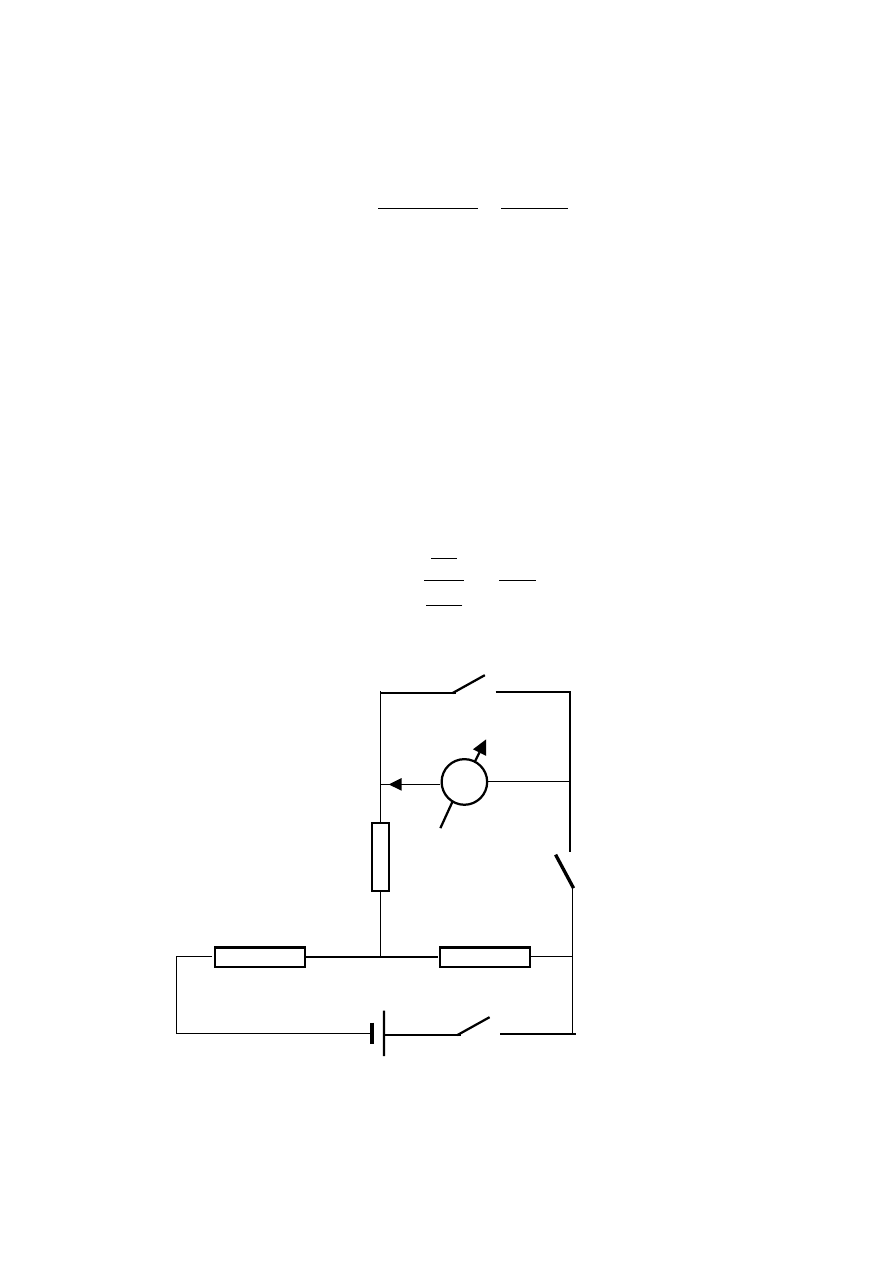
Układ pomiarowy składa się z galwanometru zwierciadłowego, zestawu oporników nastawnych
oraz źródła prądu. Schemat elektryczny układu przedstawia rys. 37.4.
Oporniki R

1

i R

n

stanowią dzielnik zmniejszający napięcie podawane do obwodu galwanometru.

Prąd I

g,

który przepłynie przez galwanometr przy zamkniętych kluczach K

1

i K

2

jest równy

)

R

R

(R

R

)

R

R

(

R

1

)

R

R

(R

R

R

U

I

n

g

1

g

n

n

g

1

n

g

+

+

+

+

+

+

=

Ponieważ R

n

1

Ω, R

≤

g

= kilkadziesiąt omów, R

≥ 1 kΩ to

n

1

n

g

R

R

R

R

U

I

+

≅

Wychylenie galwanometru przy zamkniętych kluczach K

1

i K

2

zależy od oporności R oraz różnicy

napięć między punktami A i B, regulowanej przez dzielnik napięcia (składnik

n

1

n

R

R

R

+

). Po roz-

warciu klucza K

1

pod wpływem momentu kierującego (M

K

) cewka galwanometru rozpocznie ruch

w kierunku położenia równowagi, ponieważ znajduje się ona w polu magnetycznym, popłynie
przez nią prąd indukcyjny. Jest on zależny od oporu R

z

(wzór 37.9), który w ćwiczeniu jest równy

R

z

= R + R

n

≈ R

Prąd płynie w takim kierunku, że przeciwdziała ruchowi ramki, wywołując moment hamujący
(M

H

).

Zgodnie z (37.11) współczynnik tłumienia jest równy

R

J

2

B)

S

(n

)

R

J(R

2

B)

S

(n

β

2

Z

g

2

=

+

=

(37.15)

Opornością R możemy więc regulować współczynnik tłumienia od bardzo dużej wartości, gdy R
jest małe (można dobrać tak R, aby

β = β

kr

), zwiększając R współczynnik tłumienia maleje i jest

równy zeru, gdy R =

∞ czyli otworzymy klucz K

2

. Mamy wówczas do czynienia z drganiami nie-

tłumionymi (zaniedbując oczywiście inne momenty hamujące, jak np. opór powietrza). Zauważmy
jeszcze, że takie wielkości, jak n, S, B, J są stałe w naszym układzie. Badając drgania tłumione
cewki galwanometru wygodniej jest posługiwać się wychyleniem plamki świetlnej na skali, niż
kątem skręcenia

ϕ. W przypadku dużej odległości l lusterka galwanometru od skali odczytowej,

jako amplitudę drgań możemy przyjąć odcinek A

n

równy

A

n

= l

ϕ

n

A

n

(

ϕ

n

) – kolejne amplitudy (kąty) drgań cewki.

1

n

n

1

n

n

A

A

ln

A

A

ln

λ

+

+

=

=

l

l

(37.16)

K

3

G

I

g

R

K

2

R

1

R

n

B

A

U

K

1

Rys. 37.3. Schemat elektryczny układu pomiarowego.

37.3. Przebieg pomiarów

1. Sprawdzić ustawienie położenia zerowego plamki galwanometru.

2. Ustawić na rezystorze dekadowym R maksymalną wartość rezystancji, tj. 100 k

Ω. Zamknąć

klucz K

2

, natomiast K

3

pozostawić otwarty. Ten ostatni służy do natychmiastowego zatrzyma-

nia ruchu plamki galwanometru w przypadku popłynięcia przez ramkę dużego prądu.

3. Za pomocą impulsowego zamykania klucza K

1

uzyskać wyraźne wychylenie plamki, np. 20-25

działek. Plamka galwanometru wykonuje wokół położenia zerowego ruch harmoniczny tłumio-
ny, o coraz mniejszej amplitudzie. Notować wartości kolejnych 4 amplitud przy wychyleniach
plamki w obie strony (łącznie z pierwszym).

4. Zmniejszać wartość rezystancji R kolejno dekadami najpierw co 20 k

Ω, potem co 1 kΩ, a na

końcu co 100

Ω, aż do wartości, przy której ruch plamki galwanometru stanie się ruchem ape-

riodycznym (np. 100; 80; 60; 40; 20; 10; 8; 6; 4; 3; 2; 1; 0,9; 0,8; 0,7; 0,6; itd. k

Ω)

i powtórzyć czynności opisane w pkt.2. Należy zwrócić uwagę, że przy mniejszych wartościach
R (szczególnie poniżej 10 k

Ω) należy delikatniej przyciskać klucz K

1

(szybciej puszczać).

5. Na zakończenie postępować podobnie jak w pkt.2 – spowodować wychylenie plamki galwano-

metru z położenia równowagi i otworzyć klucz K

2

(R =

∞). Wyznaczyć wartość jak największej

liczby kolejnych amplitud (przynajmniej siedmiu).

37.4. Opracowanie wyników pomiarów.

1. Dla każdej z nastawionych wartości R obliczyć z zależności (37.16) wartości

λ

N

logarytmiczne-

go dekrementu tłumienia dla każdej pary wychyleń plamki odległych o okres T (rys. 37.2), a na-
stępnie ich wartość średnią

λ .

2. Obliczyć średni błąd kwadratowy dla wartości średniej

λ

s

dla pomiaru z pkt.4 (R =

∞).

Oszacować błędy wartości

λ

N

dla R = 10 k

Ω, 1 kΩ i 0,5 kΩ.

3. Wykreślić zależność znalezionego logarytmicznego dekrementu tłumienia λ od wielkości rezy-

stancji R, uwzględniając błąd

λ

s

.

4. Wyciągnąć wnioski. Jak zmienia się błąd pomiaru ze zmniejszaniem wartość rezystancji R?

37.5. Pytania kontrolne

1. Podać zasadę działania galwanometru magnetoelektrycznego.
2. Omówić wzory na amplitudę i częstość drgań w ruchu harmonicznym tłumionym.
3. Co to jest logarytmiczny dekrement tłumienia i od czego zależy jego wartość?
4. Posługując się rys. 37.3 omówić wpływ rezystancji na prąd płynący przez galwanometr.

L i t e r a t u r a

[1] Frisz S., Timoriewa A.: Kurs fizyki, t.I. PWN, Warszawa 1964.
[2] Kittel C., Knight W.D., Ruderman M.A.: Mechanika PWN, Warszawa 1969.
[3] Szczeniowski S.: Fizyka doświadczalna, cz.I. Mechanika i akustyka. PWN, Warszawa 1972.