kierunek:

Mechatronika (WM)

Zadania uzupełniające do wykładu i ćwiczeń z Elektroniki dla sem. III

Dzielniki napięcia i prostowniki

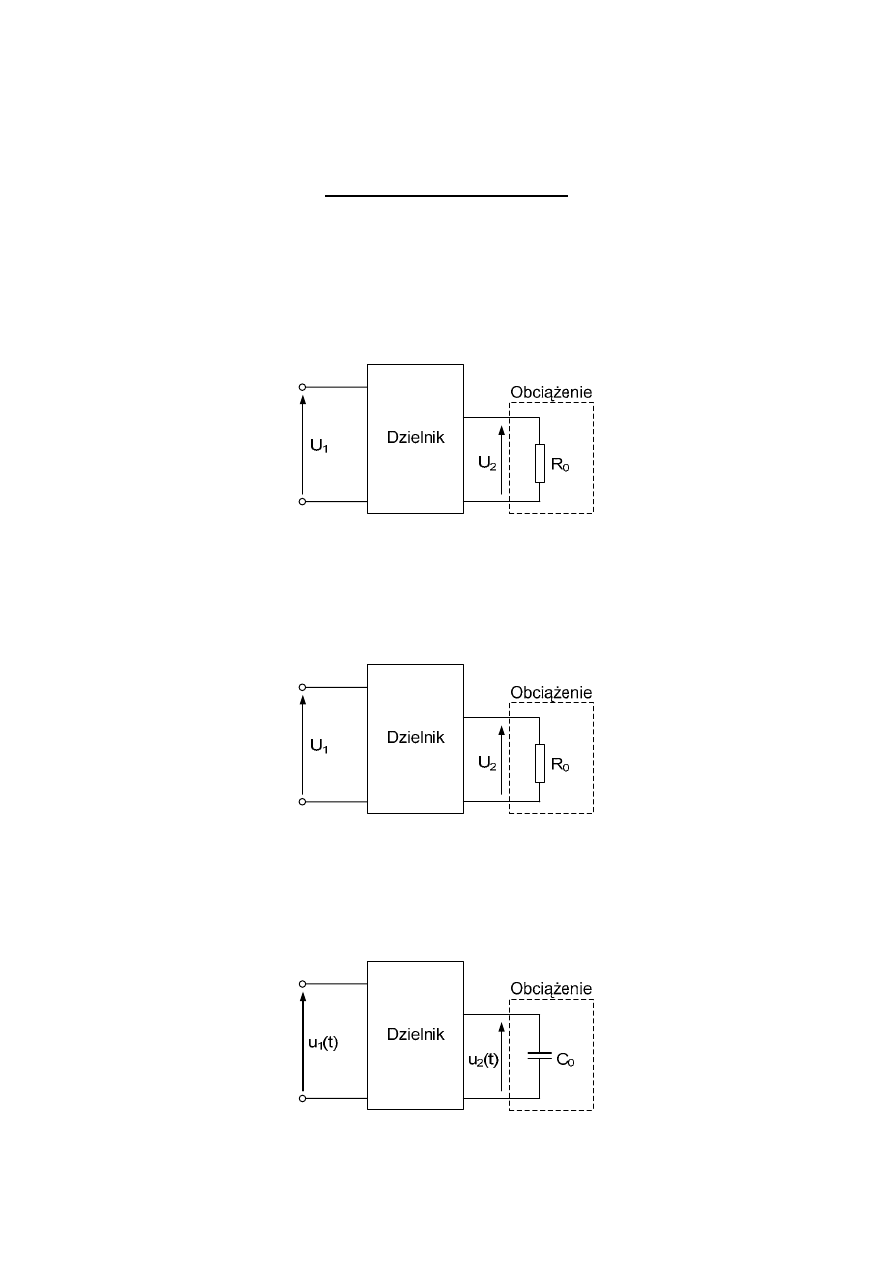
Zadanie 1

Zaprojektować dzielnik napięcia (dla napięć stałych i wolnozmiennych) tak, aby

dla napięcia wejściowego U

1

=10V uzyskać napięcia na obciążeniu dzielnika U

2

=2V, przy re-

zystancji obciążenia R

0

=100k

Ω. Rezystory dzielnika należy dobrać tak, aby źródło sygnału

wejściowego było obciążone mocą nie większą niż P

max

=0,25W.

Zadanie 2

Zaprojektować dzielnik napięcia (dla napięć stałych i wolnozmiennych) tak, aby

dla napięcia wejściowego o maksymalnej wartości U

1max

=80V uzyskać napięcia na obciążeniu

dzielnika o maksymalnej wartości U

2max

=5V, przy rezystancji obciążenia R

0

=40k

Ω. Rezysto-

ry dzielnika należy dobrać tak, aby źródło sygnału wejściowego było obciążone mocą nie
większą niż P

max

=0,5W.

Zadanie 3

Zaprojektować dzielnik napięcia (dla napięć zmiennych o dowolnym kształcie i

częstotliwości – tzn. skompensowany częstotliwościowo), dla którego spełniona jest zależ-
ność:

1

2

05

,

0

u

u

⋅

=

. Rezystancja wejściowa dzielnika winna być większa od 50 k

Ω. Przyjąć,

że obciążenie dzielnika charakteryzuje się pojemnością wejściową C

0

= 500 pF

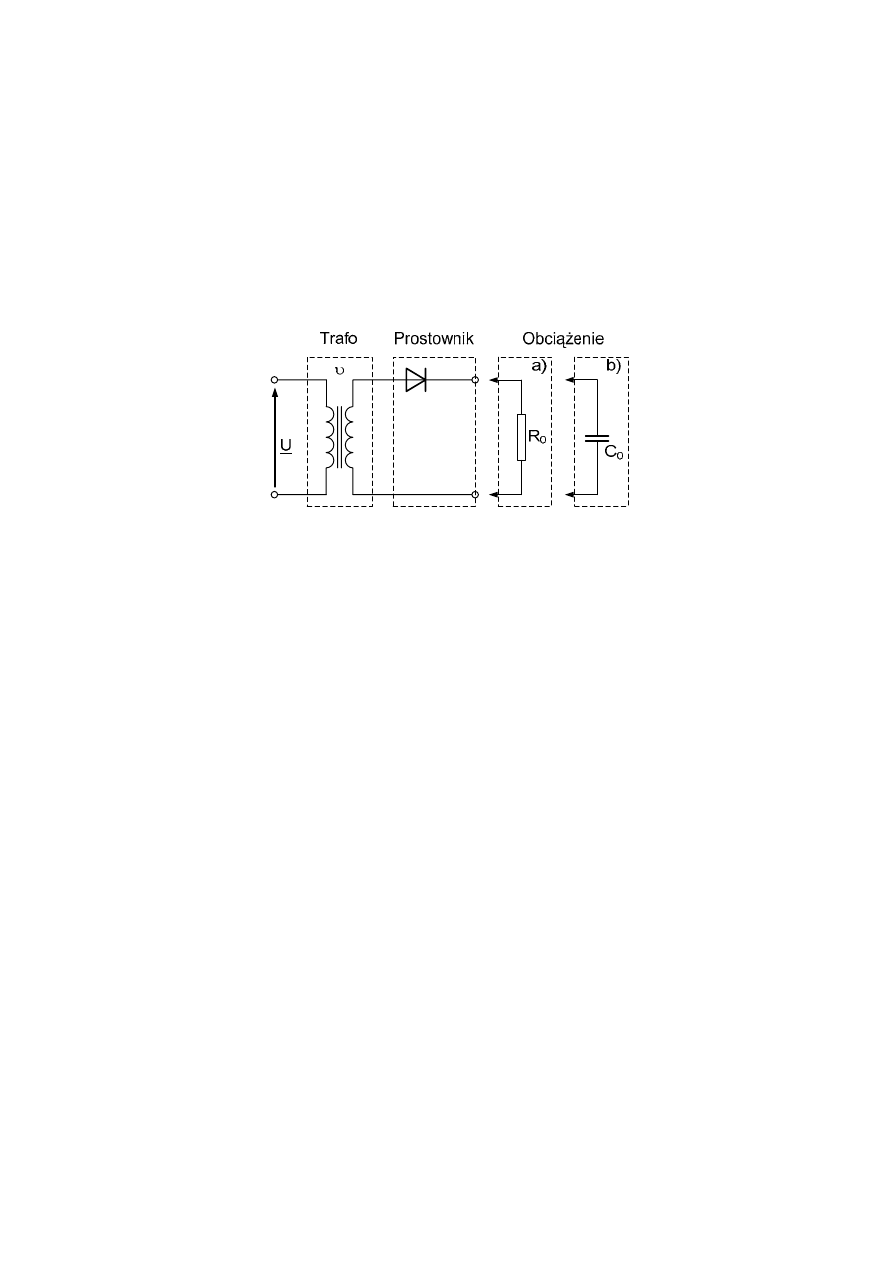
Zadanie 4

W układzie prostownika jednopulsowego, przedstawionego na rysunku, zasilane-

go napięciem sieciowym (f=50Hz) o wartości skutecznej U=230V przez transformator o prze-
kładni zwojowej υ = 5, obliczyć:
- wartość maksymalną i średnią prądu diody,
- wartość maksymalną napięcia wstecznego na diodzie,
przy obciążeniu prostownika:
a) rezystorem R

0

=40

Ω,

b) kondensatorem C

0

=2mF.

Spadek napięcia na diodzie w stanie przewodzenia zaniedbać.

Zadanie 5

W układzie prostownika jednopulsowego (schemat jak w zad. 4), zasilanego na-

pięciem sieciowym (f=50Hz) o wartości skutecznej U=230V przez transformator o przekładni
zwojowej υ = 10, obciążonego rezystorem o rezystancji R

0

=20

Ω obliczyć:

- wartość maksymalną i średnią prądu diody,
- wartość maksymalną napięcia wstecznego na diodzie.
Jak zmieni się wartość napięcia wstecznego, jeżeli zamiast rezystora włączymy kondensator o
pewnej pojemności C?
Spadek napięcia na diodzie w stanie przewodzenia zaniedbać.

Zadanie 6

W układzie prostownika jednopulsowego (schemat jak w zad. 4), zasilanego na-

pięciem sieciowym (f=50Hz) o wartości skutecznej U=230V przez transformator o przekładni
zwojowej υ = 4, dołączono do zacisków wyjściowych prostownika kondensator o pojemności
C

0

=3,3 mF i równolegle do niego odbiornik o rezystancji R

0

=10

Ω.

W układzie tym obliczyć:
- wartość średnią napięcia na rezystancji obciążenia,
- poziom tętnień napięcia (procentowo w stosunku do wartości średniej napięcia),
- moc pobieraną przez odbiornik.
Spadek napięcia na diodzie w stanie przewodzenia zaniedbać.

Zadanie 7

W układzie prostownika dwupulsowego, przedstawionego na rysunku, zasilanego

napięciem sieciowym (f=50Hz) o wartości skutecznej U=230V przez transformator o prze-
kładni zwojowej υ = 6, obliczyć:
- wartość maksymalną i średnią prądu obciążenia,
- wartość średnią napięcia obciążenia,
przy obciążeniu prostownika:
a) rezystorem R

0

=50

Ω,

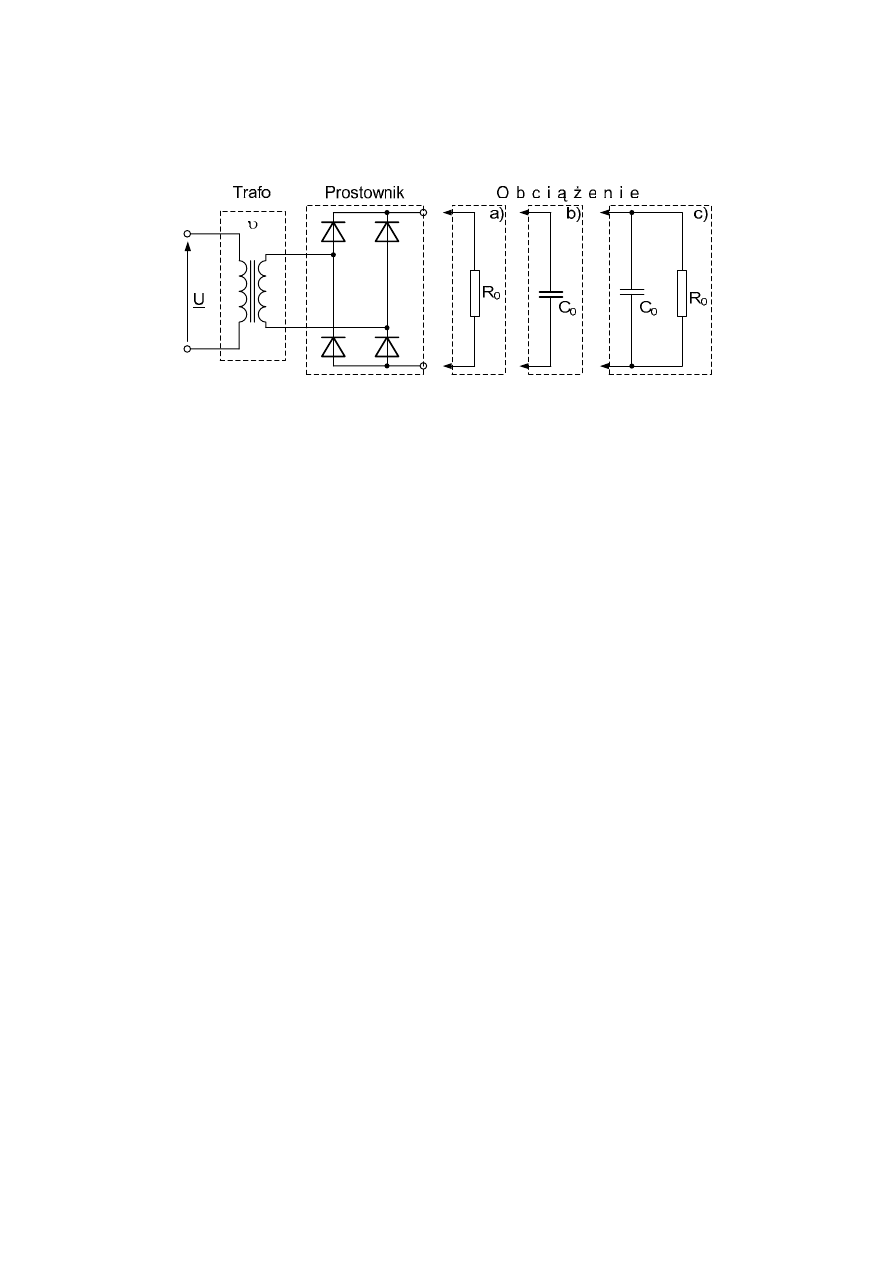
b) kondensatorem C

0

=1mF,

c) obydwoma tymi elementami połączonymi równolegle.
Spadek napięcia na diodach w stanie przewodzenia zaniedbać.

Zadanie 8
W układzie prostownika dwupulsowego (schemat jak w zadaniu 7 – wariant c), zasilanego
napięciem sieciowym (f=50Hz) o wartości skutecznej U=230V przez transformator o prze-
kładni zwojowej υ = 4, obciążonego rezystancją R

0

=36

Ω, dobrać pojemność kondensatora C

0

tak, aby tętnienia napięcia nie przekraczały 6% wartości średniej napięcia; obliczyć (w przy-
bliżeniu) tę wartość średnią.
Spadek napięcia na diodach w stanie przewodzenia zaniedbać.

Rozwiązania i odpowiedzi

Zadanie 1
Rozwiązanie:
Sumaryczna rezystancja obydwu rezystorów dzielnika, którego struktura jest przedstawiona
na rysunku poniżej, musi być nie mniejsza niż:

Ω,

400

25

,

0

100

max

2

1

min

2

1

=

=

=

+

P

U

R

R

a ponadto musimy uzyskać relację:

2

,

0

10

2

0

2

0

2

1

0

2

0

2

1

2

=

=

+

+

+

=

R

R

R

R

R

R

R

R

R

U

U

.

Jeżeli – przykładowo – przyjmiemy wartość rezystancji R

1

równą 1k

Ω, to po wykonaniu

przekształceń i podstawień, rezystancja R

2

wyjdzie nam równa 250,6

Ω. Ponieważ łączna re-

zystancja wejściowa dzielnika wynosi 1250

Ω, zatem prąd maksymalny (przy napięciu

U

1

=10V) wyniesie: I=8mA, zatem moce tracone w rezystorach dzielnika wyniosą odpowied-

nio: P

1max

=64mW, P

2max

=16mW. Wystarczą zatem rezystory o mocy znamionowej

P

n

=0,125W.

Odpowiedź:
R

1

=1k

Ω/0,125W, R

2

=250,6

Ω/0,125W.

(oczywiście podane powyżej wartości są jednym z wielu możliwych wariantów rozwiązania).

Zadanie 2

Odpowiedź:
Schemat dzielnika identyczny jak w rozwiązaniu zadania 1, wartości elementów:
R

1

=15k

Ω/0,5W, R

2

=1,026k

Ω/0,25W.

(oczywiście podane powyżej wartości są jednym z wielu możliwych wariantów rozwiązania).

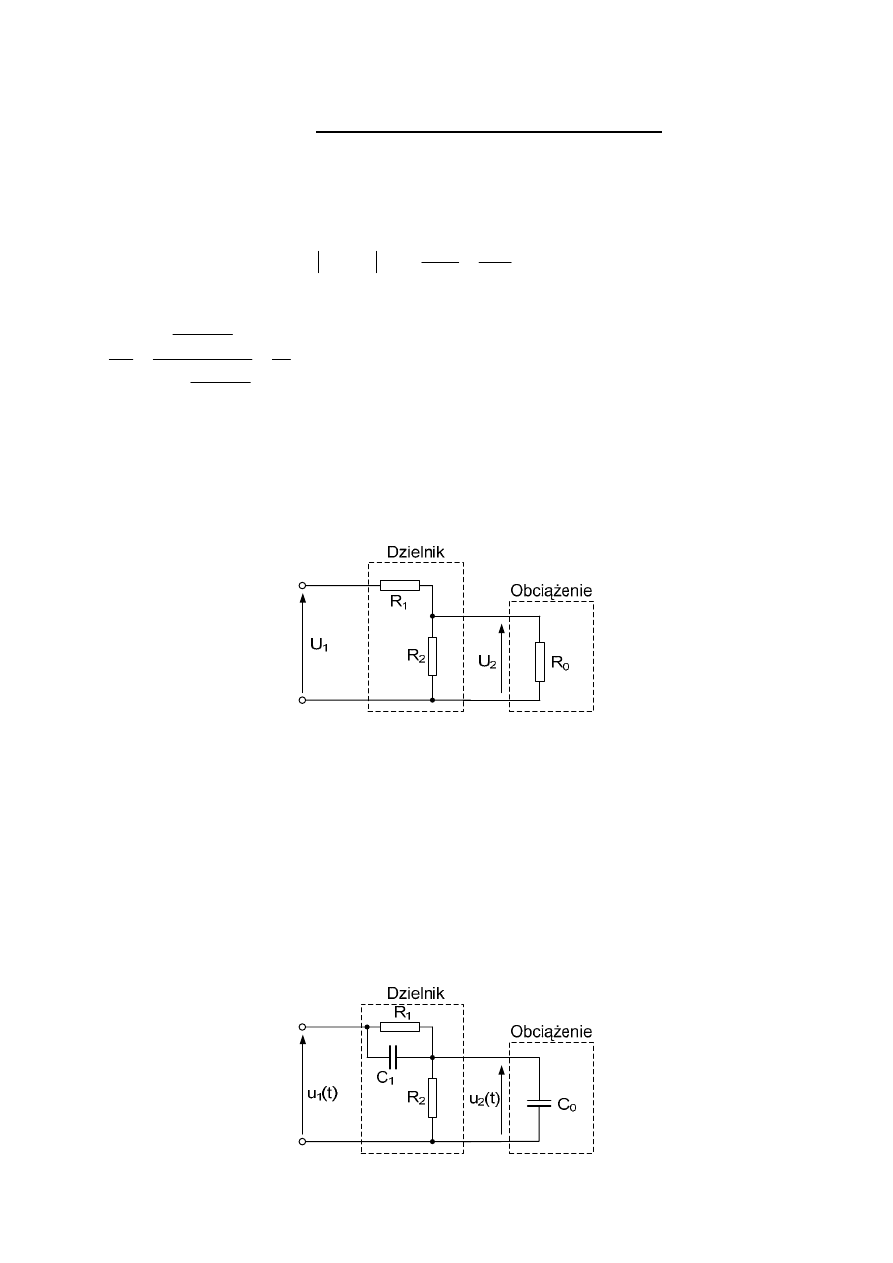
Zadanie 3

Odpowiedź:
Schemat dzielnika przedstawiono na rysunku poniżej.

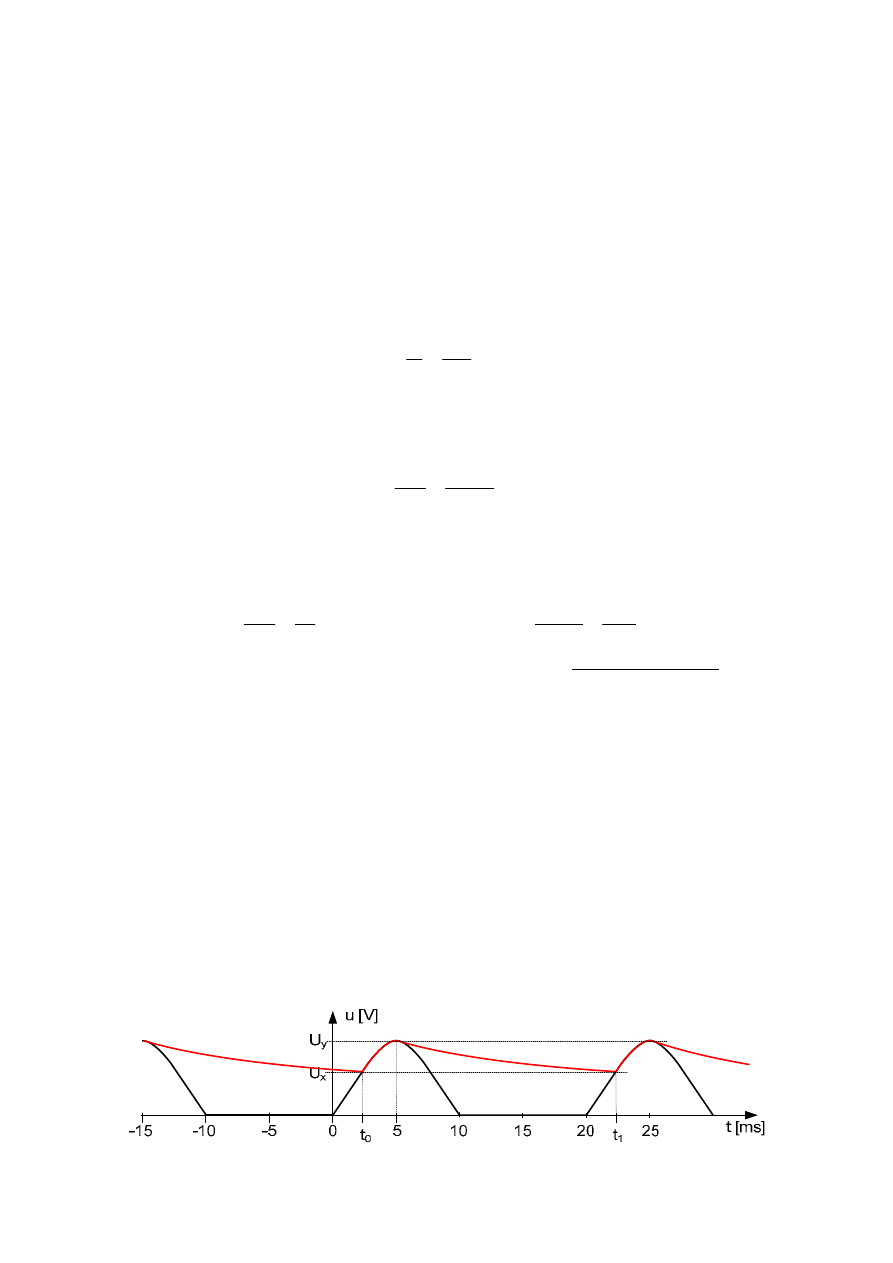
Wartości elementów: R

1

=76k

Ω, C

1

=26,3pF, R

2

=4k

Ω.

(oczywiście podane powyżej wartości rezystancji są jednym z wielu możliwych wariantów
rozwiązania, pojemność musi być dokładnie taka, jak podano – niezależnie od rezystancji.
Uwaga: w odpowiedzi nie podano nominalnej mocy rezystorów, ani moninalnego napięcia
kondensatora, ponieważ w treści zadania nie została określona maksymalna wartość napięcia
wejściowego – w woltach).

Zadanie 4

Rozwiązanie:
Wartość skuteczną napięcia na uzwojeniu wtórnym transformatora U

2

, tzn. napięcia na wej-

ściu prostownika, obliczamy korzystając z podanej przekładni transformatora:

V.

46

5

230

2

=

=

=

υ

U

U

Amplituda tego napięcia (ze względu na jego sinusoidalny przebieg) jest √2-razy większa, za-
tem: U

2m

=65V.

Przy obciążeniu rezystancyjnym prostownika (bez żadnej dołączonej do jego zacisków wyj-
ściowych pojemności), wartość średnia napięcia wyniesie:

V.

7

,

22

1416

,

3

65

2

)

(

=

=

=

π

m

śr

wy

U

U

Wartość maksymalna napięcia wstecznego na diodzie jest w tym przypadku równa amplitu-
dzie napięcia wejściowego prostownika, zatem: U

R(max)

=U

2m

=65V.

W konsekwencji w rezystancji obciążenia R

0

i w diodzie otrzymamy – jako maksymalną i

średnią wartość prądu - odpowiednio:

A,

625

,

1

40

65

0

2

(max)

=

=

=

R

U

I

m

D

oraz

A.

517

,

0

40

7

,

22

0

)

(

)

(

=

=

=

R

U

I

śr

wy

śr

D

Przy obciążeniu wyjścia prostownika tylko pojemnością C

0

, w stanie ustalonym (tzn. po

pierwszym naładowniu się kondensatora do maksymalnej wartości napięcia U

2m

=65V), prąd

nie będzie płynął, napięcie będzie stałe i równe wartości maksymalnej U

2m

, zaś największa

wartość napięcia wstecznego na diodzie osiągnie dwukrotną wartość amplitudy napięcia wej-
ściowego prostownika:
U

wy(śr)

=65V, I

D(max)

=I

D(śr)

=0, U

R(max)

=130V.

Zadanie 5

Odpowiedź:
Przy obciążeniu prostownika tylko rezystorem:
U

Rmax

=32,5V, I

Fmax

=1,625A, I

F(AV)

=0,517A.

Po zamianie rezystora na kondensator:
U

Rmax

=65V.

Zadanie 6

Rozwiązanie:
Przebieg napięcia na obciążeniu prostownika przedstawiono na rysunku poniżej (czerwony).

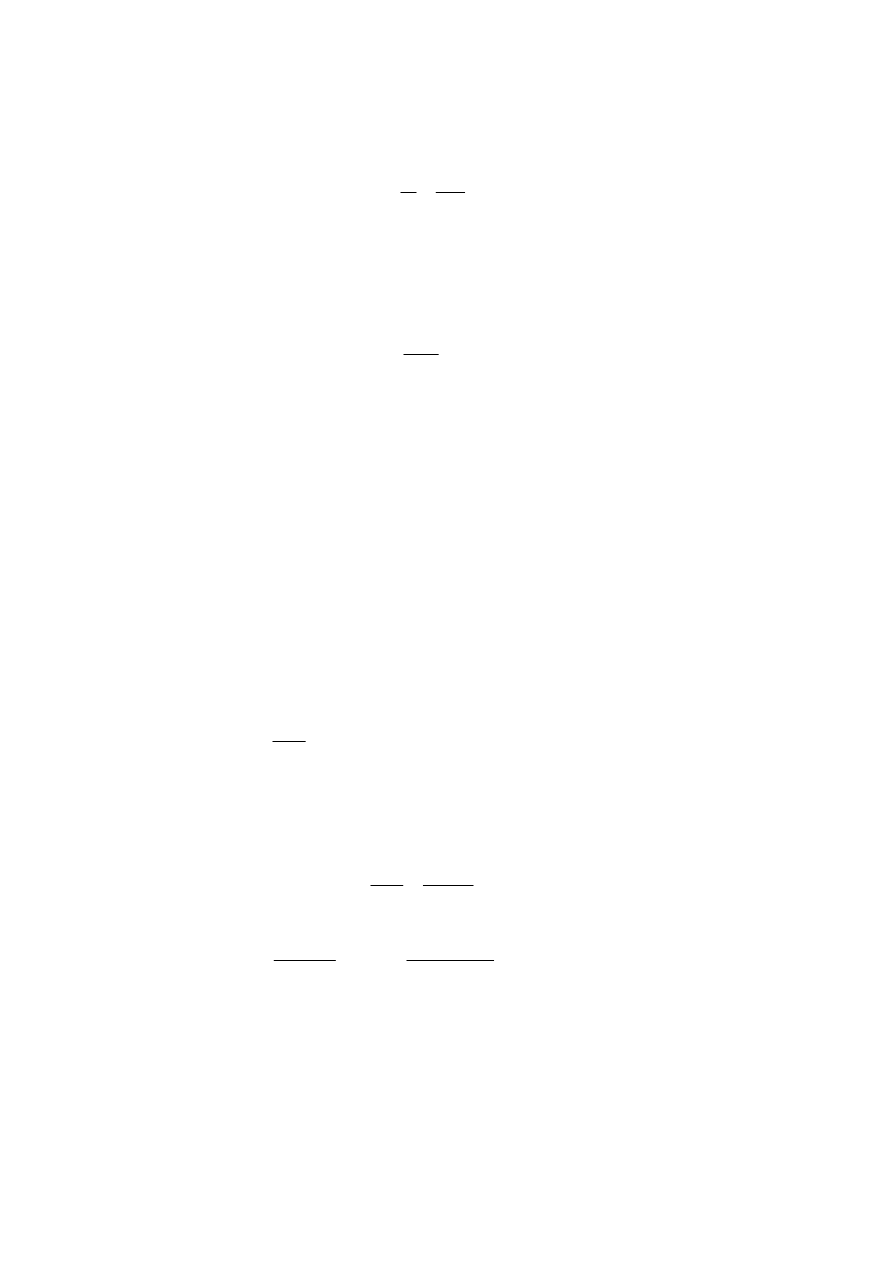
Wartość skuteczną napięcia na uzwojeniu wtórnym transformatora U

2

, tzn. napięcia na wej-

ściu prostownika, obliczamy korzystając z podanej przekładni transformatora:

V.

5

,

57

4

230

2

=

=

=

υ

U

U

Amplituda tego napięcia (ze względu na jego sinusoidalny przebieg) jest √2-razy większa, za-
tem: U

2m

=81,3V. Jest to równocześnie największa wartość napięcia na kondensatorze U

y

(patrz rys.), od której zaczyna się proces jego rozładowania w chwili t=5ms. Równocześnie
można stwierdzić, że w poprzednim okresie napięcia zasilania, kondensator zaczął się rozła-
dowywać o 20 ms wcześniej, tzn. dla t=-15ms=-0,015s. Zatem dla fragmentu przebiegu na-
pięcia, który przecina oś napięć (pionową na wykresie), można podać następujący wzór:

( )

(

)

.

3

,

81

015

,

0

3

,

30

015

,

0

0

0

+

−

⋅

+

−

⋅

=

⋅

=

t

C

R

t

y

e

e

U

t

u

Dla czasów: t

0

≤ t ≤ 5ms napięcie zmienia się sinusoidalnie wg wzoru:

( )

( )

(

)

.

314

sin

3

,

81

sin

t

t

U

t

u

y

⋅

=

⋅

=

ω

Przyrównując do siebie te dwa wzory, możemy określić chwilę czasu t

0

, w której kończy się

rozładowanie, a zaczyna doładowanie kondensatora. Ponieważ otrzymujemy równanie nieli-
niowe, można je rozwiązać numerycznie (np. iteracyjną metodą Newtona – opis metod roz-
wiązywania równań nieliniowych wykracza poza zakres tego zbioru zadań), ewentualnie
spróbować użyć aproksymacji liniowej (licząc się z niedokładnością tej metody), lub spróbo-
wać znaleźć rozwiązanie metodą „prób i błędów” (ostateczność!).
W rozważanym równaniu:

(

)

(

)

0

015

,

0

3

,

30

314

sin

3

,

81

3

,

81

0

t

e

t

⋅

=

⋅

+

−

Jako wynik uzyskamy (w przybliżeniu) wartość: t

0

=0,00204s=2,04ms. Jeżeli tę wartość pod-

stawimy do dowolnego z dwóch powyższych wzorów na napięcie u(t), to otrzymamy mini-
malną wartość napięcia na obciążeniu (na wyjściu) prostownika: U

x

=48,45V.

Dokładne obliczenie wartości średniej napięcia wyjściowego wymaga obliczenia całki (po
czasie) za jeden okres z przebiegu napięcia i podzielenia jej przez wartość okresu:

(

)

(

)

(

)

(

)

V.

48

,

64

314

sin

4065

314

sin

3

,

81

3

,

81

02

,

0

1

00204

,

0

015

,

0

005

,

0

00204

,

0

015

,

0

3

,

30

00204

,

0

015

,

0

005

,

0

00204

,

0

015

,

0

3

,

30

=

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

+

=

=

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

⋅

+

⋅

=

∫

∫

∫

∫

−

+

−

−

+

−

dt

t

dt

e

dt

t

dt

e

U

t

t

śr

Średnią moc pobieraną przez odbiornik możemy obliczyć ze wzoru:

W.

8

,

415

10

48

,

64

2

0

2

=

=

=

R

U

P

śr

Wartość tętnień napięcia wyrażoną w procentach w stosunku do wartości średniej wyniesie:

.

%

51

%

95

,

50

%

100

48

,

64

45

,

48

3

,

81

%

100

%

≈

=

⋅

−

=

⋅

−

=

śr

x

y

U

U

U

U

∆

Zadanie 7

Odpowiedź:
a) Przy obciążeniu prostownika tylko rezystorem:
I

0max

=1,08A, I

0śr

=0,69A, U

0śr

=34,5V.

b) Przy obciążeniu prostownika tylko kondensatorem:
I

0max

=0A, I

0śr

=0A, U

0śr

=54,2V.

c) Przy obciążeniu prostownika obydwoma elementami (uwaga – jako prąd obciążenia rozu-
mie się tutaj prąd rezystora, gdyż kondensator jest z reguły standardowym elementem skła-
dowym prostownika):
I

0max

=1,08A, I

0śr

=1A, U

0śr

=50,2V.

Zadanie 8

Odpowiedź:
U

0śr

=78,9V, C

0

=4,12mF.