str. 1
LABORATORIUM Z PODSTAW TEORII OKRĘTU
Sprawozdanie z ćwiczenia nr 20 (4)
Pomiar oporu ciał o różnych kształtach, wizualizacja opływu
Data realizacji ćwiczenia:
Data oddania sprawozdania:
Grupa:
Lista studentów uczestniczących w ćwiczeniu:
str. 2
1. Cel ćwiczenia
Celem ćwiczenia jest pomiar oporu ciał o różnym kształcie. Doświadczenie przeprowadzone jest w
małym kanale obiegowym ,znajdującym się w hali zajęć dydaktycznych Laboratorium Hydromechaniki
Okrętu Instytutu Okrętowego Politechniki Gdańskiej.
2. Podstawowe informacje
2.1 Opór ciał całkowicie zanurzonych.
W przypadku ciał całkowicie zanurzonych, zaniedbując wpływ ściśliwości oraz wpływ napięcia
powierzchniowego i grawitacji jest funkcją liczby Reynoldsa.
Gdzie jako charakterystyczny wymiar liniowy ciała przyjmuje się w hydrodynamice ogólnej zwykle
grubość ciała mierzoną prostopadle do kierunku przepływu, a jako powierzchnię A- powierzchnie rzutu
ciała na kierunek prostopadły do przepływu.
2.2 Co to jest paradoks d’Alemberta.
Ciało sztywne znajdujące się w przepływie płynu nielepkiego nie napotyka w ruchu jednostajnym na
żaden opór ze strony płynu.
2,3 Co to jest warstwa przyścienna?
Jest to bardzo cienka warstwa w bezpośrednim sąsiedztwie ciała, w której prędkość płynu rośnie od zera
na powierzchni ciała, zmierzając do prędkości strumienia płynu nielepkiego.
2.4 Co to jest odrywanie przepływu?
Powstaje kiedy linie prądu przestają przylegać do powierzchni ciała, prędkość przepływu w sąsiedztwie
ciała zmienia kierunek na przeciwny, tworzy się wir, który odpływa dając miejsce następnemu.
2.5 Co to jest współczynnik oporu i od czego zależy?
Współczynnik oporu (inaczej liczba Newtona) to współczynnik Cp wyrażający stosunek siły F
wywieranej na ciało przez ciecz do sił bezwładności.
2.6 Co to jest liczba Reynoldsa?
Wyraża stosunek sił bezwładności do sił ciężkości.
2.7 Jaki jest podział ciał ze względu na opór i jak wygląda ich opływ?
a) Ciała tępe
b) Ciała zaokrąglone
c) Ciała opływowe
str. 3
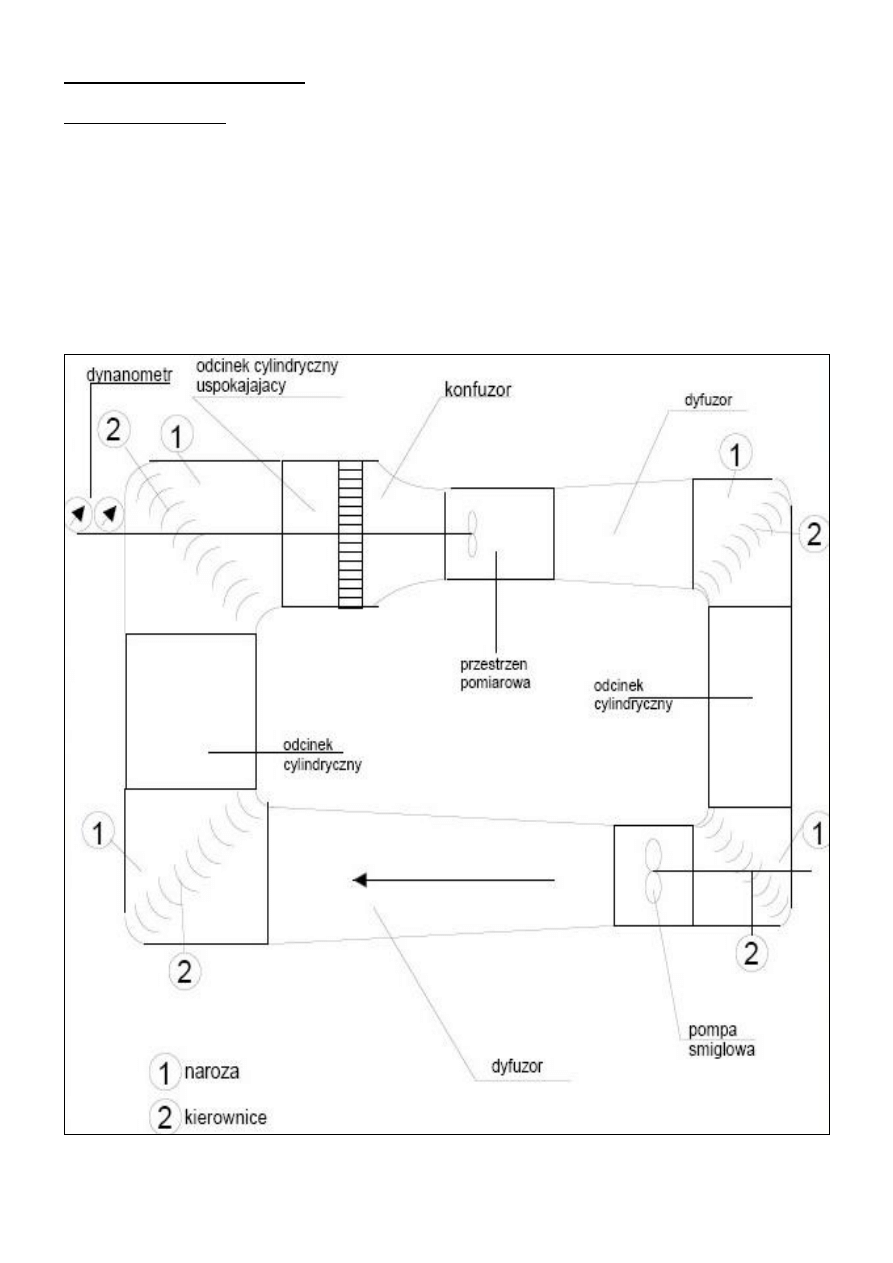
3. Opis stanowiska badawczego
3.1 Kanał kawitacyjny
Pomiar oporu ciał został przeprowadzony w małym obiegowym kanale wodnym. Przepływ wody
wytwarzany jest za pomocą dwu kół łopatkowych napędzanych przez silnik o regulowanej prędkości
obrotowej. Badane ciało było umieszczane w przestrzeni pomiarowej, umocowując do dynamometru
trzech składowych, pozwalającemu na jednoczesny pomiar oporu, siły nośnej i momentu
hydrodynamicznego. Pomiar prędkości przepływu dokonuje się za pomocą pojedynczej sondy Pitota,
pozwalającej bezpośrednio odczytać wysokość ciśnienia prędkości jako różnice pomiędzy poziomem
wody w kanale i poziomem wody w sondzie. Wyniki pomiarów rejestrowane i przetwarzane są za
pomocą komputera.
str. 4
3.2 Ciał o różnych kształtach
Podczas pomiaru oporu ciał były wykorzystywane następujące bryły:
3.2.1 Płaska płyta
3.2.2 Graniastosłup o podstawie trójkąta równoramiennego.
3.2.3 Walec kołowy.
1A
1B
1C
3
2A
2B
str. 5
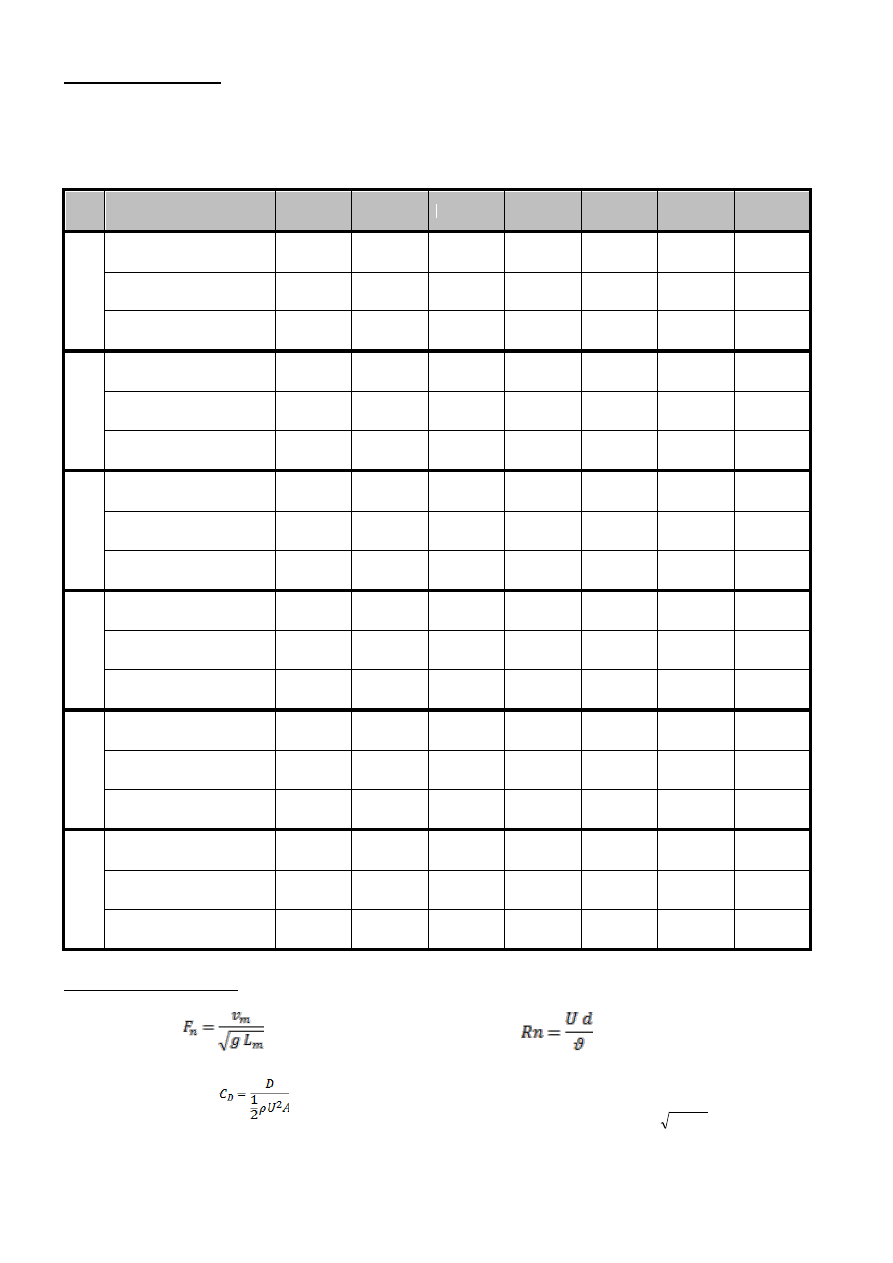
4. Wyniki pomiarów
Dla każdej wartości oporu i prędkości modelu dokonano obliczeń odpowiadających im liczb Froude’a ,
Reynoldsa i współczynnika oporu (przyjmując gęstość wody i kinematyczny współczynnik lepkości dla
temperatury 18° C).
Lp.
Charakterystyka ciała
U [ m/s ]
R* [ N ]
R** [ N ]
R*** [ N ]
Cd [ N ]
RN [ - ]
FN [ - ]
1A
L = 20 [ cm ] = 0,2 [ m ]
0,704
-1,373
-1,030
0,343
924
3338
0,50260
T = 30 [ cm ] = 0,3 [ m ]
A = 0,0015
0,576
-0,899
-1,030
0,131
527
2731
0,41122
S = 0,5 [ cm ] = 0,005 [ m ]
0,460
-1,003
-1,030
0,027
170
2181
0,32840
1B
L = 0,5 [ cm ] = 0,005 [ m ]
0,204
0,877
-1,030
1,907
1530
38689
0,92111
T = 30 [ cm ] = 0,3 [ m ]
A = 0,06
0,384
6,193
-1,030
7,223
1635
72827
1,73385
S = 20 [ cm] = 0,2 [ m ]
0,561
14,621
-1,030
15,651
1660
106395
2,53305
1C
L = 20 [ cm ] = 0,2 [ m ]
0,442
-0,960
-1,030
0,070
171
6287
0,31555
T = 30 [ cm ] = 0,28 [ m ]
A = 0,0042
0,589
-0,817
-1,030
0,213
293
8378
0,42050
S = 1,5 [ cm ] = 0,015 [ m ]
0,699
-0,612
-1,030
0,418
408
9943
0,49903
2A
L = 10 [ cm ] = 0,1 [ m ]
0,438
2,932
-1,030
3,962
1379
41534
0,44222
T = 30 [ cm ] = 0,3 [ m ]
A = 0,03
0,575
3,964
-1,030
4,994
1008
54525
0,58054
S = 10 [ cm ] = 0,1 [ m ]
0,700
6,400
-1,030
7,430
1012
66378
0,70675
2B
L = 10 [ cm ] = 0,1 [ m ]
0,398
2,359
-1,030
3,389
1428
37741
0,40184
T = 30 [ cm ] = 0,3 [ m ]
A = 0,03
0,553
6,375
-1,030
7,405
1617
52439
0,55833
S = 10 [ cm ] = 0,1 [ m ]
0,693
11,912
-1,030
12,942
1799
65715
0,69968
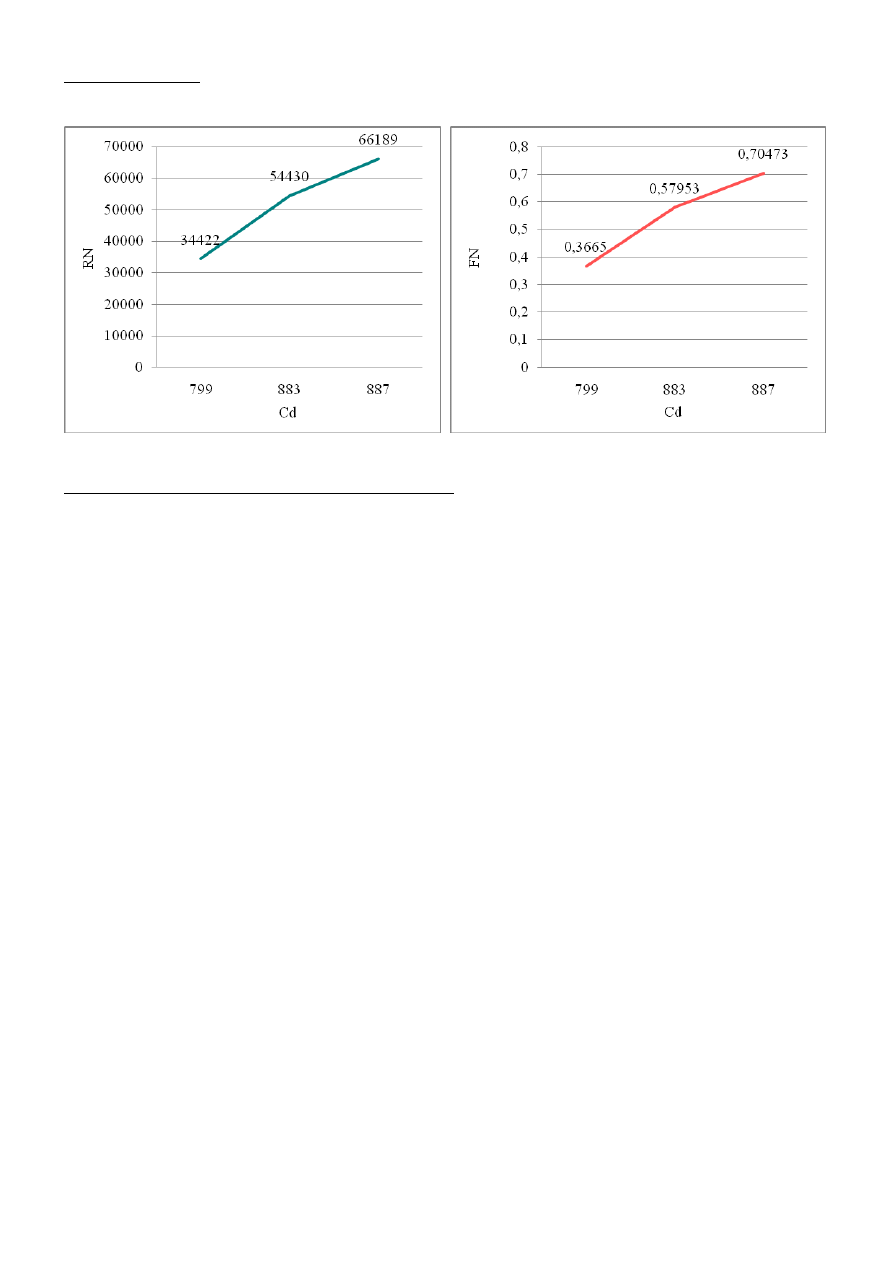
3
L = 10 [ cm ] = 0,1 [ m ]
0,363
0,547
-1,030
1,577
799
34422
0,36650
T = 30 [ cm ] = 0,3 [ m ]
A = 0,03
0,574
3,328
-1,030
4,358
883
54430
0,57953
S = 10 [ cm ] = 0,1 [ m ]
0,698
5,439
-1,030
6,469
887
66189
0,70473
Korzystając ze wzorów:
Liczba Froud’a:
Liczba Reynoldsa:
Współczynnik oporu:
Prędkość strumienia swobodnego
:
h
g
U
2
str. 6
R*
– opór statku (pomierzony)
R**
– opór statku (kalibracyjny)
R*** – opór statku (właściwy)
Cd
– współczynnik oporu całkowitego
R
N
– współczynnik związany z siłami lepkości
F
N
– środek ciężkości pola powierzchni wodnicy
A
– powierzchnie rzutu ciała na kierunek prostopadły do przepływu
U
– prędkość strumienia swobodnego
– gęstość płynu
D
– opór ciała
H
– poziom wody w sondzie
g
– przyspieszenie grawitacyjne
– lepkość dynamiczna płynu
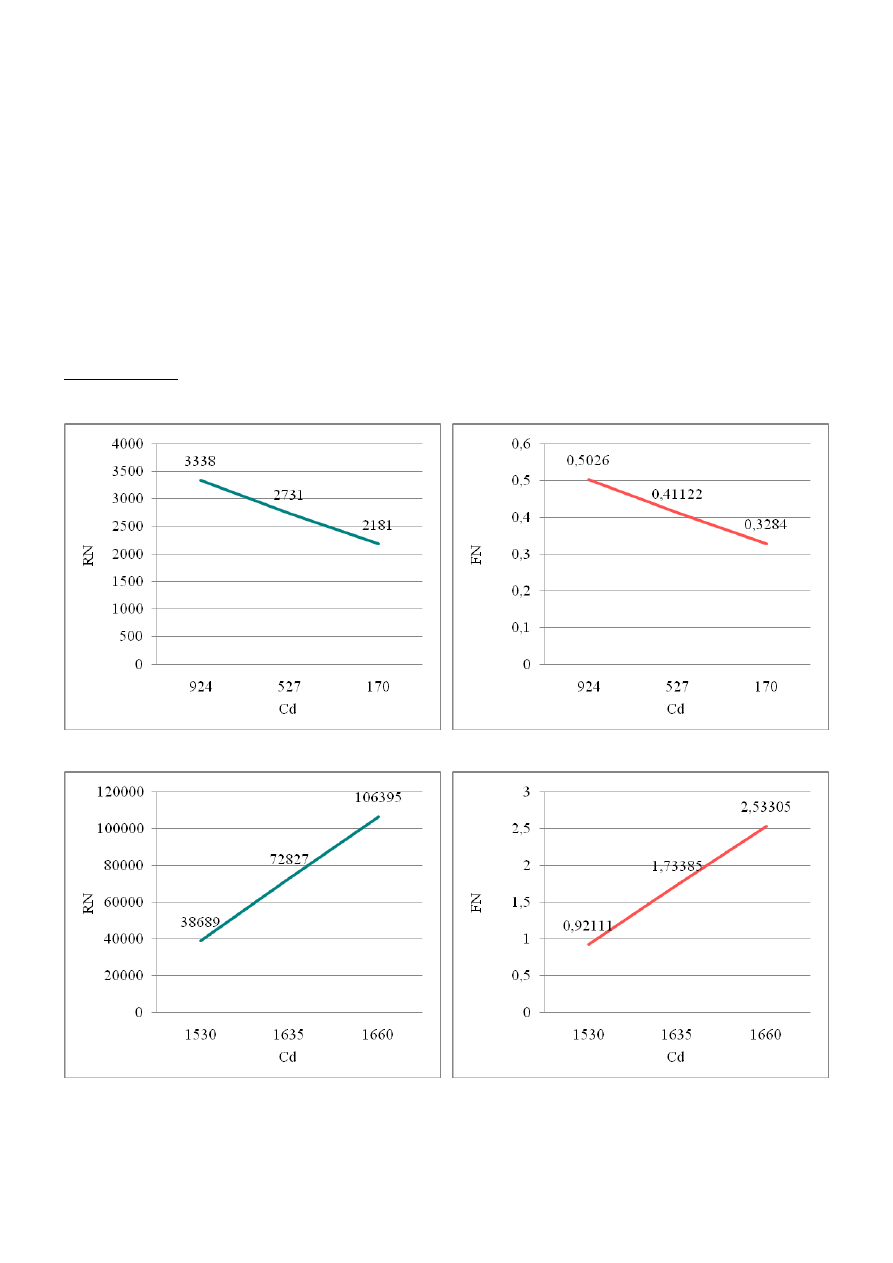
4.1 Płaska płyta
1A
1B
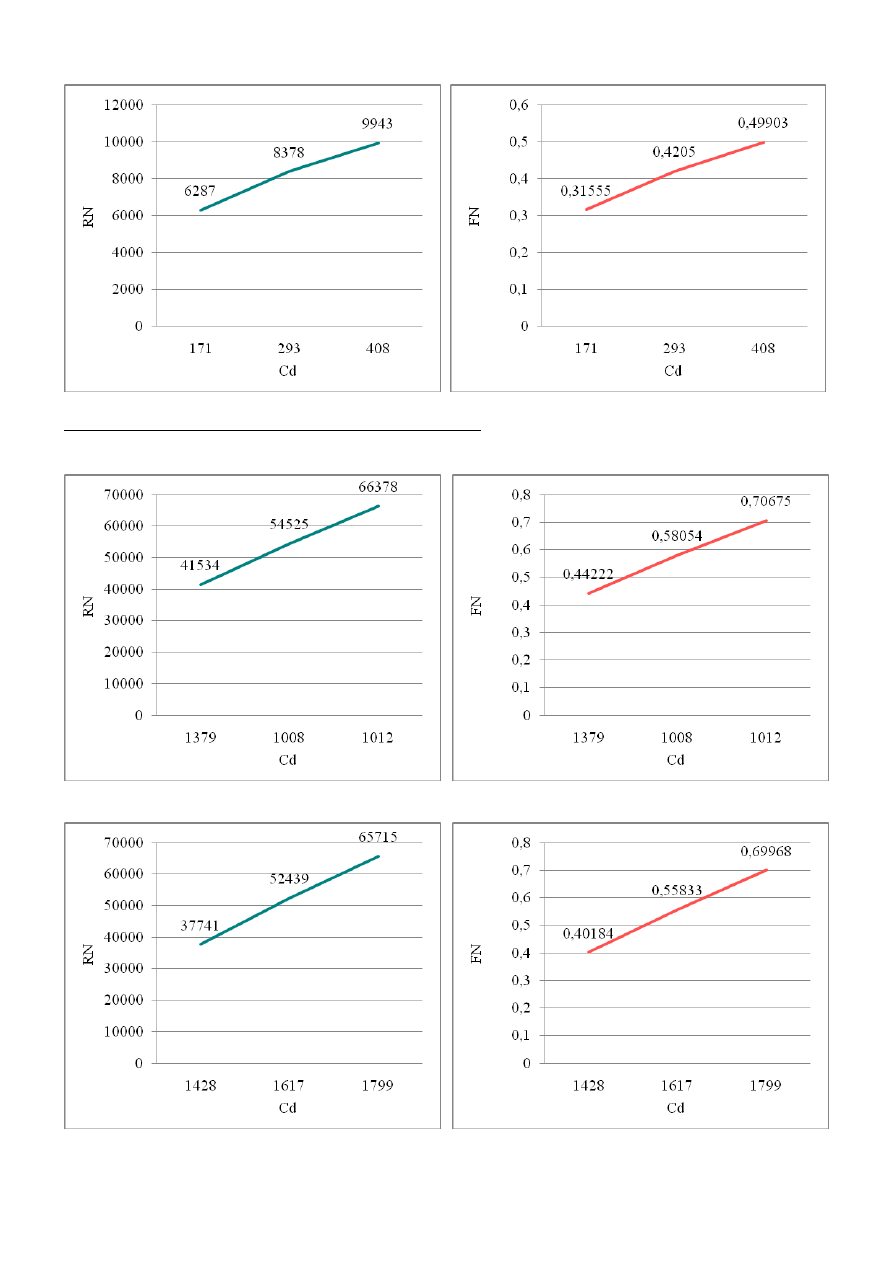
str. 7
1C
4.2 Graniastosłup o podstawie trójkąta równoramiennego.
2A
2B
str. 8
4.3 Walce kołowy.
3
5. Wnioski wynikające z przeprowadzonych badań
a) Ciała tępe – zwane również ciałem urwistym albo ciałem o dużym oporze, charakteryzują się płaską
ścianą czołową zakończoną ostrymi krawędziami i wymiarami poprzecznymi znacznymi w stosunku do
długości. Typowym przykładem takiego ciała jest:
płaska płyta ustawiona prostopadle do przepływu;
graniastosłup o podstawie trójkąta równoramiennego ustawiony prostopadle do przepływu;
Po stronie czołowej płyty prędkość przepływu spada do zera w punkcie spiętrzenia leżącym na osi
symetrii przepływu, a wzdłuż czoła płyty rośnie aż do krawędzi, gdzie następuje przymusowe oderwanie.
Za płytą powstaje ślad turbulentny. Dominującą, niemal wyłączną częścią oporu ciała tępego jest opór
ciśnienia, ponieważ naprężenie styczne działają w kierunku prostopadłym do kierunku strumienia
swobodnego. Opór ciał tępych przy liczbach Reynoldsa większych od 1000, jest niemal stały i niezależny
od R
N
.
b) Ciała zaokrąglone – podobnie jak ciało tępe, charakteryzuje się wymiarem poprzeczny znaczny w
stosunku do długości, jednak pozbawione są ostrych krawędzi, jak np.:
walec kołowy;
Występuje tu również odrywanie przepływu, jednak przyczyna odrywania jest inna, Nie jest nią
nieciągłość powierzchni opływowej, ale zahamowanie warstwy przyściennej dodatnim gradientem
ciśnienia. Punkt odrywania nie jest przymusowy, ale pojawia się w tym miejscu gdzie warstwa
przyścienna posiada zbyt małą energię kinetyczną, aby przedostać się do obszaru wysokiego ciśnienia,
kumuluje się i następnie odrywa w pewnych odstępach czasu. Dla ciał zaokrąglonych położenie punktu
oderwania zależy od liczby Reynoldsa. W odróżnieniu od ciał urwistych występuje tu również opór
tarcia, jest on jednak mały w porównaniu z oporem ciśnienia, ponieważ większa część powierzchni ciała
graniczy z obszarem odrywania. W zakresie zmienności liczb Reynoldsa od 1000 do 100000
współczynniki oporu ciał tępych i zaokrąglonych są tego samego rzędu, co wynika z podobnej szerokości
śladu.
c) Ciała opływowe – ciała o małym oporze, są to ciała o wymiarach poprzeczne małych w stosunku do
długości, zaprojektowane w taki sposób, aby zmniejszyć do minimum obszar odrywania, a więc są
smukłe, pozbawione nieciągłości powierzchni i zakończone ostrzem lub ostrą krawędzią spływu.
Typowym przykładem ciała opływowego, zwanego również aerodynamicznym, jest:
płaska płyta ustawiona w pozycji zerowego kąta natarcia;
str. 9
płaska płyta ustawiona w pozycji miedzy 45
o
do przepływu;
graniastosłup o podstawie trójkąta równoramiennego ustawiony w pozycji zerowego kąta natarcia;
Taki sposób ukształtowania ciała powoduje, ze warstwa przyścienna rozciąga się niemal na całą jego
powierzchnię, a punkt odrywania leży bardzo blisko krawędzi spływu. Opływ ciała aerodynamicznego
jest (poza wąskim śladem) zbliżony do opływu potencjalnego, bez wirowego, zachodzącego w płynie
nielepkim. Opór ciśnienia musi być wiec bardzo mały i rzeczywiści wynosi około 1/40 oporu ciśnienia
ciał tępych i zaokrąglonych. Głównym składnikiem oporu pozostaje więc opór tarcia i jakkolwiek jest on
zwiększony ze względu na dużą długość opływu, to i tak opór całkowity jest rząd mniejszy niż w
wypadku ciał tępych lub zaokrąglonych.
6. Uwagi krytyczne studentów, wynikające ze zdobytej wiedzy
a) Badanie zostało przeprowadzone w basenie modelowym co oznacza że pomiary są niezgodne z
rzeczywistością.