1 Całka podwójna w prostokącie
Na płaszczyźnie OXY dany jest prostokąt P określony nierównościami
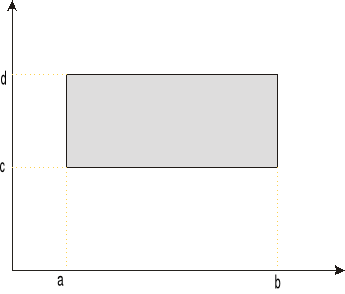
P: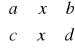
Dana jest też funkcja z = f(x,y) ograniczona i określona w tym prostokącie
Prostokąt P dzielimy na n-prostokątów częściowych, które oznaczamy przez Pi
![]()
- określamy średnicę podziału ∂i - jest to największa odległość dwóch punktów należących do prostokąta Pi
- w każdym z prostokątów Pi dobieramy punkt pośredni Ai (xi,yi) oraz wyznaczamy wartość funkcji w punkcie pośrednim f(xi,yi)
następnie tworzymy sumę Sn=![]()
- czynności te powtarzamy wiele razy tworząc ciąg .... prostokąta P, taki , że średnica δn →0 jeśli n →0
Def. Jeśli ciąg sum całkowitych Sn ma tę samą granicę przy każdym normalnym podziale prostokąta P i jeżeli granica ta nie zależy od wyboru punktów pośrednich Ai to granicę tę nazywamy całką podwójną funkcji f(x,y) w prostokącie P i oznaczamy
ją :![]()
Czyli 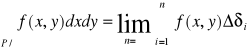
2 Całka podwójna w obszarze normalnym
Podział nazywamy normalnym jeżeli Δn → 0 gdy n → ∞
Def. Jeżeli dla każdego dowolnego normalnego ciągu podziału istnieje granica właściwa
![]()
![]()
Jeśli istnieje ta granica, to jest całką podwójną.
Tw. Z = f(x,y) jest całkowalne w P<=>kiedy f(x,y) będzie ciągła za wyjątkiem punktu zbieżnego do zera.
Def. Obszarem normalnym względem OX nazywamy obszar D spełniający nierówność
D: 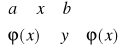
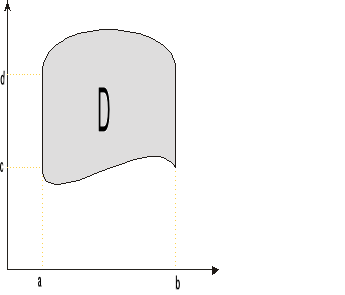
C = inf ϕ(x) d:sup ϕ(x)
x∈<a,b> x∈<a,b>
f (x,y) = 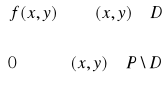
P: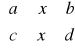
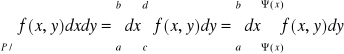
Def. Obszarem normalnym względem OY nazywamy obszar D spełniający warunek:
D: D: 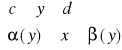
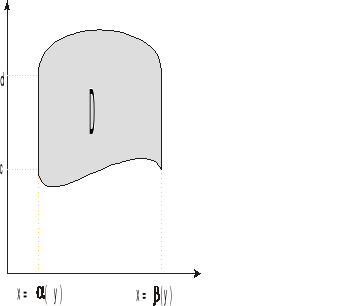
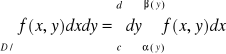
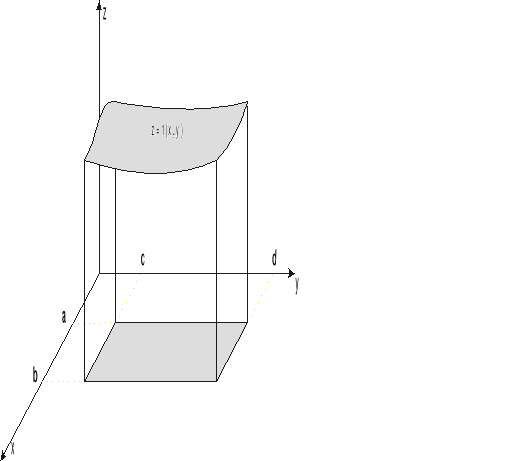
3 Interpretacja geometryczna całki podwójnych
Niech f(x,y) = k
![]()
f (x,y)≥0
![]()
P: 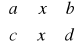
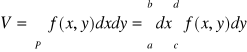
4. Interpretacja fizyczna całek podwójnych
D-regularny obszar
![]()
q (x,y)- jest to gęstość D
Moment statyczny:
![]()
-moment statyczny
względem OX
![]()
-moment statyczny
względem OY
![]()
![]()
Środek ciężkości P (x0,y0)
Moment bezwładności:
![]()
-względem OX
![]()
-względem OY
![]()
-względem OZ
5. Zmiana zmiennych w całce podwójnej
Jeżeli przekształcenie x=φ(u,v) y=ψ(u,v) odwzorowuje płaski domknięty obszar regularny ∆ w płaszczyźnie zmiennych (u,v) na obszar domknięty, regularny ∆ w płaszczyźnie zmiennych (x,y)oraz: 10 funkcje φ i ψ są klasy C1 w obszarze ∆ (ciągłe ,różniczkowalne). 20 Funkcja f jest ciągła w obszarze D. 30 Odwzorowanie wnętrz jest wzajemnie jednoznaczne. 40 Wyznacznik funkcyjny Jakobian jest różny od zera wewnątrz ∆.
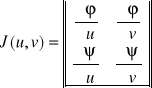
to:
![]()
Współrzędne biegunowe:
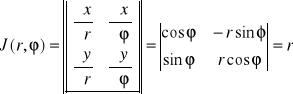
![]()
![]()
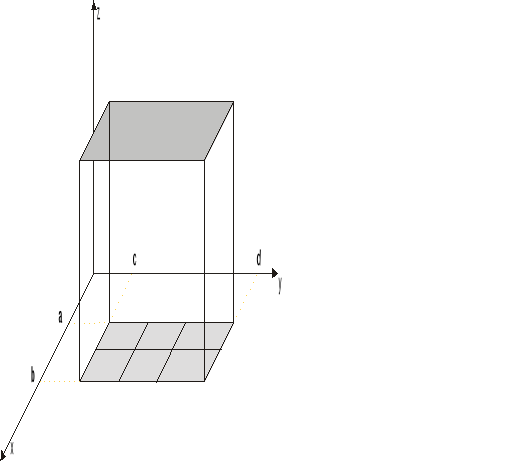
6. Całka potrójna. Interpretacja geometryczna (fizyczna)
![]()
Dany jest prostopadłościan P w przestrzeni Oxyz określony następująco :
oraz funkcja f(xyz) określona
tym prostopadłościanem:
10 Prostopadłościan ten dzielimy
na n prostopadłościanów Pi o
objętościach Vi tak by podział
był normalny tzn średnia podziału dąży do zera gdy n→∞. 20 W każdym prostopadłościanie Pi obieramy punkt pośredni Ai(xi,yi,zi) a następnie obliczamy wartość funkcji w punkcie pośrednim i tworzymy sumę całkową
![]()
Def.
Całka potrójna po prostopadłościanie-jeżeli ciąg sum całkowym Sn ma tą samą granicę przy każdym normalnym podziale prostopadłościanu P i jeżeli ta granica nie zależy od wyboru punktów pośrednich to granicę tę nazywamy całką potrójną funkcji F(x,y,z) i oznaczamy: ![]()
Interpretacja geometryczna całki potrójnej: ![]()
10 Jeżeli
V-objętość prostopadłościana
![]()
20 Jeżeli V jest objętością prostopadłościanu P, to liczbę f(c) gdzie cεP czyli:
nazywamy wartością
średnią funkcji f(x,y,z) w prostopadłościanie P.
Interpretacja fizyczna: -jeżeli u=u(x,y,z)-jest to gęstość objętościowa masy prostopadłościanu P to:
![]()
m-masa
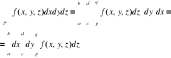
Obliczanie całki potrójej: kolejność całkowania jest dowolna
7. Obliczanie całki potrójnej
Własności całek potrójnych wykorzystane do ich obliczania: obszar całkowania wolno dzielić na części składowe, całka sumy funkcji jest równa sumie całek poszczególnych składników, czynnik stały wolno wytyczyć przed znak całki.
Tw: Jeżeli P: a≤x≤b; e≤y≤d; p≤z≤g to 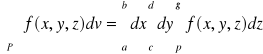
Całka iterowana
Ω: α1≤α≤α2; β1≤β≤β2; ν1≤ν≤ν2
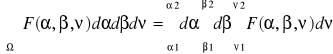
W całce iterowanej funkcja F(α,β,ν) jest najpierw całkowana względem ν, przy tym α i β traktuje się jako , następnie otrzymany wynik całkuje względem β, a α traktuje się jako . następnie otrzymany wynik całkuje się względem α.
8. Zmiana zmiennych w całce potrójnej
Tw: Jeżeli przekształcenie x=x(u,v,w) y=y(u,v,w) z=z(u,v,w) jest klasy C1 i wzajemnie jednoznaczne w obszarze Ω oraz jakobian
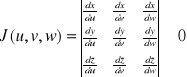
, to ![]()
![]()
W przypadku gdy obszar całkowania jest walcem, kulą lub częściom z tych brył wskazane jest zamienić współrzędne prostokątne na współrzędne walcowe:
x=rcosϕ r≥0 y=rsinϕ 0<ϕ≤2∏ z=z -∞<z<∞
Wzór na zamiane zmiennych we współrzędnych walcowych:
![]()

9. Całka krzywoliniowa nieskierowana
Dany jest na płaszczyźnie R2 łuk zwykły o końcach AB
L=AB o równaniach parametrycznych
l: x=x(t), y=y(t), t∈<t1,t2) łuk ten nie ma określonego kierunku.
1)Łuk dzielimy na części l1,l2,l3,…ln o długościach Δli gdzie i=1,2,…,n, łn=maxΔli - maksymalna długość łuków częściowych, jest to średnia podziału 1≤i≤n jeśli łn→0 przy n→∞ podział normalny.
2)Na każdym łuku obieramy punkt pośredni Pi(ξi,ni) oraz tworzymy wartość funkcji w tym punkcie.
3)Tworzymy sumę całkową dla punktów Pi=Sn=Σϕ(ξi,ni)Δl.
Def: Jeżeli dla każdego normalnego podziału łuku l granica ciągu sum całkowych Sn jest właściwa, niezależna od wyboru punktów pośrednich, to taką granicę nazywamy całką krzywoliniową nieskierowaną funkcji ϕ(x,y) po łuku l i oznaczamy
![]()
Obliczenie całki krzywoliniowej nieskierowanej:
1)Jeśli l∈R2 ma równanie parametryczne l: x=x(t); y=y(t); t∈<t1,t2> to 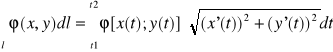
2)Jeśli l∈R3 : l:x=x(t); y=y(t); z=z(t) t∈<t1,t2> to 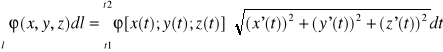
3)Jeżeli l dany jest równaniem y=f(x), x∈<a,b> 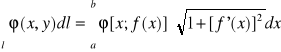
10 .Całka krzywoliniowa skierowana
Na płaszczyźnie RZ dany jest łuk zwykły skierowany o początku A i końcu B.![]()
t∈<t1,t2>
Na łuku tym określone są dwie funkcje P(x,y) oraz punkt Q(x,y). Na łuku tym budujemy funkcję. DEF.
Jeżeli dla każdego normalnego podziału łuku l ciąg sum całkowych Sn ma granicę niezależną od wyboru punktów pośrednich, to granicę tę nazywamy całką krzywoliniową skierowaną po łuku AB i oznaczamy:
![]()
Jeśli A=B, to całka określ. jest po krzywej zamkniętej K i oznaczamy ją: ![]()
Obliczanie całki skierowanej.
1. jeśli ![]()
t∈<t1,t2> to:
![]()
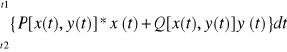
2. Jeśli y =f(x) x∈<a,b>
![]()
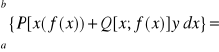
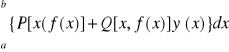
11 Twierdzenie Grenna i jego zastosowanie.
Obszar D normalny względem OX i OY.
Krzywa K=∂D
P(x,y) , Q(x,y) ∈ C1(D)- funkcja różniczkowalna w tym obszarze ;
to wtedy z tego wynika:
![]()
Przykład:
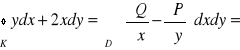
![]()
Q(x,y)=2x![]()
P(x,y) = y![]()
12. Całka różniczki zupełnej funkcji dwóch zmiennych.
P(x,y) Q(x,y) U(x,y) - funkcja dwóch zmiennych
∂u/dx=P(x,y) ∂u/dx=Q(x,y)
∂u = P(x,y) Q(x,y)dy
Jeżeli:
![]()
to: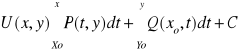
(x0,y0)=P
![]()
13) Szeregi liczbowe. Suma szeregu. Warunek konieczny zbieżności.
Sumę postaci a1+a2+...+an ,gdzie a1,a2,...an jest ciągiem liczbowym nazywamy szeregiem liczbowym i oznaczamy symbolem![]()
.
Wyraz an nazywamy wyrazem ogólnym szeregu. Liczby a1,a2,...an nazywamy wyrazami szeregu. SUMA SZEREGU-budujemy tkzw. ciąg sum częściowych: S1,S2,...,Sn, gdzie S1=a1, S2=a1+a2, Sn=a1+a2+...+an
Warunek konieczny zbieżności szeregu. Warunkiem dostatecznym i koniecznym zbieżności szeregu jest warunek istnienia granicy ciągu S1, S2, Sn gdy n→∞.
Jeżeli![]()
jest zbieżny to![]()
14.Szereg Dirichleta. Kryterium porównawcze.
1)Jeżeli dla każdego /\ n≥ no an ≤Mn i szereg
![]()
jest zbieżny, to![]()
jest też zbieżny.
2) Jeżeli /\ n≥ no an ≥Mn i szereg ![]()
jest rozbieżny, to![]()
jest też rozbieżny.
Dla porównynia szeregów stosuję się głównie szereg harmoniczny lub geometryczny.
Sz. harm. ![]()
α≤1 sz. rozbieżny ; α>1 zbieżny
Sz.geom.![]()
|q|<1 zbieżny ; |q|>1 rozb.
15.Szeregi o wyrazach nieujemnych .Kryterium d'Alamberta i kryterium Cauchy'ego.
1)Kryterium d'Alamberta . Jeśli istnieje granica
lim n![]()
![]()
an+1/an=q ,to szereg o wyrazach nieujemnych a) jest zbieżny gdy q<1 b)jest rozbieżny gdy q>1 c)gdy q=1 nie wiadomo.
2)Kryterium Cauchy'ego (pierwiastkowe).Jeśli istnieje granica lim n![]()
![]()
![]()
=q, to szereg o wyrazach nieujemnych zbudowany z ciągu ![]()
jest :a)zbieżny gdy q<1 b)q>1 rozbieżny
16)Szeregi o wyrazach dowolnych. Kryterium Leibniza.
Jeżeli wyrazy an w szeregu ![]()
(-1)n+1 an
spełniają następujące warunki:1)lim n→∞ an =0 2)an >= an+1 czyli an- an+1>=0 to szereg zbieżny
Rodzaje zbieżności szeregów o wyrazach dowolnych
1)Szereg ![]()
jest zbieżny bezwzględnie ,jeśli![]()
jest zbieżny
2)Jeśli ![]()
jest zbieżny, ale![]()
jest rozbieżny ,to szereg ![]()
jest zbieżny warunkowo
17. CIĄGI FUNKCYJNE. ZBIEŻNOŚĆ, JEDNOSTAJNA ZBIEŻNOŚĆ CIĄGU FUNKCYJNEGO.
Ciąg nieskończony którego wyrazami są funkcje określone w niepustym zbiorze liczbowym X , nazywamy ciągiem funkcyjnym, jest to ciąg: f1(x);f2(x);f3(x)...,fn(x)...
Ciąg funkcyjny może być zbieżny albo rozbieżny.
Jeżeli ciąg funkcji (fn) jest zbieżny dla każdej liczby x∈X to określa on pewną funkcję f na tym zbiorze.
Ciąg (fn) jest zbieżny w zbiorze X do funkcji granicznej f zapisujemy limn→∞fn(x) = f(x) dla x∈X
DEFINICJA.Ciąg funkcyjny (fn) nazywamy jednostajnie zbieżnym w zbiorze X do funkcji granicznej f, jeżeli dla każdego ![]()
>0 istnieje taki wskaźnik n0, że dla
każdego x∈X i dla każdego n>n0 jest spełniona nierówność ![]()
18. SZEREGI FUNKCYJNE. KRYTERIUM WEIERSTRASSA.
Szereg, którego wyrazami są funkcje
f1(x),f2(x) ... ,fn(x) czyli szereg postaci :
![]()
nazywany jest szeregiem funkcyjnym.
Kryterium Weierstrassa: Jeżeli istnieje ciąg (an) liczb dodatnich i taki wskaźnik n0 , że dla każdego naturalnego n>n0 spełniona jest nierówność |fn(x)| ≤ an
oraz szereg liczbowy ![]()
jest zbieżny, to
Szereg funkcyjny ![]()
jest zbieżny jednostajnie w zbiorze X.
19. CAŁKOWANIE (RÓŻNICZKOWANIE) SZEREGU FUNKCYJNEGO.
![]()
![]()
Twierdzenie o różniczkowaniu: jeśli szereg funkcyjny:
jest zbieżny w przedziale P i ponadto każda z funkcji fn jest w nim różniczkowalna, oraz szereg pochodnych:![]()
jest jednostajnie zbieżny w P, to funkcja:
jest różniczkowalna i zachodzi równość:
![]()
Twierdzenie o całkowaniu: jeśli szereg funkcyjny :
![]()
![]()
Jest jednostajnie zbieżny w przedziale P i ponadto każda z funkcji fn jest w nim całkowalna, to funkcja :
Jest całkowalna i zachodzi równość :
![]()
![]()
Szereg o wyrazach dodatnich (an>o), malejących an = f(n) jest zbieżny lub nie , w zależności od tego czy całka niewłaściwa
jest zbieżna lub nie. Gdzie f(x)- jest to malejąca funkcja ciągła
Kryterium to stosuje się wtedy , kiedy istnieje taka funkcja f(x), że jej wartość dla n naturalnych pokrywają się z wyrażeniami badanego szeregu, czyli an = f(n), a która jest określona dla wszystkich x większych od pewnej dodatniej liczby a.
20. Szeregi potęgowe. Promień zbieżności. Przedział zbieżności.
Wśród szeregów funkcyjnych na szczególną uwagę zasługują szeregi potęgowe - są to szeregi w postaci :
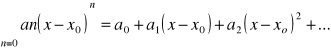
gdzie: x0 - środedek szeregu
a1, a2, a3,..., an - są to współczynniki szeregu.
Dla x0=0 mamy szeregi w postaci:
![]()
Promień zbieżności nazywamy liczbę Rrówną kresowi górnemu zbioru wszystkich x, dla którego szereg jest zbieżny. Przedział (-R;R) nazywamy przedziałem zbieżności szeregu. Możliwe są 3 przypadki:
1. R=0
2. 0<R<![]()
3. R=+![]()
Do wyznaczania promienia zbieżności stosujemy twierdzenie:
1. Jeśli istnieje granica: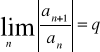
gdy q=![]()
to R=0
gdy0<R<![]()
to R=![]()
gdy q=0 to R=![]()
2. Jeżeli istnieje granica: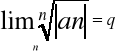
(tak jak wyżej)
21. Szereg Tailora. Rozwinięcie funkcji w szeregu Tailora.
Szereg Tailora to szereg w postaci:
![]()
![]()
np. Rozwinąć funkcję
![]()
![]()
w szereg Tailora
f(x0)=f(1)=3+5+1+2=11
f'(x0)=9x2+10x+1 f'(x0)=f'(1)=9+10+1=20
f''=(x)=18x+10 f''(x0)=f''(1)=18+10=28
f''(x)=18 f'''(x0)==f'''(1)=18
to
![]()
![]()
22.Szereg Maclaurina. Rozwinięcie w szereg Maclaurina funkcji elementarnych.
Gdy x0=0, to szereg Tailora można zapisać wzorem ![]()
Szereg ten nazywa się szeregiem Maclaurina
Rozwinięcia w szereg funkcji elementarnych:
1. ![]()
2.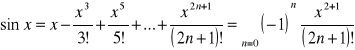
3.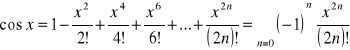
4.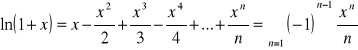
5.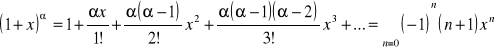
6.![]()
dla /q/<1
23) Ciągi i szeregi ortogonalne.
Szereg ortogonalny jest to szereg funkcyjny, w którym każde dwa wyrazy są funkcjami ortogalnymi, jest postać: ![]()
gdzie ciąg {fn} jest ortogonalnym układem funkcji, {an} jest ciągiem liczb rzeczywistych lub zespolonych. Szeregi ortogonalne stanowią uogólnienie szeregów trygonometrycznych. Jeżeli f(t) jest funkcją określoną na odcinku (a,b) to ![]()
w którym ![]()
nazywa się rozwiązaniem ortogonalnym funkcji.
24) Szereg Fouriera. Wzory Eulera-Fouriera
Szeregiem trygonometrycznym nazywamy szereg Fouriera postaci a0/2+(a1 cos Πx/l + b1 sin Πx/l)+(a2 cos 2Πx/l + b2 sin 2Πx/l)+... = a0/2 + ![]()
(an cos nΠx/l + bn sin nΠx/l) gdzie l>0 a0, a1, a2, b1, b2, bn, ... pewne stałe (n=1,2,...) gdzie an i bn oblicza się ze wzorów Fouriera an = 1/l ![]()
f(x) cos nΠx/l dx n=0,1,2,... bn=1/l![]()
f(x) sin nΠx/l dx n=0,1,2,...
25. Szereg trygonometryczny Fouriera
. y=f (x) w <a,b>
![]()
![]()
sz. Fouriera wzór Fouriera
{1,cosx,sinx,cos2x,sin2x,...,cosnx,sinnx,...}
Tw. Układ funkcji trygon. będzie ortogonalny
{1,cosx,sinx,...} jest ortogonalny w <-π,π>
całka tych funkcji będzie zero:
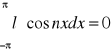
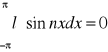
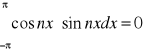
szereg trygon. Fouriera y=f(x) <-π,π> wzór ogólny:
![]()
![]()
![]()
![]()
wzory Eulera-Fouriera
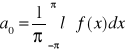
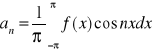
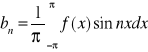
C0=2a0 C2n-1=an C2n=bn
Tw. Jeżeli szereg trygon. jednostajnie zbieżny w <-π,π> do f(x)=>
![]()
26) Warunki Dirichleta. Twierdzenie o rozwijalności w szereg trygonometryczny Fouriera.
Najprostsze warunki dostateczne rozwijalności funkcji w szereg Fouriera są podane w twierdzeniu Dirchleta. ,, Jeśli funkcja f(x) ma w przedziale <-l, l> skończoną ilość punktów nieciągłości pierwszego rodzaju ( lub jest ciągła) i ma w nim skończoną liczbę ekstremów (albo też nie ma ich wcale), to jej szereg Fouriera jest zbieżny, tzn. ma sumę S(x) w każdym punkcie tego przedziału. Przy tym: a) w punktach ciągłości funkcji f(x) szereg jest zbieżny do samej funkcji S(x)= f(x) b) w każdym punkcie nieciągłości funkcji szereg jest zbieżny do średniej arytmetycznej obu granic jednostronnych S(xk)=1/2 [lim x![]()
x- k f(x) + lim x![]()
x+k f(x)] c) na krańcach przedziału <-l, l> szereg jest zbieżny do średniej arytmetycznej jednostronnych granic funkcji , przy x zmierzającym do tych punktów od wewnątrz przedziału S(-l)= S(l)= 1/2 [ lim x![]()
-l f(x) + lim x![]()
l f(x)]
27. ROZWINIĘCIE W SZEREG TRYGONOMETRYCZNY FOURIERA FUNKCJI OKRESOWEJ.
![]()
szereg
Fouriera
1) Dla funkcji parzystej f(x) = f(-x) wszystkie współczynniki bn są równe zeru, to szereg Fouriera nie zawiera sinusów.
![]()
![]()
2) Dla funkcji nieparzystej f(x) = -f(-x) wszystkie współczynniki an są równe zeru i szereg Fouriera nie zawiera cosinusów
![]()
![]()
28. Postać zespolona szeregu trygon. Fouriera.Równość:
![]()
można zapisać w postaci zespolonej:
![]()
gdzie: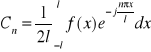
dla: n=0,±1,±2...
Równość w postaci zespolonej nazywamy równaniem funkcji f(x) na przedziale <-l,l > w zespolonym szeregu Fouriera. Jeżeli 2l jest okresem funkcji f(x), to wzór na Cn można zastąpić wzorem:
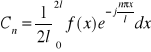
dla ![]()
29.Szereg dwumienny
mat. szereg potęgowy postaci
, gdzie a — dowolna liczba rzeczywista,
= a(a - 1)(a - 2) · ... · (a - k + 1)/k!;
1. Całka podwójna w prostokącie
2. Całka podwójna w obszarze normalnym
3. Interpretacja geometryczna całek podwójnych
4. Interpretacja fizyczna całek podwójnych
5. Zmiana zmiennych w całce podwójnej
6. Całka potrójna. Interpretacja geometryczna (fizyczna)
7. Obliczanie całki potrójnej. Całki iterowane
8. Zmiana zmiennych w całce potrójnej. Współrzędne
sferyczne i walcowe.
9. Całka krzywoliniowa nieskierowana. Obliczanie całki, interpretacja geometryczna.
10. Całka krzywoliniowa skierowana. Definicja , obliczanie
11. Twierdzenie Greena i jego zastosowania.
12. Całka różniczki zupełnej funkcji dwóch zmiennych.
13. Szeregi liczbowe. Suma szeregu. Warunek konieczny zbieżności.
14. Szereg Dirichleta. Kryterium porównawcze.
15. Szeregi o wyrazach ujemnych. Kryterium d`Alamberta. Kryterium Cauchy`ego
16. Szeregi o wyrazach dowolnych. Kryterium Lebniza.
17. Ciągi funkcyjne. Zbieżność, jednostajna zbieżność
ciągu funkcyjnego
18. Szeregi funkcyjne. Kryterium Weierstrassa.
19. Całkowanie (różniczkowanie) szeregu funkcyjnego.
20. Szeregi potęgowe. Promień zbieżności. Przedział
zbieżności.
21. Szereg Taylora. Rozwinięcie funkcji w szereg Taylora.
22. Szereg Maclaurina. Rozwinięcie w szereg Maclaurina funkcji elementarnych.
23. Ciągi i szeregi ortogonalne.
24. Szereg Fouriera. Wzory Eulera-Fouriera.
25. Szereg trygonometryczny Fouriera.
26. Warunki Dirichleta. Twierdzenie o rozwijalności w
szereg trygonometryczny Fouriera.
27. Rozwinięcie w szereg trygonometryczny Fouriera
funkcji okresowej
28. Postać zespolona szeregu trygonometrycznego Fouriera.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
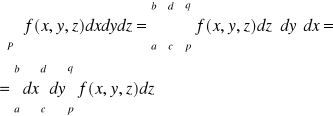
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
matmascigi, AGH Imir materiały mix, Studia
Zad 25 10 11, AGH Imir materiały mix, Studia
termo 1, AGH Imir materiały mix, Studia
sprawko M4, AGH Imir materiały mix, Studia
pnom sprawko, AGH Imir materiały mix, Studia
laborka-cw3 (1), AGH Imir materiały mix, Studia
Tob zagadnienia opracowane, AGH Imir materiały mix, Studia
sprawko M4 (1), AGH Imir materiały mix, Studia
ankietaONR, AGH Imir materiały mix, Studia
zestaw 1 - Kopia, AGH Imir materiały mix, Studia
Zad 15 11 11, AGH Imir materiały mix, Studia
Zad 6 03 12, AGH Imir materiały mix, Studia
Zad 6 12 11, AGH Imir materiały mix, Studia
p, AGH Imir materiały mix, Studia
pytanie 1, AGH Imir materiały mix, Studia
Zad 3 04 12, AGH Imir materiały mix, Studia
więcej podobnych podstron