Elementy optoelektroniki

Metody obliczania modów w światłowodzie wielomodowym.

Wykonał:

Rybicki Zbigniew

ED 8.3

1. Wstęp.

Instrumentem pozwalającym określić wiele istotnych parametrów łącza światłowodowego jest jego analiza modowa. Celem tej analizy jest określenie, w jaki sposób odbywa się propagacja fal własnych (modów) w światłowodzie. W jej rezultacie możliwa jest ocena toru światłowodowego pod kątem przepustowości informacji (pasma).

Punktem wyjścia analizy są uogólnione równania falowe w postaci wektorowej:

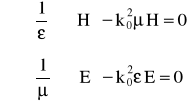
(1)

gdzie k₀=
oznacza wektor falowy,
oznaczają wektory pola odpowiednio magnetycznego i elektrycznego,ε i μ tensory przenikalności odpowiednio elektrycznej i magnetycznej.

Rozwiązanie równań falowych w takiej postaci jest bardzo żmudne i w praktyce rzadko stosowane. Jeśli mamy do czynienia z ośrodkiem izotropowym tzn.μ=1, równanie (1) przyjmuje postać:

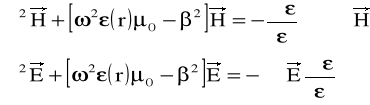
Na podstawie równań (2) można wyznaczyć mody TM i TE (Transverse Magnetic , Transverse Elektric ) z uwzględnieniem ich polaryzacji. W przypadku światłowodów, tzw. „słabo prowadzących”( weakly guiding), dla których względna różnica współczynnika załamania płaszcza i rdzenia Δ jest mała (Δ<<1), można pominąć polaryzację modów. Równanie falowe będzie wtedy miało postać:

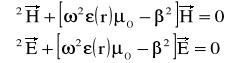
Gdzie: β- stała propagacji

β=ω²με

2. Metody obliczania modów w światłowodzie wielomodowym.

1. Metody oparte o rozwinięcie w szereg ( Power -Series Exspansion Method).

2. Metoda elementów skończonych (Finite Element Method)

3. Metoda aproksymacji schodkowej (Staircase-approximation Method)

4. Metoda Rayleigha-Ritza

5. Metody przybliżone bazujące na rozdzieleniu zmiennych (WKB Method)

Metody oparte o rozwinięcie w szereg .

Jest to metoda wykorzystująca rozwinięcie równania falowego w szereg funkcji ortonormalnych. Wybór szeregu funkcyjnego ściśle zależy od struktury konkretnie rozpatrywanego światłowodu.

Zakładając wskaźnik profilu:

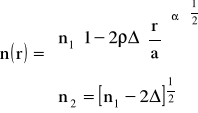
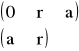
(4)

gdzie:

α- parametr profilu

1. promień rdzenia

n₁ ,n₂ -współczynniki załamania światła odpowiednio: wzdłuż osi rdzenia i w płaszczu

Δ- względny współczynnik załamania światłowodu

W początkowej fazie analizy określone zostają mody propagacji. O tym czy dany mod jest modem propagacji, decyduje częstotliwość odcięcia ν. Jeśli jest ona mniejsza od efektywnej częstotliwości znormalizowanej światłowodu gradientowego ν_eff , oznacza to że dany mod jest modem propagacji.

Wychodząc z równania falowego dla światłowodu o profilu kołowym:

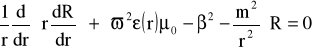
(5)

określając wielkość:

uzyskujemy:

(6)

Zakładając że w rdzeniu
otrzymujemy:

(7)

gdzie:

R- funkcja falowa,

x- promień znormalizowany

m- azymutalna liczba modowa

znormalizowana poprzeczna stała fazowa w obszarze rdzenia.

Z ciągłości R i
dla x=1 otrzymujemy:

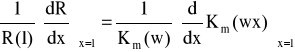
Właściwe równanie ma postać:

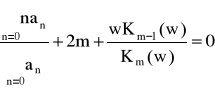
Jest to równanie dyspersji .

W warunkach odcięcia ( gdzie: u=ν=
, w=0; u -znormalizowana poprzeczna stała fazowa w obszarze rdzenia, w -znormalizowana poprzeczna stała tłumienia w obszarze płaszcza), rozwinięcie skalarnego równania falowego (6) przybiera postać.

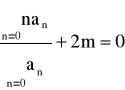
(8)

przy czym:

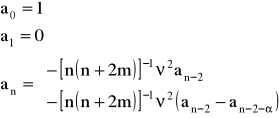
Kolejne l-te rozwiązanie powyższego równania (m = const) stanowi częstotliwość odcięcia modu LP_m.l.

W następnym kroku oblicza się czasy propagacji wszystkich modów dla jednostkowej długości światłowodu.

W końcowym efekcie wyznaczona zostaje odpowiedz toru światłowodu przy pobudzeniu impulsem gaussowskim, a w rezultacie maksymalną częstotliwość f_max zmodulowanego amplitudowo sygnału przenoszonego przez łącze.

Metoda elementów skończonych.

Polega ona na podzieleniu przekroju światłowodu na skończoną liczbę elementów. Pole elektromagnetyczne w obrębie każdego elementu jest wyrażone za pomocą zbioru wielomianów o współczynnikach określonych przez wartość natężenia pola w węzłach elementu.

Po podstawieniu do funkcjonału dla równania falowego i przyrównania wariancji tego funkcjonału do zera, otrzymamy równanie macierzowe, po rozwiązaniu którego znajdujemy wartość pola elektromagnetycznego w węzłach.

Wychodząc z równania :

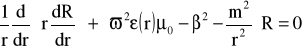
(9)

Wprowadzając do powyższego równania następujące zależności :

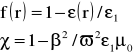
dla modów TM

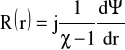
dla modów TE

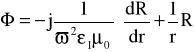
Otrzymujemy równania falowe w następującej postaci:

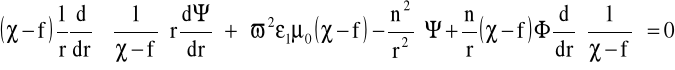
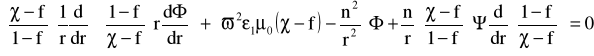
Tworzymy równanie wariacyjne( zachowując warunki graniczne ciągłość E_z, H_z, E_r, H_r, E_Θ, H_Θ , na granicy rdzeń -płaszcz r = a):

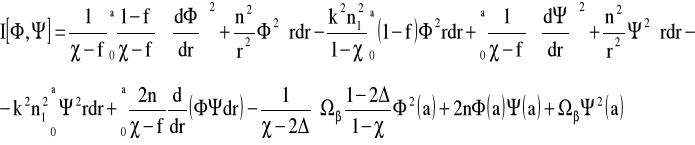
gdzie:

K_n -oznacza n-ty rząd zmodyfikowanej funkcji Bessela drugiego rzędu.

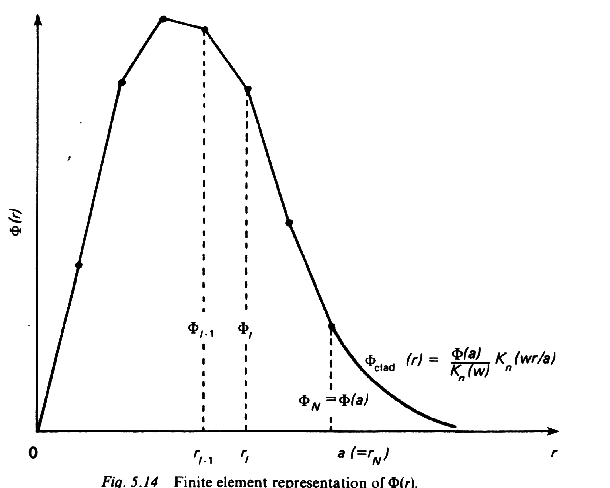
W celu rozwiązania powyższego równania stosuje się metodę elementów skończonych. Najpierw dzielimy obszar pomiędzy r=0 i r = a na N elementów i wyrażamy wartości Φ(r) i ψ(r) dla r = r_l jako:

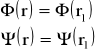
l=0,1,2,...,N

Dzielenie na N elementów jest po to aby r_p pokrywało się z r_l ,w każdym z tych elementów funkcje Φ(r) i ψ(r) są wyrażone jako:

Φ(r)= Φ_l-1F_l-1(r) +Φ_lF_l(r) (10)

ψ (r)= ψ_l-1F_l-1(r) +ψ_lF_l(r) (11)

gdzie:

F_l-1(r) i F_l(r) są ciągłymi funkcjami r spełniającymi warunki:

F_l-1(r_l-1) =1, F_l-1(r_l) = 0 (12)

F_l (r_l-1) = 0, F_l(r_l) =1 (13)

W tych elementach które nie zawierają pojedynczego punktu (r=r_p) funkcja F_l(r) jest zaproksymowana. przez liniową funkcję jak na powyższym rysunku. W elementach zawierających r_p , Φ(r) i ψ(r) są zaproksymowane , aby uniknąć rozbieżności .

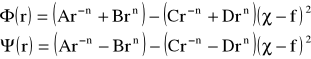
(14)

gdzie: n jest numerem modu azymutalnego, składniki A, B, C, D są tak dobrane aby Φ(r) i ψ(r) odpowiadały Φ_p i ψ_p w punkcie r=r_p oraz Φ_p-1 i ψ_p-1 w punkcie r=r_p-1 .

Podstawiając równania (12)÷(14) do równania

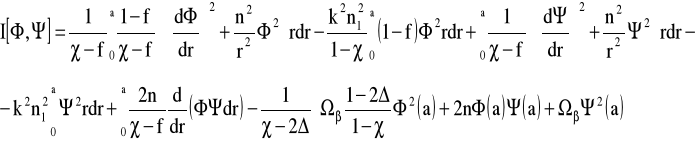
i uwzględniając warunki stacjonarne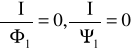
uzyskujemy równanie macierzowe w następującej formie

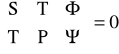
(15)

gdzie: Φ= [Φ₀, Φ₁,..., Φ_N]^T (T- oznacza transponowanie) ,Ψ=[ Ψ₀, Ψ₁,... ,Ψ_N]^T, oraz S, T, P są (N+1)*(N+1) macierzami którego elementy są przestrzennymi ograniczeniami tylko kilku typowych elementów.

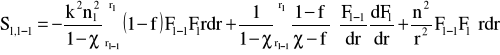
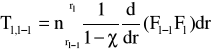
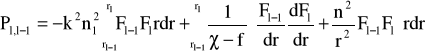
Rozwiązanie równania (15):

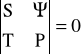
(16)

Jest to równanie dokładnie odpowiadające równaniu które określa stałe propagacji niejednorodnych światłowodów.

Metoda elementów skończonych wymaga dużej mocy obliczeniowej i stosowana jest w przypadku światłowodów anizotropowych o zadanym z góry profilu współczynnika załamania.

Metoda aproksymacji schodkowej.

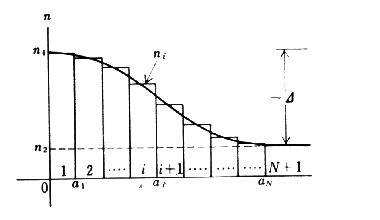
W metodzie tej współczynnik załamania jest zaproksymowany odpowiednią funkcją skokową jak na poniższym rysunku. Równanie fali (tak skalarnej jak i wektorowej) jest rozwiązane w każdym przedziale , rozwiązania są połączone granicami cylindrycznymi pomiędzy tymi przedziałami dla osiągnięcia odpowiednich równań i otrzymania charakterystyk propagacji.

W każdym przedziale przyjmujemy, że współczynnik załamania jest stały.

Rys.1 Aproksymacja współczynnika załamania funkcją schodkową

Wychodząc z równań Maxwella możemy otrzymać proste równania fali dla składowych pola elektrycznego.

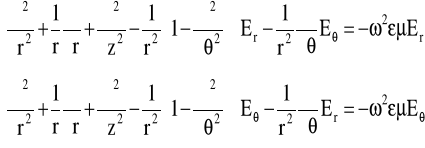
(17)

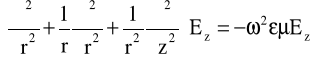
Na początku rozważamy składowe poprzeczne pola elektrycznego. W równaniach (17) zamiast E_r i E_Θ stosujemy kołowo spolaryzowane składowe

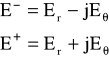
(18)

Podstawiając za
i stosując nowe zmienne (18) możemy uprościć równania (17) do następującej postaci:

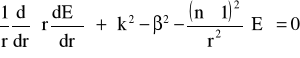
(19)

Dla składowych osiowych najpierw definiujemy parametr Z₀=ωμ/β określający impedancję falową a następnie określamy nowe zmienne w zależności od składowych pola elektrycznego i magnetycznego.

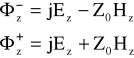
(20)

Z równania (17a) nawiązując do pola magnetycznego otrzymujemy.

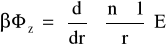
(21)

Postępując analogicznie jak dla składowych poprzecznych pola elektrycznego dla składowych poprzecznych pola magnetycznego otrzymujemy.

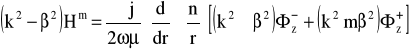
(22)

Po podstawieniu rozwiązania równania (19) do równania (21) i zróżniczkowaniu otrzymuje się zależność dla Φ^±.

Można zatem zapisać że:

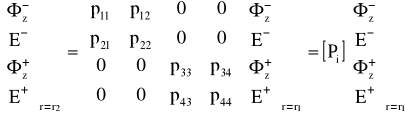
(23)

W tej postaci elementy macierzy są dane jako funkcja transcendentalna zmiennych r₁ i r₂, które są różne dla dwóch przypadków (β<kn_i i β>kn_i), gdzie n_i oznacza współczynnik załamania w i-tej warstwie. Macierz P_i jest nazwana macierzą propagacji i-tej warstwy.

Zmiana pola elektromagnetycznego na granicy pomiędzy i-tą i (i+1) warstwą jest przedstawiona w następujący sposób.

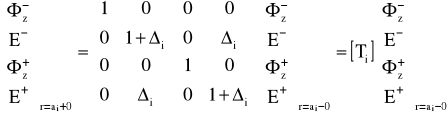
(24)

gdzie:

T_i- macierz granic

Używając P_i i T_i dla każdej warstwy możemy określić pola elektromagnetyczne na zewnętrznej powierzchni pierwszej warstwy i na wewnętrznej powierzchni warstwy (N+1) według zależności.

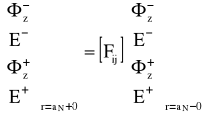
(25)

gdzie: [F_ij]=T_N(P_N-1T_N-1)…(P₁T₁) (25a)

Pole w warstwie pierwszej i ostatniej można wyrazić odpowiednio wzorami:

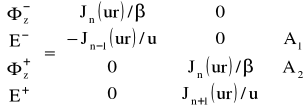
dla r<a₁ (26)

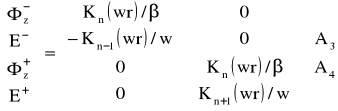
dla a_N <r (27)

gdzie A₁, A₂, A₃, A₄ są stałymi a

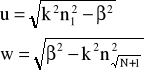
oznaczają współczynniki załamania w warstwie pierwszej i warstwie N+1

Podstawiając równania (25a)÷(27)do równania (25) możemy otrzymać równanie w postaci f(ω,β)=0 które jest równaniem dyspersji przedstawiającej charakterystyki propagacji.

O dokładności metody decyduje liczba rozpatrywanych warstw. Od ilości rozpatrywanych warstw zależy długość czasu obliczeń. Ponieważ czas obliczeń jest długi dla dużej liczby obliczeń musimy pójść na kompromis, wybierając między czasem obliczeń a dokładnością.

Metoda redukcji czasu obliczeń zakłada Δ_i<<1 i przybliża T_i do postaci T_i^''.

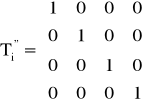
Przyjmując że P_i wyrażone równaniem:

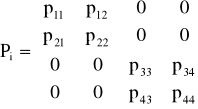
może być podzielone na dwie macierze (każda 2x2), oraz T_i może być podzielone na dwie macierze (2x2), to równanie:

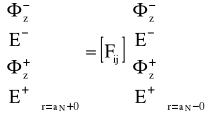
też może być podzielone na dwa niezależne równania:

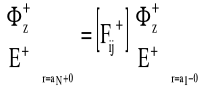
(28)

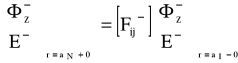
(29)

prowadzą do dwóch niezależnych równań dyspersji zmniejszając czas obliczeń.

Rozwiązanie wynikające z równania (28) nawiązują do modów HE, podczas gdy rozwiązanie równania (29) nawiązuje do modów EH, TE, TM.

Metoda Reyleigha -Ritza.

Podstawowe określenia:

1. Ilość zdeterminowanych przez kształt funkcji f(x) zdefiniowanych w danym zakresie zmiennej niezależnej x jest nazwana funkcjonałem (funkcja funkcji)

2. Równanie różniczkowe dające warunki do utworzenia stacjonarnego funkcjonału jest nazwana wzorem Eulera dla funkcjonału.

3. Kiedy rozwiązujemy równanie różniczkowe przez użycie tej metody najpierw znajdujemy funkcjonał dla którego równanie Eulera jest danym równaniem różniczkowym , a następnie znajdujemy warunek stacjonarny funkcjonału.

Wychodząc ze wzorów opisujących pole w światłowodzie:

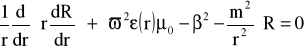
(30)

(31)

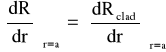
(32)

Rozwiązaniem równania różniczkowego (30) dla warunków granicznych (31) i (32) jest równanie funkcjonału :

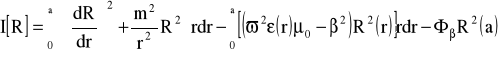
(33)

gdzie Φ_β jest zdefiniowane jako:

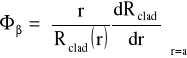
(34)

Przyjmujemy, że gdy R(r) przybiera właściwą formę , równanie (33) staje się stacjonarne dla warunku (31) , (32) i oznaczamy to wyrażenie przez R₀(r).

Następnie używając arbitralnej funkcji η(r)

Możemy zapisać:

(35)

a następnie wstawiamy do równania (33).Wtedy I[R_δ] jest funkcją δ. Według definicji R₀, I[R_δ] jest stacjonarne dla δ=0, dlatego :

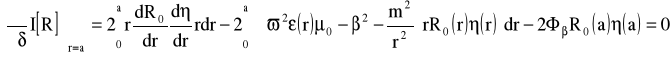
Całkując powyższe wyrażenie i używając równania (34) otrzymujemy:

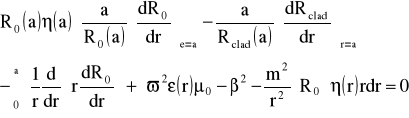
(36)

Jako, że η(r) jest arbitralną funkcją r wyrażenie w nawiasie klamrowym musi się równać zero.

Jedną z metod rozwiązywania tego problemu jest metoda Rayleigh -Ritz. W tej metodzie funkcja zdeterminowana przypadku R(r) jest najpierw używana przez serie funkcji ortogonalnych.

Zauważamy, że dla funkcji ( transverse) w obszarze płaszcza równanie dla R_clad(r) jest podobne do równania (30) (ale ε(r) zastąpione jest ε₂).

Skoro (ω²ε₂μ₀-β²)<0 , rozwiązanie w płaszczu jest dane w postaci.

(37)

gdzie K_m oznacza zmodyfikowaną funkcje Bessela drugiego rzędu n-tego stopnia, w- jest znormalizowanym numerem fali poprzecznej w obszarze płaszcza.

Z równań (34) i (37)

(38)

gdzie prim oznacza różniczkowanie funkcji Bessela względem w.

Następnie wprowadzamy funkcje ortogonalne
w celu rozszerzenia R(r). W tym wyrażeniu λ_k jest k-tym źródłem, J_m zmodyfikowana funkcja Bessela pierwszego rodzaju rzędu m.

Równanie które mamy uzyskać jest rozszerzone przez użycie funkcji F_mk(r) w następujący sposób:

(39)

gdzie C_k są stałymi które należy określić ze wzoru Bessela.

Następnie wyznaczamy warunki graniczne . Różniczkując wyrażenie (39) i używając równań

i
uzyskujemy:

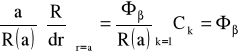
(40)

aby warunek graniczny był satysfakcjonujący.

Podstawiając równanie (39) do równania (33) oraz używając równania

i funkcji Bessela uzyskujemy:

(41)

gdzie:

l-numer funkcji ortogonalnej

(42)

Aby rozwiązanie R(r) dawało stacjonarny funkcjonał częściowe wyprowadzenie I[C₁,C₂,..] w zależności od wszystkich C_k musi być równe zero tj.

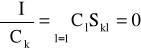
(k=1, 2, ...) (43)

gdzie:

Postać równań liniowych homogenicznych danych przez równanie (43) ma nietrywialnie rozwiązania dla C_l jedynie gdy macierz {S_kl} jest pojedyncza tj.

det{S_kl} =0 (44)

To równanie zawiera zmienne u , υ i w. Jednakże w jest związane z u i υ równaniem, podczas gdy u i υ determinuje stałą propagacji β. Stąd równanie (44) daje związek pomiędzy β i υ tj. związek dyspersji włókna światłowodowego mającego arbitralny profil wskaźnika refrakcji.

Metoda WKB.

Metodę WKB można stosować do rozwiązania równania skalarnego

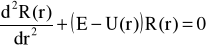
(45)

gdzie:

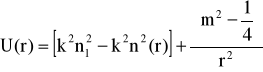
w którym: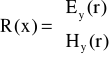
dla modów TE i TM

gdy n(r) jest funkcją wolnozmienną.

W powyższych równaniach k=ω
, n₁ -maksymalnym współczynnikiem załamania, k²n²₁ jest dodane do obydwu równań aby E i U(r) były dodatnie.

Przyjmując profil współczynnika załamania jako: n²(r)=n²₁{1-f(r)}, przy czym

n₁-jest współczynnikiem załamania w osi.

W obszarze oscylacyjnym gdzie E- U(r)>0 równanie (45) przybiera postać:

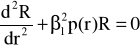
(46)

gdzie:

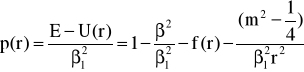
(46a)

w tych równaniach, β₁ oznacza stałą propagacji fali płaskiej rozprzestrzeniającej się w ośrodku o współczynniku załamania n₁.

W obszarze gdzie E- U(r)<0 równanie (45) przybiera postać:

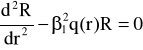
(47)

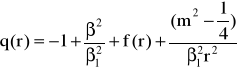
gdzie:

Korzystając z przybliżenia WKB rozwiązanie równania (46)będzie miało postać

Dla r₁< r <r₂

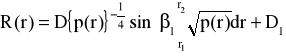
(48)

Korzystając z przybliżenia WKB rozwiązanie równania (47)będzie miało postać

Dla r<r₁

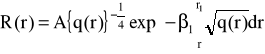
(49)

Dla r₂<r

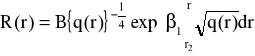
(50)

gdzie: A, B, D i D₁ nieznane stałe

Z warunku p(r)=0 otrzymuje się tzw. punkty zwrotne r₁ i r₂. W punktach r₁ i r₂ mamy jak gdyby całkowite odbicie. Funkcja R(r) reprezentuje zmiany pola wzdłuż r.

Rozważmy najpierw punkt zwroty r=r₁. Gdy p(r) jest funkcją wolno zmienną, w okolicach punktu zwrotnego R₁ możemy napisać p(r)=k(r-r₁), gdzie k-stała . Taki punkt nazywa się punktem zwrotnym pierwszego rodzaju. W takim przypadku rozwiązanie równania (46) będzie miało postać:

Dla r
r₁

(51)

gdzie: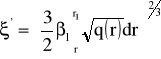

dla r₁
r

(52)

gdzie: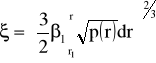
.

Dla punktu zwrotnego r=r₂, rozwiązanie równania (46) będzie miało postać:

Dla r
r₂

(53)

gdzie: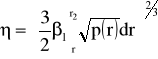

Dla r₂
r

(54)

gdzie: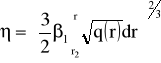

B, C, E, F nieznane stałe , Ai i Bi są funkcjami transcendentalnymi zwanymi funkcjami Airy

Uzyskaliśmy siedem rozwiązań równania (46) dla punktów zwrotnych r₁ i r₂ , zawierających osiem stałych A, B, D, D₁,E, F, G.

Żeby określić stałe musimy połączyć te rozwiązania w punktach zwrotnych używając asymptotycznych rozwiązań funkcji Airy.

Dla |z| >> 1 funkcje Airy są zaproksymowane w następujący sposób:

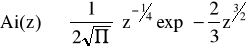
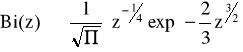
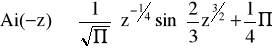
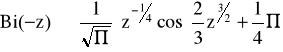
Podstawiając do rozwiązań dla punktów zwrotnych otrzymamy następujące związki pomiędzy nieznanymi stałymi:

;
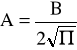
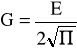
; C=0 ; F=0 ;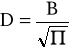
;

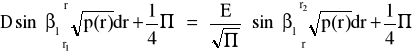
(55)

Aby powyższe równanie miało rozwiązanie dla jakiegokolwiek r :

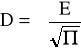
Wówczas otrzymujemy.

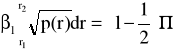
(56)

gdzie: l- jest liczbą całkowitą

Podstawiając za zmienną p(r) w równaniu (56) wyrażenie (46a) otrzymujemy:

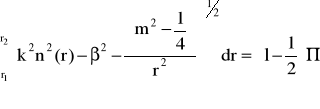
(57)

Jeżeli założymy m>>1 i l>>1 możemy przybliżyć równanie (57) do następującej postaci:

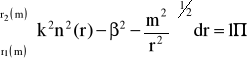
(58)

Jest to równanie charakterystyczne wyprowadzone przy zastosowaniu metody WKB. Umożliwia ono wyznaczenie stałych propagacji modu LP_ml jeśli jest znany rozkład współczynnika załamania.

Maksymalny numer modu radialnego wyraża się wzorem:

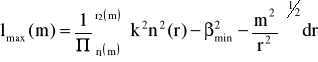
(59)

gdzie β_min - minimalna stała propagacji związana z danym m

Z równania (59) wynika że l_max(m) modów może propagować dla każdego l=1,2,.., l_{max .} Im większy jest numer modu rotacyjnego m ,tym mniejsze maksimum modu radialnego l_max(m)

Z poniższego rysunku wynika ,że E zmniejsza się gdy β wzrasta . β maleje dla większych m (gdy l = const.) i dla większych l ( gdy m = const.). Maksymalna stała propagacji β_max występuje dla m=0 i l=1. Minimalna stała propagacji β_min jest zależna od warunku odcięcia β_min=kn₂.

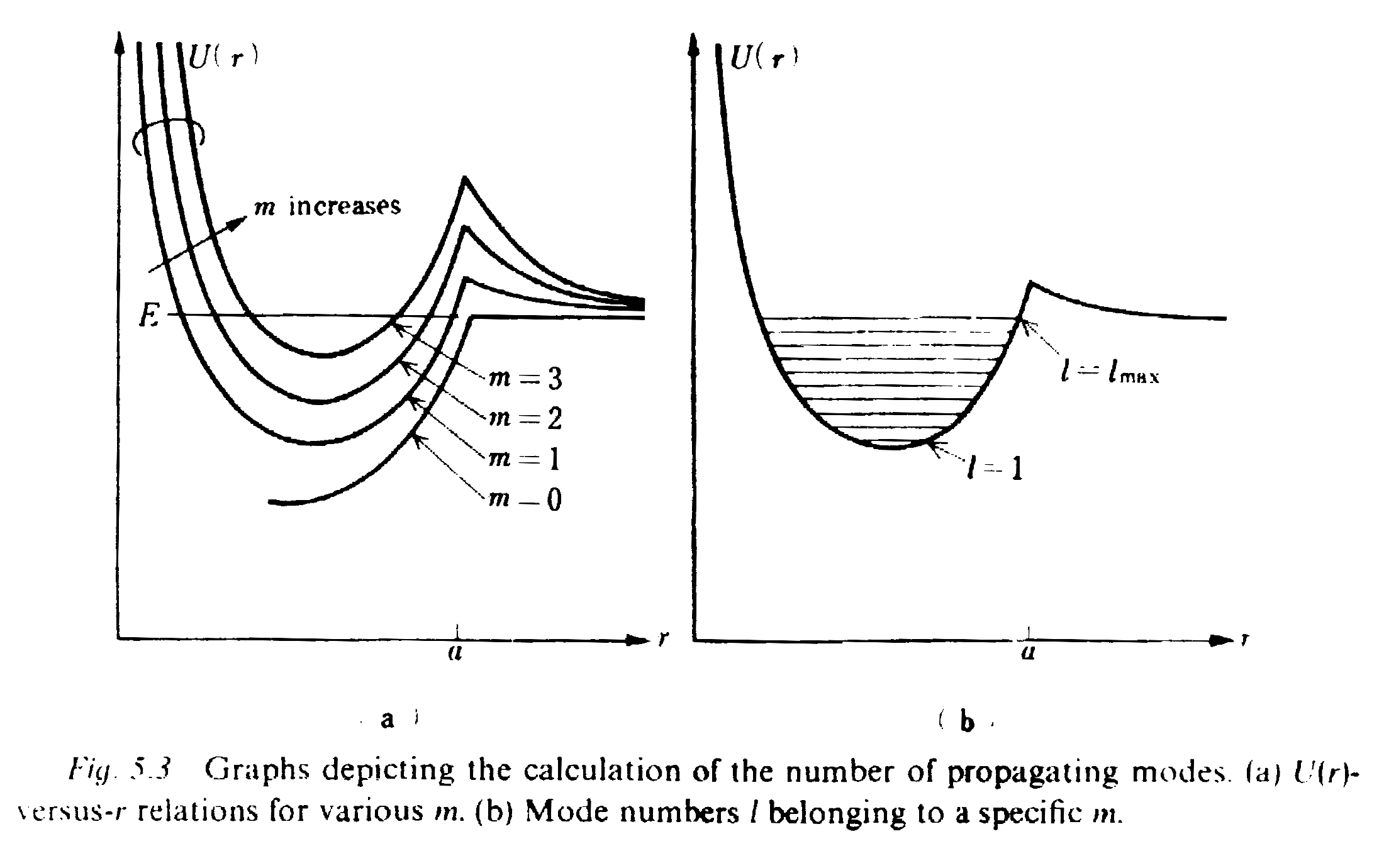
Przybliżenie WKB.

Rozważmy jednowymiarowe równanie :

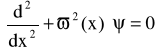
(60)

Niech rozwiązaniem tego równania będzie funkcja

(61)

Po podstawieniu jej do równania (60)otrzymamy:

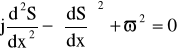
(62)

Jeżeli przyjmiemy , ze S(x) jest wolno zmienną funkcją x, to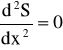
i wtedy mamy pierwsze przybliżenie dla S, a mianowicie
lub
.

Kolejne przybliżenie mamy, gdy równanie (62) zapiszemy w postaci:
, przybliżenie n+1 jako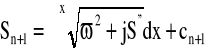
zatem dla n=0 mamy, że

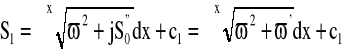
Rozwijając w szereg wyrażenie podcałkowe otrzymamy, że:

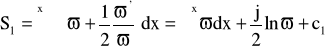
Przybliżenie WKB prowadzi do przybliżonego rozwiązania równania (60) w postaci:

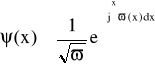
Literatura.

1. Okoshi T.: Optikal Fabers, Academic Press, New York 1982

2. Majewski A.: Teoria i projektowanie światłowodów, WNT Warszawa 1991

14

11

(2)

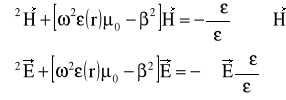
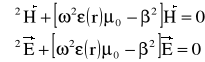
(3)

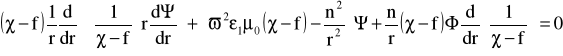
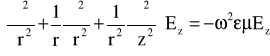
(17a)

---