Rachunek błędu

1.Wykaz:niepewność sumy wielkości:q=x+y δ
δ_x+δ_y

x=x_np
δ_x

y=y_np
δ_y wartości największe: x_max=x_np+δ_x y_max=y_np+δ_y ;q=x+y ;q_np=x_np+y_np

q_max=x_np+δy+y_np+δ_y Wartości minimalne: x_min=x_np-δ_x ;y_min=y_np-δ_y ;q_mmin=x_np-δy+y_np-δ_y

q_min=x_np+y_np
(δ_x+δ_y); q_np=x_np+y_np ;q_np=x_np+y_np ;q=q_np
(δ_x+δ_y) ; δδ_x+δ_y

Wykaż:niepewność ilorazu

jest =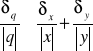

(zmierzona war. X)=x_np
δ_x

(niepewność względna x)

(wartość x)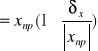

(wartość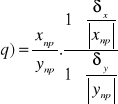

wartość max gdy mianownik najwiekszy a licznik najmniejszy,min. -odwrotnie

MAX: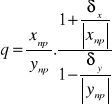
ostatni czynnik ma w wyrażeniu formę(1+a)/(1-b),gdzieaib są małe(dużomniejsze niż1) Można je uprościć stosując dwa przybliżenia.Po pierwsze,ponieważ b jest małe , więc zgodnie z twierdzeniem o dwumianie newtona

Zatem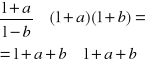

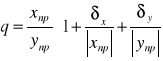
MIN: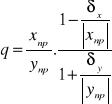
ostatni czynnik ma postać (1-a)/(1+b) gdzie a i b są mniejsze od 1

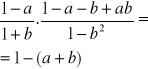
ab i b²-pomijalnie małe

nie wiem

(wartość

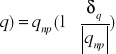
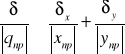
2.Wykaż: niepewność różnicy q=x-y ; q_np=x_np-y_{np ;}x=x_np
δ_x ;y=y_np
δ_y

q_max=x_max-y_min ;q_max=(x_np+δ_x)-(y_np-δ_y)

q_min=x_min-y_{max ;}q_min= (x_np-δ_x)-(y_np+δ_y)

q=x_np-y_np
(δ_x+δ_y) q=q_np
δ_q δ_q
δ_x+δ_y

b) niep.względna iloczynu q=x*y ; x_np
δ_{x ;}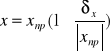

y=y_np
δ_y ;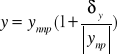
; q=x*y ; q_np=x_np*y_np

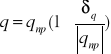
; q_max=x_max*y_max ; q_min=x_min*y_min

q_max=x_np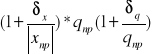
; q_max=x_np*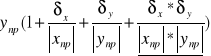

podkreślone jest pomijalnie małe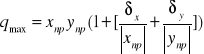

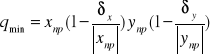
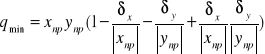
pomijalnie małe

;
;

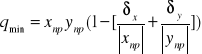
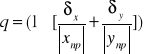
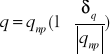
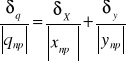
3.Omów niepewność wartości dowolnej funkcji jednej korzystając z wykresu zmiennej

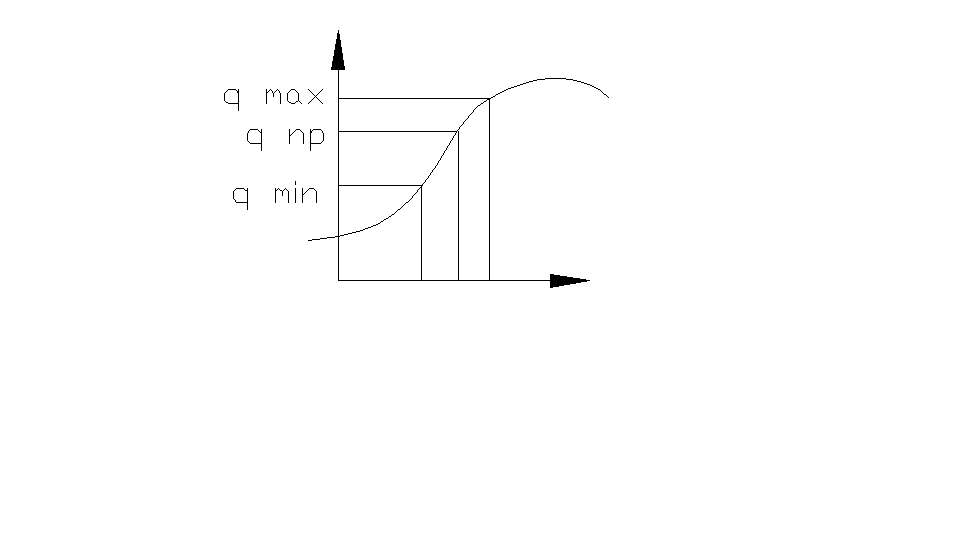
Jeśli niepewność δ_x jest mała(jak zawsze zakładamy) to interesujaca część wykresu funkcji jest w przybliżeniu prostą iłatwo przekonać się,że q_max i q_min są jednakowo oddalone od g_np.Niepewność δ_q można zatem odczytać z wykresu jako jedną z tych odległości.W ten sposób możemy zapisać q w standardowej formie:

q_np
δ_q

analitycznie:δ_q=q(x_np+δ_x)-q(x_np)

u-dostatecznie mały przedział

q(x+u)-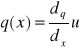

Zatem:jeśli δ_x jest mała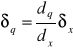

Jeśli funkcja jest malejąca to otrzymamy wynik: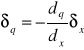

_,aby się pozbyć minusa ostateczna postać

4.Omów niepewność wartości funkcji wielu zmiennych.Kiedy stosujemy Różniczkę zupełną.

Przenoszenie krok po kroku korzystając ze wzorów na błąd sumy,różnicy oraz iloczynu i ilorazu.Różniczka zupełna: np.

(jeżeli krok po kroku,przeszacujemy:ponieważ niepewność x z licznika `znosi' się z niepewnością z mianownika).Zawsze gdy w funkcji,ta sama wielkość występuje więcej niż raz,jak w przykladzie, niektóre z niepewności mogą się znosić(efekt ten zwany jest czasem:kompensacją blędu).Może się wówczas zdarzyć,że obliczenia metodą kolejnych kroków spowodują przeszacowanie ostatecznej niepewności.Jednym sposobem, aby tego uniknąć , jest obliczenie niepewności w jednym kroku,korzystając z metody różniczki zupełnej np.

Bląd bezwzględny

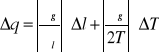
błąd względny:

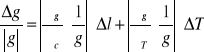
Ogólna regóła przenoszenia błędów:funcja g(x,y)

q_np=q(x_np,y_np) u:-dowolnie małe przyrosty xi y.ekstremalne wartości q są równe q(x_np
δ_x;y_np
δ_y)czyli w przybliżeniu:q(x +u,y+)=q(x,y)+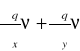

Musimy wprowadzić wartości bezwzględne ponieważ wyrażenia:

i
mogą być zarówno dodatnie jak i ujemne. Q=q(x_np,y_np)

;

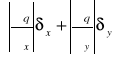
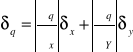
Załóżmy,że wielkości x,...,z zmierzone z niepewnościami δ_x.....δ_y do obliczenia wartości funkcjiq(x.....,z)

Jeżeli niepewności wyznaczenia wielkościx,...,z są niezależne i przypadkowe,to niepewność wyznaczenia wartości funkcji q równa jest:

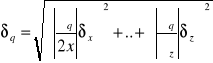
W żadnym jednak wypadku nie jest większa niż zwykła suma: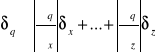

5.Przedstaw na wykresie i omów funkcję rozkładu normalnego:Błędy systematyczne ograniczone do zaniedbywalnego poziomu.Wartość prawdziwa-można ją sobie wyobrazić jak tę wartość, do której zbliżamy się coraz bardziej,wykonując coraz więcej pomiarów, z coraz wiekszą dokładnością.Jeżeli błędy systematyczne są zaniedbywalne, to odpowiadający rozkład będzie miał kształt krzywej dzwonowej wyśrodkowanej wokół wartości prawdziwej x . Funkcja matematyczna,która opisuje krzywą dzwonową,nosi nazwę funkcji: rozkladunormalnego lub funkcji Gaussa: ma postać:
gdzie δ-ustalona wartość nazywana szerokością rozkładu,krzywa dzwonowa jest szersza dla dużych wartości δ;a węższa dla małych wartości δ .Aby funkcja Gaussa była wyśrodkowana wokół x=X,a niex=0 należy we wzorze x zastapić przezx-X.

e
Funkcja ma maximum W punkcie x=X:maleje symetrycznie po obu stronach x=X;Aby rozkład graniczny,był znormalizowany(co jest wymagane) musi spełniać warunek

Zmieniając w tym kierunku zapiszemy funkcję w postaci f(x)=N

N-współczynnik normalizacji

(x-X=y dy=dx)

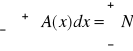
dx=n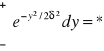

dy= δdz *=Nδ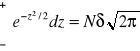

Ponieważ całka ma być równa jedności to:

Ostatecznie: rozkład Gaussa(rozkład normalny)-(x^δ^

G x,

Indeksy X; δ wskazują na środek;szerokość rozkładu

WAŻNE:Funkcja G(x), δ(x opisuje rozkład graniczny wyników pomiarów wielkości x,której wartość prawdziwa jest równa X,pod warunkiem,że pomiary są narażone na wpływ błędów przypadkowych.O dowolnych pomiarach,których rozkładem granicznym jest funkcja Gaussa mówimy ,że mają rozkład normalny.(całkowite pole powierzchni pod krzywą jest rowne 1)

f x=X

x

Mniej ważne:

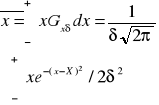
dx=* (y=x-X dx=dy)

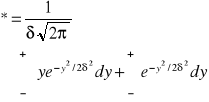
pierwsza całka równa się zero,ponieważ przyczynek od dowolnego punktu y znosi się z przyczynkiem pochodzącym od punktu -y

=X

Czyli wartość średnią obliczoną na podstawie,długiej serii pomiarów jest równa wartości prawdziwej

Odchylenie standardowe:

δ_x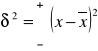
Gx,δ(x)dx

podstawienie:

=X x-X=y (
i całkujemy przez części) δx²=8²

Czyli szerokość δ funkcji Gaussa jest równa odchyleniu standardowemu otrzymanemu z wielokrotnego pomiaru.

---