Dzis przejdziemy do kombinatoryki. Na początek zbiory z powtórzeniami. Zbiór z powtórzeniami jest to para Q = (X, K), gdzie
jest zbiorem n elementowym, zaś
ciągiem liczb naturalnych. X nazywamy zbiorem podstawowym, a liczby
krotnościami elementów
w zbiorze z powtórzeniami Q. Stosujemy nastepujące oznaczenie:
. Liczność zbioru z powtórzeniami jest równa
. Podzbiorem zbioru z powtórzeniami
jest
, gdzie
dla i = 1,…,n.

Twierdzenie

Liczba wszystkich k elementowych podzbiorów zbioru z powtórzeniami
, gdzie
dla i = 1,…,n jest równa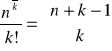
.

Przejdźmy teraz do podziałów zbioru. Podziałem zbioru X na k bloków nazywamy rodzinę zbiorów A =
spełniającą trzy warunki:

Pozdzbiory
nazywamy blokami A.

Zastosujmy nastepujące oznaczenia. Niech
będzie zbiorem wszystkich podziałów zbioru skończonego X na k bloków, a
niech będzie zbiorem wszystkich podziałów zbioru X. Wtedy
. Oznaczamy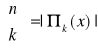
, gdzie |X| = n i nazywamy liczbą Stirlinga drugiego rodzaju.

Twierdzenie

Dla n, k
, 0 < k < n mamy, że: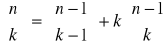
. Przyjmujemy dodatkowo: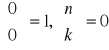
dla k > n. Mamy ponadto: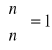
dla
, oraz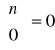
dla n > 0.

Twierdzenie

Wzór dokładny na liczby Stirlinga drugiego rodzaju:

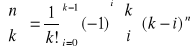
. Z tego wzoru otrzymujemy wzór na liczbę surjekcji.

Liczbe wszystkich możliwych podziałów zbioru n elementowego oznaczamy
i nazywamy entą liczbą Bella. Mamy, że: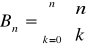
. Stąd wynika twierdzenie podstawowe, że relacja równoważności an zbiorze X wyznacza podział tego zbioru na bloki. Istnieje tez odwrotne do tego twierdzenie, które mówi, że każdy podział zbioru na bloki wyznacza relację równoważności na tym zbiorze.

Twierdzenie

Liczba wszystkich różnych relacji różnowartościowych, jakie można wprowadzić w zbiorze n elementowym jest równa entej liczbie Bella.

Popatrzmy teraz, jak wyglądają liczby Stirlinga pierwszego rodzaju (definicja rekurencyjna dla
:
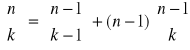
, oraz ponadto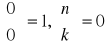
dla k > n. Liczby te mają interpretacje w teorii permutacji. Przejdźmy więc do permutacji. Niech
zbiór permutacji n elementowych. Mamy |
| = n!,
zapisujemy: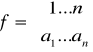
, lub
. Dla
okreslone jest złożenie permutacji
, co zapisujemy w skrócie: fg.
jest grupa, gdy:

1.
jest działaniem łącznym, czyli f (gh) = (fg) h.

2. Elementem neutralnym jest permutacja identycznościowa I = (1,…,n)
dla

3. Dla
określona jest permutacja odwrotna
. Grupa
jest nieprzemienna. W ogólności dla składania permutacji:
. Cykl długości k dla permutacji
oznaczamy
. Każda permutację można rozłożyć na cykle. Na przykład:

Twierdzenie

Liczba permutacji ze zbioru
, których rozkład na cykle rozłączne zawiera dokładnie k czynników
jest równa liczbie Stirlinga pierwszego rodzaju

. Mamy zatem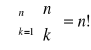

Mówimy, że permutacja
jest typu
jeśli jej rozkład na cykle rozłączne zawiera dokładnie
cykli o długości i dla i = 1,…,n. Typ permutacji zapisujemy
, gdzie będziemy pomijac czynniki, dla których
. Na przykład:

jest typu
. Inwersją permutacji
nazywamy parę (
) dla której
, oraz
. Liczbę wszystkich inwersji permutacji f oznaczamy symbolem I(f). Znakiem permutacji
nazywamy liczbę sgn (f) =
, gdzie sgn(f) = 1 to permutacja parzysta, a sgn(f) = - 1 to permutacja nieparzysta.

Twierdzenie

Niech
typu
. Wtedy sgn(f) =
. Dla
typu
mamy

sgn(f) =

---