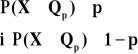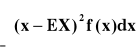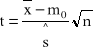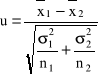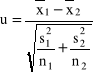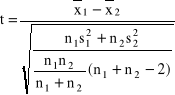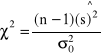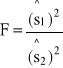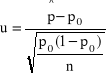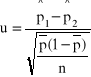JEDNOWYMIAROWE ZMIENNE LOSOWE

	ZMIENNA LOSOWA SKOKOWA	ZMIENNA LOSOWA CIĄGŁA
funkcja prawdopodobieństwa:	P(X=xi) = pi 0,
funkcja gęstości:		f(x) 0 dla x ,
dystrybuanta:	F(x) = P(Xx) = dla x	F(x) = P(Xx) = = dla x
prawdopodobieństwo:	P(X=a) = pi 0 P(ab) = F(b) - F(a)	P(X=a) = 0 P(ab)= F(b) - F(a) = =
wartość oczekiwana:	EX = W - zbiór punktów skokowych	EX =
mediana:		F(Me) = 0,5
kwantyle rzędu p:
wariancja:	D^2(X)= E(X-EX)^2= = D^2(X)= E(X^2) -E(X)^2	D^2X= E(X-EX)^2= = D^2(X)= E(X^2) -E(X)^2
odchylenie standardowe:
moment zwykły r-tego rzędu:		mr =
moment centralny r-tego rzędu:
współczynnik zmienności:

Własności dystrybuanty zmiennej losowej typu skokowego.

Dystrybuanta F(x) zmiennej losowej X typu skokowego posiada następujące własności:

1^o P(X=x_i)=F(x_i)-F(x_i-1) gdzie x_i ,x_i-1 punkty skokowe zmiennej losowej X, gdzie x_i-1<x_i

2^o P(a
=F(b)-F(a)+P(X=a)

3^o P(a<X<b)=F(b)-F(a)-P(X=b)

4^o P(a X<b)=F(b)-F(a)+P(X=a)-P(X=b)

5^o P(xa)=1-F(a)+P(X=a)

6^o P(X>a)=1-F(a)

7^o P(X<a)=F(a)-P(X=a)

Własności dystrybuanty zmiennej losowej typu ciągłego.

1^o P(a
= P(a<X<b)= P(a X<b) = F(b)-F(a)

2^o P(xa)= P(X>a)=1-F(a)

3^o P(X<a)= P(X
a)=F(a)

DWUWYMIAROWA ZMIENNA LOSOWA SKOKOWA

prawdopodobieństwo: P(X=x_i, Y=y_j) = p_ij dla i=1,2,...,k j=1,2,...,r

rozkłady brzegowe:
dla i=1,2,...,k
dla j=1,2,...,r

rozkłady warunkowe: P(X=x_i|Y=y_j) =
P(Y=y_j|X=x_i) =

dystrybuanta: F(x,y) = P(Xx, Yy) dla (x, y)

dystrybuanty rozkładów brzegowych: F₁(x) =
dla x F₂(y) =
dla y

dystrybuanty rozkładów warunkowych: F(x|y_j) = P(X
x|Y=y_j) =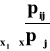

F(y|x_i) = P(Y
y|X=x_i) =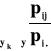

moment zwykły : m_rs = E(X^rY^s) =
dla r,s

moment centralny :
=
dla r,s

kowariancja: cov(X,Y) =
= E[(X-EX)(Y-EY)]

współczynnik korelacji: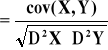

Jeśli zmienne losowe X i Y są stochastycznie niezależne, to wszystkie rozkłady warunkowe zmiennej losowej X są takie same, a ponadto identyczne z rozkładem brzegowym zmiennej losowej X. To samo można powiedzieć o rozkładach warunkowych zmiennej Y.

Zmienne losowe X i Y są stochastycznie niezależne, jeśli dla każdej pary wskaźników i=1,2,...,k j=1,2,...,r zachodzi:
.

Jeśli zmienne losowe X i Y są stochastycznie niezależne, to

Jeśli zmienne losowe X i Y są stochastycznie niezależne, to wówczas kowariancja wynosi zero: cov(X,Y)=0.

Warunkiem korelacyjnej niezależności zmiennej losowej X od zmiennej losowej Y jest równość średnich warunkowych rozkładów zmiennej X, natomiast warunkiem korelacyjnej niezależności zmiennej losowej y od zmiennej losowej X jest równość średnich warunkowych rozkładów zmiennej Y. Niezależność korelacyjna jest szczególnym przypadkiem niezależności stochastycznej.

Jeśli zmienne losowe X i Y są stochastycznie niezależne, to są również nieskorelowane. Twierdzenie odwrotne nie jest prawdziwe.

WYBRANE ROZKŁADY ZMIENNEJ LOSOWEJ

I. Rozkłady skokowe

1.Skokowy (dyskretny) rozkład równomierny

xi	x1	x2	. . .	xn
pi			. . .

Parametry rozkładu: E(X)= , D²(X)=

2. Rozkład zerojedynkowy z parametrem p, 0<p<1, gdzie p+q=1.

xi	0	1
pi	q	p

Parametry rozkładu: E(X)=p, D²(X)=pq, =pq(1-2p).

3. Rozkład dwumianowy (Bernoulliego) z parametrami (n,p), n
N, gdzie q=1-p.

P(k; n,p) =, k=0,1,2,...n.

Parametry rozkładu: E(X)=np, D²(X)=npq, =npq(1-2p).

4. Rozkład Poissona z parametrem , >0.

Funkcja prawdopodobieństwa: p_k=P(k; )=
, k.

Parametry rozkładu: E(X)= , D²(X) =, .

Dla dużych n mamy następujące przybliżenie Poissona rozkładu dwumianowego:

, , k.

Przybliżenie to jest do celów praktycznych wystarczająco dokładne gdy: n50, p0,1,      np10.

II. Rozkłady ciągłe

1.Rozkład równomierny (jednostajny, prostokątny):

Funkcja gęstości f(x)= Dystrybuanta: F(x)=

Parametry rozkładu: E(X)=Me=, D²(X)=(b-a)², dla dowolnego r, dla dowolnego r,brak mody.

2. Rozkład wykładniczy o parametrze .

Funkcja gęstości f(x)= Dystrybuanta: F(x)=

Parametry rozkładu: E(X)= , D²(X)=², Me=ln2, Do=0.

3. Rozkład normalny (de Moivre'a-Gaussa) o parametrach
, przy czym

Funkcja gęstości: f(x)= dla x

Rozkład normalny o parametrach oznaczamy symbolem N().

Parametry rozkładu: E(X)=Me=Do=, D²(X)=, dla dowolnego r, współczynnik skupienia K=3, eksces (współczynnik spłaszczenia)
.

Jeżeli zmienna losowa X ma rozkład N(), to standaryzowana zmienna losowa U= ma rozkład N(0,1) zwany standaryzowanym rozkładem normalnym.

Funkcja gęstości rozkładu N(0,1):dla u, dystrybuanta

Z symetrii wykresu funkcji gęstości względem osi OY wynika następująca zależność: 1- .

4. Rozkład chi-kwadrat. Niech U₁, U₂, ... , U_k będą niezależnymi zmiennymi losowymi o standardowym rozkładzie normalnym N(0,1) każda. Rozkład zmiennej losowej będącej sumą ich kwadratów nazywamy rozkładem o k stopniach swobody.

Parametr k rozkładu , zwany liczbą stopni swobody, oznacza liczbę niezależnych składników , które sumujemy.

Parametry rozkładu: E()=k, D² ()=2k,

Rozkład jest asymetryczny (dodatnia asymetria malejąca za wzrostem liczby stopni swobody k).

Rozkład przy liczbie stopni swobody jest zbieżny do rozkładu normalnego, tzn. gdy .

W praktyce korzysta się dla dużych k z szybszej zbieżności rozkładu zmiennej do rozkładu normalnego N(, czyli - gdy .

5. Rozkład t-Studenta. Niech U będzie zmienną losową o rozkładzie normalnym N(0,1), V zmienną losową o rozkładzie o k stopniach swobody, przy czym zmienne losowe U, V są niezależne. Rozkład zmiennej losowej postaci nazywamy rozkładem t-Studenta o k stopniach swobody.

Parametry rozkładu: E(t)=0 dla k>1, D²(t)= dla k>2, =0, rozkład jednomodalny Mo=0.

• Rozkład t-Studenta jest symetryczny względem osi OY, wykres rozkładu t-Studenta jest bardzo zbliżony do rozkładu normalnego (wykres jest nieco bardziej spłaszczony).

• Rozkład t-Studenta o k stopniach swobody jest przy liczbie stopni swobody k zbieżny do rozkładu N(0,1).

6. Rozkład F-Snedecora Niech U, V będą niezależnymi zmiennymi losowymi o rozkładach odpowiednio z k₁ oraz k₂ stopniami swobody. Rozkład zmiennej losowej nazywamy rozkładem F-Snedecora z k₁, k₂ stopniami swobody.

Parametry rozkładu: E(F)= dla k₂>2 (dla dużych k² E(F)),  D²(F)= dla k₂>4.

ROZKŁADY STATYSTYK Z PRÓBY

1. ROZKŁAD ŚREDNIEJ ARYTMETYCZNEJ Z PRÓBY

1.1. Populacja ma rozkład normalny
ze znanym odchyleniem standardowym

Średnia arytmetyczna z n-elementowej próby
ma rozkład normalny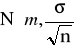
, czyli statystyka
ma standardowy rozkład normalny
.

1.2. Populacja ma rozkład normalny
z nieznanym odchyleniem standardowym

Statystyka
ma rozkład t-Studenta z n-1 stopniami swobody.

Uwaga: Rozkład t-Studenta z n-1 stopniami swobody ma graniczny standardowy rozkład normalny
(w praktyce przyjmujemy n>30).

1.3. Populacja ma dowolny rozkład z parametrami (m,
) ze znanym odchyleniem standardowym
.

Średnia arytmetyczna z n-elementowej próby
ma przy
graniczny rozkład normalny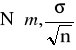
, czyli statystyka
ma standardowy rozkład normalny
.

2. ROZKŁAD RÓŻNICY ŚREDNICH ARYTMETYCZNYCH Z PRÓB

DLA DWÓCH POPULACJI NORMALNYCH

2.1. Populacje mają rozkłady normalne
oraz
ze znanymi odchyleniami standardowymi

Niech dane będą dwie populacje normalne
i
, z których pobiera się próby liczące odpowiednio
i
elementów. Wówczas statystyka
, czyli różnica średnich arytmetycznych z obu prób ma rozkład normalny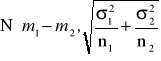
, czyli statystyka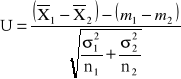
ma standardowy rozkład normalny
.

2.2. Populacje mają rozkłady normalne
oraz
z nieznanymi, ale jednakowymi odchyleniami standardowymi

Niech dane będą dwie populacje normalne
i
o identycznych odchyleniach standardowych (
), z których pobiera się niezależnie próby liczące odpowiednio
i
elementów. Dla tych prób wyznaczamy odpowiednio średnie
oraz wariancje
. Wówczas statystyka postaci: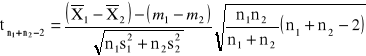
ma rozkład t-Studenta z
stopniami swobody.

3. ROZKŁAD WARIANCJI Z PRÓBY DLA POPULACJI NORMALNEJ

3.1. Populacja ma rozkład normalny
o nieznanym parametrze m, próba jest mała (n

Statystyka postaci:
ma rozkład
(chi-kwadrat) z n-1 stopniami swobody.

3.2. Populacja ma rozkład normalny
o nieznanym parametrze m, próba jest duża (n

Statystyka
ma graniczny standardowy rozkład normalny
.

4. ROZKŁAD ILORAZU WARIANCJI Z PRÓB DLA DWÓCH POPULACJI NORMALNYCH

Dane są dwie populacje generalne o dwóch niezależnych rozkładach normalnych N(m₁,
), N(m₂,
). Z populacji tych wylosowano dwie próby proste odpowiednio o liczebnościach n₁,n₂ elementów. Niech
(lub
,
) będą odpowiednio wariancjami z tych prób wówczas statystyka F=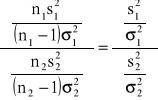
ma rozkład F-Snedecora o n₁-1, n₂-1 stopniach swobody. UWAGA!!!!! Numeracja prób powinna być taka, aby
>
.

5. ROZKŁAD WSKAŹNIKA STRUKTURY Z PRÓBY

Populacja generalna ma rozkład dwumianowy z parametrem
.

Statystyka
jest wskaźnikiem struktury z próby n-elementowej. Jeśli
(w praktyce
), to statystyka
ma graniczny rozkład normalny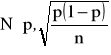
, czyli statystyka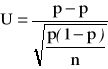
ma graniczny standardowy rozkład normalny
.

6. ROZKŁAD RÓŻNICY DWÓCH WSKAŹNIKÓW STRUKTURY Z PRÓBY

Badane są dwie populacje generalne o rozkładzie dwumianowym: z parametrem
oraz z parametrem
.

Statystyka
jest różnicą wskaźników struktury z prób
-elementowej z pierwszej populacji i
-elementowej z drugiej populacji. Statystyka
ma przy
i
(w praktyce
i
), graniczny rozkład normalny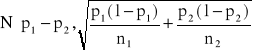
, czyli statystyka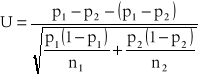
ma graniczny standardowy rozkład normalny
.

PRZEDZIAŁY UFNOŚCI

1. Przedział ufności dla wartości średniej m w populacji normalnej ze znanym odchyleniem standardowym

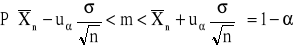
2. Przedział ufności dla wartości średniej m w populacji normalnej z nieznanym odchyleniem standardowym

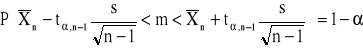
3. Przedział ufności dla wartości średniej m w populacji o nieznanym rozkładzie (duża próba)

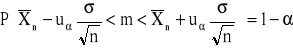
, można przyjąć

4. Przedział ufności dla wariancji
w populacji normalnej

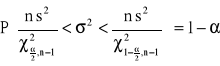
, a stąd

przedział ufności dla odchylenia standardowego
w populacji normalnej

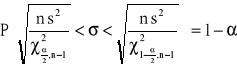
5. Przedział ufności dla odchylenia standardowego
w populacji o nieznanym rozkładzie (duża próba)

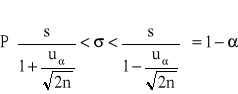
przedział ufności dla wariancji
w populacji o nieznanym rozkładzie (duża próba)

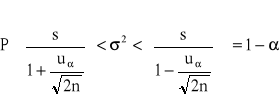
6. Przedział ufności dla parametru p (wskaźnika struktury, inaczej frakcji) w rozkładzie dwumianowym

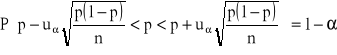
MINIMALNA LICZEBNOŚĆ PRÓBY

1. Minimalna liczebność próby przy szacowaniu wartości średniej m w populacji normalnej ze znanym odchyleniem standardowym
, d - maksymalny błąd szacunku czyli połowa długości przedziału ufności

2. Minimalna liczebność próby przy szacowaniu wartości średniej m w populacji normalnej z nieznanym odchyleniem standardowym
, d - maksymalny błąd szacunku czyli połowa długości przedziału ufności;

- liczebność próby wstępnej;
- wariancja w próbie wstępnej o liczebności

3. Minimalna liczebność próby przy szacowaniu parametru p (wskaźnika struktury, inaczej frakcji) w rozkładzie dwumianowym
, d - maksymalny błąd szacunku czyli połowa długości przedziału ufności

- wskaźnik struktury z badania pilotażowego

Jeśli nie mamy żadnych informacji o wielkości wskaźnika struktury z badania pilotażowego, to w miejsce
wstawiamy liczbę 0,5 i wówczas

PARAMETRYCZNE TESTY ISTOTNOŚCI

HIPOTEZA	CECHY CHARAKTERYSTYCZNE	STATYSTYKA	TABLICE STATYSTYCZNE		OBSZAR KRYTYCZNY
Test istotności dla wartości średniej
Ho:m=m0 HA:m m0	Populacja generalna ma rozkład normalny , jest znane.				OK=
Ho: m=m0 HA:m<m0									OK=
Ho:m=m0 HA:m>m0									OK=
Ho:m=m0 HA:m m0					Populacja generalna ma dowolny rozkład, jest znane, n>120				OK=
Ho: m=m0 HA:m<m0									OK=
Ho:m=m0 HA:m>m0									OK=
Ho:m=m0 HA:m m0					Populacja generalna ma rozkład normalny , jest nieznane, n>30				OK=
Ho: m=m0 HA:m<m0									OK=
Ho:m=m0 HA:m>m0									OK=
Ho:m=m0 HA:m m0					Populacja generalna ma dowolny rozkład, jest nieznane, n>120				OK=
Ho: m=m0 HA:m<m0									OK=
Ho:m=m0 HA:m>m0									OK=
Ho:m=m0 HA:m m0					Populacja generalna ma rozkład normalny , jest nieznane, n 30	lub			OK=
Ho: m=m0 HA:m<m0									OK=
Ho:m=m0 HA:m>m0									OK=
Test istotności dla dwóch wartości średnich
Ho:m1=m2 HA:m1 m2	Obie porównywalne populacje mają rozkłady normalne , , znane			OK=
Ho: m1=m2 HA:m1<m2							OK=
Ho:m1=m2 HA:m1>m2							OK=
Ho:m1=m2 HA:m1 m2				Obie porównywalne populacje mają rozkłady normalne , , nieznane, próby duże n1+n2-2>30			OK=
Ho: m1=m2 HA:m1<m2							OK=
Ho:m1=m2 HA:m1>m2							OK=
Ho:m1=m2 HA:m1 m2				Obie porównywalne populacje mają rozkłady normalne , , = ale nieznane, n1+n2 -2 30			OK=
Ho: m1=m2 HA:m1<m2							OK=
Ho:m1=m2 HA:m1>m2							OK=
Test istotności dla wariancji
Ho: = HA: >	Populacja generalna ma rozkład normalny , jest nieznane, n 30				OK=
Ho: = HA: >	Populacja generalna ma rozkład normalny , jest nieznane, n>30	gdzie			OK=
Test istotności dla dwóch wariancji
Ho: = HA: >	Dwie populacje o rozkładach normalnych , nieznane				OK.=
		Uwaga! Przyjmujemy taką numerację obu populacji, aby
Test istotności dla wskaźnika struktury
Ho:p=p0 HA:p p0	Populacja generalna ma rozkład zerojedynkowy z parametrem p (wskaźnik struktury), n 100				OK=
Ho: p=p0 HA:p<p0									OK=
Ho:p=p0 HA:p>p0									OK=
Test istotności dla dwóch wskaźników struktury
Ho:p1=p2 HA:p1 p2	Dwie populacje generalne o rozkładach zerojedynkowych z parametrami p1,p2 (wskaźniki struktury), duże próby n1, n2 100				OK=
Ho: p1=p2 HA:p1<p2									OK=
Ho:p1=p2 HA:p1>p2									OK=
		gdzie: , , , , .

1

---