SIATKA HYDRODYNAMICZNA
1. Wprowadzenie
Rozwiązanie konkretnego zagadnienia przepływu filtracyjnego powinno być traktowane jako zadanie trójwymiarowe. Istnieje jednak wiele zagadnień w których przepływ można rozpatrywać jako dwuwymiarowy zakładając, że w pobliżu tego przekroju właściwości ośrodka gruntowego, geometria układu warstw, a więc i parametry przepływu są w przybliżeniu takie same. Wówczas przyjmuje się, że składowa prędkości filtracji, normalna do przekroju jest równa zeru. Jeżeli natomiast w zasięgu rozpatrywanego obszaru zmienia się układ warstw lub właściwości ośrodka gruntowego, wówczas można rozwiązywać zagadnienia w kilku przekrojach, przyjmując do obliczeń schemat dwuwymiarowy.
W przypadku płaskiego przepływu wód podziemnych równanie przepływu cieczy nieściśliwej przez ośrodek jednorodny i izotropowy ma postać:
lub
gdzie:
Φ = - kH
k - współczynnik filtracji,
H - wysokość hydrauliczna.
Przy powyższych oznaczeniach składowe prędkości filtracji (mają postać):
Rozwiązaniem równania przepływu jest funkcja potencjału prędkości Φ(x, y). Przyrównując funkcję Φ do stałej C takiej, że .
kH2 ≤ C ≤ kH1
gdzie H1 i H2 są ekstremalnymi wysokościami hydraulicznymi na brzegach obszaru filtracji wywołującymi przepływ wody w rozpatrywanym obszarze, dostajemy równanie linii jednakowego potencjału C
Φ(x,y)=C
którą będziemy nazywać powierzchnią ekwipotencjalną.
Można udowodnić, że istnieje funkcja Ψ(x, y), dla której
tzn.
Powyższe związki są związkami Cauchy-Riemanna i oznaczają, że rodziny krzywych
Φ(x, y) = const. i Ψ(x, y) = const.
są wzajemnie ortogonalne. Układ tych linii w przypadku zagadnień przepływu wód podziemnych nazywamy siatką hydrodynamiczną przepływu. Rodzina krzywych
Ψ(x, y) = const.
przedstawia linie prądu (wektor prędkości jest styczny do linii prądu), które dla przepływu ustalonego pokrywają się z torami przepływających cząsteczek wody). Różniczkując powyższe związki odpowiednio po ∂x i ∂y dostajemy:
Odejmując stronami powyższe równania otrzymujemy:
lub
Rozwiązanie konkretnego zagadnienia sprowadza się więc do rozwiązania równań różniczkowych:
i
W wyniku rozwiązania możemy określić siatkę hydrodynamiczną i obliczyć wszystkie wielkości związane z przepływem wód podziemnych jak np. wysokość hydrauliczną, prędkość filtracji wielkość przepływu wód, czas przepływu na zadanym odcinku drogi.
2. Graficzna metoda obliczeń natężenia objętościowego przepływu oraz czasu przepływu zanieczyszczeń na podstawie siatki hydrodynamicznej
Rozwiązanie powyższych równań można dokonać również na drodze graficznej, korzystając z właściwości siatki hydrodynamicznej. Polega ona na tym, że siatkę hydrodynamiczną wykreśla się od ręki, traktując tak uzyskany obraz za pierwsze przybliżenie rozwiązania. Następnie siatkę poprawia się tak długo, aż spełni ona następujące warunki:
Linie prądu i linie ekwipotencjalne są ortogonalne,
Każdy wycinek siatki (wycinek ograniczony sąsiadującymi powierzchniami ekwipotencjalnymi i liniami prądu) będzie "kwadratowy" tzn. średni rozstaw linii prądu i powierzchni ekwipotencjalnych będzie taki sam.
Dla tak skonstruowanej siatki hydrodynamicznej straty wysokości hydraulicznej w każdym kwadracie siatki będą miały taką samą wartość.
Bardzo ważną właściwością siatki hydrodynamicznej jest to, że przepływ przez dowolny wycinek siatki w obrębie tej samej wstęgi (strumienia - obszar między dwoma sąsiednimi liniami prądu) ma taką samą wielkość.
Dla płaskiego zagadnienia przepływu wód podziemnych możemy określić przepływ qj na jednostkę szerokości s w i-tym wycinku siatki j-tego strumienia jako:
gdzie:
Qj - przepływ w j-tym strumieniu,
s - odległość prostopadła do przyjętego przekroju, na której geometria przekroju i właściwości gruntu są niezmienne (szerokość strumienia),
Fj,i - pole powierzchni przekroju i-tego wycinka w j-tym strumieniu,
vj,i - prędkość filtracji w i-tym wycinku j-tego strumienia
Zakładając przepływ jednostajny w poszczególnych wycinkach siatki, oraz przyjmując prawo Darcy otrzymujemy:
gdzie:
ΔHj,i - strata wysokości hydraulicznej w i-tym wycinku j-tego strumienia,
lj,i - długość drogi filtracji w i-tym wycinku j-tego strumienia,
vj,i - średni rozstaw linii prądu w i-tym wycinku j-tego strumienia.
Stąd strata wysokości hydraulicznej na i-tym wycinku j-tego strumienia wynosi:
Całkowita strata wysokości hydraulicznej wzdłuż wszystkich wycinków danego strumienia wynosi:
Stąd można określić wydatek jednostkowy pojedynczego j-tego strumienia
Całkowity przepływ wyniesie zatem
W przypadku siatki kwadratowej mamy
i w związku z tym
Na podstawie przedstawionego rozwiązania można też określić czas przepływu wody tj w poszczególnych strumieniach. W tym celu wprowadzimy pojęcie średniej prędkości rzeczywistej (prędkości porowej) u. Jest ona związana z prędkością filtracji zależnością:
gdzie n oznacza współczynnik porowatości.
Czas przepływu wody w danym strumieniu tj można określić
gdzie lj oznacza długość drogi filtracji wzdłuż j-tego strumienia.
3. Opis badań
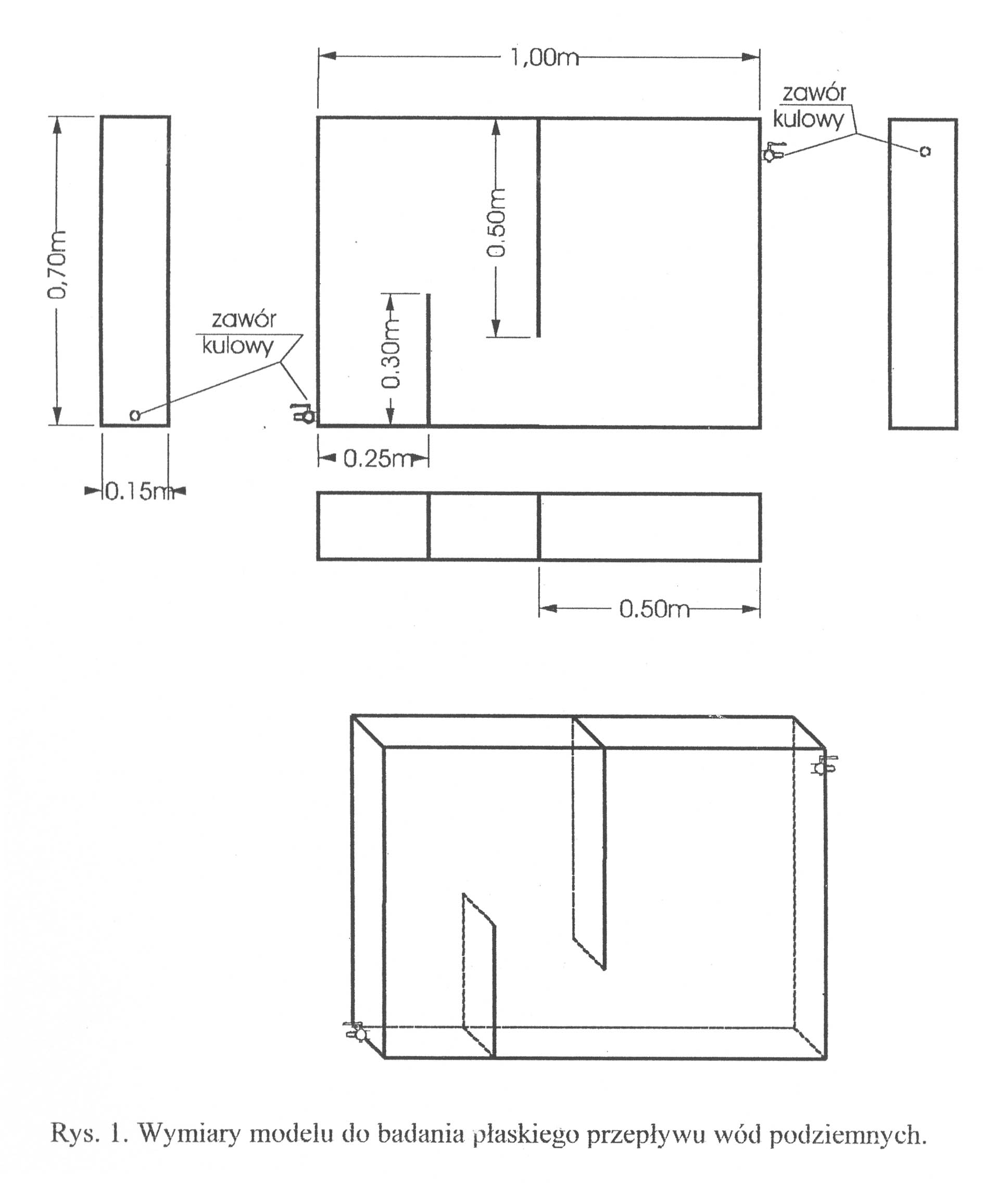
Celem ćwiczenia jest wykonanie obliczeń przepływu wód podziemnych na podstawie siatki hydrodynamicznej i porównanie uzyskanych w ten sposób wyników do wyników badań na modelu fizycznym. Geometrię modelu przedstawiono na rys. 1.
Konstrukcja siatki hydrodynamicznej będzie oparta na obserwacji linii prądu w modelu. W tym celu umieszcza się w nim piasek o znanym współczynniku filtracji oraz współczynniku porowatości. Następnie wywołuje się ustalony przepływ wody i wprowadza barwnik w kilku punktach na powierzchni wpływu wody do warstwy wodonośnej. Barwnik, rozpuszczając się w wodzie oraz płynąc razem z nią umożliwia zaznaczenie na ściance modelu przebieg linii prądu. Jednocześnie mierzy się czas przepływu barwnika przez grunt dla poszczególnych linii prądu. Ponadto mierzy się wydatek przepływającej wody.
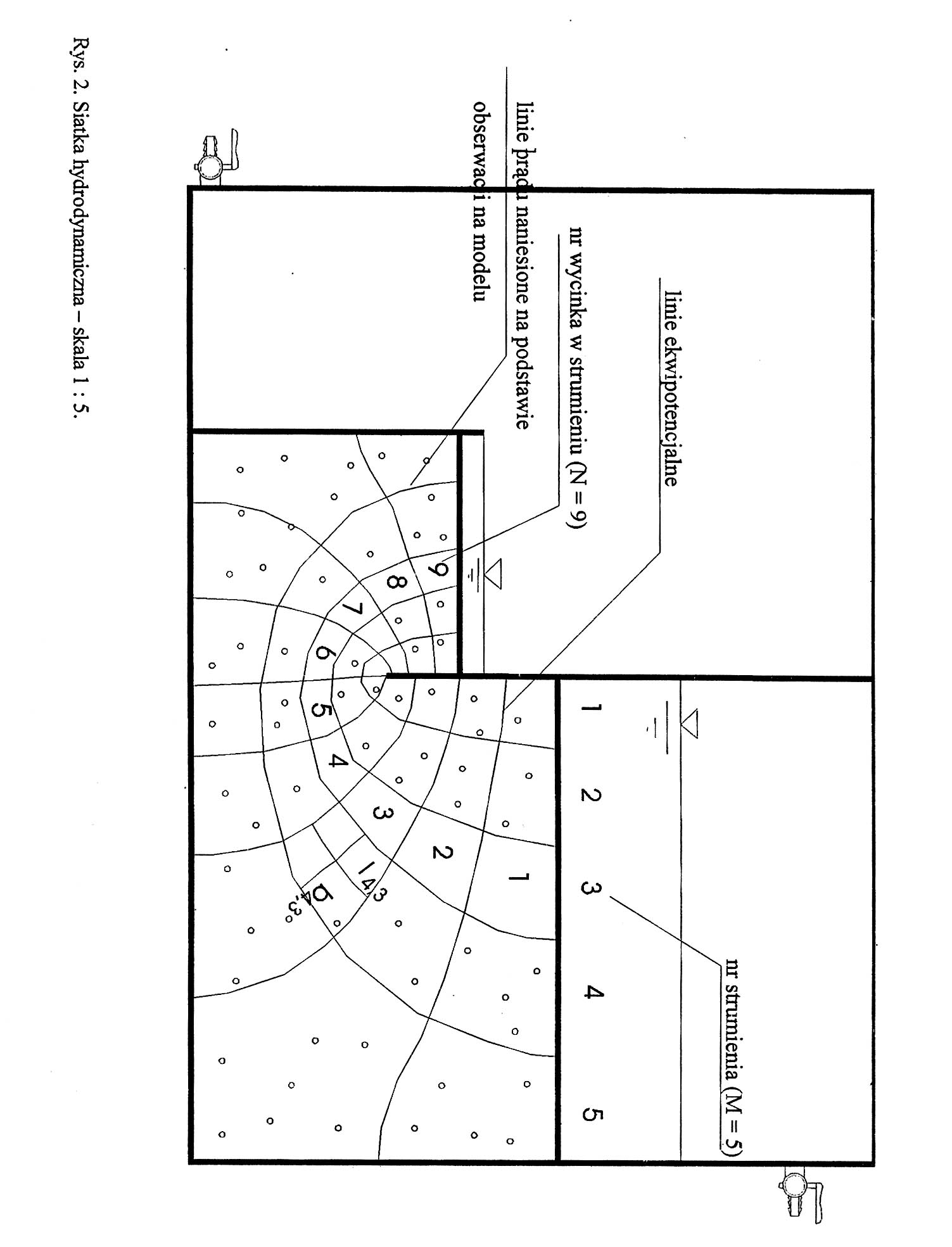
Następnie linie prądu przenosi się w skali na rysunek (rys. 2) i wykreśla siatkę hydrodynamiczną. Mając siatkę hydrodynamiczną określa się wymiary poszczególnych wycinków lj.i, oraz bj.i (tab.1) i oblicza się, wg wcześniej podanych wzorów, sumaryczny przepływ przez wszystkie strumienie (całkowity przepływ pod ścianką) oraz czas przepływu barwnika wzdłuż wybranego strumienia (obliczenia w tab.1 wykonano, przy założeniu, że współczynnik filtracji k=1,0*10-2 cm/s i współczynniku porowatości n = 0,25). Wielkości te porównuje się z otrzymywanymi na modelu.
i
i
i
i
i
i
i
i
Wyszukiwarka
Podobne podstrony:
notatek pl ci kowski,hydrogeologia L, SIATKA HYDRODYNAMICZNA
ciężkowski,hydrogeologia, górnictwo podwodne
ciężkowski,hydrogeologia, KAPILARNOŚĆ
ciężkowski,hydrogeologia, WODY PODZIEMNE
ciężkowski,hydrogeologia L, Odsączalność
ciężkowski,hydrogeologia, RUCHY CIECZY
ciężkowski,hydrogeologia, Osiadanie zapadowe gruntów
Cw5 Siatka hydrod
Siatka hydrodynamiczna
siatka hydrodynamiczna(2)
ciężkowski,hydrogeologia, erozja
ciężkowski,hydrogeologia L,ODSĄCZALNOŚĆ
ciężkowski,hydrogeologia, WIETRZENIE FIZYCZNE I CHEMICZNE
ciężkowski,hydrogeologia, DYSOCJACJA
ciężkowski,hydrogeologia, PODZIAŁ WÓD
ciężkowski,hydrogeologia, RUCHY MASOWE
ciężkowski,hydrogeologia, erozja morska
ciężkowski,hydrogeologia, Chronologia dziejów Ziemi
ciężkowski,hydrogeologia, ROZPUSZCZALNOŚC GAZÓW
więcej podobnych podstron