KLASYCZNY RACHUNEK ZDAŃ

Podstawowymi elementami języka rachunku zdań są:

zmienne zdaniowe : p, q, r...

operatory logiczne (funktory prawdziwościowe):

 - negacja

 - koniunkcja

 - alternatywa (zwykła)

→ - implikacja

 - równoważność

nawiasy ( ), [ ], { },...

Ad.1 zmienne reprezentują zdania w sensie logicznym, tzn. zdania, którym przysługują wartości logiczne: prawdy i fałszu. Prawdziwość zdania oznaczamy przez T lub 1, zaś fałszywe przez F lub 0. Omawiany rachunek zdań nazywamy klasycznym, gdyż zakłada się, że, zdanie przyjmuje jedynie jedną z dwu wymienionych wartości logicznych. Powstały inne rachunki zdań, w których nie przyjmuje się tego założenia. Nazywamy je ogólnie wielowartościowymi rachunkami zdań.

Ad. 2 .Za pomocą operatorów logicznych budujemy zdania złożone ze zdań prostych. Wartość logiczna takich zdań złożonych zależy jedynie od wartości logicznych zdań składowych.. Stąd też dla danych zdań : p i q wartości logiczne zdań złożonych: p, p  q, p  q, p → q, p  q będą całkowicie wyznaczone za pomocą wartości. Mamy więc:

p	¬p
1 0	0 1

Czyt. „nieprawda, że”

p q	p ∧ q		p q	p ∨ q		p q	p → q		p q	p ↔ q
1 0 1 0 0	1 0 0 0			1 0 1 0 0		1 1 1 0			1 1 0 1 0 0	1 0 1 1		1 1 1 0 0 1 0 0	1 0 0 1

czyt. „i” czyt. „lub” czyt. „jeżeli, to” czyt. „wtw”

Ad. 3. Nawiasy, jako znaki pomocnicze, zmieniają naturalną kolejność operacji logicznych, tzn. najmocniejsza jest negacja, później koniunkcja, alternatywa, implikacja i równoważność. Przykładowo: p → q  p oraz ( p → q )  p

Def. Matrycą logiczną zdania złożonego, zbudowanego ze zdań prostych p, q, r ..., nazywamy tablica podającą wartości logiczne tego zdania tego zdania złożonego, w zależności od wartości logicznych zdań prostych.

Wn. Wartość logiczną zdania złożonego możemy obliczyć, wyznaczając po kolei wartości logiczne zdań prostszych.

Ex. 1

Zapisz poniższe zdanie za pomocą symboliki logicznej, używając zmiennych zdaniowych: p, q, r, ... oraz operatorów logicznych: , , , →,  i podaj jego matrycę.„ Jeśli pada deszcz, to nie świeci słońce i na niebie są chmury”. Niech

p =” pada deszcz”;

q = „ świeci słońce”;

r = „na niebie są chmury”

Tak więc mamy zdanie: p → q  r

Budujemy matrycę tego zdania:

p q r	¬q	¬ q ∧ r	p → ¬q ∧ r
1 1 1 1 1 0 1 0 1 1 0 0 0 1 1 0 1 0 0 0 1 0 0 0	0 0 1 1 0 0 1 1	0 0 1 0 0 0 1 0	0 0 1 0 1 1 1 1

Kolumna 4 zawiera wartości logiczne dla całego zdania złożonego. Zdanie złożone jest prawdziwe bądź to gdy nie pada deszcz, bądź to gdy pada deszcz lecz świeci słońce i na niebie są chmury. W pozostałych przypadkach jest fałszywe.

Def 2. Zdania złożone, które są zawsze prawdziwe, niezależnie od wartości logicznych zmiennych zdaniowych w nich występujących nazywamy tautologiami (prawami logiki); te zaś, które są zawsze fałszywe nazywamy kontrtautologiami lub też wewnętrznie sprzecznymi.

Ex. 2.

Zdanie „p→p” jest tautologią, gdyż matryca przyjmuje zawsze wartość logiczną 1, zaś zdanie:

„p p” zaś jest kontrtautologią, gdyż matryca przyjmuje zawsze wartość 0.

P	p → p		p	¬p	p ∧¬p
1 0	1 1			1 0	0 1	0 0

Ex. 3.

Zbuduj matryce logiczną dla zdania złożonego P o postaci (p → q) →[ (p q) → (p  q)] i wskaż

czy jest ono tautologią, czy kontrtautologią.

p q	¬q	p → q	P ∨¬q	p ∧ q	(p ∨¬q) → (p ∧ q)	P
1 1 1 0 0 1 0 0	0 1 0 1	1 0 1 1	1 1 0 1	1 0 0 0	1 0 1 0	1 1 1 0

Ponieważ w ostatniej kolumnie w ostatnim wierszu pojawiło się 0 zatem zdanie P nie jest tautologią. Nie jest tez ono kontrtautologia, gdyż nie wystąpiły w ostatniej kolumnie same zera.

Tautologie do których często odwołujemy się w procesach dowodzenia , posiadają zwykle specjalne nazwy, nawiązujące do ich strukturalnych własności. Do tych najbardziej znanych zaliczają się

[(p → q) p] →q modus ponendo ponens

[(p → q) q ] →p modus tollendo tollens

 (p  q) p q prawa de Morgana

 (p  q ) p  q

p →(p → q) prawo Dunsa Szkota

(p →p) →p prawo redukcji do absurdu

[(p  q ) →r] →[p → (q → r)] prawo eksportacji

[p → (q → r)] →[(p  q ) →r] prawo importacji

[(p → q)  (q → r)] → (p → r) prawo sylogizmu warunkowego

IDEA DEDUKCJI

Termin dedukcja wiążę się na ogół z wyprowadzaniem jednych zdań z drugich. Dedukcja daje się sprowadzić do wyprowadzania jednych zdań z drugich, za pomocą małych kroków tzw. Reguł wyprowadzania, co do których każdy jest w stanie się zgodzić, że są poprawne. Pozostaje tylko zgodzić się, co do tego, które reguły są poprawne na mocy samej oczywistości. Omówimy dwa ujęcia systemu klasycznego rachunku zdań, w których to ujęciach będziemy mieli do czynienia z procesem dedukcji. Ujęcia te pozwalają o każdym zdaniu klasycznego rachunku zdań rozstrzygnąć, czy jest ono tautologią, czy też nie. W jednym z tych ujęć zwanym założeniowym systemem rachunku zdań będziemy mieli do czynienia z tzw. założeniowymi dowodami wprost i nie wprost, w drugim zaś będziemy mieli do czynienia ze zwykłymi dowodami wprost i nie wprost. Obydwa ujęcia dają wyobrażenia o tym, co to znaczy dowód (w sensie matematycznym) oraz na czym polega proces dowodzenia.

A. Założeniowy system klasycznego rachunku zdań.

Dowód założeniowy jest najbliższy temu co nazywamy dedukcją w potocznym tego słowa znaczeniu, niekiedy zwaną dedukcja naturalną. Żadne ze zdań nie jest w tym ujęciu wyróżnione, a w procesie dedukcji główną rolę odgrywają reguły. Zakres stosowania tej metody jest jednak dość ograniczony, gdyż odnosi się jedynie do tych systemów, czy teorii, dla których obowiązuje tzw. twierdzenie o dedukcji. W dowodach założeniowych mamy do czynienia z dwoma typami reguł, z tak zwn. (1) Regułą tworzenia założeniowych dowodów wprost i nie wprost (RDZ) oraz z (2) Regułami pierwotnymi ( przyjętymi na mocy oczywistości) oraz wtórnymi ( przyjętymi poprzez udowodnienie) dołączania nowych wierszy do dowodu (RDNW).

RDZ : jeśli istnieje założeniowy dowód wprost zdania

P* =„ P1 → (P2 → ( P3 →... →( Pn-1 → Pn )...))”

dla n  1 to zdanie to jest tezą tego rachunku( tautologia klasycznego rachunku zdań )

(2) RDNW:

P → Q P

(a) RO(reguła odrywania): P (b) DK (reguła dołączania koniunkcji) : Q

Q P  Q

P  Q P  Q

OK. (reguła opuszczania koniunkcji): P Q

P Q

DA (reguła dołącznia alternatywy: P Q P  Q

P  Q P  Q

OA (reguła opuszczania alternatywy): P Q

Q P

P → Q

DE ( dołączania równoważności): Q → P

P  Q

P  Q P  Q

(g) OE (opuszczania równoważności): P → Q Q → P

Założeniowy dowód wprost zdania P* tworzymy w następujący sposób:

Założeniowy dowód wprost zdania P^* tworzymy w następujący sposób:

1. W n-1 początkowych wierszach dowodu wypisujemy kolejno zdania, P₁, ..., P_n-1 jako założenia dowodu.

2. Do dowodu można dołączyć jako nowe wiersze:

1. tezy wcześniej udowodnione;

2. wyrażenia uzyskane na podstawie dotychczasowych wierszy według RDNW .

3. Dowód jest zakończony jeśli w ostatnim wierszu występuje wyrażenie P_n

Ex.4 P₁ P₂ P₃ P_n

Zbuduj dowód założeniowy zdania P^*=”(p → q) → [(q → r) → (p → r )]

1. p → q

2. q → r zał. dow.

3. p

4. q RO 1 i 2

5. r RO 2 i 4

Ex. 5 P1 P2 P3 Pn

Zbuduj dowód założeniowy zdania P*=”[p q → r] → [p → (q → r)]”

1. p q → r

2. p zał. dow.

3. q

4. p q DK 2 i 3

5. r RO 1 i 4

Założeniowe dowody nie wprost tworzymy podobnie jak założeniowe dowody wprost, z tym ,że dodatkowo w n- tym wierszu dowodu wpisujemy zdanie sprzeczne ze zdaniem Pn, tzn. gdy zdanie Pn nie posiada negacji lub posiada parzysta ich liczbę wpisujemy . Dowód jest zakończony po otrzymaniu w nim dwóch wierszy sprzecznych.

Ex. 6

P1 Pn

Zbuduj dowód założeniowy nie wprost zdania P*=”[(p → q)  q ] → p”

1. ( p → q)   q zał. dow.

2. p zał. dow. nwp.

3. p → q

  q OK. 1

5. q RO 3 i 2

sprzeczność wierszy 4 i 5

P1 Pn

Ex.7.

Zbuduj dowód założeniowy nie wprost zdania P*=”[(p → r)  (q → r)  (p  q )] → r”

1. (p → r)  (q)  (p q ) zał. dow.

2. r zał. dow. nwp.

3. p → r

4. q → r OK. 1

5. p q

 q MTT. (reguła wtórna z modus tollendo tolens)

9. p OA 5 i 8

10. r RO 3 i 9

sprzeczność wierszy 2 i 10

Zadanie:

Zbuduj dowód założeniowy nie wprost zdania P*=”[(p  q ) → r]  [(p r) →  q ] „

Uwaga! Udowodnić najpierw implikacje w obydwie strony, a później zwykły dowód wprost.

AKSJOMATYCZNE UJĘCIE RACHUNKU ZDAŃ

Aksjomatyzacja logiki zdań nie jest zabiegiem koniecznym dla rozstrzygnięcia czy zdanie tego rachunku jest tautologią czy też nie. Do tego celu wystarczają metoda matrycowa albo założeniowa. Powstało jednak wiele aksjomatyzacji rachunku zdań, gdyż okazały się one dogodnym obiektem badań, posiadającym specyficzne własności, a ponadto takie ujęcie logiki zdań daje pewne korzyści dydaktyczne. Do elementów systemu aksjomatycznego zdań należą:

Aksjomaty, czyli zdania będące tautologiami tego rachunku.

Reguły pierwotne, które pozwalają przejść od jednych tautologii do innych.

Definicje, które pozwalają zastąpić terminy wtórne, a więc nie występujące w aksjomatach terminami pierwotnymi, występującymi w aksjomatach.

Istnieje wiele aksjomatyzacji rachunku zdań różniących się ilością aksjomatów jak i ich doborem. Jednym z najbardziej znanych aksjomatyzacji systemu klasycznego rachunku zdań jest system ( implikacyjno-negacyjny) polskiego logika J. Łukasiewicza.

SYSTEM AKSJOMATYCZNY ŁUKASIEWICZA

Aksjomaty

A1. (p → q) → [(q → r) → (p → r)]

A2. (p → p) → p

A3. p → (p → q)

Reguły pierwotne:

RP (reguła podstawiania): Jeżeli zdanie P jest tautologią, zawierającą zmienną zdaniową v, to po podstawieniu zdania E za każde wystąpienie zmiennej v w P otrzymujemy zdanie P*, które także jest tautologią.

RO: Jeżeli zdanie złożone P* =”P→ Q” jest tautologią i P jest tautologią, to Q jest też tautologią

Definicje:

D1. P Q = P → Q

D2. P Q =  (P→ Q)

D3. PQ = (P→ Q)  (Q→ P)

Tak sformułowane definicje są regułami zastępowania (RZ) w tezach systemu zdań zawierających terminy pierwotne, przez zdania zawierające terminy zdefiniowane i odwrotnie.

Dowód prowadzimy podobnie jak dowód założeniowy, z tym, że punktem wyjścia dowodu zamiast założeń przyjmujemy aksjomaty a zamiast reguł dołączania nowych wierszy do dowodu stosujemy reguły pierwotne (RP i RO) oraz (RZ)

Ex.8 Niech P = „p→ p”. Zbuduj dowód zdania P na gruncie aksjomatyki Łukasiewicza dla klasycznego rachunku zdań.

1. (p → q) → [(q → r) → (p → r)] A1.

2 .[p → (p → p)] → [((p → p) → r) → (p → r)] RP 1 (q/p → p)

[p → (p → p)] → [((p → p) → p) → (p → p)] RP 2 (r/p)

p → (p → q) A3

p → (p → p) RP 4 (q/p)

((p → p) → p) → (p → p) RO 3 i 5

(p → p) → p A2

p → p RO 6 i 7

EX. 9 Niech P = „p  p”. Zbuduj dowód zdania P na gruncie aksjomatyki Łukasiewicza dla klasycznego rachunku zdań.

1. p → p Teza udow.

2. p  p → p  p RP 1 (p/ p  p)

3. (p → p) → p  p RZ D1 i 2

4. p → p Teza udow.

5. p → p RP 4 (p/p)

6. p  p RO 3 i 5

Metoda założeniowa a aksjomatyzacja klasycznego rachunku zdań.

a) Zarówno metoda założeniowa jak i aksjomatyczna daje wyobrażenie o tym, czym jest dowód w

sensie matematycznym

b) każde zdanie dowodu w dowodzie aksjomatycznym jest tezą systemu, tymczasem w dowodzie założeniowym nie są tezami systemu;

c) w systemie aksjomatycznym siła inferencyjna zawarta jest w aksjomatach, w systemie założeniowym w regułach;

d) metoda aksjomatyczna ma charakter bardziej uniwersalny, metoda założeniowa ma zastosowanie na gruncie tych systemów, dla których obowiązuje twierdzenie o dedukcji.

e) metoda aksjomatyczna jest na ogół trudniejsza niż założeniowa- nie wiadomo z góry jakie powinny być początkowe wiersze dowodu;

DEFINICJA DOWODU

Dowodem D zdania B w oparciu o zbiór zdań X przyjętych jako założenia nazywamy ciąg zdań, takich, że D={D₁, D₂, ..., D_n }spełniających następujące warunki:

a) B= D_n (ostatnie zdanie tego ciągu jest identyczne z B);

b) każde zdanie D_k ciągu D, gdzie (1  k  n ) albo należy do X albo jest tautologią, albo jest wyprowadzone z wcześniejszych zdań ciągu za pomocą reguł wnioskowania.

NOTACJA BEZNAWIASOWA ŁUKASIEWICZA

Beznawiasowa notacja Łukasiewicza zwana też notacja polską, polega na tym, że każdy funktor prawdziwościowy zarówno jednoargumentowy jak i dwuargumentowy poprzedza swe argumenty, zamiast, jak w przypadku dwuargumentowych, znajdować się między nimi. Argumenty zaś wypisuje się od lewa do prawa. Strukturalne własności zdania złożonego są zachowane bez używania nawiasów. Przy tym dla oznaczenia operatorów logicznych stosuje się duże litery alfabetu. I tak, dla oznaczenia negacji( N), dla koniunkcji (K), dla alternatywy (A), dla implikacji (C), dla równoważności (E).

Ex10 . (a) Niech zdanie P=”(p p). Przedstaw go w notacji beznawiasowej.

Ustalamy najpierw kolejność symboli w zdaniu P, zaczynając od funktorów

1 3 2 4 5

P=”¬ ( p ∧ ¬ p), a zatem wypisując te elementy zdania w zaznaczonej kolejności otrzymujemy zdanie P'=”NKpNp” identyczne z P.

4 3 5 2 6 7 1 8 9

P=”[( p → q) ∧ ¬ q] → ¬ p, a zatem otrzymujemy postępując jak wyżej zdanie P'

P'=”CKCpqNqNp” identyczne z P.

Ex11.

a) Przedstaw zdanie złożone P podane w symbolice beznawiasowej w postaci strukturalnej, gdzie P=”CKApqrKCprCqr”.

1 a1 a2

4 d1 d2 5 e1 e2 6 f1 f2

P=”C K A p q r K C p r C q r

2 b1 b2 3 c1 c2

Zdanie P'= [(p∨q) ∧ r ]→ [(p → r) ∧ (q → r)]

(b) Niech zdanie P=”CKKCprCqrApqr”

1 a1 a2

3 c1 c2 4 d1 d2

P=” C K K C p r C q r A p q r

2 b1 b2

Zdanie P'= [(p → r) ∧ (q → r) ∧ (p ∨ q)]→ r

Notacja polska ma duże zastosowanie przy translacji wyrażeń arytmetycznych na język wewnętrzny maszyny, przy równoczesnym wykorzystaniu stosowej organizacji pamięci komputera.

Zadanie: Przedstaw aksjomaty Łukasiewicza dla klasycznego rachunku zdań w postaci notacji polskiej.

LOGIKA WIELOWARTOŚCIOWA

U podstaw klasycznego rachunku zdań legło założenie o dwuwartościowości wszystkich zdań w sensie logicznym. Uwolnienie się od tego założenia prowadzi do rachunków zdań wielowartościowych. I tak np. J. Łukasiewicz wprowadzając trzecią wartość logiczną zbudował trójwartościowy rachunek zdań Ł3. Podobnie jak on a niezależnie od niego postą pił E. Post. Jeśli przyjąć, że n oznacza ilość dopuszczalnych wartości logicznych, w systemie wielowartościowym, to system taki ma następujące wartości:

Dla n = 3 mamy następujące wartości logiczne: 0, ˝, 1

Dla n = 4 mamy zaś: 0, 1/3, 2/3,1

Główna inspiracją zbudowania przez Łukasiewicza logiki trójwartościowej były rozważania dotyczące determinizmu. Zdania, które dotyczyły przyszłości mogły przyjmować jedną z trzech wartości logicznych. I tak:

0 - przyjmują te zdania, dla których istnieje obecnie przyczyna wykluczająca ich zajście;

1- przyjmują te zdania, dla których istnieje obecnie przyczyna powodująca ich zajście

1/2 -przyjmują te zdania, dla których nie istnieje obecnie przyczyna powodująca ich zajście, ani też przyczyna wykluczająca ich zajście.

Ex.12 Weźmy przykład zdań dotyczących przyszłości i oceńmy je pod względem wartości logicznych. Niech

p = ”Ziemia będzie kulista”;

q = ” Ziemia będzie nieruchoma”

r = „Ludzie w 2100 r. pobudują osiedla na Marsie”

a) zdanie „p” jest prawdziwe, gdyż istnieje obecnie przyczyna powodująca zajście zdarzenia, że Ziemia jest kulista

b) zdanie „q” jest fałszywe, gdyż istnieje obecnie przyczyna wykluczająca zajście zdarzenia że Ziemia jest nieruchoma”

c) r jest niezdeterminowane, czyli posiada wartość 1/2, gdyż nie istnieje obecnie przyczyna powodująca zajście zdarzenia budowania osiedli przez ludzi na Marsie, ani też przyczyna wykluczająca zajście takiego zdarzenia.

Podstawową sprawą pozostaje zbudowanie matryc dla zdań złożonych w Ł3. Oczywiście tabelki charakteryzujące klasyczne operatory są tutaj niewystarczające. Jednakże Łukasiewicz podając takie charakterystyki zachował dotychczasowe „zdrowe” intuicje logiczne jakie tkwiły w L, chodzi tu głównie o implikację, która o ile poprzednik posiada wartość logiczna mniejszą lub równą następnikowi o tyle całe przyjmuje wartość 1.

Oto główne warunki dla matryc Ł3

Np.=1-p

Apq = max{p, q}

Kpq = min{p, q}

jeśli pq, to Cpq=1

jeśli p>q, to Cpq=1-p+q

Na tej podstawie możemy zbudować matryce dla zdań złożonych w Ł3

1. dla negacji

p Np

1 0

½ ½

• 1

2. dla koniunkcji (Kpq)

q p	1	½	0
1	1	½	0
½	½	½	0
0	0	0	0

3. dla alternatywy (Apq)

q p	1	½	0
1	1	1	1
½	1	½	½
0	1	½	0

4) dla implikacji ( Cpq)

q p	1	½	0
1	1	1	1
½	½	1	1
0	0	½	1

Ex. 13 Zbuduj matrycę dla Epq wiedząc, że Epq=KCpqCqp. Najpierw zbudujemy dwie matryce dla P = Cpq i Q = Cqp, a następnie dla KPQ

p q P Q KPQ

1 1 1 1 1

1 0 0 1 0

0 1 1 0 0

0 0 1 1 1

1 ½ ½ 1 ½

½ 1 1 ½ ½

0 ½ 1 ½ ½

½ 0 ½ 1 ½

Wyniki z powyższej matrycy można więc zebrać, i przedstawić podobnie jak dla pozostałych operatorów logicznych dla Ł3.

q p	1	½	0
1	1	½	0
½	½	1	½
0	0	½	1

Rachunek zdań Ł3 można budować metoda matrycową podobnie jak w przypadku L, czyli klasycznego rachunku. Zdanie jest tautologia Ł3 gdy przyjmuje wartość 1 (prawdę) . W innych rachunkach wielowartościowych, ze względu na trudności w interpretacji nowych wartości logicznych nie mówi się o prawdzie, lecz tzw. wartości wyróżnionej. Dokonano też aksjomatyzacji tego rachunku.

Ex14. Sprawdź, czy zdanie P=” p p „oraz zdanie Q =”(p  p)” są tautologiami Ł3.

Ex3. Sprawdź, czy zdanie P=” p ∨¬p „oraz zdanie Q =”¬(p ∧ ¬p)” są tautologiami Ł3.

1. P= ApNp

p Np ApNp

1 0 1

0 1 1

½ ½ ½

2. Q= NKpNp

p Np KpNp NKpNp

1 0 0 1

0 1 0 1

½ ½ ½ ½

Logika trójwartościowa Łukasiewicza jest zawarta w logice klasycznej, tzn., że każda tautologia Ł3 jest tautologią L, lecz nie odwrotnie. Z powyższych matryc widać, że ważne prawa klasycznego rachunku zdań jak tzw. prawo wyłączonego środka i tzw. prawo niesprzeczności, posiadające przy tym ciekawe i zgodne z intuicjami interpretacje, a także długie tradycje w logice nie są tautologiami Ł3.

Szczególnie dużą klasę problemów, dla których systemy wielowartościowe znajdują zastosowanie stanowią problemy przyrodoznawstwa. Rozumowania bowiem dotyczące mikroświata prowadzone przy użyciu logiki klasycznej, okazują się rodzić sprzeczności na gruncie tych teorii, które go dotyczą. . Zauważono bowiem, że własności algebraiczne operatorów fizyki kwantowej mają charakter inny niż narzuca logika klasyczna. W tym celu m in. została zbudowana przez G. Birkhoffa i J. von Neumana tzw. logika kwantowa. Ciekawe są również analogie między logikami wielowartościowymi a tzw. logikami rozmytymi, znajdujące zastosowania w komputerowych systemach ekspertowych.

ANALIZA ROZUMOWAŃ

We wszystkich niemal rozumowaniach matematycznych i nie tylko opieramy się bezpośrednio lub pośrednio na prawach rachunku zdań. Spośród rozumowań do najważniejszych należą wnioskowanie i dowodzenie. W praktyce mamy często do czynienia z wnioskowaniami i dowodami poprawnymi i niepoprawnymi. Jeżeli rozumowanie - wnioskowanie bądź dowód spełniają warunki, które powinien spełniać wnioskowanie lub dowód wnioskowanie, to rozumowanie takie nazywamy poprawnym, w przeciwnym przypadku nazywamy go niepoprawnym. Przeprowadzane dotąd rozumowania miały charakter formalny, jednakże i faktycznie przeprowadzane rozumowania, mające charakter nieformalny, można poddać formalizacji.

Ex. 15 Mamy następujące rozumowanie: „Jeżeli będę się uczył lub jestem geniuszem, to zdam egzamin. Jeżeli zdam egzamin, to będę mógł uczęszczać na następne wykłady. Zatem, jeżeli nie zostanę dopuszczany do następnych wykładów, to nie jestem geniuszem.”

Niech

p= ”będę się uczył”

q = „jestem geniuszem”

r =” zdam egzamin”

s =”zostanę dopuszczony do następnych wykładów”

Przesłanki:

P1= ” Jeżeli będę się uczył lub jestem geniuszem, to zdam egzamin”

P2 = „ Jeżeli zdam egzamin, to będę mógł uczęszczać na następne wykłady”

Wniosek:

W= „ jeżeli nie zostanę dopuszczany do następnych wykładów, to nie jestem geniuszem.”

METODA MATRYCOWA

P1= ”p  q → r”

P2 = „r → s”

W =”s → q”

Jeżeli zdanie Q=„ P1  P2  ... Pn →W ” jest tautologią, to wnioskowanie jest formalnie poprawne, tzn. w niosek wynika logicznie z przesłanek, w przeciwnym przypadku jest formalnie niepoprawne. Sprawdzimy metodą matrycową skróconą , czy zdanie Q jest tautologią.

1 0 0

1 1 1 0

(p ∨ q → r) ∧ (r → s) → (¬s → ¬q)

0 0 0 0 0 0 11

Sprzeczność w wartościowaniu. Zdanie q=0 w pierwszym wystąpieniu, a w drugim wystąpieniu q= 1.

DOWÓD ZAŁOŻENIOWY

WPROST

1. p  q → r

2. r → s zał.

3. s

4. (r → s) → (s →r ) prawo transpozycji

5. s →r RO 4 i 2

6. r RO 5 i 3

7. (p  q → r) →[ r →( p  q )] prawo transpozycji

8. r →( p  q ) RO 7 i 1

9. ( p  q ) RO 8 i 6

10. ( p  q ) ( p  q) prawo de Morgana

11. ( p  q ) → ( p  q) OE 10

12.  p  q RO 11 i 9

13.  q OK. 12

NIE WPROST

1. p  q → r

2. r → s zał.

3. s

4 q zdnwp.

5. p  q DA 4

6. r RO 1 i 5

7. s RO 2 i 7

sprzeczność wierszy 7 i 3

EX 16. Wiemy, że jeśli program komputerowy działa poprawnie, to zaczyna i zakończy swoje działanie. Wiemy też, że nasz program rozpoczął swoje działanie i nie działał poprawnie. Wnioskujemy stąd, że program nie zakończył działania.

Niech

p = „ program rozpoczął działanie”

q = „program zakończył działanie”

r = „ program nie działa poprawnie”

P1= „r → p  q”

P2 =” p  r

W= „q „

DOWÓD ZAŁOŻENIOWY (WPROST)

1 „r → p  q

2. p  r zał..

3. p  q → q prawo opuszczania koniunkcji

4. (r → p  q)  (p  q → q) → (r → q) prawo syl. warunkowego

5. (r → p  q)  (p  q → q) DK 1 i 3

6. r → q RO 4 i 5

7. r OK. 2

8. q ? ? ? 6 i 7

Wniosek:

a) źle prowadzony dowód

b) brak dowodu

Sprawdźmy, metodą matrycową, czy zdanie Q=„(¬r → p ∧ q) ∧ ( p ∧ r) → ¬q” jest tautologią.

1 1 0

Q=”(¬r → p ∧ q) ∧ ( p ∧ r) → ¬q”

1 1 1 1 1 1

Brak sprzeczności w wartościowaniu, a zatem zdanie Q nie jest tautologią. W związku z tym zdanie q = „program nie zakończył działania” nie posiada dowodu z założeń

P1= „r → p  q” i P2 =” p  r”. Oznacza to więc, że program może zacząć działanie i zakończyć działanie i nie działać poprawnie z jakiegoś innego powodu.

Ex 17.

Na podstawie prawa (p → q) →[ (q → r) → (p → r)], reguł podstawiania i odrywania oraz następujących twierdzeń arytmetyki

Tw. 1(x * y >0) → {[(x > 0)  (y > 0)]  [( x < 0)  (y < 0)]}

Tw.2{[(x > 0)  (y > 0)]  [( x < 0)  (y < 0)]} → ( x + y = x +y )

udowodnić twierdzenie (x * y >0 ) → (x + y = x + y)

1.( p → q) →[ (q → r) → (p → r)]

2. p → q Tw1 RP p / (x * y >0) ;

3. q → r. Tw2 q / {[(x > 0)  (y > 0)]  [( x < 0)  (y<0)]}

r / x + y  = x  + y 

4. (q → r) → (p → r) RO 1 i 2

5. p → r RO 3 i 4

5'. (x * y >0 ) → (x + y = x + y)

Ex 18. Udowodnij twierdzenie:

(x + y >0) → {(x * y >0) → [(x > 0)  (y > 0)]}

Założenia:

(x + y >0) → [( x < 0)  (y < 0)]

(x * y >0) → [(x > 0)  (y > 0)]  [( x < 0)  (y < 0)]

Niech

p =” x + y >0”

q =”( x < 0)  (y < 0)”

r = „x * y >0”

s = „(x > 0)  (y > 0)”

TEZA: p→(r → s)

DOWÓD:

p → q

r → q  s zał.

(r → q  s) → [s→ (r → q)] prawo rach. zdań

s→ (r → q) RO 3 i 2

q → (r → s) RP 4 s/ q ; q/ s

(p → q) → {[( q→ (r → s )] → [p→ (r → s)]} syll. hipoteczny

[( q→ (r → s )] → [p→ (r → s)] RO 6 i 2

p→ (r → s) RO 7 i 5

8'.(x + y >0) → {(x * y >0) → [(x > 0)  (y > 0)]}

RACHUNEK KWANTYFIKATORÓW (I - RZĘDU)

Rachunek zdań nie stanowi całego języka stosowanego w rozumowaniach matematycznych. Dopiero język rachunku zdań i język rachunku kwantyfikatorów pozwala na wyrażanie myśli dowolnych teorii matematycznych i sprawdzanie ich sprawdzanie ich prawdziwości za pomocą formalnego postępowania dowodowego.

Język rachunku kwantyfikatorów I rzędu

stałe nazwowe: a, b, c, ...

zmienne nazwowe : x, y, z,...

predykaty: F,. G, ..., S,..

operatory logiczne :, , , →, 

kwantyfikatory: Ex, Ax

znaki pomocnicze: ( ), [ ], { },...

Ad 1. Stałe nazwowe pełnią taką sama rolę w omawianym języku jak nazwy jednostkowe w języku naturalnym, tzn. oznaczają one indywidua. W matematyce stałymi są np. nazwy liczb

Np. a = 5; b = żona Jana Kowalskiego

Ad. 2 zmienne nazwowe są zmiennymi, za które można podstawiać nazwy przedmiotów, ale ze ściśle określonego zbioru D zwanego dziedziną dyskursu. Dzięki zmiennym w odróżnieniu od języka naturalnego można budować tzw. funkcje zdaniowe, które nie są zdaniami oznajmującymi, a zatem nie są też zdaniami w sensie logicznym. Dopiero wstawiając za zmienne określone nazwy otrzymujemy z nich zdania w sensie logicznym: np.

1. x jest większe od 10

2. x jest mniejsze od y

3. x jest podzielne przez 2

4. x jest żoną y

Funkcjami zdaniowymi nie są takie wyrażenia, jak: x + y, czy x2 - z, gdyż po podstawieniu nie sa zdaniami lecz nazwami.

Ad 3. Predykaty oznaczają własności albo relacje. Np. F= „być liczba naturalną”, R=” jest większe niż” itp. Zamiast pisać :Maria jest żoną Andrzeja - można zapisać R(a, b), zamiast pisać : x jest liczba naturalną, można napisać N(x). Argumentami predykatu są stałe nazwowe lub zmienne nazwowe. Predykaty występują więc ze swoimi argumentami np. P(x), Q(x, y), czy S(x, y, z). Predykaty można dzielić w zależności od ilości jego argumentów na jedno, dwu, trzy i więcej argumentowe. Np. F= „być liczba naturalną”, R=” jest większe niż” itp. Zamiast pisać: Maria jest żoną Andrzeja - można zapisać R(a, b), zamiast pisać: x jest liczba naturalną, można napisać N(x). W matematyce stałymi predykatowymi są np. symbole relacji: >, <, >=, <=, identyczności: =, czy różności: .

Ad 4. Operatory logiczne pełnia analogiczna role jak w rachunku zdań, tzn. łączą zdania z predykatami np. [ (1= 0)  (2 3 )] → [ (2 > 7)  (2 + 5 = 7)] a także funkcje zdaniowe. np ( jeśli P(x, y) oznacza x > y, a R(x, y) oznacza x  y a S( x, y) oznacza x < y, to wypowiedź: ( x >y )  (x  y) → (x < y) można zapisać : P(x, y)  R(x, y) → S(x, y)

Ad 5. Zwroty takie, jak: „dla każdego x” oraz „dla pewnego x”, „ dla niektórych x” lub „ istnieje takie x, że” odgrywają w języku matematyki zasadniczą rolę i łącznie z operatorami logicznymi, stałymi i zmiennymi pozwalają już na wypowiadanie każdej myśli matematycznej. Są one nazywane kwantyfikatorami. Pierwsze z tych wyrażeń nazywamy kwantyfikatorem ogólnym lub dużym, natomiast pozostałe nazywamy szczegółowym lub egzystencjalnej albo małym. Kwantyfikator mały symbolizowany jest przez Ex, duży Ax, duży. Często alternatywnie używa się innych symboli

Kwantyfikatory wiążą zmienne. Wyrażenia znajdujące się w nawiasie występującym bezpośrednio po kwantyfikatorze nazywamy zasięgiem. Np. w wyrażeniu Ay [x + x = x + y], zasięgiem kwantyfikatora jest wyrażenie: x + x = x + y, natomiast w wyrażeniu: Ax Ay (x >y)  (x  y) zasięgiem kwantyfikatora Ay jest wyrażenie x >y a zasięgiem kwantyfikatora Ax jest wyrażenie Ay (x >y). Zamiast pisać Ax Ay piszemy często Axy. Mówimy, że zmienna występująca w wyrażeniu przy symbolu kwantyfikatora jest przez ten kwantyfikator związana, w przeciwnym przypadku jest zmienną wolna.

Ex 19. Wskazać zakresy kwantyfikatora w następujących zdaniach predykatywne. Wyróżnić zmienne wolne i związane. Kreski nad zmiennymi wskazują, że zmienna w danym wystąpieniu jest zmienną związaną

1. 
   
   
   
   
   Ax[Ey [((x + y)² < z) ∨ ( u + x < v)] ∨ ( y +x = u)]

2. 
   
   
   Ay[Ex [((x + y)² < z) ∨ ( u + x < v)] ∨ ( z +x = u)]

Zasięgiem kwantyfikatora Ax jest wyrażenie Ey [((x + y)2 < z)  ( u + x < v)]  ( y +x = u)], zaś zasięgiem kwantyfikatora Ey jest wyrażenie [((x + y)2 < z)  ( u + x < v)]. Zmienne związane są u góry podkreślone.

Zasięgiem kwantyfikatora ogólnego A jest wyrażenie Ex [((x + y)2 < z)  ( u + x < v)] 

 ( z +x = u)], zaś zasięgiem kwantyfikatora szczegółowego E jest wyrażenie [((x + y)2 < z) 

 ( z + x < v)].

Jeżeli wszystkie zmienne występujące w funkcji zdaniowej zostaną w każdym swym wystąpieniu związane kwantyfikatorami, to funkcja staje się zdaniem. Np. funkcja zdaniowa (x + y = y + x) staje się zdaniem Ax Ay (x + y = y + x), gdyż zarówno zmienna x i y w każdym swym wystąpieniu zostały związane kwantyfikatorami.

Ex 20. Które z poniższych wyrażeń są zdaniami, a które tylko funkcjami zdaniowymi?.

P(x, y, z)

Ax P(x, y, z)

E x Ax P(x, y, z)

Ax Ey Az P (x, y, z)

Ponieważ tylko w przypadku d) wszystkie zmienne zostały związane, zatem tylko w tym przypadku wyrażenie jest zdaniem.

PRAWA RACHUNKU KWANTYFIKATORÓW

W rachunku zdań rozpatrywane były takie zdania złożone, które przy dowolnym podstawieniu wartości logicznych za zdania składowe przyjmowały wartość 1 , czyli prawdę. Takie wypowiedzi są nazywane tautologiami rachunku zdań. Przez analogię z rachunkiem zdań wypowiedzi ( formuły) rachunku kwantyfikatorów, które są prawdziwe w każdej dziedzinie przy dowolnej interpretacji predykatów, które w nim występują, tzn. przy dowolnym rozumieniu symboli F, G, P, R, Q itd. jako wyrażeń odnoszących się do pewnych własności lub relacji z danej dziedziny.

I Prawa rozdzielności kwantyfikatorów

Ex [P (x) Q(x)] Ex P (x) Ex Q(x)

Ax [P (x) Q(x)] Ax P (x)  Ax Q(x)

II Prawa de Morgana dla kwantyfikatorów

1.Ex P(x) Ax P(x)

2.Ax P(x)  Ex P(x)

III. Prawa zastępowania kwantyfikatorów

Ax P(x)  Ex P(x)

Ex P(x)  Ax P(x)

IV. Prawa przestawiania kwantyfikatorów

Ax Ay R(x, y) Ay Ax R(x, y)

Ex Ey R(x, y)  Ey Ex R(x, y)

ExAy R(x, y) → Ay Ex R(x, y)

V. Inne prawa

Ax P(x) → P(a) schemat podstawiania

P(a) → E(x) P(x) prawo abstrahowania od konkretności

METODA ZAŁOŻENIOWA DOWODZENIA TEZ RACHUNKU KWANTYFIKATORÓW

Rachunek kwantyfikatorów otrzymujemy dołączając do reguł pierwotnych założeniowego systemu rachunku zdań - w odpowiednio rozszerzonej postaci i wzbogacamy je o reguły pierwotne dla kwantyfikatorów. To rozszerzenie polega na tym, że termin zdanie rozumiemy obecnie jako termin oznaczający dowolną funkcję zdaniową lub zdanie rachunku kwantyfikatorów.

Reguły pierwotne dla kwantyfikatorów:

Ax P(x)

OA: reguła opuszczania kwantyfikatora ogólnego

P(x)

Np. z założenia Ax (x = x) wyprowadzamy wyrażenie x = x

P(x)

Ax P(x) DA: reguła dołączania kwantyfikatora ogólnego ( zmienna x nie może być zmienną wolną w założeniach dowodu)

Np. z założenia x > 2 wyprowadzamy wyrażenie x >2  x=2, ale nie można wyprowadzić z niego wyrażenia Ax (x > 2  x = 2), gdyż zmienna x jest wolna w założeniu .

Ex P(x)

P(a) OE1: reguła opuszczania kwantyfikatora szczegółowego ( stosując tę regułę

kilkakrotnie wprowadzamy nową stałą różną od stałych systemu i od uprzednio

wprowadzonych w tym dowodzie za pomocą tej reguły)

Ex R( x, y)

R(a_y, y) OE2: ( stała musi być zrelatywizowana do zmiennej wolnej y będącej w zasięgu

kwantyfikatora)

Np. mamy dwa założenia 1) Ex (x =2) i 2) Ex (x = 4). Z 1) można wyprowadzić zdanie 3) a =2 , lecz z 2) nie można już wyprowadzić zdania 4) a = 4

Np. z założenia 1) Ex ( x > y) ( dla dowolnej liczby y istnieje większa od niej liczba) nie można wyprowadzić wyrażenia 2) a > y ( pewna liczba jest większa od dowolnej liczby y) ale można wyprowadzić 3) a_y >y ( od dowolnej liczby x jest większa pewna liczba ay)

P ( a) P(x) P(y)

Ex P(x) ; Ex P(x) ; Ex P(x) DE: (dołączania kwantyfikatora szczegółowego)

Np. jeżeli mamy założenie 1) a= 5, to można wyprowadzić za pomocą tej reguły zdanie

2) Ex (x = 5) ( stąd, że dowolny lub pewien określony przedmiot ma własność P wynika, żde istnieje przedmiot posiadający tę własność )

DOWODY ZAŁOŻENIOWE

Ex. 21. Zbudować dowód założeniowy poniższego twierdzenia

Ex Ay R(x, y) → Ay Ex R(x, y)

1. Ex Ay R(x, y) zał.

2. Ay R(a, y) OE 1

3. R(a, y) OA 2

4. Ex(x, y) DE 3

5. Ay Ex(x, y) DA 4

Ex 22. Zbudować dowód założeniowy poniższego twierdzenia

P(x)  Ex Q(x) → Ex [P(x)  Q(x)]

1. Ex P(x)  Ex Q(x) zał.

2. Ex P(x) OK. 1

3. Ex Q(x)

4. P(a) OE 2

5. Q(b) OE 3

6. P(a)  Q(b) DK 5 i 6

Urywa się dowód - niemożliwość zastosowania reguły DE

Ex. 23. Zbudować dowód założeniowy poniższego twierdzenia

Ay Ex R(x, y) → ExAy R(x, y)

1. Ay Ex R(x, y) zał.

2. Ex R(x, y) OA 1

3. R(a_y,y) OE 2

4. Ay R(a_y , y) DA 3

Urywa się dowód - niemożliwość zastosowania DE

Ex. 24

Udowodnij metodą założeniową, że zdanie Q=„Ex [ F(x)  G(x) ] → [Ex F(x)  Ex G(x)]” jest tautologią rachunku kwantyfikatorów.

1.Ex [ F(x)  G(x) ] zał.

2. F(a)  G(a) OE 1

3. F(a)

4. G(a) OK. 2

5. Ex F(x) DE 3 i 4

6. Ex G(x)

7. Ex F(x)  Ex G(x) DK 5 i 6

Ex. 25

Udowodnij metodą założeniową, że zdanie Q = „Ex[ F(x) → G(x) ] → [Ex F(x) → Ex G(x)]” jest tautologią rachunku kwantyfikatorów.

Ex[ F(x) → G(x)] zał.

Ex F(x)

F(a)→ G(a) OE 1

F(b) OE 2

?

Niech F(x) będzie x < 0 i a G(x) będzie x2 < 0 wtedy otrzymujemy:

Q*= „Ex[(x < 0)→ (x2 < 0)] → [Ex (x < 0)→ Ex (x2 < 0)]

Ex. 26 Udowodnij metodą założeniową, że zdanie Q = „AxAy[ R(x, y) → S(x, y)] → [ExEy R(x, y) → ExEy S(x, y )]” jest tezą rachunku kwantyfikatorów.

1. AxAy [R(x, y) → S(x, y)] zał.

2. ExEy R(x, y)

3. R(a, b) → S(a, b) OA 1

4. R(a, b) OE 2

5. S(a, b) RO 3 i 4

6. ExEy S(x, y) DE 5

Ex. 27 Udowodnij metodą założeniową, że zdanie Ax P(x)  Ax Q(x) → Ax [P(x)  Q(x)] jest tezą rachunku kwantyfikatorów.

Dowód założeniowy tzw. rozgałęziony (wiersze z podwójną numeracją)

1. Ax P(x)  Ax Q(x) zał.

1.1 Ax P(x) zał dod.

1.2. P (x) OA 1.1

1.3 P(x)  Q(x) DA 1.2

1.4 Ax [P(x)  Q(x)] DA 1.3

Ax P(x) → Ax [P(x)  Q(x)] 1.1 → 1.4

2.1 Ax Q(x) zał dod.

2.2 Q(x) OA 2.1

2.3 P(x)  Q(x)] DA 2.2

2.4 Ax [P(x)  Q(x)] DA 2.3

3. Ax Q(x)→ Ax [P(x)  Q(x)] 2.1 → 2.4

4. {Ax P(x)→Ax [P(x) Q(x)]}  {Ax Q(x)→ Ax [P(x)  Q(x)]} . {Ax P(x)  Ax Q(x)}→ Ax [P(x)  Q(x)] Prawo dyl konst. pr.{(p→r) .(q→r)  (p  q) → r}

5. {Ax P(x) → Ax [P(x)  Q(x)]}  {Ax Q(x)→ Ax [P(x)  Q(x)]} . {Ax P(x)  Ax}

DK 1, 2, 3

6. Ax [P(x)  Q(x)] RO 4i 5

Ex. 27 Zapisz następujące wypowiedzi w języku kwantyfikatorów

Każdy matematyk jest muzykalny

Niektórzy matematycy są muzykalni.

Żaden matematyk nie jest muzykalny

Niektórzy matematycy nie są muzykalni

Tylko matematycy są muzykalni

Każdy matematyk jest uczniem pewnego matematyka

Pewien matematyk nie ma uczniów wśród matematyków.

Niech F= „być matematykiem”, G =”być muzykalnym”. D =zbiór ludzi a

x należy do D. R= ” być uczniem”

Ad. 1 Ax [F(x) → G(x)]

Ad. 2 Ex [F(x)  G(x)]

Ad. 3 Ax [F(x) → G(x)]

Ad. 4 Ex [F(x)  G(x)]

Ad. 5 Ax [G(x) → F(x)]

Ad. 6 Ax [F(x) → Ey (F(y)  R(x,y))]

Ad 7. Ex[F(x)  Ey (F(y)  R(y,x))]

Ex. 28 Zapisz następujące wypowiedzi w języku kwantyfikatorów

Istnieje ktoś kto ma przyjaciela

Każdy jest czyimś przyjacielem.

Każdy jest przyjacielem wszystkich

Nikt nie jest niczyim przyjacielem

Zaimki osobowe: „ktoś”, „nikt” , „wszyscy” są synonimami wyrażeń „ pewien człowiek”, „żaden człowiek” i „ wszyscy ludzie”. Niech P=” być człowiekiem”, a R=” być przyjacielem”. D = zbiór indywiduów a zmienne z, y należą do D.

Ad. 1 Ex[P(x) Ey (P(y)  R(x,y))]

Ad. 2 Ax [P(x) → Ey (P(y)  R(x,y))]

Ad 3. Ax[P(x) → Ay (P(y) → R(x,y))]

Ad 4. Ax[P(x) →Ey (P(y)  R(x,y))]

Ex 29. Niech

będą funkcjami zdaniowymi określonymi dla liczb naturalnych. Za ich pomocą , korzystając ze znanych operacji arytmetycznych, takich jak x+y, x * y, symboli dla liczb oraz symboli logicznych, zapisać następujące funkcje

x jest liczba parzystą

x nie jest liczba parzysta

x nie jest liczba pierwszą

Nie istnieje największa liczba naturalna

Nie istnieje największa liczba pierwsza

Każda liczba przy dzieleniu przez 2 daje resztę zero lub 1

Pomiędzy liczbami n i 2n istnieje co najmniej jedna liczba pierwsza (Tw. Czebyszewa)

Każda liczba nieparzysta większa od 3 rozkłada się na sumę dwu liczb pierwszych

( hipoteza Goldbacha)

Ad 1. Ey x=2* y

Ad 2. Ey x= 2 *y

Ad 3. EyEz [((y = x)  (y=1))  x=y*z]

Ad 4. Ex Ay (x
y) co jest równoważne Ax Ey (x < y)

Ad 5. AxEt [AyAz x = y * z → y = 1 y = x] → [Ay A z ( t = y * z → y = 1 y = t)  x < t]

Ad 6. AxAyAz[(x =2*y +z → z < 2) → (z = 1  z = 0)]

Ad 7 An [ Ex(AyAz x = y * z → y = 1 y = x) 
]

Ad 8 Ax[(x>3  Ey (x=2* y) →Ez(AwAt z = w * t → w = 1 w = z)  Ev(AwAt z = w * t → w = 1 w = v) → x=z+v] lub równoważnie

Ax(2*x+1>3) →Ez Ev (AwAt ((z = w * t → w = 1 w = z)  (z = w * t → w = 1 w = v)) → x=z+v]

ZBIORY - PODSTAWOWE POJĘCIA

Zbiorami i relacjami zajmuje się nauka zwana teorią mnogości. Jednakże pojęcie zbioru można wprowadzić także na gruncie rachunku kwantyfikatorów. Możemy mówić o dwóch koncepcjach zbioru a) logicznej G. Fregego oraz matematycznej - Cantora i innych. Pojęcie zbioru ujętego logicznie będzie się przedstawiało krótko mówiąc jako własność elementów, albo inaczej obiektów spełniających pewną funkcję zdaniową.

Niech „{x: P(x)}” lub „
oznacza zbiór tych x, że P(x) . Symbol „{: }” oznacza operator abstrakcji, który tworzy nazwę zbioru z predykatu. Sens symbolu „” ustala tzw. prawo eliminacji: y {x: P(x)}  P(y). W myśl tego prawa przedmiot y jest elementem zbioru tych x, które maja własność P wtw. gdy przedmiot y ma własność P. Na oznaczenie zbiorów używamy najczęściej symboli A, B, C .... .Wyrażenie „x  A” czytamy „x jest elementem zbioru A” lub „x należy do zbioru A”. Zamiast wyrażenia „  x  A” piszemy „x A” „ x nie należy do A”.

1. Zbiór uniwersalny

V={ x: x = x}xVx = x nazywamy zbiorem pełnym (należą do niego wszystkie te przedmioty, które spełniają funkcje zdaniową x = x) . Ponieważ powyższą definicję można zapisać następująco: xVx = x a tezą jest „Ax (x = x)”, zatem tezą jest też

Ax (x = x)  AxV stwierdzającą, że każdy przedmiot należy do zbioru pełnego

2. Zbiór pusty

={x: x  x} nazywamy zbiorem pustym (należą do niego wszystkie te przedmioty, które spełniają funkcję zdaniową x  x. Ponieważ powyższą definicję można zapisać następująco: x: x  x a tezą jest „  Ex (x  x)”, zatem tezą jest też Ex (x  x)  Ex x stwierdzającą, że żaden przedmiot nie należy do zbioru pustego

Ex. 30. Niech zbiór pełny V będzie zbiorem liczb naturalnych. Przy użyciu funkcji zdaniowych

z= x*y, x/y i kwantyfikatorów zapisać funkcje zdaniowe jednej zmiennej wyznaczające zbiory

liczb parzystych - A

liczb nieparzystych - B

liczb pierwszych - C

zbiór jednoelementowy złożony z 3 - D

a) x  AEy (x=2* y)

b) x  BAy [Ez (y =2* z) → (x/y)]

c) x  C  AyAz [ x = y * z→ y =x  y =1]

d) x D  Ay[ x = y→ y =3]

Ex. 32. Elementami zbiorów mogą być również zbiory. Jeżeli A jest dowolnym zbiorem, to {A} symbolizuje zbiór jednostkowy, którego elementem jest zbiór A., co zapisujemy A∈{A}.

A≠{A}, tak samo jak a≠{a}. Ponadto porządek elementów w zbiorach nie odgrywa żadnej roli, zatem{a, b}={b, a}

Wśród podanych niżej zbiorów A,. B, C, D wskaż

1. zbiór o najmniejszej liczbie elementów

2. zbiór o największej liczbie elementów

3. zbiory identyczne

4. zbiory mające dokładnie jeden element wspólny

5. zbiory nie mające żadnego elementu wspólnego

A={1, 2, 3,. 4, 5}

B={2, {1, 4}, {3, 5, 6}}

C={{1, 2, 3, 4, 5}}

D={3, {2}, {{5}}}

E={{3-1}, 3, {{3+2}}}

OPERACJE NA ZBIORACH I ICH GEOMETRYCZNE INTERPRETACJE

1. Sumą A ∪ B nazywamy taki zbiór złożony z tych elementów, które należą do zbioru A lub do B

x ∈ (A ∪ B) ↔ x ∈ A ∨ x ∈B

2. Iloczynem ( przekrojem) A ∩ B nazywamy taki zbiór złożony z tyc elementów, które należą do A i należą do B

x ∈ (A ∩ B) ↔ x ∈ A ∧ x ∈B

V

a

3. Różnicą A - B nazywamy taki zbiór złożony z tych elemntów, które należą do A, a nie należą do B

x ∈ (A - B) ↔ x ∈ A ∧ x ∉B

V

3. Dopełnieniem zbioru A nazywamy taki zbiór A' złożony z tych wszystkich elemntów, które nie należą do zbioru A

x ∈ A'↔ x ∉A

a zatem A'=V-A

V

5. Dwa zbiory A i B są równe wtw. , gdy każdy elemnt który należy do zbioru A należy takżę do B i na odwrót

x ∈ A ↔ x ∈B

6. Między zbiorami A i B zachodzi relacja zawierania się ( inkluzji) A⊂ B wtw. gdy każdy elemnt który należy do zbioru A należy także do B

x ∈ A → x ∈B

V

Ex. 33. Obliczyć A ∪ B, A ∩ B, A-B, B-A dla następujących zbiorów

A={a, b, c}, B={c, d}

A={{a, b}, c}, B={c, d}

A={{a, {a}}, a}, B={a, {a}}

A={a, {a}, {b}}, B={{a}, {b}}

TWIERDZENIA RACHUNKU ZBIORÓW

Opierając się na wprowadzonych definicjach (sumy, iloczynu, różnicy, dopełnienia , zawierania ) oraz na prawach rachunku zdań można udowodnić odpowiednie twierdzenia dotyczące zbiorów.

Aksjomat ekstensjonalności dla zbiorów

Ax(xA xB)→A=B

Aksjomat ten stwierdza, że zbiory złożone z tych samych elementów są identyczne

DOWODY TWIERDZEŃ

Założeniowe

1. A=B → Ax (xA  xB)

1. A=B zał.

2. . xA xA taut. p  p

3. xA xB Ex I 1 i 2

4. Ax (xA  xB) DAk 3

Reguła ekstensjonalności:

Ex.I: V1= V2

P

P(V1// V2)

Reguła ExI : Jeżeli żadna zmienna wolna wyrażenia V1 nie jest związana w wyrażeniu P na miejscu zastąpienia; żadna zmienna wolna wyrażenia V2 nie staje się związana na miejscu zastąpienia w wyrażeniu stanowiącym wynik zastąpienia

2. A=BAB  BA

A=B zał.

A=B → Ax (xA  xB) Tw. Udow.

Ax (xA  xB) RO 1 i 2

Ax (xA xB) → Ax [(xA→ xB)  (xB→ xA)]

taut. (p q )→ (p→q) (q→p)

5. Ax [(xA→ xB)  (xB→ xA)] RO 4 i 3

6. Ax (xA→ xB) Ax (xB→ xA) Prwo rozkła. Kw. Ogóln. na konjuncję

7. AB  BA Def. zaw i 6

3. ABAB=A

AB zał.

Ax (xA→ xB) Def zaw.i 1

Ax(xA  xB xA) taut. (p→q) →(p  q p)

Ax(xA  Bx A) Def Ilocz. Zbiorów i 3

A  B =A RO Aks. Ekstens. i 4

Ex 34. Podać dowody praw de Morgana dla zbiorów i podać ich interpretację graficzną

( A  B)'= `A'B

(AB)'= A'  B'

PRAWA ALGEBRY ZBIORÓW

Prawa algebry zbiorów są zbudowane ze zmiennych reprezentujących nazwy zbiorów, stałych: , , -, V, , , = oraz operatorów logicznych. Nie występuje w nich symbol 

1. AA prawo zwrotności zawierania się zbiorów

2. AB BC→ AC prawo przechodniości zawierania się zbiorów

3. A  B= B A prawa przemienności iloczynu

4. AB= BA prawa sumy zbiorów

5. AB = (A'B')' prawo zastępowania sumy zbiorów iloczynem

6. A  B = (A'B')' ' prawo zastępowania iloczynu zbiorów sumą

7. A''= A dopełnienie dopełnienia zbioru A jest równe zbiorowi A

8. AA' =V suma zbioru A i jego dopełnienia jest równa zbiorowi uniwersalnemu

  A zbiór pusty jest zawarty w dowolnym zbiorze

10. AV każdy zbiór jest zawarty w zbiorze uniwersalnym

11. AB  CD → AC BD Prawo dodawania inkluzji stronami

Ex. 35. Operacja AB=(A-B)  (B-A) nazywa się różnicą symetryczną

podać interpretację graficzną

wykazać, że AA=

wykazać, że (AB) C = A(BC)

wykazać, że jeżeli A  B=, to AB= A  B

RELACJE

Zbiory jednoelementowe i dwuelementowe

Def 1.

Zbiór jednolementowy utworzony z przedmiotu x, to taki zbiór , którego jedynym elementem jest przedmiot x; oznaczamy go przez {x} i definiujemy:

y{x}y=x

Zbiór utworzony z elementów x, y, to taki zbiór którego jedynymi elementami są przedmioty x, y i tylko te; oznaczamy go przez {x, y} i definiujemy:

z{x,y}z = x  z=y

Z definicji tej wynika następująca teza:

{x,y}={y,x}

Def 2. Za pomocą pojęć rachunku zbiorów można zdefiniować pojęcie pary uporządkowanej o pierwszym elemencie x i drugim elemencie y, która będziemy oznaczać za pomocą symbolu x, y

x, y={{x}, {x,y}}

Na podstawie tej definicji można udowodnić twierdzenie:

x, y = z, u  x =z  y =u

x, y  z, u  x z  y u

x, y  y, z

Def. 3 Relacja dwuczłonowa R jest to zbiór par uporządkowanych; relacja n- członowa R jest zbiorem n- elementowych układów uporządkowanych. Na oznaczenie relacji wprowadzamy następujące symbole:

x, y R xRy

x1,..., xn R R(x1,..., xn)

Def. 4 Zbiór D(R) nazywa się dziedziną relacji R Dp(R) nazywa się przeciwdziedziną relacji

Zbiór C(R) nazywa się polem relacji R. Zbiory te określone są następująco:

a) x D(R) EyxRy

b) yDp(R) Ex xRy

c) C(R)=D(R)Dp(R)

Dla relacji n-członowej określa się pojęcie 1-ej, 2-ej,...n-ej dziedziny

C(R)=D1(R) ... Dn(R)

WYKRESY RELACJI

Iloczyn ( produkt) kartezjański dwóch zbiorów

Def. x, y  A  Bx A y B

Zbiór A  B nazywa się iloczynem kartezjańskim zbiorów A i B. Jest to zbiór par uporządkowanych, których pierwsze elementy należą do zbioru A, a drugie należą do B.

Relacja R o polu X

Zbiór R złożony z pewnych par uporządkowanych x, y, gdzie x i y należą do X nazywamy relacją dwuczłonową R o polu X , tzn. podzbiór produktu kartezjańskiego R X  X co zapisujemy x, y  R.

Ta definicja jest w istocie definicją geometryczną. Na ogół rozumie się przez nią związek a nie zbiór. Sam zbiór par nazywa się wtedy wykresem relacji R.

Ex. 36. Niech X={1, 2, 3, 4, 5, 6}. Produkt kartezjański Z= X  X składa się z 36 par. Rozpatrzmy podzbiór R produktu Z złożony z następujących par uporządkowanych:

1,1,1,2,1,3,1,4,1,5,1,6,

2,2,2,4,2,6,3,3,3,6

4,4,5,5,6,6

Jaka relacja zachodzi pomiędzy x i y?. Widać, że R jest relacja podzielności y przez x.

x, yRx/y

X 1 2 3 4 5 6

Wykres relacji podzielności R

Ex 37. Niech będzie relacja R w zbiorze A={1, 2, 3} określoną przez ..Narysuj wykres relacji R

3

0. 1 2

Wykres relacji R jest grafem skierowanym z pętlami

OPERACJE ALGEBRAICZNE NA RELACJACH

Niech R i S będą dwoma relacjami w zbiorze X.

1. Sumą relacji R i S nazywa się relację T taką, która zachodzi między elementami x i y wtedy i tylko wtedy, gdy między nimi zachodzi relacja R lub S co zapisujemy:

x R  Sy ↔ xRy ∨ xSy

2. Różnicą relacji R i S nazywamy relację Q taką, że która zachodzi między elementami x i y wtedy i tylko wtedy, gdy między nimi zachodzi relacja R, a nie zachodzi relacja S, co zapisujemy

x R-S y ↔xRy ∧ ¬ xSy

3. Iloczynem relacji R i S nazywamy relację Q taką, że która zachodzi między elementami x iy wtedy i tylko wtedy, gdy zachodzi między nimi zarówno relacja R jak i S, co zapisujemy:

xR  Sy ↔xRy ∧ xSy

4. Iloczynem względnym relacji R i S nazywamy relację Q taką, że , która zachodzi między elemntami x i y wtedy i tylko wtedy, gdy istnieje takie z, że między x i z zachodzi relacja R, a między z i y zachodzi relacja S, co zapisujemy:

x R | S y ↔E z (xRz ∧ zSy)

5. Negacją relacji (dopełnieniem) R nazywamy relację R' taką, która zachodzi między elementami x i y wtedy i tylko wtedy, gdy nie zachodzi między nimi relacja R, co zapisujemy:

xR'y   xRy

6. Konwersem relacji 6. R nazywamy relację R^-1 taką, która zachodzi między elementami x i y wtedy i tylko wtedy, gdy zachodzi między y a x relacja R, co zapisujemy

x R^-1 y  yRx

Ex 37. Udowodnić, że dla każdych x, y X

xR  Sy  (xRy  xSy)

xR  Sy  (xRy  xSy)

xR'y  (xRy)

Dowód 1.

xR  Sy x, y  R  Sx, y R  x, y S xRy  xSy

WŁASNOŚCI FORMALNE RELACJI

1. Relacje zwrotne w zbiorze X oznaczamy symbolem refl(X) i definiujemy

R  refl(X)  AxX (xRx)

2. Relacje symetryczne w zbiorze X oznaczamy symbolem sym(X) i definiujemy

R  sym(X)  AxyX (xRy→ yRx)

3. Relacje asymetryczne w zbiorze X oznaczamy symbolem as(X) i definiujemy

R  as(X)  AxyX (xRy→ yRx)

4. Relacje antysymetryczne w zbiorze X oznaczamy symbolem ants(X) i definiujemy

R  ants(X)  AxyX (xRy  yRx→ x = y)

5. Relacje przechodnie w zbiorze X oznaczamy symbolem trans(X) i definiujemy

R  trans(X)  Axyz X (xRy yRz→xRz) AxyzX (xRy  yRz → xRz)

6.Relacje spójne w zbiorze X oznaczamy symbolem con(X) i definiujemy

R  con(X)  Axy X (xRy  yRx)

RELACJA RÓWNOWAŻNOŚCI

Def. Relację R określoną w zbiorze X nazywamy relacją równoważności, jeżeli jest ona zwrotna, symetryczna i przechodnia w zbiorze X i oznaczamy symbolem .

Ex 38. Niech R będzie relacją „=” określoną w zbiorze X liczb rzeczywistych.

Dla każdych x, y, z X zachodzi

x = x,

x =y → y = x

x =y  y = z→ x = z

Relacja „=” jest relacją „ ”.

Tw.1 (Zasada abstrakcji). Jeżeli w zbiorze X określona jest relacja równoważności „ ”, to podzbiory: [x], [y],... (zwane klasami abstrakcji relacji równoważności), określone następująco:z [x]  z x

spełniają następujące warunki:

każda klasa jest niepusta

suma wszystkich klas daje zbiór X

każde dwie klasy są albo rozłączne albo identyczne

dwie klasy są identyczne [x]=[y] wtedy i tylko wtedy, gdy x  y

Niech w zbiorze X określona będzie relacja „”. Weźmy dowolne xX. Tworzymy podzbiór [x] zbioru X zwany klasa abstrakcji elementu x, złożony ze wszystkich tych elementów yX, które są równoważne x.

1. Wobec zwrotności „” x[x]

2. Wobec tego, że każdy element zbioru X tworzy klasę abstrakcji, zatem

[x]  [y] ...=X

3. Jeżeli x y, to [x]=[y], gdyż z[x]. wtw. gdy zx, wobec przechodniości relacji „”

zy, czyli z[y]. A zatem [x][y]. Podobnie z[y] wtw gdy. zy wobec przechodniości relacji „” z x, czyli z[x]. A zatem [y][x]. A zatem [x]=[y]

4. Jeżeli x  y, to [x]  [y] =. Załóżmy[x]  [y]   . Istnieje takie z, że z[x] i. z[y]. Stąd z zx i z  y, a wobec przechodniości relacji „” x  y. A zatem jeżeli x  y,

to [x]  [y] =.

Zasada abstrakcji ma dla matematyki wielkie znaczenie, gdyż pozwala z elementów jakiegoś zbioru przedmiotów, w którym jest określona relacja równoważności, tworzyć nowe obiekty - klasy abstrakcji tej relacji - klasy abstrakcji tej relacji, utożsamiając wszystkie przedmioty równoważne.

RELACJE PORZĄDKUJĄCE

Def. . Relację R określoną w zbiorze X nazywamy relacją porządkującą, jeżeli jest ona zwrotna, antysymetryczna i przechodnia w zbiorze X

Ex.39. Niech relacja R oznacza relacje podzielności (x|y) ( x jest dzielnikiem y) w zbiorze X liczb naturalnych.

x|x

jeżeli x|y i y|x, to x=y

jeżeli x|y i y|z, to x|z

Ex. 40 .Niech X będzie zbiorem podzbiorów ustalonego zbioru A={1, 2, 3}. Relacja R niech będzie relacja inkluzji „” czyli zawierania się podzbiorów. Narysuj graf tej relacji.

Podzbiory: {1, 2, 3}, {1, 2}, {1, 3}, {2, 3}, {1}, {2}, {3},

{1, 2, 3}

{1, 2} {1, 3} {2, 3}

{1} {2} {3}

∅

Graf relacji inkluzji zbioru X podzbiorów zbioru A={1, 2, 3}

Def. Relację R porządku w zbiorze X nazywamy relacją liniowego porządku, jeżeli spełnia własbość spójności.

Ex. 40 Relacją liniowo porządkującą jest relacja „” oraz relacja” ≥”. Nie jest nią natomiast relacja „>” ani też relacja „<”, które są tylko relacjami częściowego porządku, gdyż nie śą spójne. Innym ważnym przykładem relacji liniowego porządku jest tak zwane uporządkowanie leksykograficzne
.

Ex 41. Dla następujących relacji w zbiorze A={0, 1, 2, 3} określ, które z własności refl, sym, trans as spełniają następujące relacje

x, y  R1, jeśli x +y=3

x, y  R2, jeśli x -y jest liczbą parzystą

x, y  R3, jeśli x  y

x, y  R3, jeśli max{x, y}=3

Narysuj wykres każdej z tych relacji. Nie rysuj strzałek, jeśli relacja jest symetryczna.

FUNKCJE

Pojęcie funkcji, aczkolwiek było od dość dawna używane przez matematyków doczekało się stosunkowo dość późno precyzacji za sprawą G. Peano w terminach teorii relacji.

Def 1. Funkcją f określona na zbiorze X (zwanego dziedziną funkcji), o wartościach należących do zbioru Y (zwanego przeciwdziedziną), nazywamy relację R, która każdemu elementowi dziedziny, przyporządkowuje jeden i tylko jeden przedmiot przeciwdziedziny, co oznaczamy f: X→ Y, a czytamy zazwyczaj funkcja f odwzorowuje zbiór X w zbiór Y, co można opisać poniższym diagramem:.

x . f(x)

Funkcje określamy dwoma sposobami:

a) postać algebraiczna

podając zbiór X na którym jest określona i regułę lub wzór f(x) dla każdego x X.

2. postać graficzna

podając podzbiór U par uporządkowanych  x, y> iloczynu kartezjańskiego X  Y takich, że

y = f(x)  x, y> f.

Rodzaje funkcji

1. Funkcja różnowartościowa

Funkcja f: X→ Y jest funkcja różnowartościową, jeśli różnym elementom zbioru X funkcja przyporządkowuje różne wartości w zbiorze Y.

2. Funkcja „na”

Funkcja f: X→ Y jest funkcją przekształcającą zbiór X na Y, jeśli dla każdego yY, istnieje takie x, że y = f(x), tzn. każdy element przeciwdziedziny jest wartościa funkcji dla jakiegoś argumentu.

3. Funkcja jako przekształcenie wzajemnie jednoznaczne:

Funkcję f: X→ Y nazywamy przekształceniem wzajemnie jednoznacznym wtw. gdy jest różnowartościowa i przekształca zbiór X na Y.

Ex 42. Określ rodzaj funkcji

• • • • • • • •

• • • • • • •

• • • • • • • •

• • • • • •

• • • • • •

a) b) c) d)

1. funkcja „na”

2. funkcja różnowartościowa

3. przekształcenie wzajemnie jednoznaczne

4. przekształcenie nie jest funkcją

Ex. 43. Niech X={1, 2, 3, 4, 5} i weźmy następujące funkcje ze zbioru X w zbiór X

f(n) = 6-n

g(n) = max{3, n}

h(x)= max{1, n-1}

- zapisz każdą z tych funkcji jako zbiór par uporządkowanych, tzn. wypisz elementy ich wykresów

- naszkicuj wykres każdej z tych funkcji

- które z tych funkcji są jednocześnie różnowartościowe i „na”

Operacje na funkcjach

1. Superpozycja

Niech będą dane funkcje f: X→ Y i g: Y→ Z. Dla każdego elementu xX istnieje wówczas dokładnie jeden element zZ, taki że z =g(f(x)). Funkcje f i g wyznaczają więc nową funkcję h: X→ Z określoną w następujący sposób: h(x) = g(f(x)) dla każdego xX. Funkcję h nazywamy superpozycją lub złożeniem funkcji f i g i oznaczamy symbolem g  f. Z definicji mamy: (g  f)(x) = g(f(x))

f g

g ο f

Ex. 44. Niech f(x)= x² a g(x) = x+1. Niżej podane funkcje wyraź za pomocą funkcji f i g

1. h(x)= x² +1 h(x)=( g ο f) (x)

b) h(x)= (x +1)² h(x)=( f ο g) (x)

c) h(x)= x +2 h(x)=( g ο g) (x) = g²(x)

d) h(x)= x⁴ h(x)=( f ο f ) (x) = f ²(x)

e) h(x)= (x² +1)² h(x)= fο ( f ο g ) (x)

f) h(x)= (x +2)² h(x)= fο ( g ο g ) (x)

2. Odwracanie funkcji

Funkcję g: Y→ X nazywamy funkcją odwrotną do funkcji f: X→ Y jeżeli y = f(x)(zbiór argumentów funkcji g jest zbiorem wartości funkcji f) a x= g(y) (zbiór argumentów funkcji f jest zbiorem wartości funkcji g) i dla każdego x X zachodzi równość g(f(x)) = x. Funkcję g oznaczamy symbolem f ^-1. Funkcje, które posiadają funkcje odwrotne nazywamy funkcjami odwracalnymi.

f

f ^-1

Ex 45. Znajdź funkcje odwrotne następujących funkcji, przedstawiając je w podobnej formie np. f(x) = 2x f ^-1(x) =

1. f(x)= 2x - 3

2. f(x)= 3 - 5x

3. 
   

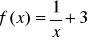
d)

e)

Funkcja identycznościowa

Funkcję f : X→X przekształcającą każdy x X na samego siebie nazywamy funkcja identycznościową i oznaczamy I.

I(x) = x

Funkcja stała

Funkcję f : X→Y nazywamy funkcją stała, jeśli istnieje element y0Y taki, że f(x)= y0 dla wszystkich x X.

Funkcja charakterystyczna

Weźmy zbiór X i jego podzbiór A. Funkcję określoną na zbiorze X, która przyjmuje wartość 1 dla elementów x A i wartość 0 dla xA, nazywamy funkcja charakterystyczna zbioru A i oznaczamy A.

1 dla x A

A =

0 dla xA

Ex. 46. Dla n  Z (zbiór liczb całkowitych) niech
funkcja f jest funkcja charakterystyczna pewnego podzbioru zbioru Z. Jaki to podzbiór?

Liczby parzyste dodatnie, gdyż f(n)= 1 dla n - parzystych i 0 dla nieparzystych

MOCE ZBIORÓW. ZBIORY NIESKOŃCZONE

Badania nad mocami zbiorów są jednym z podstawowych działów teorii mnogości. Terminem pierwotnym jaki zostaje tu użyty jest termin równoliczność zbiorów, który to termin po raz pierwszy został sprecyzowany przez G. Cantora twórcę matematycznej koncepcji zbiorów.

Def. 1. Zbiory X i Y nazywamy równolicznymi, jeśli istnieje funkcja różnowartościowa

f: X→ Y przekształcająca zbiór X na Y. Funkcja f ustala równoliczność zbiorów X i Y. Jeżeli zbiory X i Y są równoliczne, to piszemy X~Y.

Ex. 47. Jeżeli X={1, 2, 3, 4} a zbiór Y={2, 4, 6, 8}, to zbiory te są równoliczne, gdyż istnieje funkcja różnowartościowa f określona następująco f(x)=2x, która przekształca zbiór X na Y.

Własności równoliczności

X ~ X

X~ Y→ Y~ X

X~ Y  Y~ Z→ X~ Z

Zachodzi 1. gdyż istnieje Ix(x)=x, która przekształca X na X

Zachodzi 2. gdyż jeśli istnieje f przekształcająca X na Y , to istnieje f -1: Y→ X, przekształcająca Y na X

Zachodzi 3., gdyż jeśli istnieje f: X→ Y przekształcająca X na Y oraz jeśli istnieje g: Y→ Z, to istnieje f  g: X→ Z, które przekształca X na Z

Określenie mocy zbioru

Każdemu zbiorowi X przyporządkowana jest pewna własność zwana mocą zbioru lub liczba kardynalną, która nie zmienia się jeśli elementy zbioru X zastąpi się wzajemnie jednoznacznie przez inne elementy, a także wtedy gdy zmieni się uporządkowanie elementów zbioru X.. Liczbę kardynalną zbioru X oznaczamy przez
.

Zachodzą następujące zależności

(
=
)  X~ Y

Jeżeli zbiór X jest zbiorem n -elementowym, to
= n

Ex 48. Niech X={1, 4, 6, 9};
= 4. Jeśli X jest zbiorem pustym, to jego mocą jest liczba kardynalna n = 0

Zbiory skończone, nieskończone i przeliczalne

Def. 1. X jest zbiorem skończonym wtw, gdy E nN
= n

Def 2. X jest zbiorem nieskończonym wtw, gdy E nN
= n

Def. 3 Jeżeli N jest zbiorem liczb naturalnym, to
= ₀ (alef zero)

Def. 4. Zbiorami przeliczalnymi nazywamy zbiory skończone lub nieskończone równoliczne ze zbiorem N.

Ex. 49. Niech X będzie zbiorem liczb naturalnych parzystych, a Y zbiorem liczb naturalnych nieparzystych. Jakiej mocy są zbiory X i Y.

Istnieje f: N→X, określone wzorem f(n)=2n, które przekształca N na X. Zatem jeżeli N~X, to
=
. Skoro
= ₀ ,
=₀

Istnieje g: N→Y, określone wzorem f(n)=2n-1, które przekształca N na Y. Zatem jeżeli N~Y, to
=
. Skoro
=₀ ,
=₀

Ex. 50. Wykazać, że jest zbiory X i Y są mocy ₀, to X Y też jest mocy₀.

Niech f: N→X i g: N→Y przekształca zbiór N odpowiednio na X i Y. Mamy zatem pary

f(1), g (1)>, f(1), g (2)> , f(1), g (3)>,.... f(1), g (n)>,...

f(2), g (1)>, f(2), g (2)> , f(2), g (3)>,.... f(2), g (n)>,...

f(3), g (1)>, f(3), g (2)> , f(3), g (3)>,.... f(3), g (n)>,... ............................................................................................

f(m), g (1)>, f(m), g (2)> , f(m), g (3)>,.... f(m), g (n)>,...

.................................................................................................

Ustawiając pary w odpowiednim porządku można ustalić funkcję h: N→ X Y

Która przekształca zbiór N na iloczyn kartezjański zbiorów X i Y.

h(1)= f(1), g (1)> pierwsza przekątna

h(2)=f(1), g (2)>

h(3)= f(2), g (1)> druga przekątna

h(4)= f(3), g (1)>

h(5)= f(2), g (2)> trzecia przekątna

h(6)= f(1), g (3)>

.............................

Zatem Iloczyn kartezjański X i Y jest mocy ₀, co zapisujemy
=₀

Def.1 Niech  oznacza zbiór liczb rzeczywistych.. Zbiory o mocy c nazywa się zbiorami o mocy continuum.

Udowodnimy, że zbiór o mocy continuum jest nieprzeliczalny. W tym celu wystarczy udowodnić, że zbiór liczb rzeczywistych  posiada moc różną od ₀ tzn. ₀ c. Dowód taki pochodzi od Cantora i nazywa się dowodem przekątniowym. Jest on dowodem nie wprost.

Dowód.

1. Załóżmy, że
=₀

Niech  składa się z wszystkich liczb rzeczywistych uporządkowanych w różnowartościowy nieskończony ciąg: r₁, r₂, r₃,...

Dla każdej liczby rzeczywistej istnieje jej rozwinięcie na ułamek dziesiętny nieskończony, wyrazy ciągu można przedstawić następująco:

r₁= c₁, c₁₁ c₁₂...

r₂= c₂, c₂₁ c₂₂...

........................

r_n= c_n, c_n1 c_n2...

.......................

gdzie c_n jest częścią całkowitą, a c_n1 c_n2, ... kolejnymi cyframi rozwinięcia dziesiętnego liczby rn. Budujemy tabelę, która przyporządkowuje każdej liczbie naturalnej liczbę rzeczywistą.

1 2 3 4 . n .

c1, c11 c12 ................. c2,c21c22....................... c3,c31c32 c33................. c4,c41c42 c43 c44........... .......................................cn, cn1 cn2.............. cnn ..................................

1. Określmy liczbę r następująco: r = 0,d1 d2..., gdzie dla każdego n ≥1

0, gdy cnn ≠ 0

dn=

1, gdy cnn = 0

a) Z założenia liczba r jest liczba rzeczywista, a więc należy do ciągu wszystkich liczb rzeczywistych zebranych w tabeli.

b) Z drugiej strony liczba r różni się od każdej liczby rzeczywistej ciągu zebranego w tabeli, gdyż różni się od niej przynajmniej na jednej pozycji nieskończonego rozwinięcia dziesiętnego liczby rn. Wystąpiła sprzeczność a zatem
≠
i ℵ₀≠ c.

Nierówności między liczbami kardynalnymi. Twierdzenie Cantora-Bernsteina

Niech
= n i
=m. Przyjmujemy, że liczba kardynalna n jest nie większa od liczby kardynalnej m, jeżeli zbiór X jest równoliczny z podzbiorem zbioru Y. Wówczas

Każdy zbiór mocy n jest równoliczny z pewnym podzbiorem zbioru mocy m, co zapisujemy n  m

Jeżeli n  m i n  m to mówimy, że liczba kardynalna n jest mniejsza od liczby m i piszemy n m

Ex 51. Zbiór N wszystkich liczb naturalnych jest równoliczny z podzbiorem zbioru , czyli ze zbiorem N  . Ponieważ zbiór  jak to ustalono jest nieprzeliczalny, zatem

a stąd mamy ₀ c

Tw. Cantora-Bernsteina

1). Dla dowolnych liczb kardynalnych n i m zachodzi:

Jeżeli n  m i m  n, to n = m

Dla dowolnych zbiorów X, Y, Z zachodzi:

a) Jeżeli X Y Z, to



b) Jeżeli X Y Z i
=
, to
=
=

Zbiór potęgowy. Twierdzenie Cantora

Niech f: X→{0, 1} będzie funkcją charakterystyczna zbioru X. Niech {0, 1}X oznacza zbiór wszystkich takich funkcji, które nazywamy funkcjami charakterystycznymi podzbiorów zbioru X.

1. Dla każdego zbioru X zbiór wszystkich podzbiorów zbioru X jest równoliczny ze zbiorem{0, 1}^X . Zbiór wszystkich podzbiorów zbioru X będziemy oznaczać symbolem 2X i nazywać zbiorem potęgowym zbioru X. (należy pokazać, że istnieje funkcja g, która ustala równoliczność rodziny wszystkich podzbiorów zbioru X i zbioru {0, 1}^X)

2. Zbiór wszystkich podzbiorów zbioru N jest mocy c, więc
= c

Tw. Cantora

Dla każdego Zbioru X zachodzi:

<

Wniosek:

1. Twierdzenie Cantora pozwala konstruować zbiory coraz wyższych mocy. Wychodząc np. ze zbioru N wszystkich liczb naturalnych konstruujemy zbiory: N, 2^N,
, przy czym z Tw. Cantora i 2. mamy:

₀=
<
<
< ...

2. Nie istnieje zbiór wszystkich zbiorów.

Gdyby bowiem istniał zbiór wszystkich zbiorów A, to rodzina 2A wszystkich podzbiorów A byłaby sama podzbiorem A.

FUNKCJE OBLICZALNE

Funkcje obliczalne zwane też funkcjami rekurencyjnymi stanowią bardzo ważny dział logiki, pozwalają one na precyzyjne sformułowanie wielu zagadnień dotyczących algorytmów. Okazuje się bowiem, że za pomocą tego pojęcia można zdefiniować pojęcie efektywnej procedury rozstrzygania, czy też obliczania. Intuicyjna treść pojęcia funkcji obliczalnej wyjaśnia się nieraz za pomocą następującego sformułowania: Funkcja jest obliczalna, gdy istnieje efektywna metoda, za pomocą której można obliczyć jej wartość dla dowolnego ciągu jej argumentów. W latach trzydziestych udało się sprecyzować określenie pojęcia funkcji obliczalnej; podano też kilka równoważnych definicji tego pojęcia.

Zamk(X,K)

Najmniejszy zbiór, zawierający zbiór X i zamknięty ze względu na zbiór operacji K.

Zbiór funkcji obliczalnych określa się często posługując się pojęciem najmniejszego zbioru, zawierającego określone funkcje wyjściowe i zamkniętego na określone operacje.

Def 1. Zbiór X jest zamknięty ze względu na funkcję f , gdy dla każdego x f(x) X

Ex1. Niech funkcja S będzie określona w następujący sposób S(n)=n+1 dla każdego nN Zbiór liczb naturalnych N, jest zamknięty na funkcję następnika, gdyż następnik liczby naturalnej też jest liczba naturalną.

Def. 2. Zbiór X jest zamknięty ze względu na zbiór funkcji K co oznaczamy Zamk(X,K) wtedy i tylko wtedy, gdy jest zamknięty ze względu na każdą funkcję należącą do K

Def. 3. Najmniejszy zbiór zawierający zbiór X i zamknięty ze względu na zbiór operacji (funkcji) K jest to iloczyn wszystkich zbiorów, które zawierają zbiór X i są zamknięte ze ze względu na zbiór operacji (funkcji)

Ex 51. Posługując się tym pojęciem można zdefiniować wiele zbiorów np. zbiór liczb naturalnych, zbiór tautologii rachunku zdań itp.

Zbiór N liczb naturalnych, jest to najmniejszy zbiór zawierający zbiór X={0} i zamknięty ze względu na funkcję S następnika

Zbiór tez (tautologii) aksjomatycznego systemu rachunku zdań Łukasiewicza Ł3, jest to najmniejszy zbiór, do którego należą trzy aksjomaty i zamknięty ze względu na operację (reguły) odrywania, podstawiania i zastępowania członów definicji

Definicja Funkcji obliczalnych

Funkcje obliczalne należą do takiego zbioru funkcji, których zarówno dziedziną jak i przeciwdziedziną jest zbiór liczb naturalnych.

Zbiór X funkcji wyjściowych

Z(x), czyli jednoargumentowa funkcja stała, przyjmująca 0 dla dowolnego xN

S(x)= x+1, czyli funkcji następnika

(x₁,..., x_n)= x_i , czyli n-argumentowej funkcji identycznościowej

Ex. 52. Podaj wartości dla wyżej podanych funkcji, dla argumentów będących kolejnymi liczbami naturalnymi

a) Z(1)=0, Z(2)=0,..., Z(10)=0, ...

b) S(0)=1, S(1)=2,...,S(10)=11, ...

c)
(x)=x,
( x₁, x₂)= x₂,
( x₁, x_2, x₃)= x₃, ...

Zbiór operacji K określania nowych funkcji

a) Składania funkcji wyrażonej wzorem

f (x₁, . . .,x_n)=g(h₁(x₁, . . .,x_n),..., h_m(x₁, . . .,x_n))

Mając kreślone funkcje g i h_i , gdzie 1 i  m można określić nowa funkcję f będącą ich złożeniem. Gdy n=1 i m=1wtedy mamy :

f (x)= g(h(x))

b) Rekursji prostej wyrażonej wzorami :

f (x₁, . . .,x_n,0)= g(x₁, . . .,x_n)

f (x₁, . . .,x_n,y+1) = h(x₁, . . .,x_n, y, f (x₁, . . .,x_n,y )

Mając kreślone funkcje g i h, można określić nowa funkcję f. Gdy n=1 wzory te przybierają postać:

f (0)=k, gdzie kN

f (y+1)=h(y, f (y))

6) Operacja minimum efektywnego wyrażona wzorem:

f (x₁, . . .,x_n) = y[g (x₁, . . .,x_n, y)=0] , gdy dla każdego x₁, . . .,x_n istnieje takie y gdzie y oznacza najmniejsze takie yN, że funkcja g określona wzorem g(x₁, . . .,x_n, y)=0, pod warunkiem, że dla każdego x1,..., xn istnieje takie y , że g(x₁, . . .,x_n, y)=0

Mając kreśloną funkcję g można określić nową funkcję f. Gdy n=1 mamy wtedy:

f(x)= y[g(x,y)=0]. Określenie funkcji f polega na obliczeniu dla danego x kolejno wartości

g (x, 0), g (x, 1), g (x, 2),... tak długo aż natrafimy na pierwsze takie n.N, że g (x, n)=0. To znalezione n będzie wartością funkcji f.

Def 4. Zbiór funkcji obliczalnych jest to najmniejszy zbiór zawierający zbiór X funkcji określonych wzorami 1-3 i zamkniętych ze względu na zbiór operacji K określonych wzorami 4-5.

Wniosek: Jeżeli funkcja f jest obliczalna, to jest ona otrzymana z funkcji 1-3 w skończonej ilości operacji 4-6, tzn. istnieje skończony ciąg funkcji, którego ostatnim wyrazem jest funkcja f i którego każdy wyraz bądź jest jedna z funkcji 1-3, bądź jest uzyskany z wcześniejszych od niego wyrazów tego ciągu za pomocą jakiejś z operacji 4-6

Ex 53. Przykłady funkcji obliczalnych

a) f(x) = n , gdzie xN a n jest stałą i nN

Funkcję f można uzyskać z funkcji Z(x)=0 poprzez n-krotne składanie z funkcją następnika

f(x) =S(S(S...S(Z(x)))) = n

n razy

b) funkcja f(x, y)=x + y

Funkcję f można określić wychodząc od funkcji identycznościowej I i funkcji następnika S za pomocą rekursji prostej, tzn.

f(x,0)= x+0= x=I(x)

f(x, y+1)=S(x+y)=S(f(x,y))

c) funkcja f(x, y)=x * y

Funkcję f można określić wychodząc od funkcji stałej Z, takiej, że f(x,0)=Z(x) i funkcji obliczalnej g(x, y, z)= z+x za pomocą rekursji prostej, tzn.

f(x,0)=x*0=0=Z(x)

f(x, y+1)= (x*y)+x =g(x, f(x,y))

d) ) funkcja f(x)=[
], gdzie [x] oznacza cześć całkowitą z x.

Funkcję f można określić za pomocą operacji minimum efektywnego dla funkcji g określonej wzorem

g(x, y)= 0 (y+1)2>x

1 (y+1)2  x

a zatem f(x) =y [ (y+1)2>x]= y [g(x, y)=0]

Według tego określenia f(1) = [
]=1, f(2) = [
]=1,..., f(5) = [
]=2

Jest to operacja minimum, gdyż dla każdego x istnieje takie y, że (y+1)2>x. Tak np. dla x=1

g(1,y) =0 dla y=1, 2, 3, 4, ... jednakże minimalnym jest y=1, a zatem f(1) =1

Funkcja g jest zaś obliczalna z funkcji Z i S za pomocą rekursji prostej, gdyż

g(x, 0)=1=S(Z(x))

g(x, y+1)=Z(S(Zx))=Z(g(x, y), y)

Twierdzenie.

Zbiór funkcji obliczalnych jest zbiorem przeliczalnym o mocy ₀

Dowód.

W definicji zbioru funkcji obliczalnych wychodzimy z przeliczalnego zbioru funkcji

(1) Z, S oraz
. Ta ostatnia dla różnych n posiada przeliczalny zbiór układów zmiennych x1,..., xn a więc mamy także przeliczalny ciąg funkcji
. Oznaczmy zbiór (1) przez X0. Dołączmy do X0 wszystkie funkcje zdefiniowane przez a) złożenie, b) rekursję, c) minimum efektywne zastosowane do zbioru funkcji X0 i oznaczmy je przez X1. Ogólne do zbioru Xi złożonego z funkcji dołączamy za pomocą omówionych operacji nowe funkcje i tworzymy zbiór Xi+1. Powstaje ciąg X0 X1 X2. . . zbiorów przeliczalnych. Każda funkcja obliczalna należy do jednego ze zbiorów Xi. Elementy zbiorów X0 ,X1, X2... ustawiamy w ciągi:

X0=

X1=

X2=

...............................

Licząc elementy na przekątnych ustawiamy je w ciąg:
przypisując im kolejne liczby naturalne. A zatem zbiór funkcji obliczalnych jest przeliczalny.

Uwaga: Można udowodnić, że moc zbioru wszystkich funkcji wielu zmiennych, o argumentach i wartościach będących liczbami naturalnymi jest równa
.

Podanie konkretnego przykładu funkcji nieobliczalnej jest jednak bardzo trudne, gdyż większość funkcji, z którymi spotykamy się w praktyce, to funkcje obliczalne.

Funkcje obliczalne mają szerokie zastosowanie w teorii maszyn cyfrowych. Komputery w swojej pracy nie wykonują nic innego, jak operacje składania, schemat rekursji prostej i schemat minimum efektywnego. Dla każdej funkcji obliczalnej istnieje urządzenie czy to mechaniczne lub elektroniczne (np. arytmometr), o bardzo dużej pamięci do zapisywania wyników pośrednich, obliczy wartość funkcji dla dowolnych argumentów. Wielkość pamięci która maszyna musi zużyć jest dla danego argumentu skończona, choć nie daje się z góry oszacować, podobnie czas liczenia również nie daje się z góry oszacować, choć jest skończony.

Teza Turinga

Funkcjami obliczalnymi są dokładnie te funkcje, dla których istnieje maszyna cyfrowa mająca skończoną ilość stanów wewnętrznych i nieskończoną pamięć, zdolna w skończonym, choć z góry nie dającym się oszacować czasie, obliczyć wartość funkcji dla zadanego argumentu i zatrzymać się po wykonaniu obliczenia.

Teza Churcha

Każde zagadnienie dla którego istnieje efektywny sposób rozwiązania, daje się wyrazić w odpowiednim tłumaczeniu za pomocą funkcji obliczalnych.

Ex 54. Zastosowanie funkcji obliczalnych w zagadnieniu gry w szachy:

Na 64 polach szachownicy znajduje się pewna ilość figur nie więcej niż 32, a nie mniej niż 2.

Każdemu ustawieniu figur można przyporządkować numer będący liczba naturalna. Ponumerujmy pola liczbami 0d 1 do 64, figury zaś:

Białe : 1- pionek, 2- wieża, 3- skoczek, 4-goniec, 5-hetman, 6- król

Czarne: 7- pionek, 8- wieża, 9- skoczek, 10-goniec, 11-hetman, 12- król

Jeżeli na polu o numerze i nie stoi figura, to piszemy ci=0

Jeżeli na polu o numerze i stoi figura o numerze c, to piszemy ci= c. Piszemy ponadto c0=0, jeżeli ruch maja białe , a c0=1 jeżeli ruch maja czarne. Niech q=13 będzie zasada numeracji

Pi=( c64 c63 c62... c1 c0)13 i=1, 2, ...n...

Niech

P1=(8 7 10 11 12 10 9 8 7 7 7 7 7 7 7 7 0 ...0 1 1 1 1 1 1 1 1 2 3 4 5 6 4 3 2 0)13

będzie początkowym ustawieniem, zaś

Pn=(1 0 0 0 7 0 4 0 0 0 2 0 0 0 0 12 0 6 0 0 2 0)₁₃ n - tym ustawieniem zapisanym w systemie 13- nastkowym.

Można udowodnić, że funkcja f określona następująco:

1 jeżeli x jest numerem pozycji wygrywającej dla białych

2 jeżeli x jest numerem pozycji wygrywającej dla czarnych

f(x)= 3 jeżeli x jest numerem pozycji remisowej

0 jeżeli x nie jest numerem pozycji dopuszczalnej do gry w szachy

nie jest funkcją obliczalną. Wartość funkcji f dla liczby x przedstawionej przez Pn=1. Nie potrafimy jednak obliczyć wartości funkcji f dla liczby x przedstawionej zapisem P1

Algebry Boole'a

1. Definicja Algebr Boole'a

Def.1 Algebrą Boole'a nazywamy zbiór X co najmniej dwóch elementów, jeżeli spełnione są następujące warunki:

1. w zbiorze X istnieją dwa elementy wyróżnione, które oznaczamy przez 0 i 1

2. w zbiorze X określone są trzy operacje A∪ B, A ∩ B, A” zwane odpowiednio sumą boole'owską, iloczynem boole'owskim i dopełnieniem, które nie wyprowadzają poza zbiór X, tzn. dla każdych elementów A i B należących do X również A∪ B, A ∩ B, A” należą do X

3. na elementach zbioru X określona jest relacja równoważności oznaczona przez „=” spełniająca następujący warunek: dla każdych elementów A, B, C należących do X, jeżeli A=B, to również A'=B', A ∪ C =B ∪ C, A ∩ C =B∩ C

4. operacje wymienione w b) spełniają następujące aksjomaty

A1. A ∪ B =B ∪ A przemienność

B1. A ∩ B =B ∩ A

A2. A∪ (B∩ C)= (A ∪ B) ∩ (A∪ C) rozdzielność

B2. A ∩ (B ∪ C) = (A ∩ B) ∪ (A∩ C)

A3. A ∪ 0=A

B3. A ∩1=A

A4. A∪A'=1

B4. A ∩ A'=0 własności stałych

2. Przykłady Algebr Boole'a

1. Algebrą Boole'a jest algebra zbiorów

Niech Z={1, 2, 3},a X będzie zbiorem podzbiorów zbioru Z. Załóżmy, że

{1, 2, 3}=1; {1, 2}=e¹; {1, 3}=e²; {2, 3}=e³; {1}=e⁴; {2}=e⁵; {3}=e⁶; {0}=0

Czyli X={{1, 2, 3}, {1, 2}, {1, 3}, {2, 3}, {1}, {2}, {3}, {0}}={1, e¹ ,e² ,e³ ,e⁴ e⁵ ,e⁶,0}

Sprawdźmy, czy spełnione są aksjomaty algebry Boole'a dotyczące stałych 0, 1

Za A przyjmujemy pierwszy element, tzn. A={1,2,3}

A3. A ∪ =A

1 ∪ 0={1, 2, 3}∪{0}={1, 2, 3}= e¹

B3. A ∩ A'=0

1 ∩ (1 )'={1,2, 3}∩ {0}={0}=0

A4. A∪A'=1

1 ∪ (1 )' ={1,2, 3} ∪{0}={1,2, 3}=1

B4. A ∩1=A

1 ∩ 1 ={1,2, 3}∩{1,2, 3}={1,2, 3}= 1

2. Algebrą Boole'a jest też rachunek zdań

Niech X będzie zbiorem wszystkich formuł rachunku zdań, zawierających 0, 1 i zmienne p₁, p_{2,. . .,} zamkniętych ze względy na operacje : ∧, ∨. Zbiór X ma następującą postać:

X={0, 1, p_1,. p_{2, . . .,} ¬ p_{1,. . .,} p₁∧ p_{2, . . .,} p₁ ∨ p_{2 ,. . .}}

Niech

„1” - oznacza symbol zdania prawdziwego

„0” - oznacza symbol zdania fałszywego

„¬” - oznacza operację dopełnienia „ ' ”,

„∧”- oznacza operację iloczyn boole'owski „∩”

„∨”- oznacza operację sumy boole'owskiej „∪”

„↔” - oznacza relację równoważności

Sprawdźmy czy przy danej interpretackji spełnione są aksjomaty dla stałych Boole'a

A3. A ∪ 0=A

p∨ 0 ↔ p

B3. A ∩ A'=0

p ∧ ¬p ↔ 0

A4. A∪A'=1

p∨ ¬p↔1

B4. A ∩1=A

p∧1 ↔p

3. Algebrą Boole'a jest algebra sieci kontaktowych

Niech X będzie zbiorem wszystkich możliwych dwubiegunowych sieci kontaktów, z których każdy może być zamknięty, bądź otwarty. Elementami wyróżnionymi zbioru X będą:

0 - sieć składająca się z jednego, ciągle otwartego, kontaktu

1 -sieć składająca się z jednego, ciągle zamkniętego, kontaktu

operacje algebry boole'owskiej interpretujemy następująco:

„∩” - mnożenie sieci

„∪” - sumowanie sieci

„ ' ” - negacja sieci

1. Jeżeli A i B są sieciami należącymi do X, to ich A∪B jest siecią otrzymaną przez równoległe połączenie sieci:

A

B

2. Jeżeli A i B są sieciami należącymi do X, to ich A∩B jest siecią otrzymaną przez szeregowe połączenie sieci:

A B

N

3. Negacja sieci polega na zmianie kontaktów z zamkniętych na otwarte, a z otwartych na zamknięte oraz wszystkie połączenia równoległe na połączenia szeregowe, a szeregowe na równoległe

Negacją sieci:

A

B

Będzie sieć:

A B

Sprawdźmy aksjomaty dla stałych

A3. A ∪ 0=A

A

0

Sieć A ∪ 0 składa się z dwóch kontaktów A oraz 0 połączonych równolegle. Ponieważ kontakt 0 jest stale otwarty więc działanie sieci zależy jedynie od kontaktu A. Sieć A ∪ 0 oraz A są więc równoważne

A

A

=

0

B3. A ∩ A'=0

Sieć A ∩ A' składa się z sieci A oraz negacji A połączonych szeregowo

Jeżeli sieć A jest otwarta, to sieć A' jest zamknięta i na odwrót. Za każdym razem suma sięci jest jednak otwarta co odpowiada sieci zawsze otwarte 0

A A' 0

=

Podobnie sprawdzamy aksjomaty:

A4. A∪A'=1

B4. A ∩1=A

3. Twierdzenia algebry Boole'a

Tw1. W każdej algebrze Boole'a istnieje tylko jeden wyrózniony element 0 i jeden wyróżniony element 1.

Dowód ( niewprost): Załóżmy że twierdzenie nie jest prawdziwe, a więc istnieją dwa różne elementy 0 i 0* oraz 1 i 1*, takie że 0≠0* i 1≠1* spełniające aksjomaty algebry Boole'a dla wszystkich A. W aksjomacie A3 A ∪ 0=A za A podstawmy najpierw 0*.

Mamy wówczas:

0* ∪ 0 = 0*

Ponieważ A3 jest on spełniony dla 0* otrzymujemy A ∪ 0*=A W aksjomacie A3 A ∪ 0*=A za A podstawmy teraz 0.

Mamy wówczas:

0 ∪ 0* = 0

Wobec przemienności operacji sumy algebraicznej „∪” otrzymujemy:

0* ∪ 0=0 ∪ 0*

0 = 0*

co jest sprzeczne z założeniem, że 0≠0*. Analogicznie postępujemy dla 1 i 1*.

Tw. 2 Dla każdego elementu A dowolnej algebry Boole'a istnieje dokładnie jeden element B taki, że A∪B=1 i A∩B=0

Dowód (niewprost): Załóżmy że element A ma dwa uzupełnienia A' i A* :

1. A*= A* ∪ 0 A3

2. A* ∪ 0=A*∪ (A∩ A') B4

3. A*∪ (A∩ A')=(A* ∪ A) ∩ (A*∪A') A2

4. A* ∪ A) ∩ (A*∪A')= (A ∪ A*)∩ (A*∪A') A1

5. (A ∪ A*)∩ (A*∪A')=1∩ (A*∪A') A4

6. 1∩ (A*∪A')= 1∩ (A'∪A*) A1

7. 1∩ (A'∪A*)= (A∪ A') ∩ (A'∪A*) A4

8. (A∪ A') ∩ (A'∪A*) =(A'∪ A) ∩ (A'∪A*) A1

9. (A'∪ A) ∩ (A'∪A*)=A'∪ (A∩ A*) A2

10. A'∪ (A∩ A*)=A'∪0 B4

11. A'∪0=A' A3

A*=A' co jest sprzeczne z założeniem.

Tw. 3 Dla każdego elementu A algebry Boole'a A''=A

Dowód:

1. A∪A'=1 A4

2. A∩A'=0 B4

4. A'∪A=1 A1

5. A'∩A=0 B1

6. A jest dopełnieniem A'

7. A''=A Tw2.

1

01

1

A B

A B

A B

A

A B

B A

---