
Metody obliczeniowe
Semestr II
Metody numeryczne - sposoby rozwiązania
zadania matematycznego za pomocą operacji
na liczbach
1.
Rozwiązywanie układów równań liniowych. Metody bezpośrednie i iteracyjne.
2.
Sposoby rozwiązywania równań nieliniowych, zagadnienie optymalizacji.
3.
Aproksymacja i interpolacja, pojęcie modelu regresji.
4.
Wzory przybliżonego różniczkowania i całkowania.
5.
Metoda Monte Carlo.
6.
Przykłady zastosowania metod obliczeniowych w zadaniach inżynierskich.

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 2
Literatura
A.
Bjorck, G. Dahlquist
,
Metody numeryczne, PWN, Warszawa 1983.
Z. Fortuna, B. Macukow, J. Wąsowski
,
Metody numeryczne, WNT, Warszawa 2005.
J. Stoer, R. Bulirsch
,
Wstęp do metod numerycznych I-II, PWN 1990
S. Rosłaniec
,
Wybrane metody numeryczne z przykładami zastosowań w zadaniach
inżynierskich, Oficyna Wydawnicza Politechniki Warszawskiej, 2002.
A. Brozi
,
Scilab, Nakom 2007

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 3
•
http://www.put.poznan.pl/~albert.kubzdela
•
http://www.ikb.poznan.pl/zaklady/komp/
Portale internetowe

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 4
• wykład nr 1
– metody rozwiązywania układów równań
liniowych
Metody obliczeniowe

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 5
Poj
ę
cie układu równa
ń
liniowych
•
Układ powyższy nazywamy
układem m równań liniowych o n niewiadomych
.
•
Skalary a
i, j
nazywamy
współczynnikami układu
, skalary b
i
to
wyrazy wolne
.
•
Rozwiązaniem układu
nazywamy dowolną n-kę (r
1
, r
2
, ..., r
n
), które po
podstawieniu w miejsce x
i
do powyższych równań dają równości prawdziwe
=
+
+
+
=
+
+
+
=
+
+
+
m
n
mn
m
m
n
n
n
n
b
x
a
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
L
L
L
L
2
2
1
1
2
2
2
22
1
21
1
1
2
12
1
11
(sprawdzenie poprawności rozwiązania – podstawienie n-ki (r
1
, r
2
, ..., r
n
) do lewych
stron równań i porównanie z wyrazami wolnymi).

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 6
przykład układu dwóch równań z trzema niewiadomymi:
−
=
−
=
+
+
4
2
2
2
3
2
3
2
1
x
x
x
x
x
Przykład układu równa
ń
Odpowiednio:
– a
1,1
= 2, a
1,2
= 1, a
1,3
= 1, a
2,1
= 0, a
2,2
= 1, a
2,3
= -2;
– wyrazami wolnymi są liczby 2 i -4.
Układ ten ma nieskończenie wiele rozwiązań, jednym z nich
jest trójka:
x
1
= 0, x
2
= 0, x
3
= 2.
−
=
⋅
−
4
2
2
1
0
1
1
2
3
2
1
x
x
x

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 7
Postać równania
macierzowego:
b
x
A
b
b
b
x
x
x
a
a
a
a
a
a
a
a
a
m
n
mn
m
m
n
n
=
⇒
=
]
[
2
1
2
1
2
1
2
22
21
1
12
11
L
L
L
L
L
L
L
L
L
Zapis macierzowy układu równa
ń
liniowych
=
+
+
+
=
+
+
+
=
+
+
+
m
n
mn
m
m
n
n
n
n
b
x
a
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
L
L
L
L
2
2
1
1
2
2
2
22
1
21
1
1
2
12
1
11

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 8
Postać równania
macierzowego:
b
x
A
b
b
b
x
x
x
a
a
a
a
a
a
a
a
a
m
n
mn
m
m
n
n
=
⇒
=
]
[
2
1
2
1
2
1
2
22
21
1
12
11
L
L
L
L
L
L
L
L
L
=
m
mn
m
m
n
n
rozszerz
b
b
b
a
a
a
a
a
a
a
a
a
A
2
1
2
1
2
22
21
1
12
11
.
L
L
L
L
L
L
L
Z danym układem równań związane są dwie ważne macierze.
=
mn
m
m
n
n
a
a
a
a
a
a
a
a
a
A
L
L
L
L
L
L
L
2
1
2
22
21
1
12
11
macierz główna układu równań
(macierz współczynników):
macierz rozszerzona
(powstaje z macierzy głównej przez
dołączenie do niej kolumny wyrazów
wolnych:
Zapis macierzowy układu równa
ń
liniowych

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 9
Rzędem macierzy
A (rank(A), rz(A) ) nazywamy największą liczbę
liniowo niezależnych wektorów kolumnowych w macierzy A.
Istnienie rozwi
ą
zania układu równa
ń
Rz
ą
d macierzy
2
)
(
3
)
(
2
1
1
1
1
0
3
1
2
,
1
1
1
2
1
0
1
1
2
=
=
=
−
=
B
rank
A
rank
B
A
Skończony układ wektorów
{w
1
,...,w
n
}
nazywamy układem liniowo niezależnym,
gdy
a
1
w
1
+ ... +a
n
w
n
≠≠≠≠
0
jeśli skalary
a
1
,...,a
n
nie wszystkie są równe zero
=
+
2
1
3
1
1
1
1
0
2

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 10
Sprawę rozwiązalności układu równań wyjaśnia Twierdzenie
Kroneckera-Capellego:
Układ równań liniowych ma rozwiązanie wtedy i tylko wtedy,
gdy rząd macierzy głównej jest równy rzędowi macierzy
rozszerzonej.
Istnienie rozwi
ą
zania układu równa
ń
Rz
ą
d macierzy

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 11
• układ równań posiadający rozwiązanie:
=
+
+
−
=
−
=
+
+
2
4
2
2
2
3
2
1
3
2
3
2
1
x
x
x
x
x
x
x
x
[
]
[
]
T
T
2
4
2
1
2
1
*
2
−
=
−
Rz
ą
d macierzy - przykłady
3
)
(
3
)
(
2
4
2
1
1
1
2
1
0
1
1
2
,
1
1
1
2
1
0
1
1
2
=
=
−
−
=
−
=
a
rozszerzon
a
rozszerzon
A
rank
A
rank
A
A

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 12
• układ równań posiadający rozwiązanie:
=
+
+
−
=
−
=
+
+
2
4
2
2
2
3
2
1
3
2
3
2
1
x
x
x
x
x
x
x
x
2
)
(
1
)
(
5
2
2
4
1
2
,
2
4
1
2
=
=
=
=
a
rozszerzon
a
rozszerzon
A
rank
A
rank
A
A
[
]
[
]
T
T
2
4
2
1
2
1
*
2
−
=
−
Rz
ą
d macierzy - przykłady
• układ równań nie posiadający rozwiązania:
=
+
=
+
5
2
4
2
2
2
1
2
1
x
x
x
x
3
)
(
3
)
(
2
4
2
1
1
1
2
1
0
1
1
2
,
1
1
1
2
1
0
1
1
2
=
=
−
−
=
−
=
a
rozszerzon
a
rozszerzon
A
rank
A
rank
A
A

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 13
• Układ jednorodny
–
Jeżeli wszystkie wyrazy wolne są równe 0, to układ równań nazywamy
jednorodnym
. Układ jednorodny ma zawsze rozwiązanie.
=
+
+
+
=
+
+
+
=
+
+
+
n
n
nn
n
n
n
n
n
n
b
x
a
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
L
L
L
L
2
2
1
1
2
2
2
22
1
21
1
1
2
12
1
11
0
det
,
]
[
2
1
2
1
2
1
2
22
21
1
12
11
≠
=
=
A
b
x
A
b
b
b
x
x
x
a
a
a
a
a
a
a
a
a
n
n
nn
n
n
n
n
L
L
L
L
L
L
L
L
L
Typy układów równa
ń
liniowych
• Układ kwadratowy
–
Jeżeli n = m układ równań nazywamy kwadratowym
.
•
rank(A) < rank ([A,b])
brak rozwiązania;
•
rank(A) = rank ([A,b]) < n
nieskończenie wiele rozwiązań;
•
rank(A) = rank ([A,b]) = n
dokładnie jedno rozwiązanie
.
(
wówczas wyznacznik macierzy A jest różny od zera)
Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 14
Metody rozwi
ą
zywania układów równa
ń
liniowych
=
=
+
+
+
=
+
+
+
=
+
+
+
20
,...,
3
,
2
2
1
1
2
2
2
22
1
21
1
1
2
12
1
11
n
b
x
a
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
n
n
nn
n
n
n
n
n
n
L
L
L
L
=
+
=
+
2
2
22
1
21
1
2
12
1
11
b
x
a
x
a
b
x
a
x
a
=
=
+
+
+
=
+
+
+
=
+
+
+
,...
20
,
2
2
1
1
2
2
2
22
1
21
1
1
2
12
1
11
n
b
x
a
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
n
n
nn
n
n
n
n
n
n
L
L
L
L

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 15
•
bezpośrednie
(dokładne)
– metody które przy braku błędów zaokrągleń dają dokładne rozwiązanie po
skończonej liczbie przekształceń układu wejściowego
• duża efektywność dla układów o
macierzach pełnych
• duże obciążenie pamięci
• możliwa niestabilność ze względu na błędy zaokrągleń
•
iteracyjne
– polegają na konstrukcji nieskończonego ciągu wektorów, zbieżnych do
szukanego rozwiązania,
x
(0)
→
x
(1)
→
x
(2)
→
...
• efektywne dla
macierzy rzadkich
, dużych rozmiarów
• stosunkowo nieduże obciążenie pamięci
• problemy ze zbieżnością
Metody rozwi
ą
zywania układów równa
ń
liniowych

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 16
• Przy użyciu macierzy odwrotnej
• Wzory Cramera
• Układ równań z macierzą trójkątną
• Eliminacja Gaussa
• Rozkłady trójkątne macierzy
• Metoda sprzężonych gradientów
Metody bezpo
ś
rednie – sposoby rozwi
ą
za
ń

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 17
• Przy użyciu macierzy odwrotnej
Metody bezpo
ś
rednie

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 18
• Przy użyciu macierzy odwrotnej
– Układ równań A · x =b, znając macierz odwrotną można
rozwiązać:
A · x = b
A
-1
·A · x = A
-1
· b
x = A
-1
· b
Metody bezpo
ś
rednie – sposoby rozwi
ą
za
ń
x = inv(A) * b
Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 19
Metody bezpo
ś
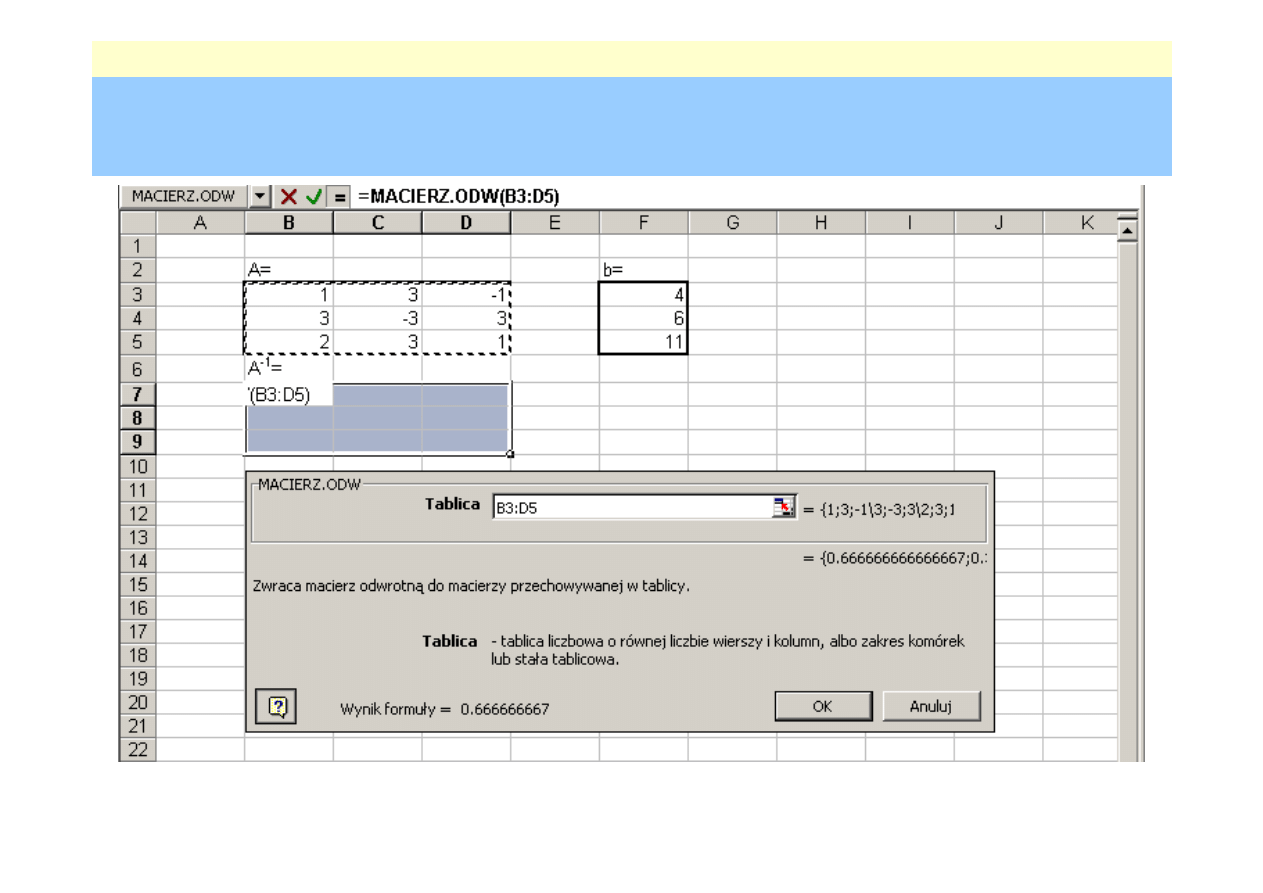
rednie – wykorzystanie macierzy odwrotnej
Przykład (wykorzystanie arkusza kalkulacyjnego MS Excel)
Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 20
Metody bezpo
ś
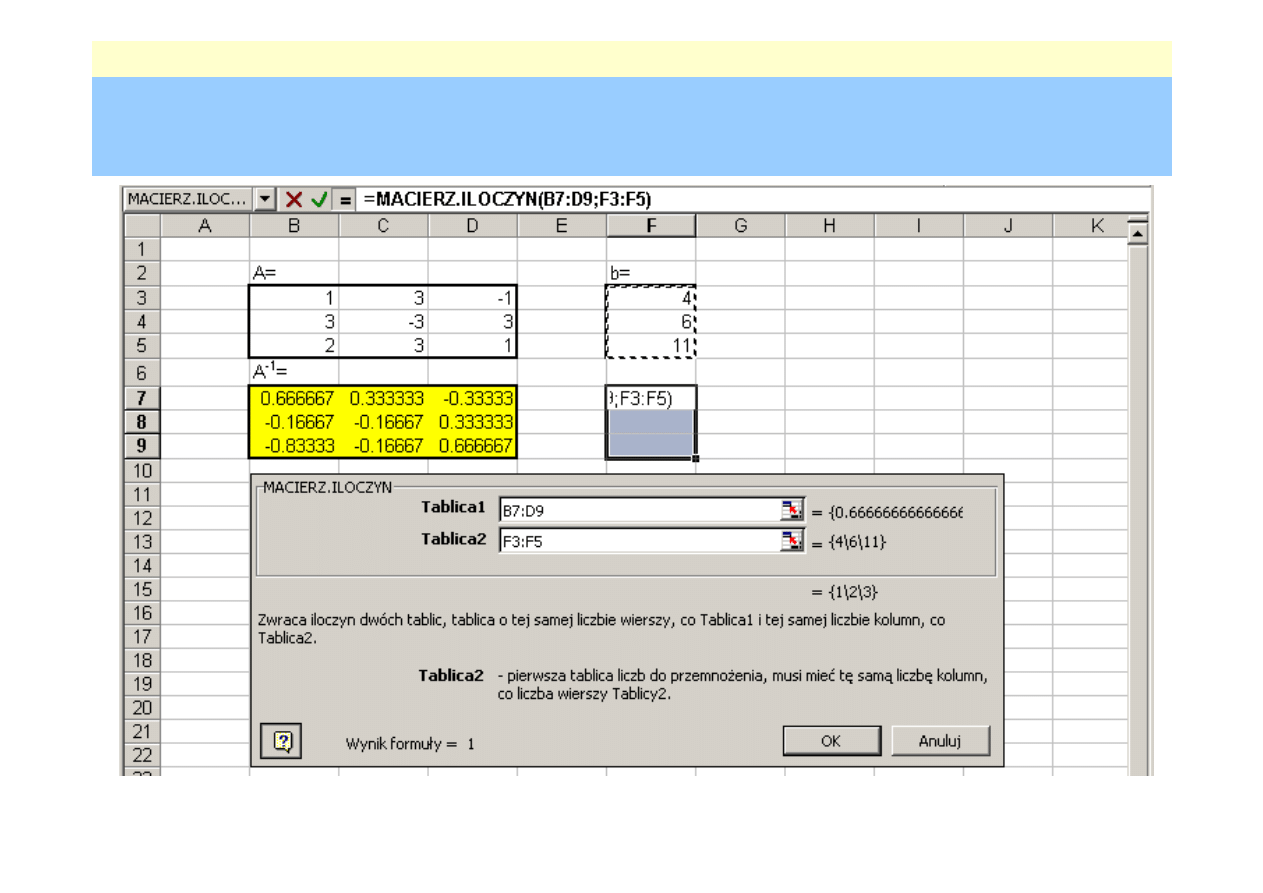
rednie – wykorzystanie macierzy odwrotnej
Przykład (wykorzystanie arkusza kalkulacyjnego MS Excel)
Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 21
Metody bezpo
ś
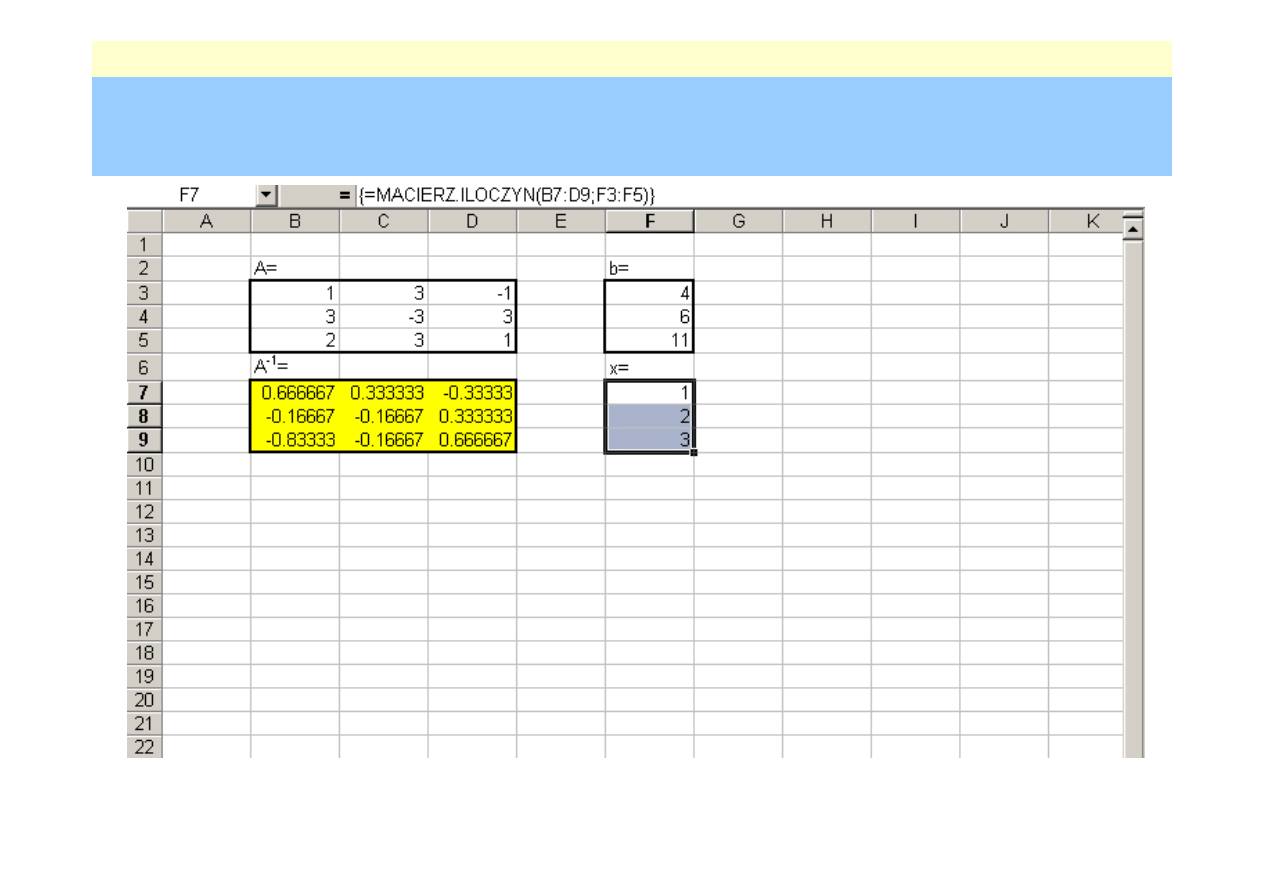
rednie – wykorzystanie macierzy odwrotnej
Przykład (wykorzystanie arkusza kalkulacyjnego MS Excel)

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 22
• Wzory Cramera
Metody bezpo
ś
rednie – sposoby rozwi
ą
za
ń

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 23
Gustaw Kramer ?
Wzory Cramera
Gabriel Cramer
1704-1752
Wybrane fakty z życiorysu
1722 – uzyskuje doktorat,
1724 – obejmuje katedrę matematyki w Genewie,
1727 – 1729 – odbywa dwuletnią podróż po Europie

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 24
• Wzory Cramera
Metody bezpo
ś
rednie – sposoby rozwi
ą
za
ń

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 25
– Układ równań A · x =b o macierzy nieosobliwej A ma dokładnie
jedno rozwiązanie postaci
– macierz A
k
powstaje z macierzy A przez zastąpienie k-tej kolumny
przez wektor b
– Cechy metody
• oszczędność pamięci
• bardzo duży nakład obliczeń (w praktyce nie do zastosowania dla
dużych układów równań)
n
k
A
A
x
k
k
,...,
1
)
det(
)
det(
=
=
Metody bezpo
ś
rednie – sposoby rozwi
ą
za
ń
• Wzory Cramera

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 26
• układ równań z macierzą trójkątną
– metoda rozwiązania – podstawianie wstecz (wprzód)
u x
u x
u
x
u x
b
u x
u
x
u x
b
u
x
u
x
b
u x
b
n
n
n n
n
n
n n
n
n
n
n
n n
n
nn n
n
11 1
12 2
1
1
1
1
1
22 2
2
1
1
2
2
1
1
1
1
1
+
+ +
+
=
+ +
+
=
+
=
=
−
−
−
−
−
−
−
−
−
...
...
...
,
,
,
,
Metody bezpo
ś
rednie – sposoby rozwi
ą
za
ń

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 27
• układ równań z macierzą trójkątną
– metoda rozwiązania – podstawianie wstecz (wprzód)
u x
u x
u
x
u x
b
u x
u
x
u x
b
u
x
u
x
b
u x
b
n
n
n n
n
n
n n
n
n
n
n
n n
n
nn n
n
11 1
12 2
1
1
1
1
1
22 2
2
1
1
2
2
1
1
1
1
1
+
+ +
+
=
+ +
+
=
+
=
=
−
−
−
−
−
−
−
−
−
...
...
...
,
,
,
,
l x
b
l x
l x
b
l
x
l
x
l
x
b
l x
l x
l
x
l x
b
n
n
n
n
n
n
n
n
n n
n
nn n
n
11 1
1
21 1
22 2
2
1 1 1
1 2 2
1
1
1
1
1 1
2 2
1
1
=
+
=
+
+ +
=
+
+ +
+
=
−
−
−
−
−
−
−
−
...
...
...
,
,
,
,
Metody bezpo
ś
rednie – sposoby rozwi
ą
za
ń

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 28
• układ równań z macierzą trójkątną
– metoda rozwiązania – podstawianie wstecz (wprzód)
u x
u x
u
x
u x
b
u x
u
x
u x
b
u
x
u
x
b
u x
b
n
n
n n
n
n
n n
n
n
n
n
n n
n
nn n
n
11 1
12 2
1
1
1
1
1
22 2
2
1
1
2
2
1
1
1
1
1
+
+ +
+
=
+ +
+
=
+
=
=
−
−
−
−
−
−
−
−
−
...
...
...
,
,
,
,
l x
b
l x
l x
b
l
x
l
x
l
x
b
l x
l x
l
x
l x
b
n
n
n
n
n
n
n
n
n n
n
nn n
n
11 1
1
21 1
22 2
2
1 1 1
1 2 2
1
1
1
1
1 1
2 2
1
1
=
+
=
+
+ +
=
+
+ +
+
=
−
−
−
−
−
−
−
−
...
...
...
,
,
,
,
x
b
u
x
u
b
u x
i
n
n
n
n
nn
i
ii
i
ij
j
j i
n
=
=
−
= −
−
= +
∑
1
1
2
1
1
,
,...,
x
b
l
x
l
b
l x
i
n
i
ii
i
ij
j
j
i
1
1
11
1
1
1
2 3
=
=
−
=
=
−
∑
, ,...,
Metody bezpo
ś
rednie – sposoby rozwi
ą
za
ń

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 29
• układ równań z macierzą trójkątną
– metoda rozwiązania – podstawianie wstecz (wprzód)
u x
u x
u
x
u x
b
u x
u
x
u x
b
u
x
u
x
b
u x
b
n
n
n n
n
n
n n
n
n
n
n
n n
n
nn n
n
11 1
12 2
1
1
1
1
1
22 2
2
1
1
2
2
1
1
1
1
1
+
+ +
+
=
+ +
+
=
+
=
=
−
−
−
−
−
−
−
−
−
...
...
...
,
,
,
,
x
b
u
x
u
b
u x
i
n
n
n
n
nn
i
ii
i
ij
j
j i
n
=
=
−
= −
−
= +
∑
1
1
2
1
1
,
,...,
Metody bezpo
ś
rednie – sposoby rozwi
ą
za
ń
x(n)= b(n)/u(n,n)

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 30
• układ równań z macierzą trójkątną
– metoda rozwiązania – podstawianie wstecz (wprzód)
u x
u x
u
x
u x
b
u x
u
x
u x
b
u
x
u
x
b
u x
b
n
n
n n
n
n
n n
n
n
n
n
n n
n
nn n
n
11 1
12 2
1
1
1
1
1
22 2
2
1
1
2
2
1
1
1
1
1
+
+ +
+
=
+ +
+
=
+
=
=
−
−
−
−
−
−
−
−
−
...
...
...
,
,
,
,
x
b
u
x
u
b
u x
i
n
n
n
n
nn
i
ii
i
ij
j
j i
n
=
=
−
= −
−
= +
∑
1
1
2
1
1
,
,...,
Metody bezpo
ś
rednie – sposoby rozwi
ą
za
ń
x(n)= b(n)/u(n,n)
for i=[n-1:-1:1]
x(i)= b(i)
end

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 31
• układ równań z macierzą trójkątną
– metoda rozwiązania – podstawianie wstecz (wprzód)
u x
u x
u
x
u x
b
u x
u
x
u x
b
u
x
u
x
b
u x
b
n
n
n n
n
n
n n
n
n
n
n
n n
n
nn n
n
11 1
12 2
1
1
1
1
1
22 2
2
1
1
2
2
1
1
1
1
1
+
+ +
+
=
+ +
+
=
+
=
=
−
−
−
−
−
−
−
−
−
...
...
...
,
,
,
,
x
b
u
x
u
b
u x
i
n
n
n
n
nn
i
ii
i
ij
j
j i
n
=
=
−
= −
−
= +
∑
1
1
2
1
1
,
,...,
Metody bezpo
ś
rednie – sposoby rozwi
ą
za
ń
x(n)= b(n)/u(n,n)
for i=[n-1:-1:1]
x(i)= b(i)
for j=[i+1:n]
x(i)=x(i)-u(i,j)*x(j)
end
end

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 32
• układ równań z macierzą trójkątną
– metoda rozwiązania – podstawianie wstecz (wprzód)
u x
u x
u
x
u x
b
u x
u
x
u x
b
u
x
u
x
b
u x
b
n
n
n n
n
n
n n
n
n
n
n
n n
n
nn n
n
11 1
12 2
1
1
1
1
1
22 2
2
1
1
2
2
1
1
1
1
1
+
+ +
+
=
+ +
+
=
+
=
=
−
−
−
−
−
−
−
−
−
...
...
...
,
,
,
,
x
b
u
x
u
b
u x
i
n
n
n
n
nn
i
ii
i
ij
j
j i
n
=
=
−
= −
−
= +
∑
1
1
2
1
1
,
,...,
Metody bezpo
ś
rednie – sposoby rozwi
ą
za
ń
x(n)= b(n)/u(n,n)
for i=[n-1:-1:1]
x(i)= b(i)
for j=[i+1:n]
x(i)=x(i)-u(i,j)*x(j)
end
x(i)=x(i)/u(i,i)
end

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 33
• Eliminacja Gaussa
Metody bezpo
ś
rednie – sposoby rozwi
ą
za
ń

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 34
Carl Friedrich Gauss 1777-1855
• matematyk, fizyk, astronom, geodeta
jedno z pierwszych odkryć:
podanie konstrukcji siedemnastokąta foremnego przy użyciu cyrkla i linijki

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 35
• sprowadzenie układu do równoważnego układu
postaci trójkątnej –
eliminacja zmiennych
• rozwiązanie układu trójkątnego –
postępowanie
odwrotne
=
+
+
+
=
+
+
+
=
+
+
+
n
n
nn
n
n
n
n
n
n
b
x
a
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
...
...
...
...
2
2
1
1
2
2
2
22
1
21
1
1
2
12
1
11
Metody bezpo
ś
rednie – Eliminacja Gaussa
( )
( )
( )
( )
( )
( )
=
=
+
+
+
=
+
+
+
+
−
−
1
1
1
2
1
2
3
1
23
2
1
22
1
3
13
2
12
1
11
...
...
...
n
n
n
n
nn
n
n
n
n
b
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
x
a
⇒
⇒
⇒
⇒

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 36
=
−
−
−
−
−
7
9
0
2
1
2
1
3
2
1
1
2
1
1
1
1
1
1
1
1
4
3
2
1
x
x
x
x
−
−
−
−
−
7
9
0
2
1
2
1
3
2
1
1
2
1
1
1
1
1
1
1
1
Układ równań zapisujemy w postaci macierzy rozszerzonej układu
Eliminacja Gaussa - przykład
⇒
⇒
⇒
⇒

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 37
Eliminacja Gaussa - przykład
⇒
⇒
⇒
⇒
−
−
−
−
−
7
9
0
2
1
2
1
3
2
1
1
2
1
1
1
1
1
1
1
1
−
−
−
−
−
−
−
−
1
5
2
2
2
1
2
0
4
3
1
0
2
2
2
0
1
1
1
1
I krok

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 38
Eliminacja Gaussa - przykład
⇒
⇒
⇒
⇒
−
−
−
−
−
7
9
0
2
1
2
1
3
2
1
1
2
1
1
1
1
1
1
1
1
−
−
−
−
−
−
−
−
1
5
2
2
2
1
2
0
4
3
1
0
2
2
2
0
1
1
1
1
I krok
( )
( )
4
,...,
1
4
,...,
2
1
11
1
1
1
11
1
1
=
=
−
=
−
=
j
i
b
a
a
b
b
a
a
a
a
a
i
i
i
j
i
ij
ij

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 39
Eliminacja Gaussa - przykład
⇒
⇒
⇒
⇒
−
−
−
−
−
7
9
0
2
1
2
1
3
2
1
1
2
1
1
1
1
1
1
1
1
−
−
−
−
−
−
−
−
1
5
2
2
2
1
2
0
4
3
1
0
2
2
2
0
1
1
1
1
I krok
−
−
−
−
−
3
6
2
2
0
1
0
0
3
2
0
0
2
2
2
0
1
1
1
1
−
−
−
−
−
−
−
−
1
5
2
2
2
1
2
0
4
3
1
0
2
2
2
0
1
1
1
1
II krok
⇒
⇒
⇒
⇒

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 40
Eliminacja Gaussa - przykład
⇒
⇒
⇒
⇒
−
−
−
−
−
7
9
0
2
1
2
1
3
2
1
1
2
1
1
1
1
1
1
1
1
−
−
−
−
−
−
−
−
1
5
2
2
2
1
2
0
4
3
1
0
2
2
2
0
1
1
1
1
I krok
−
−
−
−
−
3
6
2
2
0
1
0
0
3
2
0
0
2
2
2
0
1
1
1
1
−
−
−
−
−
−
−
−
1
5
2
2
2
1
2
0
4
3
1
0
2
2
2
0
1
1
1
1
II krok
⇒
⇒
⇒
⇒
III krok
−
−
−
−
−
3
6
2
2
0
1
0
0
3
2
0
0
2
2
2
0
1
1
1
1
⇒
⇒
⇒
⇒
−
−
−
−
−
6
6
2
2
5
.
1
0
0
0
3
2
0
0
2
2
2
0
1
1
1
1
Wykonując postępowanie odwrotne, znajdujemy rozwiązanie x = [1, 2, 3, 4]

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 41
1.
Eliminacja zmiennych
–
Krok 1
Zakładamy, że
z pozostałych n-1 równań eliminujemy zmienną x
1
odejmując od i-tego równania (i=2,3,...,n)
równanie pierwsze
pomnożone przez
0
11
≠
a
11
1
1
a
a
l
i
i
=
( )
( )
( )
( )
( )
( )
( )
( )
a x
a x
a x
b
a x
a x
b
a x
a x
b
a
a
a
a
a
b
b
a
a
b
n n
n
n
n
nn
n
n
ij
ij
i
j
i
i
i
11 1
12 2
1
1
22
1
2
2
1
2
1
2
1
2
1
1
1
1
11
1
1
1
11
1
+
+ +
=
+ +
=
+ +
=
=
−
= −
...
...
...
...
Metody bezpo
ś
rednie – Eliminacja Gaussa

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 42
1.
Eliminacja zmiennych
–
Krok 1
Zakładamy, że
z pozostałych n-1 równań eliminujemy zmienną x
1
odejmując od i-tego równania (i=2,3,...,n)
równanie pierwsze
pomnożone przez
–
Krok k-ty Zakładamy, że
z równań n-k eliminujemy zmienną x
k
odejmując od i-tego równania (i=k+1,...,n) równanie k-te
pomnożone przez
0
11
≠
a
11
1
1
a
a
l
i
i
=
( )
( )
( )
( )
( )
( )
( )
( )
a x
a x
a x
b
a x
a x
b
a x
a x
b
a
a
a
a
a
b
b
a
a
b
n n
n
n
n
nn
n
n
ij
ij
i
j
i
i
i
11 1
12 2
1
1
22
1
2
2
1
2
1
2
1
2
1
1
1
1
11
1
1
1
11
1
+
+ +
=
+ +
=
+ +
=
=
−
= −
...
...
...
...
0
)
(
≠
i
ii
a
=
+
+
=
+
+
+
=
+
+
+
+
+
=
+
+
+
+
+
+
+
+
−
−
+
−
+
−
+
+
+
+
)
(
)
(
1
)
(
1
)
1
(
)
1
(
1
)
1
(
1
)
1
(
)
1
(
2
)
1
(
2
1
)
1
(
1
2
)
1
(
2
2
)
1
(
22
1
1
1
1
1
1
2
12
1
11
...
.....
..........
..........
...
.....
..........
..........
...
...
...
...
k
n
n
k
nn
k
k
nk
k
k
n
k
kn
k
k
kk
k
k
kk
n
n
k
k
k
k
n
n
k
k
k
k
b
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
x
a
b
x
a
x
a
x
a
x
a
x
a
)
1
(
)
1
(
−
−
=
k
kk
k
ik
ik
a
a
l
Metody bezpo
ś
rednie – Eliminacja Gaussa
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
1
1
1
1
1
1
1
1
−
−
−
−
−
−
−
−
−
=
−
=
k
k
k
kk
k
ik
k
i
k
i
k
kj
k
kk
k
ik
k
ij
k
ij
b
a
a
b
b
a
a
a
a
a

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 43
1.
Eliminacja zmiennych (c.d.)
–
Po n-1 krokach ostatecznie otrzymujemy kład równań postaci:
( )
( )
( )
( )
( )
( )
( )
( )
( )
=
=
+
+
=
+
+
+
=
+
+
+
+
−
−
1
1
2
3
2
3
3
2
33
1
2
1
2
3
1
23
2
1
22
1
1
3
13
2
12
1
11
...
...
...
...
n
n
n
n
nn
n
n
n
n
n
n
b
x
a
b
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
x
a
Metody bezpo
ś
rednie – Eliminacja Gaussa

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 44
1.
Eliminacja zmiennych (c.d.)
–
Po n-1 krokach ostatecznie otrzymujemy kład równań postaci:
2.
Postępowanie odwrotne
–
Rozwiązanie układu równań o trójkątnej macierzy współczynników
zakładając, że
, rozwiązanie dla i = n,...,1 otrzymuje się wg
wzorów:
( )
( )
( )
( )
( )
( )
( )
( )
( )
=
=
+
+
=
+
+
+
=
+
+
+
+
−
−
1
1
2
3
2
3
3
2
33
1
2
1
2
3
1
23
2
1
22
1
1
3
13
2
12
1
11
...
...
...
...
n
n
n
n
nn
n
n
n
n
n
n
b
x
a
b
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
x
a
0
)
1
(
≠
−
i
ii
a
)
1
(
1
)
1
(
)
1
(
−
+
=
−
−
∑
−
=
i
ii
n
i
j
j
i
ij
i
i
i
a
x
a
b
x
Metody bezpo
ś
rednie – Eliminacja Gaussa

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 45
•
rozważmy układ równań
•
macierz układu jest nieosobliwa, więc istnieje jednoznaczne
rozwiązanie, ale ...
=
+
=
+
=
+
2
3
3
3
1
2
2
3
1
2
1
3
2
x
x
x
x
x
x
Metody bezpo
ś
rednie – Eliminacja Gaussa
wybór elementu podstawowego

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 46
•
rozważmy układ równań
•
macierz układu jest nieosobliwa, więc istnieje jednoznaczne
rozwiązanie, ale ...
•
stosując eliminację Gaussa, obliczenia zostaną przerwane w kroku
k = 1 gdyż a
11
=0.
=
+
=
+
=
+
2
3
3
3
1
2
2
3
1
2
1
3
2
x
x
x
x
x
x
Metody bezpo
ś
rednie – Eliminacja Gaussa
wybór elementu podstawowego

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 47
•
rozważmy układ równań
•
macierz układu jest nieosobliwa, więc istnieje jednoznaczne
rozwiązanie, ale ...
•
stosując eliminację Gaussa, obliczenia zostaną przerwane w kroku
k = 1 gdyż a
11
=0.
•
zmiana kolejności wierszy nie zmienia rozwiązania układu
=
+
=
+
=
+
2
3
3
3
1
2
2
3
1
2
1
3
2
x
x
x
x
x
x
Metody bezpo
ś
rednie – Eliminacja Gaussa
wybór elementu podstawowego

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 48
•
rozważmy układ równań
•
macierz układu jest nieosobliwa, więc istnieje jednoznaczne
rozwiązanie, ale ...
•
stosując eliminację Gaussa, obliczenia zostaną przerwane w kroku
k = 1 gdyż a
11
=0.
•
zmiana kolejności wierszy nie zmienia rozwiązania układu
•
Eliminację można przeprowadzić bez przestawiania wierszy bądź
kolumn gdy macierz A jest macierzą:
– z dominującą przekątną główną,
tzn.
lub
– symetryczna i dodatnio określoną
tzn. A
T
= A i x
T
A x > 0 dla każdego
niezerowego wektora x
=
+
=
+
=
+
2
3
3
3
1
2
2
3
1
2
1
3
2
x
x
x
x
x
x
∑
≠
=
=
≥
n
i
j
j
ij
ii
n
j
i
a
a
1
,...,
1
,
|
|
|
|
Metody bezpo
ś
rednie – Eliminacja Gaussa
wybór elementu podstawowego

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 49
• Elementem podstawowym (głównym)
nazywamy ten element
macierzy A, za pomocą którego dokonujemy eliminacji zmiennej z
dalszych równań
• Strategie wyboru elementu podstawowego
:
– wybór częściowy
– wybór pełny
• Strategia z częściowym wyborem elementu podstawowego (metoda Gaussa-
Crouta) jest metodą niezawodną, tzn. zakładając brak błędów obliczeń, nie
nastąpi zatrzymanie procesu obliczeń z powodu dzielenia przez zero, w
przypadku gdy istnieje jednoznaczne rozwiązanie układu
Metody bezpo
ś
rednie – Eliminacja Gaussa
wybór elementu podstawowego
Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
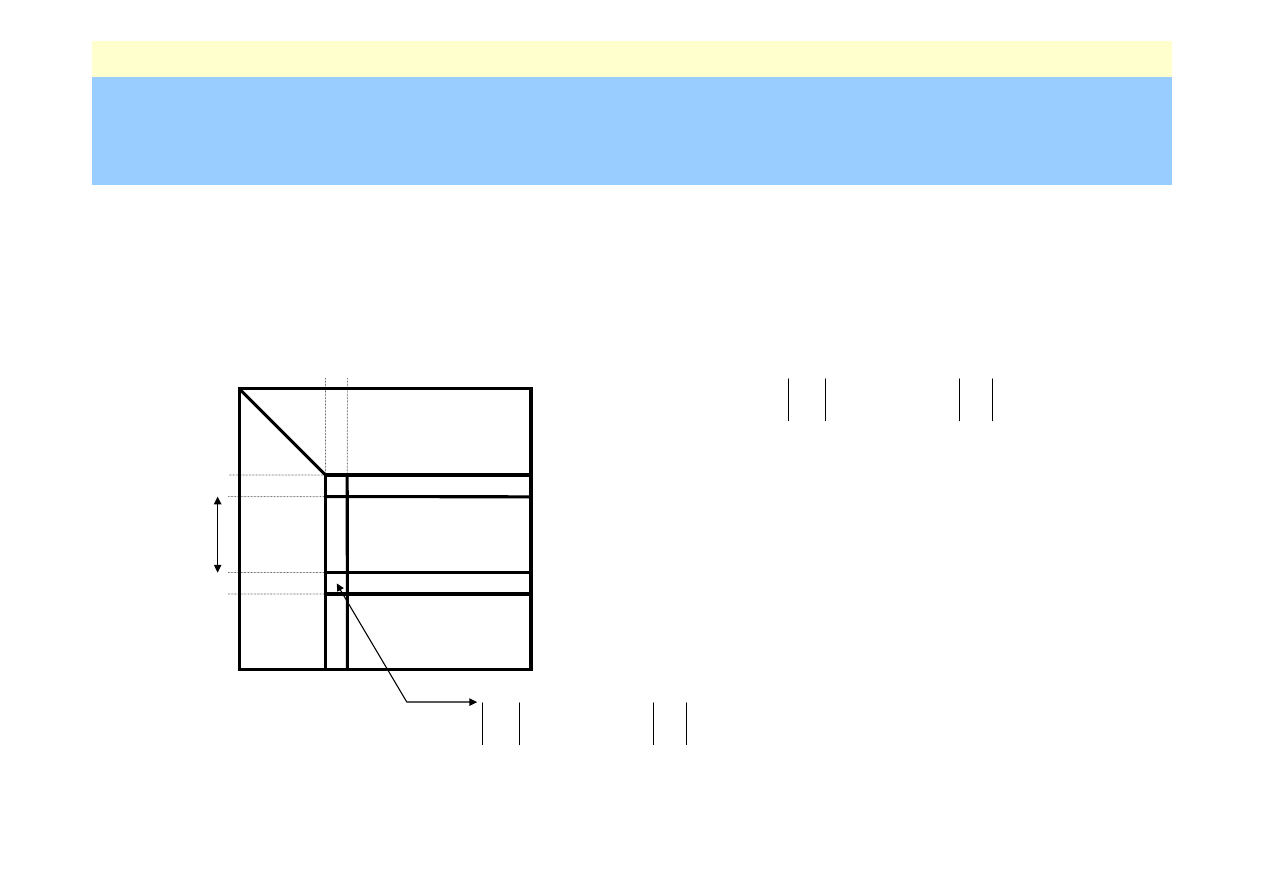
Nr: 50
wybiera się k jako najmniejszą
liczbę całkowitą dla której
i przestawia się wiersze k-ty oraz
j-ty
j
j
k
a
a
kj
i
j j
n
ij
=
=
+
max
,
,...,
1
a
a
kj
i
j j
n
ij
=
=
+
max
,
,...,
1
Metody bezpo
ś
rednie – Eliminacja Gaussa
wybór cz
ęś
ciowy elementu podstawowego
Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
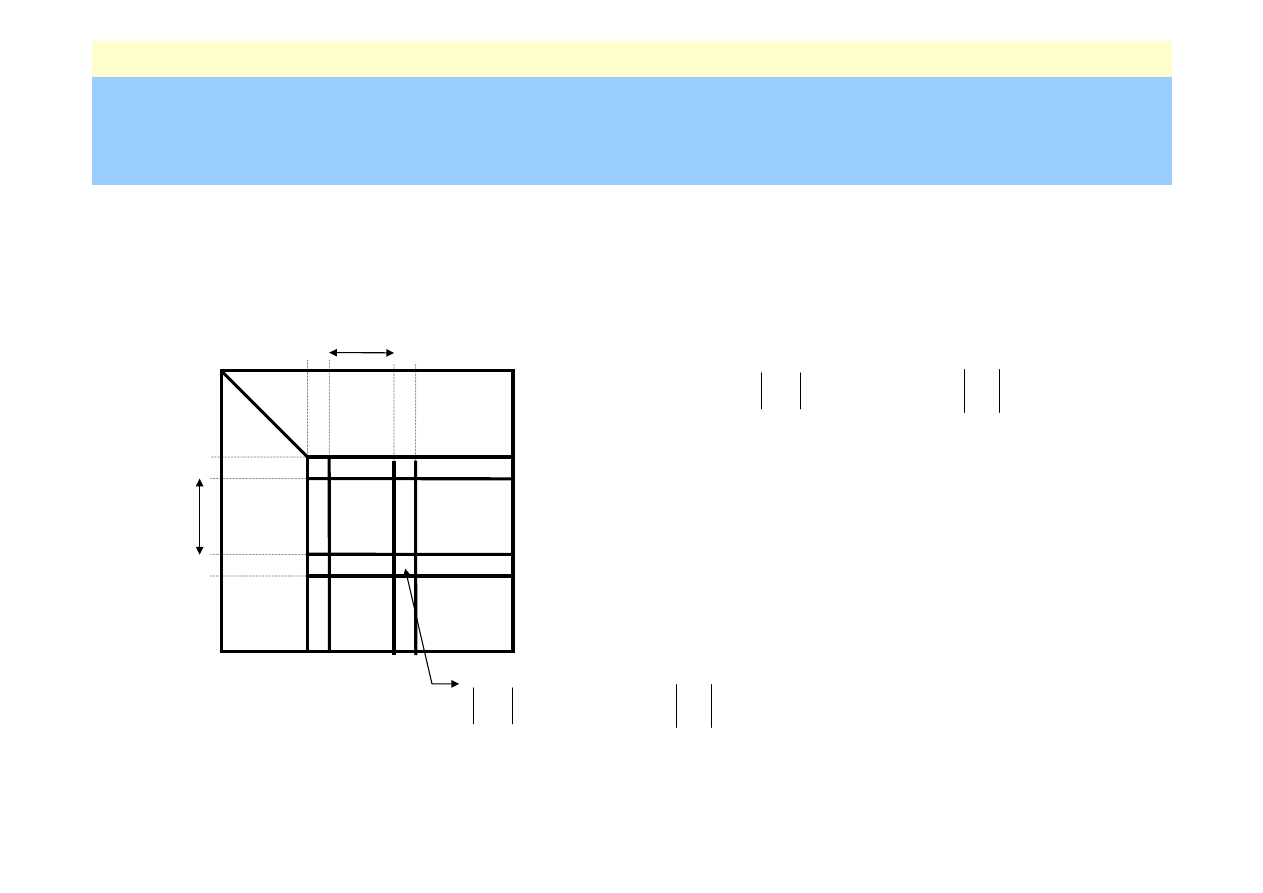
Nr: 51
wybiera się k i l jako najmniejsze
liczby całkowite dla których
i przestawia się wiersze k-ty i m-ty
oraz kolumny l-tą i m-tą,
m
m
k
l
a
a
kl
i j m m
n
ij
=
=
+
max
.
,
,...,
1
a
a
kl
i j m m
n
ij
=
=
+
max
.
,
,...,
1
Metody bezpo
ś
rednie – Eliminacja Gaussa
wybór pełny elementu podstawowego

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 52
w k-tym kroku, dla i = k+1, k+2, ..., n (wiersze) mamy
( )
( )
k
k
kk
k
ik
k
i
k
k
i
kj
k
kk
k
ik
k
k
ij
k
ij
b
a
a
b
b
n
k
k
j
a
a
a
a
a
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
,...,
1
,
,...
−
−
−
−
−
−
−
−
−
=
+
=
−
=
Metody bezpo
ś
rednie – Eliminacja Gaussa

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 53
w k-tym kroku, dla i = k+1, k+2, ..., n (wiersze) mamy
( )
( )
k
k
kk
k
ik
k
i
k
k
i
kj
k
kk
k
ik
k
k
ij
k
ij
b
a
a
b
b
n
k
k
j
a
a
a
a
a
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
,...,
1
,
,...
−
−
−
−
−
−
−
−
−
=
+
=
−
=
for k= 1:n-1
end
Metody bezpo
ś
rednie – Eliminacja Gaussa

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 54
w k-tym kroku, dla i = k+1, k+2, ..., n (wiersze) mamy
( )
( )
k
k
kk
k
ik
k
i
k
k
i
kj
k
kk
k
ik
k
k
ij
k
ij
b
a
a
b
b
n
k
k
j
a
a
a
a
a
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
,...,
1
,
,...
−
−
−
−
−
−
−
−
−
=
+
=
−
=
for k= 1:n-1
for i= k+1:n
end
end
Metody bezpo
ś
rednie – Eliminacja Gaussa

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 55
w k-tym kroku, dla i = k+1, k+2, ..., n (wiersze) mamy
( )
( )
k
k
kk
k
ik
k
i
k
k
i
kj
k
kk
k
ik
k
k
ij
k
ij
b
a
a
b
b
n
k
k
j
a
a
a
a
a
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
,...,
1
,
,...
−
−
−
−
−
−
−
−
−
=
+
=
−
=
for k= 1:n-1
for i= k+1:n
b(i)= b(i)- a(i,k)*b(k)/ a(k,k)
end
end
Metody bezpo
ś
rednie – Eliminacja Gaussa

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 56
w k-tym kroku, dla i = k+1, k+2, ..., n (wiersze) mamy
( )
( )
k
k
kk
k
ik
k
i
k
k
i
kj
k
kk
k
ik
k
k
ij
k
ij
b
a
a
b
b
n
k
k
j
a
a
a
a
a
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
,...,
1
,
,...
−
−
−
−
−
−
−
−
−
=
+
=
−
=
for k= 1:n-1
for i= k+1:n
for j= k:n
a(i,j)= a(i,j)-a(i,k)*a(k,j)/a(k,k)
end
b(i)= b(i)- a(i,k)*b(k)/ a(k,k)
end
end
Zadanie: uzupełnij kod programu o wybór częściowy elementu
podstawowego
Metody bezpo
ś
rednie – Eliminacja Gaussa
Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 57
• Odmiana eliminacji Gaussa
– Wiersze są normalizowane poprzez dzielenie przez element główny
– Kolejna zmienna jest eliminowana z wszystkich równań, a nie tylko z
następnych
– Po n krokach eliminacji
otrzymuje się macierz jednostkową
, czego
efektem jest uzyskanie rozwiązania w wektorze prawych stron
n
n
nn
n
n
n
n
n
n
b
x
a
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
=
+
+
+
=
+
+
+
=
+
+
+
...
..
..........
..........
..........
..........
...
...
2
2
1
1
2
2
2
22
1
21
)
0
(
1
)
0
(
1
2
)
0
(
12
1
)
1
(
)
1
(
2
)
1
(
2
)
1
(
2
)
1
(
2
2
)
1
(
22
)
1
(
1
)
1
(
1
2
)
1
(
12
1
...
........
..........
..........
...
...
n
n
nn
n
n
n
n
n
b
x
a
x
a
b
x
a
x
a
b
x
a
x
a
x
=
+
+
=
+
+
=
+
+
+
)
2
(
)
2
(
3
)
2
(
3
)
2
(
2
)
2
(
2
3
)
2
(
23
2
)
2
(
1
)
2
(
1
3
)
2
(
13
1
........
..........
..........
n
n
nn
n
n
n
n
n
b
x
a
x
a
b
x
a
x
a
x
b
x
a
x
a
x
=
+
+
=
+
+
+
=
+
+
+
K
K
K
)
1
(
)
1
(
2
2
)
1
(
1
1
.........
..........
..........
−
−
−
=
=
=
n
n
n
n
n
b
x
b
x
b
x
Metody bezpo
ś
rednie – Eliminacja Gaussa-Jordana
Zadanie: zapisz kod programu (wykorzystując instrukcję for) realizujący metodę
⇒
⇒
⇒
⇒
⇒
⇒
⇒
⇒

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 58
•
rozwiązanie układu równań
A x = b :
– jeśli istnieje rozkład trójkątny
A = LU
to:
LU x = b,
U x = y,
L y = b.
Twierdzenie:
Niech A będzie macierzą
n x n
. Niech A
k
oznacza macierz
k x k
utworzoną z
elementów początkowych k wierszy i kolumn macierzy A. Jeśli det(A
k
)
≠
0 dla
k=1,...,n-1
to istnieje jedyny rozkład A=LU taki, że
•
macierz L jest macierzą
trójkątną dolną
z elementami na głównej przekątnej
równymi 1,
•
macierz U jest macierzą
trójkątną górną
.
Metody bezpo
ś
rednie – Rozkład trójk
ą
tny

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 59
•
zapamiętując rozkład LU możemy szybko rozwiązać wiele układów
różniących się wektorem b
Inne zastosowania rozkładu trójkątnego macierzy:
•
obliczanie wyznacznika macierzy A
– det(A)=det(LU)=det(L)det(U)=det(U)
•
wyznaczanie macierzy odwrotnej do A
– A
-1
= (LU)
-1
= U
-1
L
-1
(odwrotności macierzy trójkątnych oblicza się łatwo)
Metody bezpo
ś
rednie – Rozkład trójk
ą
tny

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 60
• metoda Doolitle’a
a
a
a
a
a
a
a
a
a
l
l
l
u
u
u
u
u
u
n
n
n
n
nn
n
n
n
n
nn
11
12
1
21
22
2
1
2
21
1
2
11
21
1
22
2
1
1
1
K
K
M
M
O
M
K
M
M
O
K
K
K
O
M
=
n
i
i
j
u
u
l
a
l
n
i
i
j
u
l
a
u
n
i
ii
i
k
ki
jk
ji
ji
i
k
kj
ik
ij
ij
,...,
2
,
1
,
/
,...,
1
,
,
,...,
1
1
1
1
1
+
+
=
−
=
+
=
−
=
=
∑
∑
−
=
−
=
Metody bezpo
ś
rednie – Rozkład trójk
ą
tny
A = L U

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 61
• metoda Crouta
– macierz U posiada jedynki na przekątnej głównej
n
j
j
k
l
u
l
a
u
n
j
j
i
u
l
a
l
n
j
jj
j
i
ik
ji
jk
jk
j
k
kj
ik
ij
ij
,...,
2
,
1
,
/
,...,
1
,
,
,...,
1
1
1
1
1
+
+
=
−
=
+
=
−
=
=
∑
∑
−
=
−
=
=
1
1
1
2
1
21
2
1
22
21
11
2
1
2
22
21
1
12
11
M
O
K
K
K
O
M
M
K
M
O
M
M
K
K
n
n
nn
n
n
nn
n
n
n
n
u
u
u
l
l
l
l
l
l
a
a
a
a
a
a
a
a
a
Metody bezpo
ś
rednie – Rozkład trójk
ą
tny
A = L U
Zadanie: zapisz kod programu (funkcję SciLaba) realizujący metodę Crouta –
WE: macierz A, WY: macierze L, U

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 62
Przykład zastosowania metody Doolitle’a
=
?
]
0
[
?
?
?
?
?
1
?
?
1
?
]
0
[
1
1
1
3
2
1
2
1
1
1
n
i
i
j
u
u
l
a
l
n
i
i
j
u
l
a
u
n
i
ii
i
k
ki
jk
ji
ji
i
k
kj
ik
ij
ij
,...,
2
,
1
,
/
,...,
1
,
,
,...,
1
1
1
1
1
+
+
=
−
=
+
=
−
=
=
∑
∑
−
=
−
=
−
−
=
2
]
0
[
0
1
1
1
1
1
2
3
1
2
]
0
[
1
1
1
3
2
1
2
1
1
1
Metody bezpo
ś
rednie – Rozkład trójk
ą
tny
A = L U
2
2
,
3
0
1
2
,
23
32
13
31
33
33
22
12
31
32
32
11
31
31
13
21
23
23
12
21
22
22
21
21
?
1
?
1
−
=
−
−
=
=
−
=
=
=
=
−
=
=
−
=
=
=
=
u
l
u
l
a
u
u
u
l
a
l
u
a
l
u
l
a
u
u
l
a
u
a
l
a
u

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 63
Przykład zastosowania metody Doolitle’a
=
?
]
0
[
?
?
?
?
?
1
?
?
1
?
]
0
[
1
1
1
3
2
1
2
1
1
1
n
i
i
j
u
u
l
a
l
n
i
i
j
u
l
a
u
n
i
ii
i
k
ki
jk
ji
ji
i
k
kj
ik
ij
ij
,...,
2
,
1
,
/
,...,
1
,
,
,...,
1
1
1
1
1
+
+
=
−
=
+
=
−
=
=
∑
∑
−
=
−
=
2
2
,
3
0
1
2
,
23
32
13
31
33
33
22
12
31
32
32
11
31
31
13
21
23
23
12
21
22
22
21
21
?
1
?
1
−
=
−
−
=
=
−
=
=
=
=
−
=
=
−
=
=
=
=
u
l
u
l
a
u
u
u
l
a
l
u
a
l
u
l
a
u
u
l
a
u
a
l
a
u
−
−
=
2
]
0
[
0
1
1
1
1
1
2
3
1
2
]
0
[
1
1
1
3
2
1
2
1
1
1
Metody bezpo
ś
rednie – Rozkład trójk
ą
tny
A = L U

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 64
• A – macierz symetryczna, dodatnio określona
rozkład Cholesky’ego
A = L L
T
• A –macierz symetryczna
jednoznaczny rozkład
A = L D L
T
– D – macierz diagonalna
n
j
j
i
n
j
l
l
a
l
l
l
a
l
j
k
ik
jk
ij
jj
ij
j
k
jk
jj
jj
,...,
2
,
1
,...,
2
,
1
,
)
(
1
,
1
1
1
1
2
+
+
=
=
−
=
−
=
∑
∑
−
=
−
=
Układy równa
ń
z macierzami specjalnymi
Zadanie: zapisz kod programu (funkcję SciLaba, przy użyciu instrukcji
for) realizujący rozkład Cholesky’ego, WE: macierz A, WY: macierz L

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 65
•
Ax = b – układ równań
•
otrzymane przybliżone rozwiązanie x
0
–
jeśli rozwiązanie jest rozwiązaniem dokładnym to
Ax – b = [0]
–
jeśli nie jest rozwiązaniem dokładnym to obliczamy
wektor residuum
r
0
= b – Ax
0
≠≠≠≠
[0]
Jak dobrym przybliżeniem rozwiązania dokładnego jest
wektor x
0
?
Układy równa
ń
– analiza rozwi
ą
za
ń
przybli
ż
onych

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 66
• x, y – liczby rzeczywiste
– odległość d=|x – y|
• x=(x
1
,x
2
), y =(y
1
,y
2
), – punkty w przestrzeni 2D
– odległość
2
2
1
2
2
1
)
(
)
(
y
y
x
x
d
−
+
−
=
Norma – mierzenie odległo
ś
ci

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 67
• x, y – liczby rzeczywiste
– odległość
d=|x – y|
• x=(x
1
,x
2
), y =(y
1
,y
2
), – punkty w przestrzeni 2D
– odległość
2
2
1
2
2
1
)
(
)
(
y
y
x
x
d
−
+
−
=
Norma – mierzenie odległo
ś
ci
Norma
– nieujemna funkcja rzeczywistą ||.||: X
→
R, spełniającą
następujące warunki
:
1.
||x|| = 0
wtedy i tylko wtedy gdy
x = 0
2.
||ax|| = |a|*||x||
dla każdej liczby rzeczywistej
a
∈
∈
∈
∈
R
3.
||x + y||
≤≤≤≤
||x|| + ||y||
(tzw. nierówność trójkąta).
(odległość elementu przestrzeni liniowej od punktu 0)
Odległość dwóch elementów przestrzeni liniowej
x, y
d = || x-y ||

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 68
• w przestrzeni R
n
,
x =(x
1
,x
2
,..., x
n
)
∈
R
n
:
• przestrzeni ciągów
x =(x
n
)
n
p
n
i
p
i
p
n
i
i
n
i
i
i
n
i
x
x
x
x
x
x
x
x
/
1
1
1
2
2
1
1
,...,
1
)
(
||
||
,
||
||
|
|
||
||
|
|
max
||
||
∑
∑
∑
=
=
=
=
∞
=
=
=
=
|,
|
sup
||
||
,...
2
,
1
i
i
x
x
=
∞
=
Norma – przykłady

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 69
• macierzowe ( A
nm
-macierz kwadratowa n=m)
∑∑
∑
=
=
=
=
=
=
∞
=
=
=
n
i
n
j
ij
ij
n
j
n
i
n
j
ij
n
i
a
A
a
A
a
A
1
1
2
2
,...,
1
,...,
1
1
,...,
1
||
||
|
|
max
||
||
,|
|
max
||
||
=
nn
n
n
n
n
a
a
a
a
a
a
a
a
a
A
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
..
2
1
2
22
21
1
12
11
Norma – przykłady
Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 70
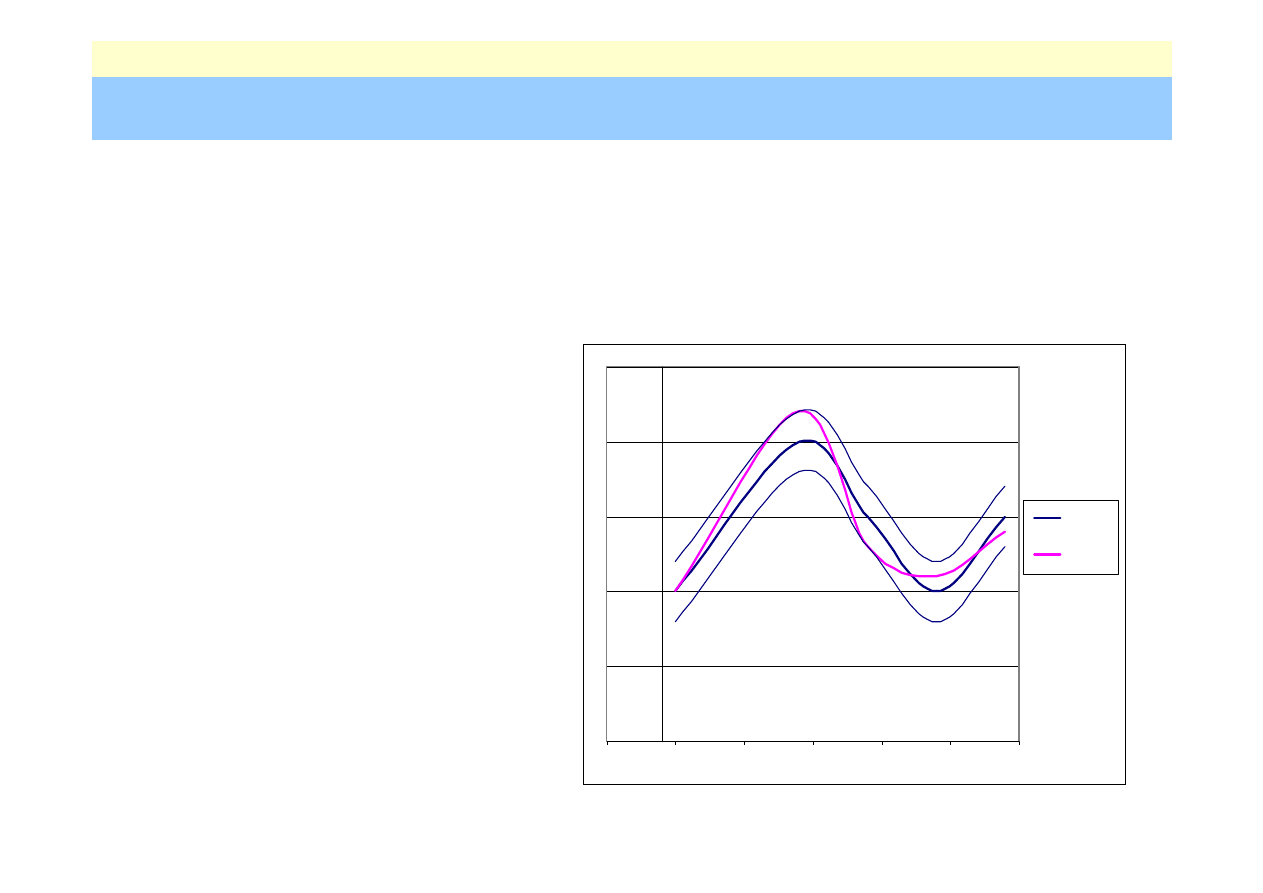
• w przestrzeni funkcji C[a,b]
f, g
∈
C[a,b]
ε
<
−
=
=
∫
∈
∞
||
||
|
)
(
|
||
||
|,
)
(
|
sup
||
||
]
,
[
2
2
]
,
[
g
f
dx
x
f
f
x
f
f
b
a
b
a
x
0
0.5
1
1.5
2
2.5
-0.8
0.2
1.2
2.2
3.2
4.2
5.2
funkc ja f
funkc ja g
Norma – przykłady

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 71
•
norma macierzowa
•
x : wektor lub macierz (rzeczywiste lub zespolone)
•
flag : rodzaj normy (domyślnie =2)
•
Opis (macierze)
–
norm(x): norm(x,2) : największa wartość bezwzględna elementu macierzy
–
norm(x,1): największa suma kolumny
–
norm(x,'inf'),norm(x,%inf): największa suma wiersza
•
wektory
–
norm(v,p): || . ||
p
–
norm(v): || . ||
2
–
norm(v,'inf'): norma supremalna
Norma – mierzenie odległo
ś
ci
[y]=norm(x [,flag])

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 72
Norma – przestrze
ń
unormowana
Przestrze
ń
liniowa w której zdefiniowano norm
ę
= przestrze
ń
unormowana
Stefan Banach
Hugo Steinhaus
Władysław Orlicz

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 73
•
Ax = b – układ równań
•
otrzymane przybliżone rozwiązanie x
0
–
jeśli rozwiązanie jest rozwiązaniem dokładnym to
Ax – b = [0]
–
jeśli nie jest rozwiązaniem dokładnym to obliczamy
wektor residuum
r
0
= b – Ax
0
≠≠≠≠
[0]
Jak dobrym przybliżeniem rozwiązania dokładnego jest
wektor x
0
?
Układy równa
ń
– analiza rozwi
ą
za
ń
przybli
ż
onych
Oszacowanie przy użyciu normy (dla rozwiązań x
1
, x
2
) :
r
1
= b–Ax
1
r
2
= b–Ax
2
Jeśli
||r
1
||<||r
2
||
to rozwiązanie
x
1
jest bardziej
dokładne niż
x
2

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 74
• A – macierz symetryczna
metoda sprzężonych gradientów
• ustalamy wektor początkowy niewiadomych x
• obliczamy wektor r
0
= b – Ax, przyjmujemy P
0
= r
0
• dla
i = 0,1,2,..., n-1
obliczamy
– podczas obliczeń
nie następuje przekształcenie
macierzy A
(wygodne dla macierzy rzadkich)
– zadawalającym przybliżeniem jest wektor x
i
dla pewnego i < n
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
T
i
i
i
P
r
P
r
r
AP
r
r
P
x
x
AP
P
r
β
β
α
α
α
+
=
=
−
=
+
=
=
+
+
+
+
+
1
1
2
1
1
1
2
,
||
||
||
||
,
,
||
||
Układy równa
ń
z macierzami specjalnymi
Metoda sprz
ęż
onych gradientów

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 75
• wektor początkowy niewiadomych x
0
= [1, 1, 1, 1]
T
• uzyskiwane kolejne przybliżenia
– [ 2.0967742 1.
2.6451613 2.0967742 ]
– [ 0.8879310 0.3060345 3.6077586 3.6637931 ]
– [ 0.8548387 0.5967742 3.6290323 3.5645161 ]
– [ 1.
2.
3.
4.
]
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
T
i
i
i
P
r
P
r
r
AP
r
r
P
x
x
AP
P
r
β
β
α
α
α
+
=
=
−
=
+
=
=
+
+
+
+
+
1
1
2
2
1
1
1
2
,
||
||
||
||
,
,
||
||
=
−
−
−
−
−
−
−
3
5
0
5
1
2
1
1
2
1
1
2
1
1
1
1
1
2
1
1
4
3
2
1
x
x
x
x
Zadanie: zapisz kod programu (funkcję SciLaba) realizujący
metodę, WE: macierz A, wektor b, WY: wektor x
Układy równa
ń
z macierzami specjalnymi
Metoda sprz
ęż
onych gradientów - przykład

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 76
Sposoby zapisu macierzy
Profil macierzy rzadkiej
=
nn
n
n
a
a
a
a
a
A
..
..
0
..
..
..
..
0
..
..
..
..
..
..
..
0
0
..
..
0
2
2
22
11
=
}
{
}
2
{
}
2
{
}
2
2
{
}
1
1
{
)
(
2
2
22
11
n
n
a
n
a
n
a
a
a
sparse
A
nn
n
n
⇒

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 77
Sposoby zapisu macierzy
Posta
ć
blokowa macierzy

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 78
Metody iteracyjne - przykład
Obliczenie pierwiastka kwadratowego
x
x
c
x
c
=
⇒
=
2

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 79
Metody iteracyjne - przykład
Obliczenie pierwiastka kwadratowego
x
x
x
c
x
x
c
x
c
2
)
(
2
=
+
⇒
=
⇒
=

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 80
Metody iteracyjne - przykład
Obliczenie pierwiastka kwadratowego
)
(
2
1
2
)
(
2
x
x
c
x
x
x
x
c
x
x
c
x
c
+
=
⇒
=
+
⇒
=
⇒
=

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 81
Metody iteracyjne - przykład
Obliczenie pierwiastka kwadratowego
)
(
2
1
2
)
(
2
x
x
c
x
x
x
x
c
x
x
c
x
c
+
=
⇒
=
+
⇒
=
⇒
=
,...
2
,
1
)
(
2
1
1
=
+
=
+
i
x
x
c
x
i
i
i
x = 1, c = 2
for i= 1:n
x = (c/x + x)/2
end
x = 1, c = 2
eps = 0.00001
while abs(c-x*x) > eps
x = (c/x + x)/2
end
...
414216
.
1
416667
.
1
5
.
1
1
4
3
2
1
=
=
=
=
x
x
x
x

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 82
– startują z przybliżenia początkowego x
(0)
– polegają na konstrukcji nieskończonego ciągu wektorów,
zbieżnych do szukanego rozwiązania,
x
(0)
→
x
(1)
→
x
(2)
→
...
– liczba operacji wykonywanych w każdym kroku iteracyjnym jest
porównywalna z mnożeniem macierzy przez wektor
– stosowane w przypadkach gdy macierz A jest dużych rozmiarów
macierzą rzadką
– problem
• doboru początkowego przybliżenia (często wektor zerowy)
• przerwania procesu iteracyjnego
Metody iteracyjne
rozwi
ą
zywania układów równa
ń
liniowych
Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 83
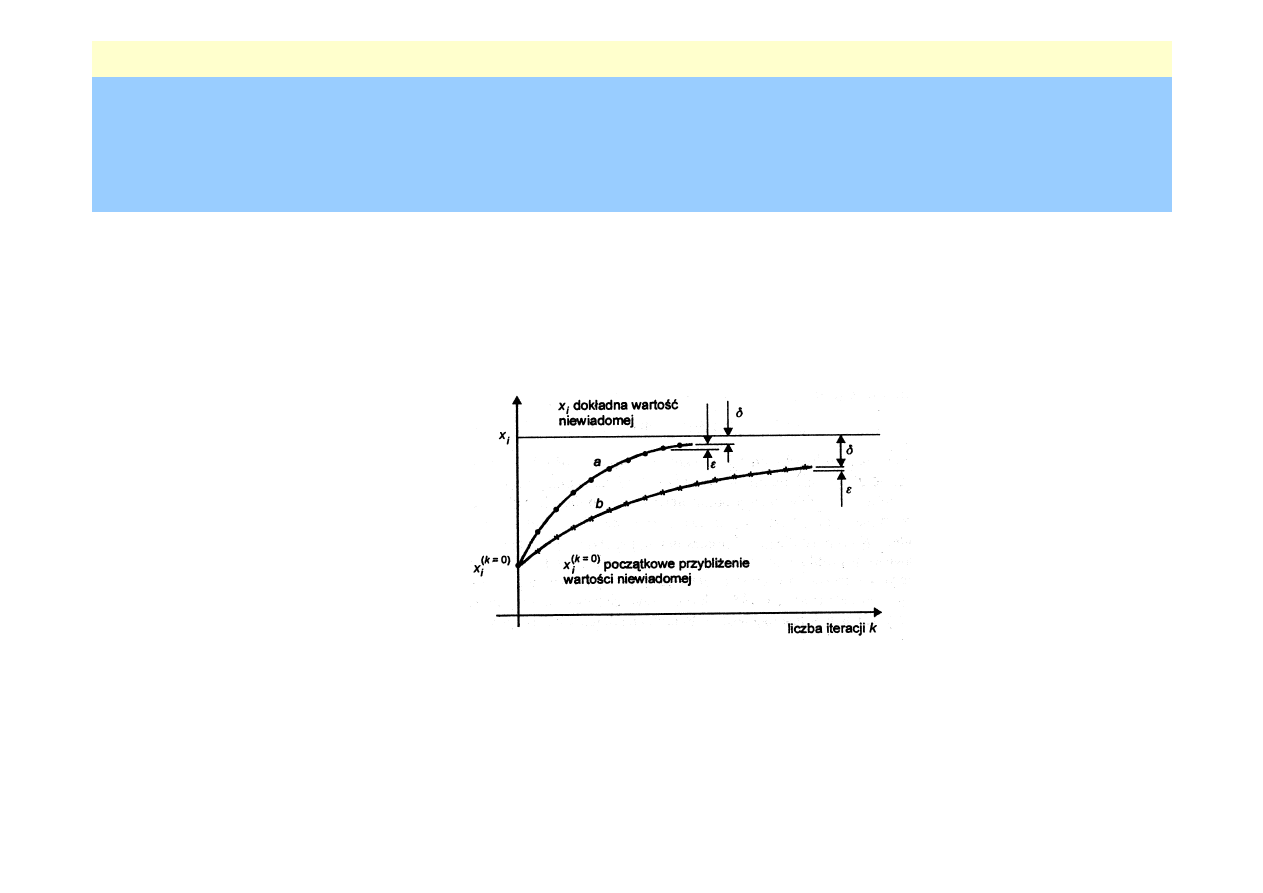
Przerwanie procesu iteracyjnego
– oszacowanie
||x
(k+1)
- x
(k)
|| <
ε
k – indeks iteracji
dobre wyniki gdy proces jest szybko zbieżny
– oszacowanie
|| r
(k)
|| = || A x
(k)
– b || <
ε
Metody iteracyjne
rozwi
ą
zywania układów równa
ń
liniowych

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 84
– dla równania
A x = b
dany jest rozkład
A = L U
– wartość obliczona
– residuum
– proces iteracyjny
• należy przyjąć
• następnie obliczyć
wg formuł
x
x
A
b
r
−
=
x
x
=
:
)
1
(
,...
3
,
2
,
)
(
=
s
x
s
)
(
)
(
)
1
(
)
(
1
1
)
(
)
(
)
(
)
(
)
(
,
)
(
,
s
s
s
s
s
s
s
s
s
x
x
x
r
L
U
x
r
x
U
L
Ax
b
r
∂
+
=
=
∂
=
∂
⋅
−
=
+
−
−
Ulepszanie iteracyjne rozwi
ą
zania
(metoda iteracji powtórnej)
Zadanie: zapisz kod programu realizujący metodę

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 85
• metoda Jacobiego
Metody iteracyjne
rozwi
ą
zywania układów równa
ń
liniowych
=
+
+
+
=
+
+
+
=
+
+
+
n
n
nn
n
n
n
n
n
n
b
x
a
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
L
L
L
L
2
2
1
1
2
2
2
22
1
21
1
1
2
12
1
11
1
2
1
1
11
b
x
a
x
a
n
k
k
k
=
+
∑
=
∑
=
−
=
n
k
k
k
x
a
b
x
a
2
1
1
1
11
11
2
1
1
1
/
)
(
a
x
a
b
x
n
k
k
k
∑
=
−
=
znane:
x
(0)
=(x
1
(0)
,..., x
n
(0)
)
szukane:
x
(1)
=(x
1
(1)
,..., x
n
(1)
)
1
,
/
)
(
11
2
)
0
(
1
1
)
1
(
1
=
−
=
∑
=
j
a
x
a
b
x
n
k
k
k
dla j =1 :
⇒
⇒
⇓
,
,...,
2
,
1
,
,
1
n
j
b
x
a
x
a
j
n
j
k
k
k
jk
j
jj
=
=
+
∑
≠
=

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 86
• metoda Jacobiego
Metody iteracyjne
rozwi
ą
zywania układów równa
ń
liniowych
=
+
+
+
=
+
+
+
=
+
+
+
n
n
nn
n
n
n
n
n
n
b
x
a
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
L
L
L
L
2
2
1
1
2
2
2
22
1
21
1
1
2
12
1
11
,
,...,
2
,
1
,
,
1
n
j
b
x
a
x
a
j
n
j
k
k
k
jk
j
jj
=
=
+
∑
≠
=
znane:
x
(m)
=(x
1
(m)
,..., x
n
(m)
)
szukane:
x
(m+1)
=(x
1
(m+1)
,..., x
n
(m+1)
)
m –ty krok :
// x(1:n,1) – rozw. pocz.
for m = 1:m_max
end
n
j
a
x
a
b
x
jj
n
j
k
k
k
m
jk
j
m
j
,...,
2
,
1
,
/
)
(
,
1
)
(
)
1
(
=
−
=
∑
≠
=
+

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 87
• metoda Jacobiego
Metody iteracyjne
rozwi
ą
zywania układów równa
ń
liniowych
=
+
+
+
=
+
+
+
=
+
+
+
n
n
nn
n
n
n
n
n
n
b
x
a
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
L
L
L
L
2
2
1
1
2
2
2
22
1
21
1
1
2
12
1
11
,
,...,
2
,
1
,
,
1
n
j
b
x
a
x
a
j
n
j
k
k
k
jk
j
jj
=
=
+
∑
≠
=
znane:
x
(m)
=(x
1
(m)
,..., x
n
(m)
)
szukane:
x
(m+1)
=(x
1
(m+1)
,..., x
n
(m+1)
)
m –ty krok :
// x(1:n,1) – rozw. pocz.
for m = 1:m_max
for j = 1:n
s = b(j)
end
end
n
j
a
x
a
b
x
jj
n
j
k
k
k
m
jk
j
m
j
,...,
2
,
1
,
/
)
(
,
1
)
(
)
1
(
=
−
=
∑
≠
=
+

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 88
• metoda Jacobiego
Metody iteracyjne
rozwi
ą
zywania układów równa
ń
liniowych
=
+
+
+
=
+
+
+
=
+
+
+
n
n
nn
n
n
n
n
n
n
b
x
a
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
L
L
L
L
2
2
1
1
2
2
2
22
1
21
1
1
2
12
1
11
,
,...,
2
,
1
,
,
1
n
j
b
x
a
x
a
j
n
j
k
k
k
jk
j
jj
=
=
+
∑
≠
=
znane:
x
(m)
=(x
1
(m)
,..., x
n
(m)
)
szukane:
x
(m+1)
=(x
1
(m+1)
,..., x
n
(m+1)
)
m –ty krok :
// x(1:n,1) – rozw. pocz.
for m = 1:m_max
for j = 1:n
s = b(j)
for k = 1:n
s = s– a(j,k)*x(k,m)
end
end
end
n
j
a
x
a
b
x
jj
n
j
k
k
k
m
jk
j
m
j
,...,
2
,
1
,
/
)
(
,
1
)
(
)
1
(
=
−
=
∑
≠
=
+

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 89
• metoda Jacobiego
Metody iteracyjne
rozwi
ą
zywania układów równa
ń
liniowych
=
+
+
+
=
+
+
+
=
+
+
+
n
n
nn
n
n
n
n
n
n
b
x
a
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
L
L
L
L
2
2
1
1
2
2
2
22
1
21
1
1
2
12
1
11
,
,...,
2
,
1
,
,
1
n
j
b
x
a
x
a
j
n
j
k
k
k
jk
j
jj
=
=
+
∑
≠
=
znane:
x
(m)
=(x
1
(m)
,..., x
n
(m)
)
szukane:
x
(m+1)
=(x
1
(m+1)
,..., x
n
(m+1)
)
m –ty krok :
// x(1:n,1) – rozw. pocz.
for m = 1:m_max
for j = 1:n
s = b(j)
for k = 1:n
if k != j then
s = s– a(j,k)*x(k,m)
end
end
end
end
n
j
a
x
a
b
x
jj
n
j
k
k
k
m
jk
j
m
j
,...,
2
,
1
,
/
)
(
,
1
)
(
)
1
(
=
−
=
∑
≠
=
+

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 90
• metoda Jacobiego
Metody iteracyjne
rozwi
ą
zywania układów równa
ń
liniowych
=
+
+
+
=
+
+
+
=
+
+
+
n
n
nn
n
n
n
n
n
n
b
x
a
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
L
L
L
L
2
2
1
1
2
2
2
22
1
21
1
1
2
12
1
11
,
,...,
2
,
1
,
,
1
n
j
b
x
a
x
a
j
n
j
k
k
k
jk
j
jj
=
=
+
∑
≠
=
znane:
x
(m)
=(x
1
(m)
,..., x
n
(m)
)
szukane:
x
(m+1)
=(x
1
(m+1)
,..., x
n
(m+1)
)
m –ty krok :
// x(1:n,1) – rozw. pocz.
for m = 1:m_max
for j = 1:n
s = b(j)
for k = 1:n
if k != j then
s = s– a(j,k)*x(k,m)
end
end
x(j,m +1) = s/a(j,j)
end
end
n
j
a
x
a
b
x
jj
n
j
k
k
k
m
jk
j
m
j
,...,
2
,
1
,
/
)
(
,
1
)
(
)
1
(
=
−
=
∑
≠
=
+

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 91
Metody iteracyjne rozwi
ą
zywania układów równa
ń
liniowych
Metoda Jacobiego - przykład
=
=
=
4
3
2
1
,
1
1
1
1
,
22
19
16
13
4
1
1
1
1
4
1
1
1
1
4
1
1
1
1
4
)
0
(
4
3
2
1
OK
x
x
x
x
x
x
=
=
=
3.9999394
2.999805
1.9999839
1.0004535
,...,
95
.
3
15
.
3
14
.
2
90
.
0
,
37
.
3
16
.
3
88
.
2
5
.
2
)
6
(
)
2
(
)
1
(
x
x
x

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 92
Metody iteracyjne rozwi
ą
zywania układów równa
ń
liniowych
Metoda Jacobiego - przykład
=
=
=
4
3
2
1
,
1
1
1
1
,
4
.
6
3
.
7
2
.
8
1
.
9
1
.
0
1
1
1
1
1
.
0
1
1
1
1
1
.
0
1
1
1
1
1
.
0
)
0
(
4
3
2
1
OK
x
x
x
x
x
x
,...
08
293
32515003
3607298
400201
,
44396
4933
548
61
)
2
(
)
1
(
+
−
−
=
−
−
=
E
x
x

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 93
Metody iteracyjne
rozwi
ą
zywania układów równa
ń
liniowych
• metoda Gaussa-Seidela
jj
n
j
k
i
k
jk
j
k
i
k
jk
j
i
j
j
n
j
k
i
k
jk
i
j
jj
j
k
i
k
jk
a
x
a
x
a
b
x
i
n
j
b
x
a
x
a
x
a
∑
∑
∑
∑
+
=
−
=
+
+
+
=
+
−
=
+
−
−
=
=
=
=
+
+
1
)
(
1
1
)
1
(
)
1
(
1
)
(
)
1
(
1
1
)
1
(
...
2
,
1
,
0
,
,...,
2
,
1
,
=
+
+
+
=
+
+
+
=
+
+
+
n
n
nn
n
n
n
n
n
n
b
x
a
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
L
L
L
L
2
2
1
1
2
2
2
22
1
21
1
1
2
12
1
11
,
,...,
2
,
1
,
1
1
1
n
j
b
x
a
x
a
x
a
j
n
j
k
k
jk
j
jj
j
k
k
jk
=
=
+
+
∑
∑
+
=
−
=

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 94
• metoda Gaussa-Seidela jest z reguły
szybciej zbieżna
niż metoda
Jacobiego
• istnieją układy dla których metoda Gaussa-Seidela jest
rozbieżna
,
a metoda Jacobiego zbieżna
• Metoda Jacobiego i metoda Gaussa-Seidela są
zbieżne
jeśli
macierz A jest
macierzą ze ściśle dominującą przekątną
główną
, tzn.
∑
≠
=
=
>
n
i
j
j
ij
ii
n
j
i
a
a
1
,...,
1
,
|
|
|
|
Metody iteracyjne
rozwi
ą
zywania układów równa
ń
liniowych

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 95
• metoda nadrelaksacji –
przyśpieszenie zbieżności metody Gaussa-
Seidela
– modyfikując wzór metody Gaussa-Seidela otrzymujemy
– parametr relaksacji
ω
ω
ω
ω
dobrany jest tak, aby zbieżność metody była jak
najszybsza (jeśli
ω
ω
ω
ω
= 1 to metoda redukuje się do metody Gaussa-Seidela
)
(
)
(
)
1
(
)
(
)
(
)
1
(
)
(
1
1
)
1
(
)
(
,
i
j
i
j
i
j
i
j
i
j
i
j
jj
n
j
k
i
k
jk
j
k
i
k
jk
j
i
j
r
x
x
r
x
x
a
x
a
x
a
b
r
ϖ
+
=
+
=
−
−
=
+
+
=
−
=
+
∑
∑
( )
...
2
,
1
,
0
,
,...,
2
,
1
,
)
(
1
1
)
1
(
1
)
(
1
1
)
1
(
)
1
(
=
=
+
−
−
=
−
−
=
∑
∑
∑
∑
=
−
=
+
+
=
−
=
+
+
i
n
j
a
x
a
x
a
x
a
b
a
x
a
x
a
b
x
jj
i
j
jj
n
j
k
i
k
jk
j
k
i
k
jk
j
jj
n
j
k
i
k
jk
j
k
i
k
jk
j
i
j
Metody iteracyjne
rozwi
ą
zywania układów równa
ń
liniowych
Zadanie: zapisz kod programu realizujący metodę Gaussa-Seidela

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 96
Złe uwarunkowanie układu równań
– układ równań postaci
A x = b
– wartość obliczona
– residuum
– wniosek : jeśli oszacowanie r jest małe to jest dobrym rozwiązaniem ?
– Przykład
x
x
A
b
r
−
=
x
[
]
[
]
T
T
T
x
rozw
r
x
b
A
2
2
.
10
10
]
4870
,
0
9911
,
0
[
1440
,
0
8642
,
0
,
1441
,
0
2161
,
0
8648
,
0
2969
,
1
8
8
−
=
−
−
=
−
=
=
=
−
−
Analiza bł
ę
dów w układach równa
ń
liniowych
Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 97
• WE: a
11
a
12
a
21
a
22
b
1
b
2
WY: x,y
-3
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
0
2
4
6
8
10
12
-3
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
0
2
4
6
8
10
12
Przykład złego uwarunkowania zadania
2
10
000000002
.
8
999999999
.
5
2
8
6
2
−
=
=
⇒
=
+
=
+
y
x
y
x
y
x
1
1
000000001
.
8
000000001
.
6
2
8
6
2
=
=
⇒
=
+
=
+
y
x
y
x
y
x
wskaźnik uwarunkowania macierzy
A
||
||
||
||
)
(
1
−
⋅
=
A
A
A
κ
jeśli jest on duży, to małe zaburzenia względne macierzy
A
i wektora
b
mogą powodować duże zaburzenia
względne wektora
x
,
zadanie jest źle uwarunkowane
08
0
.
3
||
||
6
||
||
1
+
=
=
−
E
A
A

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 98
–Matematyczny opis powiązań pomiędzy danymi wejściowymi i wyjściowymi
(sposób wyznaczenia wyników na podstawie danych wejściowych).
–Zadanie jest dobrze określone jeśli wyniki są jednoznacznie określone dla
przyjętych danych wejściowych
Zadanie numeryczne
Uwarunkowanie zadania numerycznego
• jak bardzo wynik
f(
f(
f(
f(x+D
+D
+D
+Dx)))) różni się od f(
f(
f(
f(x))))
• x – dane wejściowe
•
f- zadanie numeryczne
• y=
f(x )– wynik, D
D
D
Dy= f(
f(
f(
f(x+D
+D
+D
+Dx)))) - f(
f(
f(
f(x))))
Jeśli
to zadanie jest
źle uwarunkowane
x
x
y
y
∆
〉〉
∆
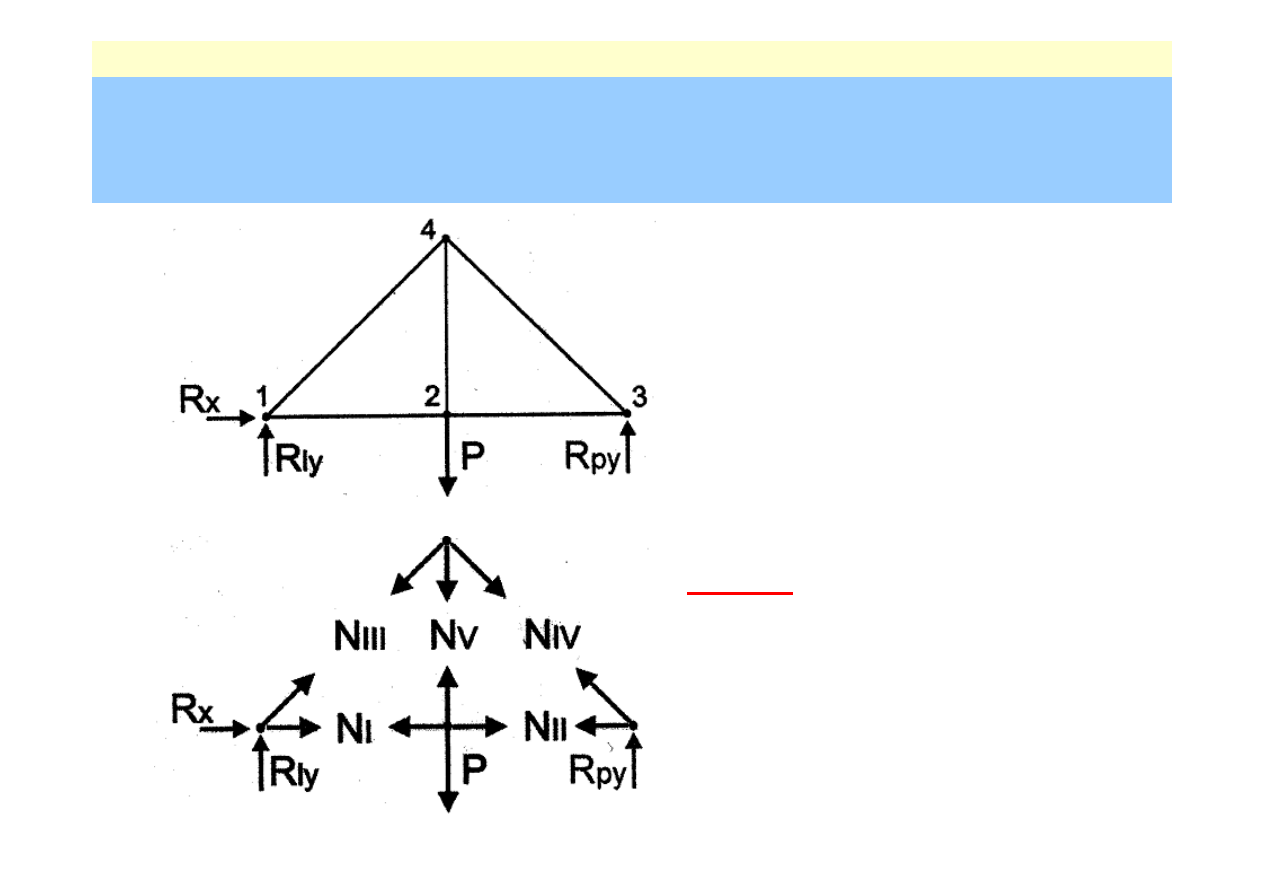
Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 99
Przykład in
ż
ynierski – zadanie kratownicy
(metoda równowa
ż
enia w
ę
złów)
0
sin
:
1
0
cos
:
1
=
+
=
+
+
α
α
III
y
y
III
I
x
x
N
R
N
N
R
P
N
N
N
V
y
II
I
x
=
=
+
−
:
2
0
:
2
Zadanie: przygotuj arkusz MS Excel
rozwiązujący zadanie kratownicy
(przyjąć długości d
12
=d
23
=d
24
=1,
P = 100kN)

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 100
•
inv()
obliczenie macierzy odwrotnej
•
linsolve()
rozwiązanie układu równań liniowych dowolnej postaci
•
lu()
rozkład LU eliminacji Gaussa
•
chol()
rozkład Cholesky'ego
•
sparse()
formowanie macierzy rzadkich
•
full()
sformowanie pełnej macierzy w oparciu o profil macierzy
rzadkiej
•
lusolve()
rozwiązanie układu równań liniowych z macierzą rzadką
•
chfact()
rozkład Cholesky'ego dla macierzy rzadkich
•
chsolve()
rozwiązanie układu równań liniowych z macierzą rzadką za
pomocą metody Cholesky'ego
•
spchol()
rozkład Cholesky'ego dla macierzy rzadkich
Poj
ę
cie układu równa
ń
liniowych
Funkcje SciLaba

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 101
• LAPACK (Linear Algebra PACKage),
LINPACK
– biblioteki procedur służących do
rozwiązywania układów równań liniowych i
metody najmniejszych kwadratów
– http://www.netlib.org/lapack/
(
L A
P A C K
)
(
L -A
P -A C -K
)
(
L A
P A
-C -K
)
(
L -A
P -A
-C K
)
(
L A -P -A
C K
)
(
L -A -P A
C -K
)
Poj
ę
cie układu równa
ń
liniowych
Procedury w j
ę
zyku FORTRAN

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 102
Podsumowanie
Metody rozwiązywania układów równań liniowych.
•
Sformułowanie zagadnienia, podstawowe pojęcia
–
macierz główna układu, macierz rozszerzona,
–
twierdzenie Kroneckera-Capellego,
–
pojecie rzędu macierzy.
•
Podział metod rozwiązywania układów równań liniowych:
–
bezpośrednie
–
iteracyjne
•
Sposoby rozwiązań przy użyciu metod bezpośrednich
–
z zastosowaniem macierzy odwrotnej,
–
za pomocą wzorów Cramera,
–
układ równań z macierzą trójkątną.
•
Eliminacja Gaussa
–
eliminacja zmiennych,
–
postępowanie odwrotne,
–
wybór elementu podstawowego,
–
metoda eliminacji Gaussa-Jordana,

Metody obliczeniowe - Budownictwo semestr 2 - wykład nr 1
Nr: 103
Podsumowanie c.d.
Metody rozwiązywania układów równań liniowych.
•
Rozkład trójkątny macierzy
–
sposób postepowania,
–
metoda Doolitle’a,
–
metoda Crouta,
–
rozkład Cholesky’ego,
•
Metoda sprzężonych gradientów.
•
Metoda wielo-frontalna (metody blokowe)
•
Analiza błędów
–
złe uwarunkowanie układu równań
–
wskaźnik uwarunkowania macierzy A
–
ulepszanie iteracyjne rozwiązania (metoda iteracji powtórnej)
•
Metody iteracyjne
–
metoda Jacobiego,
–
metoda Gaussa-Seidela,
–
metoda nadrelaksacji
Wyszukiwarka
Podobne podstrony:
2008 Metody obliczeniowe 10 D 2008 11 28 20 51 40
2008 Metody obliczeniowe 07 D 2008 10 29 19 28 1
2008 Metody obliczeniowe 06 D 2008 10 22 20 13 23
2008 Metody obliczeniowe 02 D 2008 10 1 21 28 5
2008 Metody obliczeniowe 03 D 2008 10 1 22 5 47
3 ANALITYCZNE METODY OBLICZANIA PŁYWÓW
Metody obliczeniowe
2008 Metody obliczeniowe 08 D 2008 11 11 21 31 58
Metody Obliczeniowe 2
bryły, METODY OBLICZENIOWE
moo-zadania, Elektrotechnika, Metody obliczeniowe optymalizacji, ćwiczenia
Metody badan 1 10
więcej podobnych podstron