
>
restart:
WYZNACZANIE ŚCISŁYCH ROZWIĄZAŃ
WYBRANYCH TYPÓW RÓWNAŃ
(solve, isolve, rsolve dsolve)
Znajdowanie pierwiastków, sortowanie, przypisywanie nazw pierwiastkom , sprawdzanie
rozwiązań
Ogólna budowa komendy solve
solve ( r, n );
r - układ równań lub nierówności
n - niewiadome
>
Równania algebraiczne o współczynnikach liczbowych
( solve )
Podejście najprostsze
>
solve(x^2-3*x+1=0,x);
,
+
3
2
5
2
−
3
2
5
2
>
x;
x
>
x1:=%%[2];
:=
x1
−
3
2
5
2
>
x2:=%%%[1];
:=
x2
+
3
2
5
2
>
simplify(subs(x=x1,x^2-3*x+1=0)); # sprawdzenie rozwiązań
dopiero po przypisaniu im nazw
=
0 0
>
simplify(subs(x=x2,x^2-3*x+1=0));
=
0 0
Podejście bardziej eleganckie
>
restart:
>
row:=x^2-3*x+1=0;
:=
row
=
− +
x
2
3 x 1 0
>
roz:=solve(row,x);

:=
roz
,
+
3
2
5
2
−
3
2
5
2
>
simplify(subs(x=roz[1],row)); # sprawdzenie rozwiązań przed
przypisaniem im nazw
=
0 0
>
simplify(subs(x=roz[2],row));
=
0 0
>
evalf(roz);
,
2.618033988 0.381966012
>
sort([roz]);
,
+
3
2
5
2
−
3
2
5
2
>
is(roz[1]>roz[2]);
true
>
por:=(x,y)->is(x<y);
:=
por
→
(
)
,
x y
(
)
is
<
x y
>
lpp:=sort([roz],por); # lista pierwiastków posortowanych (tylko
dla liczb rzeczywistych)
:=
lpp
,
−
3
2
5
2
+
3
2
5
2
>
seq(x||i=lpp[i],i=1..2);
,
=
x1
−
3
2
5
2
=
x2
+
3
2
5
2
>
x1, x2;
,
x1 x2
>
assign(seq(x||i=lpp[i],i=1..2)); # przypisanie nazw
pierwiastkom
>
x1;
−
3
2
5
2
>
x2;
+
3
2
5
2
Podejście bardziej efektywne
>
restart:
>
row:=x^2-3*x+1=0;
:=
row
=
− +
x
2
3 x 1 0
>
roz:=solve(row,{x}); # zbiór niewiadomych -> zbiór rozwiązań
:=
roz
,
{
}
=
x
+
3
2
5
2
{
}
=
x
−
3
2
5
2
>
simplify(eval(row,roz[1])); # inny sposób sprawdzenia rozwiązań
=
0 0
>
simplify(eval(row,roz[2]));
=
0 0
>
x;
x
>
x1:=eval(x,roz[1]);
:=
x1
+
3
2
5
2
>
x2:=eval(x,roz[2]);
:=
x2
−
3
2
5
2
Równania wyższych stopni
>
restart:
>
row:=x^10-1=0;
:=
row
=
−
x
10
1 0
>
roz:=solve(row,{x});
roz
{
}
=
x -1 {
}
=
x 1 {
}
=
x
−
− +
+
1
4
5
4
1
4
I 2
+
5
5
,
,
,
:=
{
}
=
x
−
− −
+
1
4
5
4
1
4
I 2
−
5
5
{
}
=
x
−
− −
−
1
4
5
4
1
4
I 2
−
5
5
,
,
{
}
=
x
−
− +
−
1
4
5
4
1
4
I 2
+
5
5
{
}
=
x
− +
+
1
4
5
4
1
4
I 2
+
5
5
,
,
{
}
=
x
− −
+
1
4
5
4
1
4
I 2
−
5
5
{
}
=
x
− −
−
1
4
5
4
1
4
I 2
−
5
5
,
,
{
}
=
x
− +
−
1
4
5
4
1
4
I 2
+
5
5
>
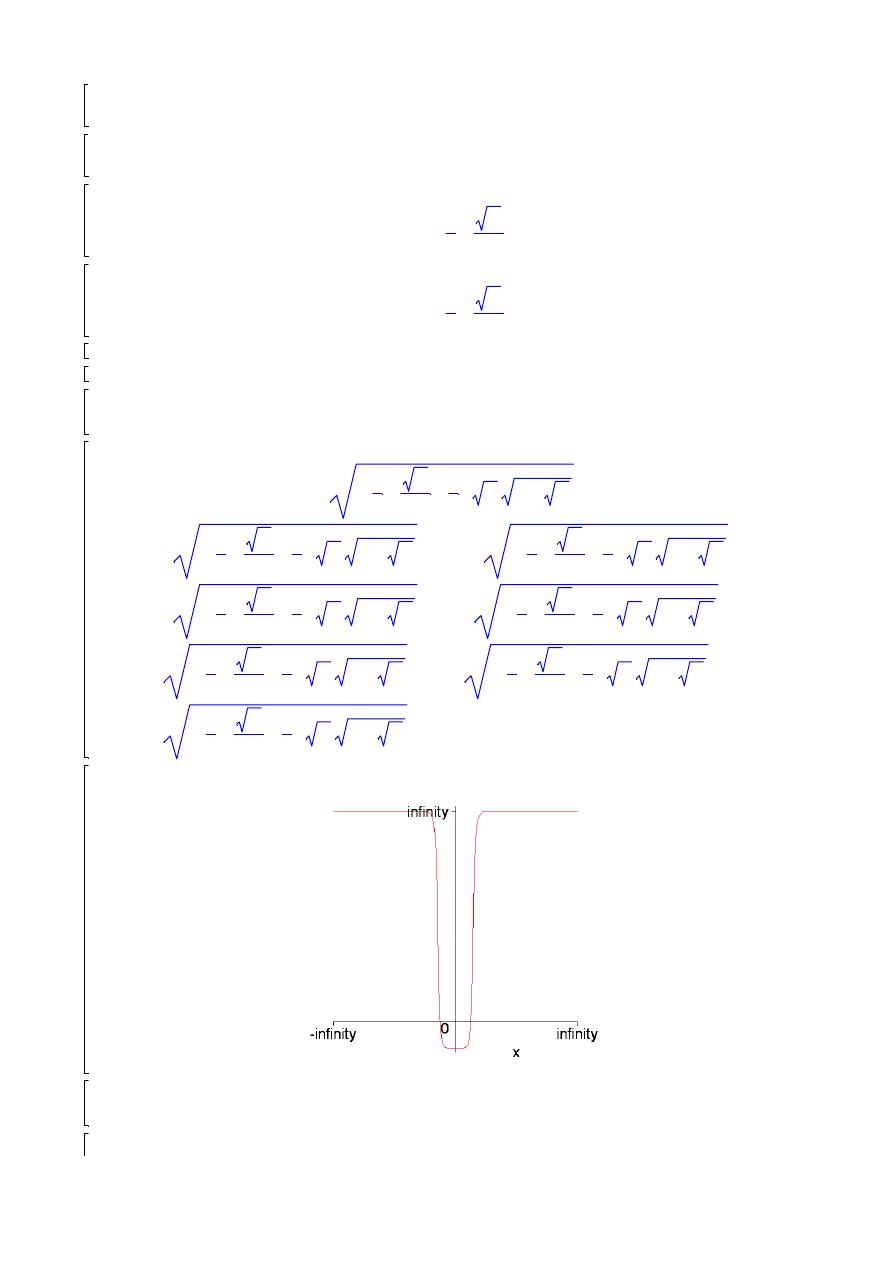
plot(lhs(row),x=-infinity..infinity);
>
row:=x^5-x+1=0;
:=
row
=
− +
x
5
x 1 0
>
roz:=solve(row,{x});

roz
{
}
=
x
(
)
RootOf
,
− +
_Z
5
_Z 1
=
index 1
{
}
=
x
(
)
RootOf
,
− +
_Z
5
_Z 1
=
index 2
,
,
:=
{
}
=
x
(
)
RootOf
,
− +
_Z
5
_Z 1
=
index 3
{
}
=
x
(
)
RootOf
,
− +
_Z
5
_Z 1
=
index 4
,
,
{
}
=
x
(
)
RootOf
,
− +
_Z
5
_Z 1
=
index 5
>
plot(lhs(row),x=-infinity..infinity);
>
evalf(roz); # evalf(roz,30); lub evalf[30](roz);
{
}
=
x
+
0.7648844336 0.3524715460 I {
}
=
x
+
-0.1812324445 1.083954101 I
,
,
{
}
=
x -1.167303978 {
}
=
x
−
-0.1812324445 1.083954101 I
,
,
{
}
=
x
−
0.7648844336 0.3524715460 I
>
fsolve(row,{x}); # rozwiązanie przybliżone, pierwiastki
rzeczywiste
{
}
=
x -1.167303978
>
fsolve(row,{x},complex); # rozwiązanie przybliżone, wszystkie
pierwiastki
{
}
=
x -1.167303978 {
}
=
x
−
-0.1812324445 1.083954101 I
,
,
{
}
=
x
+
-0.1812324445 1.083954101 I {
}
=
x
−
0.7648844336 0.3524715460 I
,
,
{
}
=
x
+
0.7648844336 0.3524715460 I
Rozwiązanie parametryczne
>
rp:=solve(x+y=1,{x(t),y(t)});
:=
rp
{
}
,
=
x
1
+
1 t
=
y
t
+
1 t
>
rp:=solve(x*y=1,{x(t),y(t)});
:=
rp
,
{
}
,
=
x
−
1
t
=
y
− t
{
}
,
=
x
1
t
=
y
t
>
rp:=solve(x^2+y^2=1,{x(t),y(t)});
:=
rp
,
{
}
,
=
x
−
1
+
1 t
2
=
y
−
t
+
1 t
2
{
}
,
=
x
1
+
1 t
2
=
y
t
+
1 t
2
>
rp:=solve(x^2+y^2+x*y=1,{x(t),y(t)});
:=
rp
,
{
}
,
=
y
−
t
+ +
t
2
t 1
=
x
−
1
+ +
t
2
t 1
{
}
,
=
x
1
+ +
t
2
t 1
=
y
t
+ +
t
2
t 1
>
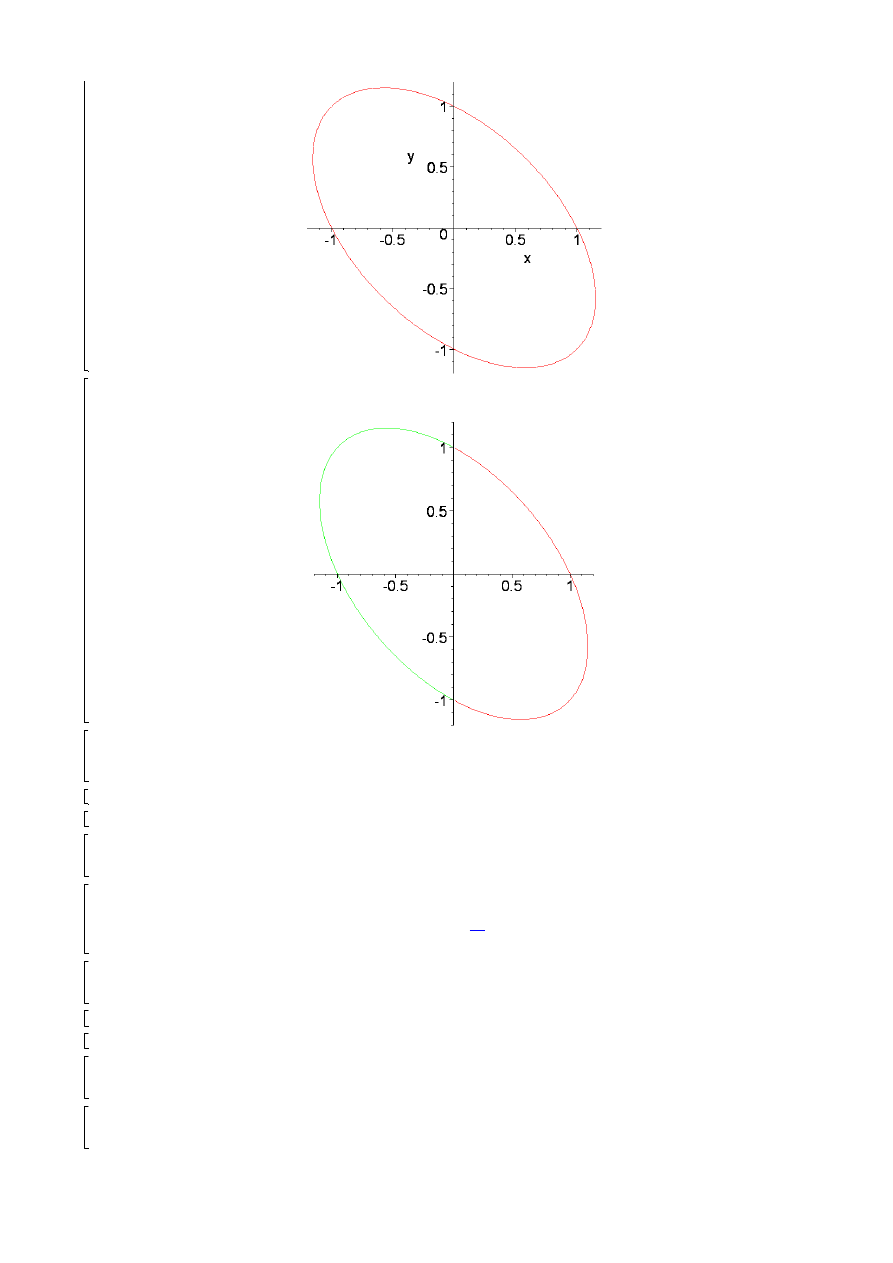
plots[implicitplot](x^2+y^2+x*y=1,x=-2..2,y=-2..2);
>
plot([[1/sqrt(t^2+t+1),t/sqrt(t^2+t+1),t=-100..100],[-1/sqrt(t^2
+t+1),-t/sqrt(t^2+t+1),t=-100..100]]);
Równania algebraiczne o współczynnikach symbolicznych
( solve )
Równanie liniowe
>
restart:
>
row:=a*x+b=0;
:=
row
=
+
a x b 0
>
x:=solve(row,x);
:=
x
−
b
a
>
row;
=
0 0
>
x:='x':
Układ równań liniowych
>
sys:={a*x+b*y=c,d*x+e*y=f};
:=
sys
{
}
,
=
+
a x b y c
=
+
d x e y f
>
niew:={x,y};
:=
niew
{
}
,
y x
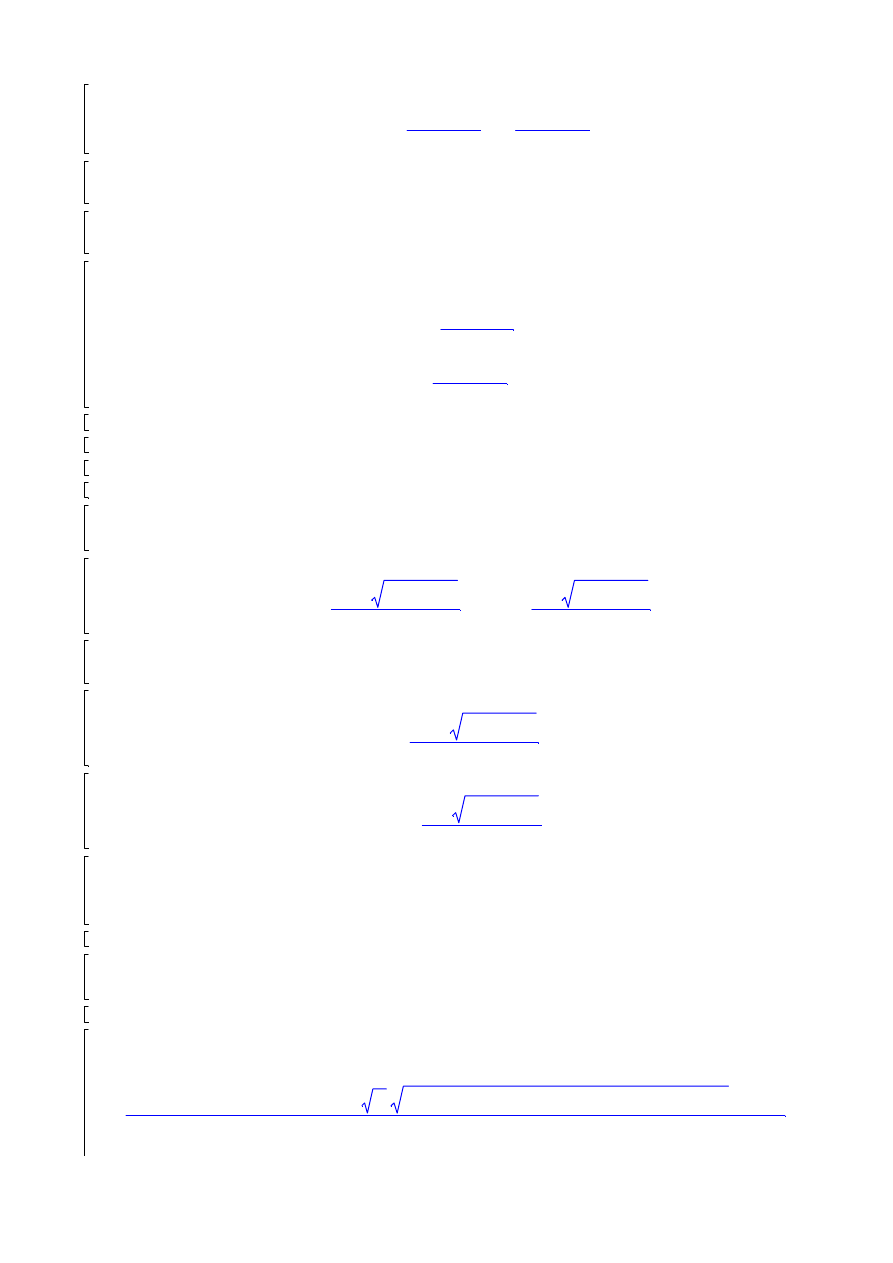
>
roz:=solve(sys,niew);
:=
roz
{
}
,
=
x
−
− +
b f e c
−
b d e a
=
y
− +
a f c d
−
b d e a
>
simplify(eval(sys,roz)); # sprawdzenie rozwiązania
{
}
,
=
c c
=
f f
>
x,y;
,
x y
>
x:=eval(x,roz); y:=eval(y,roz); # przypisanie niewiadomym
wartości pierwiastków
:=
x
−
− +
b f e c
−
b d e a
:=
y
− +
a f c d
−
b d e a
>
Równania wyższych stopni
>
restart:
Równanie kwadratowe
>
row:=a*x^2+b*x+c=0;
:=
row
=
+ +
a x
2
b x c 0
>
roz:=solve(row,{x});
:=
roz
,
{
}
=
x
− +
b
−
b
2
4 a c
2 a
{
}
=
x
−
+
b
−
b
2
4 a c
2 a
>
simplify(eval(row,roz[1])); # sprawdzenie pierwszego pierwiastka
=
0 0
>
x1:=eval(x,roz[1]); # przypisanie nazwy pierwiastkom
:=
x1
− +
b
−
b
2
4 a c
2 a
>
x2:=eval(x,roz[2]);
:=
x2
−
+
b
−
b
2
4 a c
2 a
>
expand(a*(x-x1)*(x-x2)); # sprawdzenie pierwiastków w inny
sposób
+ +
a x
2
b x c
Równanie trzeciego stopnia
>
row:=a*x^3+b*x^2+c*x+d=0;
:=
row
=
+
+ +
a x
3
b x
2
c x d 0
>
roz:=solve(row,{x}):
>
x1:=eval(x,roz[1]);
x1 :=
(
)
−
−
+
36 c b a 108 d a
2
8 b
3
12 3
−
−
+
+
4 a c
3
c
2
b
2
18 c b a d 27 d
2
a
2
4 d b
3
a
(
)
/
1 3
6 a
−

2 (
)
−
3 a c b
2
3 a
(
(
)
−
−
+
36 c b a 108 d a
2
8 b
3
12 3
−
−
+
+
4 a c
3
c
2
b
2
18 c b a d 27 d
2
a
2
4 d b
3
a
(
)
/
1 3
)
b
3 a
−
>
simplify(eval(row,x=x1));
=
0 0
>
x2:=eval(x,roz[2]):x3:=eval(x,roz[3]):
>
simplify(expand(a*(x-x1)*(x-x2)*(x-x3))); # sprawdzenie
pierwiastków w inny sposób
+
+ +
a x
3
b x
2
c x d
Równanie czwartego stopnia
>
row:=a*x^4+b*x^3+c*x^2+d*x+e=0;
:=
row
=
+
+
+ +
a x
4
b x
3
c x
2
d x e 0
>
roz:=solve(row,{x});
:=
roz
{
}
=
x
(
)
RootOf
+
+
+
+
a _Z
4
b _Z
3
c _Z
2
d _Z e
>
roz:=allvalues(%):
>
x1:=eval(x,roz[1]):
>
simplify(eval(row,x=x1));
=
0 0
Równanie piątego stopnia
>
row:=a*x^5+b*x^4+c*x^3+d*x^2+e*x+f=0;
:=
row
=
+
+
+
+ +
a x
5
b x
4
c x
3
d x
2
e x f 0
>
roz:=solve(row,{x});
:=
roz
{
}
=
x
(
)
RootOf
+
+
+
+
+
a _Z
5
b _Z
4
c _Z
3
d _Z
2
e _Z f
>
allvalues(%);
{
}
=
x
(
)
RootOf
,
+
+
+
+
+
a _Z
5
b _Z
4
c _Z
3
d _Z
2
e _Z f
=
index 1 ,
{
}
=
x
(
)
RootOf
,
+
+
+
+
+
a _Z
5
b _Z
4
c _Z
3
d _Z
2
e _Z f
=
index 2 ,
{
}
=
x
(
)
RootOf
,
+
+
+
+
+
a _Z
5
b _Z
4
c _Z
3
d _Z
2
e _Z f
=
index 3 ,
{
}
=
x
(
)
RootOf
,
+
+
+
+
+
a _Z
5
b _Z
4
c _Z
3
d _Z
2
e _Z f
=
index 4 ,
{
}
=
x
(
)
RootOf
,
+
+
+
+
+
a _Z
5
b _Z
4
c _Z
3
d _Z
2
e _Z f
=
index 5
>
evalf(roz);
{
}
=
x
(
)
RootOf
+
+
+
+
+
a _Z
5
b _Z
4
c _Z
3
d _Z
2
e _Z f
Ukady równań nieliniowych
>
sys:={a*x^2+b*y^2=c,x*y=d};
:=
sys
{
}
,
=
+
a x
2
b y
2
c
=
x y d
>
niew:={x,y};
:=
niew
{
}
,
y x
>
roz:=solve(sys,niew);
:=
roz
{
}
,
=
x
d
(
)
RootOf
+
−
d
2
a b _Z
4
c _Z
2
=
y
(
)
RootOf
+
−
d
2
a b _Z
4
c _Z
2
>
roz:=allvalues(roz);
roz
,
=
x
d b 2
b (
)
+
c
−
c
2
4 b d
2
a
=
y
2
b (
)
+
c
−
c
2
4 b d
2
a
2 b
,
:=
,
=
x
−
d b 2
b (
)
+
c
−
c
2
4 b d
2
a
=
y
−
2
b (
)
+
c
−
c
2
4 b d
2
a
2 b
,
,
=
x
d b 2
b (
)
−
c
−
c
2
4 b d
2
a
=
y
2
b (
)
−
c
−
c
2
4 b d
2
a
2 b
,
,
=
x
−
d b 2
b (
)
−
c
−
c
2
4 b d
2
a
=
y
−
2
b (
)
−
c
−
c
2
4 b d
2
a
2 b
>
simplify(map(subs,[roz],sys)); # sprawdzenie wszystkich
pierwiastków
[
]
,
,
,
{
}
,
=
c c
=
d d {
}
,
=
c c
=
d d {
}
,
=
c c
=
d d {
}
,
=
c c
=
d d
>
x:=eval(x,roz[1]); # przypisanie niewiadomym wartości pierwszej
pary pierwiastków
:=
x
d b 2
b (
)
+
c
−
c
2
4 b d
2
a
>
y:=eval(y,roz[1]);
:=
y
2
b (
)
+
c
−
c
2
4 b d
2
a
2 b
>
x:='x':y:='y':
>
a:=1:b:=1:c:=1:d:=1/4:
>
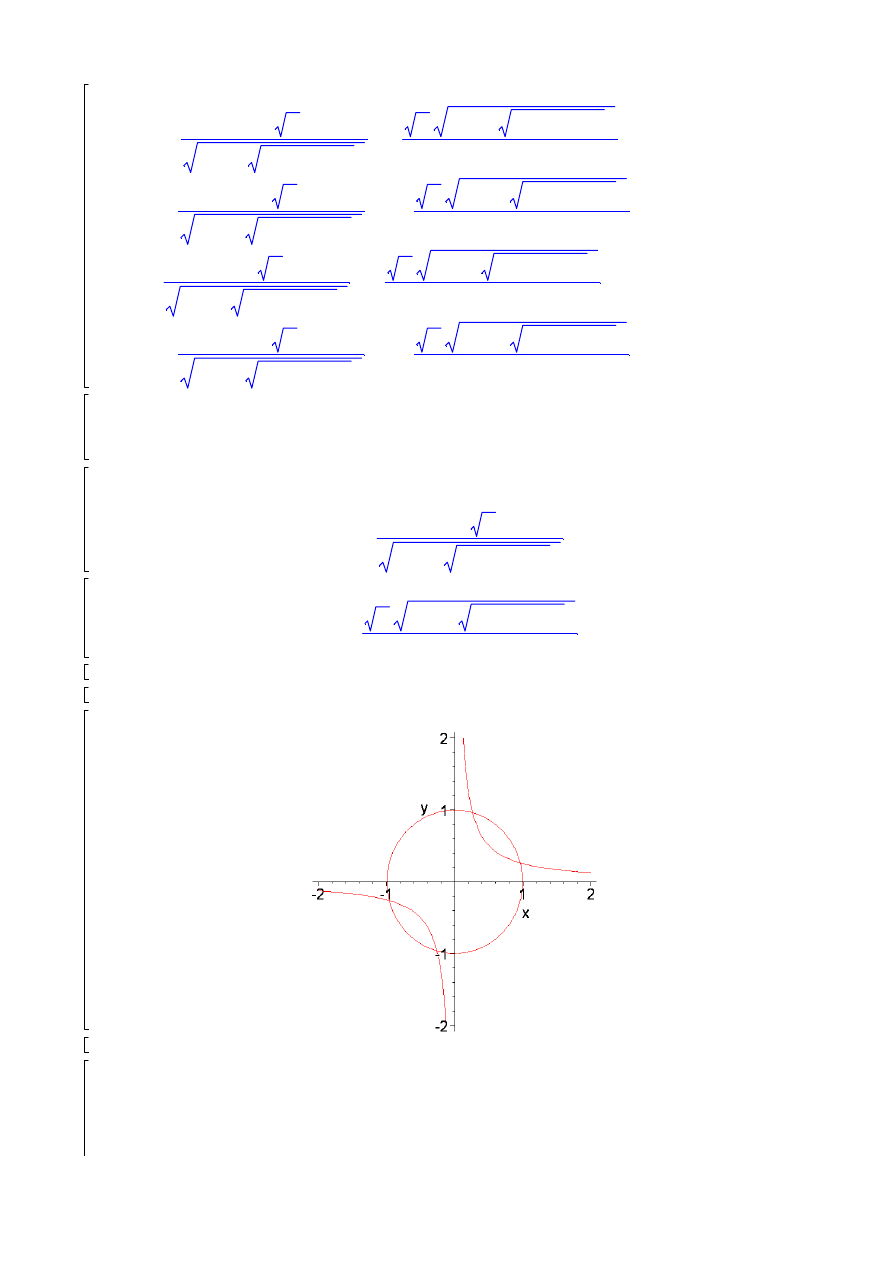
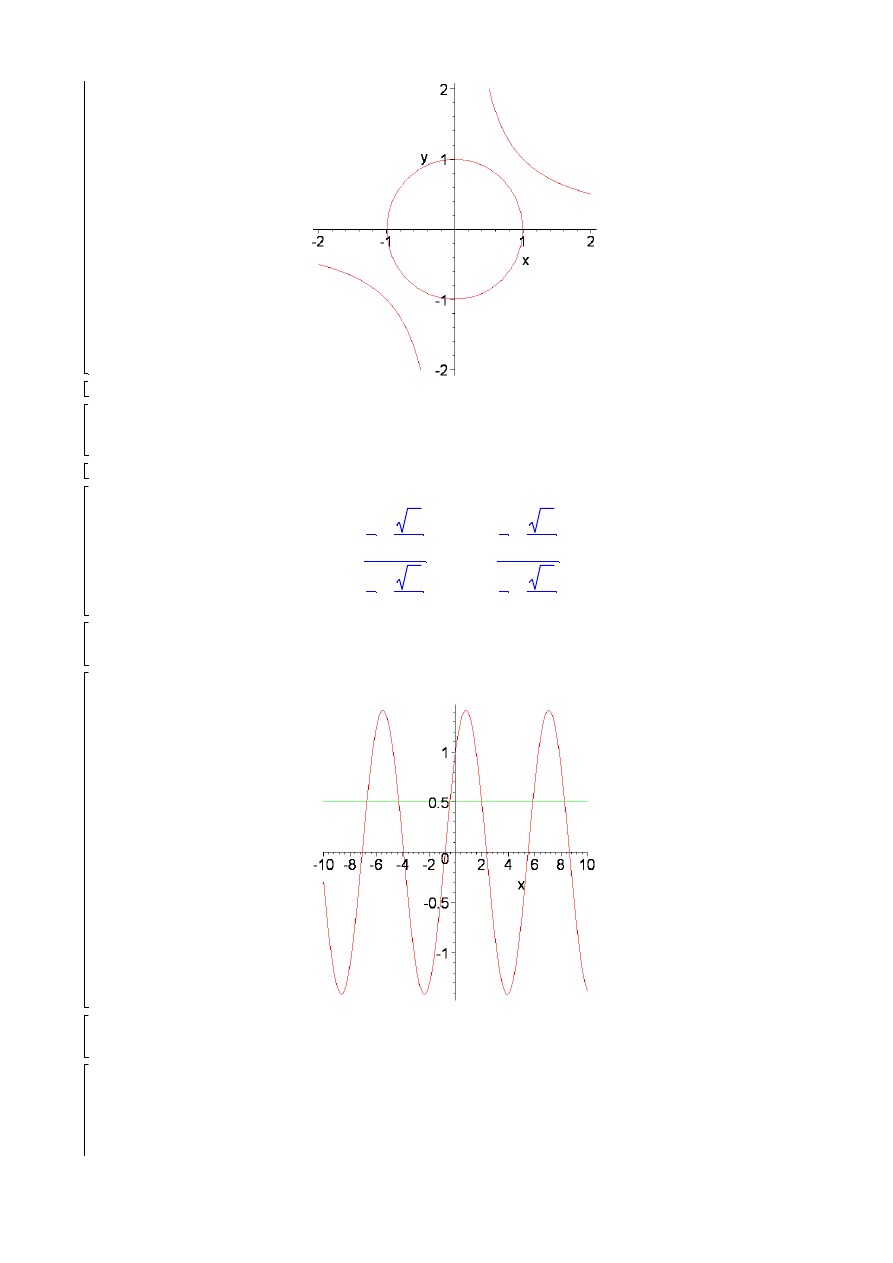
plots[implicitplot]([a*x^2+b*y^2=c,x*y=d],x=-2..2,y=-2..2);
>
a:=1:b:=1:c:=1:d:=1:
>
plots[implicitplot]([a*x^2+b*y^2=c,x*y=d],x=-2..2,y=-2..2);
>
Równania trygonometryczne
( solve )
>
restart:
>
solve(sin(x)+cos(x)=1/2,x);
,
arctan
−
1
4
7
4
+
1
4
7
4
+
arctan
+
1
4
7
4
−
1
4
7
4
π
>
evalf(%);
,
-0.4240310395 1.994827367
>
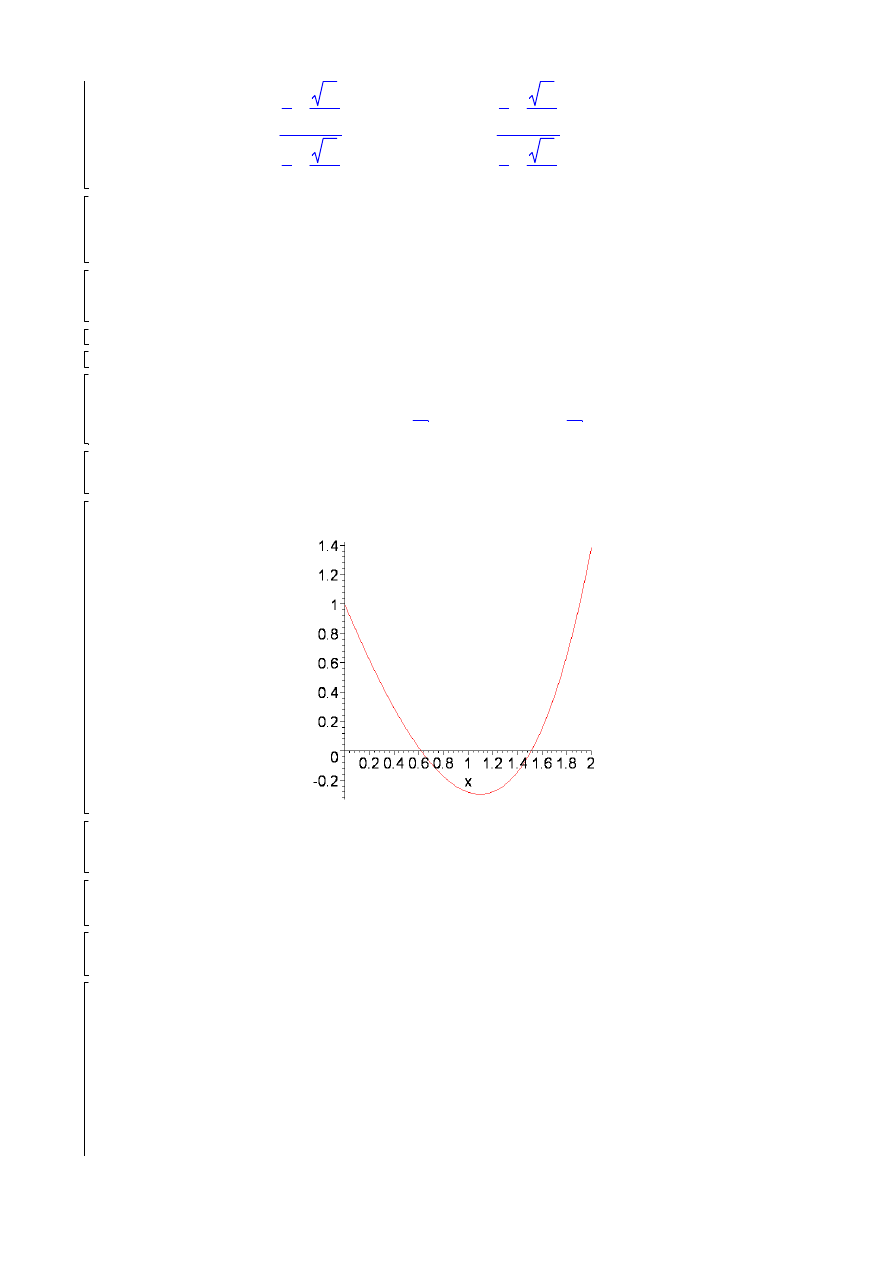
plot([sin(x)+cos(x),1/2],x);
>
_EnvAllSolutions:=true;
:=
_EnvAllSolutions
true
>
solve(sin(x)+cos(x)=1/2,x);
,
+
arctan
−
1
4
7
4
+
1
4
7
4
2
π _Z2~
+ +
arctan
+
1
4
7
4
−
1
4
7
4
π 2 π _Z2~
>
about(_Z1);
Originally _Z1, renamed _Z1~:
is assumed to be: integer
Równania wykładnicze
( solve )
>
restart;
>
solve(exp(x)-3*x,x);
,
−
LambertW
-1
3
−
LambertW
,
-1
-1
3
>
evalf(%);
,
0.6190612866 1.512134552
>
plot(exp(x)-3*x,x=0..2);
Nierówności
( solve )
>
w:=x^3-6*x^2+3*x+10;
:=
w
−
+ +
x
3
6 x
2
3 x 10
>
solve(w<=0,{x});
,
{
}
≤
x -1 {
}
,
≤
2 x
≤
x 5
>
plot(w,x=-2..6);
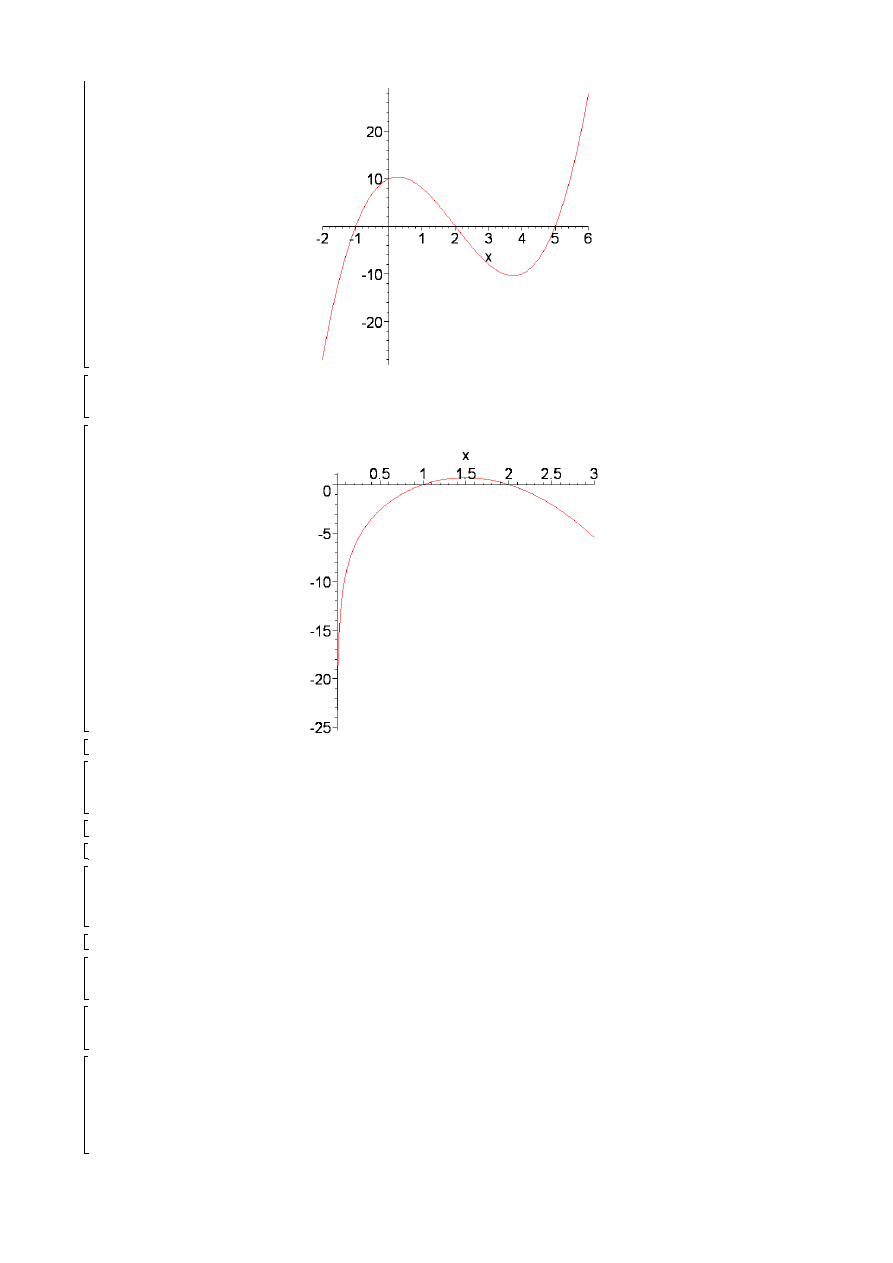
>
solve(ln(x)*(4-x^2)<0,{x});
,
{
}
,
<
0 x
<
x 1 {
}
<
2 x
>
plot(ln(x)*(4-x^2),x=0..3);
>
Rozwiązania w dziedzinie liczb całkowitych
( isolve )
- solve equations for integer solutions
>
restart:
Ogólna budowa komendy isolve
isolve ( r, n );
r - układ równań
n - nazwa zmiennej przyjmującej wartości całkowite (opcjonalna)
>
isolve(x^2+y^2=6); # =6
>
isolve(3*x+4*y=21,n);
{
}
,
=
x
−
7 4 n
=
y 3 n
>
isolve({x+2*y+3*z=4,x-y-z=0},n);
{
}
,
,
=
x
−
1 n
=
y
−4 n =
z
+
1 3 n
>
x:=eval(x,%);y:=eval(y,%%);z:=eval(z,%%%);
:=
x
−
1 n
:=
y
−4 n
:=
z
+
1 3 n

>
Równania rekurencyjne
( rsolve )
- recurrence equation solver
>
restart:
Ogólna budowa komendy rsolve
rsolve ( r, f );
r - zbiór równań
f - nazwa funkcji
>
Ciąg liczb Fibonacciego:
1
)
2
(
,
1
)
1
(
),
(
)
1
(
)
2
(
=
=
+
+
=
+
f
f
n
f
n
f
n
f
>
>
Fib:=rsolve({f(n+2)=f(n+1)+f(n),f(1)=1,f(2)=1},f);
:=
Fib
−
+
5
−
1
2
5
2
n
5
5
+
1
2
5
2
n
5
>
subs(n=15,Fib);
−
+
5
−
1
2
5
2
15
5
5
+
1
2
5
2
15
5
>
simplify(%);
610
>
seq(simplify(subs(n=i,Fib)),i=1..15);
, , , , , ,
,
,
,
,
,
,
,
,
1 1 2 3 5 8 13 21 34 55 89 144 233 377 610
>
simplify(subs(n=400,Fib));
176023680645013966468226945392411250770384383304492191886725992896575345044\
216019675
Wyznacznik macierzy pasmowej
−
−
−
−
−
−
−
−
−
−
−
x
x
x
x
x
2
1
0
0
0
1
2
0
0
0
0
0
2
1
0
0
0
1
2
1
0
0
0
1
2
"
"
#
#
%
#
#
#
"
"
"
>
x
W
W
n
W
n
W
x
n
W
−
=
=
−
+
−
=
+
2
)
1
(
,
1
)
0
(
),
(
)
1
(
)
2
(
)
2
(
>
Wg:=rsolve({W(n+2)=(2-x)*W(n+1)-W(n),W(0)=1,W(1)=2-x},W);
:=
Wg
−
+
2
−
2
− + +
2 x
− +
4 x x
2
n
− +
4 x x
2
(
)
− + +
2 x
− +
4 x x
2
2
−
2
− + −
2 x
− +
4 x x
2
n
− +
4 x x
2
(
)
− + −
2 x
− +
4 x x
2
>
subs(n=2,Wg);

−
+
8
− +
4 x x
2
(
)
− + +
2 x
− +
4 x x
2
3
8
− +
4 x x
2
(
)
− + −
2 x
− +
4 x x
2
3
>
simplify(%);
64 (
)
− +
3 4 x x
2
(
)
− + +
2 x
x (
)
− +
4 x
3
(
)
− + −
2 x
x (
)
− +
4 x
3
>
normal(%,expanded);
− +
3 4 x x
2
>
for i to 10 do
normal(subs(n=i,Wg),expanded);
end do;
−
2 x
− +
3 4 x x
2
−
+
−
4 10 x 6 x
2
x
3
−
+
+ −
5 20 x 21 x
2
x
4
8 x
3
− +
−
−
+
6 x
5
10 x
4
36 x
3
35 x 56 x
2
+
+ −
−
+
−
7 126 x
2
x
6
56 x 120 x
3
55 x
4
12 x
5
+
− +
−
−
+
−
8 252 x
2
x
7
14 x
6
84 x 330 x
3
220 x
4
78 x
5
+
−
+ +
−
−
+
−
9 462 x
2
16 x
7
x
8
105 x
6
120 x 792 x
3
715 x
4
364 x
5
+
− −
+
+
−
−
+
−
10 792 x
2
x
9
136 x
7
18 x
8
560 x
6
165 x 1716 x
3
2002 x
4
1365 x
5
+
−
+ −
+
+
−
−
+
−
11 1287 x
2
20 x
9
x
10
816 x
7
171 x
8
2380 x
6
220 x 3432 x
3
5005 x
4
4368 x
5
>
normal(subs(n=20,Wg),expanded);
33649 x
2
54627300 x
9
44352165 x
10
37442160 x
7
51895935 x
8
5379616 x
13
−
+
−
+
−
1623160 x
14
8436 x
17
741 x
18
20058300 x
6
1540 x 376992 x
15
66045 x
16
+
−
+
+
−
−
+
346104 x
3
2042975 x
4
40 x
19
7726160 x
5
x
20
28048800 x
11
13884156 x
12
21
−
+
−
−
+ −
+
+
>
Równania różniczkowe
( dsolve )
- differential equation solver
Sposób użycia komendy dsolve
dsolve ({sys,wp}, {f}, o)
sys - układ równań, wp - warunki poczatkowe lub brzegowe
f - zbiór poszukiwanych funkcji,
o - opcje
1. Zagadnienie początkowe
a) Rozwiązywanie równania różniczkowego drugiego rzędu
>
restart:
>
row:=diff(x(t),t,t)+4*diff(x(t),t)+40*x(t)=0;
:=
row
=
+
+
d
d
2
t
2
( )
x t
4
d
d
t
( )
x t
40 ( )
x t
0
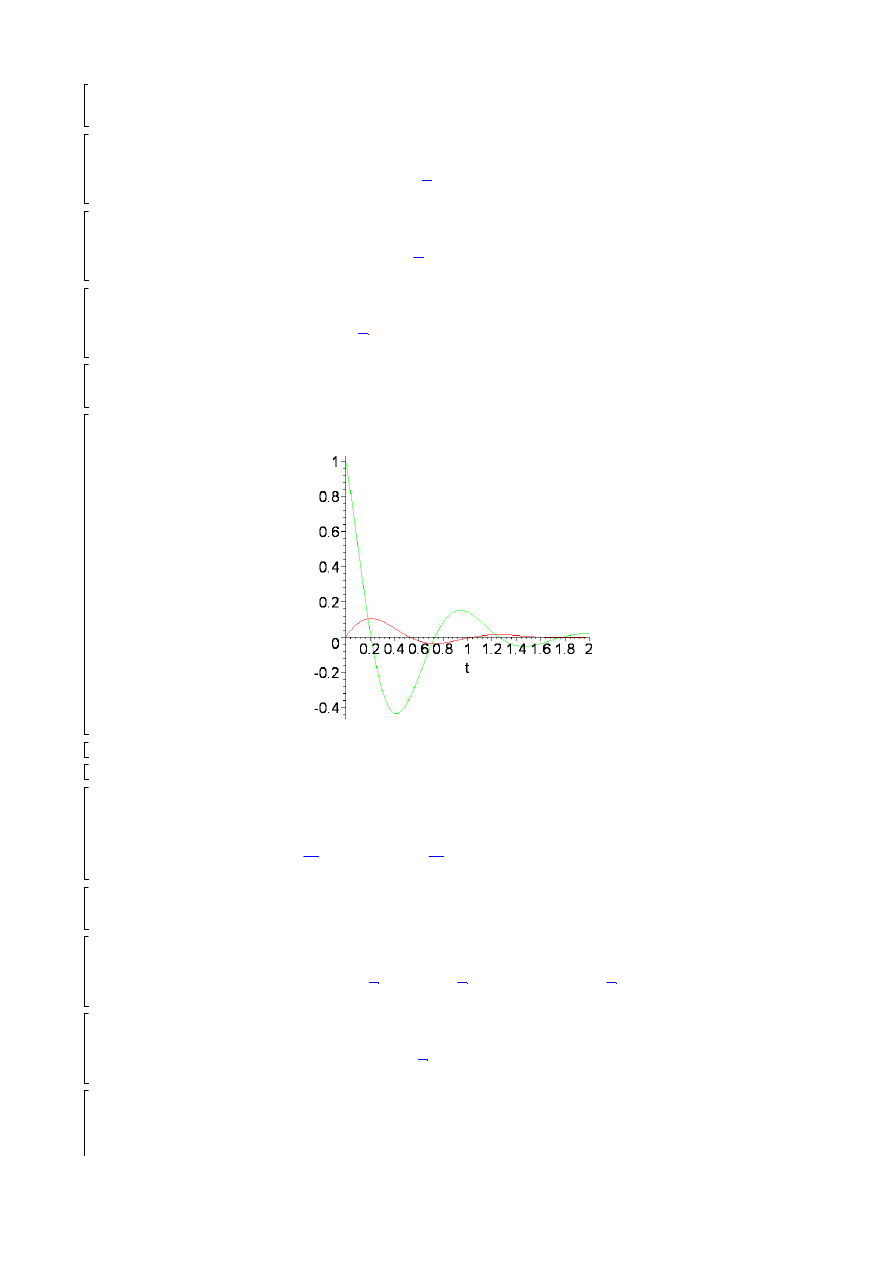
>
wp:=x(0)=0,D(x)(0)=1; # warunki początkowe
:=
wp
,
=
( )
x 0
0
=
( )
( )
D x 0
1
>
dsolve({row, wp},{x(t)});
=
( )
x t
1
6
e
(
)
−2 t
(
)
sin 6 t
>
x:=eval(x(t),%);
:=
x
1
6
e
(
)
−2 t
(
)
sin 6 t
>
v:=diff(x,t);
:=
v
−
+
1
3
e
(
)
−2 t
(
)
sin 6 t
e
(
)
−2 t
(
)
cos 6 t
>
eval(v,t=0);
1
>
plot([x,v],t=0..2);
b) Rozwiązywanie ukladu równań różniczkowych pierwszego rzędu
>
restart:
>
sys:=diff(x1(t),t)=x2(t),diff(x2(t),t)=-4*x2(t)-40*x1(t); # ten
sam problem
:=
sys
,
=
d
d
t
( )
x1 t
( )
x2 t
=
d
d
t
( )
x2 t
−
−
4
( )
x2 t
40
( )
x1 t
>
wp:=x1(0)=0,x2(0)=1;
:=
wp
,
=
( )
x1 0
0
=
( )
x2 0
1
>
roz:=dsolve({sys, wp},{x1(t),x2(t)});
:=
roz
{
}
,
=
( )
x2 t
−2 e
(
)
−2 t
−
1
6
(
)
sin 6 t
1
2
(
)
cos 6 t
=
( )
x1 t
1
6
e
(
)
−2 t
(
)
sin 6 t
>
x1:=eval(x1(t),roz);
:=
x1
1
6
e
(
)
−2 t
(
)
sin 6 t
>
x2:=eval(x2(t),roz);
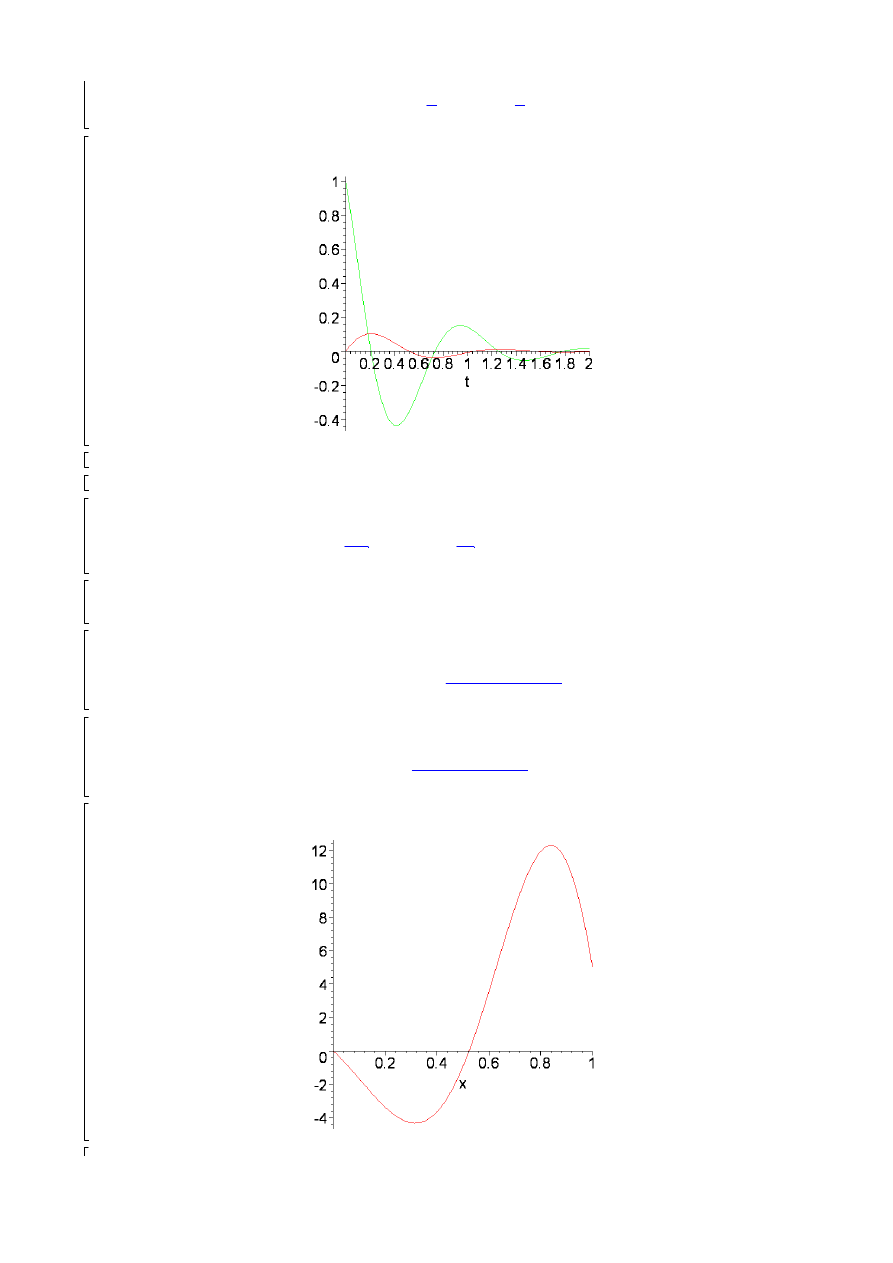
:=
x2
−2 e
(
)
−2 t
−
1
6
(
)
sin 6 t
1
2
(
)
cos 6 t
>
plot([x1,x2],t=0..2);
2. Zagdnienie brzegowe
>
restart:
>
row:=diff(y(x),x,x)-4*diff(y(x),x)+40*y(x)=0;
:=
row
=
−
+
d
d
2
x
2
( )
y x
4
d
d
x
( )
y x
40 ( )
y x
0
>
wb:=y(0)=0,y(1)=5; # warunki b
:=
wb
,
=
( )
y 0
0
=
( )
y 1
5
>
roz:=dsolve({row, wb});
:=
roz
=
( )
y x
5 e
(
)
2 x
(
)
sin 6 x
e
2
( )
sin 6
>
y:=eval(y(x),roz);
:=
y
5 e
(
)
2 x
(
)
sin 6 x
e
2
( )
sin 6
>
plot(y,x=0..1);

>
eval(y,x=1);
5
>
Wyszukiwarka
Podobne podstrony:
2008 10 29
2008 Metody obliczeniowe 06 D 2008 10 22 20 13 23
2008 Metody obliczeniowe 02 D 2008 10 1 21 28 5
2008 Metody obliczeniowe 10 D 2008 11 28 20 51 40
2008 Metody obliczeniowe 03 D 2008 10 1 22 5 47
2008 Metody obliczeniowe 08 D 2008 11 11 21 31 58
2008 Metody obliczeniowe 09 D 2008 11 11 21 32 51
2008 Metody obliczeniowe 12 D 2008 11 28 20 53 30
2008 Metody obliczeniowe 13 D 2008 11 28 20 56 53
2008 Metody obliczeniowe 08 D 2008 11 11 21 31 58
2008 10 07 SzE Utazz velem Monaco ba ( TE )
więcej podobnych podstron