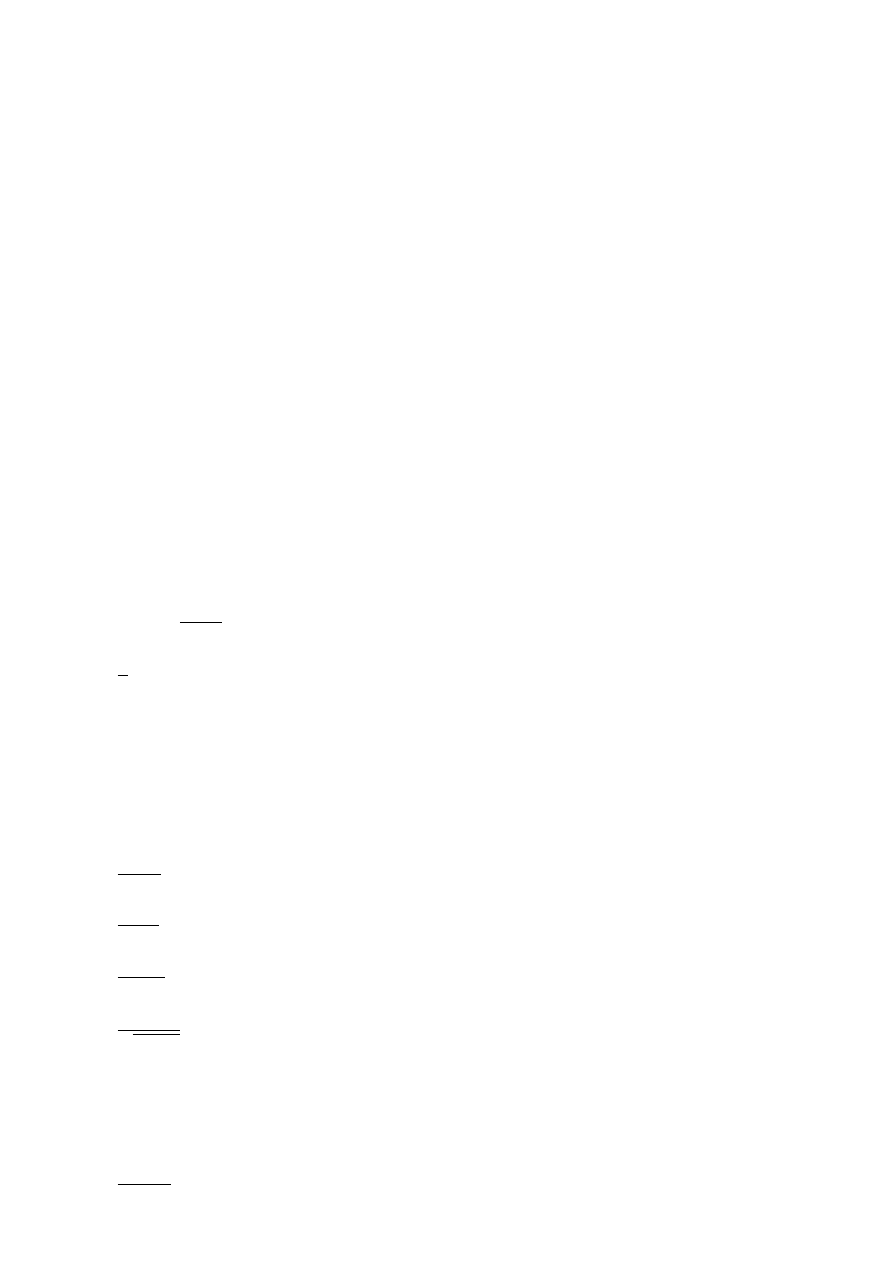
SIMR 2010/11, Analiza 1, wykład 9, 2010-12-02
Całka nieoznaczona
Definicja: Niech dana będzie funkcja f : I → R, gdize I ⊂ R jest przedziałem. Funkcją
pierwotną tej funkcji nazywamy każdą funkcję F : I → R taką, że (∀x ∈ I)
F
0
(x) = f (x).
Zbiór wszystkich funkcji pierwotnych funkcji f nazywamy całką nieoznaczoną i oznaczamy
symbolem:
Z
f (x)dx
Uwaga 1: Przedział I może być domknięty I =< a, b > . Wtedy w końcach przedziału
F
0
(a) i F
0
(b) są pochodnymi jednostronnymi.
Uwaga 2: Jeżeli istnieje funkcja pierwotna funkcji f , to istnieje nieskończenie wiele funkcji
pierwotnych różniących się tylko o stałą:
Jeżeli F
0
1
(x) = f (x) i F
0
2
(x) = f (x) to (F
1
(x) − F
2
(x))
0
= 0 czyli F
1
(x) − F
2
(x) = C na
przedziale I.
Uwaga 3: Operacją obliczania całki nieoznaczonej nazywamy całkowaniem. Całkowanie jest
operacją odwrotną do różniczkowania. Większość technik obliczania pochodnych ma swoje
odpowiedniki obliczania całek.
Całki nieoznaczone funkcji elementarnuch
1.
Z
x
α
dx =
x
α+1
α + 1
+ C , α 6= −1
2.
Z
1
x
dx = ln |x| + C
3.
Z
e
x
dx = e
x
+ C
4.
Z
sin xdx = − cos x + C
5.
Z
cos xdx = sin x + C
6.
Z
1
cos
2
x
dx = tg x + C
7.
Z
1
sin
2
x
dx = − ctg x + C
8.
Z
1
1 + x
2
dx = arc tg x + C
9.
Z
1
√
1 − x
2
dx = arc sin x + C
10.
Z
sinh xdx = cosh x + C
11.
Z
cosh xdx = sinh x + C
12.
Z
1
cosh
2
x
dx = tgh x + C
1
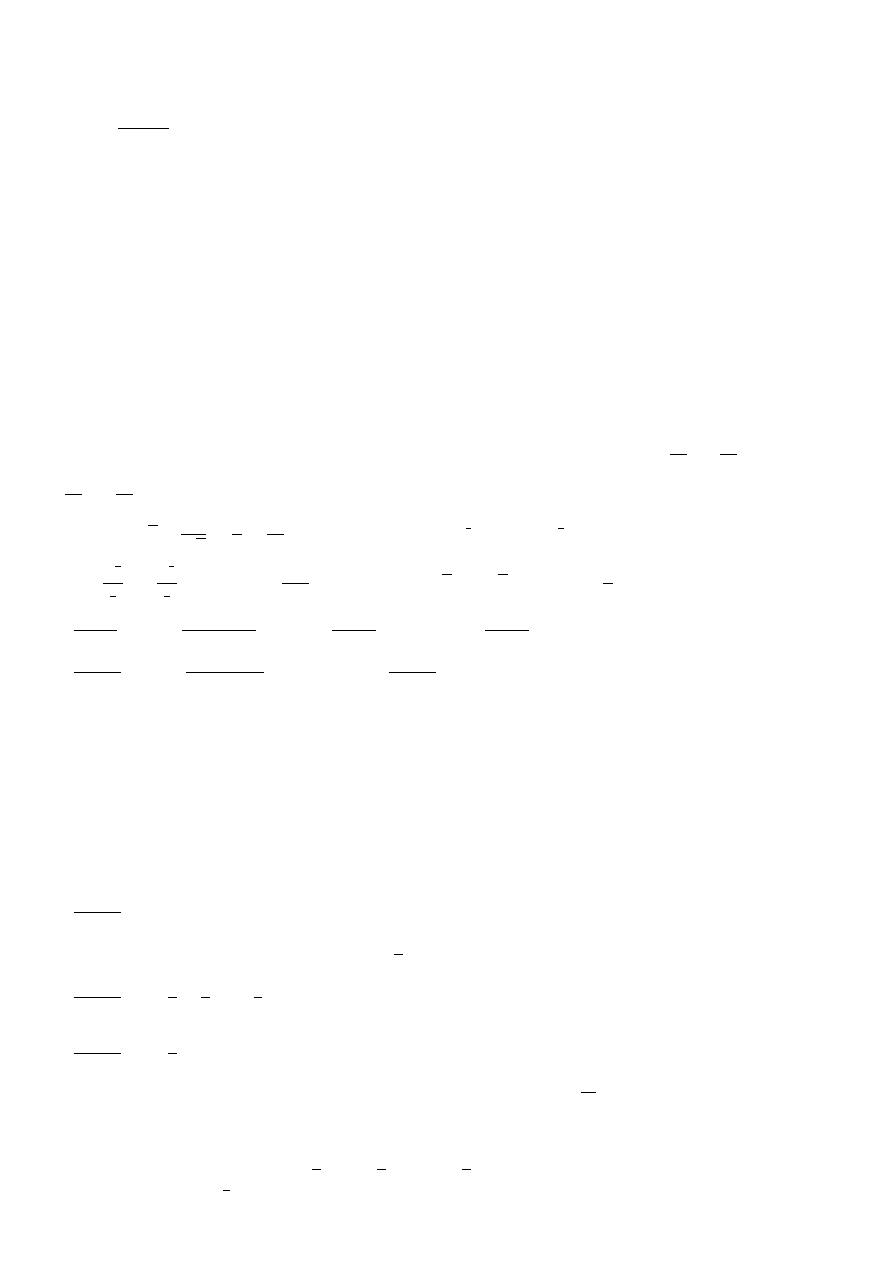
13.
Z
1
sinh
2
x
dx = − ctgh x + C
Podstawowe własności całki nieoznaczonej
Zakładamy, że funkcje f, g : I → R są całkowalne. Wtedy:
1.
Z
af (x)dx = a
Z
f (x)dx
2.
Z
(f (x) + g(x))dx =
Z
f (x)dx +
Z
g(x)dx
3.
Z
(f (x) − g(x))dx =
Z
f (x)dx −
Z
g(x)dx
Przykłady:
Z
12x
3
− 6x
2
+ 4x − 5
dx = 12
Z
x
3
dx − 6
Z
x
2
dx + 4
Z
x
1
dx − 5
Z
x
0
dx = 12
x
4
4
− 6
x
3
3
+
4
x
2
2
− 5
x
1
1
+ C = 3x
4
− 2x
3
+ 2x
2
− 5x + C
Z
2x + 6
√
x +
3
√
x
−
4
x
+
2
x
2
!
dx = 2
Z
x
1
dx+6
Z
x
1
2
dx+3
Z
x
−
1
2
dx−4
Z
x
−1
dx+2
Z
x
−2
dx =
x
2
+ 6
x
3
2
3
2
+ 3
x
1
2
1
2
− 4 ln |x| + 2
x
−1
−1
+ C = x
2
+ 4x
√
x + 6
√
x − 4 ln |x| −
2
x
+ C
Z
sin
2
x
cos
2
x
dx =
Z
1 − cos
2
x
cos
2
x
dx =
Z
1
cos
2
x
− 1
dx =
Z
1
cos
2
x
dx −
Z
dx = tg x − x + C
Z
x
2
x
2
+ 1
dx =
Z
x
2
+ 1 − 1
x
2
+ 1
dx =
Z
dx −
Z
1
x
2
+ 1
dx = x − arc tg x + C
Całkowanie przez podstawienie
Jeśli g : I
1
→ I
2
jest różniczkowalna, f : I
2
→ R, i F : I
2
→ R jest fukcją pierwotną f
((∀t ∈ I
2
)
F
0
(t) = f (t)) to istnieje poniższa całka:
Z
f (g(x)) · g
0
(x)dx = F (g(x)) + C
Uwaga: Technika ta jest odpowiednikiem obliczania pochodnej funkcji złożonej.
Przykład:
Z
x
x
2
+ 5
dx
Podstawiamy:
(
t = x
2
+ 5
dt = 2xdx
)
, stąd xdx =
1
2
dt
Z
x
x
2
+ 5
dx =
1
2
Z
1
t
dt =
1
2
ln |t| + C
Wracamy do zmiennej x
Z
x
x
2
+ 5
dx =
1
2
ln |x
2
+ 5| + C
Uwaga: W tym przykładzie t = g(x) = x
2
+ 5 , g
0
(x) = 2x , f (t) =
1
2t
Przykłady:
Z
xe
x
2
dx =
t = x
2
dt = 2xdx
xdx =
1
2
dt
=
Z
1
2
e
t
dt =
1
2
e
t
+ C =
1
2
e
x
2
+ C
2
Z
sin x
cos
2
x + 1
dx =
t = cos x
dt = − sin xdx
sin xdx = −dt
=
Z
−1
t
2
+ 1
dt = − arc tg t + C = − arc tg(cos x) + C
Z
e
x
√
1 − e
2x
dx =
(
t = e
x
dt = e
x
dx
)
=
Z
1
√
1 − t
2
dt = arc sin t + C = arc sin(e
x
) + C
Z
x
x
4
+ 1
dx =
t = x
2
dt = 2xdx
xdx =
1
2
dt
=
Z
1
2
dt
t
2
+ 1
dt =
1
2
arc tg t + C =
1
2
arc tg(x
2
) + C
Z
x
√
x
2
+ 1dx =
t = x
2
+ 1
dt = 2xdx
xdx =
1
2
dt
=
Z
1
2
√
tdt =
1
2
t
3
2
3
2
+ C =
1
3
√
x
2
+ 1
3
+ C
Z
ln
3
x
x
dx =
t = ln x
dt =
dx
x
=
Z
t
3
dt =
1
4
t
4
+ C =
1
4
ln
4
x + C
Z
sin x cos x
sin
2
x + 4
dx =
(
t = sin x
dt = cos xdx
)
=
Z
t
t
2
+ 4
dt =
s = t
2
dt = 2sds
sds =
1
2
dt
=
Z
1
2
1
s
ds =
1
2
ln |s| +
C =
1
2
ln |t
2
+ 4| + C =
1
2
ln | sin
2
x + 4| + C
Podstawienie liniowe: t = ax + b
Jeżeli F
0
(t) = f (t) oraz a, b ∈ R , a 6= 0 to
Z
f (ax + b)dx =
1
a
F (ax + b) + C
Przykłady:
Z
1
2x + 7
dx = {t = 2x + 7} =
1
2
ln |2x + 7| + C
Z
sin(4x − 1)dx = {t = 4x − 1} = −
1
4
cos(4x − 1) + C
Z
e
−2x
dx = {t = −2x} = −
1
2
e
−2x
+ C
Z
1
x
2
+ 4
dx =
Z
1
4(
x
2
4
+ 1)
dx =
1
4
Z
1
x
2
2
+ 1
dx = {t =
x
2
} =
1
2
arc tg(
x
2
) + C
Z
1
x
2
+ 4x + 13
dx =
Z
1
(x + 2)
2
+ 9
dx =
Z
1
9(
(x + 2)
2
9
+ 1)
dx =
1
9
Z
1
x + 2
3
2
+ 1
dx =
{t =
x + 2
3
} =
1
3
arc tg(
x + 2
3
) + C
Podstawienie za mianownik
Jeżeli licznik funkcji podcałkowej jest pochodną mianownika pomnożoną przez stałą, to
podstawiając nową zmienną za mianownik mamy:
Z
af
0
(x)
f (x)
dx =
(
t = f (x)
dt = f
0
(x)dx
)
=
Z
a
t
dt = a ln |t| + C = a ln |f (x)| + C
Przykłady:
Z
sin x
cos x
dx =
t = cos x
dt = − sin xdx
sin xdx = −dt
=
Z
−1
t
dt = − ln |t| + C = − ln | cos x| + C
Z
6x
2
+ 8
x
3
+ 4x
dx =
t = x
3
+ 4x
dt = (3x
2
+ 4)dx
dx = 2dt
=
Z
2
t
dt = 2 ln |t| + C = 2 ln |x
3
+ 4x| + C
Z
e
x
e
x
− 2
dx =
(
t = e
x
− 2
dt = e
x
dx
)
=
Z
1
t
dt = ln |t| + C = 2 ln |e
x
− 2| + C
3
Z
1
x ln x
dx =
t = ln x
dt =
1
x
dx
=
Z
1
t
dt = ln |t| + C = 2 ln | ln x| + C
Całkowanie przez części
Jeśli I jest przedziałem, f, g : I → R są różniczkowalne oraz funkcja f
0
g jest całkowalna to:
Z
f (x) · g
0
(x)dx = f (x) · g(x) −
Z
f
0
(x) · g(x)dx
Uwaga: Technika ta jest odpowiednikiem obliczania pochodnej iloczynu funkcji.
Przykład:
Z
x ln xdx
Całkujemy przez części:
(
f (x) = ln x g
0
(x) = x
f
0
(x) =
1
x
g(x) =
R
xdx =
x
2
2
)
Z
x ln xdx = ln x ·
x
2
2
−
Z
1
x
· xdx =
x
2
2
ln x −
Z
xdx =
x
2
2
ln x − x + C
Przykłady:
Z
x sin xdx =
(
f (x) = x
g
0
(x) = sin x
f
0
(x) = 1 g(x) = − cos x
)
= −x cos x−
Z
− cos xxdx = −x cos x+sin x+
C
Z
e
x
sin xdx =
(
f (x) = e
x
g
0
(x) = sin x
f
0
(x) = e
x
g(x) = − cos x
)
= −e
x
cos x −
Z
−e
x
cos xdx = −e
x
cos x +
Z
e
x
cos xdx
Obliczamy:
Z
e
x
cos xdx =
(
f (x) = e
x
g
0
(x) = cos x
f
0
(x) = e
x
g(x) = sin x
)
= e
x
sin x −
Z
e
x
sin xdx
Stąd mamy:
Z
e
x
sin xdx = −e
x
cos x + e
x
sin x −
Z
e
x
sin xdx
2
Z
e
x
sin xdx = e
x
(sin x − cos x) + C
Z
e
x
sin xdx =
1
2
e
x
(sin x − cos x) + C
Z
arc tg xdx =
f (x) = arc tg x g
0
(x) = 1
f
0
(x) =
1
1 + x
2
g(x) = x
= x arc tg x −
Z
x
1 + x
2
dx = {t = 1 +
x
2
,
dt = 2xdx} = x arc tg x −
Z
1
2t
dt = x arc tg x −
1
2
ln |1 + x
2
| + C
4