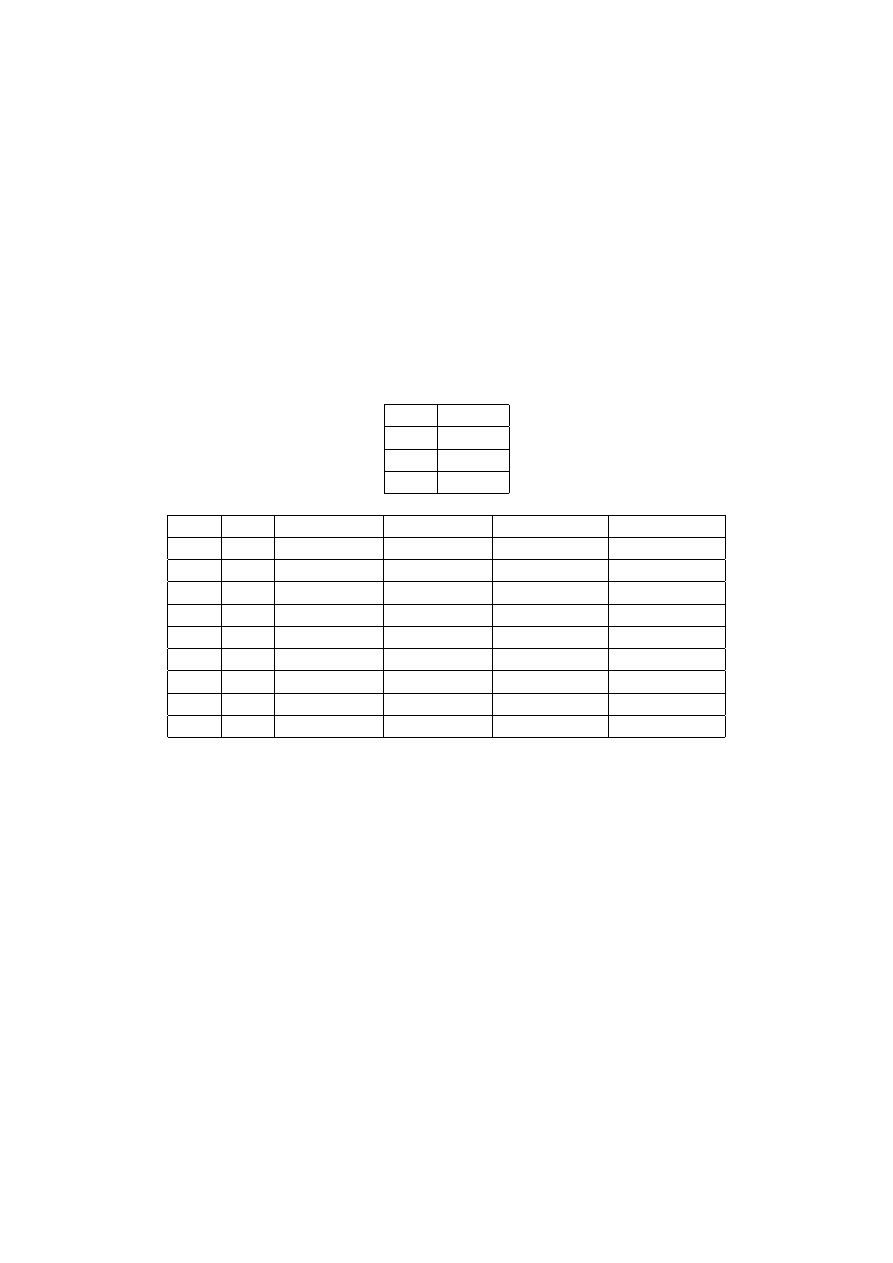
Funkcje zdaniowe, kwantyfikatory – teoria

Funkcja (forma) zdaniowa zmiennej x, której zakresem zmienności jest przestrzeń X to wyraże-
nie ϕ(x), które staje się zdaniem prawdziwym lub fałszywym po podstawieniu w miejsce x
dowolnego elementu z przestrzeni X.

Zbiory

{x : ϕ(x)}

oraz

{(x

1

, . . . , x

n

) : ϕ(x

1

, . . . , x

n

)}

nazywamy wykresami funkcji zdaniowej ϕ.

Klasyfikacja form zdaniowych jednej zmiennej

Klasa P – formy zdaniowe spełnione przez wszystkie wartości zmiennej.
Klasa F – formy zdaniowe, które nie są spełnione przez żadną wartość zmiennej.
Klasa T – formy zdaniowe spełnione przez niektóre lecz nie wszystkie wartości zmiennej.

ϕ(x)

∼ ϕ(x)

P

F

F

P

T

T

ϕ(x)

ψ(x)

ϕ(x) ∧ ψ(x)

ϕ(x) ∨ ψ(x)

ϕ(x) ⇒ ψ(x)

ϕ(x) ⇔ ψ(x)

P

P

P

P

P

P

P

F

F

P

F

F

P

T

T

P

T

T

F

P

F

P

P

F

F

F

F

F

P

P

F

T

F

T

P

T

T

P

T

P

P

T

T

F

F

T

T

T

T

T

F,T

P,T

P,T

P,F,T

Kwantyfikatory

Jeśli ϕ(x) jest funkcją zdaniową zmiennej x o zakresie zmienności X 6= ∅, to

• dla każdego x należącego do X jest ϕ(x) ≡ ∀

x∈X

ϕ(x),

• istnieje x należące do X takie, że ϕ(x) ≡ ∃

x∈X

ϕ(x).

Warunek konieczny i dostateczny na to, aby zdanie ∀

x∈X

ϕ(x) było prawdziwe można zapisać

w postaci:

∀

x∈X

ϕ(x) jest zdaniem prawdziwym ⇔ {x ∈ X : ϕ(x)} = X.

Warunek konieczny i dostateczny na to, aby zdanie ∃

x∈X

ϕ(x) było prawdziwe można zapisać

w postaci:

∃

x∈X

ϕ(x) jest zdaniem prawdziwym ⇔ {x ∈ X : ϕ(x)} 6= ∅.

Prawa rachunku funkcyjnego

1. ∀

x∈X

ϕ(x) ⇒ ϕ(y), y ∈ X

2. ϕ(y) ⇒ ∃

x∈X

ϕ(x), y ∈ X

3. ∀

x∈X

ϕ(x) ⇒ ∃

x∈X

ϕ(x)

4. Prawa de Morgana

(a) ∼ ∀

x∈X

ϕ(x) ⇔ ∃

x∈X

∼ ϕ(x)

(b) ∼ ∃

x∈X

ϕ(x) ⇔ ∀

x∈X

∼ ϕ(x)

5. ∀

x∈X

[ϕ(x)∧ψ(x)] ⇔ ∀

x∈X

ϕ(x)∧∀

x∈X

ψ(x) – prawo rozdzielności kwantyfikatora ogólnego

względem koniunkcji

6. ∀

x∈X

ϕ(x) ∨ ∀

x∈X

ψ(x) ⇒ ∀

x∈X

[ϕ(x) ∨ ψ(x)]

Uwaga: Kwantyfikator ogólny nie jest rozdzielny względem alternatywy.

7. ∃

x∈X

[ϕ(x) ∨ ψ(x)] ⇔ ∃

x∈X

ϕ(x) ∨ ∃

x∈X

ψ(x) – prawo rozdzielności kwantyfikatora

szczegółowego względem alternatywy

8. ∃

x∈X

[ϕ(x) ∧ ψ(x)] ⇒ ∃

x∈X

ϕ(x) ∧ ∃

x∈X

ψ(x)

Uwaga: Kwantyfikator szczegóły nie jest rozdzielny względem koniunkcji.

9. ∀

x∈X

[ϕ(x) ⇒ ψ(x)] ⇒ [∀

x∈X

ϕ(x) ⇒ ∀

x∈X

ψ(x)] – prawo rozkładania kwantyfikatora

ogólnego

10. ∀

x∈X

[ϕ(x) ⇒ ψ(x)] ⇒ [∃

x∈X

ϕ(x) ⇒ ∃

x∈X

ψ(x)] – prawo rozkładania kwantyfikatora

szczegółowego

11. ∀

x∈X

[ϕ(x) ⇔ ψ(x)] ⇒ [∀

x∈X

ϕ(x) ⇔ ∀

x∈X

ψ(x)]

12. ∀

x∈X

[ϕ(x) ⇔ ψ(x)] ⇒ [∃

x∈X

ϕ(x) ⇔ ∃

x∈X

ψ(x)]

13. Prawa przestawiania kwantyfikatorów

(a) ∀

x∈X

∀

y∈Y

ϕ(x, y) ⇔ ∀

y∈Y

∀

x∈X

ϕ(x, y)

(b) ∃

x∈X

∃

y∈Y

ϕ(x, y) ⇔ ∃

y∈Y

∃

x∈X

ϕ(x, y)

(c) ∃

x∈X

∀

y∈Y

ϕ(x, y) ⇒ ∀

y∈Y

∃

x∈X

ϕ(x, y)

14. Prawa włączania i wyłączania kwantyfikatorów

(a) ∀

x∈X

(ϕ(x) ∨ ψ) ⇔ ∀

x∈X

ϕ(x) ∨ ψ

(b) ∃

x∈X

(ϕ(x) ∨ ψ) ⇔ ∃

x∈X

ϕ(x) ∨ ψ

(c) ∀

x∈X

(ϕ(x) ∧ ψ) ⇔ ∀

x∈X

ϕ(x) ∧ ψ

(d) ∃

x∈X

(ϕ(x) ∧ ψ) ⇔ ∃

x∈X

ϕ(x) ∧ ψ

(e) ∀

x∈X

(ϕ(x) ⇒ ψ) ⇔ ∃

x∈X

ϕ(x) ⇒ ψ

(f) ∃

x∈X

(ϕ(x) ⇒ ψ) ⇔ ∀

x∈X

ϕ(x) ⇒ ψ

(g) ∀

x∈X

(ψ ⇒ ϕ(x)) ⇔ (ψ ⇒ ∀

x∈X

ϕ(x))

(h) ∃

x∈X

(ψ ⇒ ϕ(x)) ⇔ (ψ ⇒ ∃

x∈X

ϕ(x))

Wybrane reguły rachunku kwantyfikatorów

1.

∀

x

ϕ(x)

ϕ(y)

– reguła opuszczania kwantyfikatora ogólnego

2.

ϕ(y)

∃

x

ϕ(x)

– reguła dołączania kwantyfikatora szczegółowego

3.

∀

x

[ϕ(x) ⇔ ψ(x)]

∀

x

ϕ(x) ⇔ ∀

x

ψ(x)

4.

∀

x

[ϕ(x) ⇔ ψ(x)]

∃

x

ϕ(x) ⇔ ∃

x

ψ(x)

5.

ϕ ⇒ ψ(x)

ϕ ⇒ ∀

x

ψ(x)

– reguła dołączania kwantyfikatora ogólnego

6.

ϕ(x) ⇒ ψ

∃

x

ϕ(x) ⇒ ψ

– reguła dołączania kwantyfikatora szczegółowego

7.

ϕ ⇒ ∀

x

ψ(x)

ϕ ⇒ ψ(x)

– reguła eliminacji kwantyfikatora ogólnego

8.

∃

x

ϕ(x) ⇒ ψ

ϕ(x) ⇒ ψ

– reguła eliminacji kwantyfikatora szczegółowego

Kwantyfikatory o zakresie ograniczonym przez funkcję zdaniową

Kwantyfikatory

∀

ψ(x)

ϕ(x)

oraz

∃

ψ(x)

ϕ(x)

nazywamy kwantyfikatorami o zakresie ograniczonym przez funkcję zdaniową ψ(x).
Następujące prawa pozwalają przejść do wyrażeń, które nie zawierają kwantyfikatorów o za-
kresie ograniczonym:

• ∀

ψ(x)

ϕ(x) ⇔ ∀

x

[ψ(x) ⇒ ϕ(x)]

• ∃

ψ(x)

ϕ(x) ⇔ ∃

x

[ψ(x) ∧ ϕ(x)]