Egzamin dla Aktuariuszy z 6 października 2008 r.
Prawdopodobieństwo i Statystyka
Zadanie 1
(
)
=
−
=
−
+
+
−
+
−
=
−
)
var(
40
1600
1
40
...
var
var
40
40
2
2
1
1
Y
X
Y
X
Y
X
Y
X
Y
X
(
)
(
)
2
2
2
2
2
05
,
0
05
,
0
2
025
,
0
)
,
cov(
2
var
var
025
,
0
σ
p
σ
σ
p
σ
σ
Y
X
Y
X
−
=
−
+
=
−
+
=
*
*
,Y
X
- obserwacje gdzie obie współrzędne są znane
−
X
- tylko X znane
−
Y
- tylko Y znane
(
)
(
) (
)
=
−
+
−
=
⋅
+
⋅
−
⋅
+
⋅
=
−
−
−
−
−
Y
X
Y
X
Y
Y
X
X
Y
X
5
1
5
4
var
50
10
40
50
10
40
var
var
*
*
*
*
(
)
(
)
=
+
⋅
+
−
+
⋅
=
Y
X
Y
X
Y
X
var
var
10
100
1
25
1
)
,
cov(
2
var
var
40
1600
1
25
16
(
)
2
2
2
2
2
2
032
,
0
04
,
0
2
1
,
0
25
1
2
025
,
0
25
16
σ
p
σ
σ
σ
p
σ
σ
−
=
⋅
⋅
+
−
+
⋅
=
)
1
(
05
,
0
032
,
0
04
,
0
2
2
2
p
σ
σ
p
σ
−
=
−
0,04-0,032p=0,05-0,05p
0,018p=0,01
9
5
18
10
18
1000
100
1
=
=
=
p
Zadanie 2
(
)
(
)
(
)
4
4
4
4
4
3
4
4
4
4
4
2
1
4
4
4
4
4
3
4
4
4
4
4
2
1
II
I
Y
X
P
Y
X
z
V
t
U
P
Y
X
P
Y
X
z
V
t
U
P
z
Y
X
t
Y
X
P
)
(
,
)
(
,
)
,
max(
,
)
,
min(
>
>
<
<
+
<
<
<
<
=
<
<
I.
II.
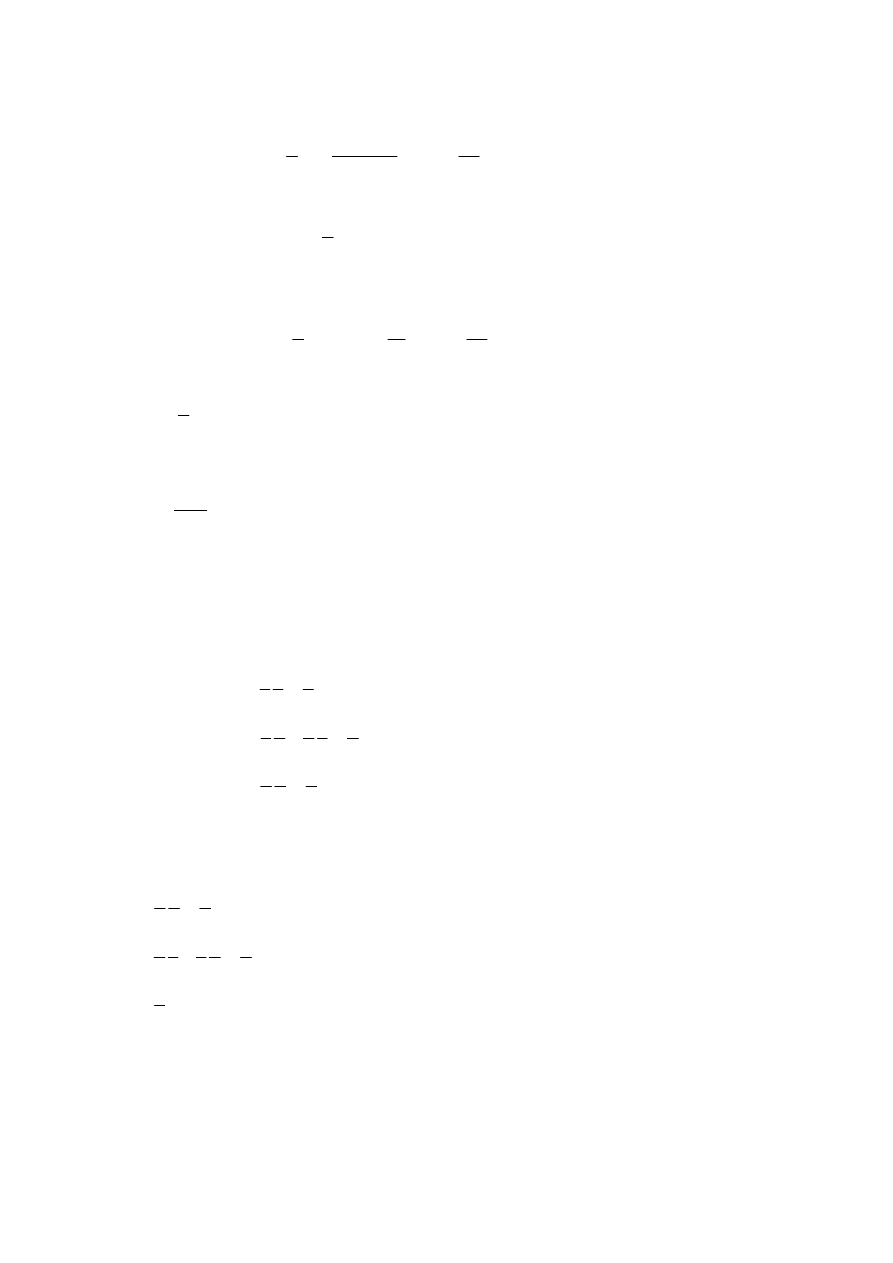
I dla z>t
∫ ∫
−
+
+
−
=
−
−
=
t z
x
t
z
z
t
z
t
dydx
y
x
I
0
2
2
3
2
2
2
)
2
(
2
1
)
2
(
dla z<t
∫ ∫
−
=
−
−
=
z y
z
z
dxdy
y
x
I
0 0
3
2
2
1
)
2
(
II dla z>t
∫ ∫
−
+
+
−
=
−
−
=
t z
y
t
z
z
t
z
t
dxdy
y
x
II
0
2
2
3
2
2
2
)
2
(
2
1
)
2
(
dla z<t
3
2
2
1
z
z
II
−
=
(
)
z
t
dla
4
)
2
(
)
,
(
2
2
3
<
−
+
+
−
=
t
z
z
t
z
t
z
t
F
t
z
dla
2
2
4
)
,
(
)
,
(
>
−
−
=
∂
∂
∂
=
z
t
z
t
F
t
z
z
t
f
czyli odpowiedź B jest prawidłowa
Zadanie 3
stan(i+1) – i kul białych w I urnie
ij
p - prawdopodobieństwo przejścia
0
0
1
0
14
13
12
11
=
=
=
=
p
p
p
p
0
9
4
3
2
3
2
9
4
3
1
3
2
3
2
3
1
9
1
3
1
3
1
24
23
22
21
=
=
=
=
+
=
=
=
p
p
p
p
9
1
9
4
3
2
3
1
3
1
3
2
9
4
3
2
3
2
0
34
33
32
31
=
=
+
=
=
=
=
p
p
p
p
0
1
0
0
44
43
42
41
=
=
=
=
p
p
p
p
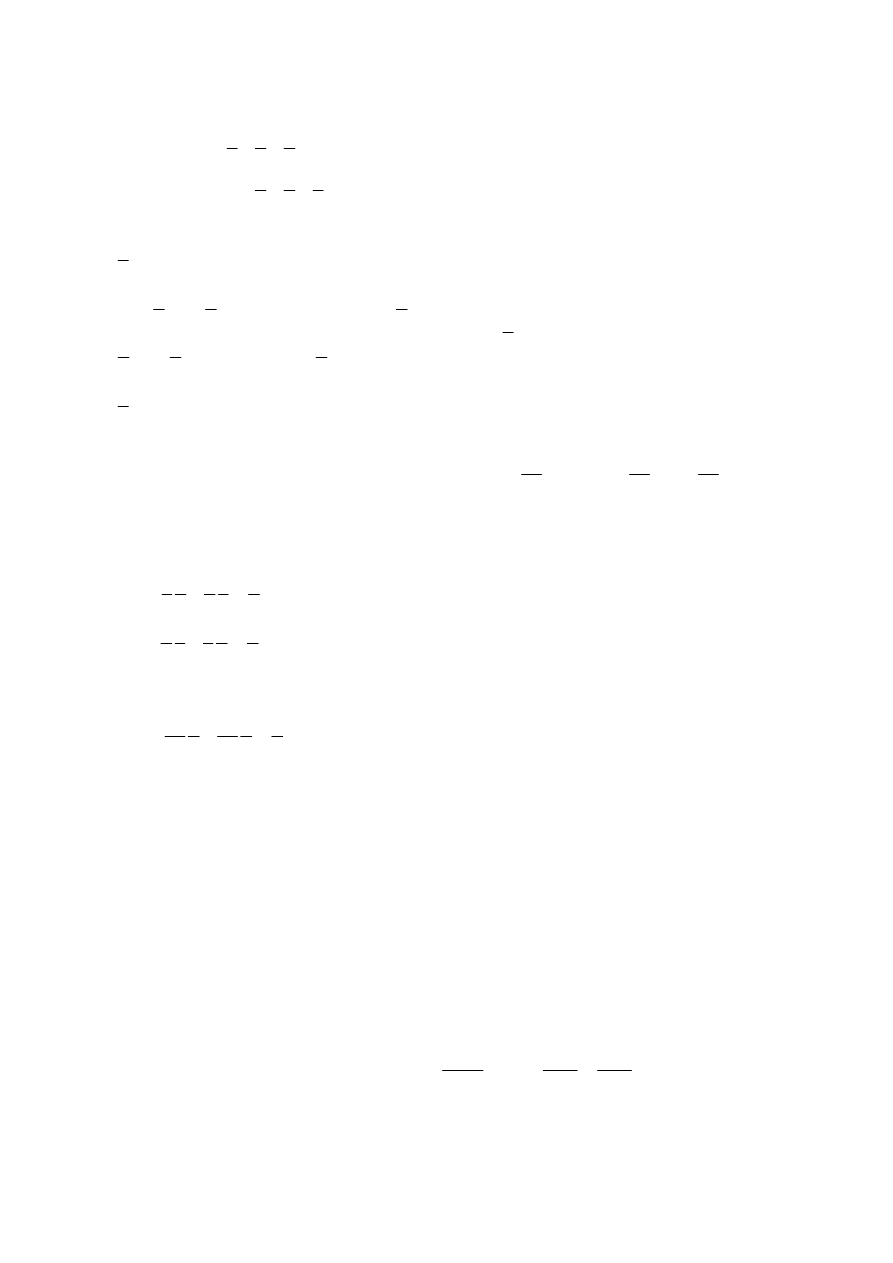
(
)
(
)
4
3
2
1
4
3
2
1
,
,
,
0
1
0
0
9
1
9
4
9
4
0
0
9
4
9
4
9
1
0
0
1
0
,
,
,
p
p
p
p
p
p
p
p
=
1
4
4
1
1
3
1
3
1
3
1
1
1
2
4
3
3
4
3
2
2
3
2
1
1
2
,
9
9
1
9
4
9
4
9
9
4
4
9
9
1
9
4
9
4
9
4
9
4
9
1
p
p
p
p
p
p
p
p
p
p
p
p
p
p
p
p
p
p
p
p
p
p
p
p
p
p
=
=
⋅
→
=
=
=
+
+
=
→
=
=
+
+
=
+
+
=
20
1
,
20
9
,
20
1
1
9
9
1
4
3
2
1
1
1
1
1
4
3
2
1
=
=
=
=
→
=
+
+
+
→
=
+
+
+
p
p
p
p
p
p
p
p
p
p
p
p
)
4
(
)
3
(
)
2
(
)
1
(
4
3
2
1
P
p
P
p
P
p
P
p
ODP
+
+
+
=
0
)
4
(
9
4
3
2
3
1
3
1
3
2
)
3
(
9
4
3
1
3
2
3
2
3
1
)
2
(
0
)
1
(
=
=
+
=
=
+
=
=
P
P
P
P
5
2
9
4
20
9
9
4
20
9
=
+
=
ODP
Zadanie 4
gdzie
y
x
x
y
n
n
y
x
f
n
,
dla
)
)(
1
(
)
,
(
2
<
−
−
=
−
(
)
(
)
)
1
,
0
(
,
,...,
max
,
,...,
min
1
1
J
J
J
J
Y
J
J
X
i
n
n
≅
=
=
u nas:
a
J
a
b
X
i
i
+
−
=
)
(
{
}
{
}
(
)
(
)
=
+
−
+
−
=
+
−
+
−
=
a
J
a
b
a
J
a
b
corr
a
J
a
b
a
J
a
b
corr
ODP
i
i
i
i
max
)
(
,
min
)
(
)
(
max
,
)
(
min
(
)
i
i
J
J
corr
max
,
min
=
1
min
)
1
(
−
−
≅
n
x
n
f
1
max
−
≅
n
nx
f
∫
∫
+
=
+
−
=
+
−
=
−
=
−
=
+
−
−
1
0
1
0
1
0
1
1
1
1
1
1
1
1
)
1
(
)
1
(
min
n
n
n
n
nx
x
x
x
n
x
nx
E
n
n
n
n
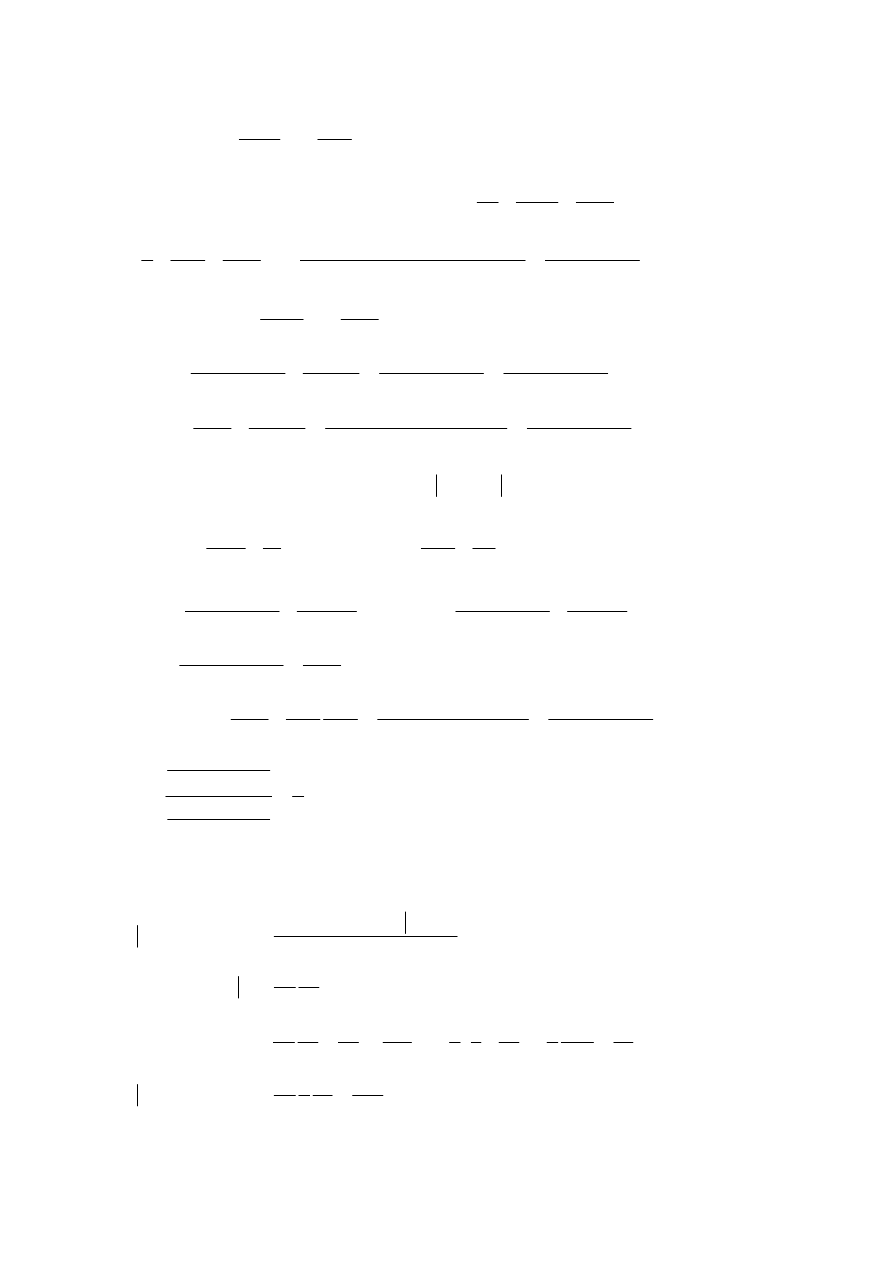
∫
+
=
+
=
=
+
1
0
1
0
1
1
1
max
n
n
n
nx
nx
E
n
n
(
)
∫
∫
=
+
+
+
−
=
+
−
=
−
=
+
+
−
−
1
0
1
0
1
0
2
1
1
2
1
2
2
2
1
2
2
1
)
1
(
min
n
x
n
x
n
x
n
x
x
x
n
x
nx
E
n
n
n
n
n
)
2
)(
1
(
2
)
2
)(
1
(
4
2
2
3
2
1
1
2
1
2
2
2
+
+
=
+
+
+
+
−
−
+
+
=
+
+
+
−
=
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
∫
+
=
+
=
=
+
+
1
0
1
0
2
1
2
2
2
max
n
n
n
nx
nx
E
n
n
2
2
2
)
1
)(
2
(
)
2
(
)
1
(
2
2
2
)
1
(
1
)
2
)(
1
(
2
var(min)
+
+
=
+
+
−
−
+
=
+
−
+
+
=
n
n
n
n
n
n
n
n
n
n
(
)
2
2
2
2
2
2
)
1
)(
2
(
)
1
)(
2
(
)
2
(
1
2
)
1
(
2
var(max)
+
+
=
+
+
+
−
+
+
=
+
−
+
=
n
n
n
n
n
n
n
n
n
n
n
n
n
n
(
)
∫ ∫
∫ ∫
=
−
−
=
=
−
=
−
−
=
⋅
−
−
1
0 0
1
0 0
2
2
)
)(
1
(
)
)(
1
(
max
min
y
y
n
n
dtdy
yt
t
y
n
n
t
x
y
xydxdy
x
y
n
n
E
∫
∫
=
−
−
−
=
−
−
−
=
−
1
0
1
0
0
1
1
)
1
(
1
)
1
(
n
y
n
y
y
n
n
dy
n
t
n
yt
y
n
n
n
n
y
n
n
=
+
−
−
+
−
=
+
−
−
+
−
=
+
+
n
n
n
n
n
n
n
n
y
n
n
y
n
n
n
n
)
2
(
1
)
1
)(
2
(
1
)
1
(
)
2
(
)
1
)(
2
(
)
1
(
1
0
2
2
2
1
)
1
)(
2
(
1
)
1
(
+
=
−
+
+
−
−
=
n
n
n
n
n
n
n
n
)
2
(
)
1
(
1
)
2
(
)
1
(
2
1
2
1
1
1
2
1
max)
cov(min,
2
2
2
2
+
+
=
+
+
−
−
+
+
=
+
+
−
+
=
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
ODP
1
)
1
)(
2
(
)
2
(
)
1
(
1
2
2
=
+
+
+
+
=
Zadanie 5
(
) (
)
(
)
4
3
2
1
4
3
2
1
4
3
2
1
,
,
,
)
(
,
,
,
,
,
,
X
X
X
X
f
θ
f
θ
X
X
X
X
f
X
X
X
X
θ
f
=
(
)
)
2
;
1
(
dla
5
,
1
1
1
,
,
,
4
4
3
2
1
∈
=
θ
θ
θ
X
X
X
X
f
(
)
∫
=
−
=
−
=
−
=
=
2
1
2
1
3
4
4
3
2
1
36
7
24
1
8
3
2
24
1
3
1
3
2
3
1
5
,
1
1
5
,
1
1
1
,
,
,
θ
θ
X
X
X
X
f
(
)
)
2
,
1
(
7
24
7
36
3
2
1
,
,
,
4
4
4
3
2
1
∈
=
=
θ
θ
θ
X
X
X
X
θ
f
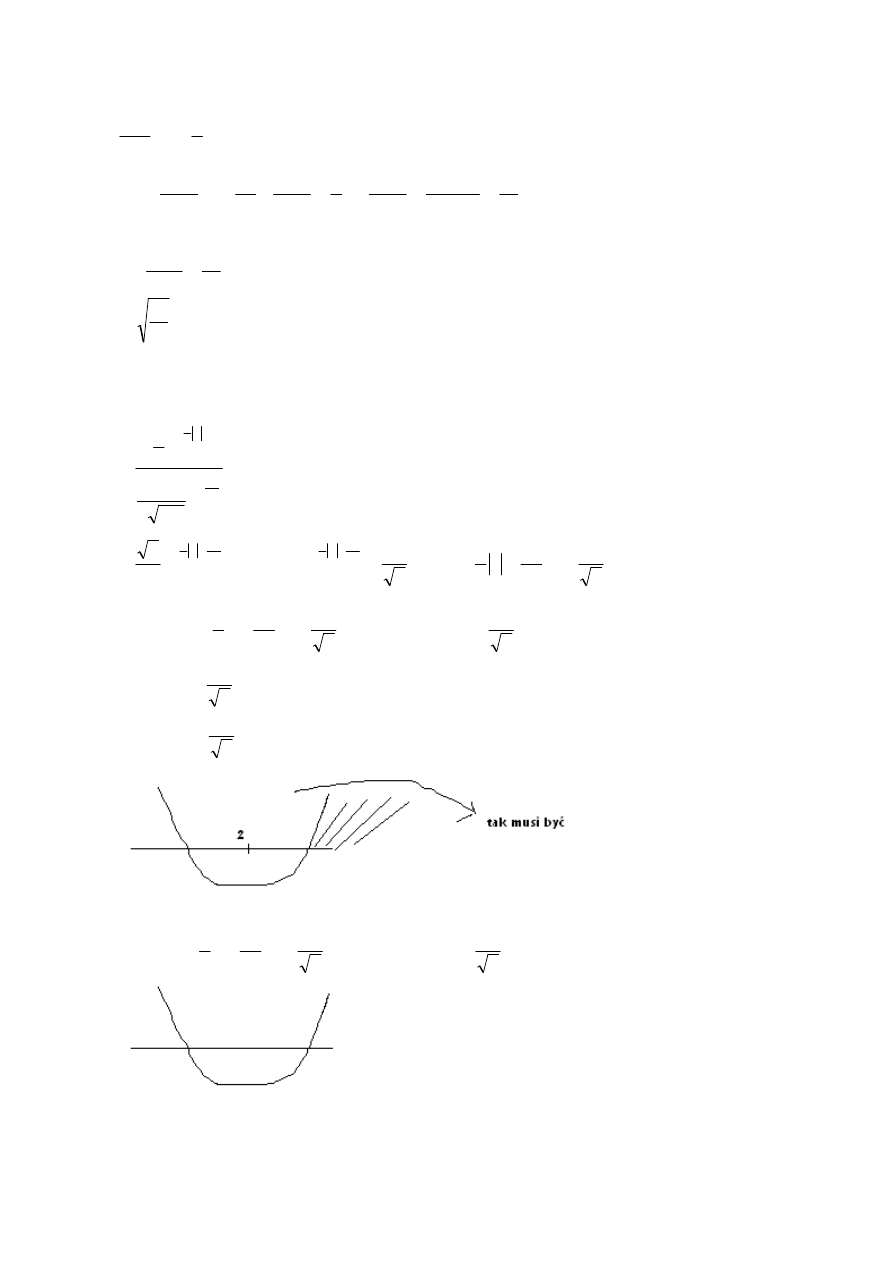
∫
=
x
θ
d
θ
1
4
2
1
7
24
14
9
42
21
48
21
24
2
1
21
24
21
24
21
24
3
3
1
3
=
−
=
→
=
−
=
−
=
x
x
θ
L
x
24
14
21
9
3
⋅
=
⋅
x
9
16
7
9
8
14
3
=
⋅
⋅
=
x
211
,
1
9
16
3
≈
=
x
Zadanie 6
α
t
e
e
P
x
x
=
>
Π
−
−
8
2
1
0
2
2
2
1
4
1
>
+
−
=
>
=
>
+
−
+
−
2
2
ln
8
2
1
2
2
2
2
2
0
8
2
1
0
8
2
1
0
2
2
t
x
x
P
t
e
P
t
e
P
x
x
x
x
dla x>0
>
−
−
=
>
+
−
0
2
2
ln
8
4
2
2
ln
8
2
1
2
0
2
0
t
x
x
P
t
x
x
P
0
2
2
ln
32
16
0
2
2
ln
8
4
2
>
+
=
∆
>
−
−
t
t
x
x
dla x<0
>
−
+
=
>
+
0
2
2
ln
8
4
2
2
ln
8
2
1
2
0
2
0
t
x
x
P
t
x
x
P
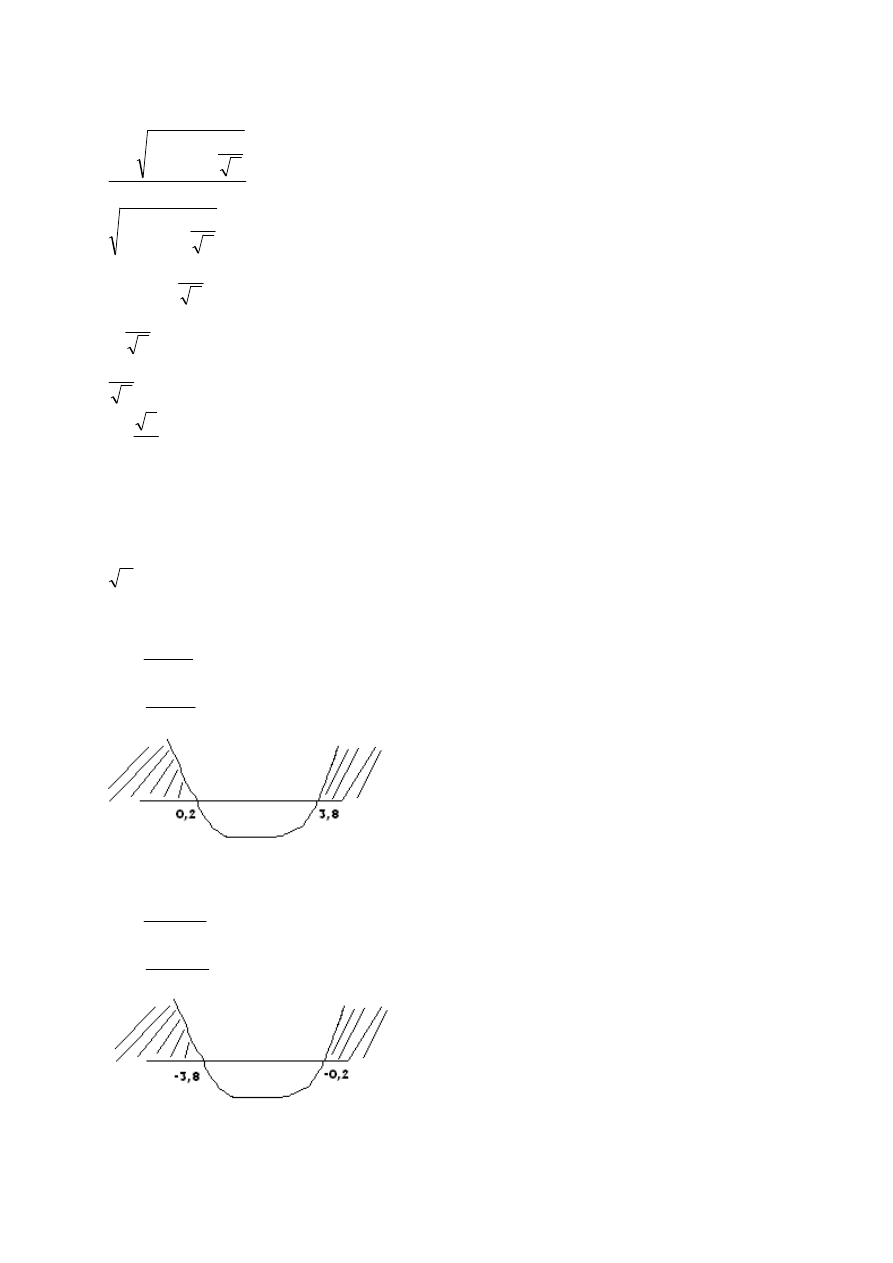
z tego i z założeń wynika, że:
8
,
3
2
2
2
ln
32
16
4
=
+
+
t
6
,
3
2
2
ln
32
16
=
+
t
96
,
12
2
2
ln
32
16
=
+
t
095
,
0
2
2
ln
−
=
t
095
,
0
2
2
−
=
e
t
095
,
0
2
2
−
=
e
t
I dla x>0
(
)
0
76
,
0
4
2
0
>
+
−
x
x
P
II dla x<0
(
)
0
76
,
0
4
2
0
>
+
+
x
x
P
6
,
3
96
,
12
76
,
0
4
16
=
∆
=
⋅
−
=
∆
dla I
8
,
3
2
6
,
3
4
2
,
0
2
6
,
3
4
2
1
=
+
=
=
−
=
x
x
dla II
2
,
0
2
6
,
3
4
8
,
3
2
6
,
3
4
2
1
−
=
+
−
=
−
=
−
−
=
x
x
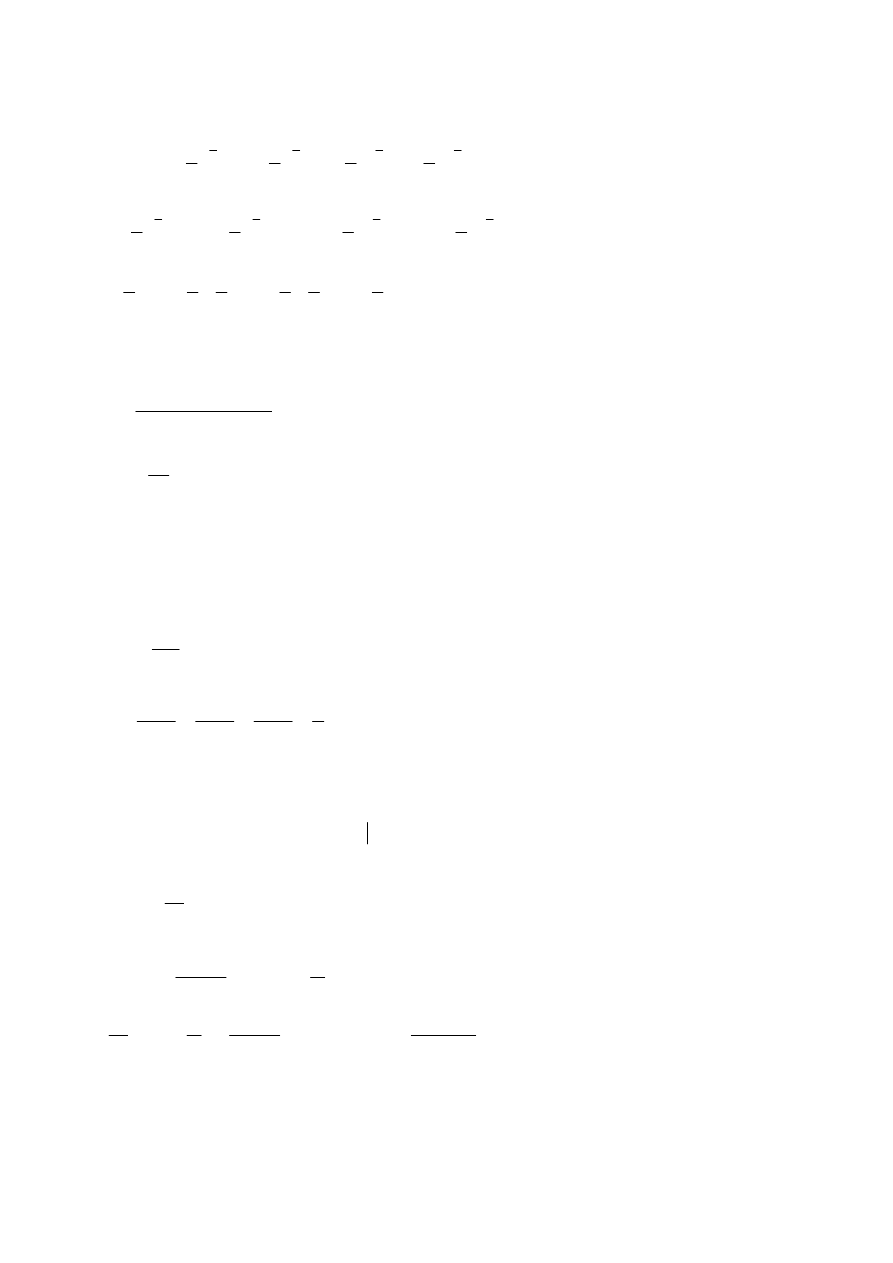
(
) (
) (
)
∞
∪
−
∪
−
∞
−
=
;
8
,
3
2
,
0
;
2
,
0
8
,
3
;
K
∫
∫
∫
∫
−
∞
−
−
∞
−
−
=
+
+
+
=
8
,
3
0
2
,
0
2
,
0
0
8
,
3
2
1
2
1
2
1
2
1
4
1
4
1
4
1
4
1
x
x
x
x
e
e
e
e
ODP
=
−
+
−
+
+
=
∞
−
−
−
−
∞
−
8
,
3
2
1
2
,
0
0
2
1
0
2
,
0
2
1
8
,
3
2
1
2
1
2
1
2
1
2
1
x
x
x
x
e
e
e
e
2447
,
0
1
2
1
2
1
2
1
2
1
2
1
2
1
1
,
0
9
,
1
9
,
1
1
,
0
1
,
0
9
,
1
≈
+
−
=
+
−
+
−
+
=
−
−
−
−
−
−
e
e
e
e
e
e
Zadanie 7
(
)
( )
(
)
θ
X
t
e
P
t
e
e
P
i
θ
n
X
n
θ
X
n
i
i
>
>
=
>
∑
∑
⋅
−
−
−
min
przy
)
3
(ln
)
3
(ln
3
ln
0
3
ln
3
ln
0
czyli
( )
( )
<
>
=
θ
X
θ
X
e
f
f
i
i
θ
n
min
gdy
0
min
gdy
3
ln
0
1
( )
(
)
01
,
0
min
=
>
γ
θ
X
P
i
(
)
n
θ
n
θ
n
θ
γ
γ
e
3
01
,
0
01
,
0
3
3
ln
⋅
=
→
=
=
−
⋅
−
czyli TEST: jeżeli
( )
θ
X
i
>
min
to z prawdopodobieństwem
n
θ
γ
3
01
,
0
⋅
=
odrzucamy
( )
(
)
81
,
0
min
3
01
,
0
1
>
>
⋅
θ
X
P
i
θ
n
81
100
100
81
3
=
≥
θ
n
81
ln
3
ln
≥
θ
n
θ
θ
θ
θ
n
4
3
ln
3
ln
4
3
ln
3
ln
3
ln
81
ln
4
=
=
=
≥
Zadanie 8
(
)
(
)
4
4
4
4
4
3
4
4
4
4
4
2
1
X
k
n
n
k
N
P
k
N
s
S
P
N
P
s
S
P
∑
∞
=
=
=
≤
+
=
=
≤
1
)
(
)
0
(
X
ds
d
ODP
=
suma wykładniczych ma rozkład gamma więc:
∑∫
∞
=
−
−
−
−
=
1 0
1
1
!
1
)!
1
(
1
k
s
w
k
e
k
dw
e
w
k
X
∑
∑
∞
=
∞
=
−
−
−
−
−
−
−
=
−
=
1
1
1
1
1
1
)!
1
(
!
)!
1
(
1
!
1
k
n
n
s
s
k
n
n
s
e
e
s
k
e
k
X
ds
d

Zadanie 9
To nie jest rozkład geometryczny tylko ujemny.dwumianowy(2,1-p)
∑
−
≅
)
1
,
2
(
.
p
n
dwum
uj
X
i
∑
∞
=
=
−
−
+
+
0
2
)
1
(
1
2
k
k
n
p
p
p
k
k
n
k
a
a
TAK CHCEMY
∑
∞
=
−
=
−
−
−
+
+
0
1
2
1
)
1
(
)!
1
2
(
!
)!
1
2
(
k
k
n
p
p
n
k
k
n
k
a
a
∑
∞
=
−
=
−
−
+
−
−
−
+
+
0
1
2
1
1
2
1
2
)
1
(
)!
2
2
(
!
)!
2
2
(
k
k
n
n
k
n
p
p
n
k
k
n
k
a
a
tu r=2n-1
jeżeli
1
1
2
1
2
=
−
−
+
+
n
k
n
k
a
a
to będzie OK.
a(2n+k-1)=(a+k)(2n-1)
a(2n+k-1-2n+1)=k(2n-1)
a=2n-1
Zadanie 10
(
)
∑
−
∏
=
4
1
3
6
6
4
i
X
θ
i
e
X
θ
L
∑
∑
−
+
−
=
4
1
ln
3
ln
6
4
ln
6
ln
i
i
X
θ
X
θ
L
6
0
6
6
4
2
4
2
4
∑
∑
∑
=
→
=
+
−
=
+
−
=
i
i
i
X
θ
θ
X
θ
θ
X
θ
θ
d
d
czyli
6
ˆ
6
1
4
∑
=
=
i
i
X
θ
(
)
∫
∫
−
−
−
−
=
=
=
=
=
=
<
=
<
4
1
4
0
0
3
4
3
4
1
4
1
1
4
4
t
t
θ
t
θ
s
θ
x
e
ds
e
θ
ds
dx
x
s
x
dx
e
x
θ
t
X
P
t
X
P
czyli
≅
θ
wykl
X
1
4
∑
Γ
≅
θ
X
i
1
;
6
4
(
)
2
6
var
;
6
,
1
;
6
,
1
,
0
6
1
1
,
0
ˆ
θ
X
θ
EX
θ
X
gdzie
θ
θ
X
P
θ
θ
θ
P
=
=
Γ
≅
<
−
=
<
−
(
)
(
)
=
<
<
=
<
−
=
θ
X
θ
P
θ
θ
X
P
ODP
6
,
6
4
,
5
6
,
0
6
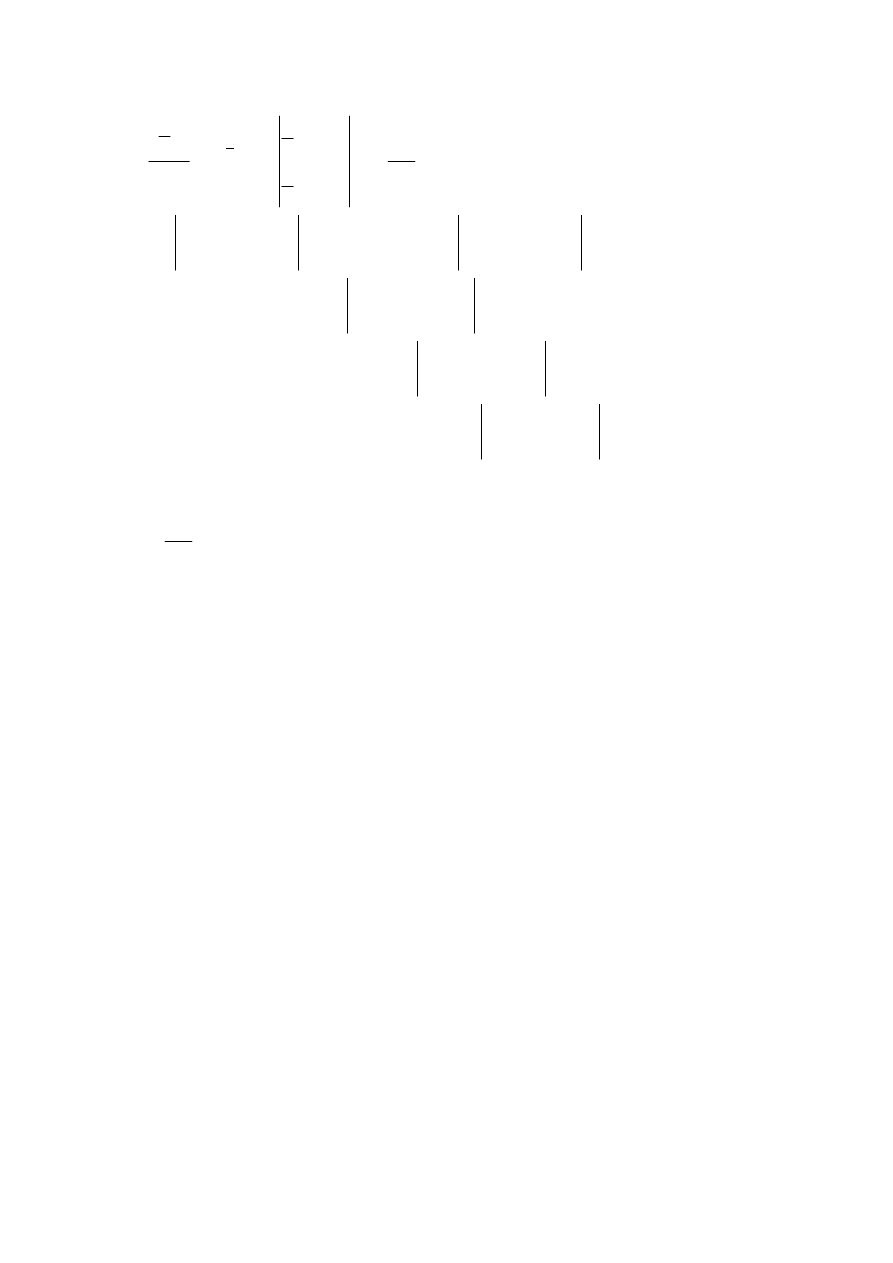
∫
∫
=
=
=
=
=
=
−
−
θ
θ
t
x
θ
dt
e
t
dt
dx
θ
t
x
θ
dx
e
x
θ
6
,
6
4
,
5
6
,
6
4
,
5
5
1
5
6
120
1
1
1
!
5
1
∫
∫
=
=
=
′
=
′
=
=
+
−
=
−
=
=
′
=
′
=
=
−
−
−
−
−
−
t
-
3
4
4
5
4
5
5
-e
v
4
5
5
t
u
e
v
t
u
e
t
e
t
e
v
t
u
e
v
t
u
e
t
t
t
t
t
t
t
(
)
=
−
=
=
′
=
′
=
=
+
−
+
−
=
−
−
−
−
−
∫
t
t
t
t
t
e
v
t
u
e
v
t
u
e
t
e
t
e
t
3
4
5
2
3
3
4
5
(
)
=
−
=
=
′
=
′
=
=
+
−
+
−
−
=
−
−
−
−
−
−
∫
t
t
t
t
t
t
e
v
t
u
e
v
t
u
e
t
e
t
e
t
e
t
2
3
20
5
2
2
3
4
5
(
)
=
−
=
=
′
=
′
=
=
+
−
+
−
−
−
=
−
−
−
−
−
−
−
∫
t
t
t
t
t
t
t
e
v
u
e
v
t
u
te
e
t
e
t
e
t
e
t
1
2
60
20
5
2
3
4
5
(
)
=
−
−
+
−
−
−
−
=
−
−
−
−
−
−
t
t
t
t
t
t
e
te
e
t
e
t
e
t
e
t
120
60
20
5
2
3
4
5
t
t
t
t
t
t
e
te
e
t
e
t
e
t
e
t
−
−
−
−
−
−
−
−
−
−
−
−
=
120
120
60
20
5
2
3
4
5
(
)
[
−
+
⋅
+
⋅
+
⋅
+
⋅
+
=
−
120
4
,
5
120
4
,
5
60
4
,
5
20
4
,
5
5
4
,
5
120
1
2
3
4
5
4
,
5
e
ODP
(
)
]
1915
,
0
120
6
,
6
120
6
,
6
60
6
,
6
20
6
,
6
5
6
,
6
2
3
4
5
6
,
6
≈
+
⋅
+
⋅
+
⋅
+
⋅
+
−
−
e
Wyszukiwarka
Podobne podstrony:
2008.10.06 prawdopodobie stwo i statystyka
2004 10 11 prawdopodobie stwo i statystykaid 25166
1998 10 03 prawdopodobie stwo i statystykaid 18585
2002 10 12 prawdopodobie stwo i statystykaid 21648
1996 10 26 prawdopodobie stwo i statystykaid 18572
2009.04.06 prawdopodobie stwo i statystyka
2003.12.06 prawdopodobie stwo i statystyka
2010.10.04 prawdopodobie stwo i statystyka
2003 12 06 prawdopodobie stwo i statystykaid 21710
2008 03 17 prawdopodobie stwo i statystykaid 26449
2008 12 15 prawdopodobie stwo i statystykaid 26466
2001.10.13 prawdopodobie stwo i statystyka
2007.10.08 prawdopodobie stwo i statystyka
2006.10.09 prawdopodobie stwo i statystyka
2004.10.11 prawdopodobie stwo i statystyka
2008.12.15 prawdopodobie stwo i statystyka
2009.10.05 prawdopodobie stwo i statystyka
1999 10 23 prawdopodobie stwo i statystykaid 18598
2009 10 05 prawdopodobie stwo i statystykaid 26670
więcej podobnych podstron