Marek Capi´

nski

Wst¸ep do matematyki finansowej

Wydzia l Matematyki Stosowanej AGH

Krak´

ow 2006

1

Podstawowe Poj¸ecia

1.1 Zasady dzia lania rynku

W celu zbudowania modelu matematycznego rynku i co za tym idzie, wyprowa-
dzenia rozmaitych wzor´

ow, przyjmiemy pewne za lo˙zenia. Dzi¸eki nim model nie

b¸edzie zbyt skomplikowany, ale b¸edzie on mniej realistyczny. Niemniej, zrozu-
mienie funkcjonowania rynku w uproszczonej wersji jest niezb¸ednym pierwszym
krokiem dla pr´

ob zbadania bardziej wyrafinowanych sytuacji.

Arbitra˙z

Sformu lujemy zasad¸e, kt´

ora pozwoli nam wyprowadzi´c wzory na ceny walor´

ow.

Przez walor (ang. asset) rozumiemy akcj¸e, got´

owk¸e, bon, obligacj¸e, inne instru-

menty finansowe, walut¸e obc¸a, z loto, surowce czy rozmaite produkty. Og´

olnie

jest to wszystko to co ma cen¸e i mo˙zna kupi´c b¸ad´z sprzeda´c.

Arbitra ˙z

oznacza mo˙zliwo´s´c uzyskania zysku z transakcji przeprowadzonej

bez ponoszenia ryzyka w wyniku z zauwa˙zenia luki na rynku. Oto przyk lad.
Przypu´s´cmy, ˙ze cena kupna dolara wynosi 3.50 z l w jednym banku, a w drugim
mo˙zemy go sprzeda´c za 3.60. Gdyby taka sytuacja zdarzy la si¸e naprawd¸e,
mogliby´smy zainwestowa´c wszystkie posiadane pieni¸adze i uzyska´c doch´

od

nie ponosz¸ac ryzyka. W praktyce jest to niemo˙zliwe w d lu˙zszym dystansie,
gdy˙z w opisanej sytuacji zakup znacznych ilo´sci dolar´

ow w pierwszym banku

spowodowa lby wzrost ich ceny, a sprzeda˙z w drugim jej spadek. St¸ad natu-

1

2

Wst¸ep do matematyki finansowej

ralne jest przyj¸a´c za lo˙zenie, ˙ze arbitra˙z w praktyce nie wyst¸epuje. Za lo˙zenie
to oznacza, ˙ze mamy do czynienia z dobrze rozwini¸etym rynkiem, w kt´

orym

sytuacje arbitra˙zu s¸a natychmiast wytropione przez ˙z¸adnych latwego zysku, a
jako konsekwencja dzia lania praw popytu i poda˙zy, ceny s¸a takie, ˙ze arbitra˙z
jest wyeliminowany.

Powy˙zszy przyk lad mo˙ze si¸e wydawa´c nieco sztuczny, lecz podobne sytu-

acje, na og´

o l bardziej skomplikowane, wyst¸epuj¸a w praktyce. Innym rodzajem

arbitra˙zu jest sytuacja, w kt´

orej jeden z inwestor´

ow ma niedost¸epne innym in-

formacje dotycz¸ace przysz lo´sci i pozwalaj¸ace na zrobienie korzystnej transakcji
bez ryzyka, lub z minimalnym ryzykiem. Na przyk lad, mo˙ze to by´c przeciek
dotycz¸acy przysz lych rozporz¸adze´

n, np. taryfy celnej czy zmiany stopy pro-

centowej. Mo˙zliwo´s´c skorzystania z tego typu informacji jest zabroniona przez
prawo, lecz egzekucja takiego przepisu mo˙ze by´c trudna. Za lo˙zenie braku arbi-
tra˙zu oznacza wi¸ec tak˙ze to, ˙ze nie dopuszczamy sytuacji b¸ed¸acych naruszeniem
zasady czystej gry.

Sformu lujmy definicj¸e:

Definicja 1.1

Przez arbitra˙z rozumiemy mo˙zliwo´s´c wyboru takiej strategii gry rynkowej, w
kt´

orej startuj¸ac z kapita lu zerowego i nie zasilaj¸ac go ze ´zr´

ode l zewn¸etrznych,

mamy w ka˙zdej chwili nieujemny kapita l, a z dodatnim prawdopodobie´

nstwem

jest on w pewnej chwili wi¸ekszy od zera.

Zerowy kapita l pocz¸atkowy oznacza, ˙ze wszelkie zakupy finansujemy z

po˙zyczek. Nieujemno´s´c kapita lu w trakcie realizacji strategii oznacza, ˙ze nie ma
potrzeby dofinansowania ze ´srodk´

ow w lasnych inwestora w celu zamkni¸ecia ot-

wartych pozycji (po˙zyczki mo˙zemy sp laci´c w ka˙zdej chwili). Przez gr¸e rynkow¸a
rozumiemy zawieranie wszelkich transakcji mo˙zliwych na danym rynku.

Konsekwencj¸a zasady braku arbitra˙zu jest zasada jednej ceny. Gdyby walor

mia l dwie ceny to kupuj¸ac taniej i sprzedajac dro˙zej mieliby´smy arbitra˙z.
Zak ladamy tutaj brak koszt´

ow transakcji czy transportu oraz r´

owno´s´c ceny

kupna i ceny sprzeda˙zy (czyli w praktyce arbitra˙z wyst¸api je´sli cena sprzeda˙zy
waloru w jednym miejscu jest ni˙zsza od ceny kupna w inym miejscu i to o tyle,
aby r´

o˙znica pokry la koszty zwi¸azane z transakcj¸a).

Ryzyko

Zak ladamy, ˙ze nie wyst¸epuje ryzyko upad lo´sci instytucji finansowych, natomi-
ast obecne jest ryzyko zwi¸azane z fluktuacjami cen na rynku.

1. Podstawowe Poj¸ecia

3

P lynno´

s´

c

Zak ladamy, ˙ze rynek jest ca lkowicie p lynny, to znaczy, ˙ze w ka˙zdej chwili
mo˙zemy sprzeda´c lub kupi´c dowoln¸a ilo´s´c walor´

ow wszelkiego rodzaju (akcji,

obligacji, walut, itp.). Ponadto mo˙zemy bez ogranicze´

n po˙zycza´c pieni¸adze.

Dodatkowo zak ladamy, ˙ze mo˙zemy sprzedawa´c walory, nie posiadaj¸ac ich.

Nosi to nazw¸e kr´

otkiej sprzeda ˙zy

(ang. short selling). Oznacza to mo˙zliwo´s´c

po˙zyczenia np. akcji w celu ich sprzeda˙zy dla uzyskania bie˙z¸acych funduszy.
Akcje te musimy odda´c, wi¸ec w strategiach uwzgl¸edniaj¸acych kr´

otk¸a sprzeda˙z

musimy uwzgl¸edni´c konieczno´s´c ich odkupienia. Ponadto w la´sciciel ma prawo
do dywidendy, wi¸ec po˙zyczaj¸acy akcj¸e musi uwzgl¸edni´c konieczno´s´c jej wyp laty
w swojej strategii.

Koszty transakcji

Nast¸epne uproszczenie dotyczy koszt´

ow transakcji. Na dobrze rozwini¸etym

rynku powinny one by´c minimalane. B¸edziemy na og´

o l zak lada´c dla up-

roszczenia, ˙ze koszty transakcji s¸a zerowe. Teoria dopuszczaj¸aca niezerowe
koszty transakcji jest bardziej skomplikowana.

Pokrewnym jest za lo˙zenie, ˙ze lokaty s¸a oprocentowane tak samo jak po˙zycz-

ki. Zak ladamy, ˙ze w ka˙zdej chwili mo˙zemy uzyska´c nieograniczon¸a po˙zyczk¸e.

Ponadto zak ladamy, ˙ze cena kupna jest taka sama jak cena sprzeda˙zy dla

wszelkich walor´

ow. Dla du˙zych instytucji finansowych jest to w przybli˙zeniu

spe lnione.

Inne za lo˙zenia

Ca lkiem naturalnym jest za lo˙zenie, ˙ze wszyscy uczestnicy rynku wol¸a zarobi´c
ni˙z straci´c. W ten spos´

ob nie uwzgl¸edniamy obecno´sci na rynku instytucji

charytatywnych czy sponsor´

ow zak ladaj¸ac, ˙ze sumy przeznaczone na tego typu

dzia lalno´s´c s¸a minimalne.

Je´sli idzie o walory, to zak ladamy ˙ze s¸a podzielne do tego stopnia, ˙ze mo˙zemy

posiada´c dowolny ich u lamek, a nawet x jednostek, gdzie x jest dowoln¸a liczb¸a
rzeczywist¸a. To jest bardzo wygodne upraszczaj¸ace za lo˙zenie, a dla du˙zych
instytucji finansowych jest ono w przybli˙zeniu spe lnione. Je´sli na przyk lad kto´s
handluje walut¸a w ilo´sciach mierzonych setkami tysi¸ecy, dla niego jednostk¸a
jest w la´snie 100.000 i mo˙ze on zakupi´c walut¸e w ilo´sci u lamka tej jednostki.

Za lo˙zenia o istnieniu kr´

otkiej sprzeda˙zy, r´

owno´sci st´

op po˙zyczek i depozyt´

ow

oraz braku koszt´

ow transakcji prowadz¸a do sytuacji w kt´

orej mo˙zemy odwr´

oci´c

4

Wst¸ep do matematyki finansowej

dowoln¸a strategi¸e zamieniaj¸ac sprzeda˙z na kupno, kupno na sprzeda˙z, lokat¸e
na po˙zyczk¸e, a po˙zyczk¸e na lokat¸e.

1.2 Uczestnicy rynku

Wyodr¸ebniamy trzy podstawowe typy uczestnik´

ow rynku. S¸a to ci, kt´

orzy

• staraj¸a si¸e wykorzystywa´c sytuacje arbitra˙zu dla uzyskania zysku bez

ryzyka. Ich aktywno´s´c powoduje, ˙ze sytuacje arbitra˙zu s¸a szybko elimi-
nowane. Dzi¸eki nim wzory wyprowadzone na podstawie zasady braku arbi-
tra˙zu s¸a zgodne z rzeczywisto´sci¸a.

• s¸a zainteresowani minimalizacj¸a ryzyka. Gotowi s¸a po´swi¸eci´c cz¸e´s´c dochodu

za cen¸e pewno´sci, ˙ze bez wzgl¸edu na zmienno´s´c rynku uzyskaj¸a zamierzony
zysk.

• s¸a gotowi ponie´s´c ryzyko, ale oczekuj¸a w zamian za to zwi¸ekszenia swoich

zysk´

ow. Ci gracze gie ldowi s¸a niezb¸edni jako partnerzy dla tych, kt´

orzy

staraj¸a si¸e wyeliminowa´c ryzyko.

Podzia l ten jest nieco umowny, bo ka˙zdy ch¸etnie skorzysta z nadarzaj¸acej

si¸e okazji zarobienia bez ryzyka i ka˙zdy te˙z jest w pewnym sensie ryzykantem.
Niemniej rozr´

o˙znienie to wyst¸epuje w praktyce i jest wygodne przy omawianiu

rozmaitych strategii.

1.3 Instrumenty pochodne

Om´

owimy kr´

otko podstawowe typy instrument´

ow pochodnych.

Kontrakt terminowy

to umowa na zakup lub sprzeda˙z w przysz lo´sci

pewnego waloru za cen¸e ustalon¸a dzi´s.

Opcja

to kontrakt daj¸acy prawo do dokonania pewnej transakcji. Mamy

dwa podstawowe rodzaje opcji:

• Europejska opcja kupna (ang. call ) to kontrakt daj¸acy prawo do kupienia

pewnego waloru w okre´slonej chwili za okre´slon¸a cen¸e.

• Europejska opcja sprzeda˙zy (ang. put) to kontrakt daj¸acy prawo do

sprzedania pewnego waloru w okre´slonej chwili za okre´slon¸a cen¸e.

Opcja ameryka´

nska

daje prawo do kupna lub sprzeda˙zy waloru za ustalon¸a

cen¸e w dowolnej chwili od momentu zawarcia kontraktu do ustalonej chwili, w
kt´

orej kontrakt wygasa.

1. Podstawowe Poj¸ecia

5

Podobnie jak kontrakty terminowe, opcje mog¸a by´c zawierane bezpo´sred-

nio pomi¸edzy zainteresowanymi stronami (ang. over the counter lub w skr´

ocie

OTC) lub poprzez instytucj¸e finansow¸a gwarantuj¸ac¸a stronom mo˙zliwo´s´c real-
izacji zawartych w niej uprawnie´

n.

Poniewa˙z opcja daje prawo do pewnych dzia la´

n, a nie nak lada ˙zadnych

zobowi¸aza´

n, jest ona korzystna dla tego kto j¸a posiada. Strona wystawiaj¸aca

opcj¸e (czyli strona gwarantuj¸aca mo˙zliwo´s´c skorzystania z zawartego w niej
uprawnienia) pobiera wi¸ec za to pewn¸a op lat¸e, tzw. premi¸e. Wyznaczenie jej
wysoko´sci to jedno z podstawowych cl´

ow matematyki finansowej.

2

Stopy Procentowe

Om´

owimy kr´

otko problem warto´sci pieni¸adza w czasie. Stawiamy sobie dwa

pytania:

• ile uzyskamy po up lywie pewnego okresu czasu je´sli maj¸ac dzi´s pewn¸a sum¸e

pieni¸edzy lokujemy j¸a bez ryzyka (w bony, obligacje, czy te˙z w banku),

• ile wynosi dzisiejsza warto´s´c konkretnej sumy pieni¸edzy (uzyskanej lub do

zap lacenia) danej w okre´slonej przysz lej chwili.

Odpowied´z na te pytania zale˙zy od przyj¸etego sposobu naliczania odsetek,

oraz oczywi´scie od ich wysoko´sci.

2.1 Oprocentowanie okresowe

2.1.1 Kapitalizacja prosta

Przypu´s´cmy, ˙ze dysponujemy w chwili obecnej got´

owk¸a w wysoko´sci X z lotych.

Przy za lo˙zeniu, ˙ze stopa procentowa dla wk lad´

ow rocznych wynosi r > 0,

z lo˙zywszy pieni¸adze w banku uzyskamy po roku rX odsetek. Liczb¸e r nazy-
wamy (roczn¸a) stop¸a oprocentowania (ang. interest rate).

Kapitalizacja prosta oznacza, ˙ze odsetki nie s¸a dopisywane do kapita lu.

Zak ladaj¸ac, ˙ze stopa procentowa pozostaje sta la, po kolejnym roku mamy do-
datkowo rX odsetek, co daje razem 2rZ odsetek. Og´

olnie, po czasie T mier-

zonym w latach uzyskujemy T rX odsetek, czyli nasze oszcz¸edno´sci X(T ) w

7

8

Wst¸ep do matematyki finansowej

chwili T wynios¸a

X

(T ) = X + T rX = X(1 + rT ).

(2.1)

Oznacza to, ˙ze stopa oprocentowania w okresie T wynosi rT . Gdy na przyk lad
T

=

1
2

, to powy˙zszy wz´

or daje sum¸e oszcz¸edno´sci po 6 miesi¸acach. Zak ladamy,

˙ze mo˙zna go stosowa´c dla dowolnej liczby rzeczywistej T > 0.

Liczba 1 + rT nosi nazw¸e czynnika wzrostu (GF - ang. growth factor ).
Przypu´s´cmy odwrotnie, ˙ze interesuje nas pewna kwota pieni¸edzy Y w chwili

T

i chcemy wyliczy´c jej dzisiejsz¸a warto´s´c X. Rozumiemy przez to tak¸a sum¸e

pieni¸edzy, kt´

ora ulokowana w banku na okres T daje nam po up lywie tego

okresu w la´snie sum¸e Y . Dla obliczenia X wystarczy zastosowa´c wz´

or (2.1) dla

X

(T ) = Y :

X

= Y

1

1 + rT

= Y (1 + rT )

−

1

.

(2.2)

Liczb¸e X nazywamy warto´

sci¸

a dzisiejsz¸

a

lub zdyskontowan¸

a

liczby Y (ang.

present value

, discounted value).

2.1.2 Kapitalizacja z lo˙zona

W sytuacji, gdy odsetki s¸a ka˙zdorazowo dopisywane do kapita lu, mamy do
czynienia z kapitalizacj¸a z lo˙zon¸a (ang. compound interest). Okres, po kt´

orym

s¸a one dopisywane mo˙ze by´c r´

o˙zny. Typowo jest to rok, 6 miesi¸ecy, kwarta l,

miesi¸ac lub dzie´

n i m´

owimy wtedy o kapitalizacji rocznej, p´

o lrocznej, kwartal-

nej, miesi¸ecznej czy dziennej (ta ostatnia nosi nazw¸e ON – ang overnight).

Przypu´s´cmy, ˙ze stopa oprocentowania jest sta la i wynosi r w skali roku. Przy

kapitalizacji rocznej po roku mamy X(1) = X(1 + r) (tak jak przy kapitalizacji
prostej). Po 2 latach nasze oszcz¸edno´sci wynios¸a 1 + r razy suma oszcz¸edno´sci
po 1 roku, czyli X(2) = X(1 + r)

2

, Og´

olniej, sum¸e oszcz¸edno´sci po T latach

obliczamy stosuj¸ac T -krotnie powy˙zsz¸a regu l¸e, co daje wz´

or

X

(T ) = X(1 + r)

T

.

(2.3)

Rozwa˙zmy sytuacj¸e, w kt´

orej odsetki s¸a dopisywane co p´

o l roku, a roczna

stopa procentowa jest bez zmian, co oznacza ˙ze w okresie p´

o lrocznym oprocen-

towanie wynosi

r
2

. Suma oszcz¸edno´sci po 6 miesiacach wyniesie X(1 +

r
2

), a po

roku X(1 +

r
2

)

2

. Og´

olnie, po k okresach p´

o lrocznych mamy

X

1 +

r
2

k

,

a po T latach,

X

(T ) = X

1 +

r
2

2T

.

2. Stopy Procentowe

9

Por´

ownajmy oszcz¸edno´sci po roku uzyskane obydwoma metodami: mamy

nier´

owno´s´c

X

(1 + r) < X(1 +

r
2

)

2

kt´

ora wynika z oczywistej nier´

owno´sci

1 + r < 1 + 2 ·

r
2

+

r

2

4

.

Zatem, zgodnie z intuicj¸a, kapitalizacja p´

o lroczna jest korzystniejsza od rocznej.

Og´

olnie, je´sli podzielimy rok na m r´

ownych okres´

ow i stosujemy kapitali-

zacj¸e m krotn¸a (dopisanie odsetek co

1

m

cz¸e´s´c roku), to po k okresach mamy

sum¸e oszcz¸edno´sci

X

1 +

r

m

k

,

a po czasie T mierzonym w latach

X

(T ) = X

1 +

r

m

T m

(2.4)

(T lat to T · m okres´

ow), gdzie T mo˙ze by´c liczb¸a rzeczywist¸a. Czynnik wzrostu

przybiera posta´c

GF

= (1 +

r

m

)

T m

.

Powy˙zsze metody kapitalizacji daj¸a nam nast¸epuj¸ace wzory na warto´s´c

dzisiejsz¸a sumy Y znanej w chwili T : przy oprocentowaniu rocznym na n lat
mamy wz´

or

X

= Y (1 + r)

−

n

,

(2.5)

a og´

olniej przy kapitalizacji m-okresowej mamy

X

= Y

1 +

r

m

−

T m

.

(2.6)

2.1.3 Renty

Renta wieczysta (ang. perpetuity) to niesko´

nczony ci¸ag kwot o tej samej

wysoko´sci C, wyp lacanych ze sta lym odst¸epem czasowym, na koniec kole-
jnych okres´

ow. Przypu´s´cmy, ˙ze odst¸ep mi¸edzy p latno´sciami wynosi jeden rok,

Warto´s´c dzisiejsza takiej renty wynosi (zak ladaj¸ac sta l¸a stop¸e z kapitalizacj¸a
roczn¸a)

∞

X

n

=1

C

(1 + r)

n

=

C

r

gdzie zastosowali´smy wz´

or na sum¸e szeregu geometrycznego o pierwszym wyra-

zie a

1

=

C

1+r

i ilorazie q =

1

1+r

.

10

Wst¸ep do matematyki finansowej

Je´sli mamy tylko sko´

nczon¸a liczb¸e p latno´sci to m´

owimy o rencie okresowej

(ang. annuity). Przy N p latno´sciach, warto´s´c dzisiejsza mo˙ze by´c obliczona
jako r´

o˙znica renty okresowej i przesuni¸etej w czasie o N lat identycznej renty

okresowej:

C

r

−

C

r

1

(1 + r)

N

= C × P A(r, N )

gdzie

P A

(r, N ) =

1
r

−

1
r

1

(1 + r)

N

nosi nazw¸e czynnika renty okresowej. Ten sam wz´

or mo˙zna uzyska´c obliczaj¸ac

sum¸e N wyraz´

ow szeregu geometrycznego. W przypadku gdy p latno´sci nast¸e-

puj¸a na pocz¸atku ka˙zdego okresu, warto´s´c dzisiejsza ro´snie o czynnik 1+r, gdy˙z
tak wzro´snie warto´s´c dzisiejsza ka˙zdego sk ladnika i mamy (1+r)×C×P A(r, N ).

Je´sli okres pomi¸edzy p latno´sciami jest inny ni˙z rok, to trzeba do dyskoton-

wania zastosowa´c stop¸e procentow¸a o odpowiedniej kapitalizacji dostosowan¸a
do d lugo´sci okresu.

Przyk lad 2.1

Przypu´s´cmy, ˙ze po˙zyczamy z banku kwot¸e 50.000 na 5 lat, stopa 12% z akpi-
talizacja miesi¸eczn¸a. Wtedy P A(60, 1%) = 44, 955 i przy sp latach w r´

ownych

ratach, musimy p laci´c miesi¸ecznie C = 1112, 22. Sp laty te obejmuj¸a odsetki i
raty kapita lowe.

2.2 Kapitalizacja ci¸

ag la

Rozwa˙zmy sytuacj¸e, w kt´

orej odsetki s¸a dopisywane m-krotnie w ci¸agu roku i

przekszta l´cmy wz´

or na warto´s´c lokaty po czasie t:

X

(t) = X

1 +

r

m

tm

= X

1 +

r

m

m

r

tr

.

Zauwa˙zmy, ˙ze wyra˙zenie (1 +

r

m

)

m

r

nie zale˙zy od okresu oszcz¸edzania, a jedynie

od cz¸esto´sci dopisywania odsetek.

Przechodz¸ac do granicy z m, m → ∞, i korzystaj¸ac z definicji liczby e mamy

X

(t) = Xe

tr

.

(2.7)

Jest to sytuacja kapitalizacji ci¸

ag lej

, kt´

ora jest matematyczn¸a idealizacj¸a

cz¸estej kapitalizacji. Uzyskany wz´

or jest do´s´c dobrym przybli˙zeniem rzeczy-

wisto´sci, a jest przy tym znacznie prostszy i latwiejszy do przekszta lcania ni˙z
wzory zwi¸azane z wielokrotn¸a kapitalizacj¸a z lo˙zon¸a.

2. Stopy Procentowe

11

Zauwa˙zmy, ˙ze pochodna funkcji X(t) = Xe

tr

wynosi rXe

tr

= rX(t), wi¸ec

spe lnione jest r´

ownanie

d

dt

X

(t) = r · X(t)

(2.8)

z warunkiem X(0) = X.

Podamy inne wyprowadzenie r´

owno´sci (2.7), (2.8), aby pokaza´c jak r´

o˙zne

podej´scia si¸e zaz¸ebiaj¸a. Ustalamy t > 0 i obliczamy warto´s´c oszcz¸edno´sci w
chwili t + h maj¸ac dane X(t) i u˙zywaj¸ac wzoru (2.1) dla kapitalizacji prostej,
co jest uzasadnione tym, ˙ze mamy na my´sli kr´

otki okres czasu h:

X

(t + h) = X(t)(1 + hr).

St¸ad po prostych przekszta lceniach dostajemy

X

(t + h) − X(t)

h

= rX(t).

Gdy h zmierza do 0, to wtedy iloraz r´

o˙znicowy z lewej strony zmierza do

pochodnej funkcji X(·) w punkcie t co daje (2.8). Jak latwo sprawdzi´c, funkcja
dana wzorem (2.7) spe lnia to r´

ownanie.

Przy kapitalizacji ci¸ag lej wz´

or na dzisiejsz¸a warto´s´c sumy Y danej w chwili

T

ma posta´c

X

= Y e

−

rT

.

(2.9)

B¸edziemy potrzebowa´c odpowiedzi na og´

olniejsze pytanie: ile wynosi warto´s´c

w chwili t < T sumy Y danej w chwili T . Wtedy mamy do czynienia z okre-
sem oszcz¸edzania d lugo´sci T − t, wi¸ec suma X(t) ulokowana w chwili t przy
kapitalizacji ci¸ag lej daje w chwili T (po czasie T − t) wielko´s´c

X

(T ) = X(t)e

r

(T −t)

.

St¸ad bior¸ac X(T ) = Y i wyliczaj¸ac X(t) uzyskujemy odpowied´z na nasze
pytanie:

X

(t) = Y e

−

r

(T −t)

.

(2.10)

Podajemy wz´

or tylko dla kapitalizacji ci¸ag lej, gdy˙z tylko dla niej b¸edziemy on

nam potrzebny. Niemniej mo˙zna r´

ownie latwo poda´c stosowny wz´

or przy innych

sposobach kapitalizacji.

12

Wst¸ep do matematyki finansowej

2.3 Stopy r´

ownowa ˙zne

Z powy˙zszych rozwa˙za´

n wynika, ˙ze cz¸estsza kapitalizacja jest korzystniejsza

przy danej stopie procentowej. Nasuwa si¸e naturalne przyk ladowe pytanie: co
lepsze, stopa 8% z kapitalizacj¸a miesi¸eczn¸a czy 7, 8% z kwartaln¸a? Lub, co na
jedno wychodzi, jaka jest wysoko´s´c stopy z kapitalizacj¸a kwartaln¸a kt´

ora daje

to samo co 8% z kapitalizacj¸a miesi¸eczn¸a? Aby m´

oc przeprowadzic pr´

ownanie

musimy si¸e donie´sc do wsp´

olnego okresu czasu. Naturalnym jest okres jednego

roku. M´

owimy, ˙ze stopy procentowe i zwi¸azane z nimi metody kapitalizacji

s¸a r´

ownowa˙zne, je´sli czyniki wzrostu za rok s¸a takie same. Czyli stopa r

m

odpowiadaj¸ac¸a kapitalizacji m-krotnej jest r´

ownowa˙zna stopie r

n

z kapitalizacj¸a

n

-krotn¸a je´sli

(1 +

r

m

m

)

m

= (1 +

r

n

n

)

n

.

M´

owimy, ˙ze stopa r

e

jest efektywna (dla danej stopy r

m

) jesli jest ona stop¸a

dla kapitalizacji rocznej r´

ownowa˙zn¸a r

m

:

1 + r

e

= (1 +

r

m

m

)

m

.

2.4 Struktura czasowa st´

op procentowych

Przez jednostkow¸a obligacj¸

e zero-kuponow¸

a

(ang. zero-coupon bond ) z

wykupem w chwili T rozumiemy zobowi¸azanie wystawione w chwili 0 przez
pewn¸a instytucj¸e (np. rz¸ad lub firm¸e), kt´

ora zobowi¸azuje si¸e wyp laci´c posi-

adaczowi obligacji jej warto´s´c nominaln¸a, czyli dla obligacji jednostkowej kwot¸e
1 z l, w chwili T (przyjmujemy umown¸a kwot¸e; w praktyce warto´s´c nominalna,
ang. face value, jest znacznie wy˙zsza). Cena obligacji zmienia si¸e w czasie i
jest dyktowana przez rynek. Oznaczmy przez B(t, T ) cen¸e obligacji w chwili t,
0 ≤ t ≤ T . Oczywi´scie, B(T, T ) = 1.

Je´sli znamy stop¸e oprocentowania, to przy ustalonym sposobie kapital-

izacji mo˙zemy obliczy´c cen¸e obligacji. Podstaw¸a jest fakt wynikaj¸acy z reg-
ulacji prawnych, ˙ze ryzyko obligacji jest bardzo ma le. Firma musi spe lni´c
zobowi¸azania wynikaj¸ace z wystawienia obligacji w pierwszej kolejno´sci gdy˙z
w przypadku ich niespe lnienia firmie grozi bankructwo. Na og´

o l inwestycja w

obligacje jest alternatyw¸a dla lokaty bankowej.

Przyjmijmy kapitalizacj¸e ci¸ag l¸a ze stop¸a procentow¸a r. Wtedy dla obliczenia

B

(0, T ) musimy obliczy´c warto´s´c dzisiejsz¸a sumy Y = 1 danej w chwili T , czyli

ze wzoru (2.9) mamy

B

(0, T ) = e

−

rT

,

2. Stopy Procentowe

13

a og´

olniej wz´

or (2.10) daje

B

(t, T ) = e

−

r

(T −t)

.

Analogiczne wzory mo˙zna poda´c dla innych rodzaj´

ow kapitalizacji.

W praktyce sytuacja jest odwrotna: mamy dane ceny obligacji i one wyz-

naczaj¸a stopy procentowe przy r´

o˙znych sposobach kapitalizacji. Oznacza to, ˙ze

stopa procentowa jest w istocie poj¸eciem wt´

ornym do ceny obligacji. Jest to

r´

ownie˙z poj¸ecie wzgl¸edne, gdy˙z wysoko´s´c stopy procentowej zale˙zy od d lugo´sci

okresu.

Cena rynkowa B(0, T ) wyznacza wysoko´s´c stopy procentowej r poprzez

rozwi¸azanie r´

ownania, w kt´

orym kapita l B(0, T ) daje po okresie T warto´s´c

1 przy zastosowaniu r´

o˙znych metod kapitalizacji ze stop¸a procentow¸a r.

Przy kapitalizacji prostej, tzw. stopa prosta rs

T

(ang. simple rate) jest

wyznaczona przez r´

ownanie

B

(0, T )(1 + rs

T

· T ) = 1.

Przy kapitalizacji z lo˙zonej m krotnej w ci¸agu roku mamy stop¸

e z lo ˙zon¸

a

rc

m,T

(ang. compound rate) wyznaczon¸a przez r´

ownanie

B

(0, T )(1 + r

m,T

1

m

)

T m

= 1.

Dla kapitalizacji ci¸ag lej stopa procentowa ci¸

ag la

r

T

(ang. continuous rate)

jest dana przez zale˙zno´s´c

B

(0, T )e

T r

T

= 1,

(2.11)

czyli

r

T

= −

1

T

log B(0, T ).

Zauwa˙zmy, ˙ze je´sli warto´s´c obligacji wzrasta, to stopa procentowa maleje,

a je´sli warto´s´c obligacji maleje, to stopa ro´snie, przy ka˙zdym sposobie kapital-
izacji.

Zauwa˙zmy, jak przy pomocy cen obligacji jednostkowych mo˙zemy zapisa´c

wz´

or na warto´s´c inwestycji w okresie d lugo´sci T . Poniewa˙z z powy˙zszych

wzor´

ow mamy

B

(0, T )

−

1

= (1 + rs

T

· T )

B

(0, T )

−

1

= (1 + r

m,T

1

m

)

T m

B

(0, T )

−

1

= e

r

T

T

14

Wst¸ep do matematyki finansowej

to wzory (2.1), (2.4), (2.7) gdzie przez r rozumiemy odpowiednio rs

T

, rc

T

, r

T

,

mo˙zemy jednolicie zapisa´c

X

(T ) = X · B(0, T )

−

1

,

natomiast zdyskontowana warto´s´c sumy Y jest dana wzorem

X

= Y · B(0, T ).

Og´

olniej, warto´sci w chwilach t i T s¸a zwi¸azane wzorem

X

(t) = X(T )B(t, T ).

Te wzory maj¸a pewne zalety. Po pierwsze, s¸a uniwersalne, tzn. jeden wz´

or

zast¸epuje kilka wyprowadzonych wcze´sniej, przy czym r´

o˙zne metody kapital-

izacji odpowiadaj¸a r´

o˙znym typom st´

op procentowych generowanych przez obli-

gacje. Ponadto, obejmuj¸a one przypadek, gdy stopy procentowe s¸a zale˙zne od
czasu, a nawet losowe.

2.5 Rynek pieni¸

e ˙zny

Lokata w walory bez ryzyka mo˙ze by´c wygodnie opisana poprzez wprowadze-
nie tak zwanego rachunku rynku pieni¸e˙znego (ang. money market account).
Oznaczmy przez A(0) kwot¸e pocz¸atkow¸a ulokowan¸a na rachunku bankowym ze
stop¸a r przy kapitalizcji ci¸ag lej. Wtedy w chwili t ta lokata ma warto´sc

A

(t) = A(0)e

rt

przy za lo˙zeniu o sta lej stopie procentowej. W praktyce taka lokata b¸edzie reali-
zowana przez depozyt na jeden dzie´

n (ON) i po czasie t, b¸ed¸acym wielokrotno´s-

ci¸a jednego dnia czyli t = n

1

365

,

mamy A(n) = (1 +

r

365

)

n

(piszemy dla wygody

A

(n) = A(t)). Je´sli dopu´scimy stop¸e zmienn¸a w czasie to A(1) = A(0)(1 + r

0

),

A

(2) = A(1)(1 + r

1

), itd. gdzie r

n

to stopa obowi¸azuj¸aca w danym dniu,

podzielona ju˙z przez 365 (kapitalizacja dzienna). Indukcyjnie

A

(n + 1) = A(n)(1 + r

n

)

(stopa r

n

jest znana w dniu n dla lokaty ko´

ncz¸acej si¸e w dniu nastepnym).

Przy za lo˙zeiu o sta lej stopie procentowej rachunek ten mo˙zna zrealizowa´c

poprzez inwestycje w obligacje. Kupujemy

A

(0)

B

(0,T )

obligacji i w chwili t mamy

warto´s´c inwestycji tak¸a sam¸a jak powy˙zej

A

(0)

B

(0, T )

B

(t, T ) =

A

(0)

e

−

rT

e

−

r

(T −t)

= A(0)e

rt

.

2. Stopy Procentowe

15

Analiza kapitalizacji dyskretnej prowadzi do skomplikowanych wzor´

ow. Po-

przestaniemy na prostym przyk ladzie, kt´

ory zilustruje r´

o˙znice mi¸edzy inwest-

ycj¸a w obligacje i rachunek pieni¸e˙zny przy zmiennych stopach.

Przyk lad.

Przypu´s´cmy, ˙ze stopa wynosi 10% i nie zmienia si¸e przez dwa

lata (kapitalizacja roczna). Lokuj¸ac A(0) = 100 mamy A(1) = 110, A(2) = 121;
co rok mamy wzrost warto´sci o 10%. Obligacje o warto´sci nominalnej B(2, 2) =
100 maj¸a ceny

B

(0, 2) =

100

1, 1

2

= 82, 64

B

(1, 2) =

100
1, 1

= 90, 91

czyli r´

ownie˙z mamy wzrost o 10% w ka˙zdym roku.

Przypu´scmy, ˙ze w drugim roku stopa spada do 5%. Wtedy A(1) = 110 jak

poprzednio, ale A(2) = 115, 50. Wzrost warto´sci przez dwa lata wynosi 15,5%.
Przechodz¸ac do obligacji mamy B(0, 2) = 82, 64 jak poprzednio, gdy˙z w chwili
zero nie wiemy ˙ze stopy spadn¸a i dyskontujemy warto´s´c nominaln¸a stop¸a znan¸a
w chwili 0. Natomiast

B

(1, 2) =

100

1, 05

= 95, 24

co daje wzrost warto´sci w pierwszym roku o 15,24%, a w drugim oczywi´scie o
5%. Przez dwa lata mamy czynnik wzrostu (1 + 15, 25%)(1 + 5%) = 1, 21 taki
jak poprzednio. Dla inwestora korzystna jest sprzeda˙z obligacji po pierwszym
roku w por´

ownaniu z tym co mo˙ze uzyska´c posiadacz rachunku pieni¸e˙znego.

Przypu´s´cmy wreszcie, ˙ze w drugim roku stopa wzrasta do 15%. Wtedy

A

(2) = 110(1 + 15%) = 126, 50 i mamy wzrost 26,5% przez dwa lata. Przy

inwestycji w obligacje wzrost przez dwa lata nadal bedzie taki sam jak w
poprzednich przypadkach, gdy˙z cena pocz¸atkowa jest taka sama oraz warto´sc
ko´

ncowa (100) jest ustalona przy emisji obligacji. Inwestor, kt´

ory zdecydowa lby

si¸e sprzeda´c obligacj¸e po pierwszym roku uzyska mniej ni˙z posiadacz rachunku
pieni¸e˙znego, gdy˙z dostanie tyko

B

(1, 2) =

100

1, 15

= 86, 96.

Wzrost w pierwszym roku wynosi 5,22%, w drugim 15%, a ca lkowity, jak ju˙z
zauwa˙zylismy, 21%.

3

Instrumenty pochodne

Najpierw om´

owimy kontrakt terminowy typu forward.

3.1 Kontrakt terminowy

Kontrakt terminowy jest wi¸a˙z¸ac¸a umow¸a zawart¸a mi¸edzy dwiema stronami i
dotycz¸ac¸a sprzeda˙zy pewnego waloru (np. papieru warto´sciowego, zbo˙za, z lota)
za ustalon¸a w umowie cen¸e w okre´slonej chwili w przysz lo´sci. Umowa obejmuje
r´

ownie˙z warunki dostawy, w tym parametry towaru. Celem zawarcia kontraktu

jest uniezale˙znienie si¸e obu stron od przysz lych waha´

n cen.

Oznaczmy przez

• t - chwil¸e zawarcia kontraktu;

• T - przysz ly termin realizacji, T > t;

• f (t, T ) - cen¸e waloru ustalon¸a w chwili t, wed lug kt´

orej w chwili T kontrakt

zostanie zrealizowany; nazywamy j¸a przysz lo´sciow¸a cen¸a realizacji (ang. for-
ward price

),

• S(t) - rynkow¸a cen¸e waloru w chwili t.

Je´sli w chwili T cena rynkowa jest wy˙zsza od przysz lo´sciowej ceny realizacji,

S

(T ) > f (t, T ),

17

18

Wst¸ep do matematyki finansowej

to jest to sytuacja korzystna dla strony, kt´

ora zawar la kontrakt kupna (czyli

zaj¸e la d lug¸a pozycj¸e) — daje on mo˙zliwo´s´c kupna poni˙zej ceny rynkowej, a
niekorzystna dla tej, kt´

ora zawar la kontrakt sprzeda˙zy (czyli zaj¸e la kr´

otka

pozycj¸e) — lepiej by loby sprzeda´c towar na wolnym rynku za wy˙zsz¸a cen¸e.
Zysk z d lugiej pozycji wynosi S(T ) − f (t, T ).

W przypadku, gdy

S

(T ) < f (t, T ),

to jest to sytuacja korzystna dla sprzedaj¸acego, a niekorzystna dla kupuj¸acego.
D luga pozycja przynosi strat¸e f (t, T ) − S(T ). W obu przypadkach dla d lugiej
pozycji mamy t¸a sam¸a zale˙zno´s´c: zysk (strata to ujemny zysk) dany jest wzorem

g

(x) = x − f (t, T ),

gdzie x oznacza cen¸e rynkow¸a. Warto´s´c funkcji g(x) jest dodatnia w przypadku
zysku, a ujemna w przypadku straty. Liczba f (t, T ) jest ustalona w kontrakcie
i jedyn¸a wielko´sci¸a zmienn¸a jest x = S(T ).

Sytuacja jest odwrotna dla pozycji kr´

otkiej gdzie bilans wynosi −S(T ) +

f

(t, T ). Jest to liczba dodatnia (zysk), gdy S(T ) < f (t, T ), a w przeciwnym

przypadku jest to strata. Wynik finansowy pozycji kr´

otkiej dany jest wzorem

g

(x) = −x + f (t, T ).

Kontrakty bezpo´srednie s¸a obci¸a˙zone pewnym ryzykiem, ˙ze kt´

ora´s ze stron

go z lamie. W zwi¸azku z tym konieczne s¸a mechanizmy zabezpieczaj¸ace. Ich
rozw´

oj doprowadzi l do powstania tzw. kontrakt´

ow futures, gdzie ryzyko to jest

wyeliminowane przez system depozyt´

ow.

3.2 Opcje

Europejska opcja kupna

(ang. call option lub kr´

otko call ) to kontrakt daj¸acy

prawo do kupienia pewnego waloru w okre´slonej chwili T za okre´slon¸a cen¸e K.

Europejska opcja sprzeda ˙zy

(ang. put option, lub put) to kontrakt

daj¸acy prawo do sprzedania pewnego waloru w okre´slonej chwili T za okre´slon¸a
cen¸e K.

Opcja ameryka´

nska

, kupna lub sprzeda˙zy, daje powy˙zsze prawa w dowol-

nej chwili pomi¸edzy momentem zawarcia kontraktu, a chwil¸a T .

Zak ladamy, ˙ze opcja jest wystawiona w chwili dzisiejszej, kt´

or¸a umownie

przyjmujemy jako chwil¸e 0. Czyli T oznacza czas do chwili realizacji.

Przy pewnych typach opcji (opcje na indeks gie ldowy czy na stopy procen-

towe) walor jest fikcyjny i ”sprzedanie” czy ”kupienie” go oznacza rozliczenie

3. Instrumenty pochodne

19

w got´

owce r´

o˙znicy mi¸edzy faktycznym rynkowym notowaniem tego waloru, a

cen¸a realizacji opcji.

Kwota K nazywana jest cen¸

a realizacji

opcji (ang. strike price, exer-

cise price

), a T nazywane jest terminem realizacji opcji, dla opcji eu-

ropejskiej (ang. exercise date), lub terminem wyga´

sni¸

ecia

opcji, dla opcji

ameryka´

nskiej (ang. expiration date). Walor, na kt´

ory wystawiona jest opcja

nazywa´c b¸edziemy instrumentem bazowym (ang. underlying asset). Dla up-
roszczenia b¸edziemy u˙zywa´c cz¸esto s lowa akcja maj¸ac na my´sli dowolny walor.

Podobnie jak przy kontraktach terminowych rozr´

o˙zniamy pozycj¸e d lug¸a

(nabywca opcji) i kr´

otk¸a (wystawiaj¸acy i sprzedaj¸acy opcj¸e).

Odnotujmy, ˙ze na rynkach ´swiatowych dominuj¸a opcje ameryka´

nskie (ter-

miny europejska/ameryka´

nska nie maj¸a znaczenia geograficznego ani histo-

rycznego). Jeden z powod´

ow to fakt, ˙ze opcje europejskie s¸a bardziej nara˙zone

na manipulacj¸e w okresie bliskim daty ich wyga´sni¸ecia.

Og´

olnie, je´sli w chwili T cena rynkowa waloru S(T ) jest wi¸eksza od K,

to posiadaj¸acy opcj¸e kupna (zajmuj¸acy d lug¸a pozycj¸e) ma zysk w wysoko´sci
S

(T ) − K, gdy˙z opcja daje mu prawo zakupienia waloru za cen¸e K, natomiast

mo˙ze go sprzeda´c po cenie rynkowej wynosz¸acej S(T ) > K. W przeciwnym
przypadku, S(T ) < K, opcja jest bezwarto´sciowa i nie zostaje zrealizowana:
nie ma sensu kupowa´c po cenie wy˙zszej ni˙z rynkowa.

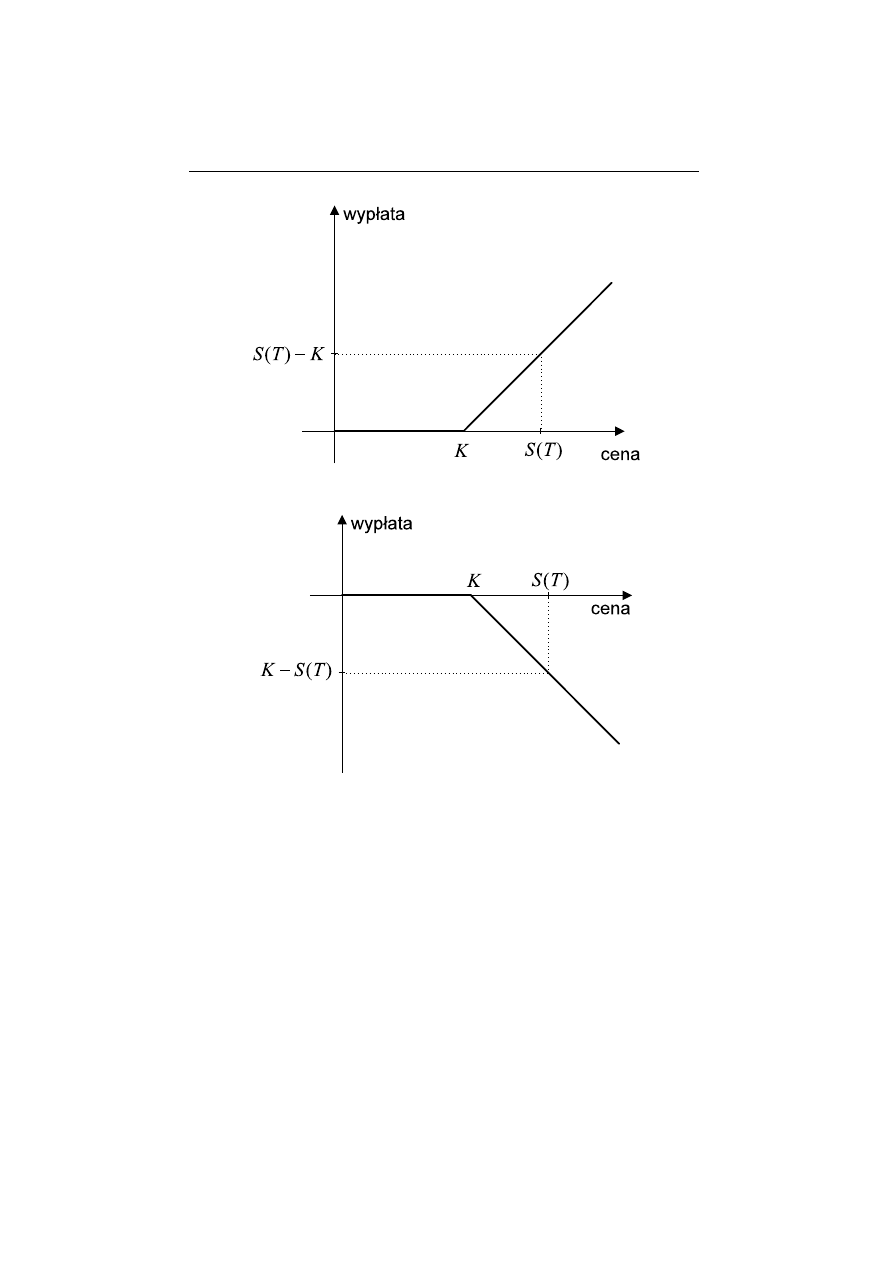
Opcja jest zdefiniowana poprzez jej funkcj¸e wyp laty. Dla d lugiej pozycji w

europejskiej opcji kupna wyp lata wynosi

S

(T ) − K

gdy S(T ) > K,

0

gdy S(T ) ≤ K.

Wyp lata ta jest zmienn¸a losow¸a, gdy˙z zale˙zy od ceny akcji w chwili T . Zilus-
trujmy t¸e zale˙zno´s´c na wykresie. Na osi x odk ladamy cen¸e S(T ), a na osi y
mamy wysoko´s´c wyp laty dla posiadacza opcji — Rysunek 3.1.

Wygodnie jest wprowadzi´c nast¸epuj¸ace oznaczenie:

x

+

=

x

gdy x > 0,

0

gdy x ≤ 0.

Nazywamy to cz¸e´sci¸a dodatni¸a liczby x. Wtedy mo˙zemy kr´

otko zapisa´c

wyp lata opcji kupna = (S(T ) − K)

+

.

Funkcj¸e x 7→ (x − K)

+

nazywamy funkcj¸

a wyp laty

opcji. Wyp lata wynosi

wi¸ec f (S(T )), gdzie f (x) = (x − K)

+

.

Wyp lata dla tego kto wystawi l opcj¸e (zaj¸a l kr´

otk¸a pozycj¸e) jest oczywi´scie

liczb¸a przeciwn¸a: −f (S(T )); ilustrujemy to na Rysunku 3.2.

Ameryka´

nska opcja kupna przynosi korzy´s´c, je´sli cho´c w jednej chwili t ≤ T

mamy S(t) − K > 0. M´

owimy wi¸ec o wyp lacie w chwili t, kt´

ora jest dana

20

Wst¸ep do matematyki finansowej

Rysunek 3.1

Rysunek 3.2

wzorem (S(t) − K)

+

, a na Rysunkach 3.1, 3.2 musimy zamieni´c T na t. Opcja

zostanie zrealizowana, gdy cho´c w jednym momencie wyp lata ta b¸edzie wi¸eksza
od zera. Teoretyczny maksymalny zysk posiadacza ameryka´

nskiej opcji kupna

wynosi

max

0≤τ ≤T

(S(τ ) − K)

+

,

a problem polega na tym, ˙ze nie wiadomo kiedy to maksimum b¸edzie osi¸agni¸ete.
Poniewa˙z zmiany cen akcji s¸a losowe, moment ten jest zmienn¸a losow¸a.

Og´

olnie, europejska opcja sprzeda˙zy posiada warto´s´c w chwili realizacji, gdy

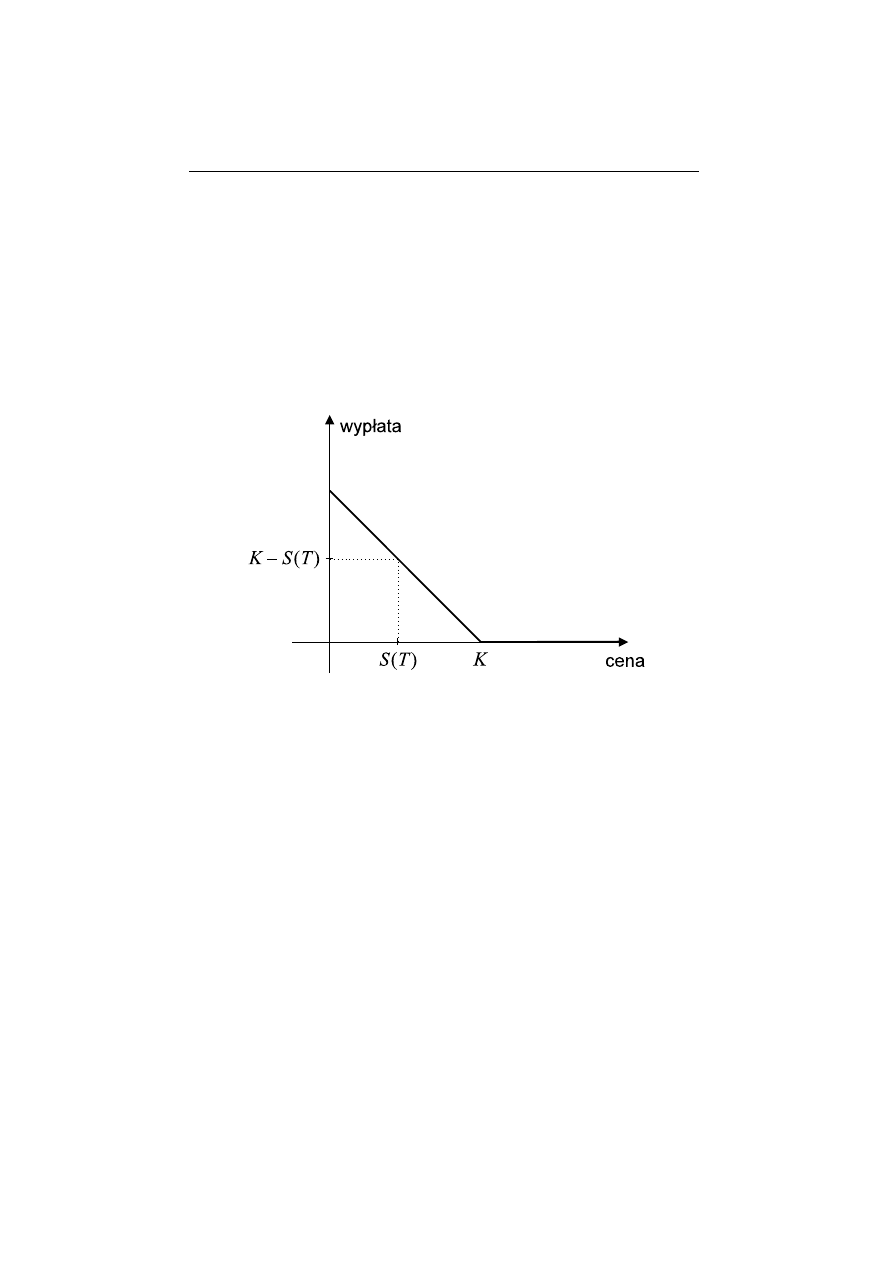
3. Instrumenty pochodne

21

cena rynkowa waloru w chwili T jest ni˙zsza ni˙z cena K gwarantowana przez
opcj¸e: S(T ) < K. Mo˙zemy sprzeda´c walor za K i odkupi´c go za S(T ), czyli zysk
wynosi K − S(T ) > 0. Gdy S(T ) ≥ K to opcja sprzeda˙zy jest bezwarto´sciowa,
czyli zysk wynosi 0. Mamy wi¸ec wyp lat¸e w wysoko´sci

K

− S(T ) gdy S(T ) < K

0

gdy S(T ) ≥ K

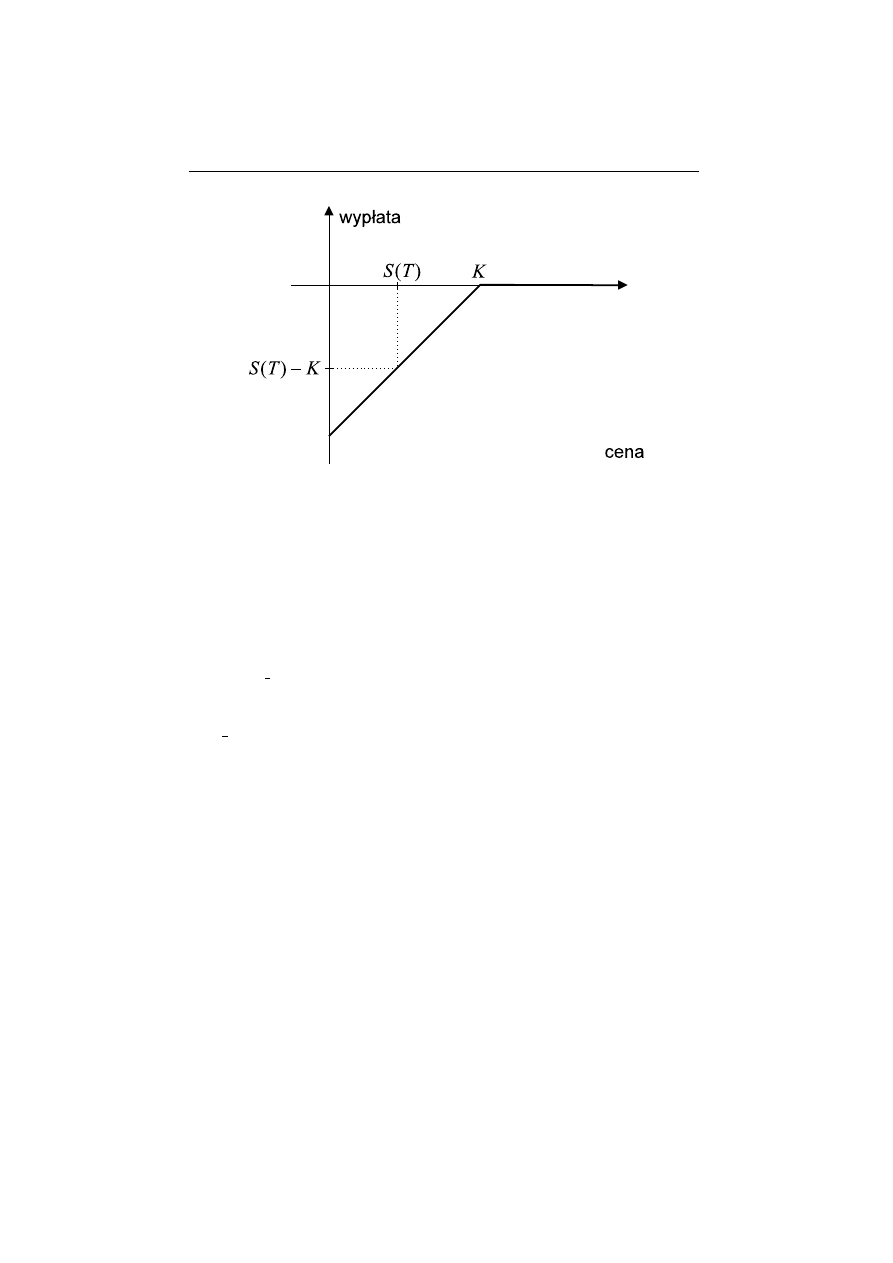
Wyp lat¸e dla d lugiej pozycji w europejskiej opcji sprzeda˙zy mo˙zemy kr´

otko

zapisa´c jako (K − S(T ))

+

, a jej wykres jako funkcji ceny S(T ) przedstawia

Rysunek 3.3.

Rysunek 3.3

Dla wystawiaj¸acego mamy liczb¸e przeciwn¸a: −(K − S(T ))

+

, a wykres na

Rysunku 3.4.

Dla posiadacza ameryka´

nskiej opcji sprzeda˙zy mamy wyp lat¸e w chwili t

dan¸a wzorem (K − S(t))

+

(dla wystawiaj¸acego mamy liczb¸e przeciwn¸a), a na

wykresach musimy zamieni´c T na t.

Poniewa˙z opcje daj¸a prawo do pewnych dzia la´

n, a nie nak ladaj¸a ˙zadnych

zobowi¸aza´

n, s¸a one korzystne dla tego kto je posiada. Strona wystawiaj¸aca

opcj¸e pobiera wi¸ec za to pewn¸a op lat¸e, tzw. premi¸

e

.

Zasygnalizujmy dwa fundamentalne problemy: ustalenie wysoko´sci tej op laty

i opracowanie strategii dla wystawiaj¸acego opcj¸e, kt´

ora umo˙zliwi mu zabez-

pieczenie si¸e przez strat¸a. Strategi¸e tak¸a nazywamy os lon¸

a

(ang. hedging).

Teraz zak ladamy, ˙ze cena opcji jest znana i wynosi C

e

dla europejskiej opcji

kupna i P

e

dla europejskiej opcji sprzeda˙zy.

22

Wst¸ep do matematyki finansowej

Rysunek 3.4

Przyk lad 3.1

Akcje Rolls-Royce’a w dniu 22 marca 1997 by ly notowane na gie ldzie londy´

n-

skiej po 233 pensy za sztuk¸e. Na londy´

nskiej gie ldzie opcji (LIFFE - London

International Financial Futures Exchange) notowano opcje o cenie realizacji
220 i 240 z terminem realizacji maj, lipiec i pa´zdziernik. Cena opcji kupna
z cen¸a realizacji 220 wynosi la 19,5 pensa. Je´sli stopa procentowa r´

owna jest

5% w skali roku (przy kapitalizacji ci¸ag lej), to 19,5 pensa dzi´s ma warto´s´c
19, 5 · e

0,05·

1
6

= 19, 663 za 2 miesi¸ace , czyli graniczn¸a warto´sci¸a ceny akcji

powy˙zej kt´

orej posiadacz opcji ma korzy´s´c jest 220 + 19, 663 = 239, 663

Opcja sprzeda˙zy o tych samych danych kosztowa la 5,5 pensa, co daje 5, 5 ·

e

0,05·

1
6

= 5, 546 i przy cenie akcji cenie poni˙zej 214,454 posiadacz opcji kupna

wyjdzie na zero: kupi akcj¸e za 214,454 i sprzeda j¸a za 220 realizj¸ac opcj¸e, a zysk
wyr´

owna op lat¸e za opcj¸e.

Zmodyfikujemy powy˙zsze wzory na wyp lat¸e i odpowiadaj¸ace im wykresy.

Za l´

o˙zmy, ˙ze stopa procentowa jest sta la w okresie [0, T ], wynosi r i rozwa˙zmy

kapitalizacj¸e ci¸ag l¸a. Oznaczmy

C

= C

e

· e

rT

,

P

= P

e

· e

rT

.

Rozpatrujemy najpierw sytuacj¸e z punktu widzenia nabywcy opcji. Poniewa˙z
zap laci l on cen¸e opcji, musimy odj¸a´c od funkcji wyp laty opcji liczb¸e C (lub P ),
czyli warto´s´c w chwili T ceny zap laconej dzi´s. To co zostaje po odj¸eciu mo˙zemy
nazwa´c zyskiem (lub strat¸a, je´sli jest to liczba ujemna) i oznaczamy go przez
G

b

C

e

, G

b

P

e

.

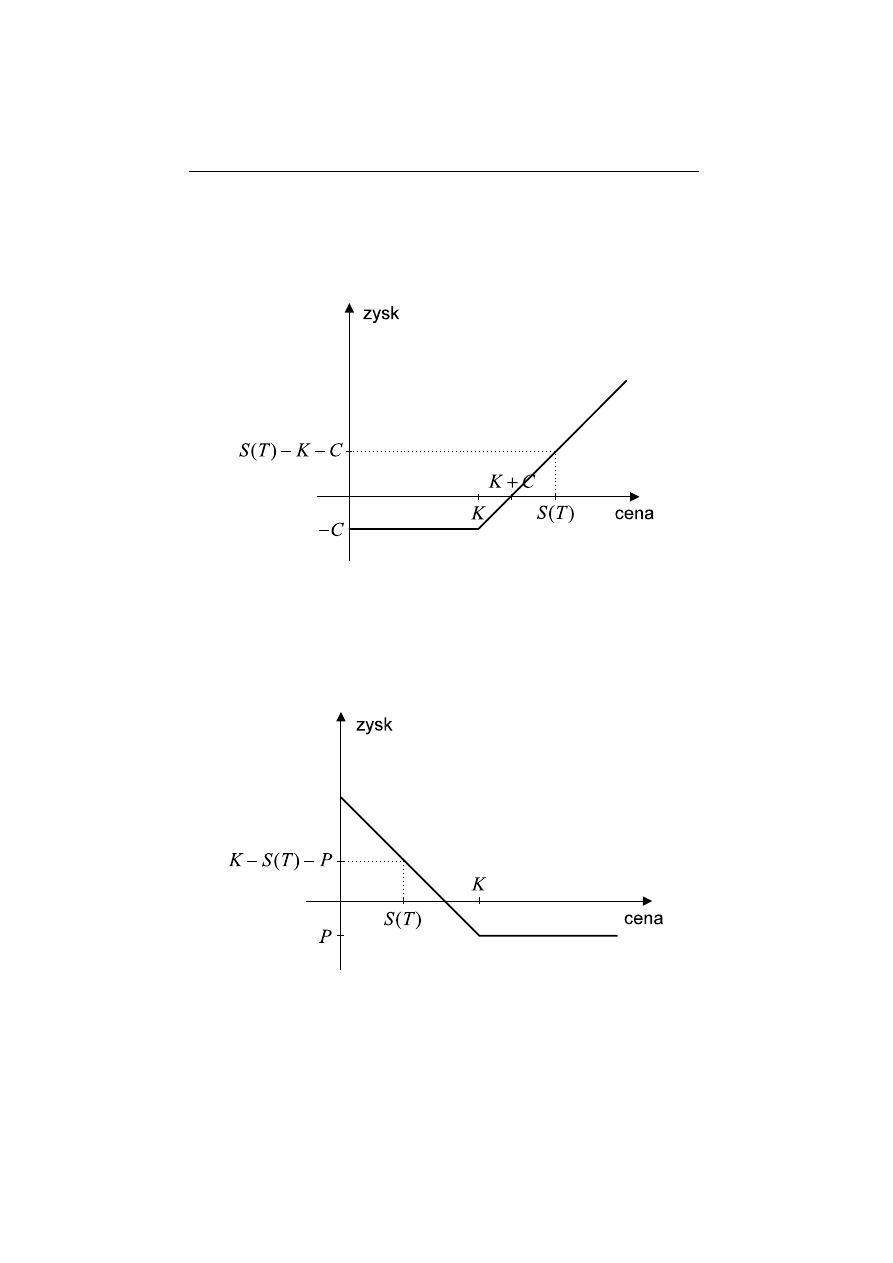
3. Instrumenty pochodne

23

Dla nabywcy opcji kupna mamy wi¸ec zysk— Rysunek 3.5 —

G

b

C

e

=

S

(T ) − K − C

gdy S(T ) > K

−C

gdy S(T ) ≤ K

Rysunek 3.5

Zysk nabywcy opcji sprzeda˙zy wynosi — Rysunek 3.6 —

G

b

P

e

=

K

− S(T ) − P

gdy S(T ) < K

−P

gdy S(T ) ≥ K

Rysunek 3.6

24

Wst¸ep do matematyki finansowej

Wida´c, ˙ze posiadacz opcji ma zysk dopiero gdy cena waloru przekracza

warto´s´c K + C dla opcji kupna lub spada poni˙zej K − P dla opcji sprzeda˙zy.
Z punktu widzenia wystawiaj¸acego opcj¸e trzeba zmieni´c znaki wyp lat na prze-
ciwne a wykresy odbi´c symetrycznie wzgl¸edem osi cen.

4

Wycena Opcji - Model Dwumianowy

4.1 Model jednoetapowy

Rozwa˙zamy najpierw bardzo uproszczony model, w kt´

orym mamy do czynienia

z czasem przyjmuj¸acym dwie warto´sci 0 i 1, cena akcji w chwili 0 wynosi S(0),
a w chwili 1 ulega ona zmianie przyjmuj¸ac losowo jedn¸a z dw´

och mo˙zliwych

warto´sci. Jednostka czasowa jest ca lkowicie umowna. Rachunkowo wygodnie
jest za lo˙zy´c, ˙ze jest to jeden rok. Niemniej, nie ma ˙zadnych przeszk´

od aby

rozwa˙zy´c bardzo kr´

otki odcinek czasowy. Wtedy naturalne jest przyj¸a´c, ˙ze ruch

cen jest zgodny z minimalnym krokiem o jakie ceny mog¸a si¸e zmienia´c na
gie ldzie (ang. tick ).

Aby model by l kompletny, powinni´smy sprecyzowa´c przestrze´

n probabili-

styczn¸a. W sytuacji, gdzie mamy tylko dwie mo˙zliwo´sci, jak przy rzucie monet¸a,
mo˙zemy wybra´c Ω = {ω

1

, ω

2

}. Prawdopodobie´

nstwo P jest wyznaczone przez

jedn¸a liczb¸e p: P = ({ω

1

}) = p, P ({ω

2

}) = 1 − p. Przyjmujemy, ˙ze

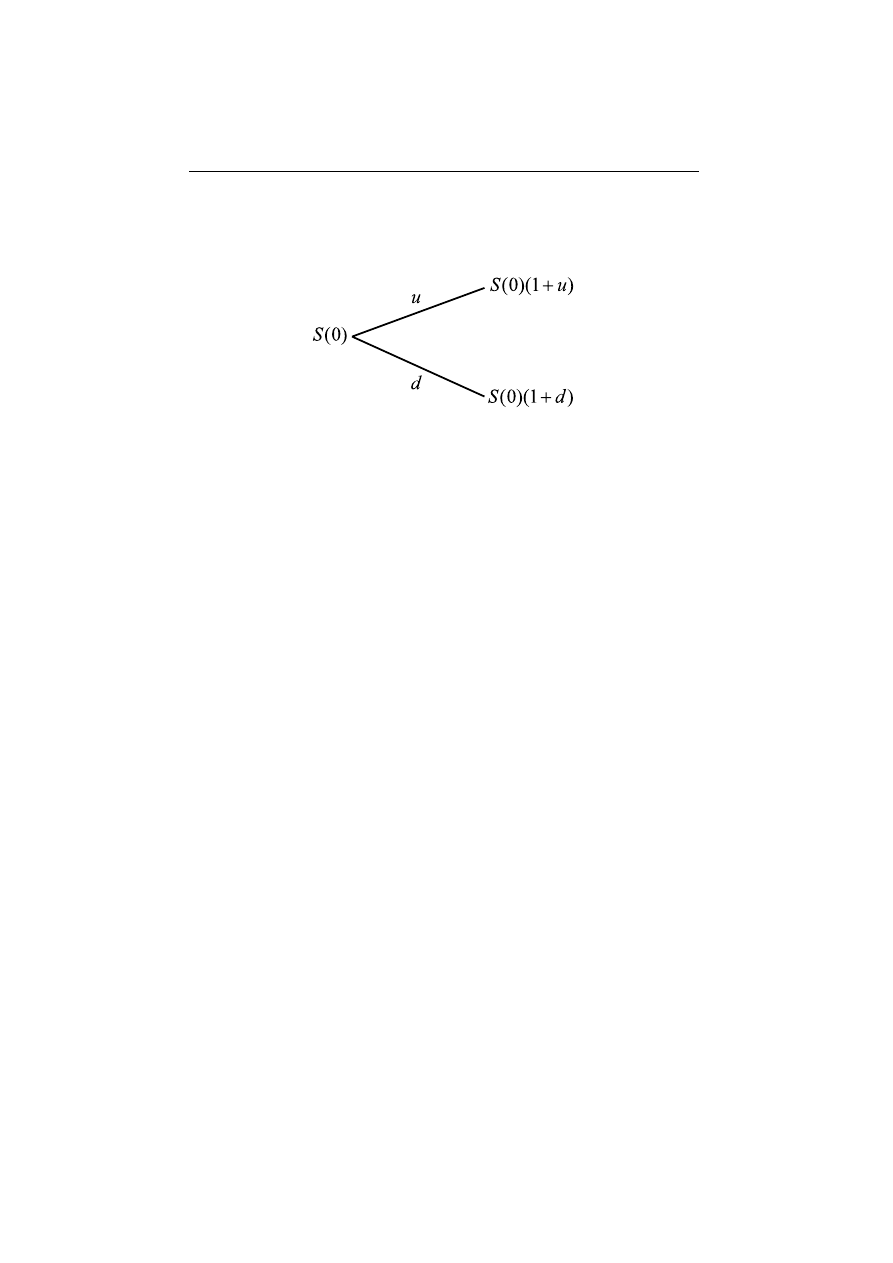
S

(1) =

S

u

(1) = S(0)(1 + u) z prawdopodobie´

nstwem p,

S

d

(1) = S(0)(1 + d)

z prawdopodobie´

nstwem 1 − p,

przy czym zak ladamy, ˙ze −1 < d < u, a p jest liczb¸a z przedzia lu (0, 1) (wyk-
luczamy p = 0 i p = 1).

Wsp´

o lczynniki d, u mierz¸a wzgl¸edn¸a zmian¸e cen akcji: u > 0 oznacza wy˙zszy

poziom ceny (up), a d < 0 — ni˙zszy (down): S

u

(1) > S

d

(1). Mimo, ˙ze Ry-

sunek 4.1 sugeruje wzrost ceny w jednym przypadku, a spadek w drugim, niem-
niej trzeba podkre´sli´c, ˙ze nie robimy takiego za lo˙zenia. Obie liczby d, u mog¸a

25

26

Wst¸ep do matematyki finansowej

by´c dodatnie, co oznacza wzrost S(1) w stosunku do S(0). Dok ladniej, S(1) jest
funkcj¸a okre´slon¸a na zbiorze Ω przyjmuj¸ac¸a warto´sci S(1)[ω

1

] = S(0)(1 + u),

S

(1)[ω

2

] = S(0)(1 + d).

Rysunek 4.1

Przypomnijmy, ˙ze inwestycja w rynek pieni¸e˙zny jest szczeg´

olnym przypad-

kiem waloru ryzykownego gdzie u = d = r, czyli mamy tak¸a sam¸a warto´s´c w
chwili 1 w obu scenariuszach, A(1) = A(0)(1 + r).

4.1.1 Portfele inwestycyjne

Przypu´s´cmy, ˙ze na pocz¸atku dysponujemy pewnym kapita lem V (0), kt´

ory in-

westujemy wybieraj¸ac portfel, czyli par¸e liczb (x, y), gdzie x oznacza liczb¸e jed-
nostek waloru ryzykownego S, a y liczb¸e jednostek rachunku rynku pieni¸e˙znego
A.

Obie te liczby mog¸a przyjmowa´c dowolne warto´sci rzeczywiste zgodnie z

za lo˙zeniem o podzielno´sci walor´

ow i dopuszczalno´sci kr´

otkich pozycji. Mamy

wi¸ec zwi¸azek

V

(x,y)

(0) = xS(0) + yA(0)

Warto´s´c naszego portfela w chwili 1 wynosi

V

(x,y)

(1) = xS(1) + yA(1),

czyli

V

(x,y)

(1) =

xS

(0)(1 + u) + yA(0)(1 + r)

z prawdopodobie´

nstwem p,

xS

(0)(1 + d) + yA(0)(1 + r)

z prawdopodobie´

nstwem 1 − p,

Przyk lad 4.1

Za l´

o˙zmy, ˙ze S(0) = 120, A(0) = 1, u = 0, 25, d = −0, 1, r = 10%. Maj¸ac kapita l

pocz¸atkowy 290 wybieramy na przyk lad x = 2, y = 50 co daje kapita l ko´

ncowy

V

(x,y)

(1) =

2 · 150 + 55 = 355 z prawdopodobie´

nstwem p,

2 · 108 + 55 = 271 z prawdopodobie´

nstwem 1 − p,

4. Wycena Opcji - Model Dwumianowy

27

Obliczmy zmian¸e warto´sci portfela

V

(x,y)

(1) − V

(x,y)

(0) = x[S(1) − S(0)] + yr

czyli zmiana warto´sci portfela ma dwa ´zr´

od la: losow¸a zmian¸e cen akcji i deter-

ministyczny przyrost lokaty bez ryzyka.

Mo˙zemy teraz doprecyzowa´c definicje arbitra˙zu w rozwa˙zanym przypadku

jednego okresu.

Definicja 4.1

M´

owimy, ˙ze portfel (x, y) jest arbitra˙zowy je´sli V

(x,y)

(0) = 0, V

(x,y)

(1) ≥ 0,

a z dodatnim prawdopodobie´

nstwem V

(x,y)

(1) > 0 (czyli V

(x,y)

(1)[ω

i

] > 0 dla

pewnego i).

Twierdzenie 4.1

Zasada braku arbitra˙zu poci¸aga nier´

owno´s´c

d < r < u.

Dow´

od.

Zobaczymy, ˙ze naruszenie tego warunku stwarza mo˙zliwo´s´c arbi-

tra˙zu.

Przypu´s´cmy, ˙ze r ≤ d, czyli

S

(0)(1 + r) ≤ S(0)(1 + d) < S(0)(1 + u).

Intuicyjnie wida´c sprzeczno´s´c, gdy˙z lokowanie w akcje by loby bardziej op la-
calne od lokaty bankowej bez wzgledu na wydarzenia na rynku. Dla ´scis lego
dowodu konstruujemy portfel arbitra˙zowy x = 1, y = −S(0), czyli w chwili 0
po˙zyczamy z banku S(0) i kupujemy za t¸e sum¸e akcj¸e. W chwili 1 mamy

V

(1,−S(0))

(1) = S(1) − S(0)(1 + r).

Z za lo˙zenia wynika, ˙ze przy scenariuszu u mamy dodatni¸a warto´s´c, a przy
scenariuszu d nieujemn¸a.

Przypu´s´cmy, ˙ze r ≥ u, czyli

S

(0)(1 + d) < S(0)(1 + u) ≤ S(0)(1 + r).

W takiej sytuacji nikt nie kupi lby akcji, bo lokata bankowa daje wi¸eksze ko-
rzy´sci. Portfel arbtra˙zowy polega na zaj¸eciu pozycji przeciwnej do poprzedniego
przypadku: x = −1, y = S(0), czyli w chwili 0 sprzedajemy kr´

otko akcj¸e za

S

(0) i lokujemy t¸e sum¸e w banku. W chwili 1 mamy

V

(1,−S(0))

(1) = −S(1) + S(0)(1 + r)

28

Wst¸ep do matematyki finansowej

co jest liczb¸a nieujemn¸a a w scenariuszu d dodatni¸a. Opisowo, odbieramy z
banku S(0)(1 + r) oraz kupujemy akcj¸e za S(1) i zwracamy j¸a, zamykaj¸ac
kr´

otk¸a sprzeda˙z. Mamy zysk S(0)(1 + r) − S(1) ≥ 0 i jest on dodatni gdy

S

(1) = S(0)(1 + d), a to zachodzi z prawdopodobie´

nstwem 1 − p > 0.

Rozwa˙zmy wreszcie zdyskontowane (dzisiejsze) warto´sci wszystkich rozwa-

˙zanych wielko´sci wyr´

o˙zniaj¸ac je przez dodanie w¸e˙zyka. Mamy wi¸ec

˜

S

(1) = S(1)(1 + r)

−

1

,

˜

V

(x,y)

(1) = V

(x,y)

(1)(1 + r)

−

1

= x ˜

S

(1) + y,

(oczywi´scie ˜

S

(0) = S(0), ˜

V

(x,y)

(0) = V

(x,y)

(0), gdy˙z s¸a to dzisiejsze warto´sci) i

obliczmy przyrost warto´sci portfela

˜

V

(x,y)

(1) − V

(x,y)

(0) = x ˜

S

(1) + y − (xS(0) + y)

= x[ ˜

S

(1) − S(0)].

Widzimy, ˙ze wielko´s´c pozycji na rynku ienie˙znym nie wp lywa na dynamik¸e
zmian zdyskontowanych warto´sci portfela.

4.1.2 Cena opcji kupna

Rozwa˙zamy europejsk¸a opcj¸e kupna z cen¸a realizacji K, zak ladaj¸ac, ˙ze

K < S

(0)(1 + u).

Taki wyb´

or K podyktowany jest zdrowym rozs¸adkiem. Gdyby zachodzi lo

K

≥ S(0)(1 + u), to bez wzgl¸edu na ruch ceny akcji opcja nie przedstawia laby

warto´sci. Analogicznie, dla opcji sprzeda˙zy zak ladamy, ˙ze

S

(0)(1 + d) < K.

Warto´s´c opcji w chwili 1, czyli w chwili jej realizacji, wynosi tyle, ile jej

funkcja wyp laty

C

e

(1) = (S(1) − K)

+

,

czyli

C

e

(1) =

S

(0)(1 + u) − K

z prawdopodobie´

nstwem p,

0

z prawdopodobie´

nstwem 1 − p,

Wybieramy teraz portfel (x, y) tak, aby w chwili 1 mia l dok ladnie tak¸a sam¸a

warto´s´c jak opcja:

V

(x,y)

(1) = C

e

(1).

Wyb´

or takiego w la´snie portfela nosi nazw¸e strategii replikuj¸

acej

.

4. Wycena Opcji - Model Dwumianowy

29

Przyk lad 4.2

Konkretnie, przypu´s´cmy, ˙ze K = 130. Wtedy

C

e

(1) =

150 − 130 = 20 z prawdopodobie´

nstwem p,

0

z prawdopodobie´

nstwem 1 − p.

Warunek replikacji daje uk lad r´

owna´

n

150x + 1, 1y = 20 gdy S(1) = 150,
100x + 1, 1y = 0

gdy S(1) = 100,

z rozwi¸azaniem







x

= 0, 4,

y

= −

40

1, 1

.

Oznacza to po˙zyczk¸e z banku w wysoko´sci 36, 36 (w zaokr¸agleniu), oraz zakup
u lamka 0,4 akcji.

Liczba 0, 4 z powy˙zszego przyk ladu m´

owi nam, jaki u lamek akcji nale˙zy za-

kupi´c, aby zreplikowa´c jedn¸a opcj¸e kupna. Wsp´

o lczynnik ten nosi nazw¸e delta.

W og´

olnej sytuacji warunek replikacji prowadzi do uk ladu r´

owna´

n

xS

(0)(1 + u) + y(1 + r) = S(0)(1 + u) − K

xS

(0)(1 + d) + y(1 + r) = 0

Po rozwi¸azaniu uk ladu dostajemy















x

=

S

(0)(1 + u) − K

S

(0)(u − d)

y

= −

(1 + d)(S(0)(1 + u) − K)

(u − d)(1 + r)

Teraz rozumujemy tak: skoro opcja i wyznaczony portfel maj¸a t¸e sam¸a warto´s´c
w chwili 1, to maj¸a te˙z t¸e sam¸a warto´s´c w chwili 0. Gdyby tak nie by lo to
mieliby´smy okazj¸e do arbitra˙zu co zostanie wyjasnione poni˙zej. Prowadzi to do
nast¸epuj¸acej definicji:

Definicja 4.2

Cena opcji

to warto´s´c w chwili 0 portfela replikuj¸acego opcj¸e.

Tego typu definicja wymaga wyja´snienia, ile jest portfeli replikuj¸acych, a

je´sli wiecej ni˙z jeden, to czy maj¸a one t¸e sam¸a warto´s´c w chwili 0. W przeciwnym
wypadku mieliby´smy wiele cen. W naszym modelu portfel replikuj¸acy zosta l

30

Wst¸ep do matematyki finansowej

wyznaczony jako rozwi¸azanie uk ladu dw´

och r´

owna´

n z dwiema niewiadomymi.

Nasze za lo˙zenie d < u, gwarantuje istnienie i jednoznaczno´s´c rozwi¸azania.

Cena opcji, czyli warto´s´c opcji w chwili 0, jest szukan¸a przez nas premi¸a C

e

,

kt´

ora nale˙zy si¸e wystawiaj¸acemu opcj¸e. Mamy wi¸ec w konkretnym przyk ladzie

C

e

= V

(x,y)

(0) = xS(0) + y = 48 − 36, 36 = 11, 64.

W og´

olnej sytuacji mamy twierdzenie poni˙zsze twierdzenie m´

owi¸ace, ˙ze

powy˙zsza definicja jest poprawna, to znaczy, ˙ze odej´scie od wyznaczonej przez
ni¸a ceny prowadzi do arbitra˙zu.

Twierdzenie 4.2

Cena europejskiej opcji kupna z cen¸a realizacji K w jednoetapowym modelu
dwumianowym wynosi

C

e

= xS(0) + y = −

(1 + d)(S(0)(1 + u) − K)

(u − d)(1 + r)

+

S

(0)(1 + u) − K

u

− d

.

Dow´

od.

Przypu´s´cmy, ˙ze C

e

> xS

(0)+y. Wystawiamy opcj¸e kupna, kupu-

jemy x akcji po˙zyczywszy y i zostajemy z dodatni¸a sum¸a pieni¸edzy. Poniewa˙z
portfel akcji i lokaty replikuje opcj¸e, w ka˙zdej sytuacji utrzymamy ten zysk.
Mianowicie, je´sli K > S(1) to opcja ma warto´s´c 0 i tak¸a sam¸a warto´s´c ma nasz
portfel. Czyli xS(1) = −y(1 + r) i sprzedaj¸ac posiadany u lamek akcji mo˙zemy
zwr´

oci´c kwot¸e y(1 + r).

Je´sli K < S(1) to musimy dokupi´c brakuj¸ace 1 − x akcji za (1 − x)S(1).

Sprzedajemy akcj¸e za K wywiazuj¸ac si¸e z wystawionej opcji. Oddajemy y(1+r)
i wychodzimy dok ladnie na zero w chwili jeden (zachowuj¸ac pocz¸atkowy zysk)
dzi¸eki temu, ˙ze nasz portfel replikuje opcj¸e, czyli xS(1) + y(1 + r) = S(1) − K.

Je´sli C

e

< xS

(0) + y to sprzedawszy kr´

otko u lamek x akcji i ulokowawszy y

bez ryzyka nabywamy opcj¸e kupna. Podobnie jak poprzednio, dzi¸eki replikacji
zachowamy pocz¸atkowy zysk.

Wyznaczyli´smy wi¸ec cen¸e za opcj¸e, jak r´

ownie˙z potrafili´smy rozwi¸aza´c prob-

lem os lony przed ryzykiem poprzez konstrukcj¸e portfela r´

ownowa˙znego wys-

tawionej opcji. Wystawiaj¸ac opcj¸e mo˙zna r´

ownocze´snie wybra´c skonstruowan¸a

powy˙zej strategi¸e. Wydaje si¸e to ja lowe, i istotnie tak jest w rozwa˙zanym mod-
elu. Zamiast kupowa´c opcj¸e mo˙zemy po prostu kupi´c portfel replikuj¸acy opcj¸e.
Niemniej w bardziej skomplikowanych sytuacjach zakup tego portfela mo˙ze
by´c k lopotliwy oraz, co istotniejsze, konieczne mo˙ze by´c ci¸ag le jego mody-
fikowanie (problem nieobecny w modelu jednoetapowym), wi¸ec stwarza to za-
potrzebowanie na wyspecjalizowanych po´srednik´

ow, kt´

orzy wystawiaj¸ac opcj¸e

4. Wycena Opcji - Model Dwumianowy

31

albo bior¸a na siebie ryzyko, albo konstruuj¸a strategi¸e zabezpieczaj¸ac¸a ich przed
ryzykiem.

Remark 4.1

Podkre´slmy, ˙ze cena opcji nie zale˙zy od prawdopodobie´

nstwa p tego, ˙ze cena

akcji p´

ojdzie w g´

or¸e. Powr´

ocimy jeszcze do tej obserwacji poni˙zej, a teraz odno-

tujmy pewne podobie´

nstwo wyceny opcji do zak lad´

ow na wy´scigach konnych.

Je´sli mamy dwa konie i tyle samo pieni¸edzy postawiono na ka˙zdego, to wyp laty
b¸ed¸a 1–1, co oznacza ˙ze wygrawszy zainwestowan¸a z lot´

owk¸e dostaniemy z

powrotem i jeszcze dostaniemy jedn¸a dodatkowo. W ten spos´

ob biuro przyj-

muj¸ace zak lady nie poniesie straty bez wzgl¸edu na wynik gonitwy (czerpi¸ac
ma ly lecz pewny zysk z koszt´

ow transakcji). Gdyby prawdopodobie´

nstwa

wygranej poszczeg´

olnych koni by ly np. 0,1 i 0,9, i przyjmuj¸acy zak lady zna l je,

nie zmieni lo by to jego polityki wyp lat, gdy˙z jakakolwiek inna ni˙z 1–1 by laby
ryzykowna.

Remark 4.2

Analizuj¸ac wz´

or z Twierdzenia 4.2 poka˙zemy najpierw, ˙ze cena opcji ro´snie

gdy u ro´snie. Cena ta r´

ownie˙z ro´snie, gdy d maleje. W tym celu przepiszmy

wz´

or na cen¸e opcji w dogodniejszej postaci:

C

e

=

1

1 + r

·

r

− d

u

− d

· [S(0)(1 + u) − K].

Teraz obliczamy pochodn¸a ceny opcji wzgl¸edem zmiennej u (wszyskie inne
czyniki s¸a teraz ustalone). Dostajemy

(r − d)[K − S(0)(1 + d)]

(1 + r)(u − d)

2

co jest dodatnie, gdy˙z r > d, K > S(0)(1 + d). Licz¸ac pochodn¸a wzgl¸edem d
dostajemy

(r − u)[S(0)(1 + u) − K]

(1 + r)(u − d)

2

co jest ujemne, gdy˙z r < u, S(0)(1 + u) > K.

Oznacza to, ˙ze cena opcji jest wi¸eksza gdy rozrzut warto´sci ceny S(1)

jest wi¸ekszy. Du˙zy rozrzut warto´sci zmiennej losowej jest zwi¸azany z du˙zym
wsp´

o lczynnikiem zmienno´sci, kt´

ory w tym modelu definiujemy jako wariancj¸e

ilorazu

S

(n+1)
S

(n)

, czyli wariancj¸e zmiennej losowej 1 + ξ, gdzie ξ = u, d. Mo˙zna

32

Wst¸ep do matematyki finansowej

latwo obliczy´c

Var(1 + ξ) = E(1 + ξ)

2

− E(1 + ξ)

2

= E(1 + 2ξ + ξ

2

) − 1 − 2E(ξ) − E(ξ)

2

= E(ξ

2

) − (up + d(1 − p))

2

= u

2

p

+ d

2

(1 − p) − u

2

p

2

− 2udp(1 − p) − d

2

(1 − p)

2

= (u − d)

2

p

(1 − p),

czyli wi¸eksza wariancja oznacza wi¸eksz¸a r´

o˙znic¸e u − d, czyli wi¸eksze u przy

ustalonym d, lub mniejsze d przy ustalonym u (niezale˙znie od prawdopodo-
bie´

nstw).

Niemniej, mo˙zna latwo zobaczy´c, ˙ze cena bynajmniej nie ro´snie wraz z wari-

ancj¸a. Dla prostoty we´zmy r = 0, S(0) = 1, K = 1 i mamy c =

−

ud

u−d

. Je´sli

u

= 0, 05 a d = −0, 05 to u − d = 0, 1 i c = 0, 025 natomiast je´sli u = 0, 01 a

d

= −0, 19 to u − d = 0, 2 i cena jest mniejsza: c = 0, 0095.

4.1.3 Cena dowolnego instrumentu pochodnego

Ustalamy pewn¸a funkcj¸e f i jako wyp lat¸e przyjmujemy

f

(S(1)) =

f

(S(0)(1 + u))

z prawdopodobie´

nswem p

f

(S(0)(1 + d))

z prawdopodobie´

nswem 1 − p

Dla opcji kupna mamy f (x) = (x−K)

+

, a dla opcji sprzeda˙zy f (x) = (K −x)

+

.

Og´

olnie, zmienn¸a losow¸a postaci f (S(1)) nazywamy instrumentem po-

chodnym

(ang. derivative security, contingent claim), a jej cen¸e dzisiejsz¸a

oznaczymy przez D

f

(0).

Wybieramy teraz portfel (x, y) replikuj¸acy instrument D

f

(1) = f (S(1))

rozwi¸azuj¸ac uk lad r´

owna´

n

xS

(0)(1 + u) + y(1 + r) = f (S

u

)

xS

(0)(1 + d) + y(1 + r) = f (S

d

)

gdzie S

u

= S(0)(1 + u), S

d

= S(0)(1 + d). Dostajemy

x

=

f

(S

u

) − f (S

d

)

S

u

− S

d

.

Ten wsp´

o lczynnik nosi nazw¸e delta. Mo˙zemy r´

ownie˙z wyliczy´c

y

=

(1 + u)f (S

d

) − (1 + d)f (S

u

)

(u − d)(1 + r)

.

4. Wycena Opcji - Model Dwumianowy

33

Cena instrumentu, to warto´s´c dzisiejsza tego portfela:

D

f

(0) = V

(x,y)

(0) = xS(0) + y

czyli

D

f

(0) =

(1 + u)f (S

d

) − (1 + d)f (S

u

)

(u − d)(1 + r)

+

f

(S

u

) − f (S

d

)

u

− d

.

(4.1)

Analogicznie jak dla szczeg´

olnego przypadku opcji kupna (rozwa˙zonego w

poprzednim podrozdziale) stosuj¸ac zasad¸e braku arbitra˙zu mo˙zemy udowodni´c

Twierdzenie 4.3

Cena instrumentu pochodnego D

f

(1) = f (S(1)) wyra˙za si¸e wzorem (4.1).

Praw¸a stron¸e wzoru (4.1) doprowad´zmy do postaci af (S

u

)+bf (S

d

). W tym

celu wy l¸aczamy przed nawias f (S

u

) i f (S

d

):

f

(S

u

)

−

1 + d

(u − d)(1 + r)

+

1

u

− d

+ f (S

d

)

1 + u

(u − d)(1 + r)

−

1

u

− d

.

U lamki w nawiasach dodajemy sprowadzaj¸ac je do wsp´

olnego mianownika

−

1 + d

(u − d)(1 + r)

+

1

u

− d

=

r

− d

(u − d)(1 + r)

=

r

− d

u

− d

1

1 + r

,

1 + u

(u − d)(1 + r)

−

1

u

− d

=

u

− r

(u − d)(1 + r)

=

1 −

r

− d

u

− d

1

1 + r

.

Oznaczmy powtarzaj¸acy si¸e u lamek przez p

∗

:

p

∗

=

r

− d

u

− d

Poniewa˙z d < r < u, wi¸ec 0 < r − d < u − d, czyli 0 < p

∗

<

1 — jest to liczba

z przedzia lu (0, 1), czyli mo˙ze by´c interpretowana jako prawdopodobie´

nstwo.

Podstawiamy do wzoru na D

f

(0):

D

f

(0) = p

∗

f

(S

u

)(1 + r)

−

1

+ (1 − p

∗

)f (S

d

)(1 + r)

−

1

.

(4.2)

Zatem liczba p

∗

jest taka, ˙ze wyliczona powy˙zej cena instrumentu D

f

jest

r´

owna warto´sci oczekiwanej zdyskontowanej jego wyp laty w chwili 1, obliczonej

przy u˙zyciu p

∗

. Poniewa˙z warto´s´c oczekiwana zale˙zy od prawdopodobie´

nstw,

oznaczmy przez E

∗

warto´s´c oczekiwan¸a liczon¸a wzgl¸edem prawdopodobie´

nstwa

p

∗

. Mamy wi¸ec

D

f

= E

∗

(1 + r)

−

1

f

(S(1))

.

(4.3)

Dla europejskich opcji kupna i sprzeda˙zy mamy odpowiednio

C

e

= E

∗

((1 + r)

−

1

(S(1) − K)

+

,

P

e

= E

∗

((1 + r)

−

1

(K − S(1))

+

.

34

Wst¸ep do matematyki finansowej

Remark 4.3

Widzimy, ˙ze wyj´sciowe prawdopodobie´

nstwo p nie wyst¸epuje we wzorze na cen¸e

opcji. U˙zywamy w nim abstrakcyjnego, nierzeczywistego prawdopodobie´

nstwa

p

∗

, kt´

ore wynika z idei replikacji opcji eliminuj¸acej wszelkie ryzyko. Wr´

o´cmy

do Uwagi 4.1. Bezpieczne od ryzyka stawki s¸a zwi¸azane z ilo´sci¸a pieni¸edzy ob-
stawionych na poszczeg´

olnego konia. Je´sli np. 5000 obstawiono na konia pier-

wszego, a 10000 na drugiego, to latwo wida´c, ˙ze wyp laty wed lug stawek 2–1,
3–2 zabezpieczaj¸a przed ryzykiem. Odpowiadaj¸a one prawdopodobie´

nstwom

1
3

,

2
3

, tzn. warto´s´c oczekiwana wyp lat jest zero gdy jest liczona wed lug nich. Aby

to zobaczy´c, przypu´s´cmy ˙ze obstawiono x z l na pierwszego, a y z l na drugiego
konia. Je´sli wygra pierwszy ko´

n to przyjmuj¸acy zak lady ma x + y − 3x, a gdy

drugi, to x + y − 1, 5y. Szukamy p

∗

aby

(−2x + y)p

∗

+ (x − 0, 5y)(1 − p

∗

) = 0

dla wszelkich x, y, co daje w la´snie p

∗

=

1
3

.

Rozwa˙zmy teraz zdyskontowane warto´sci S(t)

˜

S

(0) = S(0),

˜

S

(1) = S(1)(1 + r)

−

1

.

Obliczmy waro´s´c oczekiwan¸a E

∗

zmiennej losowej ˜

S

(1):

E

∗

˜

S

(1) = p

∗

S

(0)(1 + u)

1 + r

+ (1 − p

∗

)

S

(0)(1 + d)

1 + r

=

r

− d

u

− d

·

S

(0)(1 + u)

1 + r

+

1 −

r

− d

u

− d

·

S

(0)(1 + d)

1 + r

= ˜

S

(0)

po uproszczeniu. Okazuje si¸e wi¸ec, ˙ze warto´s´c oczekiwana E

∗

˜

S

(t) jest taka sama

dla t = 0, 1:

E

∗

˜

S

(0) = E

∗

˜

S

(1),

(4.4)

gdy˙z warto´s´c oczekiwana liczby nielosowej ˜

S

(0) jest jej r´

owna: E

∗

( ˜

S

(0)) =

˜

S

(0).

W naszej prostej sytuacji, gdzie mamy tylko dwa elementy w Ω, a proces

zmian jest jednoetapowy, ta w lasno´s´c mo˙ze by´c przyj¸eta jako definicja tego, ˙ze
ci¸ag zmiennych losowych ( ˜

S

(0), ˜

S

(1)) jest martynga lem.

Podsumujmy. Za lo˙zenie wykluczaj¸ace arbitra˙z gwarantuje istnienie praw-

dopodobie´

nstwa dla kt´

orego ( ˜

S

(t))

t

=0,1

jest martynga lem, a cena opcji jest

warto´sci¸a oczekiwan¸a jej zdyskontowanej warto´sci. Mamy kolejn¸a definicj¸e ceny
opcji:

4. Wycena Opcji - Model Dwumianowy

35

Definicja 4.3

Cena opcji

cena!opcji to warto´s´c oczekiwana zdyskontowanej warto´sci zmi-

ennej losowej (S(1) − K)

+

(dla opcji kupna, lub te˙z (K − S(1))

+

dla opcji

sprzeda˙zy) wzgl¸edem prawdopodobie´

nstwa przy kt´

orym ( ˜

S

(t))

t

=0,1

jest mar-

tynga lem.

Twierdzenie 4.4

Definicje 4.2 i 4.3 s¸a r´

ownowa˙zne, tzn. daj¸a te same ceny opcji.

Dow´

od.

Implikacj¸e w jedn¸a stron¸e ju˙z pokazali´smy powy˙zej stwierdzaj¸ac,

˙ze cena opcji dana przez Definicj¸e 4.2 spe lnia warunek Definicji 4.3. Wycho-

dz¸ac od idei replikacji opcji doszli´smy do postaci liczby p

∗

oraz pokazali´smy, ˙ze

zachodz¸a wzory (4.3) i (4.4).

Dow´

od w drug¸a stron¸e polega na wyznaczeniu liczby p

∗

aby zachodzi lo (4.4),

czyli:

S

(0) = p

∗

(1 + r)

−

1

S

u

(1) + (1 − p

∗

)(1 + r)

−

1

S

d

(1).

Mno˙z¸ac obie strony przez (1+r) i podstawiaj¸ac postacie S

u

(1), S

d

(1) dostajemy

(1 + r)S(0) = p

∗

S

(0)(1 + u) + (1 − p

∗

)S(0)(1 + d).

Dziel¸ac obustronnie przez S(0) latwo wyliczamy p

∗

=

r

− d

u

− d

. Poniewa˙z dosta-

li´smy t¸a sam¸a warto´s´c co poprzednio, wszystkie powy˙zsze rachunki pokazuj¸a,

˙ze ceny opcji s¸a takie same.

4.1.4 Zwrot

Przez stop¸e zwrotu, lub kr´

otko zwrot, rozumiemy liczb¸e

V

(1) − V (0)

V

(0)

gdzie V (0), V (1) oznacza warto´s´c dowolnego waloru. Dla A mamy wi¸ec

A

(1) − A(0)

A

(0)

= r

natomiast dla waloru ryzykownego S zwrot jest zmienn¸a losow¸a

k

=

S

(1) − S(0)

S

(0)

=

u

z prawdopodobie´

nswem p

d

z prawdopodobie´

nswem 1 − p

36

Wst¸ep do matematyki finansowej

Jej warto´sc oczekiwana dana jest wzorem E(k) = pu + (1 − p)d. Przechodz¸ac
do prwdopodobie´

nstwa p

∗

=

r−d

u−d

mamy

E

∗

(k) = p

∗

u

+ (1 − p

∗

)d

=

r

− d

u

− d

u

+

u

− r

u

− d

d

= r

Prawdopodobie´

nstwo p

∗

nazywamy neutralnym wzgl¸edem ryzyka.

Znajomos´c zwrotu pozwala wyznaczy´c przysz l¸a warto´s´c

S

(1) = S(0)(1 + k).

Jej warto´sc ocekiwana dana jest wzorem

E(S(1)) = S(0)(1 + E(k)).

Dla prawdopodobie´

nstwa neutralnego wzgl¸edem ryzyka mamy wi¸ec

E

∗

(S(1)) = S(0)(1 + r)

czyli

E

∗

(

S

(1)

1 + r

) = S(0)

– zdyskontowane ceny s¸a martynga lem i prawdopodobie´

nswto p

∗

nazywamy

martynga lowym.

4.1.5 Os lona przed ryzykiem

Wystawiaj¸ac opcj¸e ponosimy ryzyko straty. Mo˙zna si¸e przed ni¸a zabezpieczy´c
podejmuj¸ac stosown¸a gr¸e rynkow¸a. W modelu jednoetapowym sprowadza
si¸e ona do wyboru jednego portfela (x, y). Taki wyb´

or nazwiemy os lon¸

a z

g´

ory

(ang. super-hedging) je´sli warto´s´c tego portfela w chwili realizacji opcji

przewy˙zszy warto´s´c opcji:

xS

(1) + y(1 + r) ≥ f (S(1)),

gdzie f jest funkcj¸a wyp laty dowolnego instrumentu pochodnego.

Poci¸aga to nast¸epuj¸ace ograniczenia na liczby x, y:

xS

u

(1) + y(1 + r) ≥ f (S

u

(1))

xS

d

(1) + y(1 + r) ≥ f (S

d

(1))

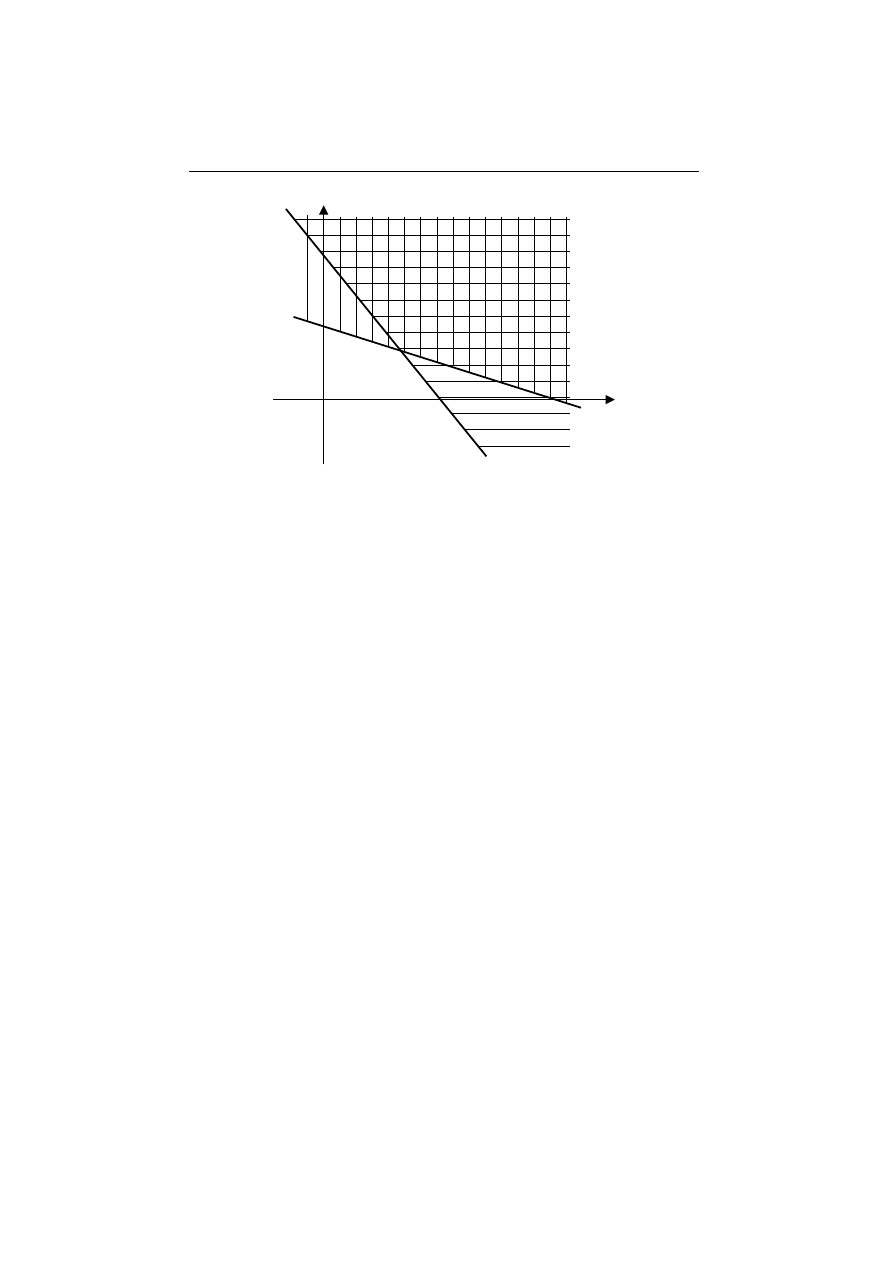
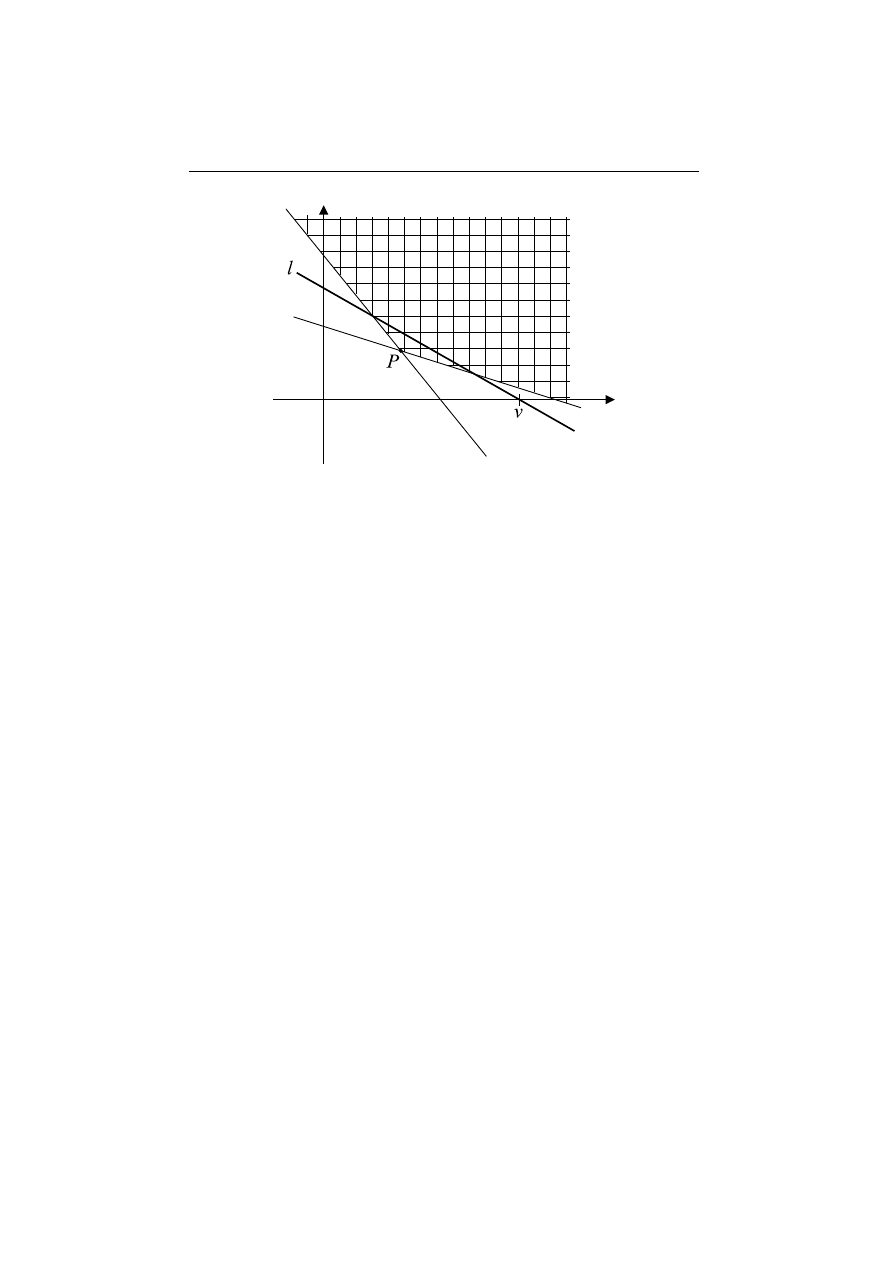
Mo˙zemy to zilustrowa´c graficznie: ka˙zda z nier´

owno´sci wyznacza p´

o lp laszczyzn¸e

w uk ladzie wsp´

o lrz¸ednych (x, y) na Rysunku 4.2.

Prowadzi to do nast¸epuj¸acej r´

ownowa˙znej definicji ceny instrumentu po-

chodnego:

4. Wycena Opcji - Model Dwumianowy

37

Rysunek 4.2

Definicja 4.4

Warto´

s´

c instrumentu

f

(S(1)) jest najmniejsz¸a liczb¸a v tak¸a, ˙ze istnieje

os lona z g´

ory o warto´sci pocz¸atkowej v:

D

f

= min{v : v = xS(0) + y, xS(1) + y(1 + r) ≥ f (S(1))}.

Aby stwierdzi´c r´

ownowa˙zno´s´c tej definicji z poprzednimi zauwa˙zmy, ˙ze port-

fel replikuj¸acy jest wyznaczony jako punkt przeci¸ecia obu prostych. Cena opcji
wed lug poprzednich definicji jest wyznaczona jako warto´s´c tego portfela w
chwili pocz¸atkowej: xS(0) + y. Problem sprowadza si¸e do tego, czy punkt
przeci¸ecia prostych odpowiada minimalnej warto´sci kapita lu pocz¸atkowego.
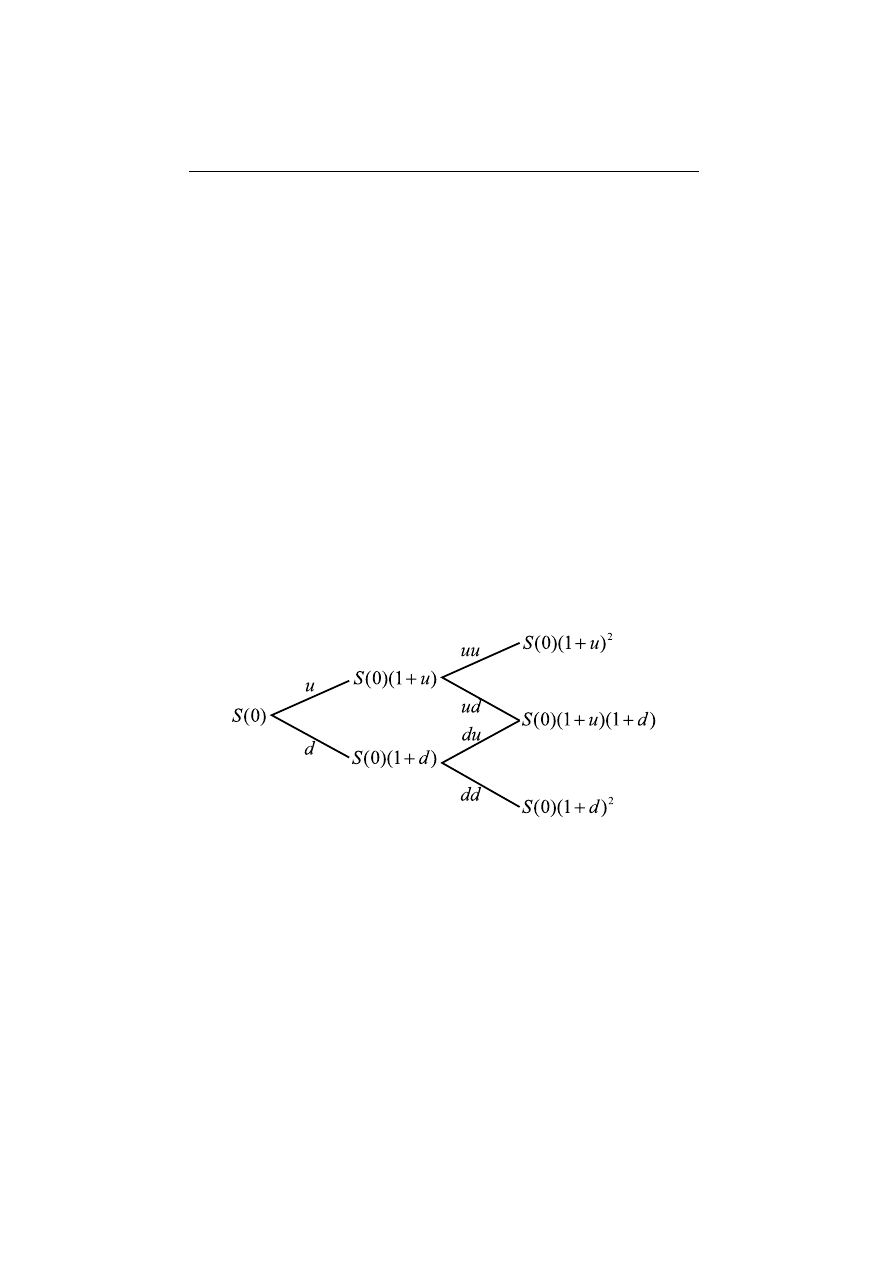
To wynika z nast¸epuj¸acej obserwacji geometrycznej. Mo˙zna latwo wyliczy´c,

˙ze punkty wyznaczaj¸ace portfele o tej samej warto´sci pocz¸atkowej le˙z¸a na

r´

ownoleg lych liniach prostych l takich jak na Rysunku 4.3, a ta warto´s´c

pocz¸atkowa wyznaczona jest przez przeci¸ecie danej prostej z osi¸a poziom¸a.
Wida´c, ˙ze jest ona najmniejsza dla prostej przechodz¸acej przez punkt P , czyli
dla portfela replikuj¸acego. Istotna jest tu zale˙zno´s´c mi¸edzy wsp´

o lczynnikami

kierunkowymi tych prostych. Jest ona zagwarantowana przez warunek d < r <
u

.

Ostatnia definicja stosuje si¸e w og´

olniejszych sytuacjach, w kt´

orych nie jest

mo˙zliwa replikacja instrumentu pochodnego, ani nie mo˙zna wyznaczy´c jed-
noznacznie prawdopodobie´

nstwa p

∗

, czyli poprzednie definicje nie mog¸a by´c

zastosowane.

Mo˙zna latwo sprawdzi´c, ˙ze podej´scie przez os lon¸e z do lu jest r´

ownowa˙zne:

38

Wst¸ep do matematyki finansowej

Rysunek 4.3

wz´

or

max{v : v = xS(0) + y, xS(1) + y(1 + r) ≤ f(S(1))}

daje ten sam wynik.

Przyk lad 4.3

Rozwa˙zmy model w kt´

orym cena S(1) mo˙ze przyj¸ac trzy warto´sci wyznac-

zone przez trzy zwroty: d < m < u. Wtedy warto´sc ko´

ncowa portfela te˙z

przyjmuje trzy warto´sci i na og´

o l nie jest mo˙zliwa replikacja gdy˙z wymaga

rozwi¸azania uk ladu trzech r´

owna´

n z dwiema niewiadomymi. Warunek na praw-

dopodobie´

nstwo neutralne wzgl¸edem ryzyka nie daje jednoznacznego rozwi¸aza-

nia: r = p

∗

u

+ q

∗

m

+ (1 − p

∗

− q

∗

)d to jedno r´

ownanie z dwiema niewiadomymi.

Wycena przez os lon¸e z do lu i z g´

ory daje r´

o˙zne wyniki. Os lona z g´

ory zabez-

piecza pozycj¸e wystawiaj¸acego opcj¸e gdy˙z pozwala na konstrukcje portfela,
kt´

orego warto´sci przewy˙zszaj¸a wyp laty opcji. Przyjmuj¸ac na przyk lad S(0) =

100, u = 20%, m = 10%, d = −20%, r = 5%, K = 100 i minimalizuj¸ac
warto´sc pocz¸atkow¸a portfela os laniaj¸acego z g´

ory dostajemy 11,90, natomiast

os laniaj¸ac z do lu mamy 7,64. Liczby te wyznaczaja przedzia l cen pomi¸edzy
kt´

orymi nabywca b¸edzie negocjowa l cen¸e z wystawiaj¸acym opcj¸e.

4. Wycena Opcji - Model Dwumianowy

39

4.2 Model dwuetapowy

Analizujemy rynek w trzech chwilach czasowych: 0, 1, 2. Rozwa˙zamy jedn¸a
akcj¸e o cenie S(n), n = 0, 1, 2. Zak ladamy, ˙ze zmiana ceny na ka˙zdym
poszczeg´

olnym etapie odbywa si¸e tak jak w modelu jednoetapowym, czyli ˙ze

mamy dwie liczby d i u spe lniaj¸ace −1 < d < r < u, kt´

ore wyznaczaj¸a wzgl¸edn¸a

zmian¸e cen:

S

(1) =

S

(0)(1 + u) z prawdopodobie´

nstwem p

S

(0)(1 + d)

z prawdopodobie´

nstwem 1 − p

S

(2) =

S

(1)(1 + u) z prawdopodobie´

nstwem p

S

(1)(1 + d)

z prawdopodobie´

nstwem 1 − p

czyli

S

(2) =







S

(0)(1 + u)

2

z prawdopodobie´

nstwem p

2

S

(0)(1 + u)(1 + d)

z prawdopodobie´

nstwem 2p(1 − p)

S

(0)(1 + d)

2

z prawdopodobie´

nstwem (1 − p)

2

Mamy wi¸ec 4 mo˙zliwo´sci wyboru liczb d, u: {dd, du, ud, uu}. Warto´sci akcji
w chwili 2 pokrywaj¸a si¸e przy dw´

och ´srodkowych wynikach. Zilustrujmy to w

formie drzewa przedstawionego na Rysunku 4.4.

Rysunek 4.4

Przyk lad 4.4

Rozwa˙zmy konkretne liczby: S(0) = 120, u = 0, 2, d = −0, 1:

S

(1) =

144 z prawdopodobie´

nstwem p,

108 z prawdopodobie´

nstwem 1 − p,

40

Wst¸ep do matematyki finansowej

S

(2) =







172, 8 z prawdopodobie´

nstwem p

2

129, 6 z prawdopodobie´

nstwem 2p(1 − p)

97, 2

z prawdopodobie´

nstwem (1 − p)

2

Tak jak w modelu jednoetapowym, warto´sci instrment´

ow pochodnych nie b¸ed¸a

zale˙za ly od prawdopodobie´

nstw, wi¸ec ich nie ustalamy.

4.2.1 Strategie inwestycyjne

Rozwa˙zamy strategi¸

e

, czyli dwa portfele (x(n), y(n)), n = 0, 1. Liczby x(n),

y

(n) oznaczaj¸a odpowiednio pozycje w akcjach i rynku pienie˙znym w chwili n.

Czyli warto´s´c inwestycji w akcje w chwilach n = 0, 1, 2 wynosi

x

(0)S(0),

x

(0)S(1),

x

(1)S(2)

a warto´sc rachunku pieni¸e˙znego

y

(0),

y

(0)(1 + r),

y

(1)(1 + r)

2

(zak ladamy, ˙ze stopa procentowa jest sta la w rozpatrywanym okresie). Widz-
imy, ˙ze powy˙zsze warto´sci w danej chwili s¸a wyznaczone poprzez wyb´

or portfela

w chwili wcze´sniejszej (z wyj¸atkiem chwili 0).

Zak ladamy, tak jak w modelu jednoetapowym, ˙ze d < r < u aby unikn¸a´c

oczywistego arbitra˙zu.

Warto´

s´

c strategii

w kolejnych chwilach n = 0, 1, 2 jest zdefiniowana w

nast¸epuj¸acy spos´

ob:

V

(x,y)

(0) = x(0)S(1) + y(0),

V

(x,y)

(1) = x(0)S(1) + y(0)(1 + r),

V

(x,y)

(2) = x(1)S(2) + y(1)(1 + r)

2

.

Definicja 4.5

M´

owimy, ˙ze strategia jest dopuszczalna (ang. admissible) je´sli V

(x,y)

(n) ≥ 0

dla ka˙zdego n, a samofinansuj¸

aca si¸

e

(ang. self-financing) je´sli

V

(x,y)

(1) = x(1)S(1) + y(1)(1 + r).

Oznacza to, ˙ze zmiana portfela w chwili 1, czyli przej´scie od pary wyznaczonej
w chwili 0, czyli (x(0), y(0)), do pary (x(1), y(1)) odbywa si¸e w ramach kapita lu
posiadanego w tej chwili:

x

(0)S(1) + y(0)(1 + r) = x(1)S(1) + y(1)(1 + r).

4. Wycena Opcji - Model Dwumianowy

41

Innymi s lowy, strategia jest dopuszczalna, je´sli nie ma bankructwa, a samofi-
nasuj¸aca si¸e, je´sli nie pobieramy ani nie dodajemy ˙zadnych sum w trakcie gry
gie ldowej (poza chwil¸a pocz¸atkow¸a).

Kolejno´s´c wydarze´

n w naszym modelu jest nast¸epuj¸aca: w chwilach 0,1,2

mamy notowania gie ldowe, a pomi¸edzy nimi podejmujemy decyzje o rozmiesz-
czeniu naszych ´srodk´

ow w ramach strategi samofinansuj¸acej si¸e

• n = 0 — mamy kapita l pocz¸atkowy V (0) i znamy cen¸e akcji S(0)

◦ wybieramy portfel x(0), y(0) tak, aby

V

(0) = V

(x,y)

(0) = xS(0) + y;

• n = 1 — cena akcji ulega zmianie na S(1), a wraz z ni¸a warto´s´c naszego

portfela na

V

(x,y)

(1) = x(0)S(1) + y(0)(1 + r);

◦ wybieramy portfel x(1), y(1) w ramach posiadanych ´srodk´

ow, czyli nie

zmieniaj¸ac warto´sci portfela

V

(x,y)

(1) = x(1)S(1) + y(1)(1 + r);

• n = 2 — cena akcji ulega zmianie na S(2), a wraz z ni¸a warto´s´c naszego

portfela na

V

(x,y)

(2) = x(1)S(2) + y(1)(1 + r)

2

.

Przyk lad 4.5

W konkretnej sytuacji z poprzedniego przyk ladu (S(0) = 120, u = 0, 2, d =
−0, 1) zak ladaj¸ac, ˙ze r = 0, 1, V (0) = 290, wybieramy x(0) = 2, y(0) = 50, i
mamy

V

(x,y)

(0) = 2 · 120 + 50 = 290

V

(x,y)

(1) =

2 · 144 + 50 · 1, 1 = 343 gdy S(1) = 144,
2 · 108 + 50 · 1, 1 = 271 gdy S(1) = 108.

Przypu´s´cmy, ˙ze zmieniamy strategi¸e sprzedaj¸ac jedn¸a akcj¸e: x(1) = 1, co wyz-
nacza pozycje na rynku pieni¸e˙znym z warunku samofinansowania si¸e

y

(1) = (V

(x,y)

(1) − x(1)S(1))(1 + r)

−

1

czyli

y

(1) =

(343 − 144) · 1, 1

−

1

= 180, 91 gdy S(1) = 144,

(271 − 108) · 1, 1

−

1

= 148, 18 gdy S(1) = 108,

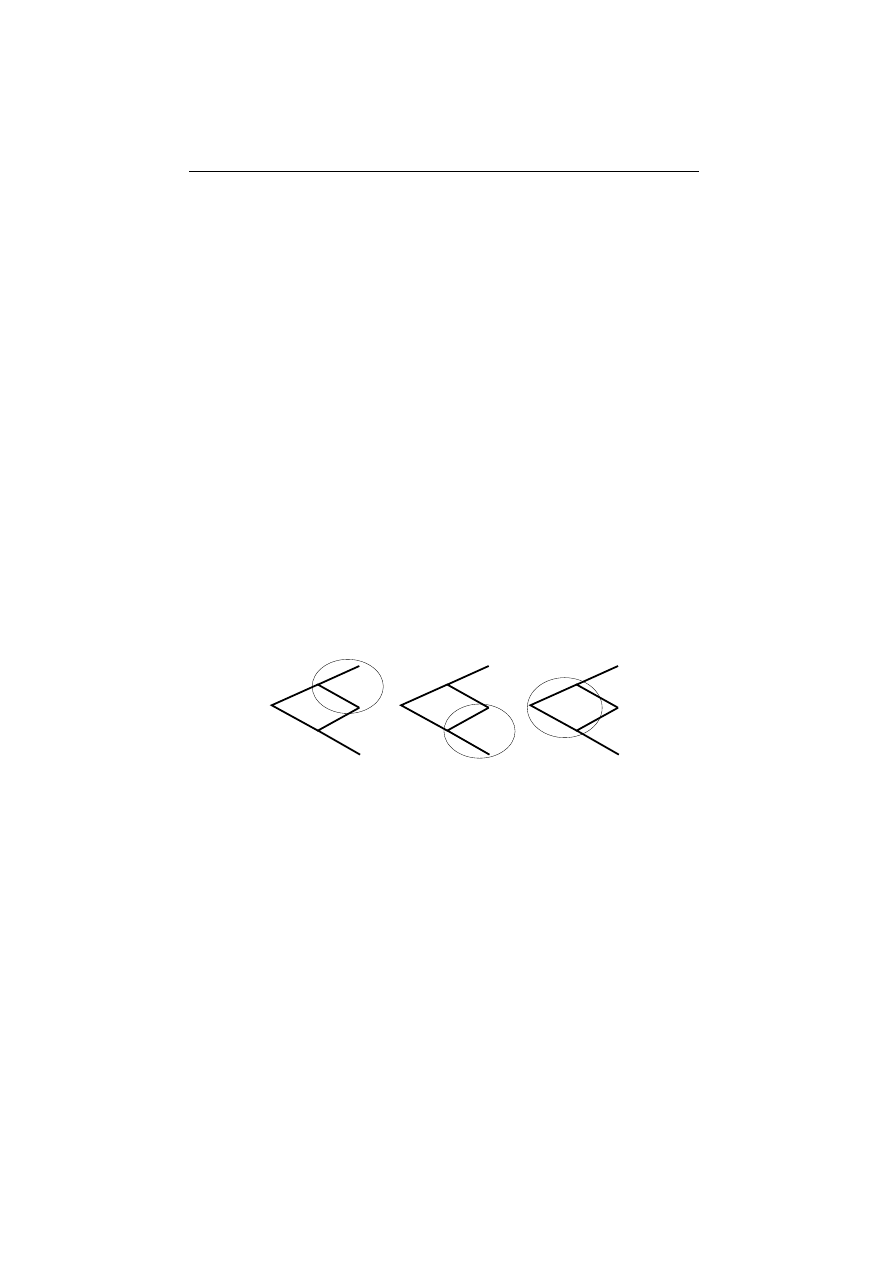
42

Wst¸ep do matematyki finansowej

W chwili 2 mamy

V

(x,y)

(2) =















218, 9 + 172, 8 = 391, 7 w wariancie uu,
218, 9 + 129, 6 = 348, 5 w wariancie ud,
179, 3 + 129, 6 = 308, 9 w wariancie du,
179, 3 + 97, 2 = 276, 5

w wariancie dd,

4.2.2 Przyk lad wyceny opcji europejskiej

Rozpatrzymy szczeg´

o lowo jeden przyk lad, gdy˙z na konkretnych liczbach na-

j latwiej jest zobaczy´c ide¸e. Przyjmijmy, tak jak w Przyk ladzie 4.4, S(0) = 120,
u

= 0, 2, d = −0, 1, r = 0, 1.

Wycenimy europejsk¸a opcj¸e kupna o chwili realizacji T = 2 z cen¸a realizacji

120 z l, czyli rozwa˙zamy zmienn¸a losow¸a f ((2)) = (S(2) − 120)

+

przyjmuj¸ac¸a

warto´sci







52, 8 gdy S(2) = 172, 8
9, 6

gdy S(2) = 129, 6

0

gdy S(2) = 97, 2

Post¸apimy analogicznie jak w modelu jednoetapowym replikuj¸ac zmienn¸a

f

(S(2)), czyli skonstruujemy strategi¸e wart¸a tyle co wyp lata opcji w chwili 2.

Zrobimy to w trzech etapach zajmuj¸ac si¸e kolejno fragmentami drzewa zaznac-
zonymi na Rysunku 4.5.

Rysunek 4.5

1 Etap.

Liczba C

u

(1) oznacza cen¸e opcji w chwili 1 pod warunkiem, ˙ze

cena akcji w chwili 1 wynosi S

u

= S(0)(1 + u) = 144. Wtedy jedyne mo˙zliwe

warto´sci S(2) to 172,8 i 129,6 i wyp laty z opcji wynosz¸a

52, 8 gdy S(2) = 172, 8, S(1) = 144
9, 6

gdy S(2) = 129, 6, S(1) = 144

Wyliczamy x(1), y(1) z uk ladu r´

owna´

n

52, 8 = x(1) · 172, 8 + y(1) · 1, 1

2

9, 6 = x(1) · 129, 6 + y(1) · 1, 1

2

4. Wycena Opcji - Model Dwumianowy

43

co daje (w przybli˙zeniu)

x

(1) = 1 y(1) = −99, 17.

Warto´s´c x(1) = 1 odpowiada temu, ˙ze opcja na pewno zostanie zrealizowana i
os lona dla wystawiaj¸acgo opcj¸e wymaga posiadania akcji. Wyliczamy warto´s´c
tego portfela w chwili 1:

C

u

(1) = 1 · 144 − 99, 17 · 1, 1 = 34, 91

(4.5)

2 Etap.

Podobnie obliczamy C

d

(1), czyli cen¸e opcji w chwili 1 gdy S(1) =

108. Mamy S(2) = 129, 6 lub S(2) = 97, 2 czyli wyp lata opcji wynosi

9, 6 gdy S(2) = 129, 6, S(1) = 108
0

gdy S(2) = 97, 2, S(1) = 108

Wyliczamy x(1), y(1) z uk ladu r´

owna´

n

9, 6 = x(1) · 129, 6 + y(1) · 1, 1

2

0 = x(1) · 97, 2 + y(1) · 1, 1

2

co daje oko lo

x

(1) = 0, 296 y(1) = −23, 78

Znajdujemy teraz warto´s´c tego portfela w chwili 1

C

d

(1) = 0, 296 · 108 − 23, 78 · 1, 1 = 5, 81

(4.6)

3 Etap.

Znale´zli´smy si¸e w sytuacji dok ladnie takiej samej jak w modelu

jednoetapowym. Znajdujemu portfel x(0), y(0) z uk ladu

34, 91 = x(0) · 144 + y(0) · 1, 1
5, 81 = x(0) · 108 + y(0) · 1, 1

traktuj¸ac warto´sci opcji C(1) jako wyp laty (co odpowiada mo˙zliwo´sci sprzeda-
nia opcji), co daje

x

(0) = 0, 81 y(0) = −74, 24.

Cen¸e opcji otrzymujemy wyliczaj¸ac warto´s´c tego portfela w chwili 0:

C

(0) = 0, 81 · 120 − 74, 24 = 22, 96.

Jak wida´c, wyznaczenie warto´sci opcji wymaga lo trzykrotnego zastosowania

procedury replikacji z modelu jednoetapowego.

Powy˙zsze obliczenia pozwol¸a nam odpowiedzie´c na nast¸epuj¸ace pytanie: jak

os loni´c si¸e przed ryzykiem straty gdy wystawilismy opcj¸e. Zainkasowali´smy jej
cen¸e 22,96 z l i teraz zgodnie z powy˙zszym schematem konstruujemy strategi¸e
zabezpieczaj¸ac¸a:

44

Wst¸ep do matematyki finansowej

• W chwili 0 kupujemy u lamek 0,81 akcji i po˙zyczamy 74,24 z l;

• Je´sli S(1) = 144 to w chwili 1 zwi¸ekszamy ilo´s´c posiadanych akcji do jednej

i finasujemy zakup zwi¸ekszaj¸ac po˙zyczk¸e do 99,17 z l;

• Je´sli S(1) = 108 to w chwili 1 redukujemy ilo´s´c akcji do 0,296 sprzedaj¸ac

odpowiedni¸a jej cz¸e´s´c; mo˙zemy wi¸ec odda´c cz¸e´sciowo po˙zyczk¸e zmniejszaj¸ac
zad lu˙zenie do 23,78 z l.

W chwili 2 bez wzgl¸edu na warto´s´c ceny S(2) nasz portfel ma tak¸a sam¸a

warto´s´c jak opcja, co wynika z przeprowadzonych powy˙zej oblicze´

n.

Jak wiadomo, warto´sci C(0), C

u

(1), C

d

(1) mo˙zemy obliczy´c innym sposo-

bem, kt´

ory nie wymaga znalezienia wszystkich portfeli strategii replikuj¸acej.

Mianowicie mamy

p

∗

=

r

− d

u

− d

=

2
3

,

oraz na podstawie wzoru na cen¸e opcji jako warto´sci oczekiwanej zdyskon-
towanej wyp laty (4.2), (4.3)

C

u

(1) = 1, 1

−

1

2

3

· 52, 8 +

1
3

· 9, 6

= 34, 91

C

d

(1) = 1, 1

−

1

2

3

· 9, 6 +

1
3

· 0

= 5, 81

C

(0) = 1, 1

−

1

2

3

· 34, 91 +

1
3

· 5, 82

= 22, 96

Widzimy, ˙ze dostajemy te same liczby, a metoda jest bardzie wygodna.

4.2.3 Wycena dowolnego instrumentu pochodnego

Rozwa˙zmy dowolny instrment pochodny f (S(2)) z terminem realizacji T = 2.
W chwili 1 definiujemy pomocniczy instrument pochodny dany przez ceny w
chwili 1 przy za lo˙zeniu jakie s¸a ceny po pierwszym etapie

D

(1) =

D

u

(1) = (1 + r)

−

1

[p

∗

f

(S

uu

) + (1 − p

∗

)f (S

ud

)] gdy S(1) = S

u

D

d

(1) = (1 + r)

−

1

[p

∗

f

(S

du

) + (1 − p

∗

)f (S

dd

)] gdy S(1) = S

d

Zauwa˙zmy, ˙ze D(1) jest instrumentem pochodnym, tzn. jest pewn¸a funkcj¸a
ceny waloru bazowego S(1):

D

(1) = g(S(1)) = (1 + r)

−

1

p

∗

f

(S(1)(1 + u)) + (1 − p

∗

)f (S(1)(1 + d))

,

g

(x) = (1 + r)

−

1

p

∗

f

(x(1 + u)) + (1 − p

∗

)f (x(1 + d))

.

4. Wycena Opcji - Model Dwumianowy

45

Obliczamy jego cen¸e w chwili 0, co da nam cen¸e D(0) instrumentu o funkcji
wyp laty f

D

(0) = (1 + r)

−

1

p

∗

D

u

(1) + (1 − p

∗

)D

d

(1)

= (1 + r)

−

1

p

∗

(1 + r)

−

1

p

∗

f

(S

uu

) + (1 − p

∗

)f (S

ud

)

+ (1 + r)

−

1

(1 − p

∗

)(1 + r)

−

1

p

∗

f

(S

du

) + (1 − p

∗

)f (S

dd

)

= (1 + r)

−

2

p

2

∗

f

(S

uu

) + 2p

∗

(1 − p

∗

)f (S

ud

) + (1 + p

∗

)

2

f

(S

dd

)

gdy˙z S

ud

= S

du

.

Jest to wz´

or na warto´s´c oczekiwan¸a zmiennej losowej o rozk ladzie dwu-

mianowym. Taki rozk lad ma zmienna losowa f (S(2)). Mo˙zemy wi¸ec kr´

otko

zapisa´c

D

(0) = E

∗

((1 + r)

−

2

f

(S(2)).

4.3 Opcja ameryka´

nska

Ograniczymy si¸e do przyk lad´

ow.

Przyk lad 4.6

Rozpatrujemy ameryka´

nsk¸a opcj¸e kupna z cen¸a realizacji K = 120 przy S(0) =

120, u = 0, 2, d = −0, 1, r = 0, 1.

• W chwili 0 oczywi´scie nie warto wykorzysta´c opcji.

• W chwili 1,

◦ gdy S(1) = 144 to wykorzystanie opcji przynosi 24 z l. Zamiast tego

lepiej sprzeda´c opcj¸e, kt´

orej warto´s´c nie mo˙ze by´c ni˙zsza ni˙z warto´s´c

wyliczonej powy˙zej opcji europejskiej, czyli 34,91 z l.

◦ gdy S(1) = 108 to opcja jest poza cen¸a i nie warto jej wykorzysta´c,

mo˙zemy natomiat j¸a sprzeda´c za 5,82 z l.

• W chwili 2 nie ma r´

o˙znicy mi¸edzy opcj¸a ameryka´

nsk¸a i europejsk¸a.

Widzimy, ˙ze nie op laca si¸e opcji wykorzysta´c przed terminem realizacji i w

zwi¸azku z tym ich ceny opcji ameryka´

nskiej i europjskiej musz¸a by´c takie same.

Teraz por´

ownamy cen¸e europejskiej i ameryka´

nskiej opcji sprzeda˙zy.

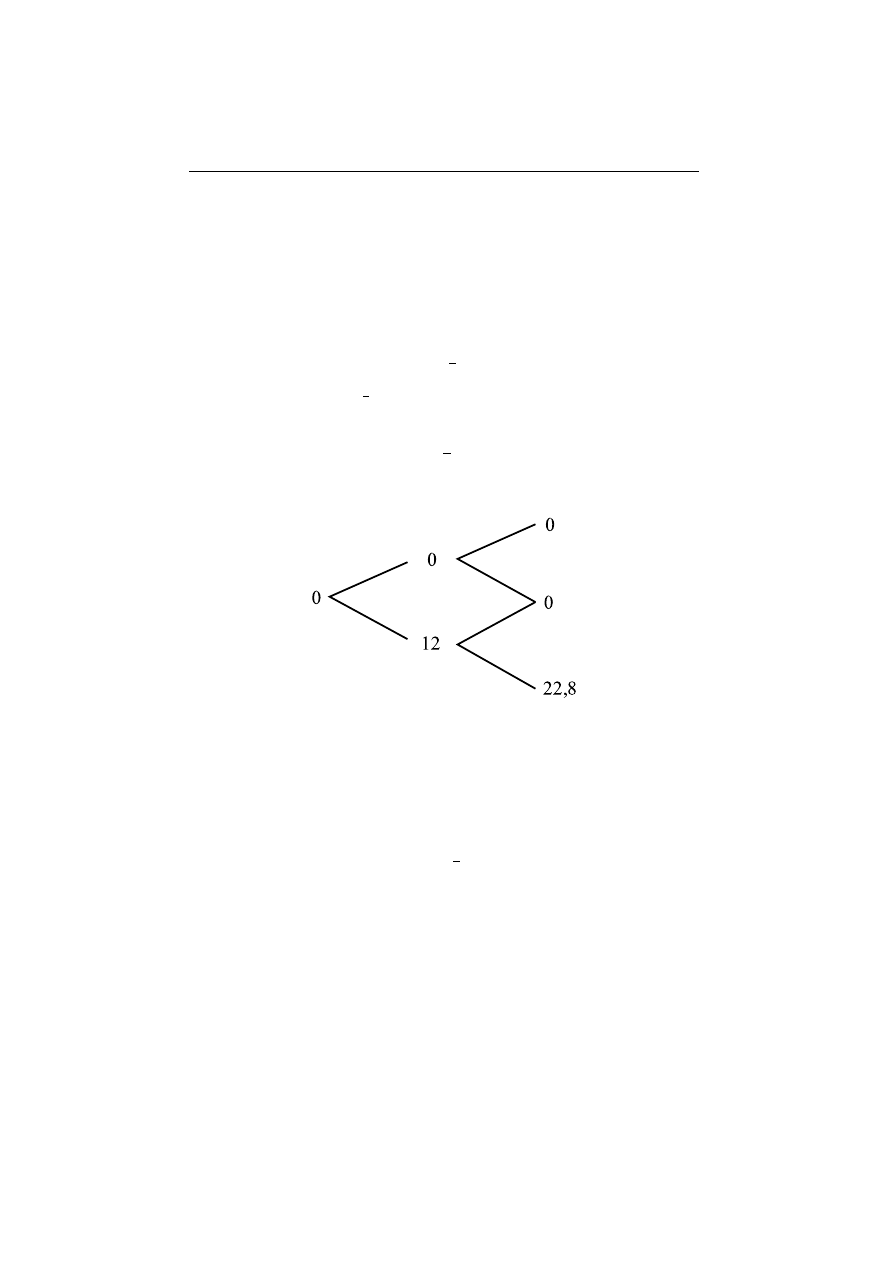
46

Wst¸ep do matematyki finansowej

Przyk lad 4.7

Pozostajemy w realiach poprzedniego przyk ladu analizuj¸ac opcj¸e sprzeda˙zy
(put) z tym samym K = 120. W chwili 2 jedynie dla wariantu dd mamy
K

− S(2) = 22, 8 > 0, a zero pojawia si¸e w pozosta lych przypadkach. A wi¸ec

dla pomocniczego instrumentu P (1) w chwili 1, jego warto´s´c w g´

ornej pozycji,

gdy na pierwszym etapie mamy u, jest zero. Gdy na pierwszym etapie mamy
d

, to

P

d

(1) = 1, 1

−

1

·

1
3

· 22, 8 = 6, 91

(przypominamy ˙ze p

∗

=

2
3

, warto´s´c 22,8 pojawia si¸e przy ruchu w d´

o l, co

odpowiada prawdopodobie´

nstwu (1 − p

∗

)). A wi¸ec w chwili 0 mamy

P

(0) = 1, 1

−

1

·

1
3

· 6, 91 = 2, 09.

Mo˙zliwe wyp laty dla ameryka´

nskiej opcji kupna przedstawia Rysunek 4.6. Je-

Rysunek 4.6

dyn¸a interesuj¸ac¸a sytuacj¸a jest chwila 1, gdy na pierwszym etapie mamy ruch
d

. Wykorzystanie opcji daje 12 czyli wi¸ecej ni˙z 6,91, co jest warto´sci¸a opcji

przy za lo˙zeniu czekania do ostatniej chwili. A wi¸ec do obliczenia ceny opcji
ameryka´

nskiej bierzemy t¸e wi¸eksz¸a liczb¸e i mamy

P

(0) = 1, 1

−

1

·

1
3

· 12 = 3, 64

— istotnie wi¸ecej ni˙z dla opcji europejskiej.

Ostatni przyk lad pokazuje, ˙ze mo˙ze si¸e op laca´c wcze´sniej zrealizowa´c ame-

ryka´

nsk¸a opcj¸e kupna tu˙z przed wyp lat¸a dywidendy.

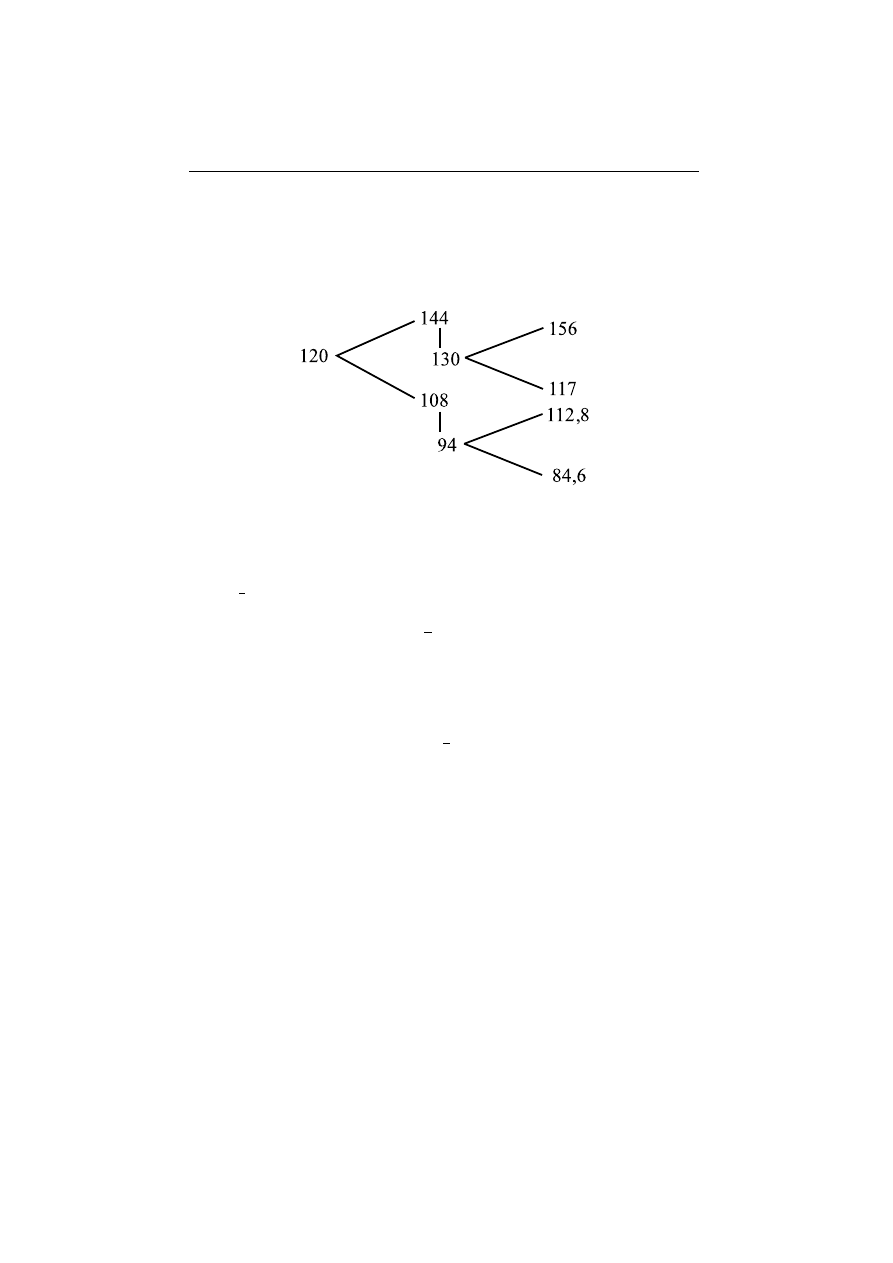
4. Wycena Opcji - Model Dwumianowy

47

Przyk lad 4.8

Za l´

o˙zmy, ˙ze w poprzedniej sytuacji mamy wyp lat¸e dywidendy pomi¸edzy chwil-

ami 1 i 2 w wysoko´sci 14 z l. Podstaw¸a wyliczenia cen w chwili 2 s¸a ceny z
chwili 1 obni˙zone o dywidend¸e, co daje liczby takie jak na Rysunku 4.7. Mamy

Rysunek 4.7

jeden przypadek, w kt´

orym opcja kupna za 120 jest w cenie w chwili 2, co

odpowiada ruchom cen uu. Dla opcji europejskiej w chwili jeden mamy warto´sci
1, 1

−

1

·

2
3

· 36 = 21, 18 i 0. Wi¸ec w chwili 0 dostajemy

C

e

= 1, 1

−

1

2
3

· 21, 18 = 12, 84.

Wida´c, ˙ze w chwili 1 przy pierwszym ruchu u op laca si¸e wykorzysta´c opcj¸e
ameryka´

nsk¸a gdy˙z daje to zysk 24, czyli wi¸ecej ni˙z 21,18 — warto´s´c opcji

wykorzystywanej w ostatniej chwili. Dostajemy

C

a

= 1, 1

−

1

·

2
3

· 24 = 14, 54

— opcja ameryka´

nska jest dro˙zsza ni˙z opcja europejska, co jest zgodne z tym,

˙ze jej wi¸eksze mo˙zliwo´sci mo˙zemy z zyskiem wykorzysta´c.