Topologia

X – przestrzeń (zbiór niepusty)

Iloczyn kartezjański zbiorów A i B





B

b

A

a

b

a

B

A









,

:

)

,

(

Metryka (odległość)

 

0

:









R

X

X

d

)

,

(

)

,

(

)

,

(

3

)

,

(

)

,

(

2

0

)

,

(

1

z

y

d

y

x

d

z

x

d

x

y

d

y

x

d

y

x

y

x

d

o

o

o













nierówność trójkąta





r

a

x

d

X

x

r

a

k

r

a







)

,

(

:

)

,

(

:

promieniu

i

środku

o

otwarta

Kula

)

,

(

)

,

(

punktu

Otoczenie

r

x

k

r

x

O







r

a

x

d

X

x

r

a

S









)

,

(

0

:

)

,

(

X



 A

x

jest punktem wewnętrznym zbioru A jeżeli istnieje takie
otoczenie punktu x , które jest zawarte w zbiorze A.

Zbiór otwarty każdy jego punkt jest punktem wewnętrznym.

Dopełnie
nie





A

y

X

y

A







:

'

Punkt x jest punktem skupienia zbioru A jeżeli każde
otoczenie tego punktu zawiera co najmniej jeden punkt
zbioru A .

Zbiór nazywa się zbiorem domkniętym, jeżeli zawiera
wszystkie swoje punkty skupienia.

Twierdzenie. Dopełnienie zbioru otwartego jest
zbiorem domkniętym, dopełnienie zbioru domkniętego
jest zbiorem otwart
Zbieżność

Mówi się, że ciąg punktów jest
zbieżny do punktu jeżeli punkt ten jest jedynym
punktem skupienia tego ciągu.





,...

,

2

1

a

a

a

n





















)

,

(

0

0

n

o

x

x

d

N

n

N

Norma Iloczyn

skalarny

V przestrzeń liniowa nad ciałem liczb rzeczywistych.
Iloczyn skalarny na przestrzeni V nazywamy funkcjonał
,
który jest dwuliniowy, symetryczny i odpowiadająca mu
forma kwadratowa jest dodatnio określona:

 

R



V

V

:

.,.

.

0

każażde

dla

0

)

,

(

(c)

,

)

,

(

)

,

(

)

(

,

,

,

)

,

(

)

,

(

)

,

(

)

(



















x

x

x

x

x

y

y

x

b

R

z

y

x

z

y

z

x

z

y

x

a

V

V

















V

V

V

V



































y

x

y

x

y

x

y

x

d

y

x

y

x

y

x

c

x

x

x

b

x

x

x

a

,

dla

2

)

(

,

dla

)

(

R

i

dla

)

(

0

0

0

i

dla

0

)

(

2

2

2

2







Norm
a

)

,

( x

x

x 

Twierdzenie (własności normy)

y

x

y

x

d





)

,

(

Twierdzenie (nierówność Schwarza)
Jeśli v, w są wektorami w przestrzeni

euklidesowej V , to

Wektorowa przestrzeń z iloczynem skalarnym
nazywana jest przestrzenią euklidesową.

w

v

w

v

,



2

,

w

w

v





2

2

2

2

2

2

2

2

2

,

,

,

2

,

,

2

,

,

0

w

w

w

w

w

w

w

w

w

w

w

v

v

v

v

v

v

v

v

v

v































w

w

w

w

w

w

w

w

v

v

v

v

v

v

v

v











,

,

,

,

0

2

2

2

2

2

2

2

2

2

Pochodna

cząstkowa

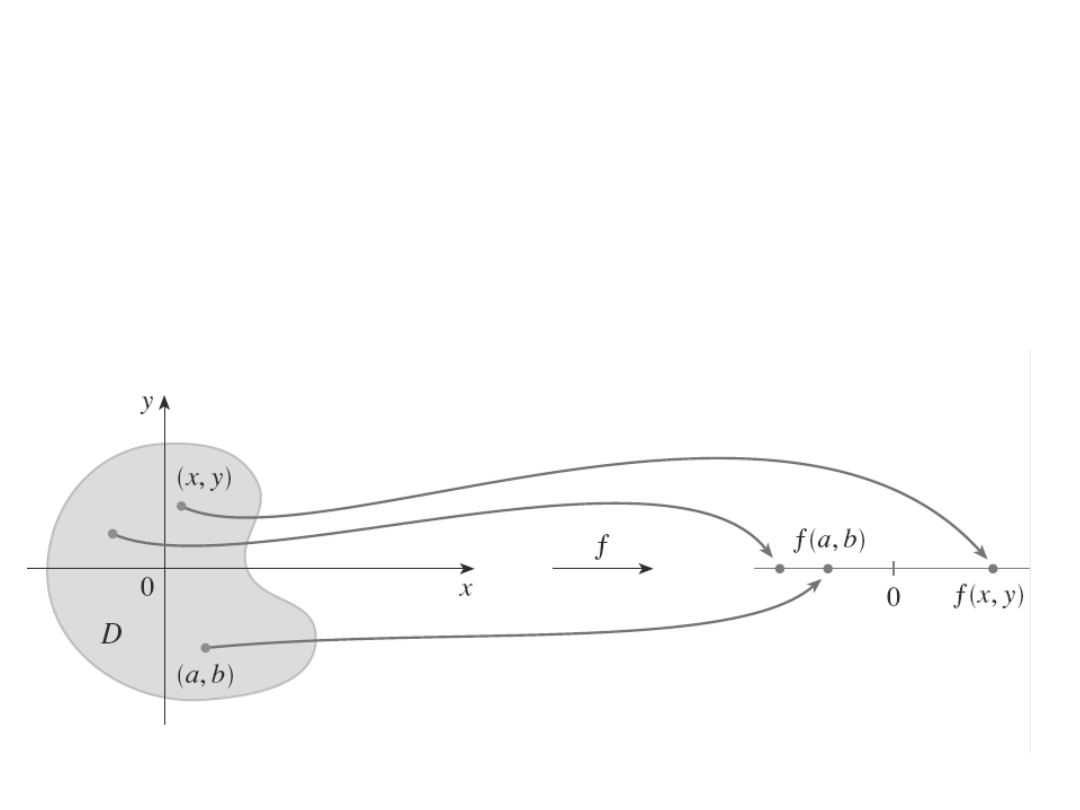
Definicja

Funkcja f dwóch zmiennych to

reguła

przyporządkowująca każdej parze

(

x, y)

liczb (ze

zbioru będącego dziedziną tej funkcji) w sposób
jednoznaczny liczbę rzeczywistą.

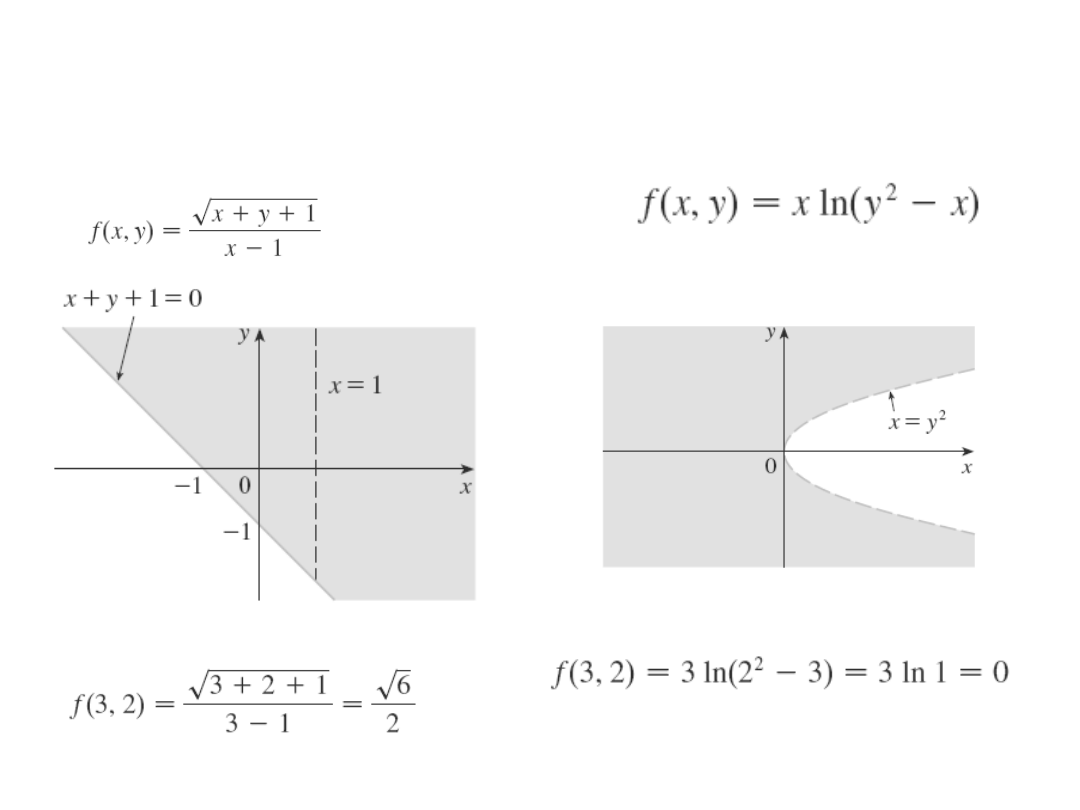
Przykład 1.

Znajdź dziedzinę następujących funkcji i oblicz ich
wartość w punkcie (2,3):

a)

b)

)

,

( y

x

f

z 

2

R

D

y

x





)

,

(

R

D

f



:

D dziedzina
funkcji

Funkcja dwóch
zmiennych

dla

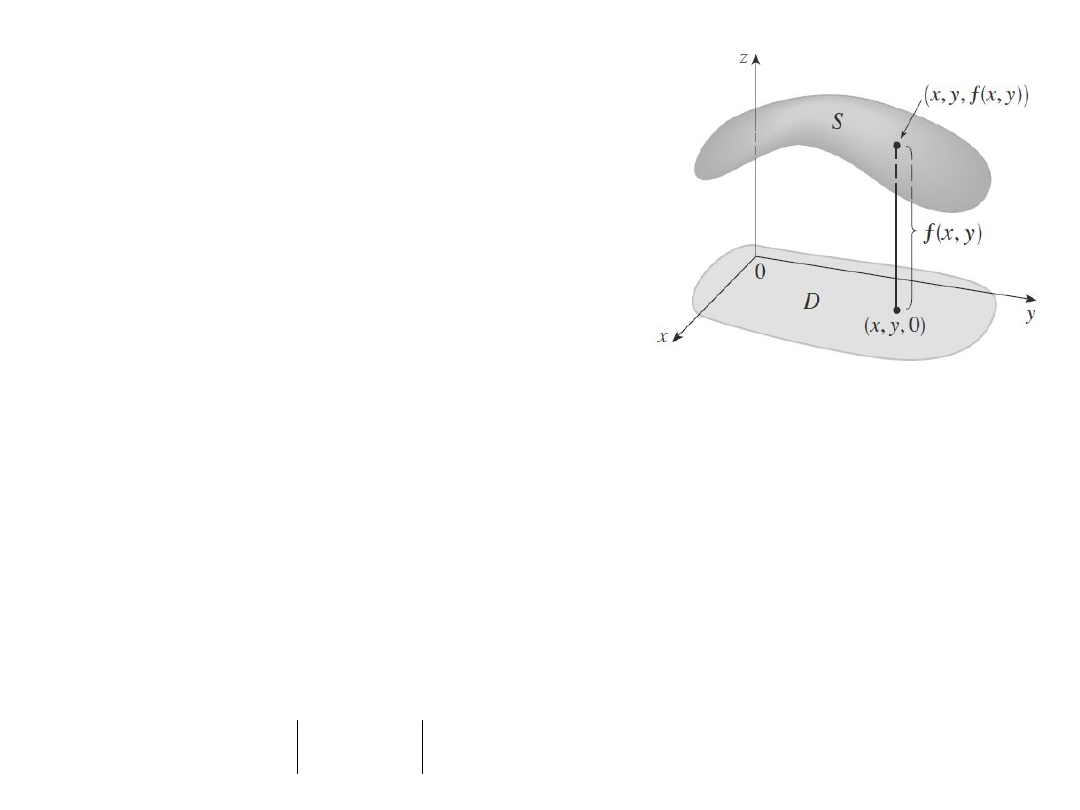
Definicja: Wykresem funkcji dwóch zmiennych
nazywamy zbiór punktów przestrzeni trójwymiarowej
postaci

3

R

))

,

(

,

,

(

y

x

f

y

x

Q

2

R

D

y

x





)

,

(

dla

Definicja: Funkcję f(x,y) nazywamy ograniczoną w
zbiorze Z , jeżeli istnieje taka liczba M , że dla
każdego spełniona jest nierówność:

Z

y

x



)

,

(

M

y

x

f



)

,

(

Różniczkowanie

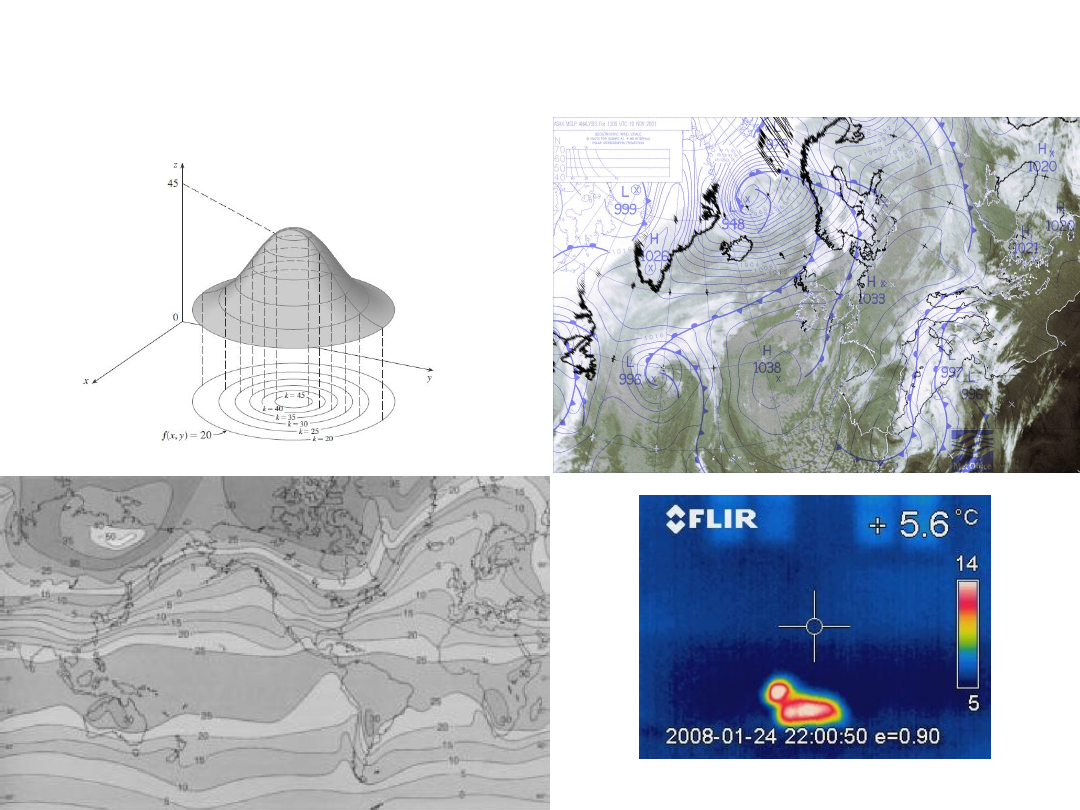
Krzywe

ekwipotencjalne

)

,

( y

x

f

k 

Funkcja wielu

zmiennych

P

x

x

x

x

x

x

f

y

n

n





)

,...,

,

(

)

,...,

,

(

2

1

2

1

Dziedzina – przeciwdziedzina





)

(

)

,...,

,

(

),

,...,

,

(

:

P

f

P

x

x

x

x

x

x

f

y

y

n

n







2

1

2

1

Definicja (granica funkcji Heinego). Liczbę g
nazywamy granicą podwójną funkcji f(x,y) w punkcie
, jeżeli dla każdego ciągu punktów
zbieżnego do odpowiadający mu ciąg
wartości jest zbieżny do g .

)

,

(

0

0

0

y

x

P

0

)

,

(

P

P

y

x

P

n

n

n

n



)

,

(

0

0

0

y

x

P





)

(

n

P

f

Granica i ciągłość

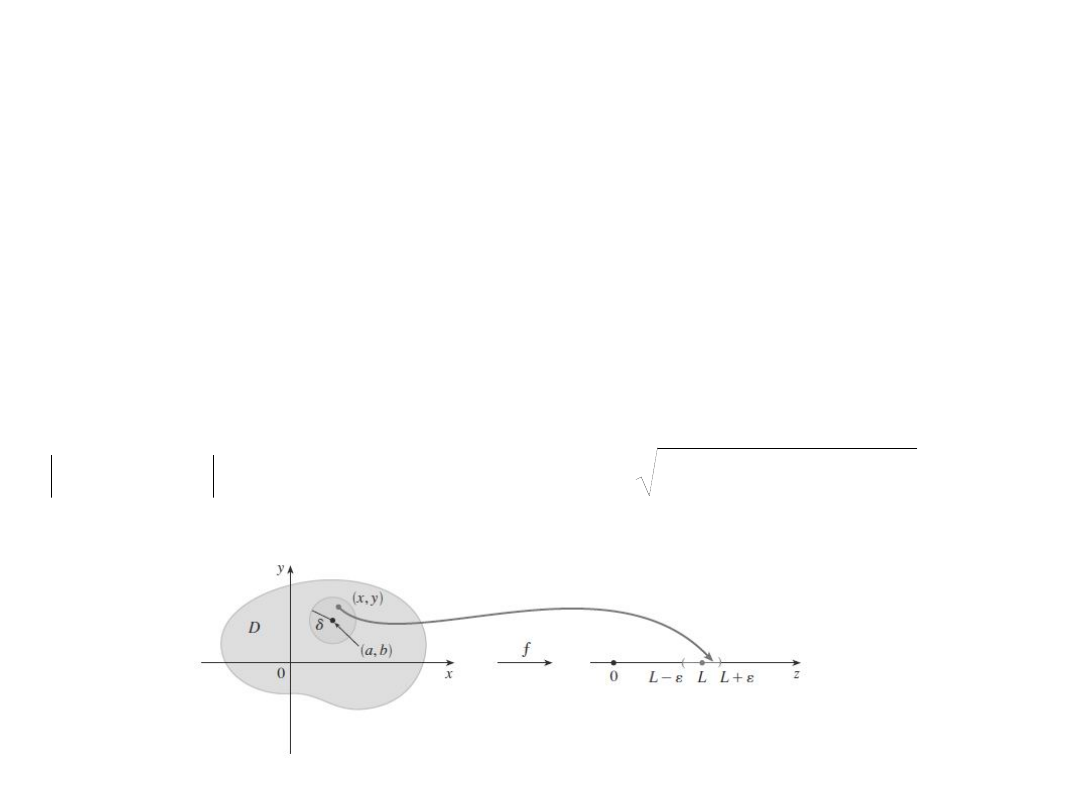
Niech f będzie funkcją dwóch zmiennych i niech
punkt (a,b). Mówimy, że granica funkcji f(x,y) gdy
(x,y) dąży do (a,b) jest równa L i zapisujemy:

 
Jeżeli dla każdego



> 0 istnieje taka liczba



> 0

taka, że

L

y

x

f

b

a

y

x





)

,

(

lim

)

,

(

)

,

(

Definicja





















2

2

)

(

)

(

0

i

)

,

(

)

,

(

b

y

a

x

D

y

x

L

y

x

f

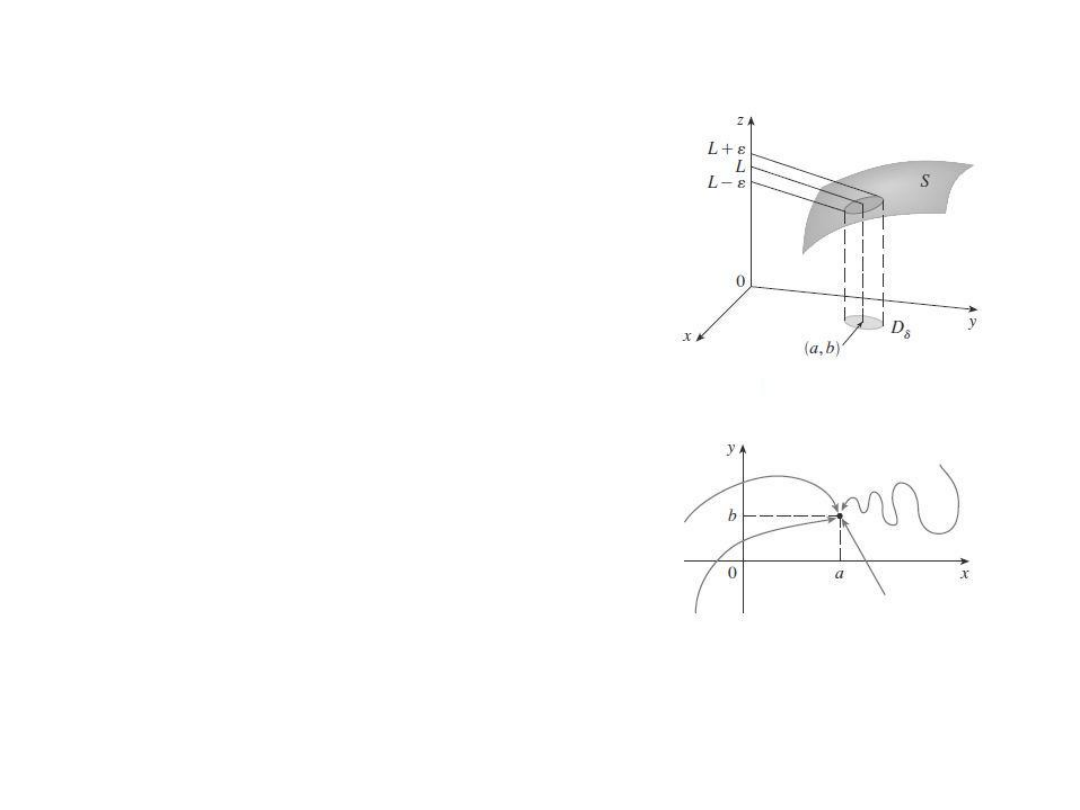
Jeżeli f(x,y)



L

1

gdy (x,y)



(a,b) wzdłuż drogi C

1

i

f(x,y)



L

2

gdy (x,y)



(a,b)

wzdłuż drogi C

2

gdzie L

1



L

2

wtedy

nie istnieje.

)

,

(

lim

)

,

(

)

,

(

y

x

f

b

a

y

x



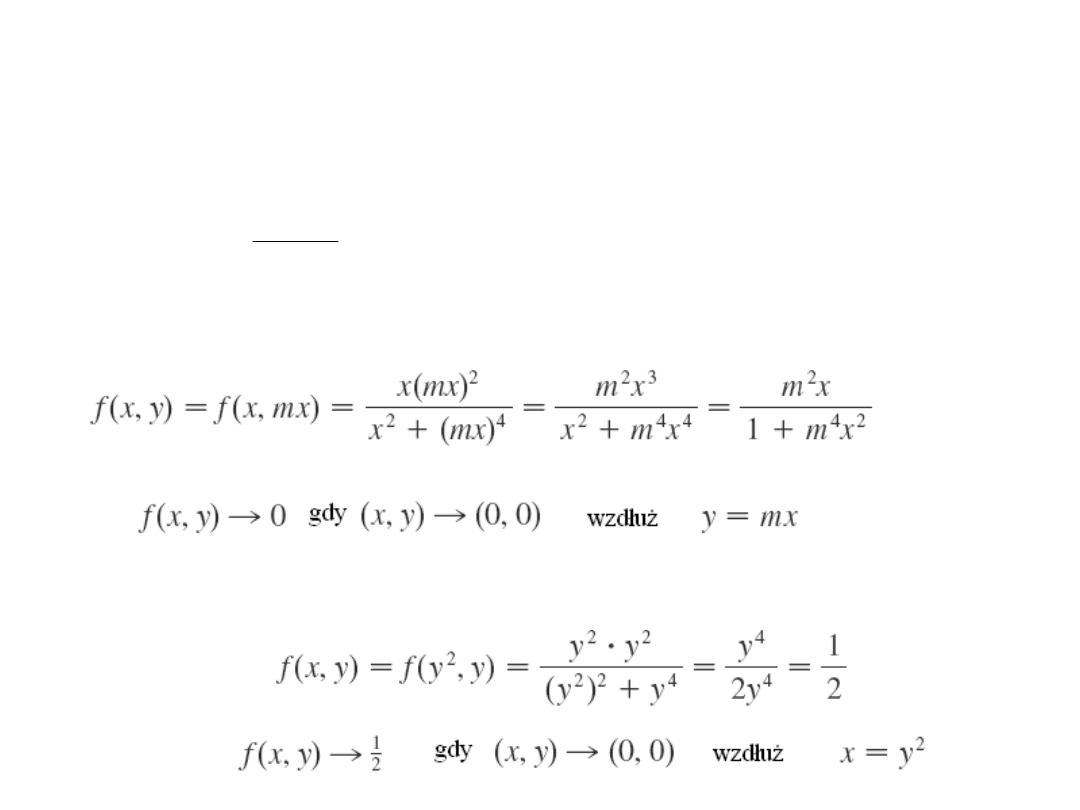
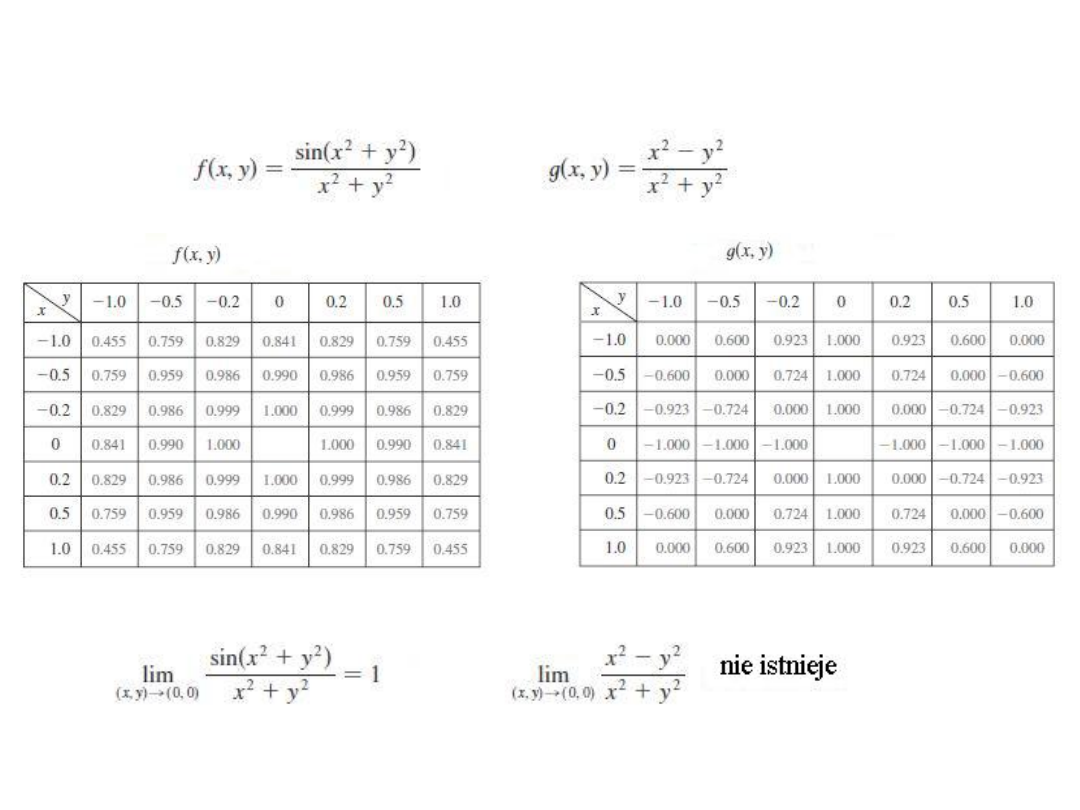
Jeżeli , czy istnieje ?

Przykład.

2

2

2

)

,

(

y

x

xy

y

x

f





)

,

(

lim

)

0

,

0

(

)

,

(

y

x

f

y

x



mx

y 

2

x

y 

Definicja  

Funkcja f(x,y) jest nazywana funkcją ciągła w
punkcie (a,b) jeżeli  

 

Mówimy, że funkcja jest ciągła na D jeżeli jest
ciągła w każdym punkcie (a,b) w D.

Ciągłość

)

,

(

)

,

(

lim

)

,

(

)

,

(

b

a

f

y

x

f

b

a

y

x





Pochodna cząstkowa

z = f(x,y)

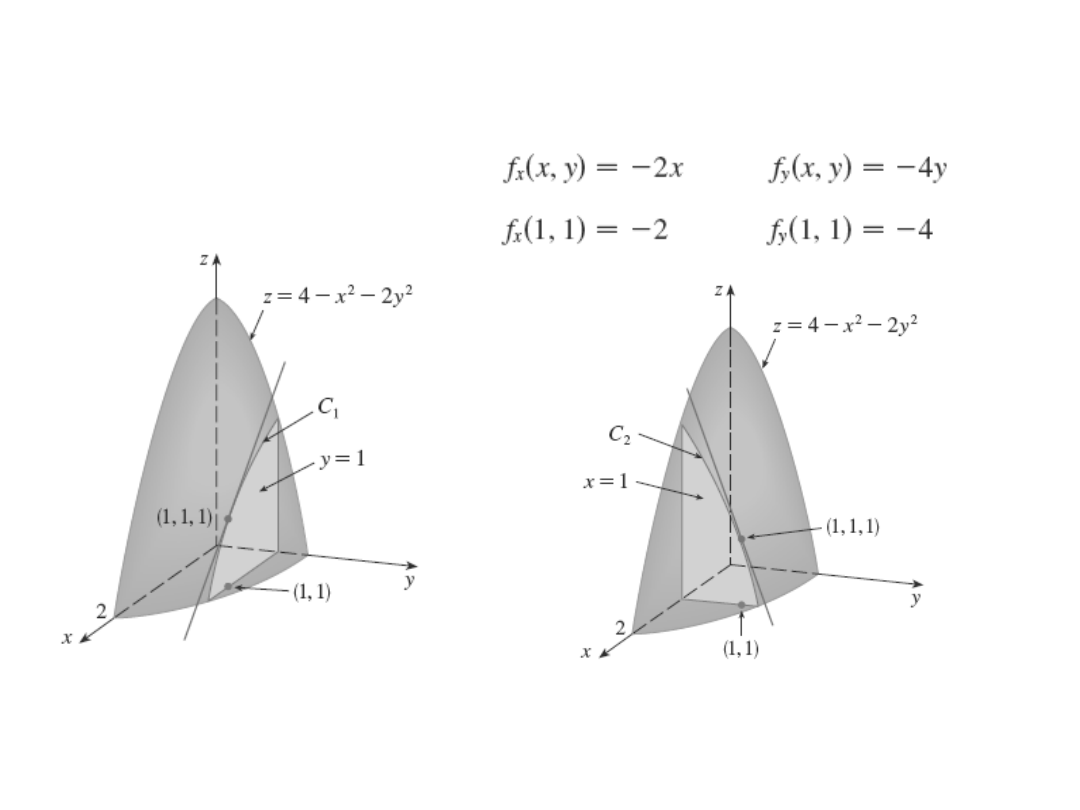
Przykłady interpretacji

geometrycznej

2

2

2

4

)

,

(

y

x

y

x

f







Krzywa C

1

jest parabolą z=2 – x

2

,

y=1

Krzywa C

2

jest parabolą z=3 – 2y

2

,

x=1

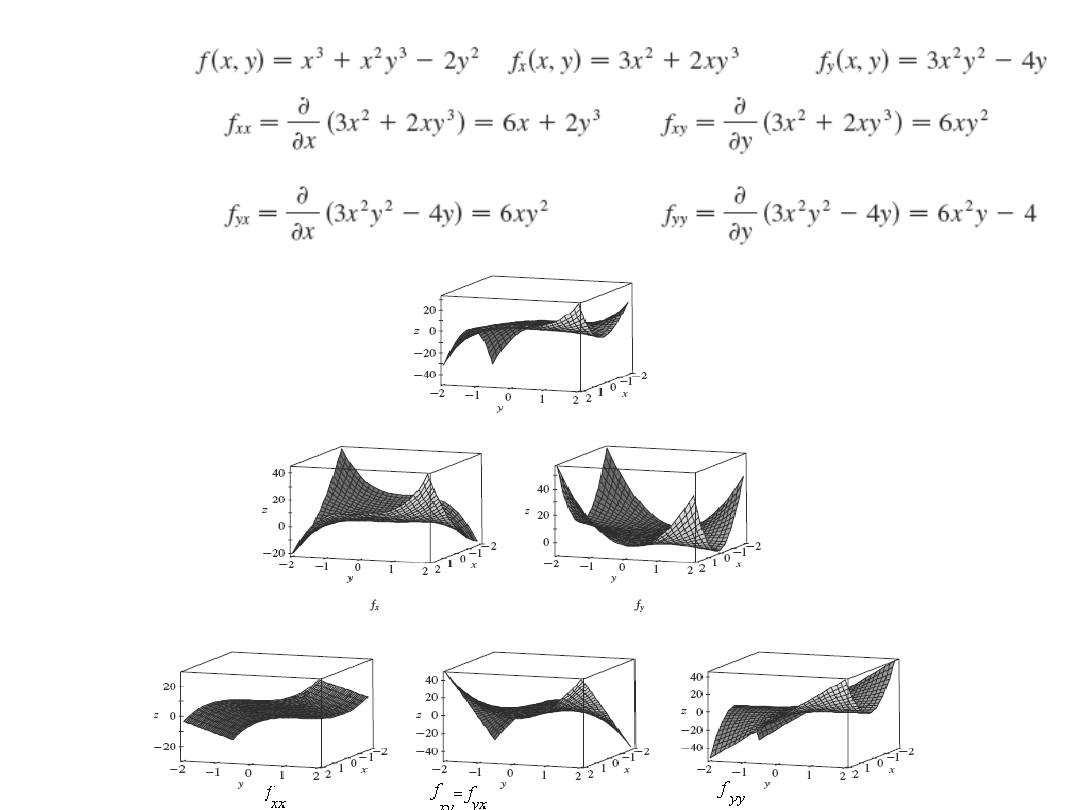
Pochodna funkcji n-zmiennych

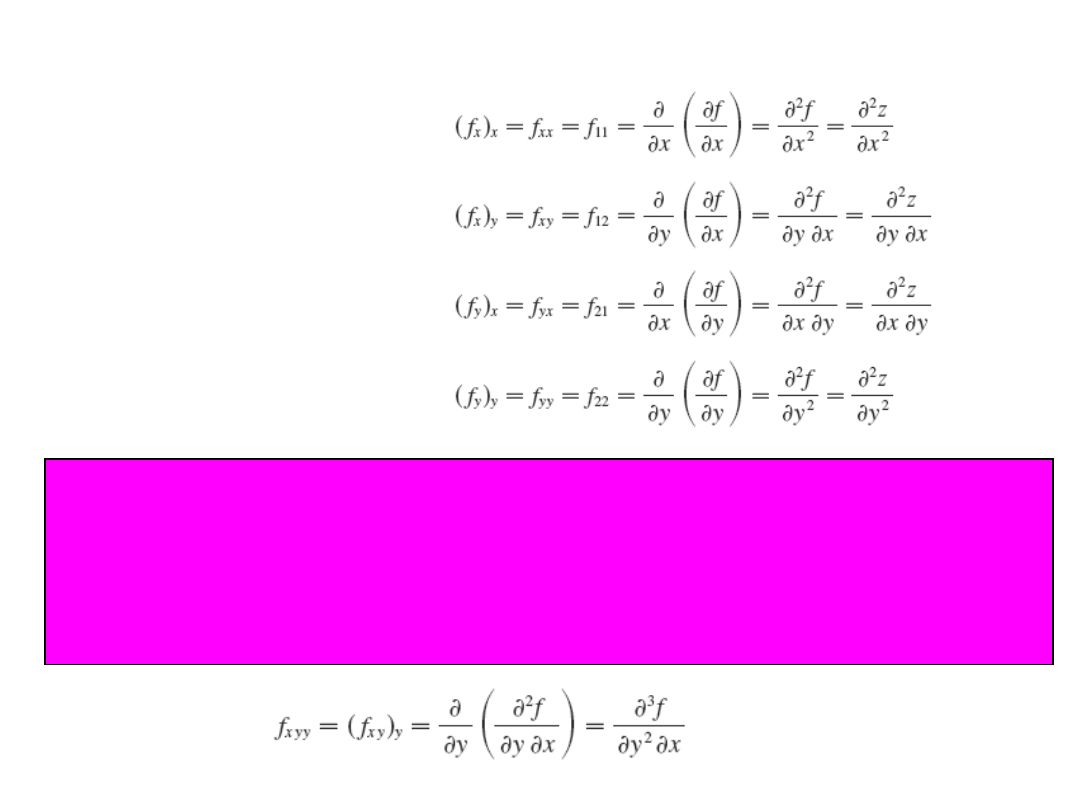
Pochodne wyższych rzędów

Twierdzenie

Niech f będzie funkcją określoną na D zawierającym (a,b). Jeżeli
funkcje f

xy

i f

yx

obie są ciągłe na D to zachodzi:

f

xy

(a,b) = f

yx

(a,b)

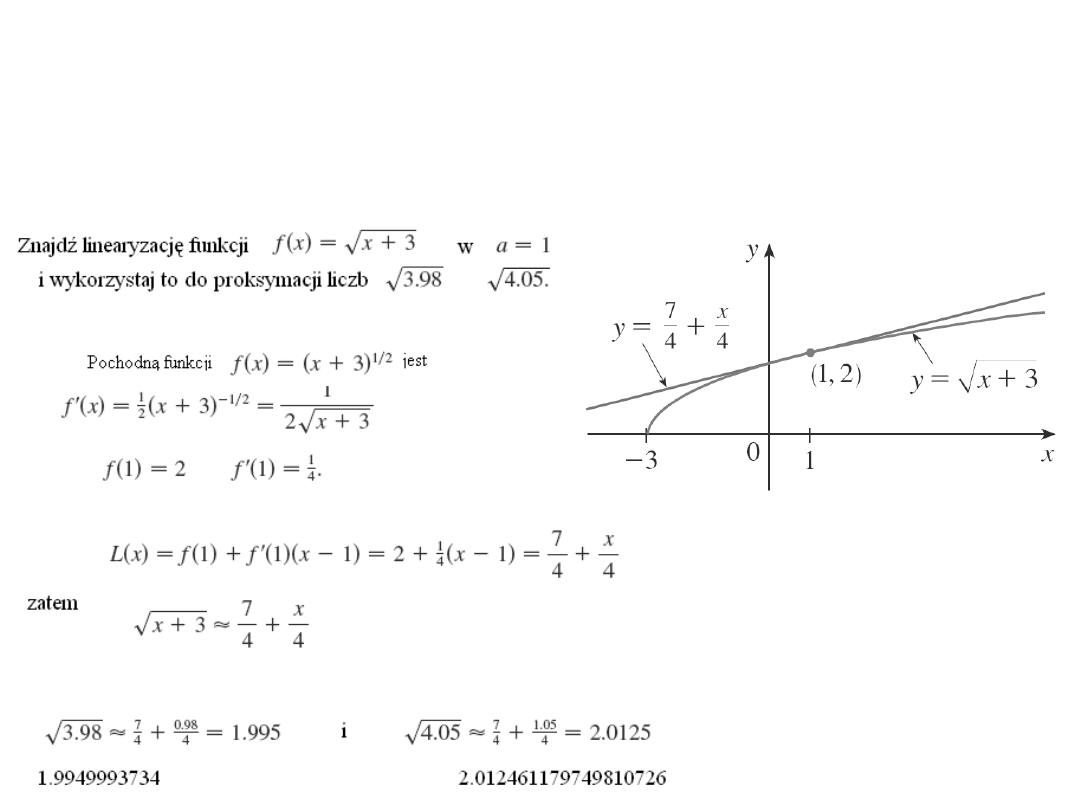
Przykła
d

Aproksymacja liniowa

Przykła
d

Przypuśćmy, że indyk po przygot

owaniu ma temperaturę 50

o

F i wkładamy go do piekarnika o temperaturze 325

o

F. Po

godzinie termometr mierzący temperaturę w mięsie
pokazuje 93

o

F, po dwóch godzinach 129

o

F . Jaka będzie

temperatura po upływie 3 godziny?
T(t) temperatura indyka po t
godzin.

Przykład

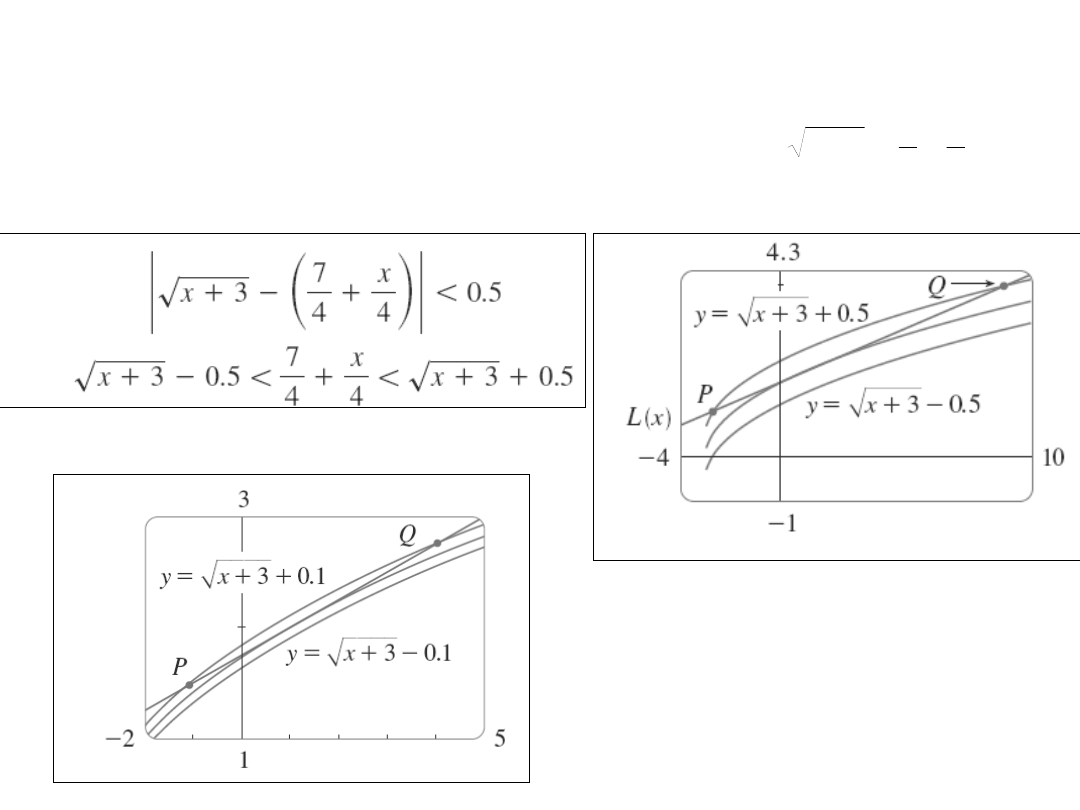
Dla jakich wartości x aproksymacja
liniowa :

daje dokładność do 0.5 ? A co dla
dokładność 0.1?

4

4

7

3

x

x







– 2,6 < x
<8,6

– 1,1 < x <3,9

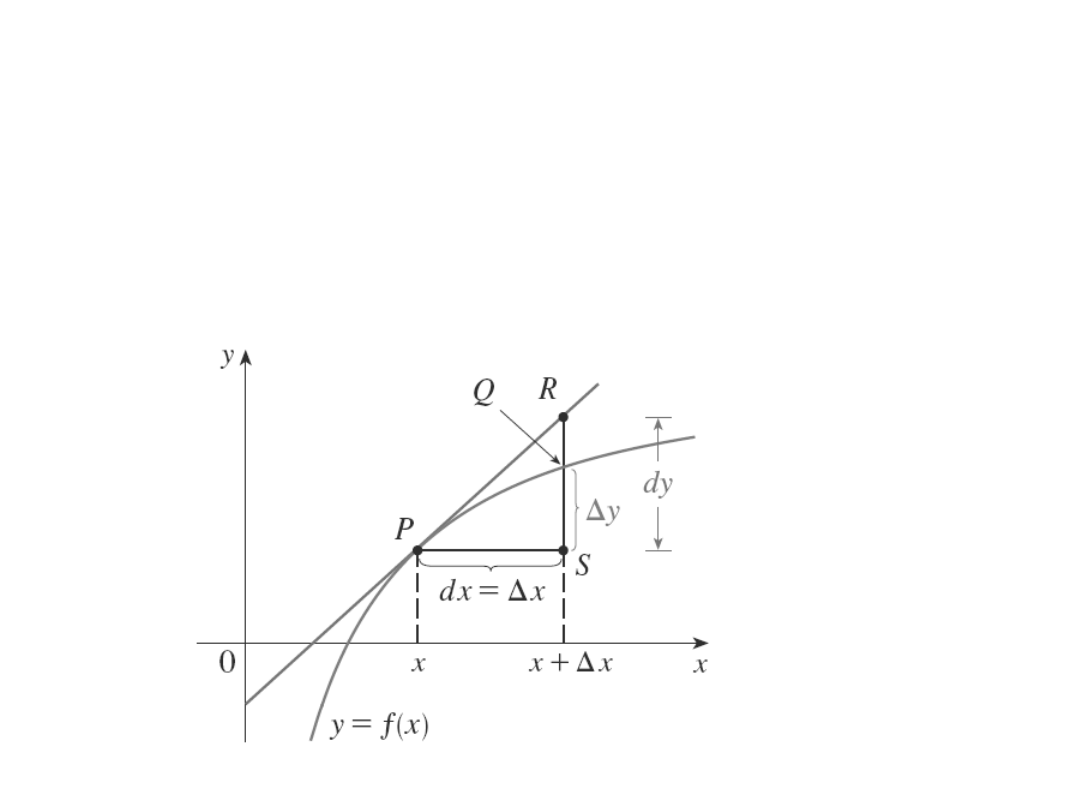
Różniczka

zupełna

)

(

)

(

))

(

,

(

)

(

x

f

x

x

f

y

x

x

f

x

x

Q

dx

x

f

dy























Przyrost wartości funkcji

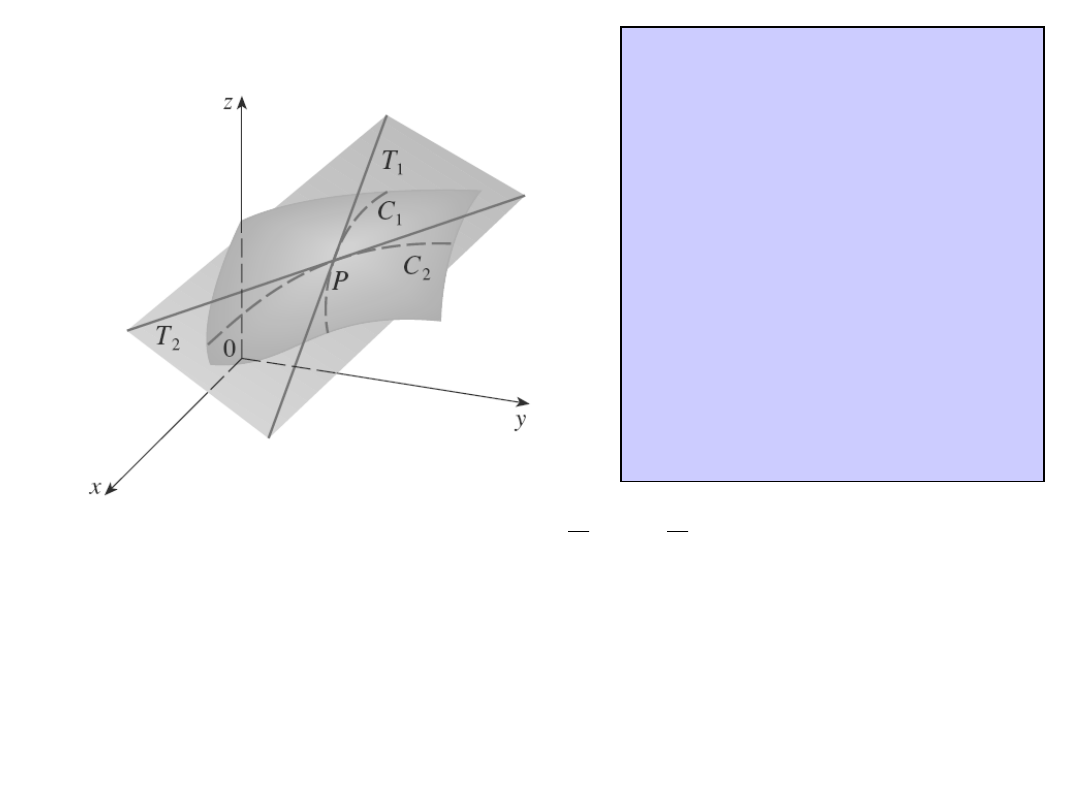
Płaszczyzna styczna

Załóżmy, że dana jest
powierzchnia S dana
równaniem z = f(x,y), gdzie f
posiada ciągłe pierwsze
pochodne cząstkowe i P(x

0

,y

0

,z

0

)

będzie punktem na S. Niech C

1

i

C

2

będą krzywymi otrzymanymi

po przecięciu powierzchni S
płaszczyznami y = y

0

i x = x

0

.

Punkt P leży na obu C

1

i C

2

.

Niech T

1

i T

2

będą liniami

stycznymi do krzywych C

1

i C

2

w

punkcie P. Powierzchnia styczna
zawiera obie proste T

1

i T

2

.

Równanie płaszczyzny
przechodzącej przez P(x

0

,y

0

,z

0

):

A(x – x

0

)+ B(y – y

0

) + C(z – z

0

)

= 0

)

,

(

)

(

)

(

)

(

0

0

0

0

0

0

0

0

y

x

f

a

y

y

x

x

a

z

z

y

y

b

x

x

a

z

z

C

B

b

C

A

a

x





























)

,

(

)

(

0

0

0

0

0

y

x

f

b

x

x

y

y

b

z

z

y











)

(

)

(

0

0

0

y

y

f

x

x

f

z

z

y

x











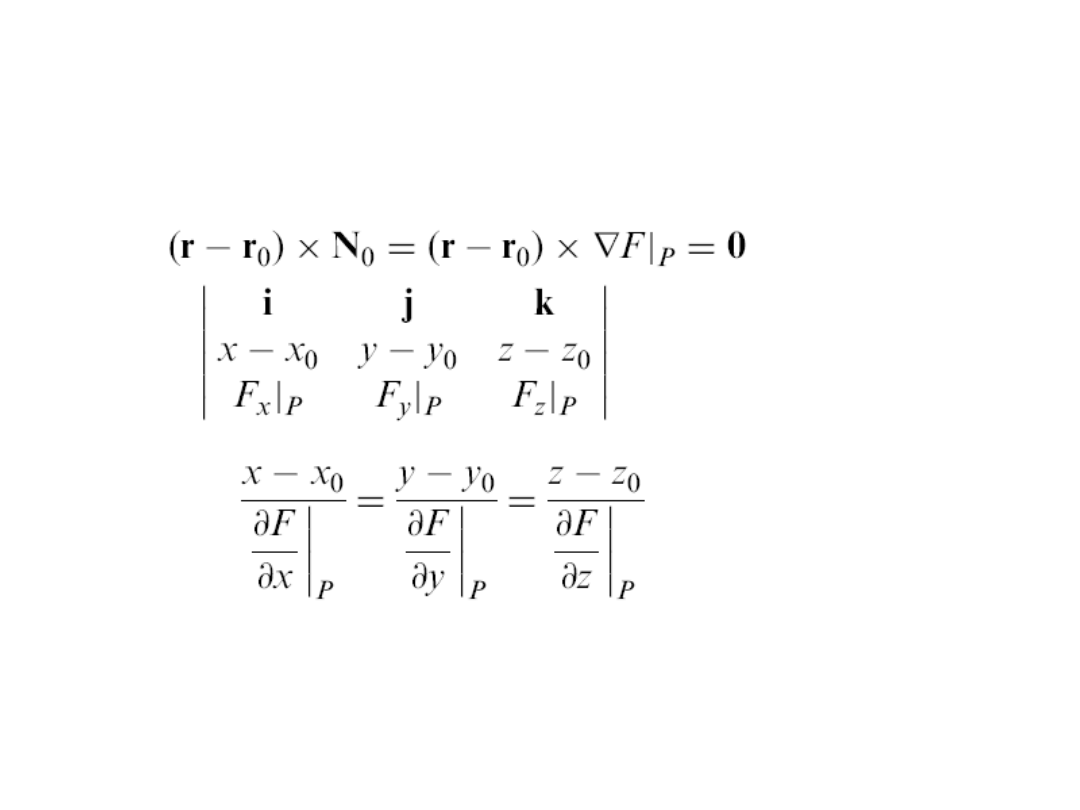
Normalna do

powierzchni

Dane powierzchnia F(x,y,z) = 0 i punkt P(x

0

,y

0

,z

0

)

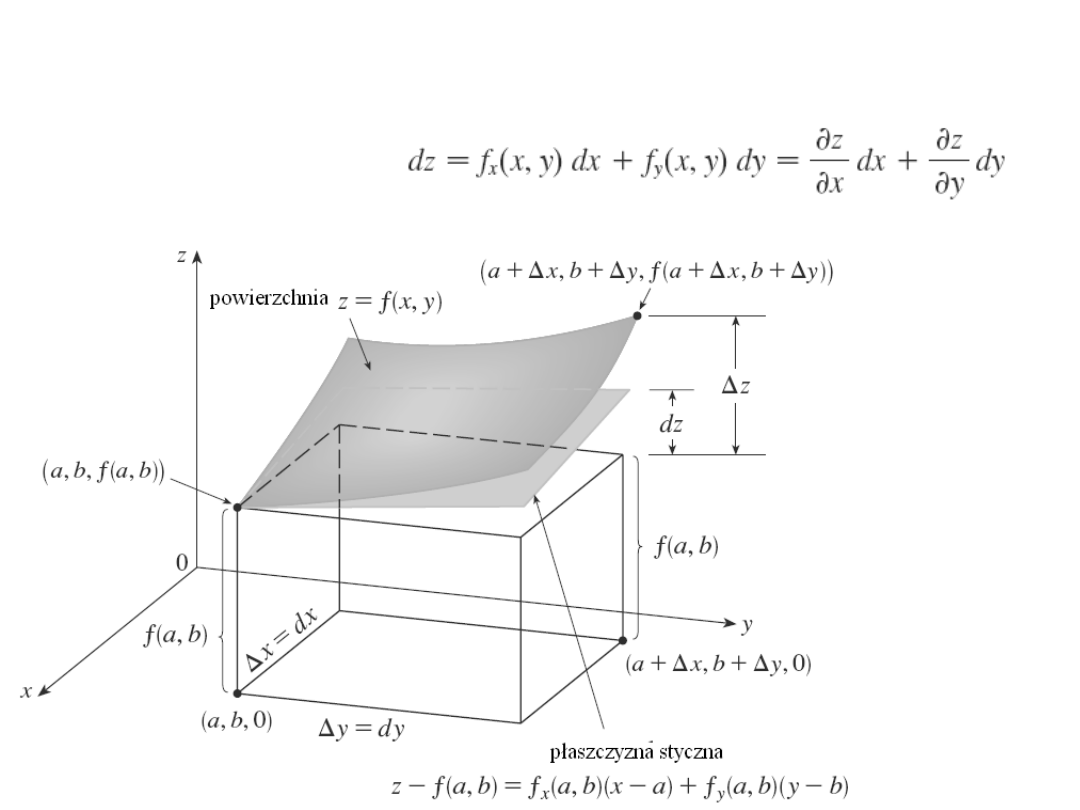
Różniczka funkcji dwóch

zmiennych

Różniczka zupełna

Różniczka funkcji wielu zmiennych

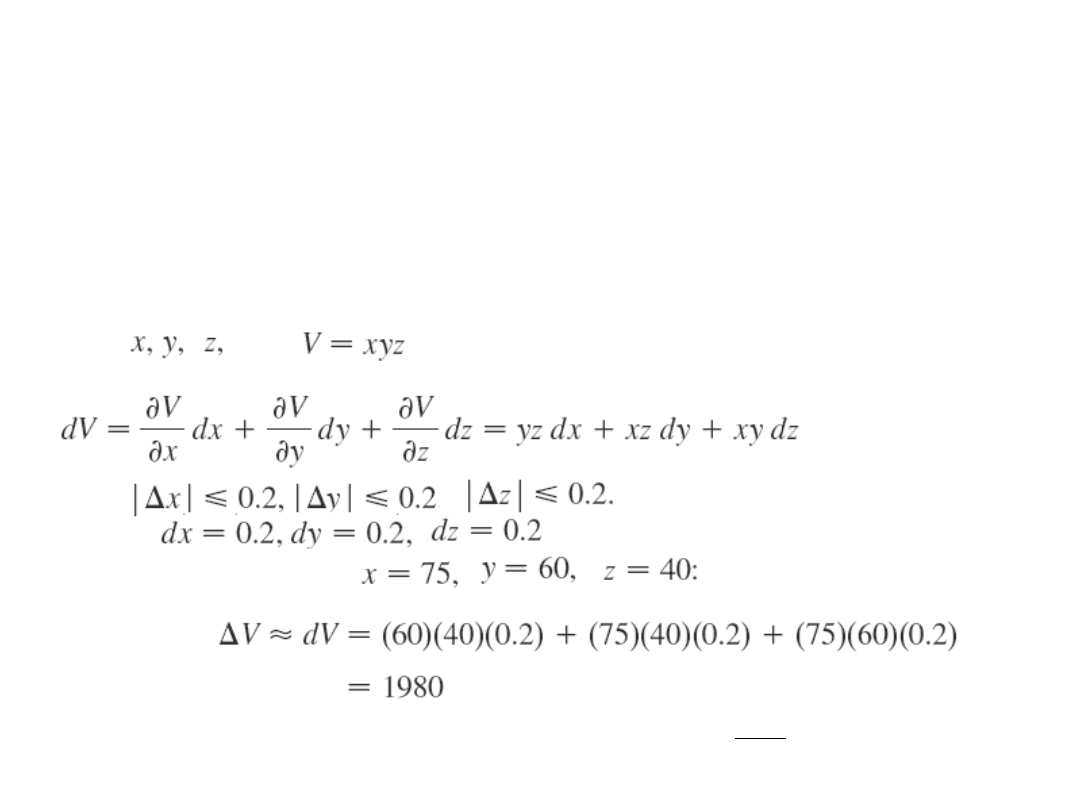
 Zmierzono krawędzie prostopadłościanu: 75 cm,
60 cm, 40 cm. Każdy z pomiarów wykonano z
dokładnością 0.2 cm. Używając różniczki oszacuj
możliwy błąd obliczonej objętości.

Przykład (analiza
błędu)

%

1





V

V

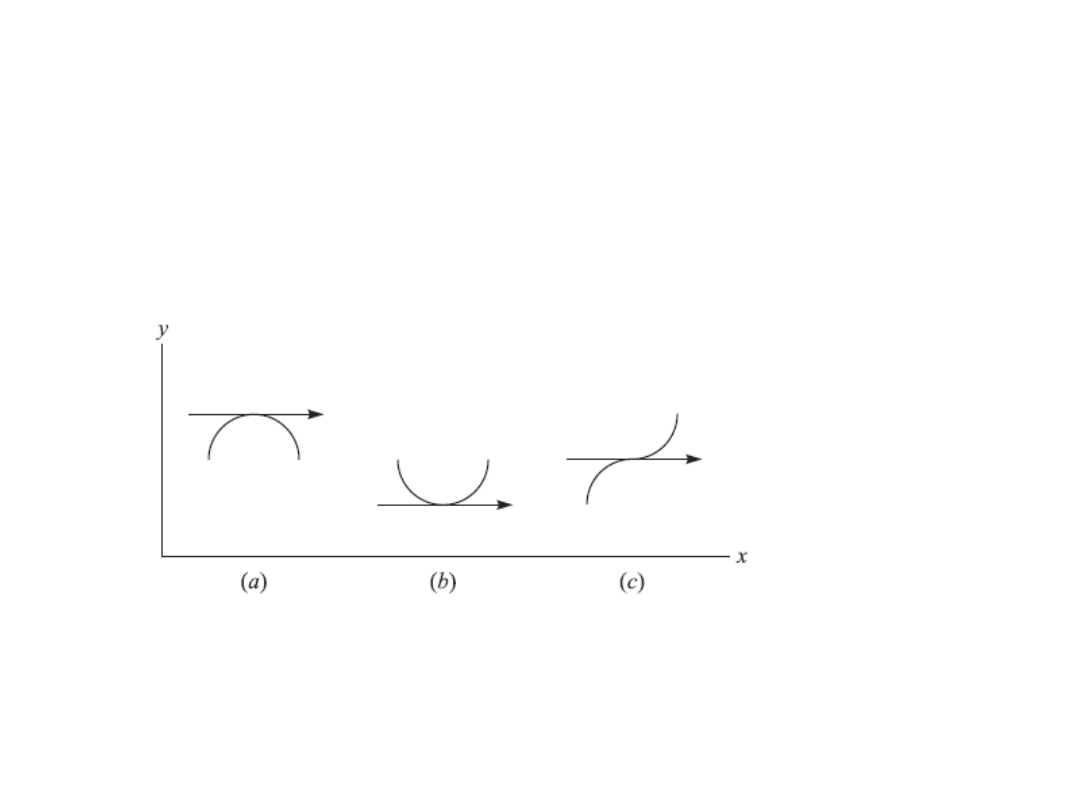
Maksimum i minimum funkcji

Funkcja jednej
zmiennej

0

0

0

)

(

)

(

0

)

(

)

(

0

0



















x

g

x

P

x

g

x

g

y

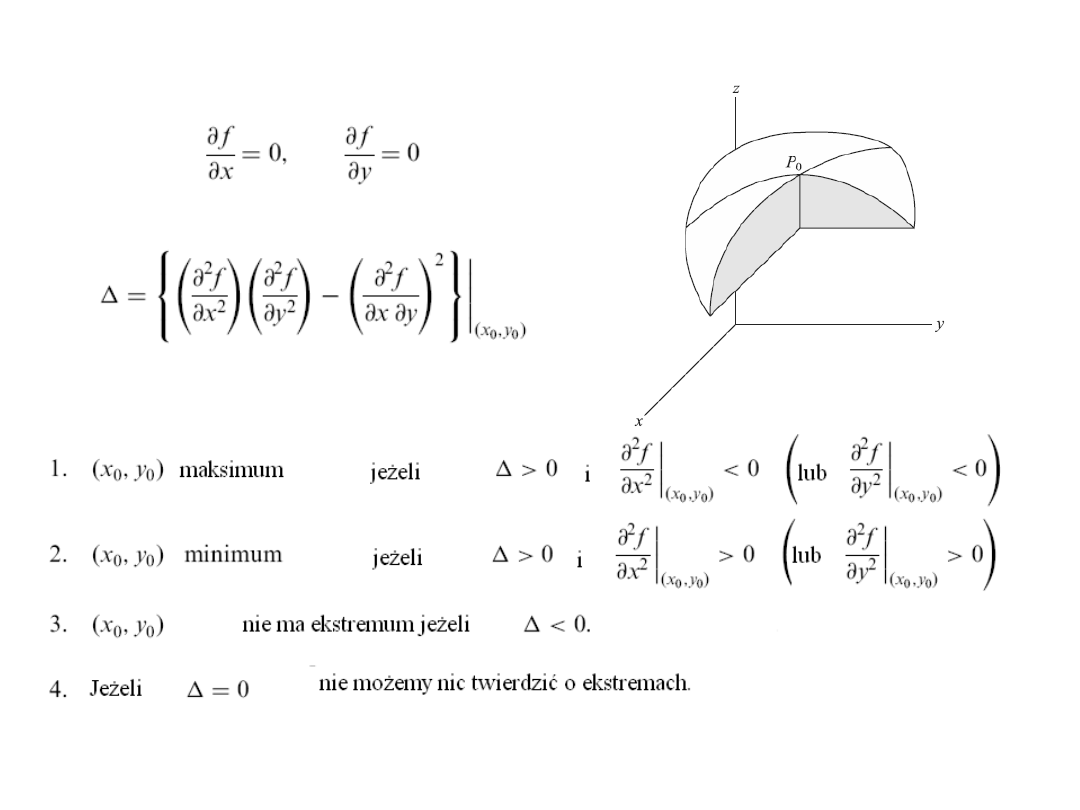
Dla

funkcji dwóch zmiennych

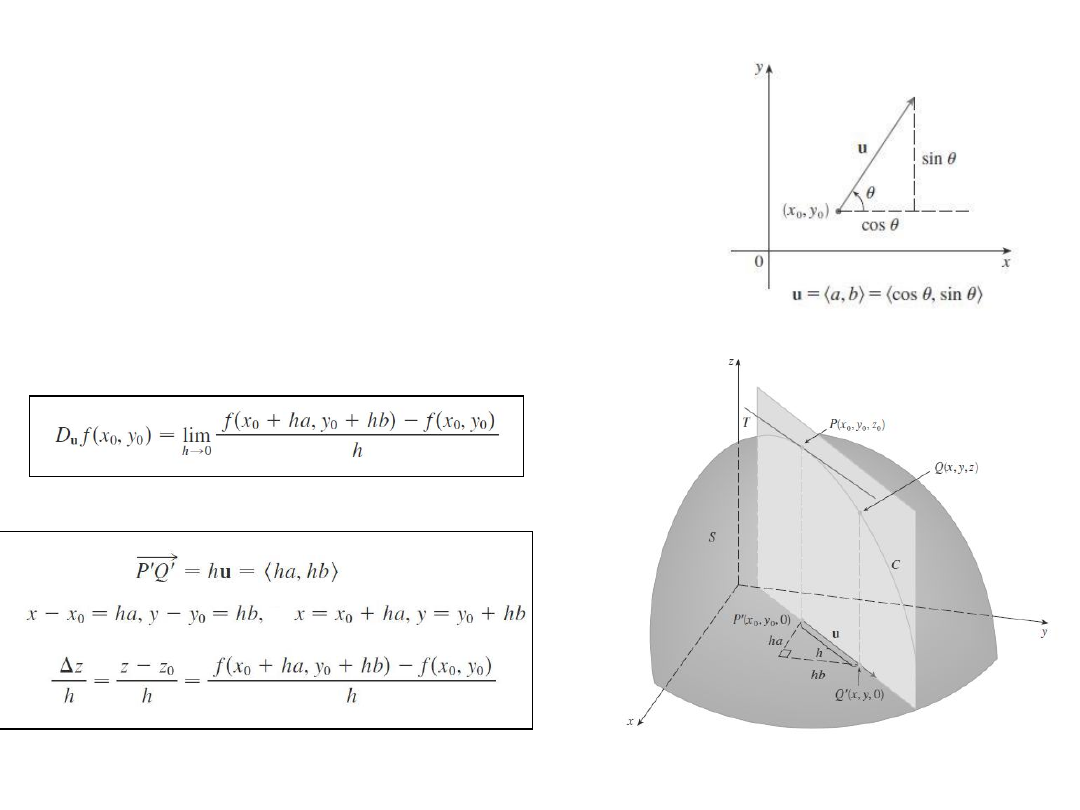
Pochodna

kierunkowa

Pochodna kierunkowa funkcji f w
punkcie (x0,y0) w kierunku wektora
jednostkowego u = (a,b)

Twierdzeni

e

Przykła
d

Oblicz pochodną kierunkową Duf(x,y) funkcji f(x,y) = x3 -
3xy + 4y2 gdzie u jest wektorem jednostkowym, który tworzy
z osią ox kąt п/6. Jaka jest wartość w punkcie (1,2).

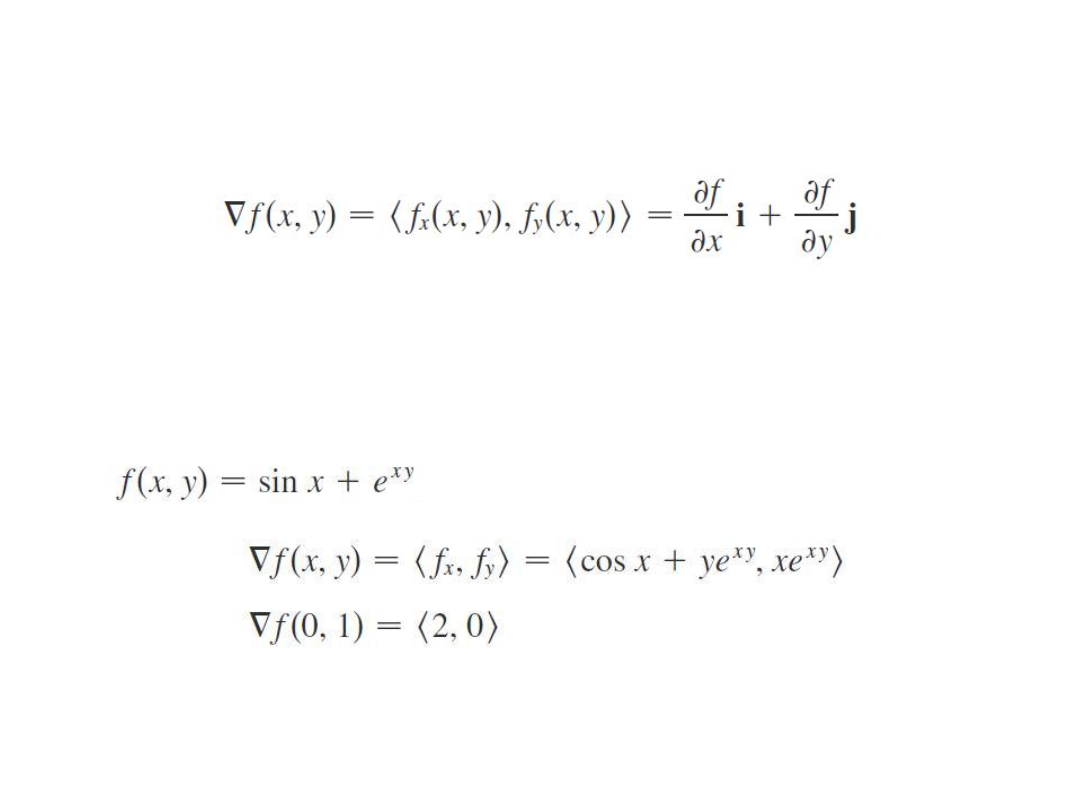
Wektor

gradientu.

Definicja

Przykład

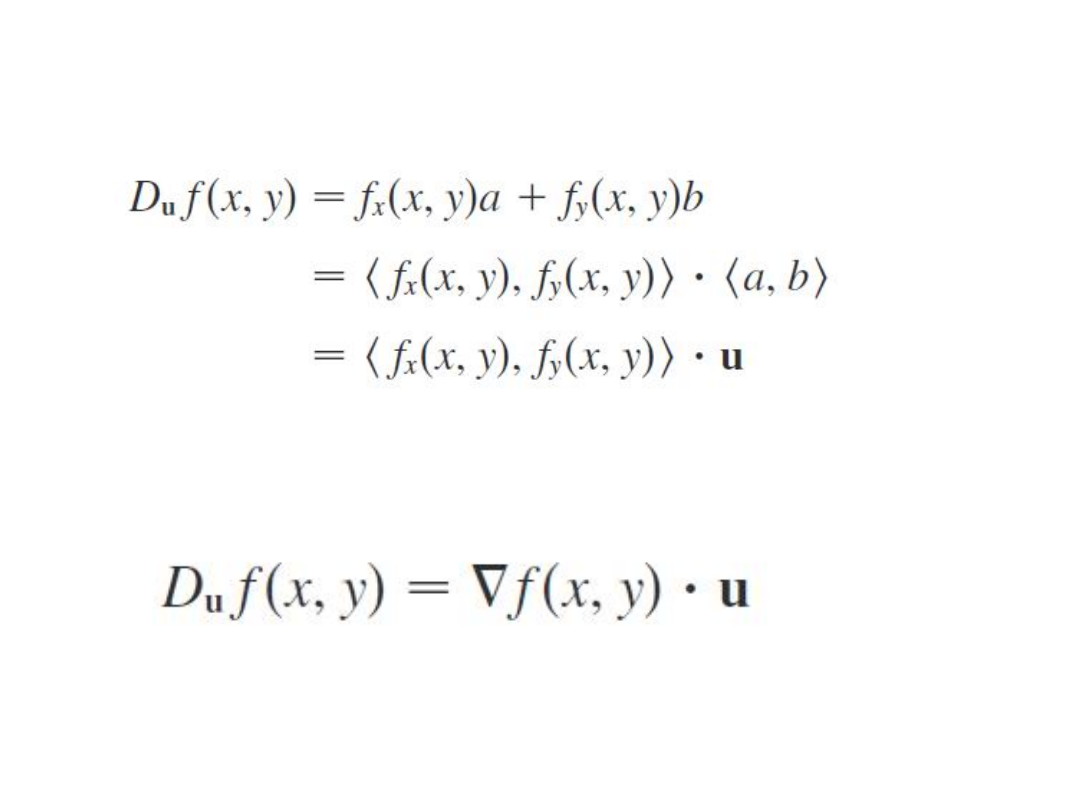
Z użyciem operatora gradientu można to zapisać:

Pochodna kierunkowa:

Funkcje trzech

zmiennych