Politechnika Wrocławska



©Roman Pietroń

PROGNOZOWANIE I

SYMULACJE

(Wybrane zagadnienia i materiały wykładu dla 4 roku ZiM)

Wrocław 2006

SPIS TREŚCI

Nr części/Str. od-do

PODSTAWY METOD PROGNOZOWANIA ................... 1/

3-51

SYMULACJA JAKO METODA PROGNOZOWANIA ............ 2/

1-15

SYMULACJA CIĄGŁA ............................... 3/

1-33

SYMULACJA DYSKRETNA ............................ 4/

1-38

GRY SYMULACYJNE ................................ 4/

39-46

SYMULACJA A SZTUCZNA INTELIGENCJA .............. 4/

47-49

ZASTOSOWANIA SYMULACJI ......................... 4/

50-56

ETYKA SYMULACJI ................................ 4/

52-53

Bibliografia ................................... 4/

54

- 1/

2

-

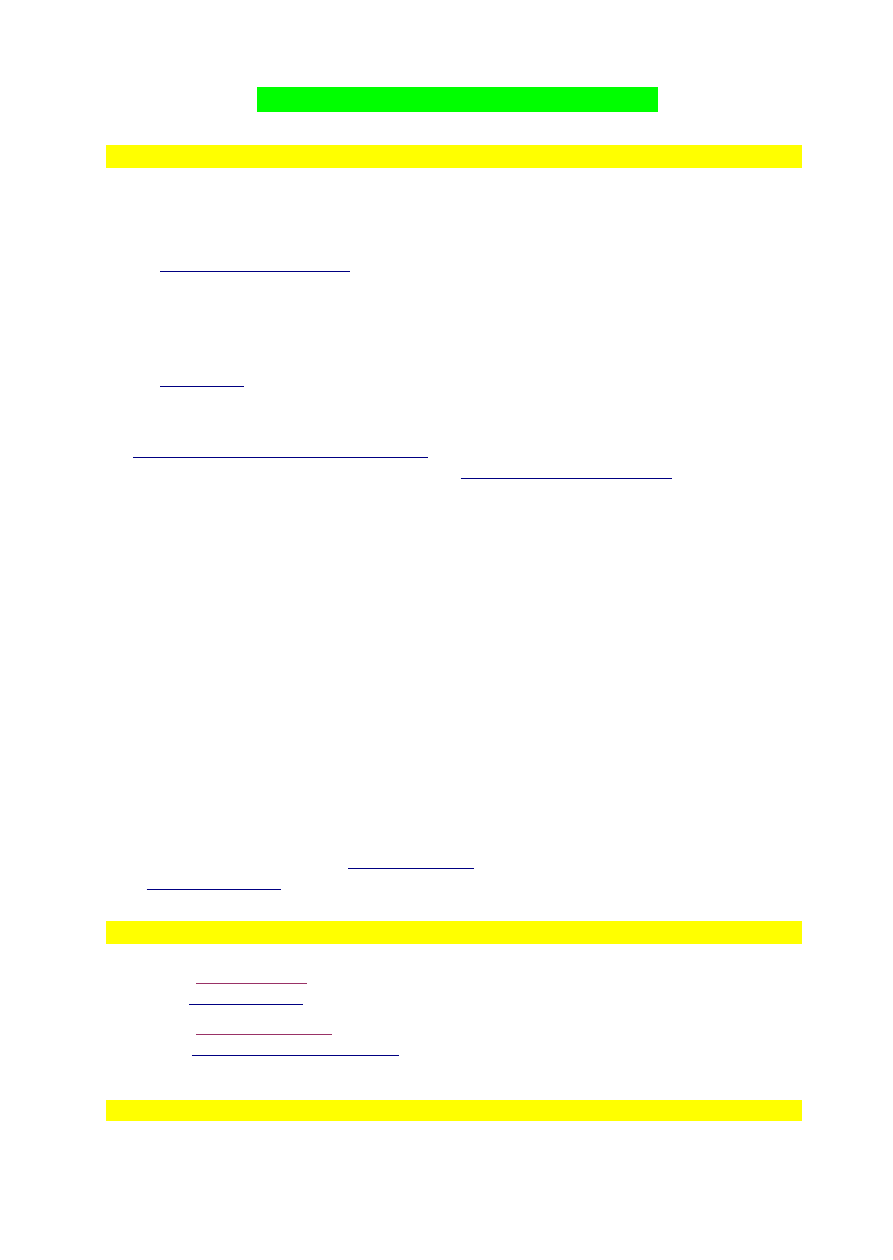
PODSTAWY METOD PROGNOZOWANIA

POJĘCIE PROGNOZY

Przewidywanie jest to wnioskowanie o zdarzeniach nieznanych na podstawie zdarzeń
znanych. Zdarzenia nieznane są to zdarzenia:

•

należące do przeszłości,

•

należące do przyszłości

.

Przewidywanie przyszłości jest to wnioskowanie o zdarzeniach, które zajdą w czasie
późniejszym niż czynność przewidywania (należących do przyszłości) odbywające się
również na podstawie informacji o przeszłości. Przewidywanie przyszłości może być:

•

nieracjonalne,

•

racjonalne

(zdroworozsądkowe, naukowe).

Przewidywanie racjonalne jest logicznym procesem przebiegającym od przesłanek
(zbioru faktów należących do przeszłości i ich interpretacji) do konkluzji.
W przewidywaniu zdroworozsądkowym przesłanki i tok wnioskowania są oparte na
doświadczeniu (brak reguł naukowych). W przewidywaniu naukowym przesłanki i tok
wnioskowania są oparte na regułach naukowych.

Prognozowanie jest to racjonalne, naukowe przewidywanie przyszłych zdarzeń.
Przewidywanie „naukowe” oznacza, że w całym procesie badawczym, obejmującym
poznawanie przeszłości (w gromadzeniu danych, diagnozowaniu, przenoszeniu
danych z przeszłości w przyszłość, formułowaniu założeń, konkluzji,...) korzysta się z
dorobku nauki (metodologie, teorie, reguły problemów).

Prognoza jest to sąd posiadający następujące właściwości:

•

jest sformułowany z wykorzystaniem dorobku nauki,

•

odnosi się do określonej przyszłości,

•

jest weryfikowalny empirycznie,

•

jest niepewny, ale akceptowalny.

Obiekt prognozowania

jest to system (układ), do którego odnosi się prognoza.

Zjawisko prognozowania

jest to zjawisko zachodzące w obiekcie prognozowania.

Zmienne prognozowania

są to Ilościowe lub jakościowe zmienne opisujące zjawisko

prognozowania. Wyróżniamy zjawiska proste – opisane za pomocą jednej zmiennej,
oraz zjawisko złożone – opisane za pomocą wielu zmiennych.

PODSTAWY PROGNOZOWANIA

Podstawa ontologiczna prognozowania

Obejmuje naturę zjawisk i ich wzajemne powiązania.

Podstawa gnoseologiczna prognozowania

Wynika z wiedzy o naturze zjawisk, ich wzajemnych powiązaniach i mechanizmach
kształtowania się.

CEL PROGNOZOWANIA

- 1/

3

-

Głównym celem prognozowania społecznego jest wspomaganie procesów
decyzyjnych.

FUNKCJE PROGNOZ

(preparacyjna, aktywizująca, informacyjna)

Funkcja preparacyjna

Prognozowanie jest działaniem, które przygotowuje inne działania (np. decyzyjne).

Funkcja aktywizująca

Prognozowanie jest pobudzeniem do podejmowania działań sprzyjających realizacji
prognozy (w przypadku zdarzeń korzystnych) albo przeciwdziałających się jej realizacji
(w przypadku zdarzeń niekorzystnych). Prognoza badawcza – prognoza, której
zadaniem jest wszechstronne rozpoznanie przyszłości i ukazanie możliwych jej wersji.
Prognoza ostrzegawcza – prognoza badawcza, której zadaniem jest przewidywanie
zdarzeń niekorzystnych.

Funkcja informacyjna

Prognozowanie jest informowaniem o nadchodzących zmianach w celu zmniejszenia
lęku przed przyszłością. Prognoza realistyczna – prognoza o wysokim stopniu zaufania
odbiorcy.

KLASYFIKACJE PROGNOZ

Wg kryterium wyrażania stanu zmiennej prognozy dzielą się na:

•

ilościowe (punktowa, przedziałowa),

•

jakościowe.

Wg kryterium przebiegu zmian zmiennej prognozy dzielą się na:

•

krótkookresowe (tylko ilościowe),

•

średniookresowe (ilościowe i małe jakościowe),

•

długookresowe (ilościowe i duże jakościowe).

Wg kryterium możliwości sterowania zmienną prognozy dzielą się na:

•

prognozy zmiennych sterowanych,

•

prognozy zmiennych nie sterowanych.

DANE WYKORZYSTYWANE W PROGNOZOWANIU

W prognozowaniu wykorzystuje się: dane wewnętrzne, dane zewnętrzne oraz
teorie naukowe. Dane wewnętrzne to dane o obiekcie

, dla którego sporządza się

prognozę (obiekcie prognozowania).

Dane zewnętrzne to dane o obiektach

stanowiących otoczenie (bliższe, dalsze) obiektu prognozowania. Z kolei

teorie

naukowe

to założenia, modele i ich interpretacje przydatne w prognozowaniu.

- 1/

4

-

Zjawisko prognozowane

Teoria

Doświadczenie

Model

Schemat wykorzystania teorii w prognozowaniu.

Kryteria doboru danych w prognozowaniu

•

Rzetelność

:

Zgodność z przedmiotem, którego dotyczą (występowanie błędów losowych i
systematycznych);

•

Jednoznaczność

:

Jednoznaczny sposób interpretowania i odbioru danych;

•

Identyfikowalność zjawiska przez zmienną

:

Wiele zjawisk można opisać przy użyciu różnych zmiennych;

•

Kompletność

:

Objęcie wszystkich ważnych wiadomości istotnych dla problemu;

•

Aktualność danych dla przyszłości

:

Określenie siły czynników w przyszłości (fakty niosące przyszłość);

•

Koszt zbierania i opracowywania danych

:

Dążenie do minimalizacji liczby danych;

•

Porównywalność danych

:

Uzyskanie porównywalności: czasowej, terytorialnej, pojęć i kategorii, metod
obliczeń.

Rodzaje szeregów czasowych w prognozowaniu

•

Jednowymiarowy szereg czasowy,

•

Wielowymiarowy szereg czasowy,

•

Jednowymiarowy szereg przekrojowy,

•

Wielowymiarowy szereg przekrojowy,

•

Szereg przekrojowo-czasowy.

PRZEGLĄD METOD PROGNOZOWANIA

Metoda – sposób zastosowany ze świadomością możliwości jego zastosowania w
przypadkach takiego typu, jakiego egzemplarz w danym przypadku rozpatruje osoba
działająca [

T.Kotarbiński, Elementy teorii poznania ..., PWN 1986, s.413

].

Metoda prognozowania

Sposób przetworzenia danych o przeszłości oraz przejścia od danych przetworzonych
do prognozy.

Reguła prognozy

Sposób przejścia od danych przetworzonych do prognozy.

Reguły prognozy – rodzaje:

•

Reguła podstawowa

:

- 1/

5

-

Prognozą jest stan zmiennej prognozowanej w należącym do przyszłości
momencie lub okresie t, otrzymany z modelu tej zmiennej przy przyjęciu
założenia, że model będzie aktualny w chwili, na którą określa się prognozę
(ekstrapolacja modelu);

•

Reguła podstawowa z poprawką

:

Występują uzasadnione przypuszczenia co do tego, że ostatnio
zaobserwowane odchylenia danych empirycznych od modelu utrzymają się w
przyszłości;

•

Reguła największego prawdopodobieństwa

:

Prognozą jest stan zmiennej, któremu odpowiada

najwyższe

prawdopodobieństwo lub maksymalna wartość funkcji gęstości rozkładu;

•

Reguła minimalnej straty

:

Prognozą jest taki stan zmiennej, którego realizacja spowoduje minimalne
straty.

Metody prognozowania – grupy:

•

Metody analizy i prognozowania szeregów czasowych,

•

Metody prognozowania przyczynowo-skutkowego,

•

Metody analogowe,

•

Metody heurystyczne,

•

Metody mieszane (np. metoda scenariuszy).

Podstawy wyboru metody prognozowania

•

Przesłanki prognostyczne,

•

Własności metod prognozowania.

Przesłanki prognostyczne

Hipotezy badawcze określające wstępnie mechanizm rozwojowy prognozowanego
zjawiska oraz dostępne o nim informacje jakościowe i ilościowe.

Postawy zajmowane przez prognostę

•

Postawa pasywna:
Widzenie przyszłości zjawiska jako nieuniknionego, pojedynczego następstwa

przeszłości, określonego przez konieczne, niezależne od woli ludzi związki
pomiędzy zjawiskami;

•

Postawa aktywna:
Uznanie przyszłości za stosunkowo niezależną od przeszłości.

ETAPY PROGNOZOWANIA

Podmioty: odbiorca prognozy, prognosta

1. Sformułowanie zadania prognostycznego

Określenie: obiektu, zjawiska (zjawisk), zmiennych, celu, wymagań dopuszczalności,
horyzontu prognozy.

2. Podanie przesłanek prognostycznych

Sformułowanie hipotez dotyczących czynników kształtujących zjawisko, deklaracja
prognosty co do postawy wobec przyszłości zjawiska, określenie zbioru danych
potrzebnych do sporządzenia prognozy, zebranie danych.

3. Wybór metody prognozowania

- 1/

6

-

Konsekwencja przesłanek prognostycznych: postawa pasywna – prognozowanie na
podstawie szeregów czasowych, prognozowanie ekonometryczne ze stałymi
parametrami; postawa aktywna – prognozowanie symulacyjne, ekonometryczne ze
zmiennymi parametrami, analogowe, heurystyczne.

4. Wyznaczenie prognozy

Odpowiada zadaniu prognostycznemu: schemat obliczeniowy metody, decyzje w
sytuacjach trudnych prognozowania, założenia, uzasadnienie, kryteria, wartości
krytyczne.

5. Ocena dopuszczalności prognozy

Zgodność z żądaniem odbiorcy: błąd prognozy ex ante, horyzont dopuszczalności,
zmiana wymagań jakościowych prognozy.

6. Weryfikacja prognozy (monitoring prognozy)

Określenie trafności prognozy: błąd prognozy ex post, analiza słuszności
postępowania prognostycznego, określenie przyczyn błędu w prognozowaniu,
systematyczność weryfikacji (monitoring).

JAKOŚĆ MODELU PROGNOSTYCZNEGO

Ocena zgodności z danymi empirycznymi

Ocena wartości prognostycznej metody

Ocena zgodności z danymi empirycznymi

Współczynnik determinacji

R

2

: miara dopasowania liniowego modelu regresji do

danych rzeczywistych, miara dopasowania modeli nieliniowych.
Skorygowany współczynnik determinacji

R

2

: miara porównawcza jakości kilku modeli,

w których liczba zmiennych objaśniających jest różna.
Odchylenie standardowe składnika resztowego

s : miara przeciętnych odchyleń

wartości rzeczywistych zmiennej prognozowanej od wartości teoretycznych.
Współczynnik wyrazistości (zmienności)

w

: miara udziału odchylenia standardowego

reszt w średniej wartości zmiennej prognozowanej (charakterystyka zmienności
losowej).
Błąd oceny estymatora parametru: miara istotności wpływu zmiennych objaśniających
na zmienną endogeniczną (średni błąd szacunku parametru).

Ocena wartości prognostycznej metody

Jakość (błąd) prognoz

ex post

i

ex ante

: miara trafności prognozy (ex post), miara

dokładności prognozy (ex ante).
Mierniki szczegółowe:

•

Błąd prognozy ex post (bezwzględny, względny, średni kwadratowy, średni
względny, medianowy, współczynnik Theila),

•

Dopuszczalność prognozy (wykazanie przez odbiorcę stopnia zaufania do
prognozy wystarczającego do wykorzystania w ustalonym celu),

•

Maksymalny horyzont prognozy (należący do przyszłości najdalszy moment lub
okres, w którym prognoza jest dopuszczalna),

•

Żądany horyzont prognozy (podany przez odbiorcę moment lub okres
dopuszczalności prognozy),

•

Błąd V

2

prognozy ex ante – wariancja prognozy (charakterystyka rozproszenia

możliwych prognoz wokół możliwych realizacji zmiennej prognozowanej w
czasie),

- 1/

7

-

•

Bezwzględny błąd v prognozy ex ante – pierwiastek kwadratowy wariancji
prognozy (prognoza jest tym dokładniejsza im mniejsza jest jego wartość),

•

Względny błąd

η

prognozy ex ante – iloraz błędu bezwzględnego i wartości

prognozowanej,

•

Prawdopodobieństwo realizacji prognozy (prawdopodobieństwo, że zmienna
prognozowa-na przyjmie określoną wartość),

•

Wiarygodność prognozy (prawdopodobieństwo, że różnica pomiędzy wartością
rzeczywistą a prognozowaną nie przekroczy określonej wartości).

WARUNKI WYKORZYSTANIA BŁĘDÓW PROGNOZY

Błędy prognoz ex post

Błędy prognoz ex post mogą być wykorzystane do określenia dopuszczalności
prognozy zmiennej gdy:

•

nowo formułowane przesłanki potwierdzają zasadność przesłanek przyjętych do
wyznaczenia poprzedniej prognozy,

•

do ustalenia nowej prognozy wykorzystuje się tę samą metodę co poprzednio,

•

przedział weryfikacji poprzedniej prognozy jest taki sam jak żądany horyzont
nowej prognozy.

Błędy prognoz wygasłych

Prognoza wygasła jest to prognoza wyznaczona na taki czas, dla którego znana jest
prawdziwa wartość zmiennej prognozowanej. Błędy prognoz wygasłych mogą być
wykorzystane do określenia dopuszczalności prognozy zmiennej, gdy nie jest możliwe
zastosowanie innych metod oceny dopuszczalności prognozy. Obliczenia podobne jak
dla błędów prognoz ex post.

Ocena dopuszczalności prognozy przez ekspertów

Może być wykorzystana do określenia dopuszczalności prognozy zmiennej, gdy nie
jest możliwe zastosowanie innych metod oceny dopuszczalności prognozy, lub gdy
przyjmuje się postawę aktywną (brak możliwości zaufania miarom ex ante i ex post).

Ocena dopuszczalności prognozy przez samego prognostę

Może być wykorzystana do określenia dopuszczalności prognozy zmiennej jedynie w
wyjątkowych sytuacjach z zachowaniem krytycyzmu (analiza krytyczna), poczucia
odpowiedzialności za wynik prognozowania, wykazaniem maksymalnej staranności
(opinia o dopuszczalności i jej uzasadnienie).

Ocena zgodności z danymi empirycznymi

Współczynnik determinacji

R

2

: miara dopasowania liniowego modelu regresji do

danych rzeczywistych, miara dopasowania modeli nieliniowych.

(

)

(

)

2

1

2

1

2

∑

∑

=

=

−

−

=

n

t

t

n

t

t

y

y

y

y

R



Skorygowany współczynnik determinacji

R

2

: miara porównawcza jakości kilku modeli,

w których liczba zmiennych objaśniających jest różna.

(

)

2

2

1

1

1

1

R

m

n

n

R

~

−

⋅

−

−

−

−

=

- 1/

8

-

Odchylenie standardowe składnika resztowego

s : miara przeciętnych odchyleń

wartości rzeczywistych zmiennej prognozowanej od wartości teoretycznych.

(

)

2

1

1

1

∑

=

−

⋅

−

−

=

n

t

t

t

y

y

m

n

s



Współczynnik wyrazistości (zmienności)

w

: miara udziału odchylenia standardowego

reszt w średniej wartości zmiennej prognozowanej (charakterystyka zmienności
losowej).

%

y

s

w

100

⋅

=

Ocena wartości prognostycznej metody

Jakość (błąd) prognoz

ex post

i

ex ante

: miara trafności prognozy (ex post), miara

dokładności prognozy (ex ante).
Mierniki szczegółowe:

•

Błąd prognozy ex post (bezwzględny, względny, średni kwadratowy, średni
względny, medianowy, współczynnik Theila),

*

t

t

t

y

y

q

−

=

,

%

y

y

y

t

*

t

t

t

100

⋅

−

=

Ψ

(

)

∑

+

=

−

−

=

T

n

t

*

t

t

*

t

y

y

n

T

s

1

2

1

,

%

y

y

y

n

T

T

n

t

t

*

t

t

100

1

1

⋅

−

−

=

∑

+

=

Ψ

(

)

∑

∑

+

=

+

=

−

=

T

n

t

t

T

n

t

*

t

t

y

y

y

I

1

2

2

1

2

•

Dopuszczalność prognozy (wykazanie przez odbiorcę stopnia zaufania do
prognozy wystarczającego do wykorzystania w ustalonym celu),

•

Maksymalny horyzont prognozy (należący do przyszłości najdalszy moment lub
okres, w którym prognoza jest dopuszczalna),

•

Żądany horyzont prognozy (podany przez odbiorcę moment lub okres
dopuszczalności prognozy),

•

Błąd V

2

prognozy ex ante – wariancja prognozy (charakterystyka rozproszenia

możliwych prognoz wokół możliwych realizacji zmiennej prognozowanej w
czasie)

(

)

2

2

*

t

t

Y

Y

E

V

−

=

•

Bezwzględny błąd v prognozy ex ante – pierwiastek kwadratowy wariancji
prognozy (prognoza jest tym dokładniejsza im mniejsza jest jego wartość)

2

t

t

v

v

=

•

Względny błąd

η

prognozy ex ante – iloraz błędu bezwzględnego i wartości

prognozowanej

%

y

v

*

t

t

t

100

⋅

=

η

•

Oszacowanie wariancji prognozy (dla modelu trendu liniowego)

- 1/

9

-

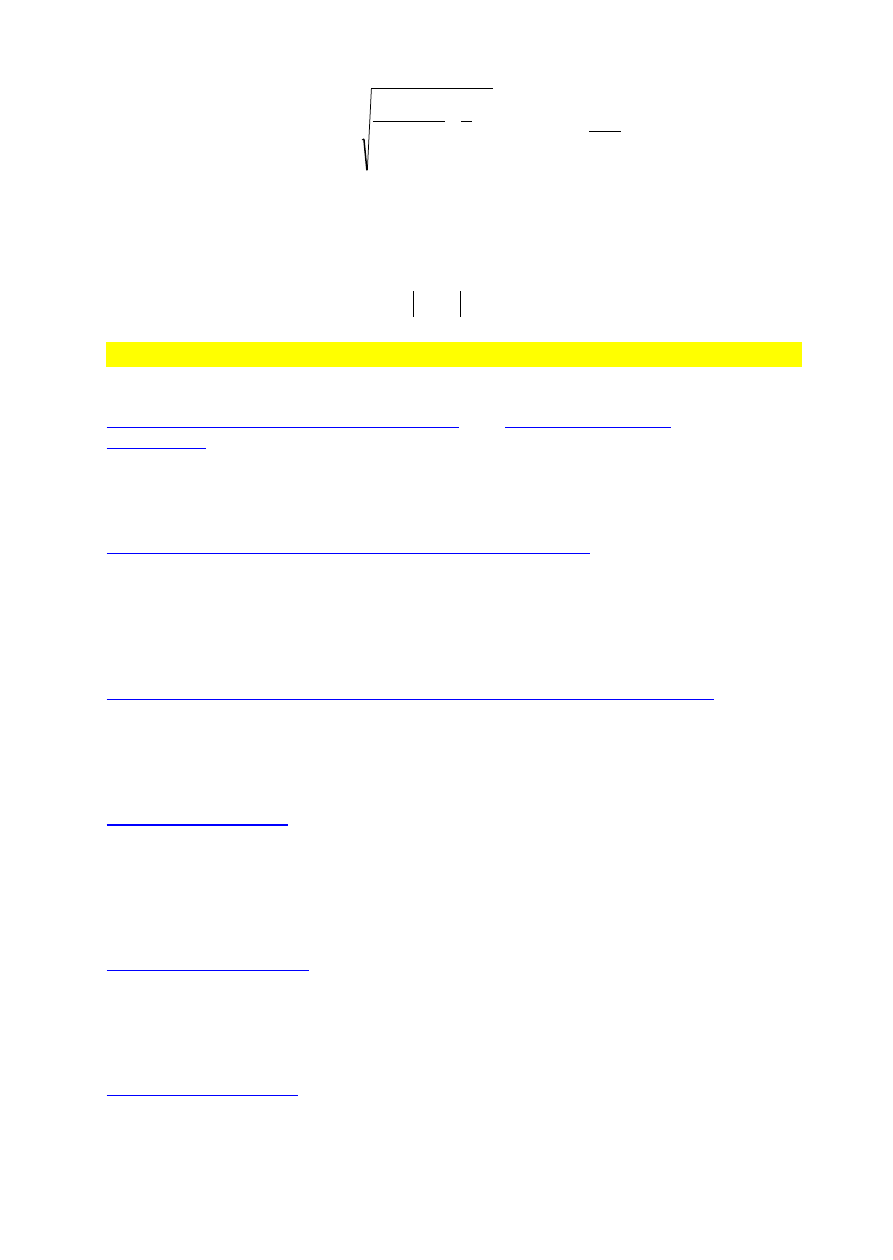
1

1

1

2

2

+

+











 −

−

⋅

=

∑

=

−

−

n

t

t

)

t

T

(

s

v

n

t

T

,

2

1

+

=

−

n

t

•

Prawdopodobieństwo realizacji prognozy (prawdopodobieństwo, że zmienna
prognozowa-na przyjmie określoną wartość)

(

)

t

*

t

t

y

Y

P

γ

=

=

•

Wiarygodność prognozy (prawdopodobieństwo, że różnica pomiędzy wartością
rzeczywistą a prognozowaną nie przekroczy określonej wartości).

(

)

t

*

t

t

y

Y

P

γ

ε =

〈

−

PRZEGLĄD METOD PROGNOZOWANIA

Metoda prognozowania

Sposób przetworzenia danych o przeszłości oraz przejścia od danych przetworzonych
do prognozy.

METODY PROGNOZOWANIA – GRUPY I RODZAJE

1. Metody analizy i prognozowania szeregów czasowych
Cecha charakterystyczna: korzystanie w diagnozowaniu zjawiska (w prognozowaniu) z
danych o dotychczasowym kształtowaniu się zmiennej lub zmiennych prognozowanych.
Przykłady: metoda naiwna, metoda średniej ruchomej (prostej, ważonej), metoda
wygładzania wykładniczego, metoda liniowa Holta, metoda analizy trendów, metoda
wskaźników, metoda analizy harmonicznej, metoda Wintersa, metoda ARMA i ARIMA.

2. Metody prognozowania przyczynowo-skutkowego (ekonometryczne)
Cecha charakterystyczna: określenie modelu wyjaśniającego mechanizm zmian
zmiennych prognozowanych przez zmiany zmiennych objaśniających.
Przykłady: metoda prosta, metoda rekurencyjna, metoda ze zmienną zero-jedynkową,
metoda ze zmienną syntetyczną.

3. Metody analogowe
Cecha charakterystyczna: przewidywanie przyszłości określonej zmiennej na podstawie
danych o zmiennych podobnych, co do których istnieją zbyt słabe podstawy,by
przypuszczać, że są przyczynowo powiązane ze zmienną prognozowaną.
Przykłady: metoda analogii biologicznej, metoda analogii przestrzennej, metoda
analogii historycznej, metoda analogii przestrzenno-czasowej.

4. Metody heurystyczne
Cecha charakterystyczna: wykorzystują opinie ekspertów,oparte na ich intuicji i
doświadczeniu.
Przykłady: metoda delficka, metoda testów rynkowych, metoda testów
koniunkturalnych.

5. Metoda scenariuszy
Cecha charakterystyczna: kombinacja wielu metod, stosowana do prognozowania
zjawisk szczególnie skomplikowanych, których przyszłość jest bardzo niepewna.

- 1/

10

-

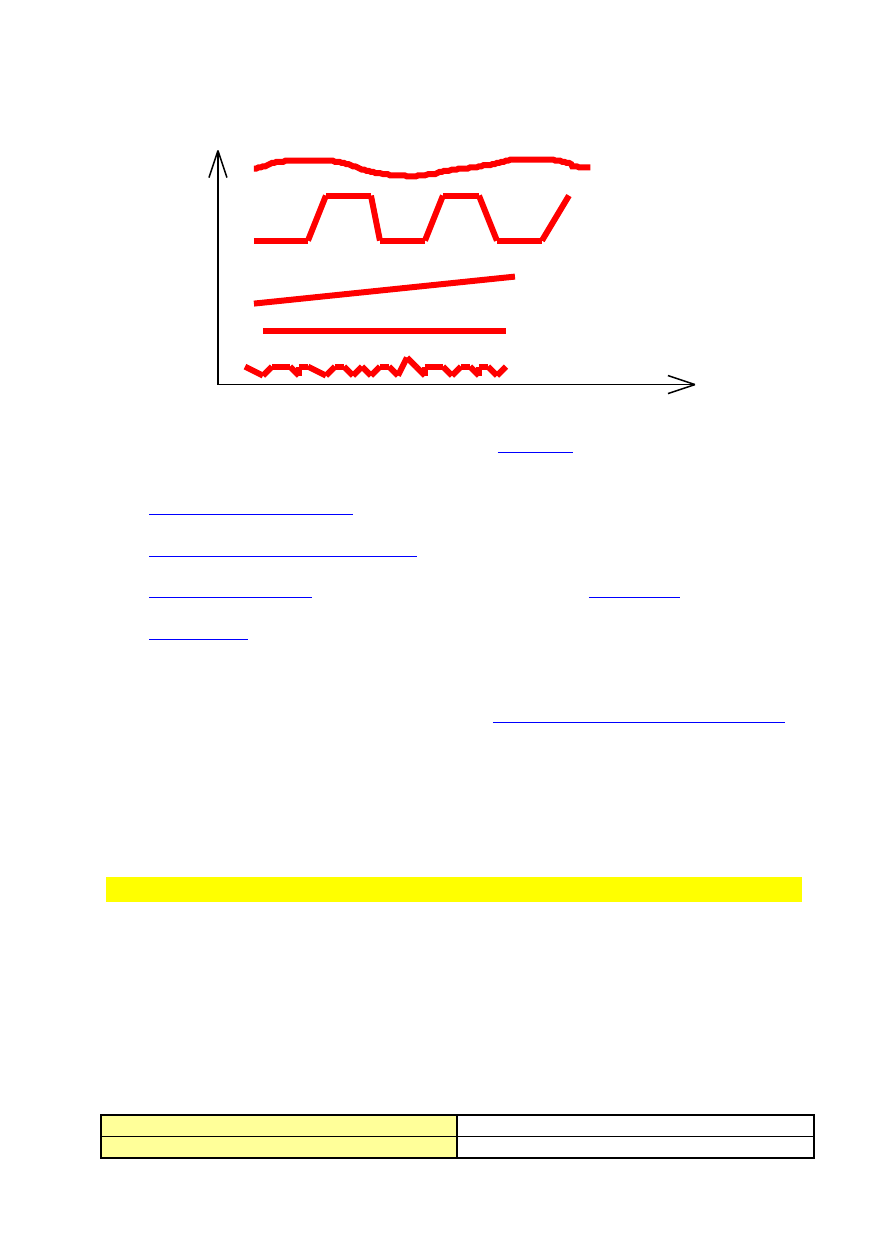
SKŁADOWE SZEREGÓW CZASOWYCH

Stały poziom

Losowość

czas

Trend liniowy

Sezonowość

Cykl

yt

Składowe szeregów czasowych.

W szeregach czasowych występują następujące składowe:
a) systematyczna, powstająca na skutek działania trwałego układu przyczyn i

prawidłowości, w tym:
- stały (przeciętny) poziom zmiennej (brak tendencji rozwojowej, oscylacje wokół

pewnego poziomu),

- tendencja rozwojowa (trend)

jako długookresowa skłonność do

jednokierunkowych zmian (wzrost lub spadek),

- składowa okresowa (periodyczna) w formie zmian cyklicznych (rytmicznych

wahań długookresowych wokół trendu lub stałego poziomu zmiennej), zmian
sezonowych (rytmicznych wahań o cyklu nie przekraczającym 1 roku),

b) losowa (przypadkowa), powstająca na skutek działania przyczyn przypadkowych z

różną siłą w różnych kierunkach.

W prognozowaniu wyróżnić można następujące rodzaje modeli szeregów czasowych:
1. Model addytywny, w którym przyjmuje się założenie, że obserwowane wartości

zmiennej prognozowanej są sumą składowych szeregu czasowego (składowe są
niezależne) a wartość oczekiwana składnika losowego wynosi 0.

2. Model multiplikatywny, w którym przyjmuje się założenie, że obserwowane wartości

zmiennej prognozowanej są iloczynem składowych szeregu czasowego (składowe
są niezależne) a wartość oczekiwana składnika losowego wynosi 1.

ALGORYTMY I CHARAKTERYSTYKA METOD PROGNOZOWANIA

PROGNOZOWANIE NA PODSTAWIE SZEREGÓW CZASOWYCH

Metoda naiwna

Algorytm prognozowania:

1

−

=

t

*

t

y

y

gdzie:

*

t

y

- prognoza zmiennej Y dla momentu t,

1

−

t

y

- obserwacja rzeczywistej wartości

zmiennej Y dla chwili t-1.

Tab. Charakterystyka metody naiwnej prognozowania

Grupa metod

Prognozowanie na podstawie szeregu czasowego

Składowe szeregu czasowego

Stały (przeciętny) poziom i wahania przypadkowe

- 1/

11

-

Przesłanki metody

Nie nastąpią zmiany w sposobie oddziaływania
czynników określających zmienną prognozowaną,
niewielkie wahania przypadkowe

Postawa, zasada, reguły prognostyczna

Postawa pasywna, zasada status quo, reguła
podstawowa prognozowania

Horyzont prognozy

Jeden okres (moment)

Ocena prognozy

Błędy ex post

Zalety metody

Prosty algorytm, łatwość zrozumienia, szybkie i
tanie prognozowanie

Wady metody

Niska jakość prognozy, ocena jedynie za pomocą
błędów ex post

Metoda średniej ruchomej prostej

Algorytm prognozowania:

∑

−

−

=

⋅

=

1

1

t

k

t

i

i

*

t

y

k

y

gdzie:

*

t

y

- prognoza zmiennej Y dla momentu t,

i

y

- obserwacja rzeczywistej wartości

zmiennej Y dla chwili i, k – liczba ruchomych składników szeregu czasowego.

Tab. Charakterystyka metody średniej ruchomej prostej prognozowania

Grupa metod

Prognozowanie na podstawie szeregu czasowego

Składowe szeregu czasowego

Stały (przeciętny) poziom i wahania przypadkowe

Przesłanki metody

Nie nastąpią zmiany w sposobie oddziaływania
czynników określających zmienną prognozowaną,
mogą wystąpić duże wahania przypadkowe

Postawa, zasada, reguły prognostyczna

Postawa pasywna, zasada status quo, reguła
podstawowa prognozowania

Horyzont prognozy

Prognoza krótkookresowa

Ocena prognozy

Ocena dopuszczalności prognozy za pomocą
średniego kwadratowego błędu s* prognozy lub
średniego błędu ψ* ex post

Zalety metody

Względnie prosty algorytm, łatwość zrozumienia,
względnie szybkie i tanie prognozowanie

Wady metody

Konieczność doboru stałej k (minimalizacja
błędów), konieczność przechowywania dużej ilości
danych dla dużego k

Metoda średniej ruchomej ważonej

Algorytm prognozowania:

∑

−

−

=

+

+

−

⋅

=

1

1

t

k

t

i

k

t

i

i

*

t

w

y

y

,

∑

=

=

k

i

i

w

1

1

gdzie:

*

t

y

- prognoza zmiennej Y dla momentu t,

i

y

- obserwacja rzeczywistej wartości

zmiennej Y dla chwili i, k – liczba ruchomych składników szeregu czasowego,

i

w

-

współczynniki wagowe z przedziału [0, 1].

Tab. Charakterystyka metody średniej ruchomej ważonej prognozowania

Grupa metod

Prognozowanie na podstawie szeregu czasowego

Składowe szeregu czasowego

Stały (przeciętny) poziom i wahania przypadkowe

Przesłanki metody

Nie nastąpią zmiany w sposobie oddziaływania
czynników określających zmienną prognozowaną,
mogą wystąpić duże wahania przypadkowe

Postawa, zasada, reguły prognostyczna

Postawa pasywna, zasada status quo, reguła
podstawowa prognozowania

Horyzont prognozy

Prognoza krótkookresowa

Ocena prognozy

Ocena dopuszczalności prognozy za pomocą

- 1/

12

-

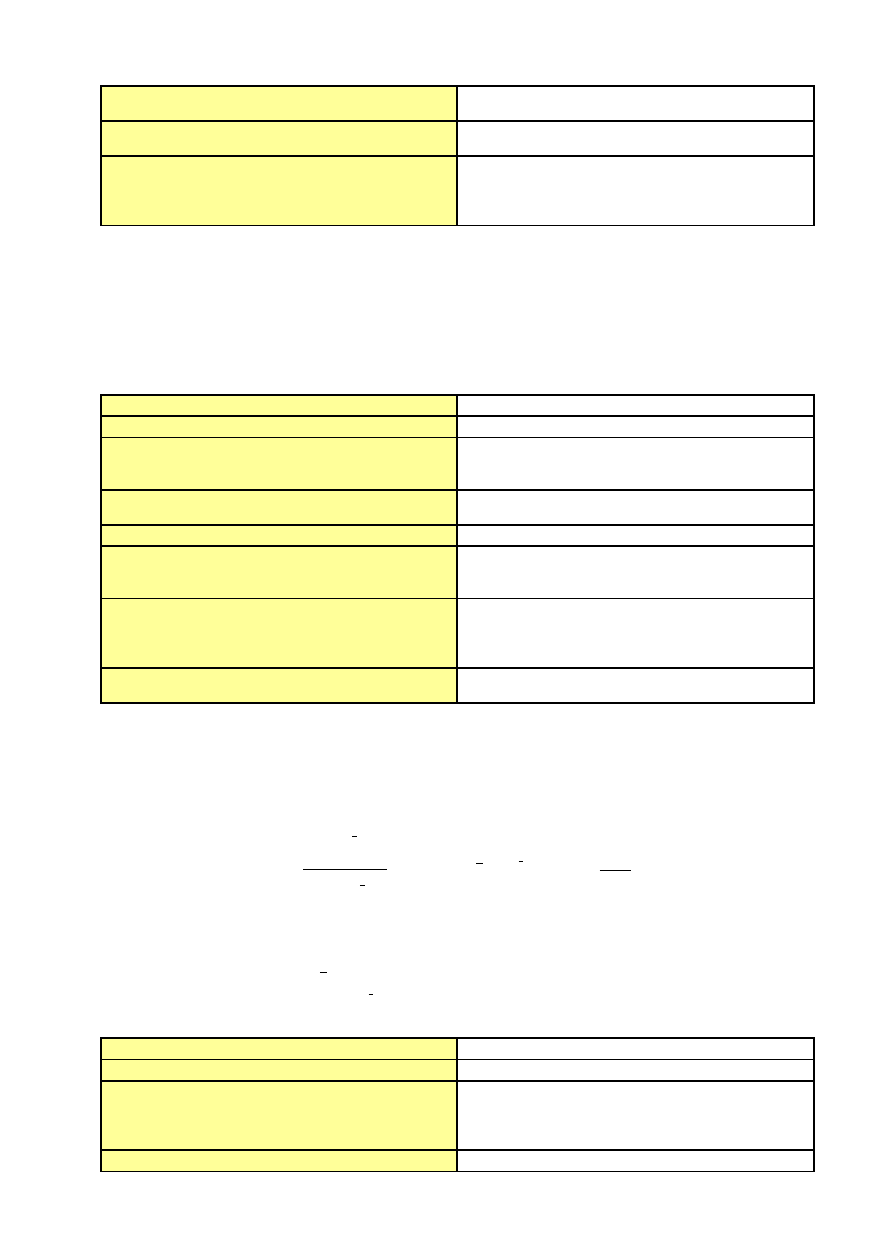
średniego kwadratowego błędu s* prognozy ex
post

Zalety metody

Względnie prosty algorytm, łatwość zrozumienia,
względnie szybkie i tanie prognozowanie

Wady metody

Konieczność doboru stałej k i współczynników
wagowych w (minimalizacja błędów), konieczność
przechowywania dużej ilości danych danych dla
dużego k

Metoda prostego uśredniania wykładniczego

Algorytm prognozowania:

(

)

(

)

*

t

t

*

t

*

t

t

*

t

y

y

y

y

y

y

1

1

1

1

1

1

−

−

−

−

−

−

⋅

+

=

⋅

−

+

⋅

=

α

α

α

gdzie:

*

t

y

- prognoza zmiennej Y dla momentu t,

1

−

t

y

- obserwacja rzeczywistej wartości

zmiennej Y dla chwili t-1, α – parametr uśredniania (wygładzania) z przedziału [0, 1].

Tab. Charakterystyka metody prostego uśredniania wykładniczego prognozowania

Grupa metod

Prognozowanie na podstawie szeregu czasowego

Składowe szeregu czasowego

Stały (przeciętny) poziom i wahania przypadkowe

Przesłanki metody

Nie nastąpią zmiany w sposobie oddziaływania
czynników określających zmienną prognozowaną,
mogą wystąpić duże wahania przypadkowe

Postawa, zasada, reguły prognostyczna

Postawa pasywna, zasada status quo, reguła
podstawowa prognozowania

Horyzont prognozy

Prognoza krótkookresowa

Ocena prognozy

Ocena dopuszczalności prognozy za pomocą
średniego kwadratowego błędu s* prognozy ex
post

Zalety metody

Względnie prosty algorytm, łatwość zrozumienia,
względnie szybkie i tanie prognozowanie,
uwzględnienie w prognozie wartości ostatniego
błędu ex post

Wady metody

Konieczność i trudność doboru parametru α
wygładzania (minimalizacja błędów)

Metoda tendencji rozwojowej modelu analitycznego (trendu
liniowego)

Algorytm prognozowania:

t

b

a

y

t

⋅

+

=



(

)

(

)

∑

∑

=

=

−

⋅

−

=

n

t

n

t

t

t

t

y

t

t

b

1

2

1

,

t

b

y

a

⋅

−

=

,

2

1

+

=

−

n

t

gdzie:

t

y



- prognoza zmiennej Y dla chwili t wyznaczona za pomocą modelu trendu

liniowego, b – współczynnik, a – współczynnik wyrazu wolnego,

t

y

- obserwacja

zmiennej Y dla chwili t,

y

- średnia obserwacja zmiennej Y, t – numer obserwacji

zmiennej, n – liczba obserwacji,

t

- średni numer obserwacji.

Tab. Charakterystyka metody trendu liniowego prognozowania

Grupa metod

Prognozowanie na podstawie szeregu czasowego

Składowe szeregu czasowego

Trend i wahania przypadkowe

Przesłanki metody

Nie nastąpią zmiany w sposobie oddziaływania
czynników określających zmienną prognozowaną,
niezmienność trendu, stałość modelu, stabilność
rozkładu czynnika losowego

Postawa, zasada, reguły prognostyczna

Postawa pasywna, zasada status quo, reguła

- 1/

13

-

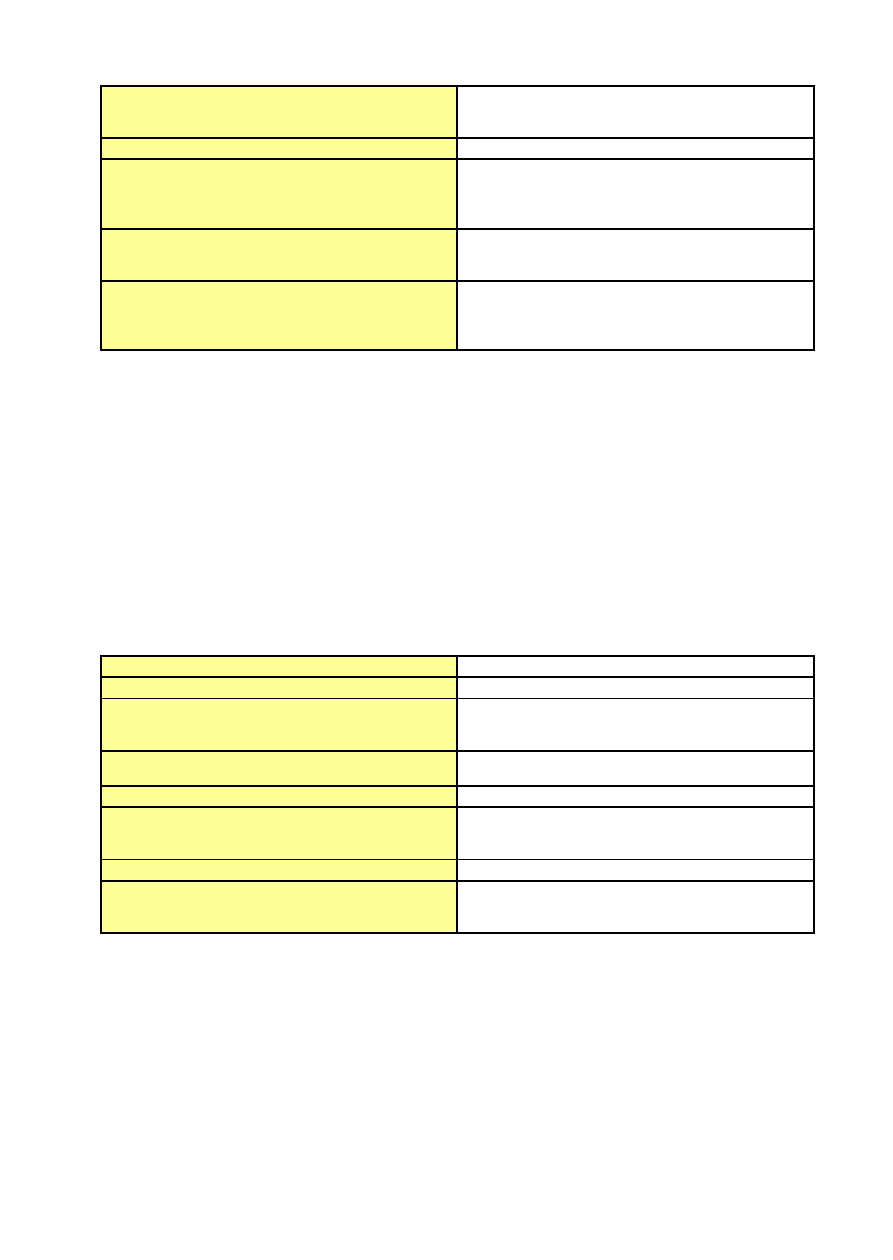
podstawowa (horyzont krótkookresowy) lub
podstawowa z poprawką prognozowania (horyzont
średniookresowy)

Horyzont prognozy

Prognoza krótkookresowa lub średniookresowa

Ocena prognozy

Ocena dopuszczalności prognozy za pomocą
błędu prognozy ex ante, ocena dopasowania
modelu za pomocą współczynnika determinacji R

2

i błędu oceny modelu s

Zalety metody

Łatwość prognozowania, określenie trendu zmian,
dobór dobrego modelu, umożliwia wyznaczenie
błędu ex ante

Wady metody

Ryzyko oparcia prognozy na dobrym modelu, ale
nieaktualnym dla ostatnich obserwacji, ostre
założenie o niezmienności mechanizmu
rozwojowego zjawisk

Metoda tendencji rozwojowej liniowego modelu Holta (wygładzania
wykładniczego)

Algorytm prognozowania:
Równanie I (uśrednienie szeregu czasowego):

(

) (

)

2

2

1

1

1

−

−

−

−

+

⋅

−

+

⋅

=

t

t

t

t

S

F

y

F

α

α

Równanie II (uśrednienie trendu):

(

) (

)

2

2

1

1

1

−

−

−

−

⋅

−

+

−

⋅

=

t

t

t

t

S

F

F

S

β

β

Równanie III (wyznaczenie prognozy):

(

)

n

n

*

T

S

n

T

F

y

⋅

−

+

=

gdzie:

1

−

t

F

- uśredniona prognoza zmiennej Y dla chwili t-1,

1

−

t

S

- uśredniony trend

zmiany wartości zmiennej Y dla chwili t-1,

1

−

t

y

- rzeczywista wartość obserwacji

zmiennej Y dla chwili t-1, α, β – parametry uśredniania z przedziału [0, 1],

*

T

y

-

prognoza zmiennej Y dla chwili T, n – liczba elementów szeregu czasowego
(obserwacji).

Tab. Charakterystyka metody Holta liniowego wygładzania wykładniczego prognozowania

Grupa metod

Prognozowanie na podstawie szeregu czasowego

Składowe szeregu czasowego

Trend i wahania przypadkowe

Przesłanki metody

Nie nastąpią zmiany w sposobie oddziaływania
czynników określających zmienną prognozowaną,
niezmienność trendu i regularność zmian

Postawa, zasada, reguły prognostyczna

Postawa pasywna, zasada status quo, reguła
podstawowa prognozowania

Horyzont prognozy

Prognoza krótkookresowa

Ocena prognozy

Ocena dopuszczalności prognozy za pomocą
średniego kwadratowego błędu s* prognozy ex
post

Zalety metody

Elastyczność metody (model adaptacyjny)

Wady metody

Konieczność i trudność doboru parametrów
wygładzania α i β (minimalizacja błędów),
konieczność przechowywania dużej ilości danych

Metoda tendencji rozwojowej trendu pełzającego z wagami
harmonicznymi

Algorytm prognozowania:

Trend pełzający jest modelem adaptacyjnym służącym do budowy prognoz
krótkookresowych. Procedura konstrukcji i ekstrapolacji trendu pełzającego jest
następująca:

Krok 1

: Ustalenie wartości stałej wygładzania k < n.

Krok 2

: Oszacowanie na podstawie kolejnych fragmentów szeregu o długości k

liniowych funkcji trendu.

- 1/

14

-

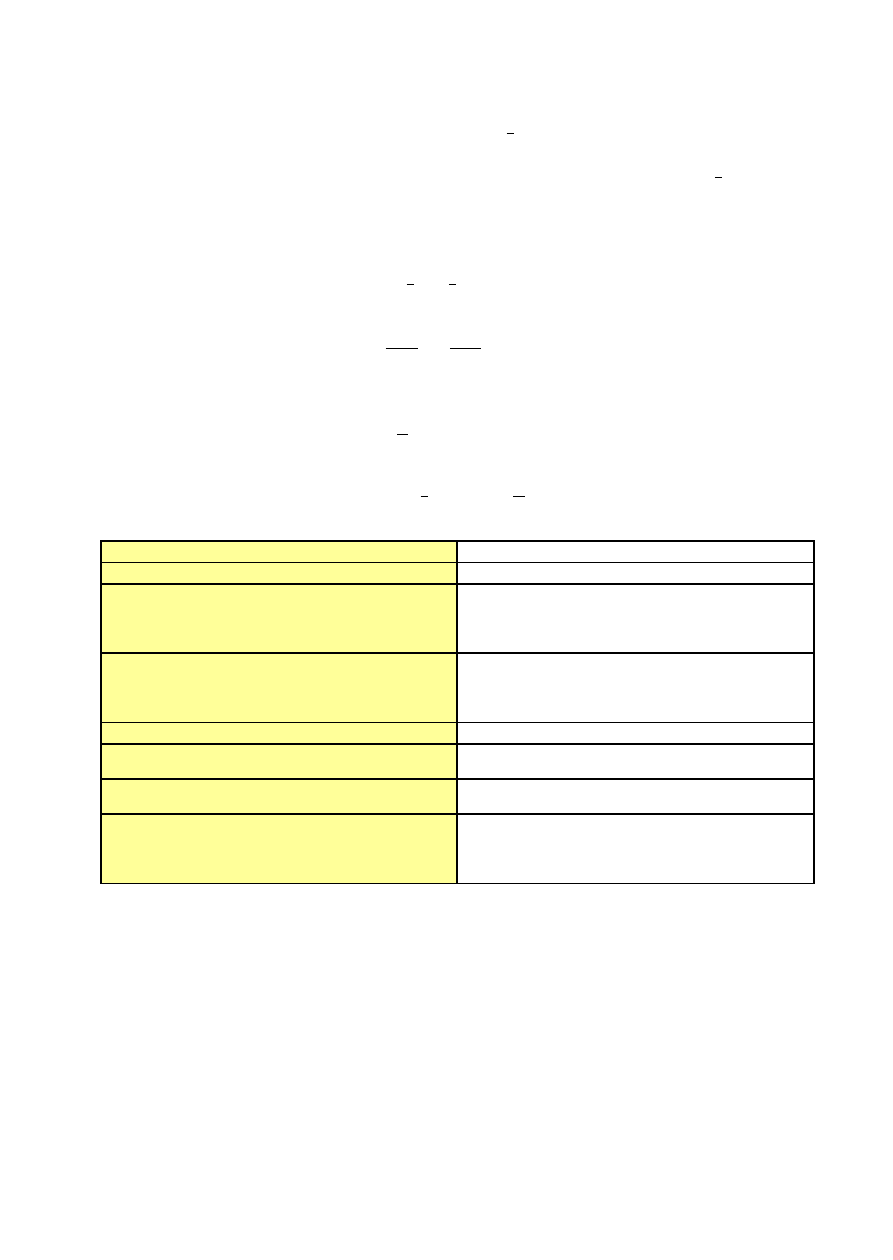
Krok 3

: Obliczenie wygładzonych wartości zmiennej ŷ

t(i)

, tzn. wartości teoretycznych

wynikających z i-tej funkcji trendu.

Krok 4

: Obliczenie średniej wartości wygładzonej

t

y

dla każdego okresu t jako

średniej arytmetycznej wartości wygładzonych obliczonych dla tego okresu w
kroku 3. Po połączeniu odcinkami liniowymi kolejnych punktów (t,

t

y

)

otrzymuje się wykres wygładzonych wartości szeregu czasowego w postaci
funkcji segmentowej, zwanej trendem pełzającym.

Krok 5

: Ekstrapolacja modelu trendu pełzającego. Obliczenie przyrostów funkcji

trendu dla wartości wygładzonych:

1

1

1

1

−

=

−

=

+

+

n

,...,

t

,

y

y

w

t

t

t

Krok 6

: Nadanie wag poszczególnym przyrostom. Są to tzw. wagi harmoniczne.

1

1

1

1

1

1

1

−

=

−

⋅

−

=

∑

=

+

n

,...,

t

,

i

n

n

C

t

i

n

t

Krok 7

: Określenie średniego przyrostu trendu jako średniej ważonej (wagami

harmonicznymi) wszystkich obliczonych w kroku 5. przyrostów.

∑

−

=

+

+

⋅

=

1

1

1

1

n

t

t

n

t

w

C

w

Krok 8

: Wyznaczenie prognozy punktowej na moment/okres T.

w

)

n

T

(

y

y

n

*

T

⋅

−

+

=

Tab. Charakterystyka metody trendu pełzającego prognozowania

Grupa metod

Prognozowanie na podstawie szeregu czasowego

Składowe szeregu czasowego

Trend i wahania przypadkowe

Przesłanki metody

Nie nastąpią zmiany w sposobie oddziaływania
czynników określających zmienną prognozowaną,
utrzymanie trendu,

zmiany mechanizmu

rozwojowego badanego zjawiska

Postawa, zasada, reguły prognostyczna

Postawa pasywna, zasada status quo, reguła
podstawowa prognozowania, model addytywny
(wahania bezwzględnie stałe), model
multiplikatywny (wahania względnie stałe)

Horyzont prognozy

Prognoza krótkookresowa i średniookresowa

Ocena prognozy

Ocena dopuszczalności prognozy za pomocą
błędu prognozy ex ante

Zalety metody

Pozwala na adaptacyjność do tendencji zmian
trendu, umożliwia wyznaczenie błędu ex ante

Wady metody

Złożoność obliczeniowa i trudność doboru stałej
wygładzania

k

(minimalizacja błędów),

konieczność posiadania dużej ilości danych i ich
przechowywania

Metoda wskaźników sezonowych

Algorytm prognozowania:

i

)

w

*(

t

*

ti

c

y

y

⋅

=

(model multiplikatywny)

lub

i

)

w

*(

t

*

ti

c

y

y

+

=

(model addytywny)

gdzie:

*

ti

y

- prognoza zmiennej Y dla chwili t oraz i-tego cyklu,

)

w

*(

t

y

- wstępna prognoza

w oparciu o trend liniowy,

i

c

- czysty wskaźnik sezonowości dla i-tego cyklu.

W metodzie wskaźników sezonowych prognozę wyznaczamy jako ekstrapolację
dotychczasowej tendencji korygowanej wskaźnikiem sezonowości.
Procedura konstrukcji prognozy jest następująca:

Krok 1

: Identyfikacja cykli i faz występujących w cyklach.

Krok 2

: Opracowanie prognozy wstępnej jako ekstrapolacji zaobserwowanej

tendencji rozwojowej z oszacowaniem parametrów za pomocą KMNK.

- 1/

15

-

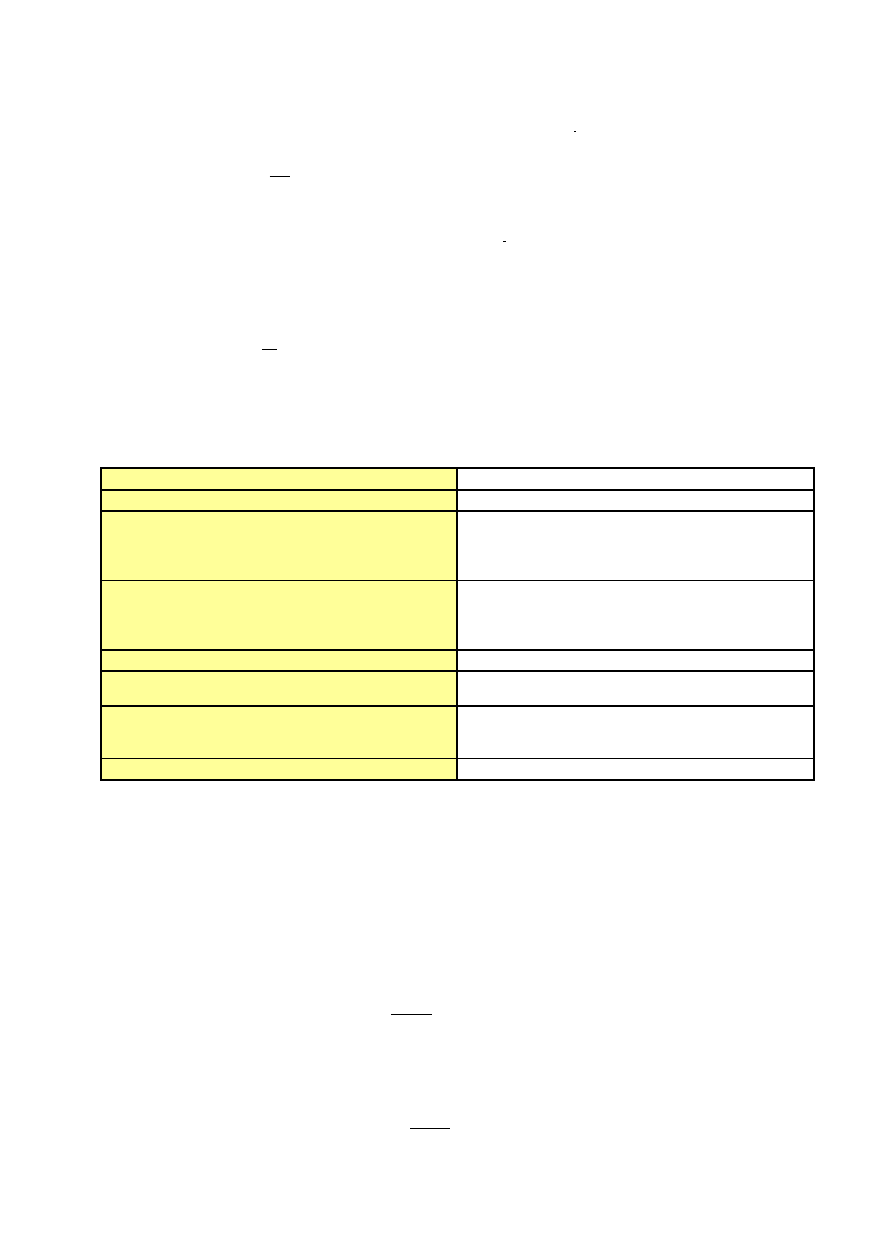
t

b

a

y

)

w

(

t

⋅

+

=



Krok 3

: Wyznaczenie wartości wskaźników sezonowości z

ti

jako ilorazu lub różnicy

wartości rzeczywistych i wartości teoretycznych:

t

ti

ti

y

y

z



=

(model multiplikatywny)

t

ti

ti

y

y

z



−

=

(model addytywny)

Krok 4

: Wyznaczenie surowych wskaźników sezonowości z

i

w celu wyeliminowania

wahań przypadkowych we wskaźnikach z

ti

przez wyznaczenie średniej

arytmetycznej tych wartości z

ti

, które odpowiadają jednoimiennym okresom.

Krok 5

: Obliczenie średniej arytmetycznej q surowych wskaźników sezonowości z

i

.

Krok 6

: Wyznaczenie czystych wskaźników sezonowości jako ilorazów lub różnic

surowych wskaźników sezonowosci z

i

i wielkości q:

q

z

c

i

i

=

(model multiplikatywny)

q

z

c

i

i

−

=

(model addytywny)

Krok 7

: Wyznaczenie prognozy jako korektę prognozy wstępnej za pomocą

czystego wskaźnika sezonowości dla danej fazy cyklu:

i

)

w

*(

t

*

ti

c

y

y

⋅

=

(model multiplikatywny)

i

)

w

*(

t

*

ti

c

y

y

+

=

(model addytywny)

Tab. Charakterystyka metody wskaźników sezonowych prognozowania

Grupa metod

Prognozowanie na podstawie szeregu czasowego

Składowe szeregu czasowego

Trend lub stały poziom i wahania sezonowe

Przesłanki metody

Nie nastąpią zmiany w sposobie oddziaływania
czynników określających zmienną prognozowaną,
utrzymanie trendu, niezmienność siły i rodzaju
wahań sezonowych

Postawa, zasada, reguły prognostyczna

Postawa pasywna, zasada status quo, reguła
podstawowa prognozowania, model addytywny
(wahania bezwzględnie stałe), model
multiplikatywny (wahania względnie stałe)

Horyzont prognozy

Prognoza krótkookresowa lub średniookresowa

Ocena prognozy

Ocena dopuszczalności prognozy za pomocą
błędu prognozy ex ante

Zalety metody

Pozwala na obserwację tendencji zmian wahań
sezonowych, umożliwia wyznaczenie błędu ex
ante

Wady metody

Złożoność obliczeń

Metoda Wintersa

Algorytm prognozowania:

Gdy szereg czasowy zmiennej prognozowanej zawiera tendencję rozwojową, wahania
sezonowe i wahania przypadkowe, wtedy stosuje się model Wintersa należący do
klasy modeli wygładzania wykładniczego. Prognozę wyznacza się w sposób
sekwencyjny, korzystając z 3 równań zawierających 3 parametry wygładzania. Model
prognozy w metodzie Wintersa może mieć postać: addytywną lub multiplikatywną.
Wygładzona wartość zmiennej po eliminacji wahań sezonowych na moment t-1 dana
jest wzorem:

(

)(

)

2

2

1

1

1

1

−

−

−

−

−

−

+

−

+

=

t

t

r

t

t

t

S

F

C

y

F

α

α

Wygładzona wartość przyrostu trendu na moment t-1 dana jest wzorem:

(

) (

)

2

2

1

1

1

−

−

−

−

⋅

−

+

−

=

t

t

t

t

S

F

F

S

β

β

Ocena wskaźników sezonowości na moment t-1 dana jest wzorem:

(

)

r

t

r

t

t

t

C

F

y

C

−

−

−

−

−

−

⋅

−

+

=

1

1

1

1

1

γ

γ

- 1/

16

-

Gdzie r – długość cyklu sezonowego (liczba faz w cyklu)
Równanie prognozy na moment t>n:

(

)

(

)

r

t

n

n

*

t

C

S

n

t

F

y

−

+

⋅

−

+

=

(postać addytywna modelu)

(

)

(

)

r

t

n

n

*

t

C

S

n

t

F

y

−

⋅

⋅

−

+

=

(postać multiplikatywna modelu)

Wyboru parametrów wygładzania dokonuje prognosta.
Wartości początkowe:

- dla komponenty F przyjąć wartość rzeczywistą zmiennej z szeregu czasowego

odpowiadającą 1. fazie drugiego cyklu lub średnią wartość z 1. cyklu,

- dla komponenty S przyjąć różnicę średnich wartości z 2. i 1. cyklu bądź przyjąć 0,
- dla komponenty C (w poszczególnych fazach 1. cyklu) przyjąć ilorazy wartości

rzeczywistej zmiennej z 1. cyklu w odniesieniu do średniej wartości w 1. cyklu
bądź przyjąć 1.

Tab. Charakterystyka metody Wintersa prognozowania

Grupa metod

Prognozowanie na podstawie szeregu czasowego

Składowe szeregu czasowego

Tendencja rozwojowa, wahania sezonowe,
wahania przypadkowe

Przesłanki metody

Nie nastąpią zmiany w sposobie oddziaływania
czynników określających zmienną prognozowaną,
utrzymanie trendu, niezmienność siły i rodzaju
wahań sezonowych

Postawa, zasada, reguły prognostyczna

Postawa pasywna, zasada status quo, reguła
podstawowa prognozowania, model addytywny
(wahania bezwzględnie stałe), model
multiplikatywny (wahania względnie stałe)

Horyzont prognozy

Prognoza krótkookresowa

Ocena prognozy

Ocena dopuszczalności prognozy za pomocą
błędu prognozy ex ante

Zalety metody

Pozwala na obserwację tendencji zmian wahań
sezonowych, umożliwia wyznaczenie błędu ex
ante

Wady metody

Trudności obliczeniowe (obliczenia sekwencyjne),
konieczność i trudność doboru parametrów α, β, γ
(minimalizacja błędów)

Metoda trendów jednoimiennych okresów

Algorytm prognozowania:

Oszacowanie parametrów trendu następuje oddzielnie dla poszczególnych faz cyklu.
Każdy szereg czasowy określonej fazy cyklu opisany jest modelem:

ji

ji

i

i

ji

t

y

ξ

α

α

+

+

=

1

0

gdzie:

ji

y

- prognoza zmiennej Y dla chwili t, i-tej fazy oraz j-tego cyklu,

ji

t

- zmienna

czasowa taka, że

(

)

1

−

⋅

+

=

j

r

i

t

ji

, α - parametry strukturalne i-tego modelu,

ξ

- składnik

losowy.

Tab. Charakterystyka metody trendów jednoimiennych okresów prognozowania

Grupa metod

Prognozowanie na podstawie szeregu czasowego

Składowe szeregu czasowego

Trend lub stały poziom, wahania sezonowe i
wahania przypadkowe

Przesłanki metody

Nie nastąpią zmiany w sposobie oddziaływania
czynników określających zmienną prognozowaną,
utrzymanie trendu, zmiany intensywności wahań
sezonowych, dużo danych

Postawa, zasada, reguły prognostyczna

Postawa pasywna, zasada status quo, reguła
podstawowa prognozowania, model liniowy dla
każdej fazy cyklu

Horyzont prognozy

Prognoza krótkookresowa

- 1/

17

-

Ocena prognozy

Ocena dopuszczalności prognozy za pomocą
błędu prognozy ex ante

Zalety metody

Pozwala na obserwację tendencji zmian wahań
sezonowych, umożliwia wyznaczenie błędu ex
ante

Wady metody

Konieczność i trudność doboru parametrów
strukturalnych

α

(minimalizacja błędów),

konieczność posiadania dużej ilości danych i ich
przechowywania

Metoda analizy harmonicznej

Algorytm prognozowania:

Analiza harmoniczna polega na budowie modelu w postaci sumy harmonik, czyli
funkcji sinusoidalnych lub cosinusoidalnych o danych okresach. Pierwsza harmonika
ma okres równy długości okresu badanego, druga – połowie tego okresu, trzecia –
jednej trzeciej, itd. W przypadku n obserwacji liczba wszystkich możliwych harmonik
jest równa n/2.
Przypadek 1
W przypadku, gdy w szeregu czasowym występuje pewien

stały poziom i wahania

sezonowe

, szereg czasowy można przedstawić jako sumę harmonik:

∑

=













−

⋅

+

=

2

1

0

2

/

n

i

i

i

t

it

n

cos

A

y

ε

π

α

lub korzystając z własności funkcji cosinus:

∑

=

























⋅

+













⋅

+

=

2

1

0

2

2

/

n

i

i

i

t

it

n

cos

it

n

sin

y

π

β

π

α

α

Wartości parametrów α

0

, α

i

, β

i

, szacuje się za pomocą KMNK. Stosuje się wzory:

∑

=

⋅

=

n

t

t

y

n

a

1

0

1

,

∑

=

−

=













⋅

⋅

=

n

t

t

i

n

,...,

i,

it

n

sin

y

n

a

1

1

2

1

2

2

π

∑

=

−

=













⋅

⋅

=

n

t

t

i

n

,...,

i,

it

n

cos

y

n

b

1

1

2

1

2

2

π

Dla ostatniej harmoniki o numerze n/2:

0

2

=

/

n

a

,

( )

∑

=

⋅

⋅

=

n

t

t

/

n

t

cos

y

n

b

1

2

1

π

Amplituda A

i

jest to największa (co do wartości bezwzględnej) różnica pomiędzy

wartością harmoniki a poziomem przeciętnym. Wartości amplitud dla poszczególnych
harmonik oblicza się wg wzoru:

2

2

i

i

b

a

A

i

+

=

Wartości przesunięcia fazowego oblicza się jako:

i

i

i

t

θ

ε

=

, gdzie:









=

i

i

i

b

a

arctg

ε

oraz

i

n

i

⋅

= π

θ

2

Przypadek 2
W przypadku, gdy w szeregu czasowym występuje pewna

tendencja rozwojowa i

wahania sezonowe

, szereg czasowy można przedstawić jako sumę harmonik:

( )

∑

=

























⋅

+













⋅

+

=

2

1

2

2

/

n

i

i

i

t

it

n

cos

it

n

sin

t

f

y

π

β

π

α

- 1/

18

-

gdzie f(t) – funkcja trendu:

1.

Oszacowujemy parametry funkcji f(t) za pomocą KMNK

2.

Oszacowujemy parametry harmonik, wartości amplitud, procent wyjaśnianej
zmienności, wielkości faz oraz przesunięcia fazowego.

Tab. Charakterystyka metody analizy harmonicznej w prognozowaniu

Grupa metod

Prognozowanie na podstawie szeregu czasowego

Składowe szeregu czasowego

Trend lub stały poziom i wahania sezonowe

Przesłanki metody

Nie nastąpią zmiany w sposobie oddziaływania
czynników określających zmienną prognozowaną,
utrzymanie trendu, niezmienność siły i rodzaju
wahań sezonowych

Postawa, zasada, reguły prognostyczna

Postawa pasywna, zasada status quo, reguła
podstawowa prognozowania, model addytywny
(wahania bezwzględnie stałe), model
multiplikatywny (wahania względnie stałe)

Horyzont prognozy

Prognoza krótkookresowa lub średniookresowa

Ocena prognozy

Ocena dopuszczalności prognozy za pomocą
błędu prognozy ex ante

Zalety metody

Pozwala na obserwację tendencji zmian wahań
sezonowych, umożliwia wyznaczenie błędu ex
ante

Wady metody

Bardzo duża złożoność obliczeń

PROGNOZOWANIE EKONOMETRYCZNE

Ogólny algorytm prognozowania:

Krok 1

: Specyfikacja zmiennych

Krok 2

: Wybór postaci modelu

Krok 3

: Estymacja parametrów modelu

Krok 4

: Weryfikacja modelu

Krok 5

: Wyznaczenie prognozy

Metoda prognozowania ekonometrycznego ze zmienną syntetyczną

Algorytm prognozowania:

Krok 1

: Normalizacja zmiennych cząstkowych (stymulant, nominant, destymulant)

Stymulanta jako zmienna, której wzrost wartości jest pożądany, jest określona
na zbiorze R+. Normalizacja tej zmiennej przebiega wg algorytmu: z

it

= (x

it

/

max x

it

).

Nominanta jako zmienna, której wartości powinna należeć do zalecanego
przedziału wartości [x

i,min

, x

i,max

] (lub jest równa x

i,norm

=x

i,min

=x

i,max

) jest określona

na zbiorze R+. Normalizacja tej zmiennej przebiega wg algorytmu:

z

it

= (x

it

/ x

i,min

),

gdy x

it

≤ x

i,min

;

z

it

= 1,

gdy x

i,min

≤ x

it

≤ x

i,max

;

z

it

= (x

i,max

/ x

it

),

gdy x

it

> x

i,max

Destymulanta jako zmienna, której wzrost spadek wartości jest pożądany, jest
określona na zbiorze R+. Normalizacja tej zmiennej przebiega wg algorytmu:

z

it

= (min x

it

/ x

it

).

Krok 2

: Wyznaczenie zmiennej syntetycznej

- 1/

19

-

Opierając się na znormalizowanych zmiennych cząstkowych konstruuje się
zmienną syntetyczną o charakterze stymulanty. Zmienna syntetyczna może
być obliczona jako suma lub jako średnia arytmetyczna.

∑

=

⋅

=

m

i

t,

i

t

z

m

Z

1

1

Krok 3

: Wyznaczenie prognozy

Prognozę wyznacza się z zastosowaniem modelu liniowego

t

t

Z

b

a

y

⋅

+

=



, dla

którego parametry a i b oszacowane są metodą KMNK. Następnie po
podstawieniu wartości dla Z

t

wyznaczana jest prognoza.

Tab. Charakterystyka metody ekonometrycznej prognozowania

Grupa metod

Prognozowanie ekonometryczne

Składowe szeregu czasowego

Dowolne

Przesłanki metody

Stabilność relacji strukturalnych w czasie, stały
rozkład w czasie składnika losowego, znajomość
wartości zmiennych objaśniających

Postawa, zasada, reguły prognostyczna

Postawa aktywna, zasada status quo, reguła
podstawowa prognozowania, model prosty,
rekurencyjny, ze zmienną zero-jedynkową, ze
zmienną syntetyczną

Horyzont prognozy

Prognoza krótkookresowa lub średniookresowa

Ocena prognozy

Ocena dopuszczalności prognozy za pomocą
błędu prognozy ex ante, ocena modelu za pomocą
współczynnika determinacji

R

2

, odchylenia

standardowego s reszt oraz macierzy wariancji i
kowariancji D

2

(a)

Zalety metody

Umożliwia poznawanie związków pomiędzy
czynnikami zjawisk (cel wyjaśniający), pozwala na
formalne

sprawdzenie

przesłanek

prognostycznych, umożliwia ocenę wpływu
zmiennych objaśniających na zmienną
prognozowania, pozwala na wyznaczenie błędu ex
ante, znany jest „dobry model”, możliwość
ekstrapolacji modelu poza jego dziedzinę

Wady metody

Złożoność obliczeniowa, duży koszt zbierania
danych i szacowania parametrów modelu,
występowanie autokorelacji składnika losowego

PROGNOZOWANIA PRZEZ ANALOGIE

W metodzie prognozowania za pomocą analogii wykorzystujemy podobieństwo
zmiennych prognozowanych w tym samym lub w różnych obiektach. Kryteria
podobieństwa to:
a) podobieństwo poziomu (dwie zmienne są podobne, jeżeli w pewnym momencie lub
okresie osiągnęły jednakową wartość),
b) podobieństwo kształtu (dwie zmienne są podobne, jeżeli charakteryzują się
podobnymi zmianami w czasie, np. mają podobne tendencje rozwojowe, podobne
wahania).

Prognozowanie za pomocą analogii przestrznno-czasowej

Algorytm prognozowania:

Krok 1

: Wybór obiektów podobnych (k)

Przyjmujemy graniczną wartość miary podobieństwa m

*

. Wybieramy obiekty

podobne do obiektu, dla którego wyznaczana jest prognoza. Na całej długości

- 1/

20

-

szeregów czasowych charakteryzujących obiekty podobne szukamy
przedziałów podobieństwa o tej samej długości, których miara podobieństwa
m

(o,k)

przekroczy krytyczną miarę podobieństwa m

*

i wybieramy spośród nich

takie pary, których miara podobieństwa osiąga wartość maksymalną.

Krok 2

: Ustalenie stałej przesunięcia ∆

(o,k)

Przed wyznaczeniem prognozy cząstkowej należy ustalić stałą przesunięcia:

∆

(o,k)

= y

0

(o)

– y

0

(k)

gdzie y

0

(o)

– wartość zmiennej przypadająca na koniec przedziału

podobieństwa obiektu prognozowanego, y

0

(k)

– wartość zmiennej przypadająca

na koniec przedziału podobieństwa obiektu podobnego k.

Krok 3

: Wyznaczenie prognozy cząstkowej y

t

*

(o,k)

Wartości w szeregach czasowych odpowiadające numerom okresów od t=1
dla obiektów podobnych zostaną wykorzystane do wyznaczenia prognozy
cząstkowej:

y

t

*

(o,k)

= y

t

(k)

+ ∆

(o,k)

,

t=1, ..., n

(k)

gdzie y

t

*

(o,k)

– prognoza cząstkowa zmiennej Y dla obiektu (o) w chwili t według

obiektu (k), y

t

(k)

- wartość zmiennej Y w k-tym obiekcie w chwili t, ∆

(o,k)

- stała

przesunięcia, n

(k)

– długość przedziału podobieństwa.

Krok 4

: Wyznaczenie prognozy globalnej y

t

*

Prognoza globalna dla obiektu na podstawie podobieństwa kształtowania się
zmiennej prognozowanej w innych obiektach zostanie wyznaczona w
następujący sposób:

∑

=

⋅

=

q

k

)

k

,

o

(

)

k

,

o

(

*

t

*

t

w

y

y

1

∑

=

=

q

k

)

k

,

o

(

)

k

,

o

(

)

k

,

o

(

m

m

w

1

Prognozowanie za pomocą analogii historycznej

Algorytm prognozowania:

W metodzie prognozowania za pomocą analogii historycznej informacja o
prawidłowościach zmian danego zjawiska (zmienna wiodąca) wykorzystywana jest w
prognozowaniu innych zjawisk w danym obiekcie, które są opóźnione (zmienna
naśladująca).

Krok 1

: Podział zmiennych na dwie grupy: zmienne wiodące i zmienne naśladujące.

Zmienne wiodące (wyprzedzające) x

t

służą wyznaczeniu prognozy, zmienne

naśladujące (opóźnione) y

t

są zmiennymi prognozowanymi.

Krok 2

: Ustalenie opóźnienia p zmiennej naśladującej.

Opóźnienie ustalane jest z wykresów zmiennych, wykorzystując kryteria
podobieństwa: poziomu (wartości) i kształtu

Krok 3

: Budowa modelu ekonometrycznego uwzględniającego opóźnienie p.

Parametry modelu oszacowywane są za pomocą KMNK. Model ma postać:

p

t

t

x

b

a

y

−

⋅

+

=



Krok 4

: Budowa modelu ekonometrycznego uwzględniającego opóźnienie p.

Prognozowanie za pomocą analogii biologicznej

Algorytm prognozowania:

W metodzie prognozowania za pomocą analogii biologicznej informacja o budowie i
funkcjonowaniu organizmów żywych wykorzystywana jest w opisie innych obiektów
(„przeniesienie na inne obiekty”).

- 1/

21

-

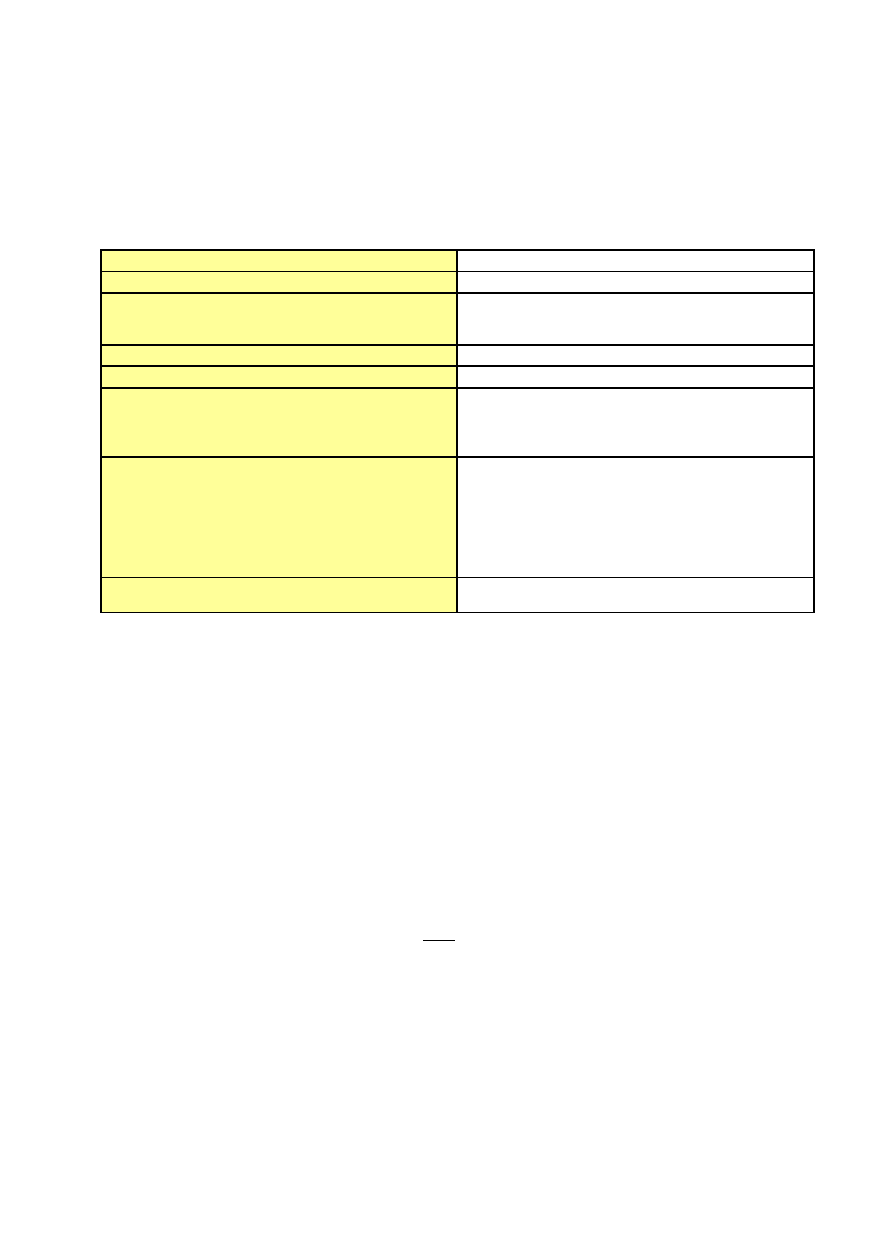
Prognozowanie za pomocą analogii przestrzennej

Algorytm prognozowania:

W metodzie prognozowania za pomocą analogii przestrzennej informacja o zajściu
danego zjawiska w innej przestrzeni (na innym terytorium) wykorzystywana jest w
przewidywaniu i prognozowaniu tego zjawiska w danej przestrzeni (na danym
terytorium), do której odnosi się prognozowane zjawisko.

Tab. Charakterystyka metod analogowych prognozowania

Grupa metod

Prognozowanie na podstawie analogii

Składowe szeregu czasowego

Dowolne

Przesłanki metody

Istnienie obiektów podobnych (podobieństwo
poziomu

lub

kształtu),

niemożność

ekstrapolowania tendencji z przeszłości

Postawa, zasada, reguły prognostyczna

Postawa aktywna

Horyzont prognozy

Prognoza średniookresowa lub długookresowa

Ocena prognozy

Ocena dopuszczalności prognozy za pomocą
długości przedziałów podobieństwa (liczby
obserwacji), wartości miar podobieństwa, błędów
ex ante (analogie historyczne)

Zalety metody

Możliwość prognozowania przy braku dla danego
obiektu szeregów czasowych z przeszłości,
przewidywanie zajścia nowych zdarzeń w
obiekcie, przewidywanie trendu i związków
pomiędzy zmiennymi w przyszłości, przewidywanie
punktów zwrotnych trendu i zmiany postaci
związków między zmiennymi

Wady metody

Brak możliwości ekstrapolowania tendencji z
przeszłości

PROGNOZOWANIE HEURYSTYCZNE

Metoda heurystyczna Delphi

Prognozowanie i ocena zgodności ekspertów wg współczynnika h dyspersji
opinii ekspertów

Algorytm prognozowania:

W metodzie delfickiej prognosta przyjmuje postawę aktywną. Prognoza zostaje
sformułowana wg reguły największego prawdopodobieństwa. Jest nią wartość
modalna, czyli ten wariant cechy, któremu odpowiada największa liczba udzielonych
odpowiedzi przez ekspertów. Zgodność opinii ekspertów oceniana jest na podstawie
współczynnika dyspersji, którego wartość zawiera się w przedziale [0, 1] i powinna być
jak najmniejsza. Współczynnik ten obliczany jest jako:















−

⋅

−

=

∑

=

k

j

rj

r

f

k

k

h

1

2

1

1

gdzie: k – liczba kategorii odpowiedzi w r-tym pytaniu, f

rj

- częstość odpowiedzi dla j-tej

kategorii w r-tym pytaniu.

Prognozowanie i ocena zgodności ekspertów wg współczynnika W konkordancji
(zgodności) opinii ekspertów

Algorytm prognozowania:

W metodzie delfickiej prognosta przyjmuje postawę aktywną. Eksperci nadają rangi
poszczególnym wariantom odpowiedzi, wskazując w ten sposób kolejność wg szans
realizacji prognozy. Prognoza zostaje sformułowana wg reguły największego

- 1/

22

-

prawdopodobieństwa (szans) realizacji prognozy. Jest nią wartość modalna, czyli ten
wariant cechy, któremu odpowiada największe prawdopodobieństwo realizacji.
Zgodność opinii ekspertów oceniana jest na podstawie współczynnika konkordancji,
którego wartość zawiera się w przedziale [0, 1] i powinna być jak największa.
Współczynnik ten obliczany jest jako:

(

)

k

k

n

S

W

−

⋅

⋅

=

3

2

12

,

∑ ∑

=

=









−

=

k

j

n

i

ij

x

x

S

1

2

1

,

∑ ∑

=

=

⋅

=

n

i

k

j

ij

x

k

x

1

1

1

gdzie n – liczba ekspertów, k – liczba wariantów odpowiedzi, S – parametr sumowania
odchyleń od przeciętnej rangi,

x

- przeciętna ranga. Następnie obliczana jest

statystyka

χ

2

:

(

)

1

12

2

+

⋅

⋅

⋅

=

k

k

n

S

χ

Z tablic rozkładu

χ

2

dla przyjętego w prognozowaniu poziomu istotności α oraz k-1

stopni swobody odczytywana jest wartość krytyczna

χ

2

kr

i następuje jej porównanie z

wartością obliczonej statystyki. Jeżeli

χ

2

>

χ

2

kr

, to można uznać, że eksperci byli zgodni

w swych opiniach.

Prognozowanie i ocena zgodności ekspertów wg mediany

Algorytm prognozowania:

Prognozą jest wartość środkowa szeregu, czyli mediana. Mediana dzieli szereg
odpowiedzi na 2 równoliczne grupy. Porządkujemy odpowiedzi ekspertów wg
wzrastających ocen liczbowych. Miejsce mediany wyznacza relacja (N+1)/2, gdzie N
jest liczbą ocen (liczbą ekspertów). By ocenić zgodność opinii ekspertów możemy
posłużyć się rozstępem międzykwartylowym

∆

= Q

3

– Q

1

, gdzie: Q

3

– kwartyl górny,

Q

1

– kwartyl dolny. Kwartyl dolny Q

1

= (N+1)/4, kwartyl górny Q

3

= 3(N+1)/4. Jeżeli

obliczony rozstęp międzykwartylowy

∆

≤

∆

*

,

gdzie

∆

* jest pożądanym rozstępem, to

oznacza, że eksperci są zgodni w swoich opiniach.

Metoda testu koniunktury

Algorytm prognozowania:

Test koniunktury to ankietowe badanie przedsiębiorstw. Ankieta zawiera pytania
diagnostyczne i pytania prognostyczne dotyczące określonych aspektów
przedsiębiorstwa. Wyniki badania prezentowane są w postaci: wykresów, procentowej,
ważonej oraz w formie ważonego salda. Saldo jest różnicą pomiędzy procentem
odpowiedzi wskazujących na polepszenie a procentem odpowiedzi
wskazujących na pogorszenie sytuacji przedsiębiorstwa lub różnicą pomiędzy
procentem odpowiedzi wskazujących na sytuację korzystną dla
przedsiębiorstwa a procentem odpowiedzi wskazujących na sytuację
niekorzystną dla przedsiębiorstwa. Saldo oblicza się w odniesieniu do danego
pytania w badaniu i pytań tych jest n. Wskaźnik koniunktury w formie sald przyjmuje
wartość z przedziału od -100 do +100. Dodatnia wartość wskaźnika oznacza dobrą
koniunkturę, ujemna zaś złą. Wzrost wskaźnika oznacza poprawę koniunktury, a jego
spadek – pogorszenie koniunktury z punktu widzenia badanych przedsiębiorstw.
Procedura prognozowania jest następująca:

Krok 1

: Przeprowadzenie ankiety z pytaniami diagnostycznymi i prognostycznymi.

Krok 2

: Obliczenie sald S

i

(i=1, ..., n) jako wskaźników koniunktury.

Krok 3

: Obliczenie wskaźnika w klimatu koniunktury.

Wskaźnik klimatu koniunktury ten obliczany jest jako średnia arytmetyczna
sald odpowiedzi na pytania dotyczące aktualnej i przewidywanej sytuacji

- 1/

23

-

przedsiębiorstwa. „Dobry” klimat koniunktury mają przedsiębiorstwa, dla
których wartość wskaźnika jest większa od 0.

n

S

w

n

i

i

∑

=

=

1

Tab. Charakterystyka metody heurystycznej prognozowania

Grupa metod

Prognozowanie heurystyczne

Składowe szeregu czasowego

Brak szeregów czasowych

Przesłanki metody

Brak danych z przeszłości, istnienie dostępu do
prognoz ekspertów

Postawa, zasada, reguły prognostyczna

Postawa aktywna, badanie opinii ekspertów na
dany temat, zastosowanie reguły największego
prawdopodobieństwa (prognozą jest wartość
modalna opinii ekspertów), niezależność i wielość
opinii ekspertów, wieloetapowość postępowania,
ocena statystyczna opinii ekspertów

Horyzont prognozy

Prognoza średniookresowa lub długookresowa

Ocena prognozy

Ocena dopuszczalności prognozy za pomocą miar
zgodności opinii ekspertów

Zalety metody

Możliwość prognozowania zjawisk nowych

Wady metody

Wieloetapowość postępowania, subiektywizm
opinii ekspertów

PRZYKŁADY ZASTOSOWANIA METOD PROGNOZOWANIA

Przykład 1

Dochody ze sprzedaży (w tys. zł w cenach stałych) rakiet tenisowych przedsiębiorstwa
”Master” w latach 1996-2004 w Polsce kształtowały się następująco: 46,5; 46,4; 46,7; 45,9;
46,0; 45,9; 46,2; 46,6; 46,5.

a) Określić składowe szeregu czasowego.
b) Wybrać metodę prognozowania dochodów ze sprzedaży rakiet tenisowych na rok 2005.

Wybór uzasadnić.

c) Wyznaczyć prognozę wybraną metodą.

Rozwiązanie:

a) Składowe szeregu czasowego: stały poziom + wahania przypadkowe

45,5

46,0

46,5

47,0

Seria 1

Ocena wzrokowa wykresy wskazuje, że w badanym szeregu czasowym występują: składowa
systematyczna w postaci stałego (przeciętnego) poziomu oraz wahania przypadkowe. Do oceny siły
wahań przypadkowych zastosowano współczynnik zmienności.

(

)

∑

=

−

⋅

−

=

n

t

t

y

y

n

s

1

2

1

1

∑

=

⋅

=

n

t

t

y

n

y

1

1

%

y

s

V

Z

100

⋅

=

%

,

,

/

.

%

y

s

V

Z

66

0

3

46

30822

0

100

=

=

⋅

=

- 1/

24

-

Niska wartość współczynnika zmienności badanej zmiennej dopuszcza zastosowanie metody naiwnej do
prognozowania na następny okres.

b) Metoda prognozowania dochodów ze sprzedaży rakiet

Ponieważ w badanym szeregu czasowym występuje składowa systematyczna stałego poziomu oraz
niewielkie wahania przypadkowe, w prognozowaniu można wykorzystać metody prognozowania na
podstawie szeregu czasowego (w tym: metodę naiwną, wygładzania wykładniczego, itp.).

c) Wyznaczenie prognozy

- metoda naiwna: y

10

*

= 46,5

- metoda wygładzania wykładniczego: przyjęto, że α=0,2

y

10

*

= α · y

9

+ (1 – α) · y

9

*

= 0,2· 46,5 + (1 – 0,2) · 46,30271 = 46,34217

t

y

y*

e

y-ysr

(y-y

sr

)

2

1

46,5

46,5

0

0,2

0,04

2

46,4

46,5

-0,1

0,1

0,01

3

46,7

46,48

0,22

0,4

0,16

4

45,9

46,524

-0,624

-0,4

0,16

5

46

46,3992

-0,3992

-0,3

0,09

6

45,9 46,31936

-0,41936

-0,4

0,16

7

46,2 46,23549

-0,03549

-0,1

0,01

8

46,6 46,22839

0,37161

0,3

0,09

9

46,5 46,30271 0,197288

0,2

0,04

10

46,34217

416,7

0,76

y

sr

46,3

s

0,308221

V

z

[%]

0,665703

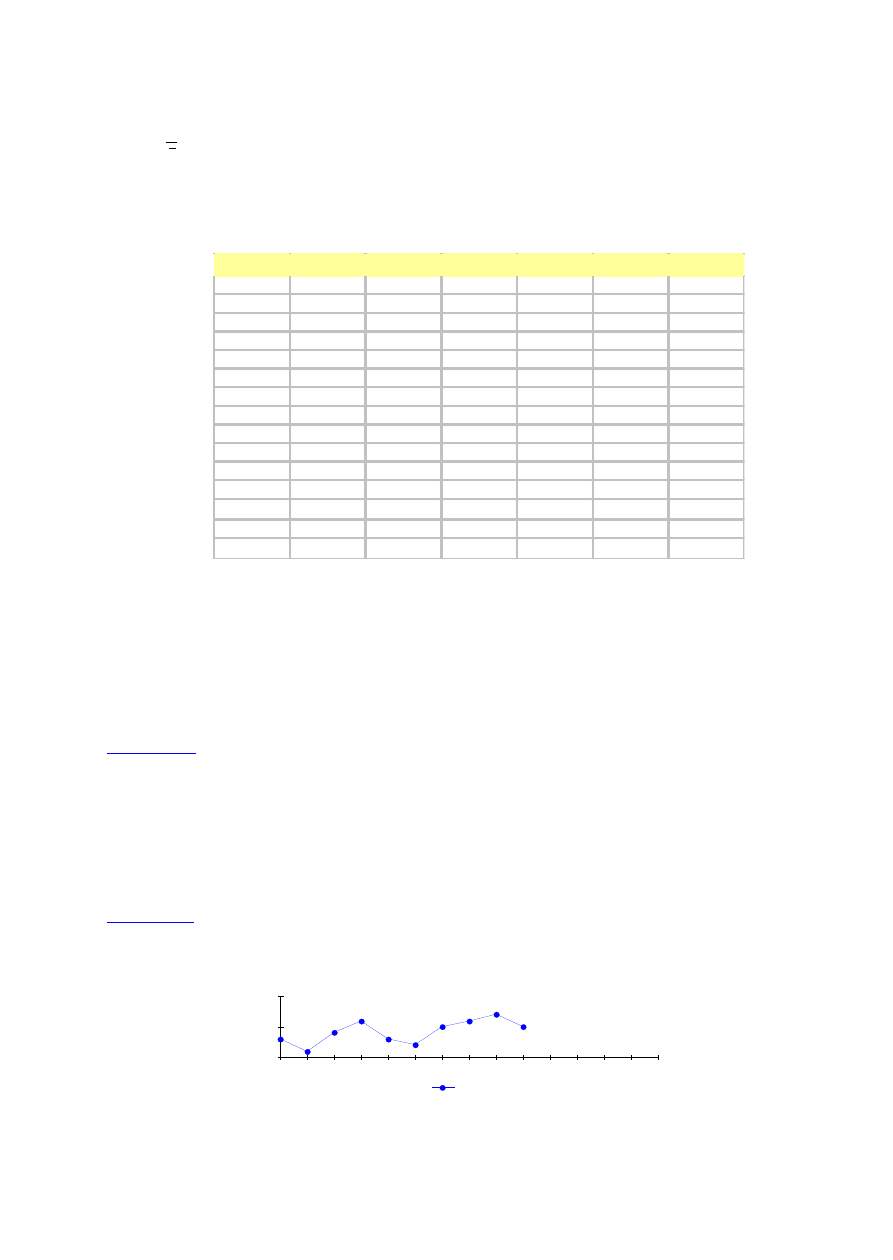
Przykład 2

Ilość sprzedanego masła (w kostkach) w sklepie "Wrocławianka" w kolejnych 10 tygodniach
kształtowała się następująco: 30, 32, 28, 31, 29, 33, 30, 31, 30, 32.

a) Określić obiekt, zjawisko, zmienną.
b) Sformułować przesłanki do wyznaczenia prognozy na następny tydzień.
c) Wybrać metodę do wyznaczenia prognozy sprzedaży masła na następny tydzień. Wybór

uzasadnić.

d) Wyznaczyć prognozę wybraną metodą.
e) Ocenić trafność prognozy, wiedząc, że w prognozowanym okresie sprzedano 33 kostki

masła.

Rozwiązanie:

a)

Obiekt: system „sklep Wrocławianka”

Zjawisko: gospodarcze – sprzedaż masła
Zmienna: ilość sprzedanego masła w kostkach w kolejnych 10 tygodniach (zmienna ilościowa)

b)

Przesłanki: hipotezy badawcze określające wstępnie mechanizm rozwojowy (wskazanie zjawisk i
kierunki wpływów). Mechanizm: przypadkowy wzrost-spadek wokół wartości sredniej

0

20

40

Seria 1

c)

Wybór metody: na podstawie szeregu czasowego

- metoda naiwna
- metoda średniej ruchomej prostej

- 1/

25

-

- metoda średniej ruchomej ważonej
- metoda wyrównywania wykładniczego

%

,

,

/

,

%

y

s

V

Z

92

4

6

30

5055

1

100

=

=

⋅

=

Niska wartość współczynnika zmienności badanej zmiennej dopuszcza zastosowanie metody naiwnej
do prognozowania na następny okres.

t

y

y*

e

y-y

sr

(y-y

sr

)

2

1

30

30

0

-0,6

0,36

2

32

30

2

1,4

1,96

3

28

30,4

-2,4

-2,6

6,76

4

31

29,92

1,08

0,4

0,16

5

29

30,136

-1,136

-1,6

2,56

6

33

29,9088

3,0912

2,4

5,76

7

30 30,52704

-0,52704

-0,6

0,36

8

31 30,42163 0,578368

0,4

0,16

9

30 30,53731

-0,53731

-0,6

0,36

10

32 30,42984 1,570156

1,4

1,96

11

30,74388

Suma

306

20,4

y

sr

30,6

s

1,505545

V

z

[%]

4,920083

d) Wyznaczenie prognozy:

- metoda naiwna: y

11

*

= 32

- metoda wygładzania wykładniczego: przyjęto α=0,2

y

11

*

= α · y

10

+ (1 – α) · y

10

*

= 0,2· 32 + (1 – 0,2) · 30,43 = 30,74

e)

Trafność prognozy;.

- metoda naiwna

Ψ

*

= 5%, (graniczny błąd ex post)

Ψ

11

= (33-32)/33 = 3%  (prognoza trafna)

Przykład 3

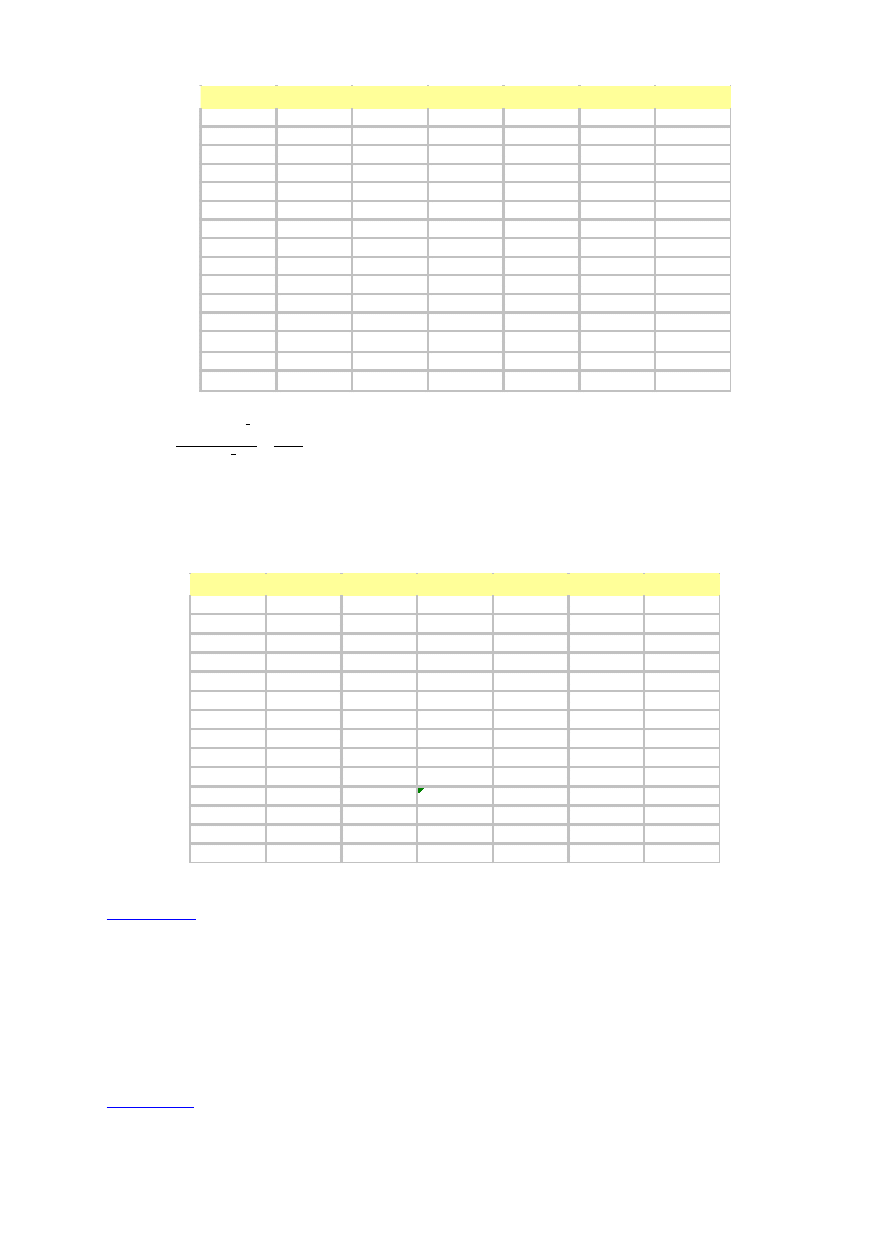
Liczba pasażerów przewożonych środkami komunikacji miejskiej w latach 1996-2005 (w mln
osób) w pewnym mieście była następująca: 12,8; 12,6; 12,9; 13,1; 12,8; 12,7; 13,0; 13,1; 13,2;
13,0.
a) Sformułować przesłanki do wyznaczenia prognozy na 2006 r.
b) Jaką postawę można przyjąć przy konstrukcji prognozy na 2006 r. i dlaczego?
c) Wybrać metodę prognozowania. Wybór uzasadnić.
d) Wyznaczyć prognozę liczby przewożonych pasażerów w 2006 r.

Rozwiązanie:

a)

Przesłanki: hipotezy badawcze określające wstępnie mechanizm rozwojowy (wskazanie zjawisk i
kierunki wpływów). Mechanizm: trend liniowy + wahania przypadkowe.

12,5

13,0

13,5

Seria 1

b)

Postawa: pasywna (widzenie przyszłości zjawiska jako nieuniknionego, pojedynczego następstwa

przeszłości). Oznacza to, że „prawa ruchu” zjawiska wyrażają przyszłe stany przez stany przeszłe.

c)

Wybór metody: prognozowanie na podstawie szeregu czasowego z trendem liniowym.

- 1/

26

-

t

y

y*

e

y-y

sr

(y-y

sr

)

2

1

12,8

12,8

0

-0,12

0,0144

2

12,6

12,8

-0,2

-0,32

0,1024

3

12,9

12,76

0,14

-0,02

0,0004

4

13,1

12,788

0,312

0,18

0,0324

5

12,8

12,8504

-0,0504

-0,12

0,0144

6

12,7 12,84032

-0,14032

-0,22

0,0484

7

13 12,81226 0,187744

0,08

0,0064

8

13,1

12,8498 0,250195

0,18

0,0324

9

13,2 12,89984 0,300156

0,28

0,0784

10

13 12,95988 0,040125

0,08

0,0064

11

12,9679

Suma

129,2

0,336

y

sr

12,92

s

0,193218

V

z

[%]

1,495498

d) Wyznaczenie prognozy

(

)

(

)

=

=

−

−

⋅

=

∑

∑

5

82

3

3

2

,

,

t

t

t

t

y

b

0,04

−

−

⋅

−

=

t

b

y

a

=

12,7

y

t

*

= 0,04 · t + 12,7

y

11

*

= 0,04 · 11 + 12,7 = 13,14 mln osób.

t

t-t

śr

(t-t

śr

)2

y

y(t-t

sr

)

y*

1

-4,5

20,25

12,8

-57,6

2

-3,5

12,25

12,6

-44,1

3

-2,5

6,25

12,9

-32,25

4

-1,5

2,25

13,1

-19,65

5

-0,5

0,25

12,8

-6,4

6

0,5

0,25

12,7

6,35

7

1,5

2,25

13

19,5

8

2,5

6,25

13,1

32,75

9

3,5

12,25

13,2

46,2

10

4,5

20,25

13

58,5

0

82,5

12,92

3,3

13,14

b

0,04

a

12,7

Przykład 4

Liczba nowo otwartych kont osobistych w banku „AmiBank” w ciągu ostatnich 12 miesięcy była
następująca: 40, 39, 45, 47, 50, 48, 42, 47, 43, 38, 40, 41.
a) Określić składowe szeregu czasowego.
b) Wybrać metodę do wyznaczania prognozy liczby nowo otwartych kont na następny

miesiąc. Wybór uzasadnić.

c) Wyznaczyć prognozę wybraną metodą.
d) Ocenić trafność wyznaczonej prognozy, wiedząc, że rzeczywista liczba nowo otwartych kont
w trzynastym miesiącu wynosiła 42.

Rozwiązanie:

a) Określenie składowych szeregu czasowego. Ocena wzrokowa i współczynnik V

z

wskazują na

następujące składowe: stała wartość + duże wahania przypadkowe.

- 1/

27

-

0

50

Seria 1

t

y

y-y

sr

(y-y

sr

)

2

1

40

-3,33333 11,11111

2

39

-4,33333 18,77778

3

45 1,666667 2,777778

4

47 3,666667 13,44444

5

50 6,666667 44,44444

6

48 4,666667 21,77778

7

42

-1,33333 1,777778

8

47 3,666667 13,44444

9

43

-0,33333 0,111111

10

38

-5,33333 28,44444

11

40

-3,33333 11,11111

12

41

-2,33333 5,444444

Suma

520

172,6667

y

sr

43,33333

s

3,96194

V

z

[%]

9,142939

b) Wybór metody.

Metoda prognozowania na podstawie szeregu czasowego:
- metoda uśredniania wykładniczego
- metoda trendu liniowego

c) Wyznaczenie prognozy wybraną metodą.

- metoda uśredniania wykładniczego dla α = 0,25 (dla α = 0,3 y*=41,622)

y* = 42

t

y

y*

e

1

40

40

0

2

39

40

-1

3

45

39,75

5,25

4

47

41,0625

5,9375

5

50 42,54688 7,453125

6

48 44,41016 3,589844

7

42 45,30762

-3,30762

8

47 44,48071 2,519287

9

43 45,11053

-2,11053

10

38

44,5829

-6,5829

11

40 42,93718

-2,93718

12

41 42,20288

-1,20288

13

41,90216

- metoda trendu liniowego: y* = 42

- 1/

28

-

t

t-t

śr

(t-t

śr

)2

y

y(t-t

sr

)

y*

1

-5,5

30,25

40

-220

2

-4,5

20,25

39

-175,5

3

-3,5

12,25

45

-157,5

4

-2,5

6,25

47

-117,5

5

-1,5

2,25

50

-75

6

-0,5

0,25

48

-24

7

0,5

0,25

42

21

8

1,5

2,25

47

70,5

9

2,5

6,25

43

107,5

10

3,5

12,25

38

133

11

4,5

20,25

40

180

12

5,5

30,25

41

225,5

0

143 43,33333

-32

42,32634

b

-0,22378

a

44,78788

d) Ocena trafności wyznaczonej prognozy, wiedząc, że rzeczywista liczba nowo otwartych kont w

trzynastym miesiącu (T=13) wynosiła 42.
- metoda uśredniania wykładniczego dla α = 0,25

Ψ

*

= 5%

Ψ

13

= ((42-42)/42)·100% = 0,00 %

Wniosek: prognoza jest dopuszczalna

- metoda trendu liniowego

Ψ

*

= 5%

Ψ

13

= ((42-42)/42)·100% = 0,00 %

Wniosek: prognoza jest dopuszczalna

Przykład 5

Liczba produkowanych i sprzedawanych czajników bezprzewodowych (w tys. sztuk) przez
pewną firmę w poszczególnych kwartałach lat 2003-2005 została opisana modelem:

ŷ

t

= 15 + 0,5·t

s = 0,5 tys. sztuk

R

2

= 0.90

Przy sprzedaży 20 tys. sztuk czajników w IV kwartale 2005 r. firma wykorzystała swoje
możliwości produkcyjne w 83%. Przyjmując postawę pasywną, ocenić z
prawdopodobieństwem 0,9 słuszność wypowiedzi dyrektora firmy, twierdzącego, iż do końca
2006 r. zdolności produkcyjne firmy będą wystarczające do zaspokojenia zgłaszanego popytu
na czajniki bezprzewodowe. Przyjąć, że w danym kwartale sprzedawane są tylko czajniki
produkowane w tym kwartale.

Rozwiązanie:

Zastosowanie: metoda trendu liniowego i konstrukcja prognozy przedziałowej

Obliczenie zdolności produkcyjnych firmy:
0.83 · 20 tys. sztuk / 0.83 = 24,096 tys. sztuk ≈ 24,1 tys. sztuk

Obliczenie prognoz na kolejne kwartały 2006 r.:
y*

13

= 15 + 0,5·13 = 15 + 6,5 = 21,5 tys. szt.

y*

14

= 15 + 0,5·14 = 15 + 6,5 = 22,0 tys. szt.

y*

15

= 15 + 0,5·15 = 15 + 6,5 = 22,5 tys. szt.

y*

16

= 15 + 0,5·16 = 15 + 6,5 = 23,0 tys. szt.

Błędy ex ante obliczonych prognoz są następujące:

(

)

(

)

1

12

1

5

6

5

6

13

12

1

2

2

13

+

+

−

−

⋅

=

∑

=

=

t

t

,

t

,

s

v

=0,5871 [tys. sztuk]

- 1/

29

-

t

t-t

sr

(t-tsr)

2

v

13

v

14

v

15

v

16

1

-5,5

30,25 0,587109 0,607596 0,630194 0,654685

2

-4,5

20,25

3

-3,5

12,25

4

-2,5

6,25

5

-1,5

2,25

6

-0,5

0,25

7

0,5

0,25

8

1,5

2,25

9

2,5

6,25

10

3,5

12,25

11

4,5

20,25

12

5,5

30,25

6,5

143

Konstrukcja prognozy przedziałowej
Prognozę przedziałową dla zadanej z góry wiarygodności prognozy (p) konstruuje się w następujący
sposób:

{

}

p

v

u

y

y

v

u

y

P

T

*

T

T

T

*

T

=

⋅

+

≤

≤

⋅

−

gdzie u – współczynnik związany z wiarygodnością prognozy, rozkładem reszt modelu oraz długością
szeregu czasowego. Przyjmujemy założenie o rozkładzie reszt.
a) nie weryfikowano hipotezy o normalnym rozkładzie reszt (lub przy odrzuceniu hipotezy)

Wartość współczynnika u znaleziona z nierówności Czebyszewa jest równa sqrt[1/(1-0.9)] = 3.1623

1623

3

9

0

1

1

,

,

u

=

−

=

Prognoza przedziałowa dla T=13 ma postać:
[21,5 - 3,1623 · 0,5871; 21,5 + 3,1623 · 0,5871] = [19,64; 23,36]
Prognoza przedziałowa dla T=14 ma postać:
[22,0 - 3,1623 · 0,6076; 22,0 + 3,1623 · 0,6076] = [20,08; 23,92]
Prognoza przedziałowa dla T=15 ma postać:
[22,5 - 3,1623 · 0,6302; 22,5 + 3,1623 · 0,6302] = [20,51;

24,49

]

Prognoza przedziałowa dla T=16 ma postać:
[23,0 - 3,1623 · 0,6547; 23,0 + 3,1623 · 0,6547] = [20,93;

25,07

]

b) rozkład reszt jest normalny

Uznając, że podany przedział jest za szeroki przetestowano hipotezę o normalności rozkładu reszt
modelu i nie było podstaw do jej odrzucenia. Jeżeli zatem rozkład reszt jest normalny wartość
współczynnika u odczytuje się z tablic rozkładu t-Studenta dla n-2 stopni swobody i

α

=1-p (przy n>30

korzystamy z tablic rozkładu normalnego). W naszym przypadku mamy:

n-2 = 12-2 = 10 stopni swobody oraz

α

=1-0,9=0,1,

a zatem u = 1,812

Prognoza przedziałowa dla T=16 ma postać:
[23 - 1,812 · 0,6547; 23 + 1,812 · 0,6547] = [21,81;

24,19

]

Wniosek:
Dyrektor firmy nie miał racji – zdolności produkcyjne mogą nie wystarczyć na produkcję w roku 2006.
Maksymalny zgłaszany popyt może wynosić ok. 25 tys. sztuk (25,07 tys. sztuk)).

Przykład 6

Dane jest ostatnie równanie trendu pełzającego: ŷ

t

= 7 + 1,2·t, dla t = 4, 5, 6 oraz przyrosty

wyrównanych wartości szeregu czasowego: 2,5 2,0 3,1 2,3 1,8. Wyznaczyć prognozę
zjawiska na okres T = 8.

Rozwiązanie:

Trend pełzający jest modelem adaptacyjnym służącym do budowy prognoz krótkookresowych.
Procedura konstrukcji i ekstrapolacji trendu pełzającego jest następująca:
a) Krok 1: Ustalenie wartości stałej wygładzania k < n

b)

Krok 2: Oszacowanie na podstawie kolejnych fragmentów szeregu o długości k liniowych funkcji

trendu.

- 1/

30

-

c)

Krok 3: Obliczenie wygładzonych wartości zmiennej ŷ

t(i)

, tzn. wartości teoretycznych wynikających z i-

tej funkcji trendu.

d)

Krok 4: Obliczenie średniej wartości wygładzonej

t

y

dla każdego okresu t jako średniej arytmetycznej

wartości wygładzonych obliczonych dla tego okresu w kroku 3. Po połączeniu odcinkami liniowymi
kolejnych punktów (t,

t

y

) otrzymuje się wykres wygładzonych wartości szeregu czasowego w

postaci funkcji segmentowej, zwanej trendem pełzającym.

e)

Krok 5: Ekstrapolacja modelu trendu pełzającego. Obliczenie przyrostów funkcji trendu dla wartości

wygładzonych:

1

1

1

1

−

=

−

=

+

+

n

,...,

t

,

y

y

w

t

t

t

f)

Krok 6: Nadanie wag poszczególnym przyrostom. Są to tzw. wagi harmoniczne.

1

1

1

1

1

1

1

−

=

−

⋅

−

=

∑

=

+

n

,...,

t

,

i

n

n

C

t

i

n

t

g)

Krok 7: Określenie średniego przyrostu trendu jako średniej ważonej (wagami harmonicznymi)

wszystkich obliczonych w kroku 5 przyrostów.

∑

−

=

+

+

⋅

=

1

1

1

1

n

t

t

n

t

w

C

w

h) Krok 8: Wyznaczenie prognozy punktowej na moment/okres T.

w

)

n

T

(

y

y

n

*

T

⋅

−

+

=

Dane: n=6, k=3
Obliczenie wygładzonych wartości zmiennej y:
ŷ

4

= 7 + 1,2·4 = 11,8

ŷ

5

= 7 + 1,2·5 = 13

ŷ

6

= 7 + 1,2·6 = 14,2

Obliczenie średniej wartości wygładzonej w ostatnim okresie:

13

3

2

14

13

8

11

=

+

+

=

/

)

,

,

(

y

t

Nadanie wag poszczególnym przyrostom:
t=1

=

=

+

6

2

6

1

1

C

C

(1/(6-1)) ·(1/(6-1))=0,04

t=2

=

=

+

6

3

6

1

2

C

C

(1/(6-1)) ·((1/(6-1))+(1/(6-2)))=0,09

t=3

=

=

+

6

4

6

1

3

C

C

(1/(6-1)) ·((1/(6-1))+(1/(6-2))+(1/(6-3)))=0,1566

t=4

=

=

+

6

5

6

1

4

C

C

(1/(6-1)) ·((1/(6-1))+(1/(6-2))+(1/(6-3))+(1/(6-4)))=0,2566

t=5

=

=

+

6

6

6

1

5

C

C

(1/(6-1))·((1/(6-1))+(1/(6-2))+(1/(6-3))+(1/(6-4))+(1/(6-5)))=0,4566

Określenie średniego przyrostu trendu jako średniej ważonej:

∑

−

=

+

+

⋅

=

1

1

1

1

n

t

t

n

t

w

C

w

=0,04·2,5+0,090·2,0+0,157·3,1+0,257·2,3+0,456·1,8=2,18

Wyznaczenie prognozy:

w

)

n

T

(

y

y

n

*

T

⋅

−

+

=

56

18

18

2

6

8

2

14

8

,

,

)

(

,

y

*

=

⋅

−

+

=

y

8

*

=18,56

Przykład 7

Na podstawie danych o kształtowaniu się sprzedaży firmy „Trefl” S.A. (w mln zł) w
poszczególnych kwartałach lat z lat 2002-2005 wyznaczono następujące funkcje trendu:

ŷ

t

= 18,54 + 0,75·t

s = 1,04 mln zł

R

2

= 0.91

ŷ

t

= 17,35 · 1,104

t

s = 3,55 mln zł

R

2

= 0.72

Wybierając odpowiedni model (wybór uzasadnić), wyznaczyć prognozę zmiennej na I kwartał
2006 r. stosując regułę podstawową. Ocenić jej dopuszczalność, wiedząc, że prognoza może
być obarczona błędem względnym co najwyżej 4%.

Rozwiązanie:

Wybór modelu: funkcja liniowa (większe dopasowanie R

2

, mniejszy błąd s)

- 1/

31

-

Błąd ex ante prognozy:

(

)

(

)

1

n

1

t

t

t

T

s

v

2

2

+

+

−

−

⋅

=

∑

Względny błąd ex ante prognozy:

%

100

y

v

*

T

T

T

⋅

=

η

t

t-t

śr

(t-t

śr

)

2

y

t

*

v

17

n

17

1

-7,5

56,25

19,29 1,1743253 3,753037

2

-6,5

42,25

20,04

3

-5,5

30,25

20,79

4

-4,5

20,25

21,54

5

-3,5

12,25

22,29

6

-2,5

6,25

23,04

7

-1,5

2,25

23,79

8

-0,5

0,25

24,54

9

0,5

0,25

25,29

10

1,5

2,25

26,04

11

2,5

6,25

26,79

12

3,5

12,25

27,54

13

4,5

20,25

28,29

14

5,5

30,25

29,04

15

6,5

42,25

29,79

16

7,5

56,25

30,54

17

31,29

340

ŷ

t

= 18,54 + 0,75·t

y*

17

= 18,54 + 0,75·t = 31,29 mln zł.

η

*

= 5%

η

17

= 3,75% < 4%

Wniosek: prognoza jest dopuszczalna

Przykład 8

Liczba zawartych umów leasingowych w firmie finansowo-leasingowej w poszczególnych
kwartałach lat 2002-2005 kształtowała się następująco:

20 10 4 11 33 17 9 18 45 23 14 11 25 60 30 13.

Sporządzić prognozy liczby zawartych umów leasingowych na kolejny rok (2006), stosując
model Wintersa.

Rozwiązanie:

Sprawdzenie zmienności szeregu czasowego:

0

50

100

Seria 1

Gdy szereg czasowy zmiennej prognozowanej zawiera tendencję rozwojową, wahania sezonowe i
wahania przypadkowe, wtedy stosuje się model Wintersa należący do klasy modeli wygładzania
wykładniczego. Prognozę wyznacza się w sposób sekwencyjny, korzystając z 3 równań zawierających 3
parametry wygładzania.

- 1/

32

-

t

y

y-y

sr

(y-y

sr

)

2

1

20

-1,4375 2,066406

2

10

-11,4375 130,8164

3

4

-17,4375 304,0664

4

11

-10,4375 108,9414

5

33

11,5625 133,6914

6

17

-4,4375 19,69141

7

9

-12,4375 154,6914

8

18

-3,4375 11,81641

9

45

23,5625 555,1914

10

23

1,5625 2,441406

11

14

-7,4375 55,31641

12

11

-10,4375 108,9414

13

25

3,5625 12,69141

14

60

38,5625 1487,066

15

30

8,5625 73,31641

16

13

-8,4375 71,19141

Suma

343

3231,938

y

sr

21,4375

s

14,67864

V

z

[%]

68,47179

Postawa prognosty: pasywna. Horyzont prognozy: prognoza krótkookresowa. Postaci modelu Wintersa:
wybieramy postać multiplikatywną. Liczba umów jest najwyższa w 1. kwartałach i 4 kwartałach, najniższa
w 3. kwartałach. Zauważyć można tendencję wzrostową liczby zawieranych umów.

Postać multiplikatywna:

Wygładzona wartość zmiennej po eliminacji wahań sezonowych na moment t-1 dana jest wzorem:

(

)(

)

2

2

1

1

1

1

−

−

−

−

−

−

+

−

+

=

t

t

r

t

t

t

S

F

C

y

F

α

α

Wygładzona wartość przyrostu trendu na moment t-1 dana jest wzorem:

(

) (

)

2

2

1

1

1

−

−

−

−

⋅

−

+

−

=

t

t

t

t

S

F

F

S

β

β

Ocena wskaźników sezonowości na moment t-1 dana jest wzorem:

(

)

r

t

r

t

t

t

C

F

y

C

−

−

−

−

−

−

⋅

−

+

=

1

1

1

1

1

γ

γ

Gdzie r – długość cyklu sezonowego (liczba faz w cyklu)

Równanie prognozy na moment t>n:

(

)

(

)

r

t

n

n

*

t

C

S

n

t

F

y

−

⋅

⋅

−

+

=

Wyboru parametrów wygładzania dokonuje prognosta.

Wartości początkowe:

- dla komponenty F przyjąć wartość rzeczywistą zmiennej z szeregu czasowego odpowiadającą 1.

fazie drugiego cyklu lub średnią wartość z 1. cyklu,

- dla komponenty S przyjąć różnicę średnich wartości z 2. i 1. cyklu bądź przyjąć 0,

- dla komponenty C (w poszczególnych fazach 1. cyklu) przyjąć ilorazy wartości rzeczywistej

zmiennej z 1. cyklu w odniesieniu do średniej wartości w 1. cyklu bądź przyjąć 1.

W tabeli podano obliczenia prognoz na dla kolejnych kwartałów 2006 r. (t=17, 18, 19, 20) przyjmując
założenie, że wartości parametrów są równe: α = 0.5, β = 0.95, γ = 0.2 (obliczenie 1), α = 0.5, β = 0.95, γ
= 0.5 (obliczenie 2).

- 1/

33

-

Obliczenie 1.

t

y

t

F

t

S

t

C

t

y

t

*

(y

t

-yt

*

)

2

1

20

1,777778

2

10

0,888889

3

4

0,355556

4

11

0,977778

5

33

33

32 1,622222

6

17

42,0625 10,20938 0,791943

7

9 38,79219

-2,59633 0,330846

8

18 27,30248

-11,045 0,914078

9

45 21,99858

-5,59095 1,706895

10

23 22,72506 0,410606 0,835974

11

14 32,72574

9,52118 0,350236

12

11 27,14045

-4,82997 0,812323

13

25 18,47848

-8,47037 1,636101

14

60 40,89033 20,86773 0,962247

15

30

73,7073 32,21951 0,361592

16

13 60,96515

-10,4941 0,692505

17

82,5758

18

38,46779

19

10,6608

20

13,14991

α

0,5

β

0,95

γ

0,2

Obliczenie 2.

t

y

t

F

t

S

t

C

t

y

t

*

(y

t

-yt

*

)

2

1

20

1,777778

2

10

0,888889

3

4

0,355556

4

11

0,977778

5

33

33

32 1,388889

6

17

42,0625 10,20938 0,646525

7

9 38,79219

-2,59633 0,293781

8

18 27,30248

-11,045 0,818529

9

45 24,32872

-3,37732 1,619277

10

23 28,26311 3,568805 0,730153

11

14 39,74327 11,08459 0,323021

12

11

32,1333

-6,67524 0,580427

13

25 20,44852

-11,4343

1,42093

14

60 45,59438 23,31685 1,023052

15

30 80,89226 34,69883 0,346942

16

13 68,99421

-9,56821 0,384424

17

84,44017

18

51,00713

19

13,97815

20

11,81003

α

0,5

β

0,95

γ

0,5

Przykład 9

- 1/

34

-

Kwartalna wielkość sprzedaży skuterów wodnych w firmie „Jacek” (w sztukach) w latach
2002-2005 kształtowała się następująco:

20

30

39

60

40

51

62

81

50

64

74

95

55

68

77

96.

Wyznaczyć prognozę sprzedaży na 2006 r. korzystając z:

a)

metody wskaźników,

b)

metody harmonicznej.

Rozwiązanie:

0

50

100

Seria 1

a) Metoda wskaźników
Z metody wskaźników można korzystać przy prognozowaniu charakteryzującym się wahaniami
sezonowymi występującymi wraz z tendencją rozwojową lub wraz ze stałym (przeciętnym)
poziomem zmiennej. Prognozę wyznaczamy jako ekstrapolację dotychczasowej tendencji korygowanej
wskaźnikiem sezonowości. Postawa prognosty: pasywna. Zaobserwowano: składowa systematyczna
(rosnący trend liniowy) oraz wahania sezonowe (względnie stałe). Występuje też składnik losowy. Cykl
składa się z 3 faz: Faza 1: kwartał 1, 2 – rzeczywista wartość zmiennej znajduje się poniżej linii trendu.
Faza 2: kwartał 3 – rzeczywista wartość zmiennej znajduje się na linii trendu. Faza 3 – rzeczywista
wartość zmiennej znajduje się powyżej linii trendu. Zatem t=1,...,12 oraz i =1,..3. Przyjmujemy model
multiplikatywny:

y

ti

*

= y

t

*(w)

· c

i

gdzie y

ti

*

- prognoza na okres t w i-tej fazie cyklu, y

t

*(w)

– prognoza wstępna na okres t, c

i

- czysty

wskaźnik sezonowości w i-tej fazie cyklu.

y

t

t-tsr

(t-tsr)2

(t-tsr)y

zti

z1

z1

2 0

1

- 7 , 5

5 6 , 2 5

- 1 5 0

0 , 6 1 4 4 1 1 6

0 , 8 2 9 4 8 6 5

3 0

2

- 6 , 5

4 2 , 2 5

- 1 9 5

0 , 8 2 8 0 9 0 1

z2

z2

3 9

3

- 5 , 5

3 0 , 2 5

- 2 1 4 , 5

0 , 9 7 7 3 3 5 5

1 , 0 2 4 1 6 2 6

6 0

4

- 4 , 5

2 0 , 2 5

- 2 7 0

1 , 3 7 6 7 5 0 5

z3

z3

4 0

5

- 3 , 5

1 2 , 2 5

- 1 4 0

0 , 8 4 6 4 2 9 1

1 , 2 9 0 6 4 7 9

5 1

6

- 2 , 5

6 , 2 5

- 1 2 7 , 5

1 , 0 0 1 2 9 9 3

6 2

7

- 1 , 5

2 , 2 5

- 9 3

1 , 1 3 5 3 1 7 1

q

q

8 1

8

- 0 , 5

0 , 2 5

- 4 0 , 5

1 , 3 8 9 6 8 0 8

1 , 0 4 8 0 9 9

5 0

9

0 , 5

0 , 2 5

2 5

0 , 8 0 6 9 3 0 1

6 4

1 0

1 , 5

2 , 2 5

9 6

0 , 9 7 5 0 1 9 6

0,79142

7 4

1 1

2 , 5

6 , 2 5

1 8 5

1 , 0 6 7 5 7 1 9

0,9771621

9 5

1 2

3 , 5

1 2 , 2 5

3 3 2 , 5

1 , 3 0 1 5 0 1

1,2314179

5 5

1 3

4 , 5

2 0 , 2 5

2 4 7 , 5

0 , 7 1 7 3 6 8 4

6 8

1 4

5 , 5

3 0 , 2 5

3 7 4

0 , 8 4 6 3 4 3 9

7 7

1 5

6 , 5

4 2 , 2 5

5 0 0 , 5

0 , 9 1 6 4 2 6

9 6

1 6

7 , 5

5 6 , 2 5

7 2 0

1 , 0 9 4 6 5 9 2

60,125

340

1250

b=

3,6764706

a=

28,875

Prognoza wstępna: ekstrapolacja zaobserwowanej tendencji rozwojowej. Parametry linii trendu
oszacowujemy KMNK.

t

,

,

y

t

⋅

+

=

68

3

88

28



t=1,...12. Wyznaczona postać funkcji trendu posłuży do konstrukcji prognozy wstępnej. By wyznaczyć
wartości czystych wskaźników sezonowości c

i

należy:

1)

obliczyć wartości z

ti

jako ilorazy wartości rzeczywistych i wartości teoretycznych

- 1/

35

-

t

ti

ti

y

y

z



=

i tak:dla t=1, i=1

z

1,1

= 20 / (28,68 + 3,68 · t) = 0,6144,

itd. (zob. tabela)

2)

Wartości z

ti

zawierają efekt oddziaływania wahań sezonowych oraz przypadkowych. W celu

wyeliminowania wahań przypadkowych obliczamy surowe wskaźniki sezonowości z

i

(i=1,...,3)

przez wyznaczenie średniej arytmetycznej tych wartości z

ti

, które odpowiadają jednoimiennym

okresom, zatem:
Dla 1 i 2 kwartału: z

1

= 0,8295

Dla 3 kwartału: z

2

= 1,0242

Dla 4 kwartału: z

3

= 1,2906

3)

Obliczyć średnią arytmetyczną surowych wskaźników sezonowości q:

q = 1,0481

4)

Czyste wskaźniki sezonowości wyznaczamy jako ilorazy surowych wskaźników sezonowosci z

i

i

wielkości q.

q

z

c

i

i

=

Dla 1 i 2 kwartału: c

1

= 79,1%

Dla 3 kwartału: c

2

= 97,7%

Dla 4 kwartału: c

3

= 123,1%.

Suma czystych wskaźników sezonowości w modelu multiplikatywnym powinna być równa liczbie
wyróżnionych faz. W przykładzie suma (0,791 + 0,977 + 1,231) = 2,999 ≈ 3.

5) Wyznaczenie prognozy:

y

17

* = (28,88 + 3,68 ·17) ·79,1% = 91,44 · 79,1% = 72,33 ≈ 72 szt.

y

18

* = (28,88 + 3,68 ·18) ·79,1% = 95,12 · 79,1% = 75,24 ≈ 75 szt.

y

19

* = (28,88 + 3,68 ·19) ·97,71% = 98,80 · 97,7% = 96,53 ≈ 97 szt.

y

20

* = (28,88 + 3,68 ·20) ·123,1% = 102,48 · 123,1% = 126,15 ≈ 126 szt.

b) Metoda analizy harmonicznej

Analiza harmoniczna polega na budowie modelu w postaci sumy harmonik, czyli funkcji
sinusoidalnych lub cosinusoidalnych o danych okresach. Pierwsza harmonika ma okres równy długości
okresu badanego, druga – połowie tego okresu, trzecia – jednej trzeciej, itd. W przypadku n obserwacji
liczba wszystkich możliwych harmonik jest równa n/2.

Przypadek 1

W przypadku, gdy w szeregu czasowym występuje pewien stały poziom (

w tym przykładzie raczej

obserwujemy tendencję rozwojową

) i wahania sezonowe, szereg czasowy można przedstawić jako sumę

harmonik:

∑

=













−

⋅

+

=

2

1

0

2

/

n

i

i

i

t

it

n

cos

A

y

ε

π

α

lub korzystając z własności funkcji cosinus:

∑

=

























⋅

+













⋅

+

=

2

1

0

2

2

/

n

i

i

i

t

it

n

cos

it

n

sin

y

π

β

π

α

α

W podanym przykładzie liczba harmonik jest równa n/2 = 16/2 = 8
Pierwsza harmonika ma okres 16 kwartałów (4 lata)
Druga harmonika ma okres 16/2 = 8 kwartałów (2 lata)
Trzecia harmonika ma okres 16/3 = 5,33 kwartałów (ponad rok)
Czwarta harmonika ma okres 16/4 = 4 kwartałów (1 rok)
Piąta harmonika ma okres 16/5 = 3,2 kwartałów (trzy czwarte roku)
Szósta harmonika ma okres 16/6 = 2,5 kwartałów (trochę ponad pół roku)
Siódma harmonika ma okres 16/7 = 2,28 kwartałów (trochę ponad pół roku)
Ósma harmonika ma okres 16/8 = 2 kwartały (pół roku)

Wartości parametrów

α

0

,

α

i

,

β

i

, szacuje się za pomocą KMNK. Stosuje się wzory:

∑

=

⋅

=

n

t

t

y

n

a

1

0

1

∑

=

−

=













⋅

⋅

=

n

t

t

i

n

,...,

i,

it

n

sin

y

n

a

1

1

2

1

2

2

π

- 1/

36

-

∑

=

−

=













⋅

⋅

=

n

t

t

i

n

,...,

i,

it

n

cos

y

n

b

1

1

2

1

2

2

π

Dla ostatniej harmoniki o numerze n/2:

0

2

=

/

n

a

( )

∑

=

⋅

⋅

=

n

t

t

/

n

t

cos

y

n

b

1

2

1

π

Amplituda A

i

jest to największa (co do wartości bezwzględnej) różnica pomiędzy wartością harmoniki a

poziomem przeciętnym. Wartości amplitud dla poszczególnych harmonik oblicza się wg wzoru:

i

i

i

c

b

a

A

i

=

+

=

2

2

Wartości przesunięcia fazowego oblicza się jako:

i

i

i

t

θ

ε

=

gdzie:









=

i

i

i

b

a

arctg

ε

oraz

i

n

i

⋅

= π

θ

2

Udział części wariancji zmiennej Y w poszczególnych harmonikach przedstawić można jako:

2

2

2 s

c

i

i

⋅

=

ϖ

, dla i=1,...,(n/2)-1

2

2

s

c

i

i

=

ϖ

, dla i=n/2

gdzie: s

2

– ocena wariancji zmiennej Y

Jeżeli przyjmiemy założenie o istnieniu w szeregu czasowym stałego poziomu zjawiska i wahań
sezonowych, to dalsze obliczenia przebiegają następująco. Wartości parametrów α

0

, α

i

, β

i

szacuje się za

pomocą KMNK. Dla przykładu, obliczenia dla pierwszej harmoniki byłyby wtedy następujące:

a

0

= 962/16 = 60,125

a

1

= (2/16) · (-134,4772) = -16,8097

b

1

= (2/16) · (-18,5327) = -2,3166

t

y

t

x=(2π/16)·t

sin x

cos x

y

t

·sin x

y

t

·cos x

1

20

0,3927

0,3827

0,9239

7,6537

18,4776

2

30

0,7854

0,7071

0,7071

21,2132

21,2132

3

39

1,1781

0,9239

0,3827

36,0313

14,9247

4

60

1,5708

1,0000

0,0000

60,0000

0,0000

5

40

1,9635

0,9239

-0,3827

36,9552

-15,3073

6

51

2,3562

0,7071

-0,7071

36,0624

-36,0624

7

62

2,7489

0,3827

-0,9239

23,7264

-57,2805

8

81

3,1416

0,0000

-1,0000

0,0000

-81,0000

9

50

3,5343

-0,3827

-0,9239

-19,1342

-46,1940

10

64

3,9270

-0,7071

-0,7071

-45,2548

-45,2548

11

74

4,3197

-0,9239

-0,3827

-68,3671

-28,3186

12

95

4,7124

-1,0000

0,0000

-95,0000

0,0000

13

55

5,1051

-0,9239

0,3827

-50,8134

21,0476

14

68

5,4978

-0,7071

0,7071

-48,0833

48,0833

15

77

5,8905

-0,3827

0,9239

-29,4666

71,1387

16

96

6,2832

0,0000

1,0000

0,0000

96,0000

Suma

962

-134,4772

-18,5327

W podobny sposób należy przeprowadzić obliczenia dla następnych harmonik z obliczeniami dla 2x,
3x,..., 8x. Łącznie otrzymamy 8 tabel. Następnie oszacowywane są parametry modelu zgodnie z
podanymi wyżej wzorami. Podstawiając następnie numer prognozowanego kwartału do opracowanego
modelu z 8 harmonikami otrzymamy prognozy. Jest to zatem prognozowanie przez ekstrapolację
otrzymanego modelu z zastosowaniem reguły podstawowej i przyjęciem postawy pasywnej w
prognozowaniu.

W naszym przykładzie występuje jednak przypadek 2

– obserwowana jest tendencja

rozwojowa, zatem do rozwiązania użyjemy modelu z funkcją trendu liniowego.

Przypadek 2

W przypadku, gdy w szeregu czasowym występuje pewna tendencja rozwojowa (

tak jak w tym

przykładzie

) i wahania sezonowe, szereg czasowy można przedstawić jako sumę harmonik:

( )

∑

=

























⋅

+













⋅

+

=

2

1

2

2

/

n

i

i

i

t

it

n

cos

it

n

sin

t

f

y

π

β

π

α

gdzie f(t) – funkcja trendu. Postępowanie obliczeniowe jest następujące:

1. Oszacowujemy parametry funkcji f(t) za pomocą KMNK

- 1/

37

-

2.

Oszacowujemy parametry harmonik (8 harmonik), wartości amplitud, procent wyjaśnianej
zmienności, wielkości faz oraz przesunięcia fazowego.

t

t-t

śr

(t-t

śr

)

2

y

y(t-t

sr

)

y*

1

-7,5

56,25

20

-150

2

-6,5

42,25

30

-195

3

-5,5

30,25

39

-214,5

4

-4,5

20,25

60

-270

5

-3,5

12,25

40

-140

6

-2,5

6,25

51

-127,5

7

-1,5

2,25

62

-93

8

-0,5

0,25

81

-40,5

9

0,5

0,25

50

25

10

1,5

2,25

64

96

11

2,5

6,25

74

185

12

3,5

12,25

95

332,5

13

4,5

20,25

55

247,5

14

5,5

30,25

68

374

15

6,5

42,25

77

500,5

16

7,5

56,25

96

720

Suma

0

340

60,125

1250

17

91,375

18

95,05147

b

3,676471

a

28,875

Oszacowana funkcja trendu ma postać:

t

,

,

t

b

a

y

t

⋅

+

=

⋅

+

=

6765

3

875

28



Szereg zawiera 16 obserwacji, zatem należy oszacować parametry 8 harmonik stosując wzory jak
powyżej w przypadku 1 (założenie o braku tendencji rozwojowej) ale z wykorzystaniem wartości zmiennej

t

t

t

y

y

y



−

=

′

zamiast zmiennej y

t

. Postępowanie to jest uzasadnione istnieniem w szeregu czasowym

tendencji rozwojowej. Dalsze obliczenia przedstawiono w tabelach.

t

y

t

y

t

'=y

t

-ŷ

t

x=(2π/16)·t

sin x

cos x

y

t

'·sin x

y

t

'·cos x

1

20 -12,5515

0,3927

0,3827

0,9239

-4,8032

-11,5960

2

30

-6,2279

0,7854

0,7071

0,7071

-4,4038

-4,4038

3

39

-0,9044

1,1781

0,9239

0,3827

-0,8356

-0,3461

4

60

16,4191

1,5708

1,0000

0,0000

16,4191

0,0000

5

40

-7,2574

1,9635

0,9239

-0,3827

-6,7049

2,7773

6

51

0,0662

2,3562

0,7071

-0,7071

0,0468

-0,0468

7

62

7,3897

2,7489

0,3827

-0,9239

2,8279

-6,8272

8

81

22,7132

3,1416

0,0000

-1,0000

0,0000

-22,7132

9

50 -11,9632

3,5343

-0,3827

-0,9239

4,5781

11,0526

10

64

-1,6397

3,9270

-0,7071

-0,7071

1,1595

1,1595

11

74

4,6838

4,3197

-0,9239

-0,3827

-4,3273

-1,7924

12

95

22,0073

4,7124

-1,0000

0,0000

-22,0073

0,0000

13

55 -21,6691

5,1051

-0,9239

0,3827

20,0197

-8,2924

14

68 -12,3456

5,4978

-0,7071

0,7071

8,7297

-8,7297

15

77

-7,0221

5,8905

-0,3827

0,9239

2,6872

-6,4875

16

96

8,3015

6,2832

0,0000

1,0000

0,0000

8,3015

Suma

962

-0,0001

13,3858

-47,9444

- 1/

38

-

t

y

t

y

t

'=y

t

-ŷ

t

2x=2·(2π/16)·t

sin 2x

cos 2x

y

t

'·sin 2x

y

t

'·cos 2x

1

20 -12,5515

0,7854

0,7071

0,7071

-8,8752

-8,8752

2

30

-6,2279

1,5708

1,0000

0,0000

-6,2279

0,0000

3

39

-0,9044

2,3562

0,7071

-0,7071

-0,6395

0,6395

4

60

16,4191

3,1416

0,0000

-1,0000

0,0000

-16,4191

5

40

-7,2574

3,9270

-0,7071

-0,7071

5,1317

5,1317

6

51

0,0662

4,7124

-1,0000

0,0000

-0,0662

0,0000

7

62

7,3897

5,4978

-0,7071

0,7071

-5,2253

5,2253

8

81

22,7132

6,2832

0,0000

1,0000

0,0000

22,7132

9

50 -11,9632

7,0686

0,7071

0,7071

-8,4593

-8,4593

10

64

-1,6397

7,8540

1,0000

0,0000

-1,6397

0,0000

11

74

4,6838

8,6394

0,7071

-0,7071

3,3120

-3,3120

12

95

22,0073

9,4248

0,0000

-1,0000

0,0000

-22,0073

13

55 -21,6691

10,2102

-0,7071

-0,7071

15,3224

15,3224

14

68 -12,3456

10,9956

-1,0000

0,0000

12,3456

0,0000

15

77

-7,0221

11,7810

-0,7071

0,7071

4,9653

-4,9653

16

96

8,3015

12,5664

0,0000

1,0000

0,0000

8,3015

Suma

962

-0,0001

9,9438

-6,7047

t

y

t

y

t

'=y

t

-ŷ

t

3x=3·(2π/16)·t

sin 3x

cos 3x

y

t

'·sin 3x

y

t

'·cos 3x

1

20 -12,5515

1,1781

0,9239

0,3827

-11,5960

-4,8032

2

30

-6,2279

2,3562

0,7071

-0,7071

-4,4038

4,4038

3

39

-0,9044

3,5343

-0,3827

-0,9239

0,3461

0,8356

4

60

16,4191

4,7124

-1,0000

0,0000

-16,4191

0,0000

5

40

-7,2574

5,8905

-0,3827

0,9239

2,7773

-6,7049

6

51

0,0662

7,0686

0,7071

0,7071

0,0468

0,0468

7

62

7,3897

8,2467

0,9239

-0,3827

6,8272

-2,8279

8

81

22,7132

9,4248

0,0000

-1,0000

0,0000

-22,7132

9

50 -11,9632

10,6029

-0,9239

-0,3827

11,0526

4,5781

10

64

-1,6397

11,7810

-0,7071

0,7071

1,1595

-1,1595

11

74

4,6838

12,9591

0,3827

0,9239

1,7924

4,3273

12

95

22,0073

14,1372

1,0000

0,0000

22,0073

0,0000

13

55 -21,6691

15,3153

0,3827

-0,9239

-8,2924

20,0197

14

68 -12,3456

16,4934

-0,7071

-0,7071

8,7297

8,7297

15

77

-7,0221

17,6715

-0,9239

0,3827

6,4875

-2,6872

16

96

8,3015

18,8496

0,0000

1,0000

0,0000

8,3015

Suma

962

-0,0001

20,5150

10,3464

t

y

t

y

t

'=y

t

-ŷ

t

4x=4·(2π/16)·t

sin 4x

cos 4x

y

t

'·sin 4x

y

t

'·cos 4x

1

20 -12,5515

1,5708

1,0000

0,0000

-12,5515

0,0000

2

30

-6,2279

3,1416

0,0000

-1,0000

0,0000

6,2279

3

39

-0,9044

4,7124

-1,0000

0,0000

0,9044

0,0000

4

60

16,4191

6,2832

0,0000

1,0000

0,0000

16,4191

5

40

-7,2574

7,8540

1,0000

0,0000

-7,2574

0,0000

6

51

0,0662

9,4248

0,0000

-1,0000

0,0000

-0,0662

7

62

7,3897

10,9956

-1,0000

0,0000

-7,3897

0,0000

8

81

22,7132

12,5664

0,0000

1,0000

0,0000

22,7132

9

50 -11,9632

14,1372

1,0000

0,0000

-11,9632

0,0000

10

64

-1,6397

15,7080

0,0000

-1,0000

0,0000

1,6397

11

74

4,6838

17,2788

-1,0000

0,0000

-4,6838

0,0000

12

95

22,0073

18,8496

0,0000

1,0000

0,0000

22,0073

13

55 -21,6691

20,4204

1,0000

0,0000

-21,6691

0,0000

14

68 -12,3456

21,9911

0,0000

-1,0000

0,0000

12,3456

15

77

-7,0221

23,5619

-1,0000

0,0000

7,0221

0,0000

16

96

8,3015

25,1327

0,0000

1,0000

0,0000

8,3015

Suma

962

-0,0001

-57,5882

89,5882

- 1/

39

-

t

y

t

y

t

'=y

t

-ŷ

t

5x=5·(2π/16)·t

sin 5x

cos 5x

y

t

'·sin 5x

y

t

'·cos 5x

1

20 -12,5515

1,9635

0,9239

-0,3827

-11,5960

4,8032

2

30

-6,2279

3,9270

-0,7071

-0,7071

4,4038

4,4038

3

39

-0,9044

5,8905

-0,3827

0,9239

0,3461

-0,8356

4

60

16,4191

7,8540

1,0000

0,0000

16,4191

0,0000

5

40

-7,2574

9,8175

-0,3827

-0,9239

2,7773

6,7049

6

51

0,0662

11,7810

-0,7071

0,7071

-0,0468

0,0468

7

62

7,3897

13,7445

0,9239

0,3827

6,8272

2,8279

8

81

22,7132

15,7080

0,0000

-1,0000

0,0000

-22,7132

9

50 -11,9632

17,6715

-0,9239

0,3827

11,0526

-4,5781

10

64

-1,6397

19,6350

0,7071

0,7071

-1,1595

-1,1595

11

74

4,6838

21,5984

0,3827

-0,9239

1,7924

-4,3273

12

95

22,0073

23,5619

-1,0000

0,0000

-22,0073

0,0000

13

55 -21,6691

25,5254

0,3827

0,9239

-8,2924

-20,0197

14

68 -12,3456

27,4889

0,7071

-0,7071

-8,7297

8,7297

15

77

-7,0221

29,4524

-0,9239

-0,3827

6,4875

2,6872

16

96

8,3015

31,4159

0,0000

1,0000

0,0000

8,3015

Suma

962

-0,0001

-1,7256

-15,1283

t

y

t

y

t

'=y

t

-ŷ

t

6x=6·(2π/16)·t

sin 6x

cos 6x

y

t

'·sin 6x

y

t

'·cos 6x

1

20 -12,5515

2,3562

0,7071

-0,7071

-8,8752

8,8752

2

30

-6,2279

4,7124

-1,0000

0,0000

6,2279

0,0000

3

39

-0,9044

7,0686

0,7071

0,7071

-0,6395

-0,6395

4

60

16,4191

9,4248

0,0000

-1,0000

0,0000

-16,4191

5

40

-7,2574

11,7810

-0,7071

0,7071

5,1317

-5,1317

6

51

0,0662

14,1372

1,0000

0,0000

0,0662

0,0000

7

62

7,3897

16,4934

-0,7071

-0,7071

-5,2253

-5,2253

8

81

22,7132

18,8496

0,0000

1,0000

0,0000

22,7132

9

50 -11,9632

21,2058

0,7071

-0,7071

-8,4593

8,4593

10

64

-1,6397

23,5619

-1,0000

0,0000

1,6397

0,0000

11

74

4,6838

25,9181

0,7071

0,7071

3,3120

3,3120

12

95

22,0073

28,2743

0,0000

-1,0000

0,0000

-22,0073

13

55 -21,6691

30,6305

-0,7071

0,7071

15,3224

-15,3224

14

68 -12,3456

32,9867

1,0000

0,0000

-12,3456

0,0000

15

77

-7,0221

35,3429

-0,7071

-0,7071

4,9653

4,9653

16

96

8,3015

37,6991

0,0000

1,0000

0,0000

8,3015

Suma

962

-0,0001

1,1203

-8,1189

t

y

t

y

t

'=y

t

-ŷ

t

7x=7·(2π/16)·t

sin 7x

cos 7x

y

t

'·sin 7x

y

t

'·cos 7x

1

20 -12,5515

2,7489

0,3827

-0,9239

-4,8032

11,5960

2

30

-6,2279

5,4978

-0,7071

0,7071

4,4038

-4,4038

3

39

-0,9044

8,2467

0,9239

-0,3827

-0,8356

0,3461

4

60

16,4191

10,9956

-1,0000

0,0000

-16,4191

0,0000

5

40

-7,2574

13,7445

0,9239

0,3827

-6,7049

-2,7773

6

51

0,0662

16,4934

-0,7071

-0,7071

-0,0468

-0,0468

7

62

7,3897

19,2423

0,3827

0,9239

2,8279

6,8272

8

81

22,7132

21,9911

0,0000

-1,0000

0,0000

-22,7132

9

50 -11,9632

24,7400

-0,3827

0,9239

4,5781

-11,0526

10

64

-1,6397

27,4889

0,7071

-0,7071

-1,1595

1,1595

11

74

4,6838

30,2378

-0,9239

0,3827

-4,3273

1,7924

12

95

22,0073

32,9867

1,0000

0,0000

22,0073

0,0000

13

55 -21,6691

35,7356

-0,9239

-0,3827

20,0197

8,2924

14

68 -12,3456

38,4845

0,7071

0,7071

-8,7297

-8,7297

15

77

-7,0221

41,2334

-0,3827

-0,9239

2,6872

6,4875

16

96

8,3015

43,9823

0,0000

1,0000

0,0000

8,3015

Suma

962

-0,0001

13,4981

-4,9207

- 1/

40

-

t

y

t

y

t

'=y

t

-ŷ

t

8x=8·(2π/16)·t

sin 8x

cos 8x

y

t

'·sin 8x

y

t

'·cos 8x

1

20 -12,5515

3,1416

0,0000

-1,0000

0,0000

12,5515

2

30

-6,2279

6,2832

0,0000

1,0000

0,0000

-6,2279

3

39

-0,9044

9,4248

0,0000

-1,0000

0,0000

0,9044

4

60

16,4191

12,5664

0,0000

1,0000

0,0000

16,4191

5

40

-7,2574

15,7080

0,0000

-1,0000

0,0000

7,2574

6

51

0,0662

18,8496

0,0000

1,0000

0,0000

0,0662

7

62

7,3897

21,9911

0,0000

-1,0000

0,0000

-7,3897

8

81

22,7132

25,1327

0,0000

1,0000

0,0000

22,7132

9

50 -11,9632

28,2743

0,0000

-1,0000

0,0000

11,9632

10

64

-1,6397

31,4159

0,0000

1,0000

0,0000

-1,6397

11

74

4,6838

34,5575

0,0000

-1,0000

0,0000

-4,6838

12

95

22,0073

37,6991

0,0000

1,0000

0,0000

22,0073

13

55 -21,6691

40,8407

0,0000

-1,0000

0,0000

21,6691

14

68 -12,3456

43,9823

0,0000

1,0000

0,0000

-12,3456

15

77

-7,0221

47,1239

0,0000

-1,0000

0,0000

7,0221

16

96

8,3015

50,2655

0,0000

1,0000

0,0000

8,3015

Suma

962

-0,0001

0,0000

98,5882

Ocena wariancji zmiennej Y niezbędna do określenia części wariancji uwzględnianej przez poszczególne
harmoniki est następująca:

t

y

t

y

t

'=y

t

-ŷ

t

(y

t

')

2

1

20 -12,5515

157,5394

2

30

-6,2279

38,7873

3

39

-0,9044

0,8180

4

60

16,4191

269,5874

5

40

-7,2574

52,6692

6

51

0,0662

0,0044

7

62

7,3897

54,6077

8

81

22,7132

515,8909

9

50 -11,9632

143,1191

10

64

-1,6397

2,6886

11

74

4,6838

21,9382

12

95

22,0073

484,3234

13

55 -21,6691

469,5509

14

68 -12,3456

152,4137

15

77

-7,0221

49,3094

16

96

8,3015

68,9143

Suma

-0,0001

2482,1618

s

2

= 165,4775

Nr harmoniki

a

i

b

i

a

i

2

b

i

2

c

i

2

=a

i

2

+b

i

2

A

i

=√(c

i

2

ω

i

[%]

1

1,6732

-5,9931

2,7997

35,9166

38,7163

6,2222

11,70

2

1,2430

-0,8381

1,5450

0,7024

2,2474

1,4991

0,68

3

2,5644

1,2933

6,5760

1,6726

8,2486

2,8720

2,49

4

-7,1985

11,1985

51,8188 125,4070

177,2257

13,3126

53,55

5

-0,2157

-1,8910

0,0465

3,5760

3,6225

1,9033

1,09

6

0,1400

-1,0149

0,0196

1,0299

1,0496

1,0245

0,32

7

1,6873

-0,6151

2,8469

0,3783

3,2252

1,7959

0,97

8

0,0000

6,1618

0,0000

37,9673

37,9673

6,1618

22,94

Oszacowane parametry modelu obliczane są następująco:
a

1

= (2/16) · (13,3858) = 1,6732

b

1

= (2/16) · (-47,9444) = -5,9931

a

2

= (2/16) · (9,9438) = 1,2430

b

2

= (2/16) · (-6,7047) = -0,8381

a

3

= (2/16) · (20,5150) = 2,5644

b

3

= (2/16) · (10,3464) = 1,2933

a

4

= (2/16) · (-57,5882) = -7,1985

b

4

= (2/16) · (89,5882) = 11,1985

a

5

= (2/16) · (-1,7256) = -0,2157

b

5

= (2/16) · (-15,1283) = -1,8910

a

6

= (2/16) · (1,1203) = 0,1400

b

6

= (2/16) · (-8,1189) = -1,0149

a

7

= (2/16) · (13,4981) = 1,6873

b

7

= (2/16) · (-4,9207) = -0,6151

- 1/

41

-

a

8

= (2/16) · (0) = 0,0000

b

8

= (1/16) · (98,5882) = 6,1618

Oszacowany model ma postać:













⋅

⋅

⋅

+













⋅

⋅

⋅

−













⋅

⋅

⋅

+













⋅

⋅

⋅

−













⋅

⋅

⋅

+













⋅

⋅

⋅

−













⋅

⋅

⋅

−













⋅

⋅

⋅

+













⋅

⋅

⋅

−













⋅

⋅

⋅

+













⋅

⋅

⋅

+













⋅

⋅

⋅

−













⋅

⋅

⋅

+













⋅

⋅

−













⋅

⋅

+

⋅

+

=

t

cos

,

t

cos

,

t

sin

,

t

cos

,

t

sin

,

t

cos

,

t

sin

,

t

cos

,

t

sin

,

t

cos

,

t

sin

,

t

cos

,

t

sin

,

t

cos

,

t

sin

,

t

,

,

y

t

8

16

2

1618

6

7

16

2

6151

0

7

16

2

6873

1

6

16

2

0149

1

6

16

2

14

0

5

16

2

8910

1

5

16

2

2157

0

4

16

2

1985

11

4

16

2

1985

7

3

16

2

2933

1

3

16

2

5644

2

2

16

2

8381

0

2

16

2

2430

1

16

2

9931

5

16

2

6732

1

6765

3

875

28

π

π

π

π

π

π

π

π

π

π

π

π

π

π

π



Prognozy na kolejne kwartały 2006 r. otrzymujemy podstawiając do oszacowanego modelu kolejne
wartości zmiennej czasowej. Jest to zatem prognozowanie przez ekstrapolację otrzymanego modelu z
zastosowaniem reguły podstawowej i przyjęciem postawy pasywnej w prognozowaniu.

t

y

t

*

17

78,8240

18

88,8241

19

97,8240

20

118,8241

y

17

* = 79 szt.

y

18

* = 89 szt.

y

19

* = 98 szt.

y

20

* = 119 szt.

Przykład 10

Liczbę komputerów sprzedanych przez pewną firmę w poszczególnych kwartałach lat
2003-2005 przedsiębiorstwom przemysłowym opisano za pomocą modelu:

t

t

t

x

x

y

2

1

11

12

50

⋅

+

⋅

+

=



90

0

2

,

R

=

,

gdzie:

y

t

– liczba sprzedanych komputerów w kwartale t, x

1t

– procentowy udział wydatków na

reklamę w kosztach sprzedaży w kwartale t, x

2t

– wartość zmiennej syntetycznej

charakteryzującej koniunkturę w przemyśle w kwartale t. Do konstrukcji zmiennej syntetycznej
wykorzystano następujące zmienne: liczba zawartych w danym kwartale kontraktów w
przemyśle (w tysiącach), średnie oprocentowanie kredytów w poszczególnych kwartałach,
stopa inflacji w kolejnych kwartałach. Zaobserwowane w badanym okresie minimalne i
maksymalne wartości tych zmiennych były następujące: dla liczby zawartych w danym
kwartale kontraktów w przemyśle – 150 i 300 tysięcy, dla oprocentowania kredytów – 22 i 37%,
dla stopy inflacji -2 i 6%.

a)

Sporządzić prognozę wielkości sprzedaży komputerów w I kwartale 2006 r., wiedząc, że:
firma planuje w I kwartale 2006 r. udział wydatków na reklamę w kosztach sprzedaży na
poziomie 3%, przewidywana liczba zawartych kontraktów w przemyśle w I kwartale 2006 r.
wynosi 200 tysięcy, średnie oprocentowanie kredytów w I kwartale 2006 r. wyniesie 24%,
przewidywana stopa inflacji w I kwartale 2006 r. wynosi 3%.

b)

Ocenić dopuszczalność wyznaczonej prognozy, wiedząc, że: bezwzględny błąd prognozy
ex ante dla I kwartału wynosi 5 sztuk, wartość krytyczną błędu ustalono na poziomie 5%.

Rozwiązanie:

Zastosowanie: model ze zmienną syntetyczną

a) Krok 1: normalizacja zmiennych cząstkowych (stymulant, nominant, destymulant)

Stymulanta jako zmienna, której wzrost wartości jest pożądany, jest określona na zbiorze R+.
Normalizacja tej zmiennej przebiega wg algorytmu: z

it

= (x

it

/ max x

it

). Stymulanta w zadaniu: liczba

zawartych kontraktów w przemyśle.

Nominanta jako zmienna, której wartości powinna należeć do zalecanego przedziału wartości [x

i,min

,

x

i,max

] (lub jest równa x

i,norm

=x

i,min

=x

i,max

) jest określona na zbiorze R+. Normalizacja tej zmiennej

przebiega wg algorytmu:

z

it

= (x

it

/ x

i,min

),

gdy x

it

≤ x

i,min

;

- 1/

42

-

z

it

= 1,

gdy x

i,min

≤ x

it

≤ x

i,max

;

z

it

= (x

i,max

/ x

it

),

gdy x

it

> x

i,max

;

Nominanta w zadaniu: brak.

Destymulanta jako zmienna, której spadek wartości jest pożądany, jest określona na zbiorze R+.
Normalizacja tej zmiennej przebiega wg algorytmu: z

it

= (min x

it

/ x

it

). Destymulanta w zadaniu: średnie

oprocentowanie kredytów, przewidywana stopa inflacji.

a) Krok 2: opierając się na znormalizowanych zmiennych cząstkowych konstruuje się zmienną

syntetyczną o charakterze stymulanty (suma zmiennych cząstkowych lub ich średnia arytmetyczna).

W przykładzie wybrano sumę. Dane: m = 12 (lata 2003-2005). Normalizacja i zmienne cząstkowe
x

2,1,t

, x

2,2,t

, x

2,3,t

obliczane są w sposób następujący:

Dla stymulanty:

max

,

t,

,

t,

,

x

x

x

1

2

1

2

1

2

=

Dla destymulant:

t,

,

min

,

t,

,

x

x

x

2

2

2

2

2

2

=

,

t,

,

min

,

t,

,

x

x

x

3

2

3

2

3

2

=

x

2,1,t

= 200/300 (stymulanta)

x

2,2,t

= 22/24 (destymulanta)

x

2,3,t

= 2/3 (destymulanta)

Zmienna syntetyczna może być obliczona jako suma lub jako średnia arytmetyczna.

∑

=

⋅

=

m

i

t,

i,

x

m

x

1

2

2

1

= (1/3) * [(200/300) + (22/24) + (2/3)]

Wybieramy sumę:

∑

=

=

m

i

t,

i,

x

x

1

2

2

= (200/300) + (22/24) + (2/3) = 2,249999 ≈ 2,25

Wyznaczenie prognozy:
y

13

*

= 50 + 12·3 + 11·2,25 = 110,75 sztuk ≈ 111 sztuk.

Dopuszczalność prognozy:
η*

13

= 5%

v

13

= 5 sztuk

η

13

= (5/111) · 100% = 4,505% < η*

13

= 5%

Prognoza jest dopuszczalna.

Przykład 11

Spożycie owoców w kg na mieszkańca w trzech krajach przedstawia tabela:

Kraj

1984

1985

1986

1987

1988

1989

1990

Francja

49

51

51

54

57

58

59

Włochy

73

72

72

74

73

75

75

Austria

52

54

59

60

67

69

72

W Polsce w 2005 r. spożycie owoców wynosiło 54 kg na mieszkańca. Miara podobieństwa
szeregu spożycia owoców w Polsce w latach 1995-2005 do szeregów: Francji w latach
1977-1987 wynosiła 0,85, Włoch w latach 1976-1986 wynosiła 0,35 i Austrii w latach
1976-1986 wynosiła 0,95. Wyznaczyć prognozę spożycia owoców w Polsce na lata 2007-2008.

Rozwiązanie:

Zastosowanie: model z analogiami przestrzenno-czasowymi (obiekty podobne: Francja, Włochy,
Austria)
Krok 1: ustalenie stałej przesunięcia
Krok 2: wyznaczenie prognozy cząstkowej
Krok 3: wyznaczenie prognozy globalnej

Dane:

Przyjmujemy graniczną wartość miary podobieństwa m

*

= 0,8

Polska w 2005 r.: 54 kg/mieszkańca
Francja w latach 1977-1987 (podobieństwo: 0,85)

- 1/

43

-

Włochy w latach 1976-1986 (podobieństwo: 0,35)
Austria w latach 1976-1986 (podobieństwo: 0,95)

Francja

Włochy

Austria

1984

49

73

52

1985

51

72

54

1986

51

72

59

1987

54

74

60

1988

57

73

67

1989

58

75

69

1990

59

75

72

Spożycie owoców w

kg/mieszkańca

0

100

200

300

1

2

3

4

5

6

7

Lata 1980-1989

Serie3

Serie2

Serie1

Obiektem prognozowanym jest Polska. Obiekty podobne to: Francja, Austria (odrzucamy Włochy ze
względu na niskie podobieństwo). Jako przedział podobieństwa dla obiektu prognozowanego (dla Polski)
wybieramy jeden rok (2005).

Na całej długości szeregów czasowych charakteryzujących obiekty podobne szukamy przedziałów
podobieństwa o tej samej długości, których miara podobieństwa m

(o,k)

przekroczy krytyczną miarę

podobieństwa m

*

i wybieramy spośród nich takie pary, których miara podobieństwa osiąga wartość

maksymalną. Wartość krytyczna przekroczona jest dla Francji i Austrii. Przed wyznaczeniem prognozy
cząstkowej należy ustalić stałą przesunięcia:

∆

(o,k)

= y

0

(o)

– y

0

(k)

gdzie y

0

(o)

– wartość zmiennej przypadająca na koniec przedziału podobieństwa obiektu

prognozowanego, y

0

(k)

– wartość zmiennej przypadająca na koniec przedziału podobieństwa obiektu

podobnego k.

Polska

Francja

Włochy

Austria

54

54

72

59

57

74

60

58

73

67

59

75

69

75

72

Wartości w szeregach czasowych odpowiadające numerom okresów od t=1 dla obiektów podobnych
zostaną wykorzystane do wyznaczenia prognozy cząstkowej:

y

t

*

(o,k)

= y

t

(k)

+ ∆

(o,k)

,

t=1, ..., n

(k)

gdzie y

t

*

(o,k)

– prognoza cząstkowa zmiennej Y dla obiektu (o) w chwili t według obiektu (k), y

t

(k)

- wartość

zmiennej Y w k-tym obiekcie w chwili t, ∆

(o,k)

- stała przesunięcia, n

(k)

– długość przedziału podobieństwa.

Wyznaczamy prognozy cząstkowe spożycia owoców dla Polski w 2006 r., tj. dla t=1.

Według Francji:

∆

(Polska,Francja)

= 54 – 54 = 0

y

*(Polska,Francja)

2006

= 57 + (0) = 57

Według Austrii:

∆

(Polska,Austria)

= 54 – 59 = -5

y

*(Polska,Austria)

2006

= 60 + (-5) = 55

Wyznaczamy prognozy cząstkowe spożycia owoców dla Polski w 2007 r., tj. dla t=2.

Według Francji:

y

*(Polska,Francja)

2007

= 58 + (0) = 58

Według Austrii:

y

*(Polska,Austria)

2007

= 67 + (-5) = 62

Wyznaczamy prognozy cząstkowe spożycia owoców dla Polski w 2008 r., tj. dla t=3.

Według Francji:

y

*(Polska,Francja)

2008

= 59 + (0) = 59

Według Austrii:

y

*(Polska,Austria)

2008

= 69 + (-5) = 64

Prognoza globalna dla Polski na lata 2007-2008 na podstawie podobieństwa kształtowania się zmiennej
w dwóch krajach zostanie wyznaczona w następujący sposób:

∑

=

⋅

=

q

k

)

k

,

o

(

)

k

,

o

(

*

t

*

t

w

y

y

1

∑

=

=

q

k

)

k

,

o

(

)

k

,

o

(

)

k

,

o

(

m

m

w

1

Prognoza globalna dla Polski w 2007 r. jest następująca:

- 1/

44

-

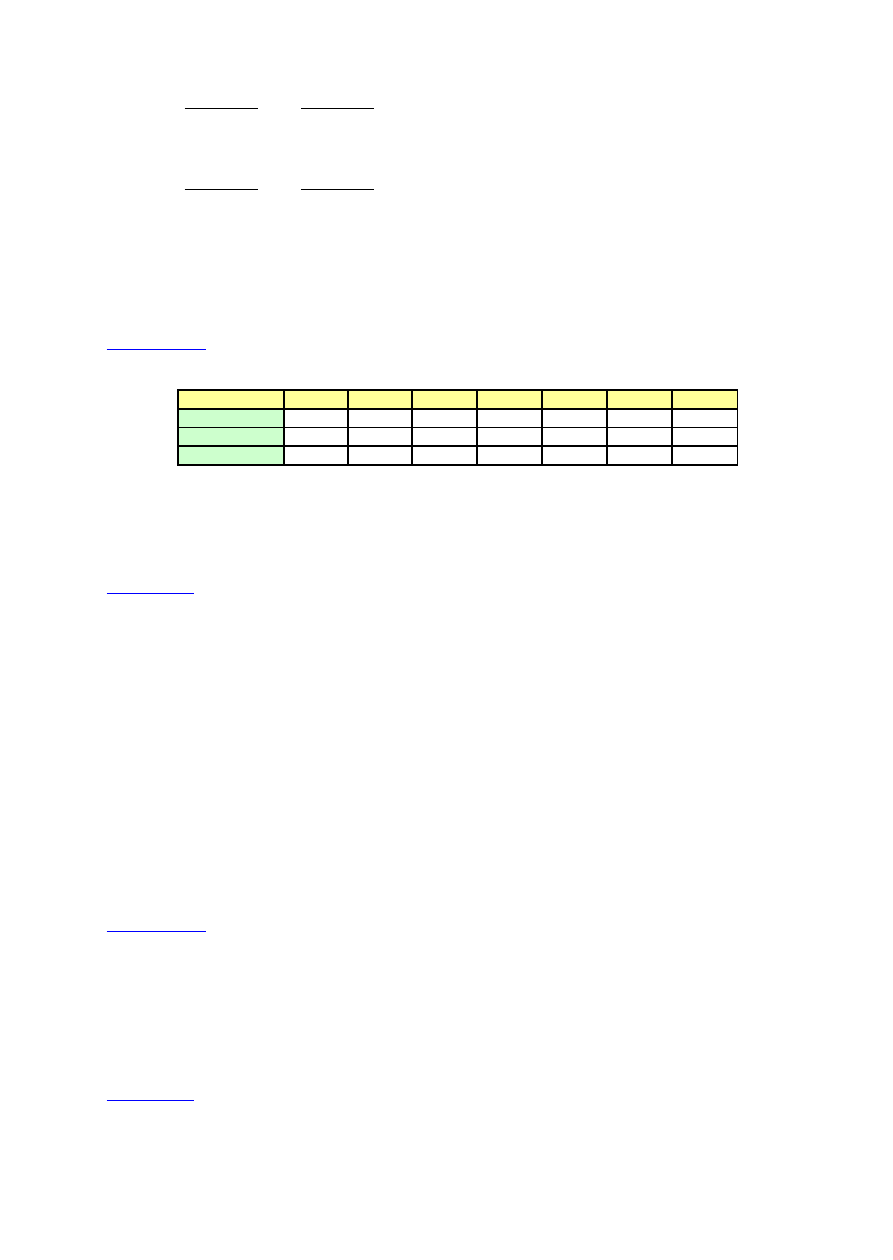
60

111

60

722

32

389

27

95

0

85

0

95

0

62

95

0

85

0

85

0

58

2007

≈

=

+

=

+

⋅

+

+

⋅

=

,

,

,

,

,

,

,

,

,

y

*

Prognoza globalna dla Polski w 2008 r. jest następująca:

62

639

61

778

37

861

27

95

0

85

0

95

0

64

95

0

85

0

85

0

59

2008

≈

=

+

=

+

⋅

+

+

⋅

=

,

,

,

,

,

,

,

,

,

y

*

Dopuszczalność prognoz:
Maksymalnie można wyznaczać prognozy do 2008 r. (t=3), ponieważ tylko do tego roku posiadamy
wartości z szeregów czasowych każdego kraju. Długie przedziały podobieństwa (11 obserwacji) oraz
stosunkowo wysokie wartości miary podobieństwa pomiędzy Polską a rozważanymi krajami pozwalają
uznać wyznaczone prognozy za dopuszczalne.

Przykład 12

Spożycie cukru w kg na mieszkańca w trzech krajach europejskich przedstawia tabela.

K ra j

1979

1980

1981

1982

1983

1984

1985

Belgia

36

37

37

37

38

38

39

Dania

35

35

36

36

37

39

38

Węgry

36

35

34

35

34

35

35

W Polsce w 2005 r. spożycie cukru wynosiło 42 kg na mieszkańca. Miara podobieństwa
szeregu spożycia cukru w Polsce w latach 1995-2005 do szeregów: Belgii w latach 1971-1981
wynosiła 0,8, Danii w latach 1972-1982 wynosiła 0,9 i Węgier w latach 1971-1981 wynosiła
0,3. Sporządzić prognozy spożycia cukru w Polsce na następne 3 lata. Ocenić dopuszczalność
wyznaczonych prognoz.

Rozwiązanie:

Zastosowanie: model z analogiami przestrzenno-czasowymi
Obiekty podobne: Belgia, Dania (odrzucamy Węgry ze względu na niską wartość miary podobieństwa).
Krok 1: ustalenie stałej przesunięcia
Krok 2: wyznaczenie prognozy cząstkowej
Krok 3: wyznaczenie prognozy globalnej

y

*(P,B)

2006

= 37 + (42 - 37) = 42

y

*(P,D)

2006

= 37 + (42 - 36) = 43

y

*

2006

= 42 x ((0,8/(0,8+0,9)) + 43 x ((0,9/(0,8+0,9)) = 42,5 = 43 kg/mieszkańca

y

*(P,B)

2007

= 38 + (42 – 37) = 43

y

*(P,D)

2007

= 39 + (42 – 36) = 45

y

*

2007

= 44 kg/mieszkańca

y

*(P,B)

2008

= 43

y

*(P,D)

2008

= 44

y

*

2008

= 43,5 = 44 kg/mieszkańca

Dopuszczalność prognoz: długie przedziały podobieństwa (11 obserwacji) oraz stosunkowo wysokie
wartości miary podobieństwa pomiędzy Polską a wybranymi krajami (0,9; 0,8). Wniosek: wyznaczone
prognozy są dopuszczalne.

Przykład 13

W latach 2004-2005 miesięczna wielkość sprzedaży płynu do płukania (w litrach) kształtowała
się następująco: 80, 70, 60, 101, 130, 168, 210, 255, 220, 209, 260, 348, 330, 380, 430, 542,
524, 411, 375, 332, 295, 270, 240, 216, natomiast wielkość sprzedaży proszku do prania tej
samej marki (w kg) kształtowała się następująco: 132, 168, 215, 256, 221, 211, 264, 341, 335,
375, 438, 560, 525, 380, 376, 330, 296, 271, 237, 217, 190, 175, 166, 140. Zaproponować
metodę prognozowania i wyznaczyć przewidywaną wielkość sprzedaży płynu do płukania na
styczeń i kwiecień 2006 r.

Rozwiązanie:

Dane: Szeregi czasowe: X – miesięczna sprzedaż proszku do prania (w kg) w latach 2004-2005, Y –

miesięczna sprzedaż płynu do płukania (w litrach) w latach 2004-2005. Wyznaczyć: y

*

I 2006

, y

*

IV 2006

- 1/

45

-

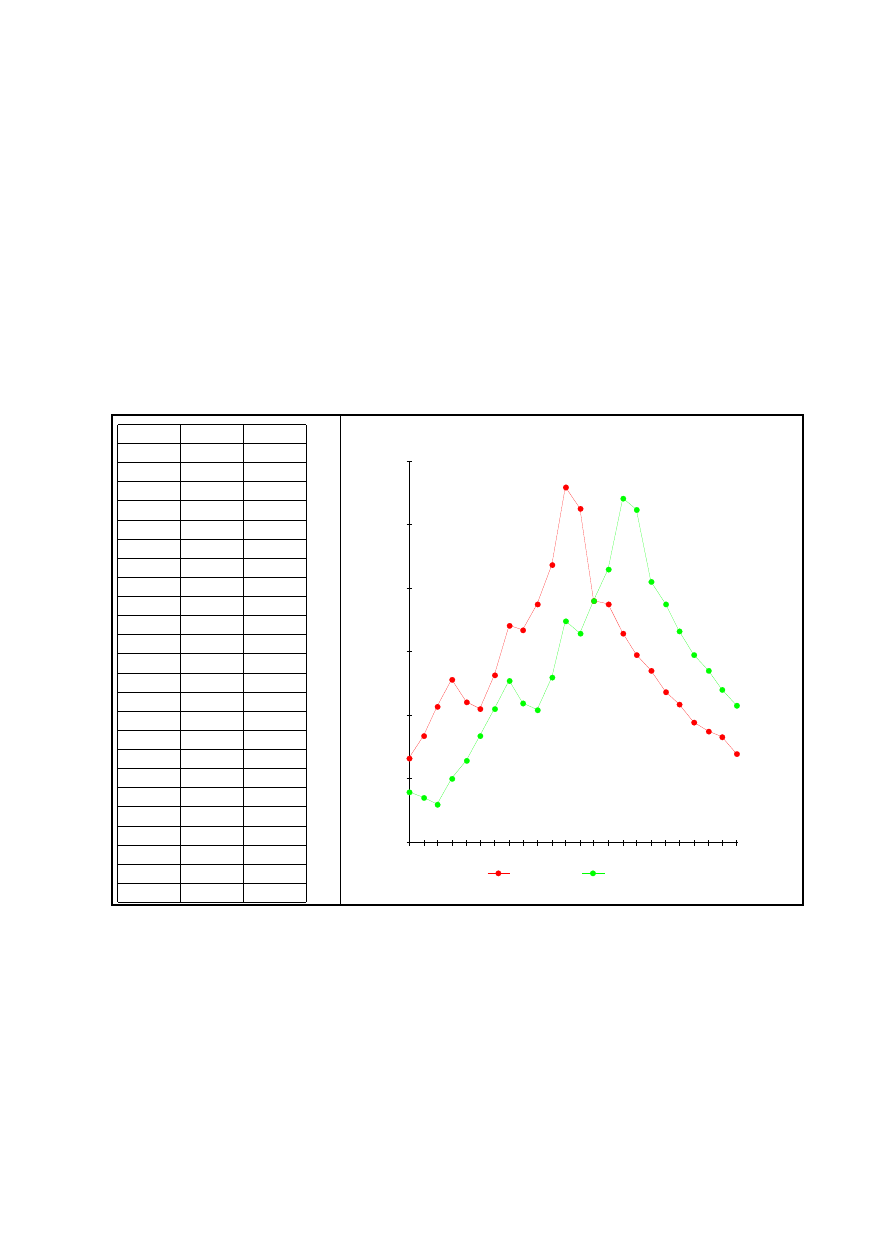
Zastosowanie: model z analogiami historycznymi polegający na przeniesieniu prawidłowości zmian w
czasie jednych zmiennych na inne zmienne występujące w tym samym obiekcie.

Krok 1: podział zmiennych na dwie grupy: zmienne wiodące (wyprzedzające) i zmienne

opóźnione (naśladujące). Zmienne wyprzedzające służą wyznaczeniu prognozy, zmienne
naśladujące są zmiennymi prognozowanymi. Postawa prognosty: aktywna

Krok 2: oszacowanie parametrów modelu liniowego dla zmiennych (KMNK).
Krok 3: oszacowanie błędu ex ante.

Analiza wykresów wskazuje na duże podobieństwo w kształtowaniu się wielkości sprzedaży obu środków
chemii gospodarczej, zarówno w przebiegu zmian, jak i w wielkości sprzedaży. Do wyznaczenia prognozy
wielkości sprzedaży płynu skorzystamy z analogii historycznych. Największa sprzedaż proszku wystąpiła
w grudniu (t=12) 2004 r., natomiast największa sprzedaż płynu wystąpiła w kwietniu (t=16) 2005 r. Można
zatem uznać, że wielkość sprzedaży płynu będzie się kształtowała podobnie jak wielkość sprzedaży
proszku, z tym, że będzie opóźniona o 4 okresy (p=4). Zbudujemy model uwzględniający rząd opóźnienia
p=4. Postać oszacowanego modelu jest następująca:

4

−

⋅

+

=

t

t

x

b

a

y



=

2

R

?

gdzie: y

t

– sprzedaż płynu, x

t-4

– sprzedaż proszku. Parametry modelu oszacowujemy metodą KMNK.

M

i e s i ą c

P r o s z e k

P ł y n

1

1 3 2

8 0

2

1 6 8

7 0

3

2 1 5

6 0

4

2 5 6

1 0 1

5

2 2 1

1 3 0

6

2 1 1

1 6 8

7

2 6 4

2 1 0

8

3 4 1

2 5 5

9

3 3 5

2 2 0

1 0

3 7 5

2 0 9

1 1

4 3 8

2 6 0

1 2

5 6 0

3 4 8

1 3

5 2 5

3 3 0

1 4

3 8 0

3 8 0

1 5

3 7 6

4 3 0

1 6

3 3 0

5 4 2

1 7

2 9 6

5 2 4

1 8

2 7 1

4 1 1

1 9

2 3 7

3 7 5

2 0

2 1 7

3 3 2

2 1

1 9 0

2 9 5

2 2

1 7 5

2 7 0

2 3

1 6 6

2 4 0

2 4

1 4 0

2 1 6

0

100

200

300

400

500

600

Seria 1

Seria 2

- 1/

46

-

Miesiąc

x(t)

y(t)

x^2

y^2

x*y

(yp-ysr)^2 (y-ysr)^2

(y-yp)^2

1

1 3 2

1 3 0

1 7 4 2 4

1 6 9 0 0

1 7 1 6 0 3 0 2 7 8 , 7 8 2 3 1 4 1 7 , 5 6 3 1 0 , 5 1 0 5 9 9

2

1 6 8

1 6 8

2 8 2 2 4

2 8 2 2 4

2 8 2 2 4 1 9 1 2 5 , 1 4 7 1 9 3 9 0 , 5 6 3 0 , 9 1 4 5 1 5 5

3

2 1 5

2 1 0

4 6 2 2 5

4 4 1 0 0

4 5 1 5 0 8 4 0 2 , 7 8 3 4 9 4 5 7 , 5 6 2 5

3 1 , 1 7 3 2 7

4

2 5 6

2 5 5

6 5 5 3 6

6 5 0 2 5

6 5 2 8 0 2 6 0 0 , 1 9 2 3 2 7 3 0 , 0 6 2 5 1 , 5 8 2 3 6 1 5

5

2 2 1

2 2 0

4 8 8 4 1

4 8 4 0 0

4 8 6 2 0 7 3 4 6 , 9 4 3 7 7 6 1 2 , 5 6 2 5 2 , 3 5 8 3 3 0 5

6

2 1 1

2 0 9

4 4 5 2 1

4 3 6 8 1

4 4 0 9 9 9 1 4 6 , 0 4 4 1 9 6 5 3 , 0 6 2 5 6 , 8 3 8 4 7 3 2

7

2 6 4

2 6 0

6 9 6 9 6

6 7 6 0 0

6 8 6 4 0 1 8 5 3 , 7 8 2 1 2 2 3 2 , 5 6 2 5 1 7 , 5 9 3 2 4 4

8

3 4 1

3 4 8

1 1 6 2 8 1

1 2 1 1 0 4

1 1 8 6 6 8 1 1 1 1 , 1 1 1 9 1 6 6 0 , 5 6 2 5 5 5 , 0 0 6 7 7 9

9

3 3 5

3 3 0

1 1 2 2 2 5

1 0 8 9 0 0

1 1 0 5 5 0 7 4 9 , 7 1 7 0 5

5 1 7 , 5 6 2 5 2 1 , 4 4 5 8 0 5

1 0

3 7 5

3 8 0

1 4 0 6 2 5

1 4 4 4 0 0

1 4 2 5 0 0

4 4 9 7 , 5 1 5 5 2 9 2 , 5 6 2 5 3 2 , 3 3 6 1 1 8

1 1

4 3 8

4 3 0

1 9 1 8 4 4

1 8 4 9 0 0

1 8 8 3 4 0

1 6 7 8 6 , 7 1 1 5 0 6 7 , 5 6 3 4 6 , 4 2 4 2 6 3

1 2

5 6 0

5 4 2

3 1 3 6 0 0

2 9 3 7 6 4

3 0 3 5 2 0 6 2 7 9 8 , 0 1 5 5 5 1 0 7 , 5 6 3 2 5 1 , 0 7 4 2 2

1 3

5 2 5

5 2 4

2 7 5 6 2 5

2 7 4 5 7 6

2 7 5 1 0 0

4 6 6 0 1 , 1 9 4 6 9 8 0 , 5 6 3 0 , 7 6 8 9 7 4 8

1 4

3 8 0

4 1 1

1 4 4 4 0 0

1 6 8 9 2 1

1 5 6 1 8 0 5 1 8 7 , 4 3 2 6 1 0 7 6 4 , 0 6 3 1 0 0 6 , 5 4 9 6

1 5

3 7 6

3 7 5

1 4 1 3 7 6

1 4 0 6 2 5

1 4 1 0 0 0 4 6 3 1 , 5 6 1 7 4 5 9 0 , 0 6 2 5 0 , 0 9 3 3 7 8 1

1 6

3 3 0

3 3 2

1 0 8 9 0 0

1 1 0 2 2 4

1 0 9 5 6 0 5 0 2 , 6 8 5 2 1

6 1 2 , 5 6 2 5 5 , 4 2 5 9 0 6 8

1 7

2 9 6

2 9 5

8 7 6 1 6

8 7 0 2 5

8 7 3 2 0 1 2 7 , 9 0 5 4 1

1 5 0 , 0 6 2 5 0 , 8 8 4 4 8 8 4

1 8

2 7 1

2 7 0

7 3 4 4 1

7 2 9 0 0

7 3 1 7 0 1 3 0 4 , 0 1 3 2 1 3 8 7 , 5 6 2 5 1 , 2 9 7 0 4 0 5

1 9

2 3 7

2 4 0

5 6 1 6 9

5 7 6 0 0

5 6 8 8 0 4 8 7 7 , 8 0 6 2 4 5 2 2 , 5 6 2 5 6 , 7 1 4 8 0 0 2

2 0

2 1 7

2 1 6

4 7 0 8 9

4 6 6 5 6

4 6 8 7 2 8 0 4 2 , 9 6 3 3 8 3 2 6 , 5 6 2 5

2 , 4 5 6 8 3 8

6148

6145

2129658

2125525

2126833 235972,3 237473,75 1501,449

307,4 307,25

R ^ 2 =

0,9936774

b =

0,99206

s =

9,1331175

a =

2,28958

4

99

0

29

2

−

⋅

+

=

t

t

x

,

,

y



=

2

R

0,994

Dopasowanie modelu do danych empirycznych jest bardzo dobre. Przewidywana sprzedaż płynu na
styczeń i kwiecień 2006 r. wynosi:

39

190

190

99

0

29

2

99

0

29

2

21

25

,

,

,

x

,

,

y

*

=

⋅

+

=

⋅

+

=

89

140

140

99

0

29

2

99

0

29

2

24

28

,

,

,

x

,

,

y

*

=

⋅

+

=

⋅

+

=

- 1/

47

-

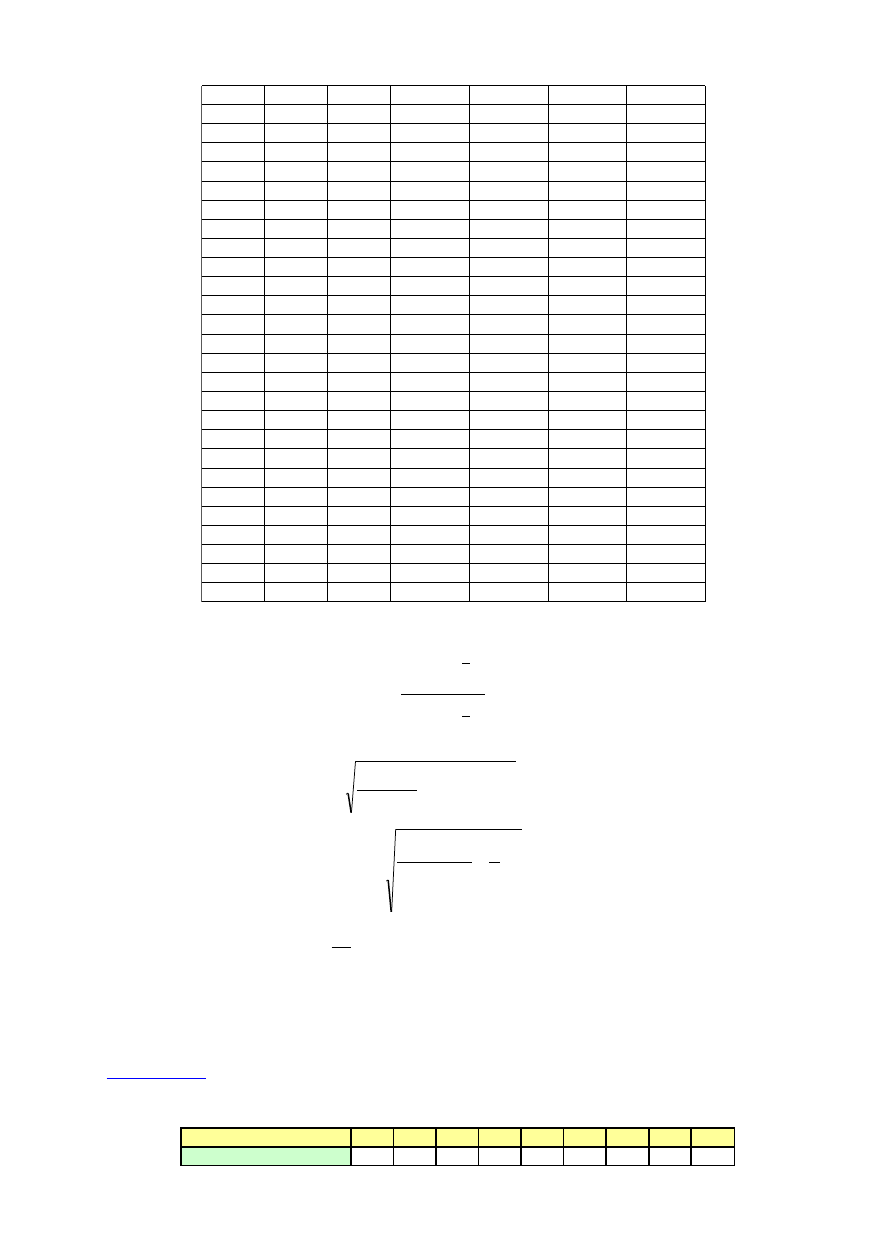
Miesiąc

x(t)

y(t)

x-xsr

(x-xsr)^2

t-tsr

(t-tsr)^2

(t-tsr)^2

1

1 3 2

1 3 0

- 1 7 5 , 4

3 0 7 6 5 , 1 6

- 9 , 5

9 0 , 2 5

2

1 6 8

1 6 8

- 1 3 9 , 4

1 9 4 3 2 , 3 6

- 8 , 5

7 2 , 2 5

3

2 1 5

2 1 0

- 9 2 , 4

8 5 3 7 , 7 6

- 7 , 5

5 6 , 2 5

4

2 5 6

2 5 5

- 5 1 , 4

2 6 4 1 , 9 6

- 6 , 5

4 2 , 2 5

5

2 2 1

2 2 0

- 8 6 , 4

7 4 6 4 , 9 6

- 5 , 5

3 0 , 2 5

6

2 1 1

2 0 9

- 9 6 , 4

9 2 9 2 , 9 6

- 4 , 5

2 0 , 2 5

7

2 6 4

2 6 0

- 4 3 , 4

1 8 8 3 , 5 6

- 3 , 5

1 2 , 2 5

8

3 4 1

3 4 8

3 3 , 6

1 1 2 8 , 9 6

- 2 , 5

6 , 2 5

9

3 3 5

3 3 0

2 7 , 6

7 6 1 , 7 6

- 1 , 5

2 , 2 5

1 0

3 7 5

3 8 0

6 7 , 6

4 5 6 9 , 7 6

- 0 , 5

0 , 2 5

1 1

4 3 8

4 3 0

1 3 0 , 6

1 7 0 5 6 , 3 6

0 , 5

0 , 2 5

1 2

5 6 0

5 4 2

2 5 2 , 6

6 3 8 0 6 , 7 6

1 , 5

2 , 2 5

1 3

5 2 5

5 2 4

2 1 7 , 6

4 7 3 4 9 , 7 6

2 , 5

6 , 2 5

1 4

3 8 0

4 1 1

7 2 , 6

5 2 7 0 , 7 6

3 , 5

1 2 , 2 5

1 5

3 7 6

3 7 5

6 8 , 6

4 7 0 5 , 9 6

4 , 5

2 0 , 2 5

1 6

3 3 0

3 3 2

2 2 , 6

5 1 0 , 7 6

5 , 5

3 0 , 2 5

1 7

2 9 6

2 9 5

- 1 1 , 4

1 2 9 , 9 6

6 , 5

4 2 , 2 5

1 8

2 7 1

2 7 0

- 3 6 , 4

1 3 2 4 , 9 6

7 , 5

5 6 , 2 5

1 9

2 3 7

2 4 0

- 7 0 , 4

4 9 5 6 , 1 6

8 , 5

7 2 , 2 5

2 0

2 1 7

2 1 6

- 9 0 , 4

8 1 7 2 , 1 6

9 , 5

9 0 , 2 5

6148

6145

239762,8

665

307,4 307,25

s =

9 , 1 3 3 1 1 7 5

v ( I 2 0 0 6 ) = 1 0 , 0 7 0 4 3 5 k g

n ( I 2 0 0 6 ) = 5 , 2 8 9 3 7 1 9 %

Bezwzględne i względne błędy ex ante opracowanej prognozy na T=21 (styczeń 2006 r.) są następujące:

(

)

(

)

2

1

2

1

2

∑

∑

=

=

−

−

=

n

t

t

n

t

t

y

y

y

y

R



= 0,994

(

)

2

1

1

1

∑

=

−

⋅

−

−

=

n

t

t

t

y

y

m

n

s



= 9,13 kg

1

1

1

2

2

+

+











 −

−

⋅

=

∑

=

−

−

n

t

t

)

t

T

(

s

v

n

t

T

= 10,07 kg

%

y

v

*

t

t

t

100

⋅

=

η

= (10,07 / 190,39) · 100% = 5,29%

Zatem można uznać, że błąd względny jest powyżej 5% (prognoza jest na granicy dopuszczalności, gdy
graniczny błąd ex ante jest równy 5%).

Przykład 14

Eksperci podali, kiedy ich zdaniem nastąpi dewaluacja złotówki względem dolara w 2006 r.,
wskazując na numer miesiąca.

Nr eksperta

1

2

3

4

5

6

7

8

9

Nr miesiąca

8

6

9

8

11

7

9

7

8

- 1/

48

-

a)

Sformułować prognozę terminu dewaluacji złotówki względem dolara w 2006 r.

b)

Ocenić, czy eksperci byli zgodni w swych opiniach, jeżeli ∆

*

= 2 miesiące.

Rozwiązanie:

Ad a)
Prognozą jest wartość środkowa szeregu, czyli mediana. Mediana dzieli szereg odpowiedzi na 2
równoliczne grupy. Porządkujemy odpowiedzi ekspertów podających numer miesiąca: 6, 7, 7, 8, 8, 8, 9,
9, 11. Miejsce mediany wyznacza relacja (N+1)/2 = 5. W tym przykładzie zatem mediana znajduje się na
5 miejscu w uporządkowanym szeregu odpowiedzi. Wniosek: ósmy miesiąc

Ad b)
By ocenić zgodność opinii ekspertów możemy posłużyć się rozstępem międzykwartylowym

∆

= Q

3

– Q

1

, gdzie: Q

3

– kwartyl górny, Q

1

– kwartyl dolny

Q

1

= (N+1)/4 = 10/4 = 2,5 (średnia arytmetyczna obserwacji 2 i 3 (7)

Q

3

= 3(N+1)/4 = 7,5 (średnia arytmetyczna obserwacji 7 i 8 (9)

∆

= 9 – 7 = 2 miesiące ≤

∆

*

= 2 miesiące. Wniosek: eksperci są zgodni

Przykład 15

Zapytano 100 ekspertów reprezentujących różne dziedziny przemysłu, co sądzą o tempie
rozwoju gospodarki w roku 2006. Po opracowaniu ankiety otrzymano wyniki:

Tempo rozwoju

Niskie

słabe

średnie

wysokie

bardzo wysokie

% odpowiedzi

1

4

90

3

2

Sformułować prognozę tempa rozwoju polskiej gospodarki w 2006 r. i ocenić jej
dopuszczalność.

Rozwiązanie:

Odpowiedzi układają się w 5 kategorii odpowiedzi (k=5). Do oceny zgodności opinii ekspertów zostanie
wykorzystany współczynnik dyspersji względnej klasyfikacji dla zadanego pytania.















−

⋅

−

=

∑

=

k

j

j

f

k

k

h

1

2

1

1

= (5/4) x [1 – ( 1/100)

2

+(4/100)

2

+ (90/100)

2

+ (3/100)

2

+ (2/100)

2

)] = (5/4) x [1 -

0,813] = 0,23375

Wartość współczynnika dyspersji świadczy o zgodności opinii ekspertów (relatywnie niska wartość
współczynnika dyspersji). Zatem prognoza tempa rozwoju gospodarki w 2006 r. może być określona
jako wartość modalna (średnie tempo rozwoju).

Dopuszczalność: prognoza jest dopuszczalna (duża zgodność ekspertów).

Przykład 16

Poproszono 50 ekspertów o podanie opinii na temat znaczenia dla środowiska Górnego
Śląska zagrożeń spowodowanych przez różne czynniki w 2005 r. Opinie ekspertów dotyczące
trzech czynników powodujących zagrożenie zestawiono w tabeli:

Czynnik powodujący
zagrożenie

Znaczenie zagrożenia

bardzo ważne

ważne

niezbyt ważne

nieistotne

Zanieczyszczenie powietrza

15

25

7

3

Odpady

32

11

5

2

Obniżenie jakości wody pitnej

6

12

27

5

Ocenić, czy eksperci byli zgodni w swych opiniach dotyczących czynników powodujących
zagrożenia dla środowiska.

Rozwiązanie:

Odpowiedzi dotyczące znaczenia czynników zagrożenia w odniesieniu do 3 pytań (powietrze, odpady,
woda) układają się w 4 kategorie (bardzo ważne, ważne, niezbyt ważne, nieistotne). Do oceny zgodności
opinii ekspertów zostanie wykorzystany współczynnik dyspersji względnej klasyfikacji dla zadanego
pytania. Zatem liczba kategorii odpowiedzi k=4, liczba zadawanych pytań jest równa 3 (r=1,2,3).

- 1/

49

-















−

⋅

−

=

∑

=

k

j

j

f

k

k

h

1

2

1

1

1

1

= (4/3) x [1 – (15/50)

2

+(25/50)

2

+ (7/50)

2

+ (3/50)

2

] = 0,849















−

⋅

−

=

∑

=

k

j

j

f

k

k

h

1

2

2

2

1

1

= (4/3) x [1 – (32/50)

2

+(11/50)

2

+ (5/50)

2

+ (2/50)

2

] = 0,707















−

⋅

−

=

∑

=

k

j

j

f

k

k

h

1

2

3

3

1

1

= (4/3) x [1 – (6/50)

2

+(12/50)

2

+ (27/50)

2

+ (5/50)

2

] = 0,835

15

25

7

3

h

1

=

0,849067

32

11

5

2

h

2

=

0,7072

6

12

27

5

h

3

=

0,8352

Wartości współczynnika dyspersji świadczą o niezgodności opinii ekspertów (duże wartości
współczynnika dyspersji). Zatem opinia na temat czynników zagrożeń dla środowiska Górnego
Śląska jest niezgodna. Dopuszczalność prognozy: prognoza jest niedopuszczalna.

Przykład 17

Pięciu ekspertów poproszono o opinie dotyczące wzrostu PKB w Polsce w 2006 r. Przyjęto, że
mogą wystąpić cztery warianty wzrostu. Rangi nadane przez ekspertów poszczególnym
wariantom określają kolejność według szans realizacji wzrostu PKB, co przedstawiono w
poniższej tabeli:

Wzrost PKB (w %)

Ekspert

Wariant

A

B

C

D

3,5-4,0

4,0-4,5

4,5-5,0

5,0-5,5

I

1

2

4

3

II

2

1

3

4

III

1

3

4

2

IV

1

2

4

3

V

1

2

4

3

a) Ocenić, czy eksperci byli zgodni w swych opiniach dotyczących wzrostu PKB w 2006 r.
b) Uporządkować warianty wzrostu PKB według szans realizacji.

Rozwiązanie:

a) Ocena zgodności ekspertów w opiniach nt. wzrostu PKB

Uzyskane odpowiedzi są pomiarami na skali porządkowej, ponieważ eksperci nadawali rangi (znaczenie)
poszczególnym wariantom wzrostu PKB. Do oceny zgodności opinii ekspertów wykorzystany zostanie
współczynnik konkordancji:

(

)

k

k

n

S

W

−

⋅

⋅

=

3

2

12

,

gdzie n – liczba ekspertów, k – liczba wariantów odpowiedzi,

∑ ∑

=

=









−

=

k

j

n

i

ij

x

x

S

1

2

1

,

∑ ∑

=

=

⋅

=

n

i

k

j

ij

x

k

x

1

1

1

- przeciętna ranga.

Odpowiedzi udzielało 5 ekspertów (n=5), były 4 kategorie odpowiedzi (k=4). Obliczamy przecietną rangę
oraz parametr S a następnie współczynnik konkordancji W.

Nastepnie obliczamy statystykę χ

2

:

(

)

5

12

4

50

15

19

10

6

4

1

,

x

=

=

+

+

+

⋅

=

- 1/

50

-

1

2

4

3

2

1

3

4

1

3

4

2

1

2

4

3

1

2

4

3

6

10

19

15

x

sr

12,5

S

97

W

0,776

(

)

64

11

100

1164

5

4

5

97

12

1

12

2

,

k

k

n

S

=

=

⋅

⋅

⋅

=

+

⋅

⋅

⋅

=

χ

Z tablic rozkładu χ

2

dla przyjętego w badaniu poziomu istotności α=0,1 oraz k-1 = 3 stopni swobody

odczytano wartość krytyczną wynoszącą 6,251. Ponieważ wyznaczona statystyka przekracza wartość
odczytaną z tablic, można uznać, że eksperci byli zgodni w swych opiniach dotyczących wzrostu PKB
(zgodność nie jest przypadkowa).

b) Uporządkowanie wariantów wzrostu PKB według szans realizacji

Na podstawie zgodnej opinii ekspertów można uporządkować warianty według szans realizacji wzrostu
PKB. Uporządkowanie wynika z rang łącznych przypisanych wariantom. Oznacza to, że najmniejszą
szansę realizacji ma wzrost wg wariantu A (3,5-5,0), następnie wzrost wg wariantu B (4,0-4,5), następnie
D (5,0-5,5), następnie C (4,5-5,0). Zatem wg szans realizacji kolejność wariantów jest następująca:
C, D, B, A.

Przykład 18

Zbudowany na podstawie wypowiedzi ankietowych wskaźnik koniunktury w przemyśle
szklarskim dla stycznia 2006 r. wyniósł +2%. Dla następnego miesiąca uzyskano następujące
odpowiedzi: nastąpi poprawa koniunktury - 32% odpowiedzi, koniunktura nie ulegnie zmianie –
40% odpowiedzi, koniunktura pogorszy się – 28% odpowiedzi. Czy według przewidywań
respondentów koniunktura w przemyśle szklarskim w lutym w porównaniu ze styczniem
poprawi się, pogorszy, czy pozostanie bez zmian?

Rozwiązanie:

Test koniunktury jest to ankietowe badanie przedsiębiorstw. Anieta zawiera pytania diagnostyczne i
pytania prognostyczne. Wyniki badania prezentowane są w postaci: wykresów, procentowej, ważonej
oraz w formie ważonego salda. Saldo jest różnicą pomiędzy procentem odpowiedzi wskazujących
na polepszenie a procentem odpowiedzi wskazujących na pogorszenie sytuacji przedsiębiorstwa
lub różnicą pomiędzy procentem odpowiedzi wskazujących na sytuację korzystną dla
przedsiębiorstwa a procentem odpowiedzi wskazujących na sytuację niekorzystną dla
przedsiębiorstwa. Wskaźnik koniunktury w formie sald przyjmuje wartość z przedziału od -100 do +100.
Dodatnia wartość wskaźnika oznacza dobrą koniunkturę, ujemna zaś złą. Wzrost wskaźnika oznacza
poprawę koniunktury, a jego spadek – pogorszenie koniunktury z punktu widzenia badanych
przedsiębiorstw.

Większość odpowiedzi (40%) wskazuje na to, że koniunktura dla lutego 2006 r. nie ulegnie zmianie
(wariant 2.). Sytuacja korzystna występuje w wariancie 1. (poprawa koniunktury). Saldo jest więc
obliczane jako % odpowiedzi na wariant pierwszy (poprawa koniunktury) minus % odpowiedzi na wariant
3. pogorszenia koniunktury. Wskaźnik koniunktury w formie salda obliczany jest jako:

Saldo w styczniu 2006 r.: +2%
Saldo w lutym 2006 r.: 32 – 28% = +4%
Porównując saldo z lutego (+4%) z saldem ze stycznia (+2%) oceniamy, że nastąpi poprawa koniunktury.

Przykład 19

Mamy następujące dane pochodzące z badań koniunktury gospodarczej:

- 1/

51

-

Ogólna sytuacja gospodarcza przedsiębiorstwa jest:

dobra

25

zadowalająca

30

zła

45

Ogólna sytuacja gospodarcza przedsiębiorstwa w ciągu najbliższych 3 miesięcy w
stosunku do danego miesiąca:

poprawi się

38

pozostanie bez zmian 41
pogorszy się

21

a)

Czy badane przedsiębiorstwa lepiej oceniają swą aktualną sytuację gospodarczą czy

przyszłą?

b) Obliczyć wskaźnik ogólnego klimatu koniunktury i podać jego interpretację.

Rozwiązanie:

Ad a) Ocena sytuacji gospodarczej aktualnej i przyszłej
Saldo sytuacji obecnej: 25% - 45% = -20%
Saldo sytuacji przyszłej: 38% - 21% = +17% (sytuacja gospodarcza będzie lepsza)
Badane przedsiębiorstwa lepiej oceniają swą przyszłą sytuację niż aktualną.

Ad b) Wskaźnik ogólnego klimatu koniunktury

Wskaźnik ten obliczany jest jako średnia arytmetyczna sald odpowiedzi na pytania dotyczące aktualnej i
przewidywanej sytuacji przedsiębiorstwa. „Dobry” klimat koniunktury mają przedsiębiorstwa, dla których
wartość wskaźnika jest większa od 0.

(

) (

)

(

)

%

,

%

%

w

5

1

2

17

20

−

=

+

+

−

=

Interpretacja wskaźnika w: ogólny klimat koniunktury nie jest dobry (w<0).

- 1/

52

-