J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 5 • KMBiM WILiŚ PG
1
Ćwiczenie 5
Rozwiązania tarcz we współrzędnych biegunowych
Związki między składowymi stanu naprężeń w układzie prostokątnym i biegunowym
1.
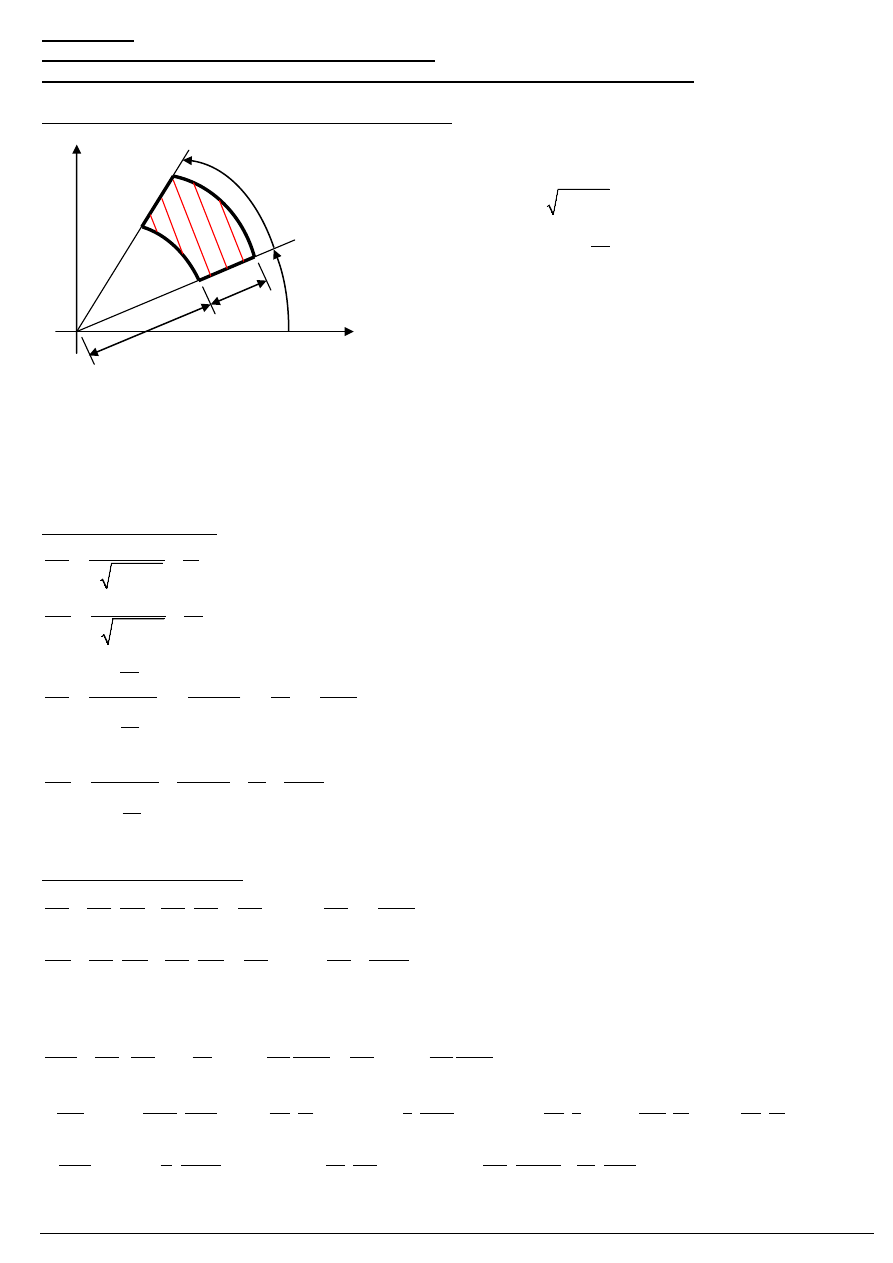
Rozwiązania tarcz we współrzędnych biegunowych
Współrzędne biegunowe – współrzędne krzywoliniowe, ortogonalne, na płaszczyźnie
W celu wyprowadzenia wzorów transformacyjnych dla operatora biharmonicznego
4
F
∇
z układu
prostokątnego do biegunowego obliczamy pochodne cząstkowe funkcji złożonej:
(
)
( )
1
2
,
,
F x x
F r
ϕ
⇒
(
)
(
)
(
)
1
2
1
2
,
,
,
x x
x x
F r
ϕ
=
1
r
x
∂
∂
Obliczenia pomocnicze:
1
1
2
2
1
2
2
cos
2
x
x
r
x
x
ϕ
=
=
=
+
2
r
x
∂
∂
2
2
2
2
1
2
2
sin
2
x
x
r
x
x
ϕ
=
=
=
+
1
x
ϕ
∂
∂
2
2
1
2
2
2
2
2
2
1
2
2
1
sin
1
x
x
x
x
x
x
r
r
x
x
ϕ
−
=
= −
= −
= −
+
+
2
x
ϕ
∂
∂
1
1
1
1
2
2
2
2
1
2
2
1
cos
1
x
x
x
x
x
r
r
x
x
ϕ
−
=
=
=
=
+
+
1
1
1
F
F
r
F
x
r
x
x
ϕ
ϕ
∂
∂
∂
∂
∂
=
⋅
+
⋅
∂
∂ ∂
∂
∂
Pochodne funkcji naprężeń:
sin
cos
F
F
r
r
ϕ
ϕ
ϕ
∂
∂
=
⋅
+
⋅ −
∂
∂
2
2
2
F
F
r
F
x
r
x
x
ϕ
ϕ
∂
∂
∂
∂
∂
=
⋅
+
⋅
∂
∂ ∂
∂
∂
cos
sin
F
F
r
r
ϕ
ϕ
ϕ
∂
∂
=
⋅
+
⋅
∂
∂
Następnie:
2
2
1
1
1
F
F
x
x
x
∂
∂ ∂
=
∂
∂
∂
sin
sin
cos
cos
F
F
r
r
r
r
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
∂
∂
∂
∂
=
−
−
∂
∂
∂
∂
2
2
2
2
2
2
2
2
2
2
2
2
sin
1
1
1
1
1
cos
cos
sin
cos
sin
cos
sin
sin
sin
cos
F
F
F
F
F
F
F
r
r
r
r
r
r
r r
r
r
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
∂
∂
∂
∂
∂
∂
∂
=
⋅
−
⋅
⋅
+
⋅ ⋅
⋅
− ⋅
⋅
⋅
+
⋅ ⋅
+
⋅
−
⋅ ⋅
⋅
∂
∂ ∂
∂
∂ ∂
∂
∂
∂
2
2
2
2
2
2
2
2
2
2
2
2
sin
1
cos
sin
cos
sin
cos
sin
F
F
F
F
F
r
r
r
r
r
r
r
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
∂
∂
∂
∂
∂
=
⋅
− ⋅
⋅
⋅
+
⋅
⋅
⋅
+
⋅
+
⋅
⋅
∂
∂ ∂
∂
∂
∂
1
x
2
x
dr
r
1
2
cos
sin
x
r
x
r
ϕ
ϕ
= ⋅
= ⋅
ϕ
d
ϕ
r d
ϕ
⋅
2
2
1
2
2
1
r
x
x
x
arctg
x
ϕ
=
+
⇒
=
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 5 • KMBiM WILiŚ PG
2
Podobnie:
2
2
2
2
2
F
F
x
x
x
∂
∂
∂
=
∂
∂
∂
( )
cos
cos
sin
sin
...
F
F
r
r
r
r
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
∂
∂
∂
∂
=
+
+
=
∂
∂
∂
∂
2
2
2
2
2
2
2
2
2
2
2
2
cos
1
sin
sin
cos
sin
cos
cos
F
F
F
F
F
r
r
r
r
r
r
r
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
∂
∂
∂
∂
∂
=
⋅
+ ⋅
⋅
⋅
−
⋅
⋅
⋅
+
⋅
+
⋅
⋅
∂
∂ ∂
∂
∂
∂
2
2
2
2
2
2
2
2
2
2
1
2
1
1
F
F
F
F
F
F
x
x
r
r
r
r
ϕ
∂
∂
∂
∂
∂
∇
=
+
=
+ ⋅
+
⋅
∂
∂
∂
∂
∂
Zatem operator Laplace’a we współrzędnych biegunowych:
Równanie tarczy we współrzędnych biegunowych:
( )
,
F
F r
ϕ
=
–
funkcja naprężeń
(
)
4
2
2
0
F
F
∇
= ∇ ∇
=
( )
( )
( )
( )
( )
( )
2
2
2
2
2
2
2
2
2
2
,
,
,
1
1
1
1
0
F r
F r
F r
r
r
r
r
r
r
r
r
ϕ
ϕ
ϕ
ϕ
ϕ
∂
∂
∂
∂
∂
∂
+ ⋅
+
⋅
+ ⋅
+
⋅
=
∂
∂
∂
∂
∂
∂
Uwaga:
Do wyznaczenia naprężeń stycznych w ukł. biegunowym potrzebna jest również pochodna mieszana!
2
1
2
1
2
F
F
x x
x
x
∂
∂ ∂
=
∂ ∂
∂
∂
( )
cos
sin
sin
cos
...
F
F
r
r
r
r
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
∂
∂
∂
∂
=
+
−
=
∂
∂
∂
∂
2
2
2
2
2
2
2
1
1
1
1
sin
cos
cos 2
cos 2
sin
cos
sin
cos
F
F
F
F
F
r
r
r
r
r
r
r
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
∂
∂
∂
∂
∂
=
⋅
⋅
+ ⋅
⋅
−
⋅
⋅
− ⋅
⋅
⋅
−
⋅
⋅
⋅
∂
∂ ∂
∂
∂
∂
PSN w układzie biegunowym:
2.
Związki między składowymi stanu naprężeń w układzie prostokątnym i biegunowym
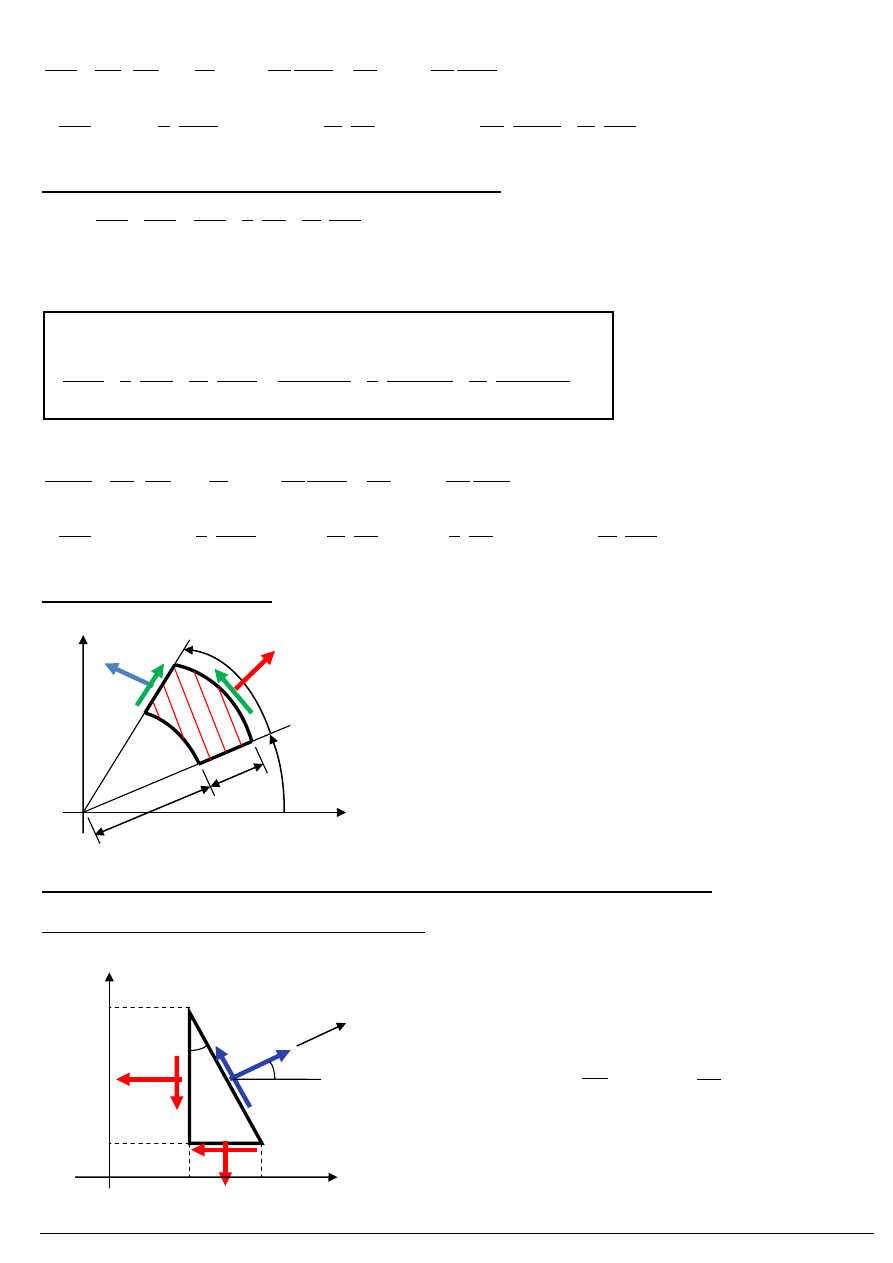
Elementarne wyprowadzenie (z równań równowagi):
Rzut na oś w kierunku
r
:
11
2
22
1
21
1
12
2
cos
sin
cos
sin
rr
ds
ds
ds
ds
ds
σ
σ
ϕ σ
ϕ σ
ϕ σ
ϕ
=
+
+
+
2
2
11
22
21
cos
sin
sin 2
rr
σ
σ
ϕ σ
ϕ σ
ϕ
→
=
+
+
Rzut na oś prostopadłą do kierunku
r
:
11
22
21
sin
cos
sin
cos
cos 2
r
ϕ
σ
σ
ϕ
ϕ σ
ϕ
ϕ σ
ϕ
→
= −
⋅
+
⋅
+
2
cos
ds
ds
ϕ
=
1
sin
ds
ds
ϕ
=
Dane:
11
22
12
21
,
,
σ σ
σ
σ
=
Szukane:
,
,
rr
r
r
ϕϕ
ϕ
ϕ
σ
σ
σ
σ
=
ds
–
powierzchnia ścianki ukośnej,
stąd:
–
powierzchnie ścianek:
1
1
ds
g dx
= ⋅
oraz:
2
2
ds
g dx
= ⋅
1
x
2
x
dr
r
ϕ
d
ϕ
rr
σ
r
ϕ
σ
ϕϕ
σ
r
ϕ
σ
→ naprężenia:
rr
σ
–
naprężenia promieniowe (radialne)
ϕϕ
σ
–
naprężenia obwodowe (pierścieniowe)
r
ϕ
σ =
r
ϕ
σ – naprężenia styczne
rr
σ
12
σ
11
σ
21
σ
1
ds
ϕ
22
σ
1
x
2
ds
2
x
r
ϕ
σ
ds
ϕ
r
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 5 • KMBiM WILiŚ PG
3
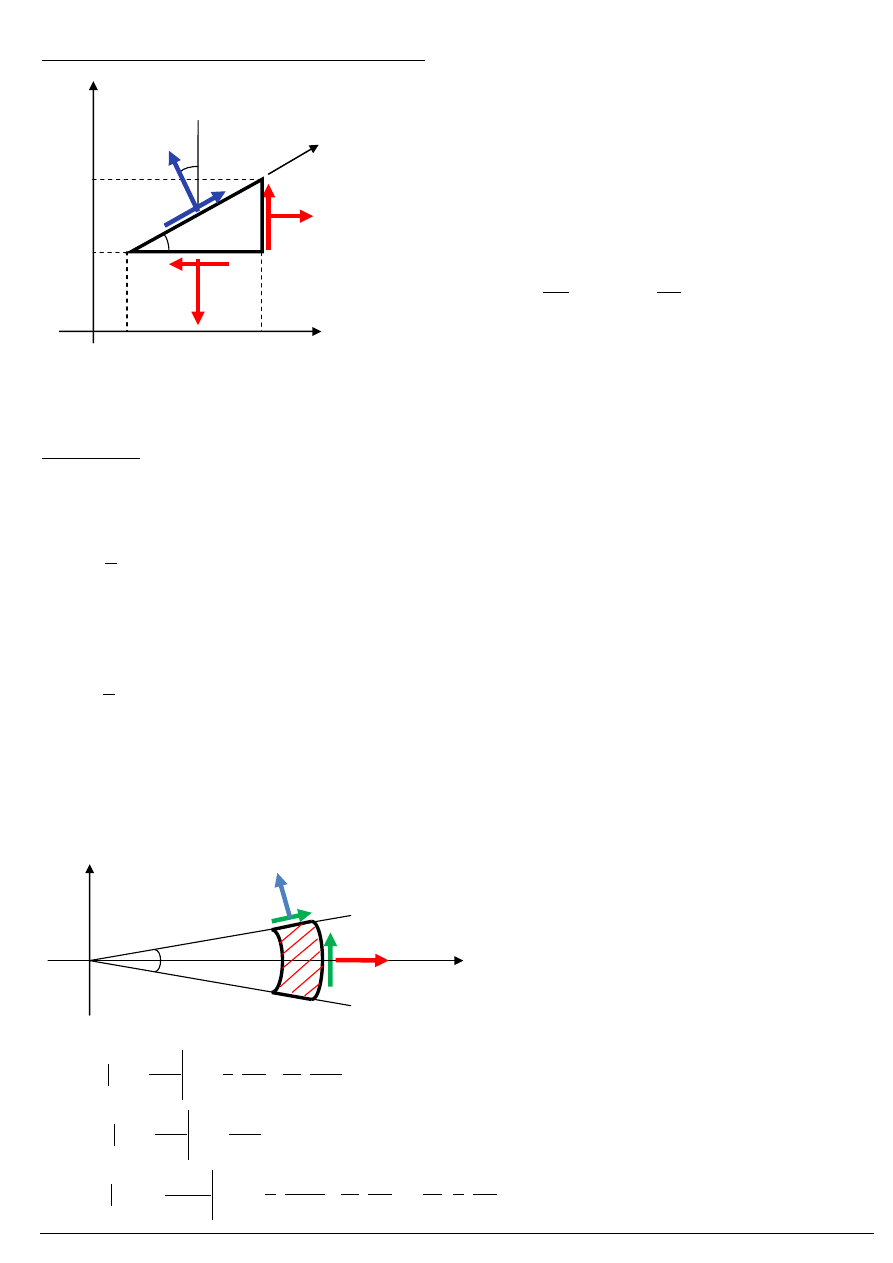
Analogiczne wyprowadzenie (z równań równowagi):
Rzut na oś prostopadłą do kierunku r :
2
2
11
22
21
sin
cos
sin 2
ϕϕ
σ
σ
ϕ σ
ϕ σ
ϕ
→
=
+
−
Niezmiennik:
11
22
rr
ϕϕ
σ
σ
σ
σ
+
=
+
!
Rozwiązując poniższy układ trzech równań równowagi:
(
)
2
2
11
22
21
22
11
21
2
2
11
22
21
cos
sin
sin 2
1
sin 2
cos 2
2
sin
cos
sin 2
rr
r
ϕ
ϕϕ
σ
σ
ϕ σ
ϕ σ
ϕ
σ
σ
σ
ϕ σ
ϕ
σ
σ
ϕ σ
ϕ σ
ϕ
=
+
+
=
−
+
=
+
−
otrzymamy tzw.
związki odwrotne:
(
)
2
2
11
12
2
2
22
cos
sin
sin 2
1
sin 2
cos 2
2
sin
cos
sin 2
rr
r
rr
r
rr
r
ϕϕ
ϕ
ϕϕ
ϕ
ϕϕ
ϕ
σ
σ
ϕ σ
ϕ σ
ϕ
σ
σ
σ
ϕ σ
ϕ
σ
σ
ϕ σ
ϕ σ
ϕ
=
+
−
=
−
+
=
+
+
Naprężenia w tarczy (w układzie biegunowym) wyznaczymy z funkcji naprężeń (jako odpowiednie pochodne
funkcji naprężeń), przyjmując element różniczkowy leżący na osi
1
x , tzn. dla
0
ϕ
=
!
11
0
rr
ϕ
σ
σ
=
=
2
2
2
0
F
x
ϕ =
∂
=
∂
2
2
2
1
1
F
F
r
r
r
ϕ
∂
∂
= ⋅
+
⋅
∂
∂
22
0
ϕϕ
ϕ
σ
σ
=
=
2
2
1
0
F
x
ϕ =
∂
=
∂
2
2
F
r
∂
=
∂
12
0
r
ϕ
ϕ
σ
σ
=
=
2
1
2
0
F
x x
ϕ =
∂
= −
∂ ∂
2
2
1
1
1
F
F
F
r
r
r
r r
ϕ
ϕ
ϕ
∂
∂
∂
∂
= − ⋅
+
⋅
= −
⋅
∂ ∂
∂
∂
∂
Gdy:
0
d
ϕ
→
to:
22
ϕϕ
σ
σ
=
itd.
22
σ
12
σ
11
σ
21
σ
ϕ
r
1
x
2
ds
2
x
1
ds
ds
ϕ
ϕϕ
σ
r
ϕ
σ
2
cos
ds
ds
ϕ =
1
sin
ds
ds
ϕ
=
Dane:
11
22
12
21
,
,
σ σ
σ
σ
=
Szukane:
,
,
rr
r
r
ϕϕ
ϕ
ϕ
σ
σ
σ
σ
=
ds
–
powierzchnia ścianki ukośnej,
stąd:
–
powierzchnie ścianek:
1
1
ds
g dx
= ⋅
oraz:
2
2
ds
g dx
= ⋅
1
x
2
x
dr
r
d
ϕ
rr
σ
r
ϕ
σ
ϕϕ
σ
r
ϕ
σ
Document Outline
- Ćwiczenie 5
- Rozwiązania tarcz we współrzędnych biegunowych
- Związki między składowymi stanu naprężeń w układzie prostokątnym i biegunowym
- 1. Rozwiązania tarcz we współrzędnych biegunowych
- 2. Związki między składowymi stanu naprężeń w układzie prostokątnym i biegunowym
Wyszukiwarka
Podobne podstrony:
TSiP Cw 05-notatki
TSiP Cw 10-notatki
TSiP Cw 02-notatki
TSiP Cw 13-notatki
TSiP Cw 12-notatki
16) TSiP Cw 04 notatki
TSiP Cw 13 notatki
TSiP Cw 09 notatki
TSiP Cw 03 notatki
Degeneracje i Regeneracje Ćw 9.05.2010, Notatki Studia Fizjoterapia
MD cw 05
podst fin ćw " 05 2010
Cw 05 Pomiar punktu Curie ferro Nieznany
ĆW. VII, Notatki AWF
cw 05 instrukcja id 121376 Nieznany
Cw 05 Rezonans w obwodzie szeregowym
ćw.5, 05 Gorski, Politechnika Krakowska
więcej podobnych podstron