Józef Szymczak
Pochodna funkcji jednej zmiennej
(notatki z wykładu)
Niech
0
x
i
1
x
będą pewnymi argumentami funkcji
)
(x
f
, a
)
(
0
x
f
i
)
(
1
x
f
wartościami funkcji
odpowiadającymi tym argumentom.
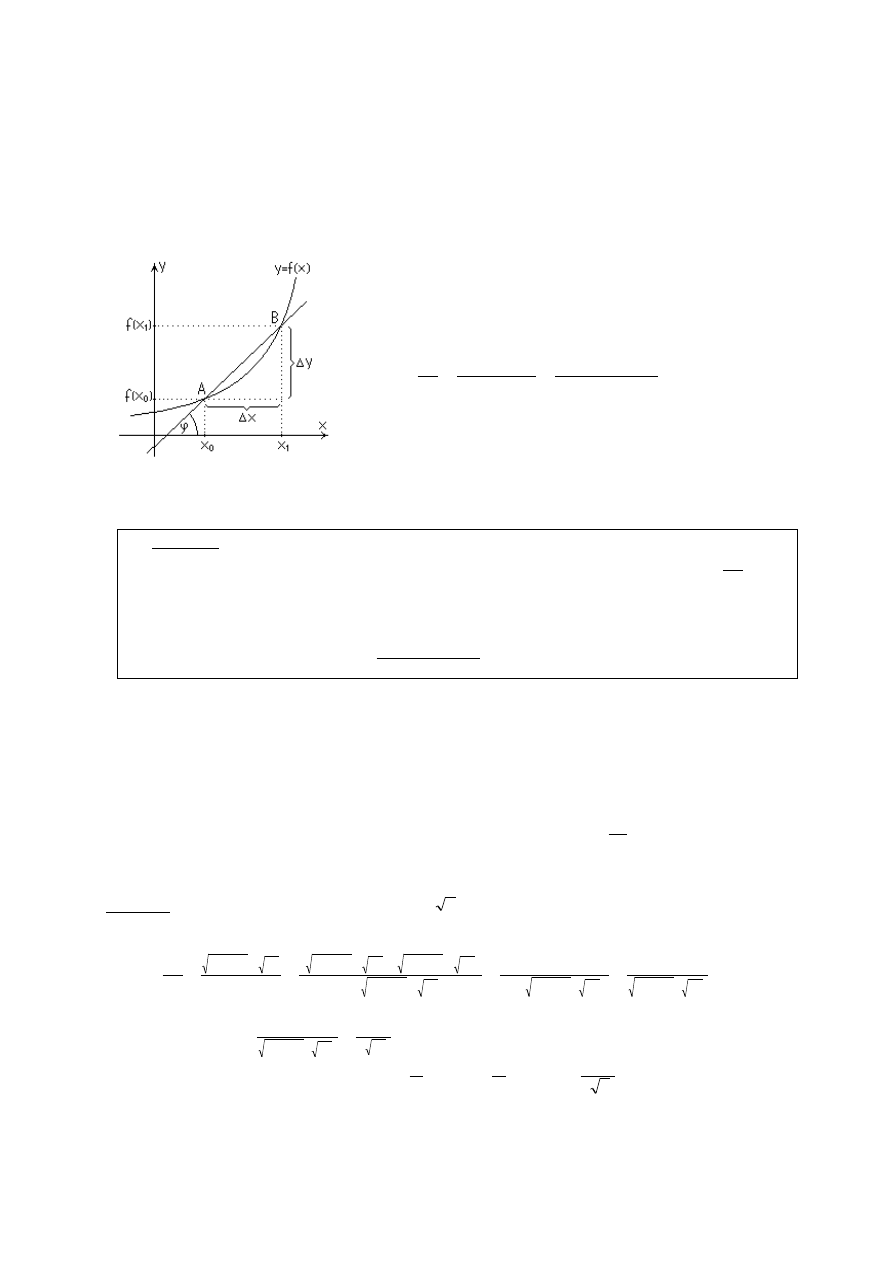
Oznaczmy:
0
1
x
x
x
– przyrost argumentu,
)
(
)
(
0
1
x
f
x
f
y
– przyrost funkcji odpowiadający
danemu przyrostowi argumentu.
x
x
x
x
y
x
f
x
x
f
x
f
x
f
)
(
)
(
)
(
)
(
0
0
0
1
0
1
to iloraz różnicowy wyrażający stosunek przyrostu funkcji
y
do przyrostu argumentu
x
(czyli stosunek przyrostu
zmiennej zależnej do przyrostu zmiennej niezależnej).
Definicja pochodnej funkcji
Pochodną funkcji
)
(x
f
w punkcie
0
x
nazywamy granicę ilorazu różnicowego
x
y
(o ile
istnieje) przy założeniu, że przyrost argumentu
x
dąży do zera.
Zapisujemy ten fakt symbolicznie:
x
x
f
x
x
f
x
x
f
)
(
)
(
0
0
0
0
lim
)
(
.
Pochodna funkcji w punkcie jest to zatem ściśle określona liczba.
Jeżeli funkcja
)
(x
f
ma w punkcie
0
x
pochodną skończoną, to mówimy, że jest ona
różniczkowalna w punkcie
0
x
.
Wyznaczanie pochodnej funkcji nazywamy różniczkowaniem.
Pochodną funkcji zapisujemy używając symboli:
)
(x
f
, y
lub
dx
dy
.
Przykład. Obliczyć pochodną funkcji
x
x
f
)
(
w punkcie
0
x
(na podstawie definicji).
Wyznaczamy iloraz różnicowy dla tej funkcji:
1
)
(
)
(
)
(
)
(
0
0
0
0
0
0
0
0
0
0
0
0
0
0
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
y
.
Z definicji pochodnej mamy:
2
1
1
0
0
0
0
0
lim
)
(
x
x
x
x
x
x
f
.
Stąd możemy policzyć, że np.
4
1
)
4
(
f
,
2
1
)
1
(
f
,
2
1
2
)
2
(
f
,
)
0
(
f
nie istnieje.
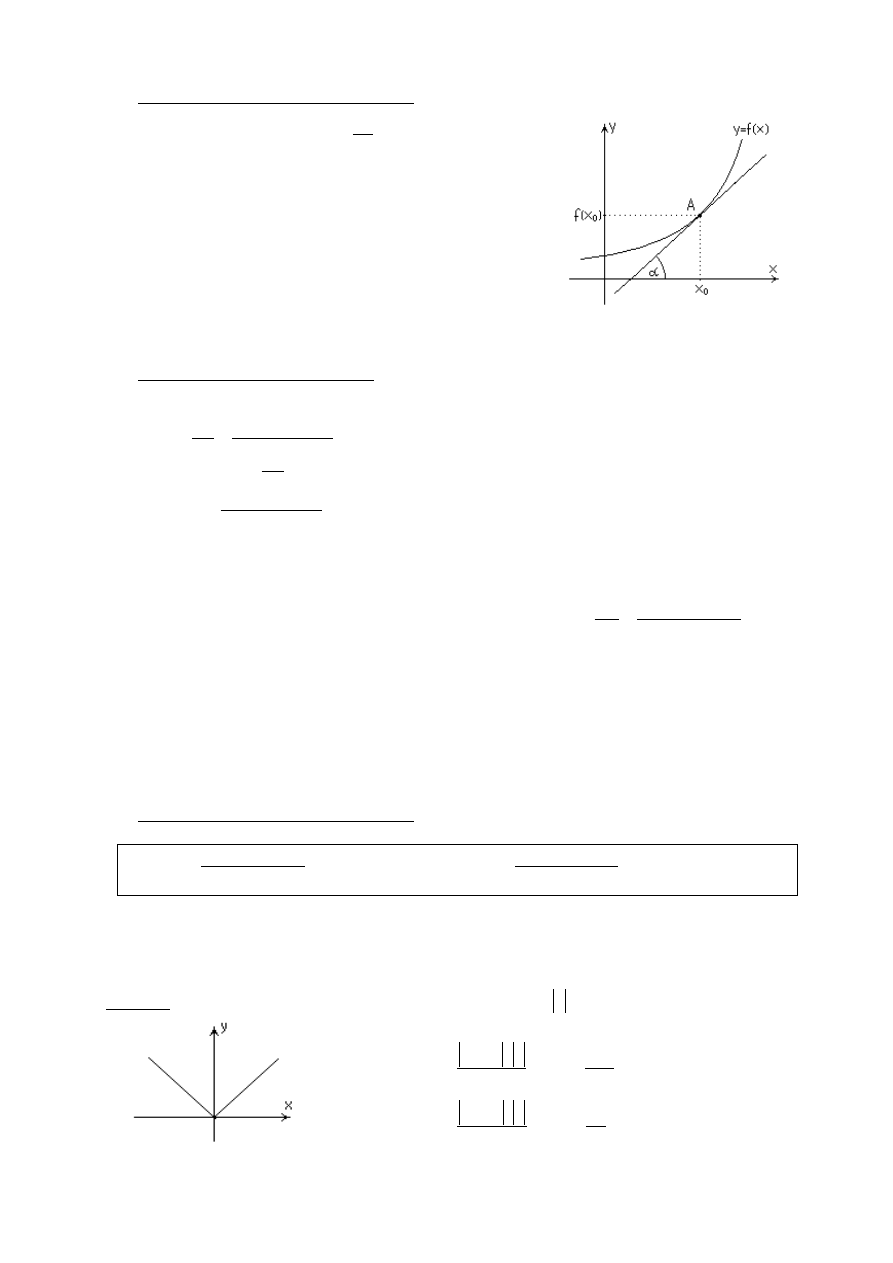
Interpretacja geometryczna pochodnej
Zauważmy, że iloraz różnicowy
x
y
wyraża tangens kąta
między dodatnią półosią
Ox
a sieczną przechodzącą
przez punkty
))
(
,
(
0
0
x
f
x
A
i
))
(
,
(
1
1
x
f
x
B
. Gdy
x
dąży do
zera, sieczna zmienia swoje położenie stając się w końcu
styczną. Tak więc
tg
x
f
)
(
0
,
gdzie kąt
jest kątem zawartym między dodatnią półosią
Ox
, a styczną do wykresu funkcji
)
(x
f
w punkcie
))
(
,
(
0
0
x
f
x
A
.
Interpretacja fizyczna pochodnej
Traktując drogę S jako funkcję zależną od czasu t, czyli
)
(t
S
S
, możemy powiedzieć, że iloraz
różnicowy
t
t
S
t
t
S
t
S
)
(
)
(
0
0
oznacza prędkość średnią poruszającego się ciała w przedziale
czasu
t
, czyli
t
S
V
sr
.
t
t
S
t
t
S
t
t
S
)
(
)
(
0
0
0
0
lim
)
(
oznacza prędkość poruszającego się ciała w chwili
0
t
(prędkość
chwilowa), czyli
)
(
)
(
0
0
t
V
t
S
.
Traktując ładunek elektryczny Q przepływający przez przekrój przewodnika jako funkcję
czasu t, czyli
)
(t
f
Q
, możemy powiedzieć, że iloraz różnicowy
t
t
f
t
t
f
t
Q
)
(
)
(
0
0
oznacza
średnie natężenie prądu w przedziale czasu
t
. Granica tego ilorazu różnicowego przy
0
t
oznaczać będzie natężenie prądu w chwili
0
t
.
____________________________________________
Ogólnie możemy powiedzieć, że pochodną interpretujemy jako szybkość zmiany funkcji w
danym punkcie
0
x
x
.
______________________________________________
Pochodna lewostronna i prawostronna.
)
(
0
0
0
)
(
)
(
0
lim
x
f
x
x
f
x
x
f
x
,
)
(
0
0
0
)
(
)
(
0
lim
x
f
x
x
f
x
x
f
x
.
Pochodna funkcji w punkcie
0
x istnieje wtedy i tylko wtedy, gdy istnieją pochodne
jednostronne w tym punkcie i są sobie równe.
Przykład. Wyznaczyć pochodne jednostronne funkcji
x
x
f
)
(
w punkcie
0
0
x
.
W tym przypadku mamy , że
1
lim
0
0
lim
)
(
0
0
0
x
x
x
x
x
f
x
x
,
1
lim
0
0
lim
)
(
0
0
0
x
x
x
x
x
f
x
x
.
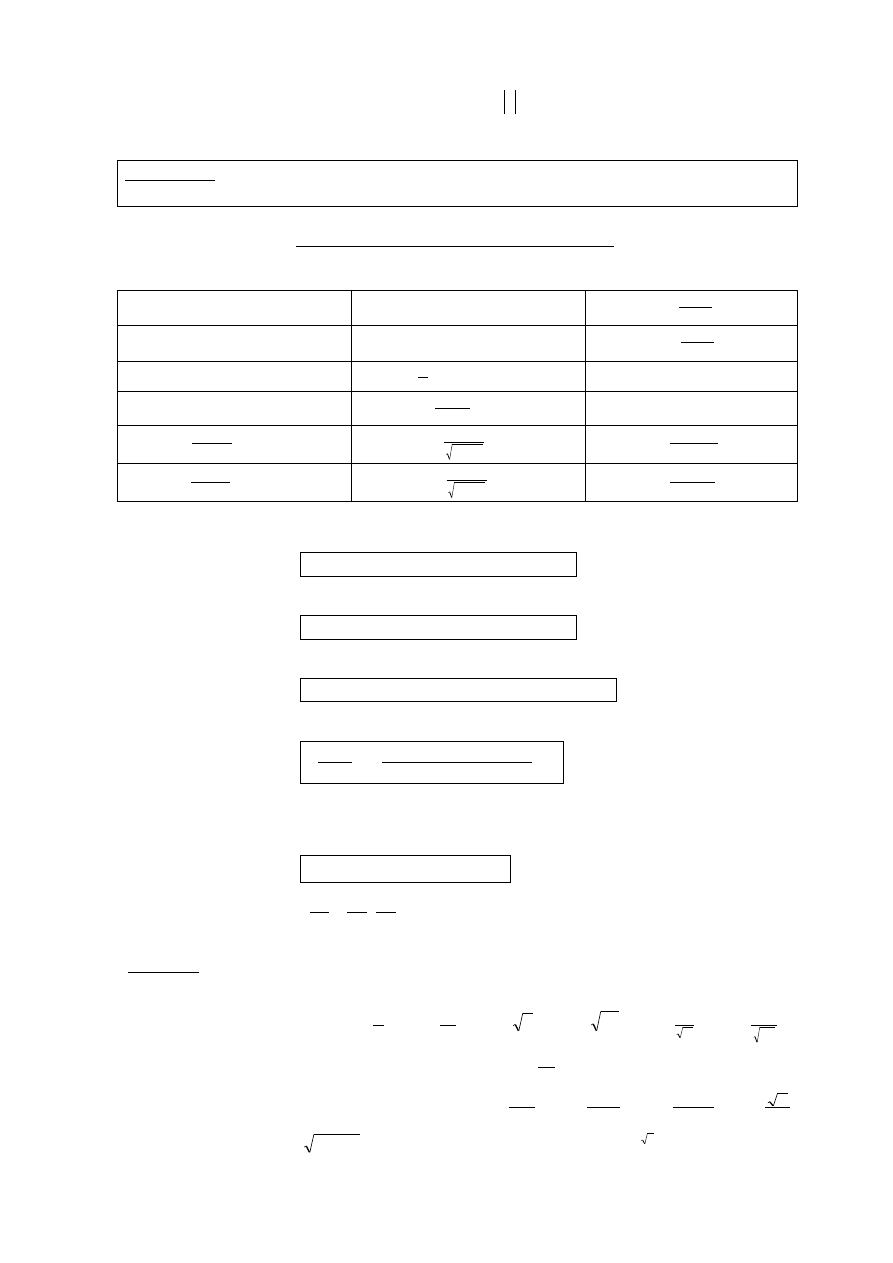
Widać stąd, że nie istnieje pochodna funkcji
x
x
f
)
(
w punkcie
0
0
x
, ponieważ pochodne
jednostronne w tym punkcie są różne.
Twierdzenie. Funkcja różniczkowalna w danym punkcie
0
0
x
jest w tym punkcie ciągła
(odwrotne twierdzenie nie zachodzi, co pokazuje wcześniejszy przykład).
Ważniejsze wzory rachunku różniczkowego.
Pochodne podstawowych funkcji elementarnych:
0
)
(
c
x
x
e
e
)
(
1
1
)
(arctan
2
x
x
1
)
(
x
x
1
,
0
,
ln
(
)
a
a
a
a
a
x
x
1
1
)
cot
arc
(
2
x
x
x
x
cos
)
(sin
x
x
1
)
(ln
x
x
cosh
)
(sinh
x
x
sin
)
(cos
a
x
x
a
ln
1
)
(log
x
x
sinh
)
(cosh
x
x
2
cos
1
)
(tan
2
1
1
)
(arcsin
x
x
x
x
2
cosh
1
)
(tanh
x
x
2
sin
1
)
(cot
2
1
1
)
(arccos
x
x
x
x
2
sinh
1
)
(coth
Pochodna funkcji mającej pewien stały współczynnik:
)
(
)
)
(
(
x
f
c
x
f
c
Pochodna sumy (różnicy) funkcji:
)
(
)
(
)
)
(
)
(
(
x
g
x
f
x
g
x
f
Pochodna iloczynu funkcji:
)
(
)
(
)
(
)
(
)
)
(
)
(
(
x
g
x
f
x
g
x
f
x
g
x
f
Pochodna ilorazu funkcji:
)
(
)
(
)
(
)
(
)
(
)
(
)
(
2
)
(
x
g
x
g
x
f
x
g
x
f
x
g
x
f
Pochodna funkcji złożonej (oblicza się ją jako iloczyn pochodnej funkcji zewnętrznej i
pochodnej funkcji wewnętrznej):
)
(
)
(
))
(
(
)
(
x
g
g
f
x
g
f
czyli jeśli
))
(
(
x
g
f
y
, to
dx
dg
dg
df
dx
df
Zadanie 1.
Wyznaczyć pochodne następujących funkcji:
a)
x
y
,
2
x
y
,
4
5x
y
,
x
y
1
,
3
2
x
y
,
x
y
,
3
5
x
y
,
x
y
1
,
4
3
2
x
y
.
b)
x
x
y
cos
2
3
,
x
x
e
y
x
sin
3
ln
2
5
,
2
1
arctan
x
x
y
.
c)
x
x
xe
y
x
ln
,
x
x
y
sin
2
,
x
y
x
arctan
2
,
x
x
y
ln
,
1
2
1
x
x
y
,
2
3
1
2
x
x
y
,
1
x
x
y
.
d)
3
2
)
1
2
(
x
x
y
,
x
x
y
cos
,
)
4
3
ln(
x
y
,
x
e
x
y
3
2
,
x
xe
y
.
e)
Jak wyznaczamy pochodną funkcji typu:
)
(
))
(
(
x
g
x
f
y
? Wyznaczyć pochodną funkcji
x
x
y
cos
.
Zadanie 2.
Wyznaczyć równanie stycznej i normalnej do wykresu funkcji
a)
3
2
x
x
y
w punkcie
)
2
,
1
(
;
b)
x
y
1
w punkcie
)
,
2
(
2
1
P
.
Pochodna funkcji określonej parametrycznie.
Jeżeli funkcja
)
(x
f
określona jest parametrycznie równaniami
)
(
)
(
t
y
y
t
x
x
i istnieją pochodne
)
(t
y
i
0
)
(
t
x
, to
)
(
)
(
t
x
t
y
dx
dy
(można też zapisać
dt
dx
dt
dy
)
Na przykład
a) dla funkcji
1
5
3
1
3
3
5
3
t
t
y
t
t
x
mamy
3
3
2
t
dt
dx
,
2
4
15
15
t
t
dt
dy
, więc
2
5
)
1
(
3
)
1
(
15
3
3
15
15
2
2
2
2
2
4
t
t
t
t
t
t
t
dx
dy
.
b) dla funkcji
t
a
y
t
a
x
sin
cos
mamy
t
a
t
x
sin
)
(
,
t
a
t
y
cos
)
(
, więc
t
t
a
t
a
dx
dy
cot
sin
cos
.
Można podać też interpretację wektorową pochodnej dla
funkcji określonej parametrycznie.
Jeśli
)]
(
),
(
[
t
y
t
x
r
przedstawia wektor wodzący pewnej
krzywej płaskiej określonej odpowiednimi równaniami para-
metrycznymi, to
)]
(
),
(
[
t
y
t
x
dt
r
d
jest wektorem stycznym do
danej krzywej w określonym punkcie
))
(
),
(
(
0
0
t
y
t
x
.
Pochodne wyższych rzędów.
Pochodną rzędu II funkcji
)
(x
f
y
będziemy oznaczać symbolem
y
(lub
)
(x
f
czy też
2
2
dx
y
d
).
Analogicznie będziemy oznaczać pochodne rzędu wyższego niż II.
Przykłady:
a) Jeśli
4
5
2
3
x
x
x
y
, to
1
10
3
2
x
x
y
,
10
6
x
y
,
6
y
,
0
...
)
5
(
)
4
(
y
y
.
b) Jeśli
x
y
ln
, to
x
y
1
,
2
1
x
y
,
3
2
x
y
,
4
)
4
(
6
x
y
,…,
n
n
n
x
n
y
)!
1
(
)
1
(
1
)
(
.
Różniczka funkcji
Niech funkcja
)
(x
f
ma pochodną właściwą w punkcie
0
x
.
Różniczką funkcji w punkcie
0
x
nazywamy funkcję df zmiennej
0
x
x
x
określoną
wzorem
x
x
f
x
df
)
(
)
(
0
Geometrycznie różniczka funkcji przedstawia część
liniową przyrostu funkcji.
W ogólnym przypadku dla funkcji
)
(x
f
y
zapisujemy:
dx
x
f
dy
)
(
.
Przykład. Obliczyć różniczkę
dy
funkcji
3
)
(
x
x
f
y
w punkcie
1
0
x
odpowiadającą
przyrostowi
01
,
0
x
. Obliczyć też przyrost
y
tej funkcji przy podanych warunkach.
a) różniczka:
ponieważ
2
3
)
(
x
x
f
, więc
03
,
0
)
01
,
0
(
1
3
)
1
(
2
x
f
dy
;
b) przyrost funkcji:
ponieważ
)
(
)
(
0
0
x
f
x
x
f
y
, więc
029701
,
0
1
970299
,
0
)
1
(
)
99
,
0
(
3
3
y
.
Uwaga.
Dla małych przyrostów argumentu
x
można przyjąć, że
dy
y
, czyli
x
x
f
x
f
x
x
f
)
(
)
(
)
(
0
0
0
, skąd
x
x
f
x
f
x
x
f
)
(
)
(
)
(
0
0
0
,
co można wykorzystać do niektórych przybliżonych obliczeń.
Przykład. Obliczyć przybliżoną wartość potęgi:
4
)
01
,
2
(
.
Mamy tu przypadek funkcji potęgowej
4
)
(
x
x
f
y
, skąd
3
4
)
(
x
x
f
. Dalej zauważmy, że
2
0
x
,
01
,
0
x
, a więc
32
,
16
01
,
0
32
16
)
01
,
0
(
2
4
2
)
01
,
2
(
)
(
3
4
4
0
x
x
f
.
Przypomnijmy, że symbolem
)
,
(
0
x
S
oznaczamy pewne sąsiedztwo punktu
0
x o
promieniu
.
Twierdzenie de l’Hospitala.
Jeżeli funkcje
)
(
)
(
x
g
x
f
oraz
)
(
)
(
x
g
x
f
są określone w pewnym sąsiedztwie
)
,
(
0
x
S
i istnieje
granica
)
(
)
(
lim
0
x
g
x
f
x
x
(właściwa lub niewłaściwa) oraz
0
)
(
)
(
0
0
lim
lim
x
g
x
f
x
x
x
x
albo
)
(
)
(
0
0
lim
lim
x
g
x
f
x
x
x
x
(lub
), to istnieje
)
(
)
(
lim
0
x
g
x
f
x
x
, przy czym
)
(
)
(
lim
0
x
g
x
f
x
x
=
)
(
)
(
lim
0
x
g
x
f
x
x
.
Twierdzenie to jest prawdziwe również dla granic jednostronnych oraz granic w
nieskończoności.
Przykłady.
a)
x
x
x
arcsin
sin
lim
0
H
]
[
0
0
2
0
1
1
cos
lim
x
x
x
=
1
1
= 1.
b)
1
1
lim
3
0
x
x
x
e
e
H
]
[
0
0
x
x
x
e
e
3
3
lim
0
=
3
1
.
c)
x
x
x
ln
lim
0
H
]
[
x
x
x
1
1
lim
2
0
=
x
x
x
2
lim
0
=
2
lim
0
x
x
=
.
d)
)
1
sh
1
(
lim
0
x
x
x
]
[
x
x
x
x
x
sh
sh
lim
0
H
]
[
0
0
x
x
x
x
x
ch
sh
ch
1
lim
0
H
]
[
0
0
x
x
x
x
x
x
sh
ch
ch
sh
lim
0
=
2
0
= 0.
e)
x
x
x
ln
lim
H
]
[
1
1
lim
2
1
x
x
= 0.
Zadanie. Wyznaczyć
x
x
x
1
)
(
lim
.