Tomasz Kowalski

Wykłady z matematyki dla studentów kierunków ekonomicznych

Wykład 14

ZASTOSOWANIA RACHUNKU RÓŻNICZKOWEGO

FUNKCJI JEDNEJ ZMIENNEJ W EKONOMII

1. Funkcje w zagadnieniach ekonomicznych

Przykład 1. Przeprowadzić w zbiorze

)

;





 c

D

badanie funkcji Tőrnquista

b

x

c

x

ax

x

T







)

(

3

przyjmując, że a, b, c są pewnymi stałymi dodatnimi.
Rozwiązanie.

Ponieważ

0

)

(

lim

3













c

T

b

x

c

x

ax

c

x

,





























]

[

1

1

1

lim

lim

x

b

x

c

x

x

ax

b

x

c

x

ax

, to funkcja nie posiada

asymptoty poziomej, może jednak posiadać asymptotę ukośną prawostronną.

a

a

b

x

c

x

a

x

x

T

m

x

b

x

c

x

x

x





























1

1

lim

lim

)

(

lim

3

,



































b

x

c

b

ax

x

b

x

c

x

ax

mx

x

T

n

x

x

x

)

(

lim

]

[

lim

]

)

(

[

lim

3

)

(

1

)

(

lim

c

b

a

c

b

a

x

b

x

















.

Prosta jest asymptotą ukośną prawostronną.

)

(

c

b

a

ax

y







Obliczając pochodną funkcji dostajemy



























2

2

/

2

/

/

3

)

(

)

(

)

)(

2

(

)

(

)

(

))

(

(

b

x

acx

ax

b

x

ac

ax

b

x

acx

ax

b

x

c

x

ax

x

T

2

2

2

2

)

(

)

(

)

(

)

(

2

b

x

c

x

ab

bx

x

a

b

x

abc

abx

ax



















.

Ponieważ zarówno mianownik jak i licznik wyrażenia (który jest sumą wyrażeń dodatnich) są
w rozpatrywanym zbiorze dodatnie, to otrzymana pochodna jest dodatnia i tym samym

jest rosnąca

w przedziale

T

2

)

;





 c

D

.













/

2

2

//

3

)

)

(

)

(

)

(

(

))

(

(

b

x

c

x

ab

bx

x

a

x

T

4

2

4

2

2

)

(

)

)(

(

2

)

(

)

(

2

)

2

(

)

)(

2

2

(

b

x

bc

b

b

x

a

b

x

b

x

bc

bx

x

a

b

x

b

x

a

























.

Druga pochodna jest dodatnia w rozpatrywanym przedziale, zatem jest wypukła.

3

T

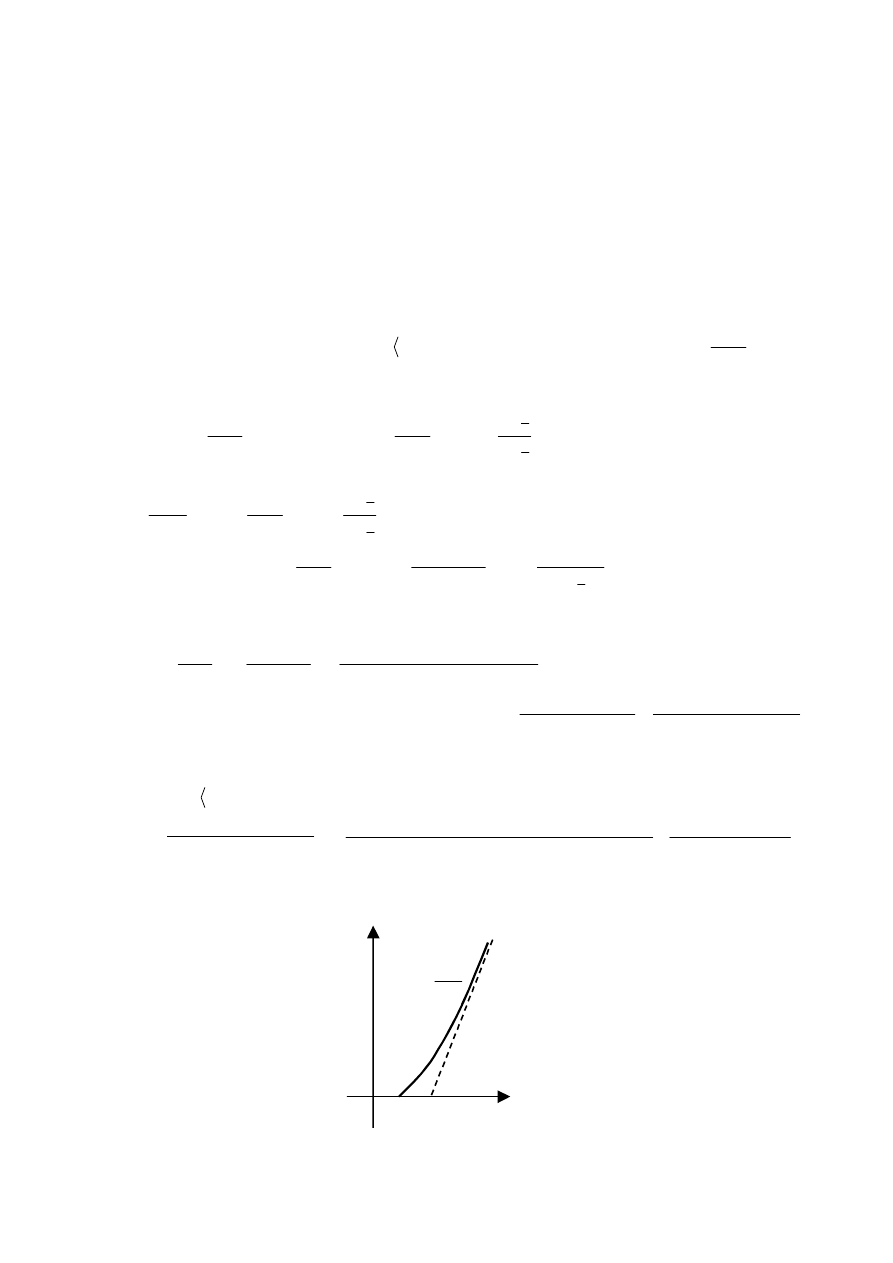
Wykres funkcji przedstawia rys.1.

Y

b

x

c

x

ax

x

T







)

(

3

c

b+c

X

Rys. 1.

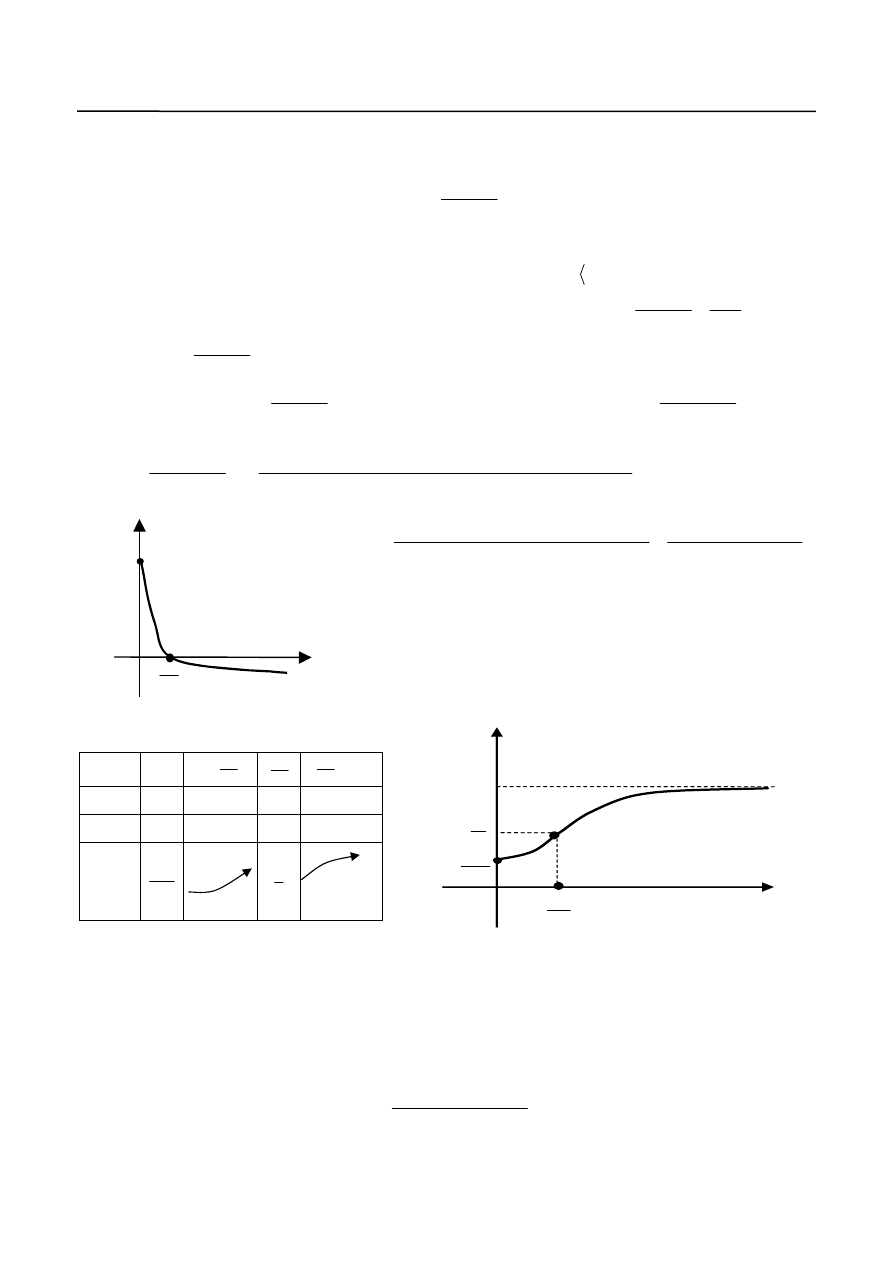
Wykład 14. Zastosowania rachunku różniczkowego w ekonomii

2

W badaniach ekonomicznych ważne znaczenie ma tzw. funkcja logistyczna opisująca popyt na nowo
wprowadzone na rynek dobro w zależności od czasu t, określona wzorem:

ct

be

a

t

f







1

)

(

,

gdzie a, c są stałymi dodatnimi,

.

1



b

Przykład 2. Przeprowadzić badanie funkcji logistycznej w zbiorze

)

;

0







D

.

Rozwiązanie. Obliczając granice na końcach przedziału dostajemy

b

a

be

a

t

f

ct

t

t



















1

1

lim

)

(

lim

0

0

oraz

a

be

a

t

f

ct

t

t

















1

lim

)

(

lim

. Oznacza to, że funkcja posiada asymptotę poziomą prawostronną

a

y

 .

Pochodna funkcji:































)

(

)

1

(

]

)

1

(

[

)

1

(

)

(

2

/

1

/

/

c

be

be

a

be

a

be

a

t

f

ct

ct

ct

ct

2

)

1

(

ct

ct

be

abce







.

Otrzymana pochodna jest dodatnia w zbiorze D, zatem f jest rosnąca i nie posiada ekstremów.











/

2

//

)

)

1

(

(

)

(

ct

ct

be

abce

t

f































4

2

)

1

(

)

(

)

1

(

2

)

1

)(

(

ct

ct

ct

ct

ct

ct

be

c

be

be

abce

be

c

abce

3

2

4

2

)

1

(

)

1

(

)

1

(

]

2

1

)[

1

(

ct

ct

ct

ct

ct

ct

ct

ct

be

be

e

abc

be

be

be

be

e

abc





































X

b

1

Y

lnb

c

+

_ _ _

h t

be

ct

( )







1

.

Znak drugiej pochodnej jest w rozpatrywanym zbiorze identyczny
jak znak funkcji

, której wykres przedstawiony jest

na rys.2.

1

)

(





ct

be

t

h

Rys. 2.

Y

X

a

a
2

a

b

1



l n b

c

Układamy tabelkę zmienności:

t

0

)

;

0

(

ln

c

b

)

;

(

ln





c

b

/

f

+

+

//

f

+ 0 –

f

a

b

1



a
2

p.p.

c

b

ln

a

Wykres funkcji przedstawiony jest na rys.3.

Rys. 3.

2. Zastosowanie rachunku różniczkowego w ekonomii

Niech

będzie funkcją oznaczającą zależność kosztów produkcji od wielkości produkcji

x.

Załóżmy, że

. Wówczas iloraz

)

(

x

K

0



x

0

,

0



x

x

x

K

x

x

K









)

(

)

(

0

0

oznacza koszt przeciętny wytworzenia

jednostki produktu przy zwiększeniu produkcji o

x

 jednostek, przyjmując jako wyjściową produkcję

jednostek.

0

x

Wykład 14. Zastosowania rachunku różniczkowego w ekonomii

3

Jeżeli jest funkcją różniczkowalną, to

)

(

x

K

)

(

)

(

)

(

lim

0

/

0

0

0

x

K

x

x

K

x

x

K

x















nazywamy kosztem

krańcowym

.

Ze wzoru przybliżonego

przyjmując

x

x

K

x

K

x

x

K













)

(

)

(

)

(

0

/

0

0

1



x

otrzymujemy:

)

(

)

(

)

1

(

0

/

0

0

x

K

x

K

x

K







.

Z ostatniego wzoru wynika, że koszt krańcowy jest w przybliżeniu równy kosztowi, jaki należy ponieść, aby
zwiększyć produkcję o jednostkę.

Przykład 3.

Całkowity koszt w złotych wyprodukowania w małej fabryce w ciągu tygodnia

x artykułów

dany jest wzorem:

2

100

1

5

50

)

(

x

x

x

K







. Obliczyć

)

25

(

)

26

(

K

K



i porównać z

.

)

25

(

/

K

Rozwiązanie.

Mamy tutaj

49

,

4

)

25

100

1

25

5

50

(

26

100

1

26

5

50

)

25

(

)

26

(

2

2



















 K

K

.

Ponieważ

x

x

K

50

1

5

)

(

/





, to

5

,

4

2

1

5

)

25

(

/







K

. Jak widać obie wielkości różnią się nieznacznie.

W podobny sposób można interpretować pochodną w przypadku, gdy funkcja opisuje zależność dwóch

innych wielkości ekonomicznych: popyt-cena, wynagrodzenie -wydajność, utarg-ilość.

Niech

będzie funkcją oznaczającą zależność kosztów produkcji od wielkości produkcji x.

Załóżmy, że

. Wówczas iloraz

)

(

x

f

0

x

0

,

0







x

0

0

0

:

)

(

)

(

x

x

x

x

f

x

x

f











nazywamy elastycznością

przeciętną funkcji f w przedziale

x

x





0

;

i oznaczamy sym

x

0

bolem

E.

Jeżeli jest funkcją różniczkowalną, to

)

(

x

f

)

(

)

(

:

)

(

)

(

lim

0

0

0

/

0

0

0

0

x

f

x

x

f

x

x

x

x

f

x

x

f

x



















nazywamy

elastycznością funkcji f w punkcie

i oznaczamy przez

.

0

x

)

(

0

x

E

Elastyczność funkcji w punkcie określa przybliżoną procentową zmianę wartości funkcji odpowiadającą

zmianie argumentu o 1%.

Przykład 4.

Obliczyć elastyczność funkcji

6

3

)

(



 x

x

f

.

Rozwiązanie. Z określenia elastyczności mamy

2

3

6

3

)

(

)

(

)

(

/













x

x

x

x

x

f

x

f

x

x

E

.

Tak więc dla

elastyczność

2 . Oznacza to, że jeżeli wartość x wzrośnie o 1%, to wartość

funkcji wzrośnie o około 2%. (Tutaj wzrost argumentu funkcji o 1%, tzn. od wartości 4 do wartości 4,04
pociąga za sobą wzrost wartości funkcji od 6 do 6,12 czyli dokładnie o 2%).

4



x

)

4

(



E