Granica i ci

ą

gło

ść

funkcji zespolonych

1/5

380 Granica i ci

ą

gło

ść

funkcji zespolonych

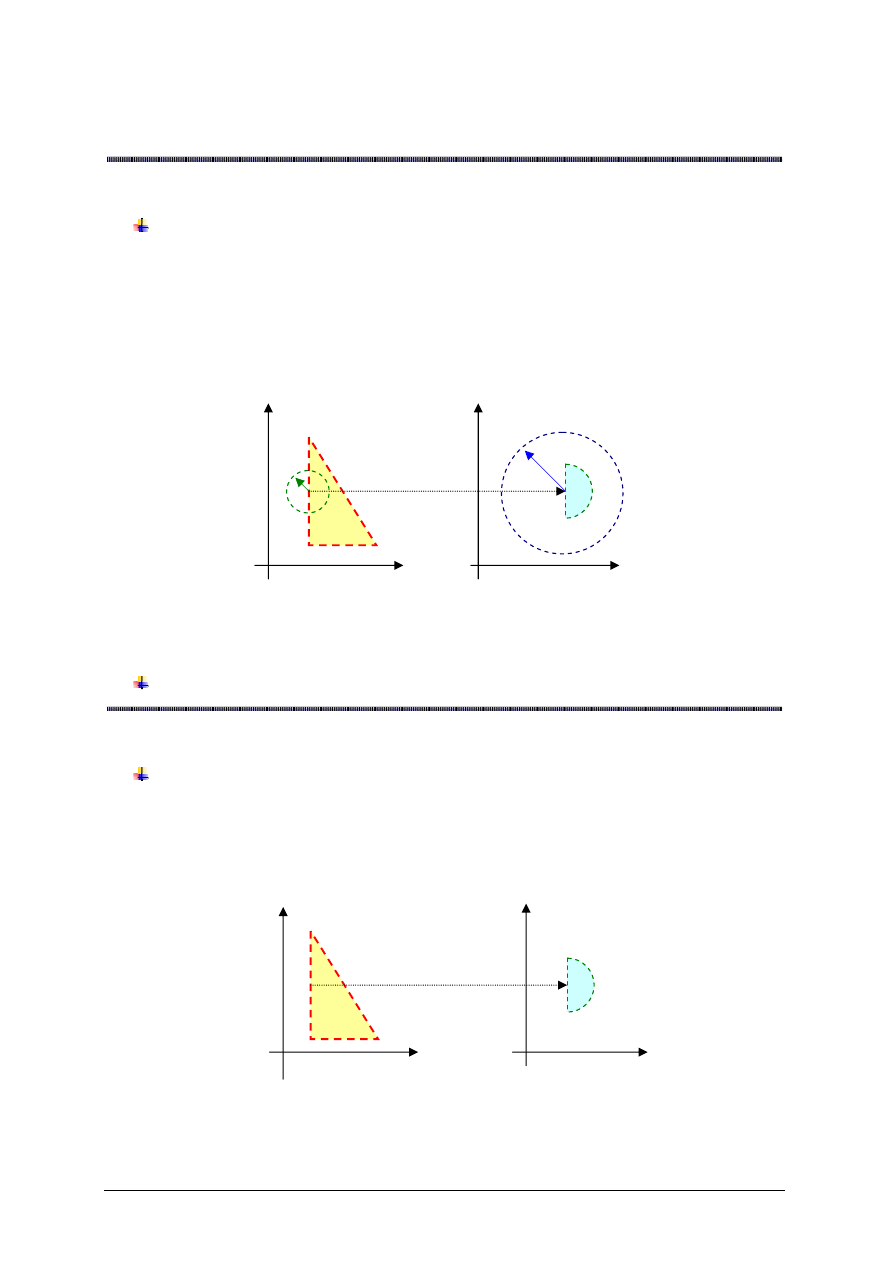
Definicja Cauchy’ego granicy funkcji

Niech

C

⊂

Ω

i niech

C

f

→

Ω

:

. Mówimy,

ż

e element

C

b

∈

jest

granic

ą

funkcji

f

w punkcie

d

a

Ω

∈

(a wi

ę

c w punkcie skupienia zbioru

Ω

), gdy

ε

δ

δ

ε

<

−

⇒

<

−

Ω

∈

∀

>

∃

>

∀

|

)

(

|

|

|

}

{

\

0

0

b

z

f

a

z

a

z

.

Inaczej:

)

,

(

)

(

}

{

\

)

,

(

ε

δ

b

K

z

f

a

a

K

z

∈

⇒

Ω

∩

∈

Inaczej:

)

,

(

})

{

\

)

,

(

(

ε

δ

b

K

a

a

K

f

⊂

Ω

∩

.

Piszemy

b

x

f

a

z

=

→

)

(

lim

.

Uwaga

Funkcja

f

nie

musi by

ć

okre

ś

lona w punkcie

a

.

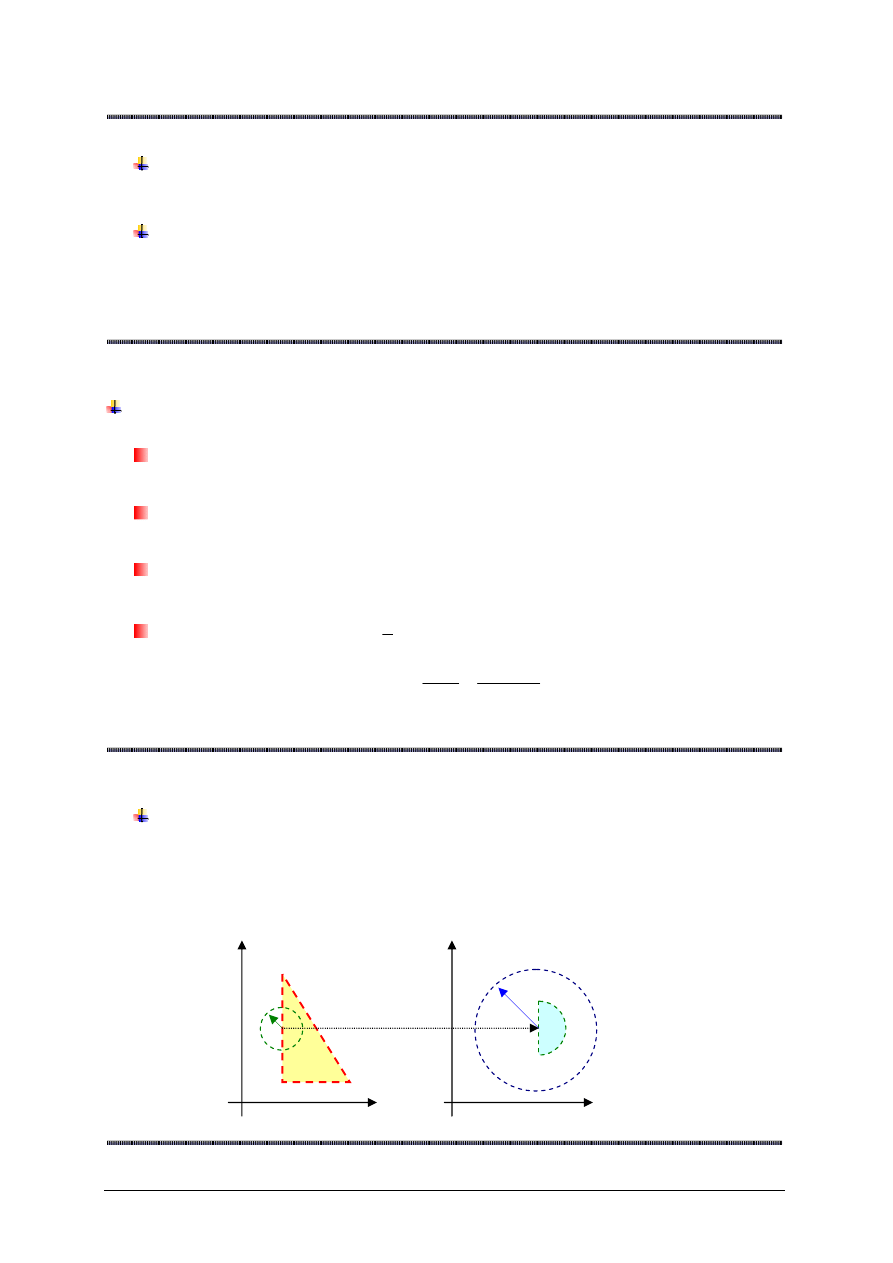
Definicja Heinego granicy funkcji

Niech

C

⊂

Ω

i niech

C

f

→

Ω

:

. Mówimy,

ż

e element

C

b

∈

jest

granic

ą

funkcji

f

w punkcie

d

a

Ω

∈

(a wi

ę

c w punkcie skupienia zbioru

Ω

), gdy dla

dowolnego ci

ą

gu

)

(

n

z

elementów zbioru

}

{

\ a

Ω

b

z

f

a

z

n

n

→

⇒

→

)

(

.

C

C

Ω

f

a

b

)

(

n

x

f

•

•

•

•

•

n

x

•

C

C

Ω

f

a

b

ε

δ

Granica i ci

ą

gło

ść

funkcji zespolonych

2/5

Twierdzenie o równowa

ż

no

ś

ci

Definicje Cauchy’ego i Heinego granicy funkcji s

ą

równowa

ż

ne.

Twierdzenie o jednoznaczno

ś

ci granicy

Niech

C

⊂

Ω

i niech

C

f

→

Ω

:

. Je

ż

eli funkcja

f

ma granic

ę

w punkcie

d

a

Ω

∈

, to jest ona tylko jedna.

Dowody analogiczne, jak w przypadku funkcji rzeczywistych.

Twierdzenie o działaniach arytmetycznych na granicach

Niech

C

⊂

Ω

i niech

C

g

f

→

Ω

:

,

posiadaj

ą

sko

ń

czone granice w punkcie

d

a

Ω

∈

.

Funkcja

g

f

+

posiada granic

ę

w punkcie

a

oraz

)

(

lim

)

(

lim

))

(

)

(

(

lim

z

g

z

f

z

g

z

f

a

z

a

z

a

z

→

→

→

+

=

+

.

Funkcja

g

f

−

posiada granic

ę

w punkcie

a

oraz

)

(

lim

)

(

lim

))

(

)

(

(

lim

z

g

z

f

z

g

z

f

a

z

a

z

a

z

→

→

→

−

=

−

.

Funkcja

g

f

⋅

posiada granic

ę

w punkcie

a

oraz

)

(

lim

)

(

lim

))

(

)

(

(

lim

z

g

z

f

z

g

z

f

a

z

a

z

a

z

→

→

→

⋅

=

⋅

.

Je

ś

li

0

)

(

lim

≠

→

z

g

a

z

to funkcja

g

f

posiada granic

ę

w punkcie

a

oraz

)

(

lim

)

(

lim

)

(

)

(

lim

z

g

z

f

z

g

z

f

a

z

a

z

a

z

→

→

→

=

.

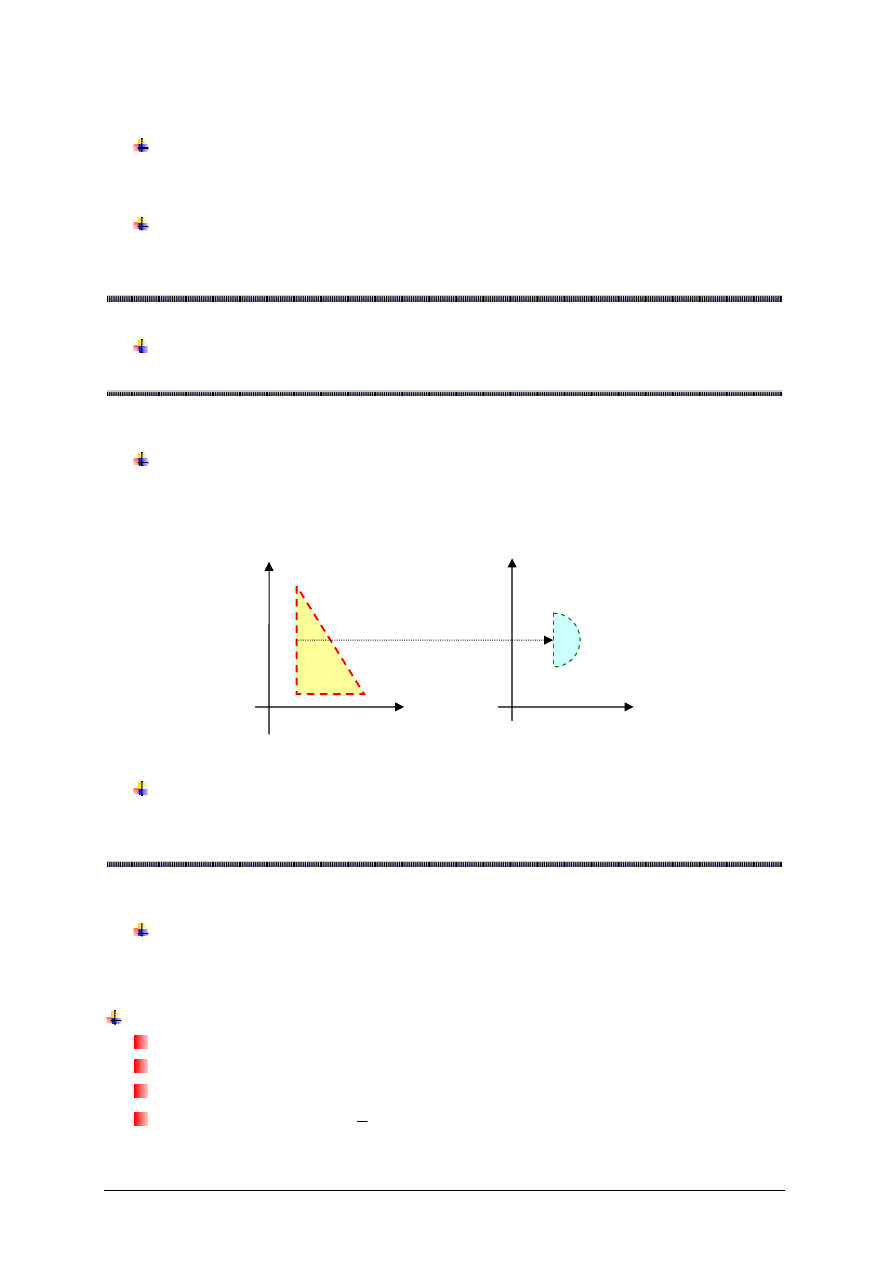
Definicja Cauchy’ego ci

ą

gło

ś

ci funkcji w punkcie

Niech

C

⊂

Ω

i niech

C

f

→

Ω

:

. Mówimy,

ż

e funkcja

f

jest

ci

ą

gła w punkcie

Ω

∈

a

, gdy

ε

δ

δ

ε

<

−

⇒

<

−

Ω

∈

∀

>

∃

>

∀

|

)

(

)

(

|

|

|

0

0

a

f

z

f

a

z

z

.

Inaczej:

)

),

(

(

)

(

)

,

(

ε

δ

a

f

K

x

f

a

K

x

∈

⇒

Ω

∩

∈

Inaczej:

)

),

(

(

)

)

,

(

(

ε

δ

a

f

K

a

K

f

⊂

Ω

∩

.

C

C

Ω

f

a

)

(a

f

ε

δ

Granica i ci

ą

gło

ść

funkcji zespolonych

3/5

Uwaga

Funkcja

f

jest zawsze ci

ą

gła w punktach izolowanych swojej dziedziny.

Rzeczywi

ś

cie, je

ś

li

d

a

Ω

Ω

∈

\

, to

∅

=

Ω

∩

}

{

\

)

,

(

a

a

K

δ

dla pewnego

0

>

δ

, a

st

ą

d

)

),

(

(

)

(

})

({

)

)

,

(

(

ε

δ

a

f

K

a

f

a

f

a

K

f

∈

=

=

Ω

∩

dla wszystkich

0

>

ε

.

Funkcja

f

jest ci

ą

gła w punkcie

d

a

Ω

∩

Ω

∈

skupienia swojej dziedziny wtedy

i tylko wtedy, gdy posiada granic

ę

w punkcie

a

oraz

).

(

)

(

lim

a

f

z

f

a

z

=

→

Definicja ci

ą

gło

ś

ci funkcji na zbiorze

Niech

C

⊂

Ω

i niech

C

f

→

Ω

:

. Mówimy,

ż

e funkcja

f

jest

ci

ą

gła na zbiorze

Ω

, gdy jest ona ci

ą

gła w ka

ż

dym punkcie

a

zbioru

Ω

.

Definicja Heinego ci

ą

gło

ś

ci funkcji w punkcie

Niech

C

⊂

Ω

i niech

C

f

→

Ω

:

. Mówimy,

ż

e funkcja

f

jest

ci

ą

gła w punkcie

Ω

∈

a

, gdy dla dowolnego ci

ą

gu

)

(

n

z

elementów zbioru

Ω

)

(

)

(

a

f

z

f

a

z

n

n

→

⇒

→

.

Uwaga

Je

ż

eli

f

jest ci

ą

gła na zbiorze

Ω

, to dla dowolnego ci

ą

gu

)

(

n

z

elementów

zbioru

Ω

zbie

ż

nego do elementu zbioru

Ω

mamy

)

(lim

)

(

lim

n

n

z

f

z

f

=

.

Twierdzenie

W przestrzeniach metrycznych definicje Cauchy’ego i Heinego ci

ą

gło

ś

ci

funkcji s

ą

równowa

ż

ne.

Twierdzenie o sumie, ró

ż

nicy, iloczynie i ilorazie funkcji ci

ą

głych

Niech

C

⊂

Ω

i niech funkcje

C

g

f

→

Ω

:

,

b

ę

d

ą

ci

ą

głe w punkcie

Ω

∈

a

.

Funkcja

g

f

+

jest ci

ą

gła w punkcie

a

.

Funkcja

g

f

−

jest ci

ą

gła w punkcie

a

.

Funkcja

g

f

⋅

jest ci

ą

gła w punkcie

a

.

Je

ś

li

0

)

(

≠

a

g

to funkcja

g

f

jest ci

ą

gła w punkcie

a

.

C

C

Ω

f

a

)

(

a

f

)

(

n

z

f

•

•

•

•

•

n

x

•

Granica i ci

ą

gło

ść

funkcji zespolonych

4/5

)

(

Ω

f

Ω

C

f

g

h

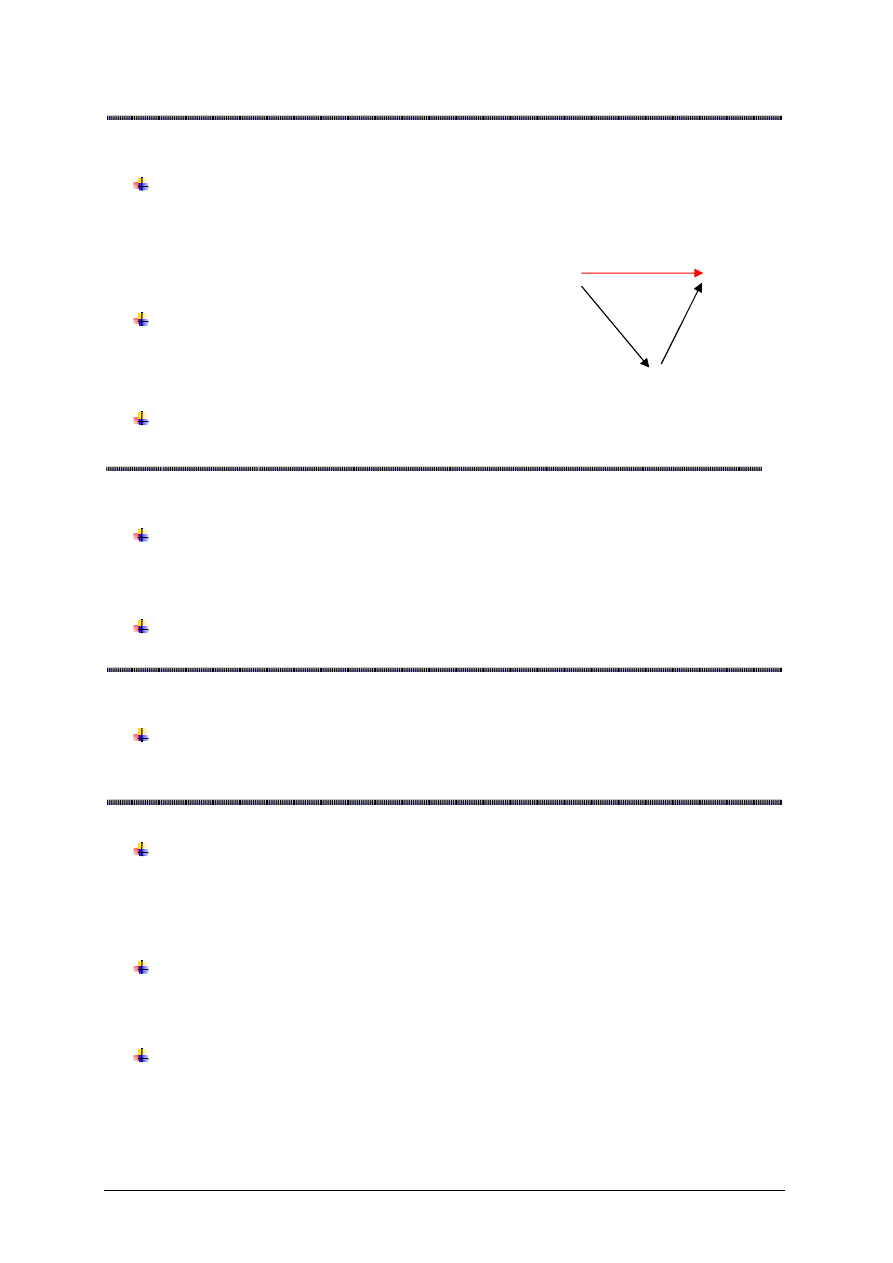
Twierdzenie o ci

ą

gło

ś

ci zło

ż

enia

Niech

C

⊂

Ω

,

C

f

→

Ω

:

i

C

f

g

→

Ω

)

(

:

. Je

ż

eli funkcja

f

jest ci

ą

gła w punkcie

Ω

∈

a

i funkcja

g

jest ci

ą

gła w punkcie

)

(

a

f

, to funkcja

C

h

→

Ω

:

,

f

g

h

o

=

jest ci

ą

gła w punkcie

Ω

∈

a

.

Dowód

Je

ż

eli

a

z

n

→

, to

)

(

)

(

a

f

z

f

n

→

, a st

ą

d

)

(

))

(

(

))

(

(

)

(

a

h

a

f

g

z

f

g

z

h

n

n

=

→

=

.

Wniosek

Je

ż

eli funkcja

f

jest ci

ą

gła na

Ω

i funkcja

g

jest ci

ą

gła na

)

(

Ω

f

, to funkcja

C

h

→

Ω

:

,

f

g

h

o

=

jest ci

ą

gła na

Ω

.

Twierdzenie o obrazie zbioru spójnego

Niech

C

⊂

Ω

i niech

C

f

→

Ω

:

b

ę

dzie funkcj

ą

ci

ą

gł

ą

na

Ω

. Je

ż

eli

Ω

⊂

A

jest

zbiorem spójnym w

Ω

, to zbiór

)

(

Ω

f

jest zbiorem spójnym w

C

.

Uwaga

Mówi

ą

c mniej formalnym j

ę

zykiem: „Funkcja ci

ą

gła nie rozrywa zbioru

spójnego na kilka kawałków”.

Twierdzenie o obrazie zbioru zwartego

Niech

C

⊂

Ω

i niech

C

f

→

Ω

:

b

ę

dzie funkcj

ą

ci

ą

gł

ą

na

Ω

. Je

ż

eli

Ω

⊂

A

jest

zbiorem zwartym w

Ω

, to zbiór

)

(

Ω

f

jest zbiorem zwartym w

C

.

Definicja funkcji jednostajnie ci

ą

głej

Niech

C

⊂

Ω

i niech

C

f

→

Ω

:

b

ę

dzie funkcj

ą

ci

ą

gł

ą

na

Ω

. Mówimy,

ż

e

funkcja

f

jest

jednostajnie ci

ą

gła na zbiorze

Ω

, gdy

ε

δ

δ

ε

<

−

⇒

<

−

Ω

∈

∀

>

∃

>

∀

|

)

(

)

(

|

|

|

,

0

0

2

1

2

1

2

1

x

f

x

f

x

x

x

x

.

Uwaga

Liczba

δ

zale

ż

y tylko od liczby

ε

, a wi

ę

c nie zale

ż

y od

ż

adnego punktu

zbioru

Ω

.

Wniosek

Ka

ż

da funkcja jednostajnie ci

ą

gła na zbiorze

Ω

jest równie

ż

ci

ą

gła na

Ω

.

Granica i ci

ą

gło

ść

funkcji zespolonych

5/5

Twierdzenie Cantora

Niech

C

⊂

Ω

i niech

C

f

→

Ω

:

b

ę

dzie funkcj

ą

ci

ą

gł

ą

na

Ω

. Je

ż

eli

Ω

⊂

A

jest

zbiorem zwartym w

Ω

, to NWSR:

f

jest funkcj

ą

ci

ą

gł

ą

na

Ω

,

f

jest funkcj

ą

jednostajnie ci

ą

gł

ą

na

Ω

.

Funkcje zdefiniowane na zb. zwartym

ci

ą

głe = jednostajnie ci

ą

głe

Funkcje

ci

ą

głe

jednostajnie ci

ą

głe