13/10/2014

1

METODY STATYSTYCZNE 2014

materiały do W1-2

Joanna Rotnicka

1

Etap I: METODA REPREZENTACYJNA  próba

Etap II: STATYSTYKA OPISOWA

Etap III: WNIOSKOWANIE STATYSTYCZNE

Techniki statystyki opisowej:

1. Opis tabelaryczny

2. Graficzna prezentacja wyników

3. Wyznaczanie miar rozkładu

Etapy analizy statystycznej:

Szereg rozdzielczy przedziałowy

1. Grupowanie danych w klasy/przedziały

Rozstęp – długość najmniejszego przedziału, w którym znajdują się
wszystkie wartości próbki losowej:

R = x

max

– x

min

k



5 log n

k = 1 + 3,322 log n

k = ¾ √n

k = √n

Ilość klas k oblicza się ze wzorów:

gdzie: n – liczba obserwacji (danych)

6 – 8

7 – 10
9 – 12

11 – 17
16 – 25

30 – 60

60 – 100

100 – 200
200 – 500

500 – 1500

K – liczba klas

n – liczebnosc populacji

6 – 8

7 – 10
9 – 12

11 – 17
16 – 25

30 – 60

60 – 100

100 – 200
200 – 500

500 – 1500

k – liczba klas

n – liczebność próby

Przy dobieraniu ilości klas standardowo
można posłużyć się także tabelką:

STATYSTYKA OPISOWA:

1. opis tabelaryczny

2. Rozpiętość przedziałów i sposób określania granic

Jeżeli: R – rozstęp danej próby,

k – ilość klas

to długość klasy b: b ≈ R / k i b ≥ R / k

Próbę musimy tak pokryć przedziałami, aby 1 dana należała tylko
do jednej klasy!!! Czyli:

[x

min

, a] (a, b] (b, c] … (z, x

max

]

przedziały 1-stronnie zamknięte (…]

przedział 2-stronnie zamknięty […]

a dla zmiennej skokowej np. 4-6, 7-9, 10-12, ...

3. Liczebność klas – zliczanie, ile obserwacji wpada do każdej z klas

Jeżeli i – nr klasy

n

i

– liczebność i-tej klasy

k – ilość klas

to: n

1

+ n

2

+ ... n

K

= n (n – liczebność próby:



n

i

= n )

Pary liczb (

i

; n

i

) gdzie: i = 1, 2, …, K

i

- środek i-tej klasy

n

i

– liczebność i-tej klasy

nazywamy

szeregiem rozdzielczym przedziałowym

Dla prostoty wszystkie
elementy danej klasy
utożsamia się z jej
środkiem

i

STATYSTYKA OPISOWA:

2. graficzna prezentacja wyników

6

Dane prezentowane w formie:

 HISTOGRAMU



 WIELOBOKU LICZEBNOŚCI

 KRZYWEJ LICZEBNOŚCI

wykreślane bezpośrednio na
podstawie

szeregu rozdzielczego

HISTOGRAM

– wykres słupkowy, gdzie na osi:

dla szeregu rozdzielczego

przedziałowego

• odciętych (X)  środki i końce klas
• rzędnych (Y)  liczebność klas (n

i

), tzw.

częstość

13/10/2014

2

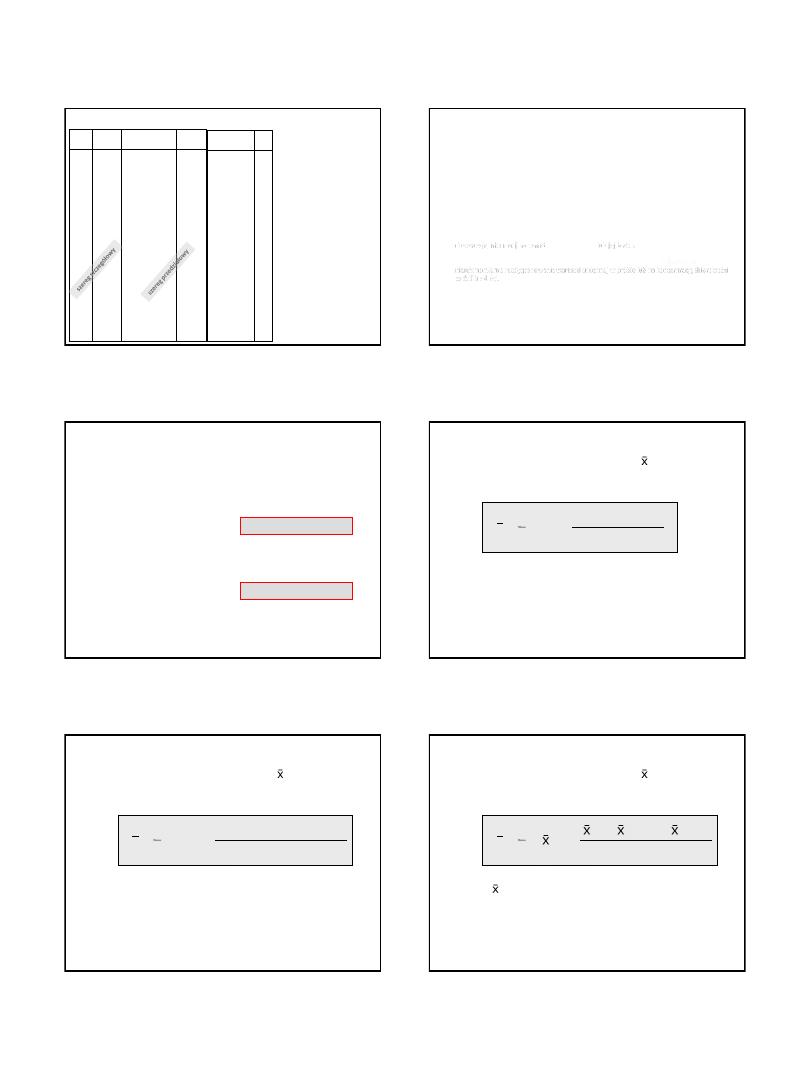
dane
[mm]

klasy

n

i

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

22,47

24,01

24,87

25,15

25,18

25,19

25,27

25,57

25,78

25,97

26,02

26,57

26,83

28,00

28,08

28,45

28,59

28,90

28,95

29,11

29,12

30,17

30,59

30,92

31,93

32,87

33,34

34,42

34,81

36,50

[21

– 23)

[23

– 25)

[25

– 27)

[27

– 29)

[29

– 31)

[31

– 33)

[33

– 35)

[35

– 37]

1

2

10

6

5

2

3

1

Różnie dobrane
przedziały

klasy

(inny podział)

n

i

[22

– 24)

[24

– 26)

[26

– 28)

[28

– 30)

[30

– 32)

[32

– 34)

[34

– 36)

[36

– 38]

1

9

3

8

4

2

2

1

Przykład: opady w stacji meteorologicznej X w 30-leciu

7

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu częstości

1. Miary tendencji centralnej (średnie, moda, mediana, kwantyle) –

służą do

określania wartości zmiennej opisanej przez rozkład, wokół której skupiają się pozostałe wartości
zmiennej.

2. Miary zróżnicowania (wariancja, odchylenie standardowe, … ) –

określają, w jakim

stopniu poszczególne wartości jednostek próby są rozproszone wokół wartości centralnej (średniej)

3. Miary asymetrii (trzeci moment centralny, współczynniki asymetrii, skośności) –

dostarczają informacji na temat symetrii rozkładu lub jej braku.

4. Miary koncentracji (czwarty moment centralny, kurtoza)

– wskazują na

nierównomierne rozdysponowanie wartości zmiennej w próbie lub na koncentrację zbiorowości
wokół średniej.

8

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

1. MIARY TENDENCJI CENTRALNEJ

Do najczęściej stosowanych miar należą:
 średnie klasyczne

- arytmetyczna
- harmoniczna
- geometryczna
- kwadratowa

 średnie pozycyjne

- mediana
- moda
- kwantyl

Miary klasyczne

Miary pozycyjne

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

1. M

IARY

K

LASYCZNE

:

średnia arytmetyczna (wartość przeciętna)

n

x

1

+ x

2

+ … + x

n

=

gdzie: x

i

– kolejne dane z próby

n – liczebność populacji

Dla szeregu szczegółowego 

średnia arytmet. nieważona

x

n

x

i

i

n

=

=



1

1

10

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

n

=

gdzie: x

i

– kolejne dane z próby

n

i

– liczebność x

i

p – ilość wariantów zmiennej skokowej X

Dla szeregu punktowego 

średnia arytmetyczna ważona

x

n

x n

i

i

i

p

=

=



1

1

x

1

n

1

+ x

2

n

2

+ … + x

p

n

p

11

1. M

IARY

K

LASYCZNE

:

średnia arytmetyczna (wartość przeciętna)

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

n

=

gdzie:

i

– środek i-tej klasy:

[dln granica + grn granica] / 2

n

i

– liczebność i-tej klasy

k – ilość klas

Dla szeregu przedziałowego 

średnia arytmet. ważona

x

n

n

i

i

i

k

=

=



1

1

1

n

1

+

2

n

2

+ … +

k

n

k

12

1. M

IARY

K

LASYCZNE

:

średnia arytmetyczna (wartość przeciętna)

13/10/2014

3

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

1. M

IARY

K

LASYCZNE

:

średnia arytmetyczna

 Na wartość silny wpływ wywierają wartości ekstremalne

(skrajne)  średniej nie powinno się stosować przy szeregach
asymetrycznych, bo jej wartość będzie zaniżona lub zawyżona.



obliczana jest wyłącznie dla przedziałów zamkniętych – przedział

można zamknąć pod warunkiem, że n

i



5% z N; domknięcie

następuje zazwyczaj szerokością przedziału poprzedzającego.

Jeżeli przedziału nie można domknąć  stosuje się miary
pozycyjne.

UWAGA!!

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

1. M

IARY

K

LASYCZNE

:

średnia harmoniczna

h

n

=

gdzie: x

i

– kolejne dane z próby

n – liczebność próby

Dla szeregu szczegółowego

x

h

n

x

i

i

n

=

=



1

1

1

-1

x

1

x

2

… x

n

1 1

1

+ + +

Założenie: 1/x

i

≠ 0

∑ 1/x

i

≠ 0

14

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

1. M

IARY

K

LASYCZNE

:

średnia harmoniczna

h

=

gdzie:

i

– środek i-tej klasy

n

i

– liczebność i-tej klasy

k – ilość klas

Dla szeregu przedziałowego

x

h

n

i

i

k

=

=



1

1

n

i

-1

n

1

2

…

k

n

1

n

2

n

k

+

+

+

Założenie: 1/

i

≠ 0

∑ 1/

i

≠ 0

15

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

1. M

IARY

K

LASYCZNE

:

średnia geometryczna

g

Stosowana przy badaniu średniego tempa zmian zjawisk, gdy

wielkości opisywane są dynamicznie 

PRZYKŁAD

.

Dla szeregu szczegółowego

Założenie: x

i

≥ 0

g

=

x

1

x

2

… x

n

n

gdzie: x

i

– kolejne dane z próby

n – liczebność próby

16

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

1. M

IARY

K

LASYCZNE

:

średnia geometryczna

g

Stosowana przy badaniu średniego tempa zmian zjawisk, gdy

wielkości opisywane są dynamicznie 

PRZYKŁAD

.

Dla szeregu przedziałowego

Założenie: x

i

≥ 0

g

=

1

2

…

k

n

gdzie:

i

– środek i-tej klasy

n

i

– liczebność i-tej klasy

k – ilość klas

n

1

n

2

n

k

17

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

1. M

IARY

C

ENTRALNE:

moda (Mo)

(wartość / klasa modalna, dominanta)

Ta wartość zmiennej, która w danym rozkładzie empirycznym występuje
najczęściej (o ile w ogóle istnieje), ponadto:

Mo ≠ x

min

i Mo ≠ x

max

Wyznaczanie mody ma sens jedynie wówczas, gdy

:

 rozkład częstości jest jednomodalny
 asymetria rozkładu jest umiarkowana
 przedział, w którym występuje Mo oraz dwa sąsiadujące

z nim przedziały mają jednakowe rozpiętości

13/10/2014

4

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

1. M

IARY

C

ENTRALNE:

mediana (Me)

(wartość środkowa)

Dzieli próbę na dwie równe części: połowa danych ma wartości



Me,

a połowa ma wartości > Me

Kiedy stosujemy?

 gdy nie można obliczyć , czyli w szeregach z

otwartymi przedziałami

 przy szeregach asymetrycznych (nie reaguje na wartości

skrajne!!)

 gdy nie można obliczyć Mo, czyli gdy szereg z dominantą

i szeregi z nim sąsiadujące mają różną rozpiętość

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

1. M

IARY

P

OZYCYJNE

:

mediana (Me)

Dla szeregu szczegółowego i punktowego:

Niech {x

1



x

2



…



x

n

} – próba uporządkowana rosnąco

x

(n+1)/2

gdy n – nieparzyste (liczba środkowa)

[x

n/2

+ x

(n+1)/2

] / 2 gdy n – parzyste (średnia arytmetyczna

dwóch liczb środkowych)

Me =

20

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

1. M

IARY

P

OZYCYJNE

:

mediana (Me)

Dla szeregu przedziałowego:

gdzie: x

Me

– wartość zmiennej dla dolnej granicy przedziału z Me

n

Me

– liczebność klasy z Me



n

Me-1

– skumulowana liczebność klas do klasy z Me

d

Me

– rozpiętość przedziału z Me

50%, czyli ½ obserwacji

n /2 - ∑ n

Me-1

Me = x

Me

+

* d

Me

n

Me

21

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

1. M

IARY

P

OZYCYJNE

:

kwantyle

Wartości zmiennej z danej próby, które dzielą tę próbę na dwie
określone pod względem liczby jednostek części. Części te pozostają
względem siebie w określonych proporcjach.

Rodzaje kwantyli:



kwartyle (Q

i

)

– dzielą próbę na 4 części



decyle (D

i

)

– dzielą próbę na 10 części



percentyle (P

i

)

– dzielą próbę na 100 części

22

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

1. M

IARY

P

OZYCYJNE

:

kwantyle

Kwartyle (Q

i

)

Q

1

– 25% zmiennych ma wartości



Q

1

,

a 75% ma wartości > Q

1

Q

2

– 50% zmiennych ma wartości



Q

2

,

a 50% ma wartości > Q

2

Q

3

– 75% zmiennych ma wartości



Q

3

,

a 25% ma wartości > Q

3

Q

2

= Me

 szeregi, z których wyznacza się kwantyle muszą być

uporządkowane rosnąco lub malejąco

 stosowane wtedy, gdy nie można obliczyć ani ani Mo

kwartyl dolny

kwartyl górny

23

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

1. M

IARY

P

OZYCYJNE

:

kwantyle

Kwartyle (Q

i

)

n/4 -

∑ n

Q1

– 1

Q

1

= x

Q1

+

* d

Q1

n

Q1

2n/4 -

∑ n

Me

– 1

Q

2

=

x

Me

+

* d

Me

= Me

n

Me

3n/4 -

∑ n

Q3

– 1

Q

3

= x

Q3

+

* d

Q3

n

Q3

25%, czyli ¼ obserwacji

75%, czyli ¾ obserwacji

gdzie: x

Q1

– wartość zmiennej dla dolnej granicy przedziału z Q

1

n

Q1

– liczebność klasy z Q

1



n

Q1-1

– skumulowana liczebność klasy do klasy z Q

1

d

Q1

– rozpiętość przedziału z Q

1

24

13/10/2014

5

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

1. M

IARY

P

OZYCYJNE

:

kwantyle

Kwartyle (Q

i

)

n/4 -

∑ n

Q1

– 1

Q

1

= x

Q1

+

* d

Q1

n

Q1

2n/4 -

∑ n

Me

– 1

Q

2

=

x

Me

+

* d

Me

= Me

n

Me

3n/4 -

∑ n

Q3

– 1

Q

3

= x

Q3

+

* d

Q3

n

Q3

25%, czyli ¼ obserwacji

75%, czyli ¾ obserwacji

25

1. M

IARY

P

OZYCYJNE

:

kwantyle

Decyle (D

i

)

np. D

1

–

10% zmiennych ma wartości



D

1

,

a 90% ma wartości > D

1

D

5

= Q

2

= Me

Percentyle (P

i

)

np. P

17

–

17% zmiennych ma wartości



P

17

,

a 83% ma wartości > P

17

P

10

= D

1

P

50

= D

5

= Q

2

= Me

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

26

1. M

IARY

P

OZYCYJNE

:

kwantyle

Percentyle (P

i

):

i-ty (i = 1–99) percentyl obliczamy ze wzoru:

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

n * i/100 -

∑ n

Pi

– 1

P

i

= x

Pi

+

* d

Pi

n

Pi

gdzie: x

Pi

– wartość zmiennej dla dolnej granicy przedziału z P

i

n

Pi

– liczebność klasy z P

i



n

Pi-1

– skumulowana liczebność klas do klasy z P

i

d

Pi

– rozpiętość przedziału z P

i

i%, czyli i/100 obserwacji

27

1. M

IARY

C

ENTRALNE:

graficzne wyznaczanie Me, Q

i

, P

i

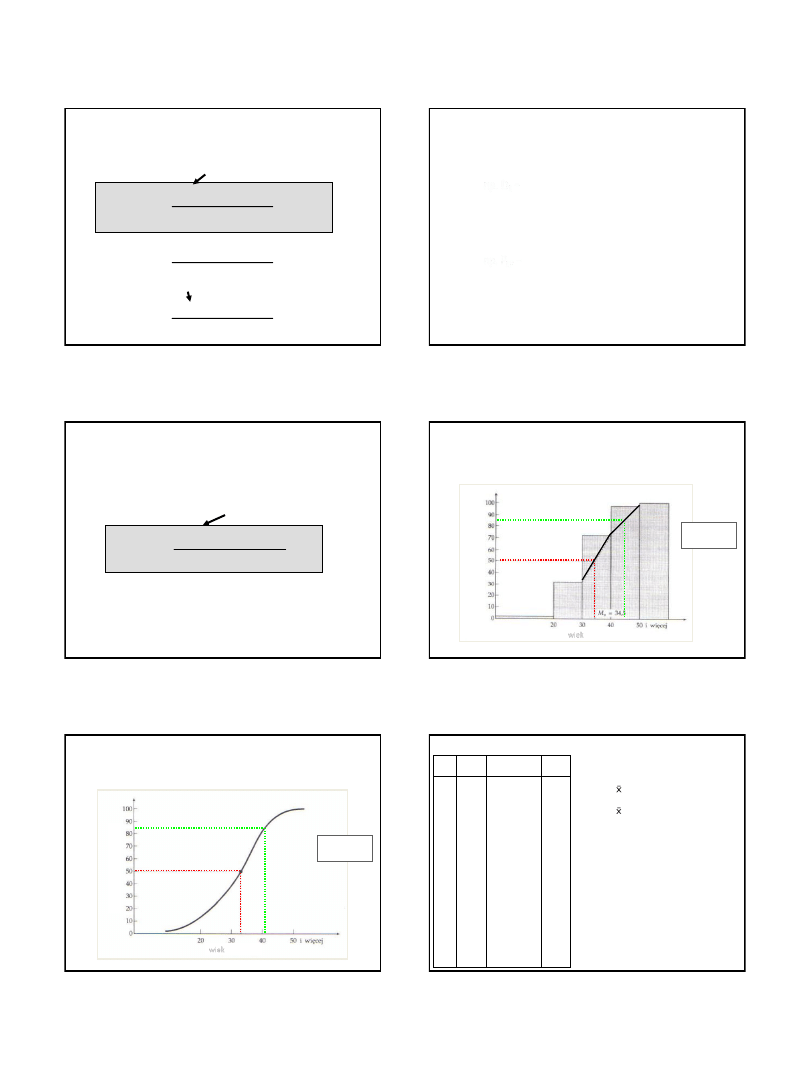
STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

wiek

lic

zebno

ść

(

%

)

na podstawie histogramu kumulacyjnego

Me = Q

2

P

85

45

35

Me = 34,5

(policzone)

1. M

IARY

C

ENTRALNE:

graficzne wyznaczanie Me, Q

i

, P

i

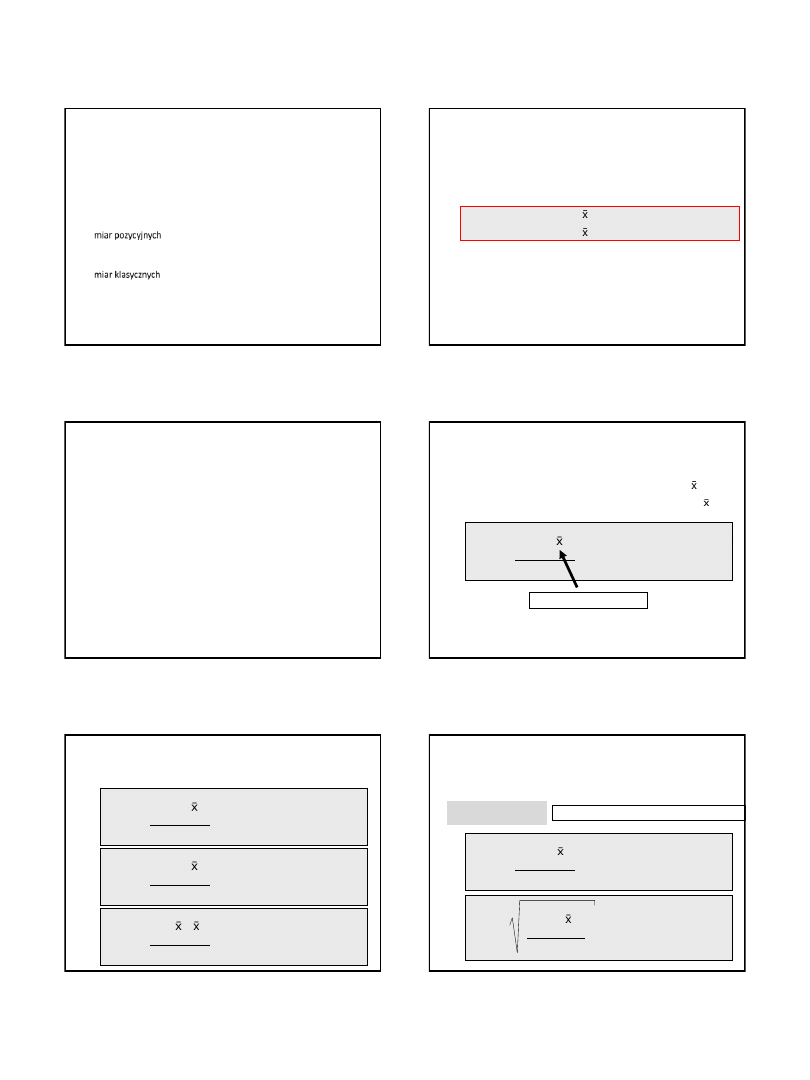
STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

wiek

lic

zebno

ść

(

%

)

na podstawie krzywej kumulacyjnej

Me = Q

2

P

85

41

33

Me = 34,5

(policzone)

dane
[mm]

klasy

n

i

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

22,47

24,01

24,87

25,15

25,18

25,19

25,27

25,57

25,78

25,97

26,02

26,57

26,83

28,00

28,08

28,45

28,59

28,90

28,95

29,11

29,12

30,17

30,59

30,92

31,93

32,87

33,34

34,42

34,81

36,50

[21

– 23)

[23

– 25)

[25

– 27)

[27

– 29)

[29

– 31)

[31

– 33)

[33

– 35)

[35

– 37]

1

2

10

6

5

2

3

1

Przykład: opady w stacji X w 30-leciu

Średnia arytmetyczna:
- dla szeregu szczegółowego

= 853,63/30 = 28,45

-dla szeregu przedziałowego

= 28,33

Klasa modalna ???

Mediana (Me)
-dla szeregu szczegółowego

Me = (28,45 + 28,08)/2 = 28,27

-dla szeregu przedziałowego

Me = obliczenia = 27,67

Kwartyle – dla szeregu przedziałowego:

Q

1

= obliczenia = 25,9

Q

2

= ??? = 27,67

Q

3

= ??? = 30,4

ZADANIE – cz. 1

30

13/10/2014

6

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

2. MIARY ZRÓŻNICOWANIA

Stopień zmienności mniejszy



większe znaczenie danej miary!

Im mniejsze są różnice, tym bardziej jednorodna jest badana zbiorowość i
tym mniejsza próba potrzebna jest do uzyskania miarodajnego wyniku.

Siłę zróżnicowania oceniamy za pomocą:


miar pozycyjnych

- rozstęp (obszar zmienności)
- odchylenie międzykwarytlowe (ćwiartkowe)



miar klasycznych

- odchylenie przeciętne
- wariancja
- odchylenie standardowe

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

R = x

max

– x

min

2. M

IARY

Z

RÓŻNICOWANIA:

rozstęp R

(obszar zmienności)

Niech Z

1

= {1, 3, 5, 7, 9}



= 25/5 = 5 i

R = 1



9

Niech Z

2

= {3, 4, 5, 6, 7}



= 25/5 = 5 i

R = 3



7

Daje pewne wyobrażenie o rozproszeniu, ale nie jest zbyt
precyzyjną miarą rozrzutu !!!

Dla rozkładu normalnego Q

1

i Q

3

oddalone są od Me o ten sam

dystans:

Q = (Q

3

– Q

1

) / 2  tzw. odchylenie ćwiartkowe

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

Stosowane, gdy dane przedstawione są sumarycznie przez Me.

2. M

IARY

Z

RÓŻNICOWANIA:

odchylenie ćwiartkowe Q

Q

3

– Q

1

 rozstęp międzykwartylowy

33

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

Stosowane, gdy dane przedstawione są sumarycznie przez .

Jest to przeciętna różnica pomiędzy poszczególnymi danymi a .

2. M

IARY

Z

RÓŻNICOWANIA:

odchylenie przeciętne OP

OP =

Ix

i

-

I

i

n

=



1

n

dla szeregu szczegółowego

wartość bezwzględna!!!

34

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

2. M

IARY

Z

RÓŻNICOWANIA:

odchylenie przeciętne OP

OP =

I

x

i

-

I

i

n

=



1

n

dla szeregu szczegółowego

OP =

I

x

i

-

I n

i

i

p

=



1

n

dla szeregu punktowego

OP =

I

i

-

I n

i

i

k

=



1

n

dla szeregu przedziałowego

gdzie: p – ilość wariantów

zmiennej skokowej

gdzie: k – ilość klas

35

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

S

2

=

(x

i

-

)

2

i

n

=



1

n

dla szeregu szczegółowego

S =

(x

i

-

)

2

i

n

=



1

n

σ

2

i σ – dla zbiorowości

S

2

i S – dla próby

2. M

IARY

Z

RÓŻNICOWANIA:

wariancja

σ

2

/ S

2

odchylenie standardowe

σ / S

Wariancja = moment centralny 2-ego rzędu

36

13/10/2014

7

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

S

2

=

(x

i

-

)

2

* n

i

i

p

=



1

n

dla szeregu punktowego

S =

(x

i

-

)

2

* n

i

i

p

=



1

n

σ

2

i σ – dla zbiorowości

S

2

i S – dla próby

2. M

IARY

Z

RÓŻNICOWANIA:

wariancja

σ

2

/ S

2

odchylenie standardowe

σ / S

37

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

S

2

=

(

i

-

)

2

* n

i

i

k

=



1

n

dla szeregu przedziałowego

S =

(

i

-

)

2

* n

i

i

k

=



1

n

gdzie:

i

– środek i-tej klasy

σ

2

i σ – dla zbiorowości

S

2

i S – dla próby

2. M

IARY

Z

RÓŻNICOWANIA:

wariancja

σ

2

/ S

2

odchylenie standardowe

σ / S

38

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

Mianem σ

2

/ S

2

jest kwadrat jednostki fizycznej, w jakiej badana jest

mierzona cecha.

Im zbiorowość bardziej zróżnicowana tym wyższa jest wartość σ

2

.

Typowy obszar zmienności – w tym obszarze mieści się ok. 2/3
wszystkich jednostek badanej populacji statystycznej, gdyż jest on
zawarty w granicach dwóch S:

- S < x

typ

< + S

2. M

IARY

Z

RÓŻNICOWANIA:

wariancja

σ

2

/ S

2

odchylenie standardowe

σ / S

39

2. M

IARY

Z

RÓŻNICOWANIA:

współczynnik zmienności V

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

odchylenie ćwiartkowe Q

Me

* 100% = wskaźnik zmienności

odchylenie przeciętne OP

* 100% = zmienność względna

odchylenie standardowe S

* 100% = współczynnik zmienności

Przy dokonywaniu porównań fakt, że na wartość

odchylenia wpływa wielkość średniej jest niewygodny.

m

ia

ry

kl

a

sy

cz

n

e

m

ia

ra

p

o

zy

cy

jn

a

40

dane
[mm]

klasy

n

i

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

22,47

24,01

24,87

25,15

25,18

25,19

25,27

25,57

25,78

25,97

26,02

26,57

26,83

28,00

28,08

28,45

28,59

28,90

28,95

29,11

29,12

30,17

30,59

30,92

31,93

32,87

33,34

34,42

34,81

36,50

[21

– 23)

[23

– 25)

[25

– 27)

[27

– 29)

[29

– 31)

[31

– 33)

[33

– 35)

[35

– 37]

1

2

10

6

5

2

3

1

Przykład: opady w stacji X w 30-leciu

Odchylenie ćwiartkowe:

Q = obliczenia = 2,25

Odchylenie przeciętne (OP)
-dla szeregu szczegółowego

OP = obliczenia = 2,79

-dla szeregu przedziałowego

OP = obliczenia =2,69

Wariancja ( S

2

) i odchylenie standardowe (S)

-dla szeregu szczegółowego

S

2

= obliczenia = 11,86

S = obliczenia = 3,45

-dla szeregu przedziałowego

S

2

= obliczenia = 10,96

S = obliczenia = 3,31

Ponadto dla szeregu przedziałowego:

Wskaźnik zmienności = 8,13%
Zmienność względna = 9,50%
Współczynnik zmienności V = 11,68%

ZADANIE – cz. 2

41

3. M

IARY

A

SYMETRII:

trzeci moment centralny

M

3

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

Suma trzecich potęg odchyleń wartości zmiennej od wartości
podzielona przez n. Miara jest mianowana.

M

3

=

(x

i

-

)

3

i

n

=



1

n

dla szeregu szczegółowego

M

3

=

(x

i

-

)

3

* n

i

i

p

=



1

n

dla szeregu punktowego

gdzie: p – ilość wariantów

zmiennej skokowej

42

13/10/2014

8

3. M

IARY

A

SYMETRII:

trzeci moment centralny

M

3

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

Moment centralny 3-ego rzędu to suma trzecich potęg odchyleń
wartości zmiennej od wartości podzielona przez n.

M

3

=

(

i

-

)

3

* n

i

i

k

=



1

n

dla szeregu przedziałowego

M

3

= 0 

rozkład symetryczny

M

3

< 0 

asymetria lewostronna

M

3

> 0 

asymetria prawostronna

43

3. M

IARY

A

SYMETRII:

współczynnik asymetrii A

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

Jest to standaryzowany M

3

(miara niemianowana).

Ma tę przewagę nad M

3

, że pozwala porównywać różne rozkłady.

A = 0 

rozkład symetryczny

A < 0 

asymetria lewostronna

A > 0 

asymetria prawostronna

M

3

S

3

A =

44

3. M

IARY

A

SYMETRII:

współczynnik skośności

A

S - klasyczny

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

Miara niemianowana i unormowana, co umożliwia porównywanie
różnych rozkładów.

Zazwyczaj -1



A

S



+1

Tylko przy bardzo silnej asymetrii As >



1

gdzie: – przeciętna

Mo – moda (dominanta)
S – odchylenie standardowe

A

S

= 0 

rozkład symetryczny

A

S

< 0 

asymetria lewostronna

A

S

> 0 

asymetria prawostronna

A

S

=

- Mo
S

45

3. M

IARY

A

SYMETRII:

współczynnik skośności

A

Q - pozycyjny

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

Miara pozycyjna, uzupełniająca. Stosowana wtedy, gdy nie można
obliczyć i / lub Mo.

gdzie: Me – przeciętna

Q

1

– dolny kwartyl

Q

3

– górny kwartyl

Q – odchylenie ćwiartkowe

A

Q

= =

(Q

3

– Me) – (Me – Q

1

)

(Q

3

– Me) + (Me – Q

1

)

Q

3

+ Q

1

– 2 Me

2Q

46

4. M

IARY

K

ONCENTRACJI:

czwarty moment centralny M

4

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

W celu określenia koncentracji obserwacji wokół średniej należy badany
rozkład porównywać z innym, w którym skupienie elementów będzie
typowe  czyli z rozkładem normalnym.

Miara jest mianowana.

M

4

=

(

i

-

)

4

* n

i

i

k

=



1

n

dla szeregu przedziałowego

47

4. M

IARY

K

ONCENTRACJI:

kurtoza (wsp. spłaszczenia) K

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

Jest to standaryzowany M

4

. Miara niemianowana będąca miarą spłaszczenia rozkładu.

M

4

S

4

K =

M

4

S

4

eK = - 3

lub

K = 3 

rozkład symetryczny – normalny

K < 3 

rozkład platykurtyczny (spłaszczony)

K > 3 

rozkład leptokurtyczny (szpiczasty)

eK = 0



rozkład symetryczny – normalny

eK < 0



rozkład platykurtyczny (spłaszczony)

eK > 0



rozkład leptokurtyczny (szpiczasty)

cz

ęs

toś

ć

przedziały

48

wsp. ekscesu

13/10/2014

9

3. M

IARY

A

SYMETRII:

wskaźnik asymetrii (skośności)

W

S

STATYSTYKA OPISOWA:

3. wyznaczanie miar rozkładu

Miara bezwzględna asymetrii; nie można go używać do porównywania
asymetrii w zbiorowościach, w których wartość zmiennej wyrażona jest
w różnych jednostkach miary.

W

S

= - Mo

gdzie: – przeciętna

Mo – moda (dominanta)

W

S

= 0 

rozkład symetryczny

W

S

< 0 

asymetria lewostronna

W

S

> 0 

asymetria prawostronna

49

dane
[mm]

klasy

n

i

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

22,47

24,01

24,87

25,15

25,18

25,19

25,27

25,57

25,78

25,97

26,02

26,57

26,83

28,00

28,08

28,45

28,59

28,90

28,95

29,11

29,12

30,17

30,59

30,92

31,93

32,87

33,34

34,42

34,81

36,50

[21

– 23)

[23

– 25)

[25

– 27)

[27

– 29)

[29

– 31)

[31

– 33)

[33

– 35)

[35

– 37]

1

2

10

6

5

2

3

1

Przykład: opady w stacji X w 30-leciu

Trzeci moment centralny:

dla szeregu [21,23)

- M

3

= 19,25

- A = M

3

/ S

3

= 19,25 / 3,31

3

= 0,53 (S = 3,31)

- As = (28,33 – 26,00) / 3,31 = 0,70

Czwarty moment centralny
- M

3

= obliczenia = ???

- K = obliczenia = ???

ZADANIE – cz. 3

50