www.zadania-projekty.pl
1
1.1. Przedmiot ekonomii matematycznej
Przedmiotem ekonomii matematycznej są modeli realnych ekonomicznych
procesów.
Model to jest obiekt, który zastępuje oryginał i odwzorowuje najistotniejsze dla
danego badania cechy i właściwości oryginału.
Metoda ekonomii ekonomicznej to jest systemowa analiza ekonomiki jak
skomplikowanego dynamicznego układu. Ekonomia Matematyczna tworze modele
matematyczne w postaci założeń o powiązaniu zmiennych ekonomicznych. W skutek
różnorodności podmiotów gospodarczych i zmienności warunków, Ekonomia Matematyczna
dzieli się na szereg różnych modeli nie mających wartości uniwersalnej.
Główni podstawowe matematyczne modele mikro- i makroekonomii:
Modele zachowania konsumenta
Teoria produkcji
Modele rynku
Modele równowagi
Modele wzrostu gospodarczego
Modele cyklu koniunkturalnego
1.2. Modele zachowania konsumenta
Jednej z najistotniejszych pojęciem teorii ekonomicznej jest teoria konsumenta.
Głównym pytaniem tu jest ustalenie konsumpcji dla danych cen na dobra i dochodzie.
Konkretna decyzja o zakupach określonego koszyka dóbr matematycznie może być
pokazana jako wybór punktu w przestrzeni towarów. Niech
n
- jest ograniczona ilość dóbr,
a
n
n
R
x
x
x
x
)
,...,
,
(
2
1
koszyk określonych dóbr w przestrzeni
n
R
Przestrzenią dóbr nazywa się zbiór wszystkich możliwych dóbr z dodatnimi
współrzędnymi
0
:
x
x
X
X
.
W przestrzeni dóbr wprowadzimy normę
i
i
x
max
x
,
i odpowiednio metrykę (odległość pomiędzy elementami)
i
i
i
y
x
max
y
,
x
.
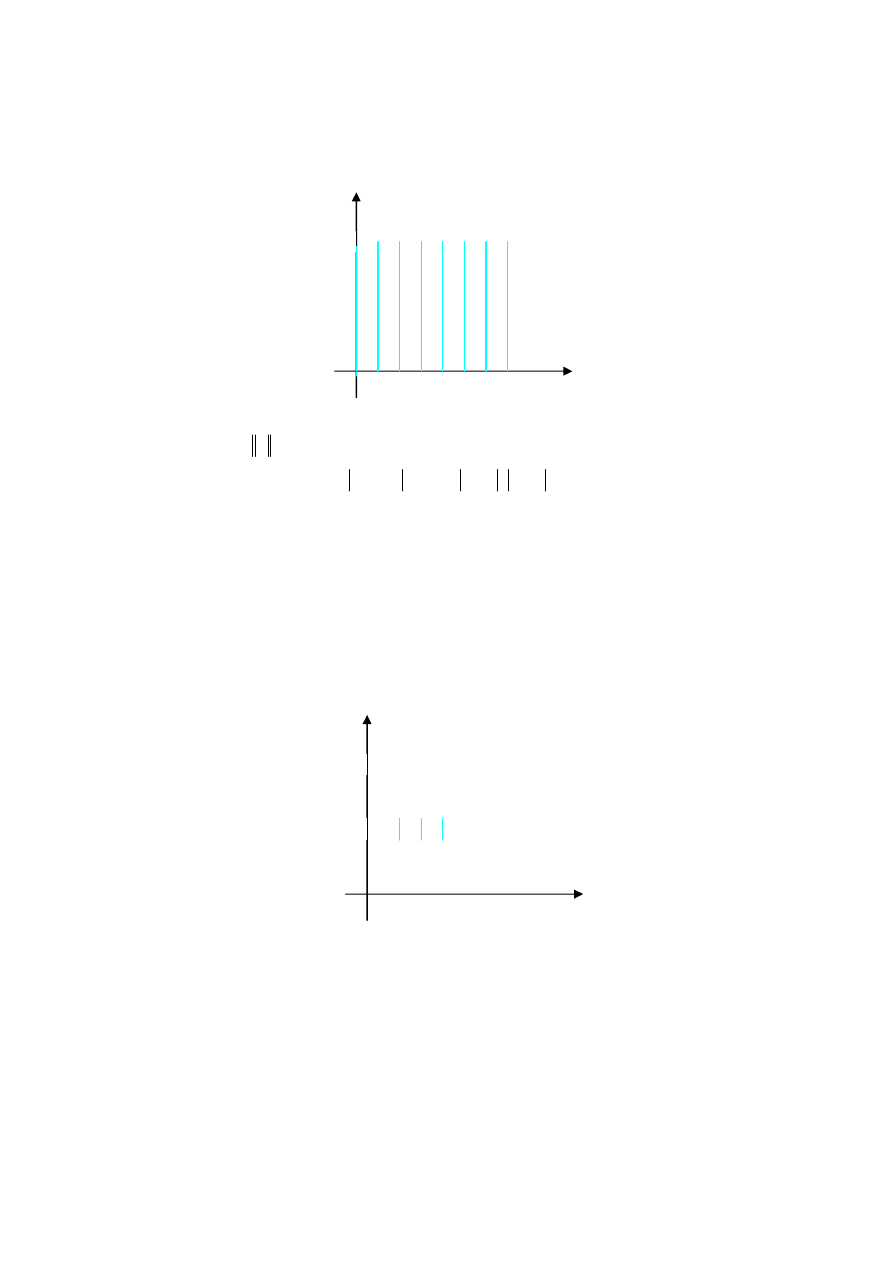
2
Przykład. 1.1 Narysować w przestrzeni dóbr wszystkie koszyki
20
x
,
7
x
|
x
;
x
x
2
1
2
1
, gdzie
1
x
są jajka,
2
x
męka. Obliczyć wielkość koszyka
5
,
7
i odległość pomiędzy koszykami
5
,
7
i
7
,
3
.
Rozwiązanie.
Wielkość koszyka:
7
5
,
7
max
x
i
.
Odległość:
4
7
5
;
3
7
max
y
x
max
7
,
3
;
5
,
7
i
i
i
i
.
Definicja 1.1. Zbiór
0
0
x
,
x
|
x
x
U
nazywa się
- otoczeniem.
Definicja 1.2. Zbiór
X
Y
nazywa się otwarty, jeżeli każdy element x zbioru Y
należy do niego razem z pewnym otoczeniem
0
x
U
.
Przykład. 1.2 Narysować w przestrzeni dóbr wszystkie koszyki należące do
otoczenia
10
;
3
U
2
z przykładu 1.1.
Rozwiązanie.
1
2
3
4
5
6
7
X
1
X
2
20
X
1
1
2
3
4
5
6
7
X
2
20
10
www.zadania-projekty.pl
3
Definicja 1.3. Punkt
A
a
nazywa się punktem brzegowym zboru A, gdy w
dowolnym otoczeniu tego punktu znajdują się punkty należące i punkty nie należące do
zbioru A.
Definicja 1.4. Zbiór
X
Y
nazywa się domknięty, jeżeli Y jest sumą niektórego
otwartego zbioru A i wszystkich brzegowych punktów A.
1.3. Ograniczenie budżetowe
Załóżmy, że możemy obserwować ceny wszystkich dóbr
n
n
R
p
p
p
P
)
,...,
,
(
2
1
,
oraz budżet konsumenta
m
. Wtedy ograniczenie budżetowe może być zapisane jako
m
x
p
x
p
x
p
n
n
...
2
2
1
1
Zbiór punktów
n
n
R
x
x
x
X
)
,...,
,
(
2
1
, który spełniają ten warunek nazywa się
zbiorem budżetowym lub zbiorem dopuszczalnych koszyków.
1.4. Własności zbioru budżetowego w
2
R
.
Definicja 1.5. Linią budżetu nazywamy zbiór koszyków
2
2
1
)
,
(
R
x
x
X
, który
spełniają warunek
m
x
p
x
p
2
2
1
1
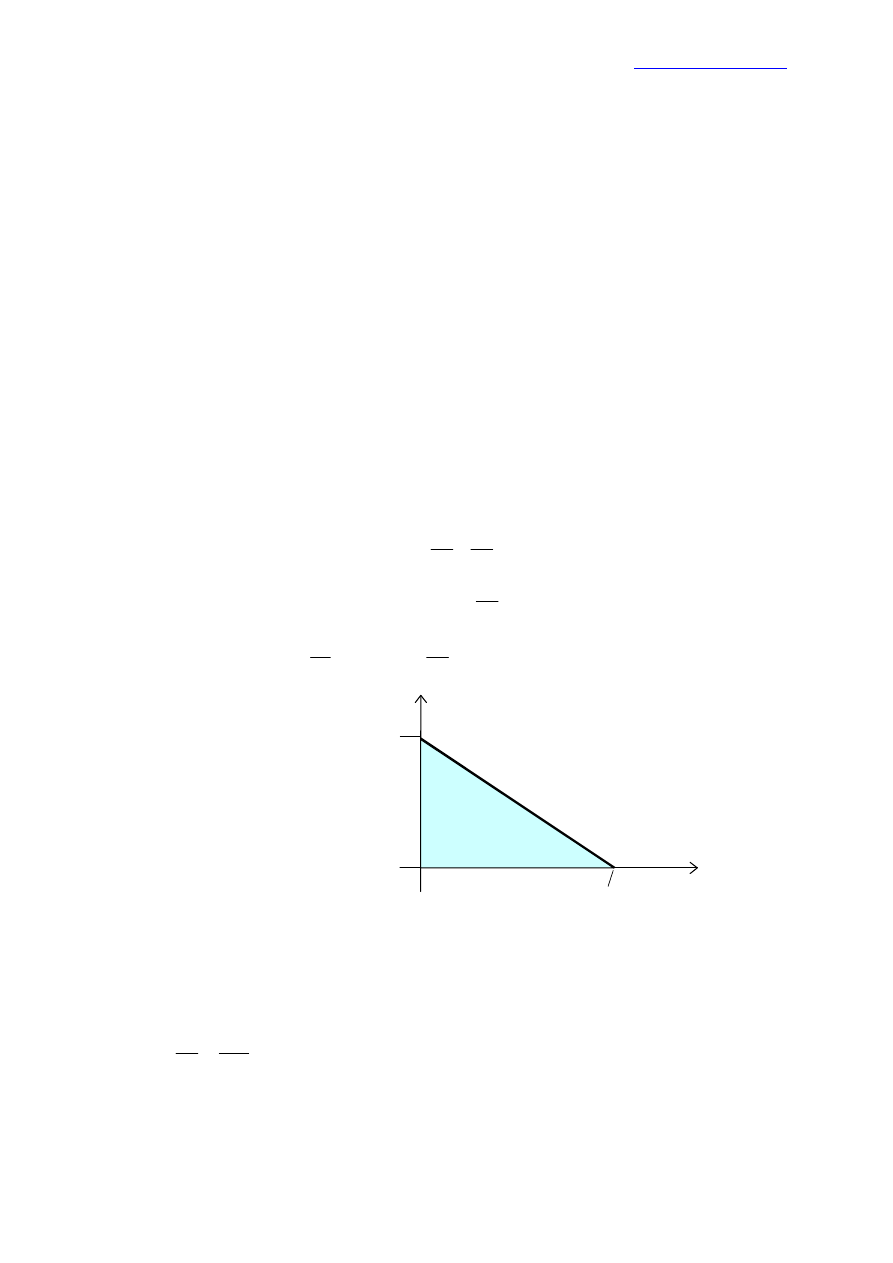
Równanie linię budżetu może być również zapisane w postaci
1
2
1
2
2
x
p
p
p
m
x
Jest to równanie prostej z nachyleniem
2
1
p
p
. Najprostszy sposób narysowania tej
linii – to połączyć punkty
0
,
1
p
m
oraz
2
,
0
p
m
.
Nachylenie linii budżetu ma jasną interpretacje ekonomiczną: mierzy ono stopę
według której konsument jest skłonny zamienić dobro 1 na dobro 2:
m
x
p
x
p
2
2
1
1
m
x
x
p
x
x
p
)
(
)
(
2
2
2
1
1
1
...
2
1
p
p
1
2
x
x
.
Występuje minus, ponieważ
2
1
, x
x
zawsze mają znaki przeciwne.
Eliminacja jednego parametru.
Linia budżetu
1
x
2
x
1
p
m
2
p
m
4
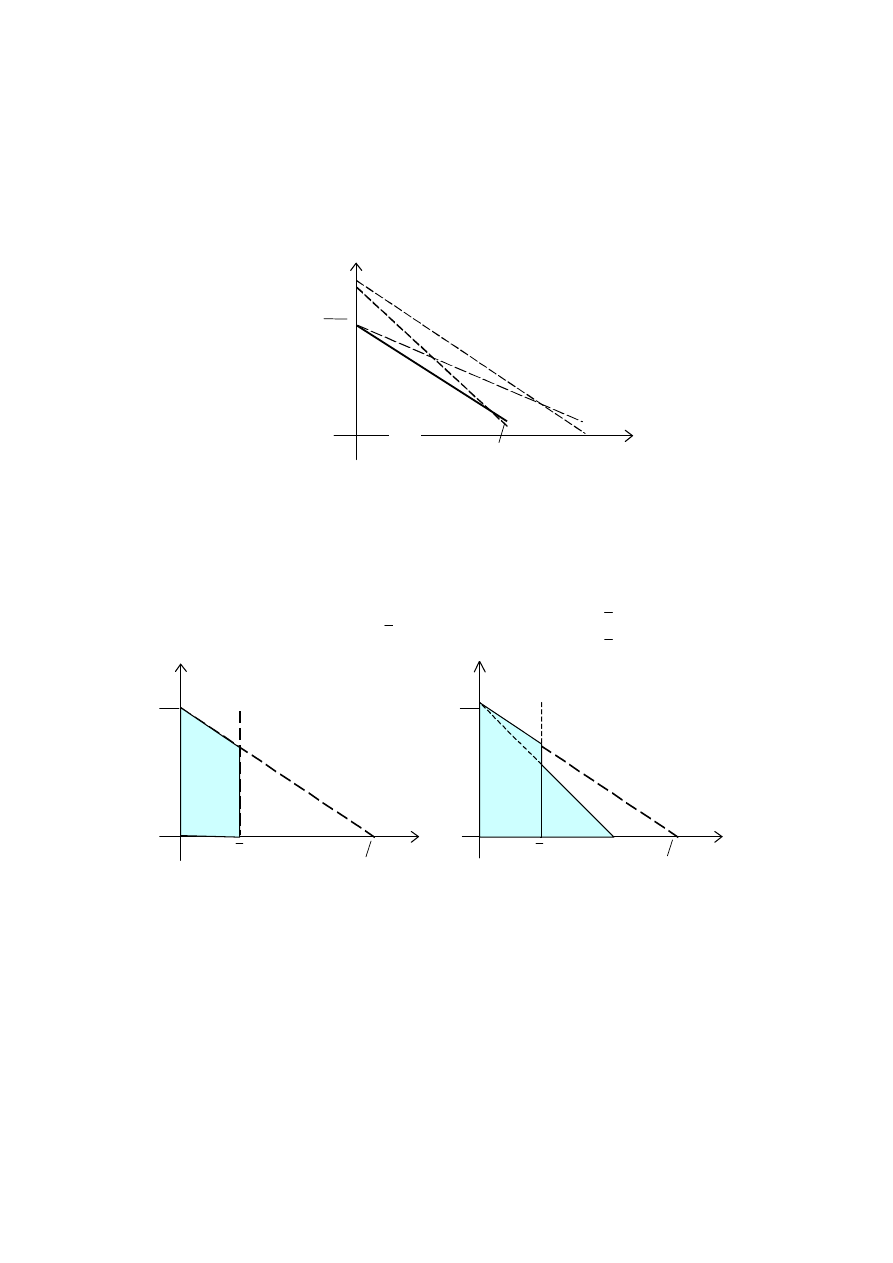
1.5. Zmiany linii budżetu
Linia budżetu ma 3 parametry
m
p
p
,
,
2
1
, które mogą się zmienić. Z równania
wynika, że wzrost dochodu (budżetu) przesunie równolegle do góry linię budżetu i nie
zmieni kont nachylenia. Zmniejszenie ceny dobra 1 powoduje przesunięcie punktu
przecięcia linii budżetu z poziomą osią na prawo. To znaczy, prosta staje się mniej stroma.
Zmniejsza się kąt nachylenia.
Zmniejszenie ceny dobra 2 – bardziej stroma.
Zbiór budżetowy w przypadku racjonowania.
Rząd czasem nakłada ograniczenia w postaci racjonowania lub opodatkowania
konsumpcji większej niektórego poziomu. Niech
1
x
– racjonowane dobro.
a) Kartki konsumpcyjne:
1
1
x
x
b)
1
1
1
1
1
1
1
,
,
x
x
t
p
x
x
p
cena
(t – podatek)
Racjonowanie
1
x
2
x
1
p
m
2
p
m
1
x
1
x
1
x
1
p
m
2
p
m
max
1
x
Później zobaczymy, że czasem sytuacji b) wynikają i w modelach bez racjonowania
(konsumpcja międzyokresowa).
W teorii konsumpcji zakłada się, że każdy konsument ma własne preferencji na
niektórym podzbiorze przestrzeni dóbr x. To oznacza, że dla dwóch dowolnych koszyków
X
x
i
X
y
konsument potrafi ich uszeregować według stopnia pożądania i zawsze
mamy jedną z trzech relacji:
1.
x
y
, (mówimy y silnie preferowany nad x);
2.
y
x
, (mówimy x silnie preferowany nad y);
3.
y
x ~
, (koszyki x, y są obojętne (indyferentne)).
Zmiany linii bud
żetu
1
x
2
x
1
p
m
2
p
m
x
10
x
20
www.zadania-projekty.pl
5
Wprowadzimy następujące relacji preferencji:
1.
y
x ~
, (mówimy x słabo preferowany nad y), co oznacza, że koszyk „y nie gorszy od
koszyka x”.
2.
y
x
, (mówimy x silnie preferowany nad y), co oznacza, że koszyk x jest z pewnością
lepszy od koszyka y.
3.
y
x ~
, (koszyki x, y są obojętne (indyferentne)).
Pierwsza relacja nazywają się relacja słabej preferencji, druga relacja silnej
preferencji, trzecia relacja indeferentności.
Podstawową relacją jest relacja słabej preferencji, na podstawie której możemy
zdefiniować pozostałe relacji.
Definicja 1.5. Parę
~
,
X
nazywamy polem preferencji konsumenta.
Definicja 1.6. Niech
X
y
x
,
.
1. Mówimy, że koszyki x, y są indyferentne, jeżeli równocześnie
y
x ~
i
x
y
~
.
2. Mówimy, że koszyk x jest silnie preferowany nad koszykiem y, jeżeli
y
x ~
i
x
y
~
1.6. Właściwości preferencji.
Relacja słabej preferencji ma następujące właściwości:
1. Dla
X
x
,
x
x ~
(refleksyjność, zwrotność).
2. Dla
X
y
x
,
x
y
y
x
~
~
(zupełność).
3. Jeżeli
dla
X
z
y
x
,
,
z
x
to
z
y
y
x
~
,
~
~
(przechodniość,
tranzytywność).
Aksjomat 3 wprowadza liniowy porządek w przestrzeni dóbr i daje możliwość
konsumentowi zawsze dokonywać konkretnego wyboru i nie zamykać się w błędnym kole,
natomiast aksjomat 2 wyklucza istnienie sytuacji, gdy konsument nie jest w stanie
powiedzieć, który z koszyków jest lepszy.
Relacja indeferencji spełnia warunki ekwiwalentności:
1. Dla
X
x
,
x
x ~
(refleksyjność, zwrotność).
2. Dla
X
y
x
,
y
x ~
x
y ~
(symetryczność).
3.
Jeżeli
dla
X
z
y
x
,
,
z
x
to
z
y
y
x
~
,
~
~
(przechodniość,
tranzytywność).
To znaczy, przestrzeń dóbr rozbija się na zbiory, które nie mają wspólnych punktów. Takie
zbiory nazywają się obszary obojętności. Obszar obojętności w przypadku 2 dóbr
nazywamy linią obojętności.
Własności relacji silnej preferencji.
1. Dla
X
y
x
,
x
y
y
x
(zupełność).
2. Jeżeli dla
X
z
y
x
,
,
z
x
to
z
y
y
x
~
,
~
~
(przechodniość,
tranzytywność).
6
1.7. Dodatkowe założenia.
Definicja 1.7. Relację preferencji nazywamy ciągłą, jeżeli
y
zbiory
y
x
x
|
i
x
y
x
|
są zbiorami otwartymi w przestrzeni dóbr X.
Przykład. 1.3 Konsument kupuje bezpośrednio u rybaków skrzynie ze słabo
słonymi śledziami. Relacja preferencji wygląda następująco: nie gorsze śledzie to takie,
które są wcześniej wyłowione, ale nie wcześniej niż po 2 dobach i nie później niż po 5
dobach (tylko po takim terminie śledzie będą odpowiednio słone). Czy relacja preferencji
jest relacją ekwiwalentności? Czy spełnia założenie zupełności? Czy relacja preferencji jest
ciągła? Narysować na osi czasu wszystkie koszyki należące do otoczenia
2
1
U
i
5
2
U
.
Rozwiązanie.
2
1
U
5
2
U
Definicja 1.8. Niech M jest niepustym podzbiorem pola preferencji
~
,
X
.
M
x
nazywamy M – preferowanym koszykiem i oznaczamy
x=m.pref.M, jeżeli
M
y
jest słabo preferowany nad
y
x
~
.
Definicja 1.9. Zbiór M nazywa się wypukły, jeżeli dowolne dwa jego punkty
można połączyć odcinkiem, należącym do zbioru M.
Definicja 1.10. Pole preferencji
~
,
X
nazywamy słabo wypukłe, jeżeli
1. Przestrzeń towarów jest zbiorem wypukłym
2. Dla
X
y
zbiór
y
x
X
x
~
|
jest zbiorem wypukłym w przestrzeni dóbr X.
Interpretacja w R
2
Definicja 1.11. Pole preferencji
~
,
X
nazywamy silnie wypukłe, jeżeli
1. Przestrzeń towarów jest zbiorem wypukłym
2. Dla
1
,
0
,
,
X
y
x
,
(
y
x ~
,
y
x
)
y
y
x
.
X
y
zbiór
y
x
X
x
~
|
jest zbiorem wypukłym w przestrzeni dóbr X.
W większości modeli przypuszczamy, że są spełnione 3 dodatkowe założenia:
Z1. Monotoniczność (zjawisko niedosytu): jeżeli x<y
x
y
.
Z2. Pole preferencji
~
,
X
- wypukłe.
Z3.
y
x ~
- relacja ciągła.
Twierdzenie 1.1. Jeżeli pole preferencji
~
,
X
jest słabo wypukłym, M jest
niepustym, wypukłym podzbiorem X i istnieje M preferowany koszyk, to zbiór wszystkich
M- preferowanych koszyków jest wypukły.
Twierdzenie 1.2. Jeżeli pole preferencji
~
,
X
jest silnie wypukłym, to w
wypukłym zbiorze M istnieje nie więcej niż jeden M - preferowany koszyk.
t
1
2
3
4
5
6
7
www.zadania-projekty.pl
7
1.8. Funkcja użyteczności.
Relację preferencji jest nie zbyt wygodna dla praktycznego zastosowania. Dla
niektórych słabych założeniach
preferencji wygodnie przedstawiać w postaci liczbowego indykatora preferencji funkcji
użyteczności, która dozwala zastąpić relację preferencji zwykłej relacją więcej.
Definicja 1.12. Określoną na przestrzeni dóbr funkcje
R
R
U
n
:
nazywamy
funkcją użyteczności konsumenta związaną z relacją
~
, jeżeli
X
y
x
,
spełnia ona
następujące warunki:
1.
)
(
)
(
y
U
x
U
y
x ~
2.
)
(
)
(
y
U
x
U
y
x
Twierdzenie. 1.3. (Debreu). Jeżeli relacja preferencji jest ciągła, to istnieje ciągła
funkcja użyteczności, związana z tą relacją
Twierdzenie 1.4. Jeżeli U(x) – funkcja użyteczności,
R
R
f
:
– funkcja
rosnąca, to superpozycja f(U(x)) jest funkcją użyteczności związaną z tą samą relacją.
Przykłady funkcji użyteczności w
2
R
:
multiplikatywna -
2
1
2
1
2
1
;
x
ax
x
x
U
, dla
0
;
1
;
,
;
0
,
2
1
1
1
2
1
a
o
x
x
;
logarytmiczna -
2
2
1
1
2
1
ln
ln
;
x
x
x
x
U
, dla
0
,
;
0
,
1
1
2
1
x
x
;
addytywna -
2
1
2
2
1
1
2
1
;
x
x
x
x
U
, dla
1
,
0
,
,
;
0
,
2
1
1
1
2
1
o
x
x
;
1.9. Właściwości funkcji użyteczności.
W dalszych rozważaniach zakładamy, że spełnione warunki następnego twierdzenia
Twierdzenie 1.5. Niech relacja preferencji jest słabo wypukła i znajdujemy się w
warunkach niedosytu, wtedy odpowiednia funkcja użyteczności jest quasi wklęsłą i
rosnącą.
Więc funkcja użyteczności ma następujące właściwości:
1.
0
;
;
2
1
i
n
x
x
x
x
U
- zjawisko niedosytu (większe koszyki zawsze lepszy).
2.
0
;
;
2
2
1
2
i
x
x
x
x
U
n
- dla zwiększających się koszyków różnica w korzyści
pomiędzy koszykami dla konsumenta maleje (prawo Gossena: macierz drugich
pochodnych jest ujemne określona).
3.
i
n
o
x
x
x
x
x
U
i
;
;
2
1
lim
- olbrzymie korzyści dla konsumenta od bardzo
małych koszyków.
8
4.
0
;
;
2
1
lim
i
n
x
x
x
x
x
U
i
- dla olbrzymich koszyków dalsze ich zwiększenie nie
zwiększa ich przydatność.
Więc w przypadku dwuwymiarowych koszyków krzywa obojętności
const
x
x
U
2
1
;
jako
funkcja uwikłana może być zapisana w postaci
1
2
x
g
x
, gdzie funkcja g ma poziomą i
pionową asymptoty i jest wklęsła.
Nie ma sensu mówić o użyteczności, jako o liczbowej mierze zadowolenia. F.Uż. po
prostu wprowadzają liczbową charakterystykę relacji preferencji.Przykład. U=x
1
2
x
2
,
U’=x
1
2/3
x
2
1/3
. Te same linii obojętności, różne wartości.
1.10. Stopa substytucji i elastyczność
Definicja 1.13. Krańcową użytecznością i-tego towaru nazywamy
i
MU
i
n
x
x
x
x
U
;
;
2
1
.
Dla naszych założeń krańcowa użyteczność i-tego dobra maleje wraz z zrostem jego
spożycia.
Definicja 1.14. Wyrażenie
ij
s
ij
MRS
s
=
j
i
MU
MU
nazywamy krańcową stopą substytucji i-tego dobra przez j-te dobro.
Definicja 1.15. Wyrażenie
j
i
ij
ij
x
x
s
nazywamy elastycznością substytucji i-tego dobra przez j-te dobro.
MRS pokazuje o ile powinna zwiększyć się ilość j-tego dobra przy zmniejszeniu o
jednostkę i-tego dobra, aby użyteczność koszyka nie zmieniła się.
Elastyczność mierzy to samo dla procentowych zmian. Elastyczność nie zależy od skali
pomiaru dóbr.
Model zachowania konsumenta
W teorii konsumpcji zakłada się, że konsument zawsze dąży do tego, żeby
maksymalizować użyteczność dla swoich ograniczonych możliwości
x
u
x
u
m
px
X
B
x
max
max
(3.1)
www.zadania-projekty.pl
9
Zakładamy, że punkt, który jest rozwiązaniem zadania (3.1) należy do dziedziny
dostępnych koszyków
X
x
*
. Więc dla rozwiązania (3.1) musimy obliczyć bezwarunkowe
maksimum funkcji Lagranżego
m
px
x
u
x
L
(3.2)
Lokalne warunki lokalnego ekstremum to są
m
x
p
j
n
j
j
*
1
, (3.3)
0
*
*
i
i
i
p
x
x
u
x
L
,
n
i
,
1
. (3.4)
Z (3.4) widać, że stosunek krańcowych stóp substytucji równa się stosunkowi cen
na odpowiednie dobra
j
i
j
i
p
p
x
x
u
x
x
u
*
*
. (3.5)
Rozwiązując (3.3) i (3.4) odnośnie
*
x
otrzymujemy funkcję popytu
m
p
x
x
,
*
*
. (3.6)
Definicja 3.1. Funkcję
m
p
x
x
,
*
*
uzależniającą popyt konsumenta na towary
od cen towarów i dochodu konsumenta nazywamy funkcję popytu konsumpcyjnego.
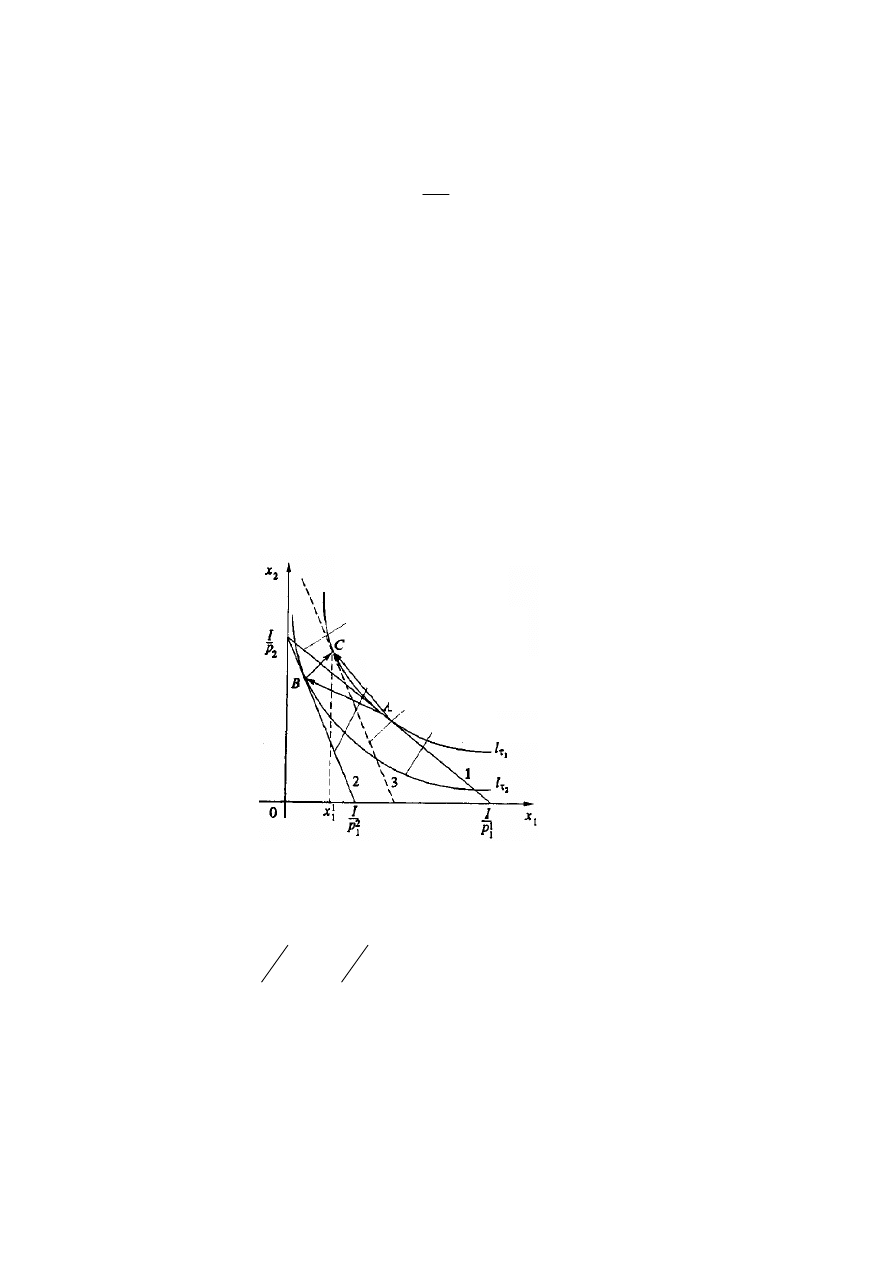
Definicja 3.2. Krzywa zapotrzebowania
*
*
( )
,
o
x
x m p
(czyli krzywa ekspansji
dochodu) przedstawia optymalny wybór konsumenta przy różnych poziomach dochodu, ale
przy stałych cenach
( )
o
p
.
Definicja 3.3. Krzywe Engla
*
*
( )
,
o
x
x m p
- są wykresy zależności popytu na
jedno dobro jako funkcji dochodu przy założeniu stałości wszystkich cen
( )
o
p
.
10
3.2. Wzajemna zamienialność dóbr
Rozpatrzymy funkcję popytu
i
i
np
m
x
. Widać, że popyt na i-te dobro maleje wraz
ze wzrostem ceny na i-te dobro, rośnie wraz ze wzrostem dochodu i nie zależy od ceny na
j-te dobro.
Definicja 3.4. Jeżeli popyt na i-te dobro maleje wraz ze wzrostem ceny na i-te
dobro i jednocześnie rośnie popyt na j-te dobro to takie dobra nazywają się wzajemnie
zamienialne.
Definicja 3.5. Jeżeli popyt na i-te dobro maleje wraz ze wzrostem ceny na i-te
dobro i jednocześnie maleje popyt na j-te dobro ta takie dobra nazywają się wzajemnie
dopełniające się.
W rzeczywistości wraz ze wzrostem ceny na i-te dobro może występować
zakłócenie w postaci ogólnego obniżenia dochodu konsumenta, co może doprowadzić do
obniżenia popytu na wzajemnie zamienialne j-te dobro. Dla usunięcia takiego zakłócenia
wprowadza się
Definicja 3.6. Budżet dostosowany to jest taki budżet, który zachowuje siłą
nabywczą konsumenta. Inaczej mówiąc budżet , który dozwala nabyć równoznaczny
koszyk.
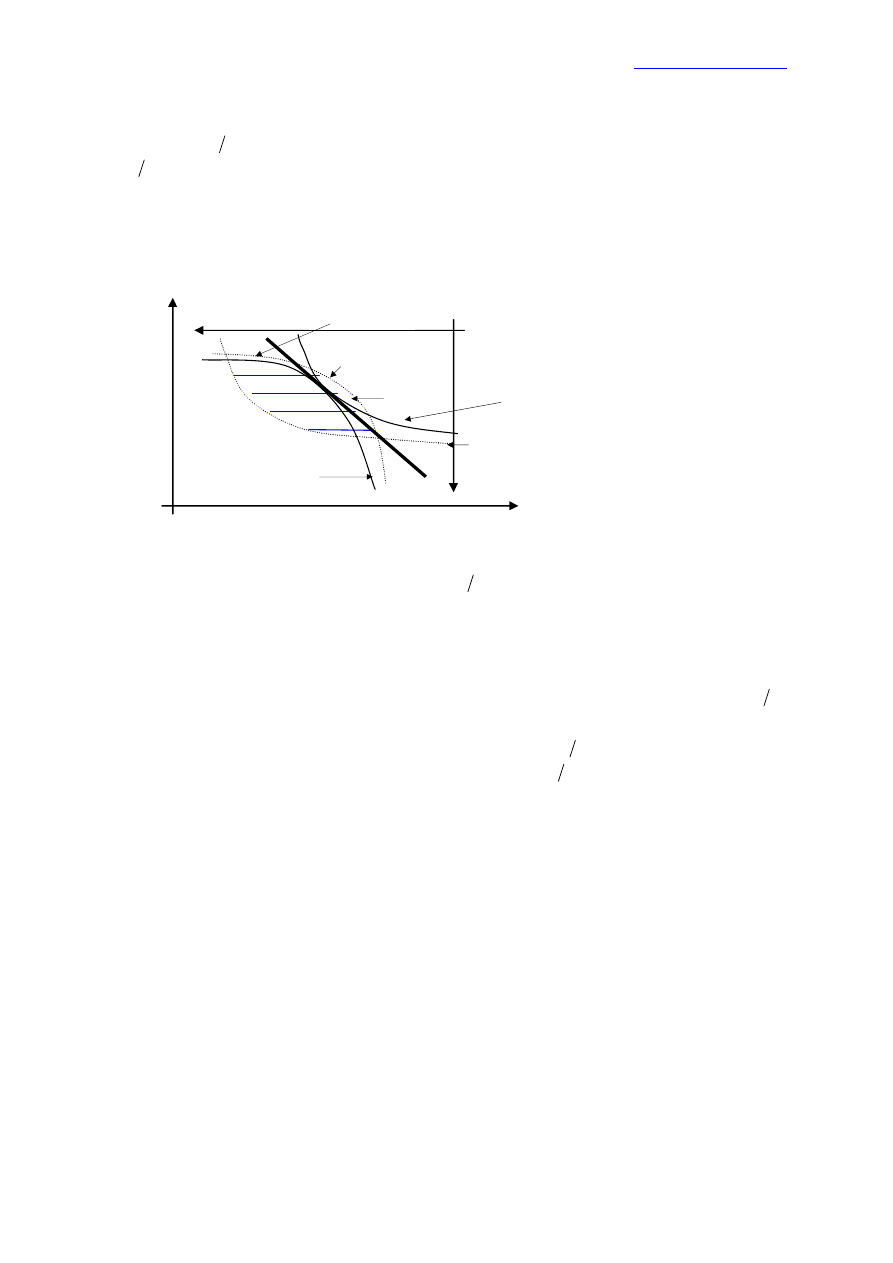
Rys. 4.1
Kiedy cena dobra ulega zmianie, pojawiają się dwa rodzaje efektów:
zmienia się stosunek, według którego wymienia się jedno dobro na drugie;
zmienia się ogólna siła nabywcza dochodu konsumenta;
Na przykład, jeżeli cena pierwszego dobra zmieniła się od
1
p
do
1
'
p
, to stosunek
cen zmienia się od
1
2
p
p
do
1
2
'
p
p
, a ogólna siła nabywcza (budżet) zmienia się od
m
do
'
m
(Rys. 4.1).
Definicja 3.7. Pierwszy efekt – zmiana popytu z tytułu zmiany stopy wymiany
między dwoma dobrami – jest nazywany efektem substytucyjnym.
Definicja 3.8. Drugi efekt – zmiana popytu z tytułu osiągnięcia innej (większej lub
mniejszej) siły nabywczej - jest nazywany efektem dochodowym.
Nowa linia budżetu
Stara linia budżetu
Skompensowana linia budżetu
CB- Efekt dochodowy
AC - Efekt substytucyjny
AB – Efekt ogólny
Krzywe obojętności
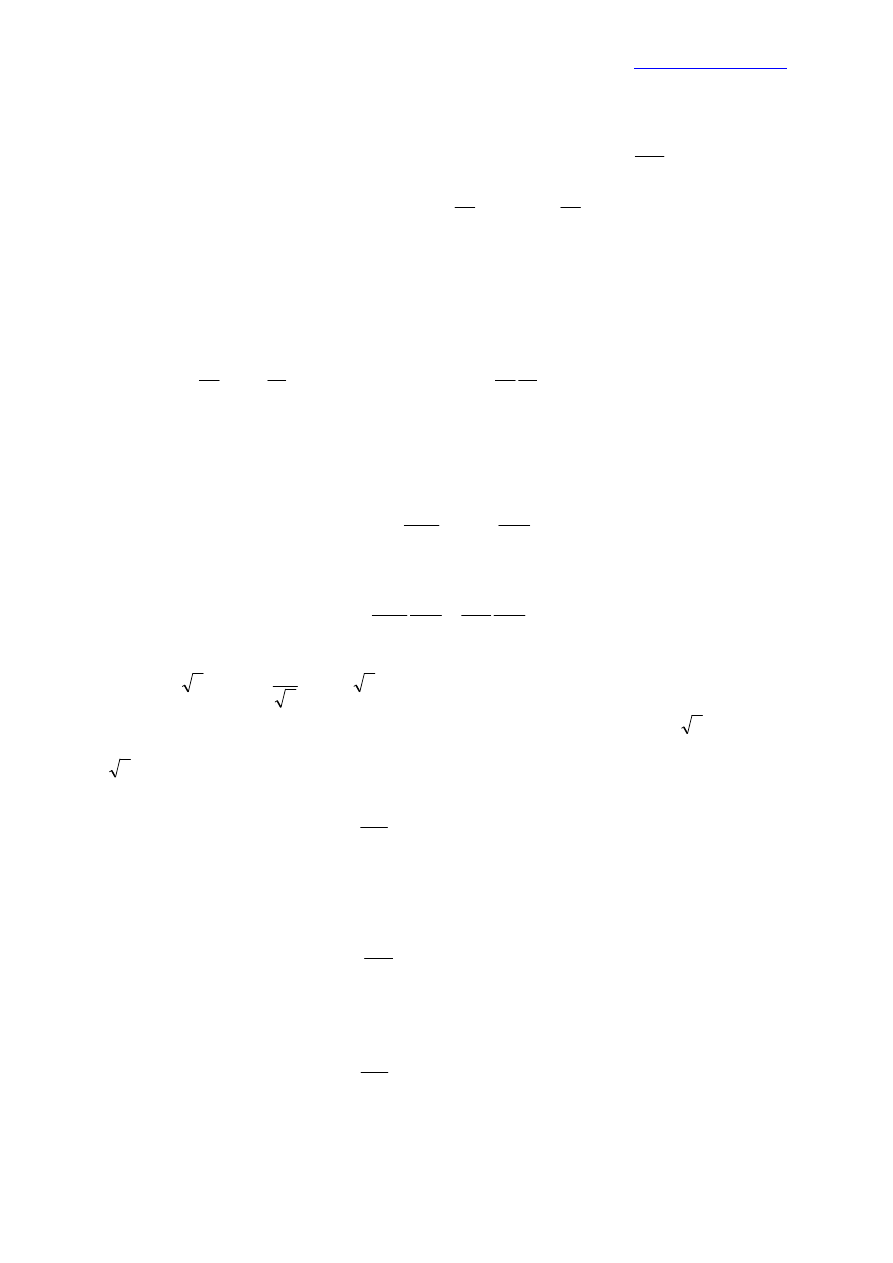
www.zadania-projekty.pl
11
Rozpatrzymy funkcję użyteczności dwóch dóbr
2
1
2
1
,
x
x
x
x
U
, budżet 60, ceny
dóbr odpowiednio 10 i 2. Więc funkcje popytu mają postać
i
i
p
m
x
2
,
2
,
1
i
. Wtedy
wybór początkowy konsumenta będzie
3
20
60
1
p
x
,
15
4
60
2
p
x
i funkcja użyteczności
przyjmie wartość
45
,
2
1
x
x
U
. Niech teraz cena dobra drugiego wzrośnie do 7. Żeby
kupić ten sam koszyk konsument musi wydać dodatkowo (7-2)15=75 jednostek
pieniężnych. Ale wraz ze wzrostem ceny zmieni się stopa wymiany dóbr i więc musimy
kupić nie ten sam koszyk tylko koszyk równoznaczny tj. koszyk dla którego
45
,
2
1
x
x
U
.
Obliczymy budżet dostosowany
'
m
. Mamy:
20
'
1
m
x
,
14
'
2
m
x
, wtedy.
45
14
'
20
'
,
2
1
2
1
m
m
x
x
x
x
U
Stąd
25
,
112
'
m
.
Więc dodatkowo musimy wydać tylko 52,25.
Zapiszemy teraz rozwiązanie w ogólnej postaci. Po wzroście ceny z
1
p
do
1
zp
funkcje popytu mają postać
1
1
2
'
'
zp
m
x
i
2
2
2
'
'
p
m
x
,
gdzie
'
m
jest to budżet dostosowany. Warunek równej użyteczności
2
1
2
1
2
2
2
'
2
'
p
m
p
m
p
m
zp
m
.
Stąd
m
z
m
'
i
z
x
x
1
1
'
,
2
2
'
x
z
x
.
W przypadku budżetu dostosowanego popyt na pierwsze dobro zmaleje w
z
razy (jeżeli
budżet nie jest dostosowany to w z razy), natomiast popyt na drugie dobro wzrośnie w
z
razy.
Więc
0
subst
1
2
p
x
. (3.7)
Dolny indeks subst oznacza, że jest usunięty efekt dochodowy i zostaje się tylko
efekt substytucyjny.
Dla wzrostu ceny na drugie dobro mamy analogicznie
0
subst
2
1
p
x
. (3.8)
Warunek (3.7) lub (3.8) to jest warunek tego, że dobra są wzajemnie zamienialne.
Warunek
0
subst
1
2
p
x
(3.9)
i warunek
12
0
subst
2
1
p
x
(3.10)
to warunki wzajemnie dopełniających się dóbr. Obliczymy cząstkowe pochodne. Mamy
odpowiednio przyrosty:
1
1
1
x
z
x
x
,
2
2
2
x
x
z
x
,.
1
1
1
p
zp
p
Stąd
2
1
1
1
1
1
1
1
1
1
1
1
1
1
1
subst
1
1
4
2
1
1
1
lim
lim
lim
p
m
p
x
z
z
p
x
z
z
p
z
x
p
zp
x
z
x
p
x
z
z
z
,
2
1
1
2
1
2
1
1
2
1
1
1
2
2
1
subst
1
2
4
2
1
1
1
lim
lim
lim
p
p
m
p
x
z
p
x
z
p
z
x
p
zp
x
x
z
p
x
z
z
z
.
Więc mamy wzajemnie zamienialne dobra.
3.3. Równanie Słuckiego
Jednym z podstawowych równań w teorii wyboru konsumpcyjnego jest równanie
Słuckiego, które było udowodnione w 1915 r. Rosyjskim matematykiem Słuckim.
Równanie Słuckiego pokazuje zależność pomiędzy efektami substytucyjnym i dochodowym
a ogólnym popytem. Zapiszemy bez dowodu Równanie Słuckiego:
j
i
subst
j
i
j
i
x
m
x
p
x
p
x
,
2
,
1
i
,
2
,
1
j
. (3.10)
Pierwszy składnik w prawej części opisuje efekt substytucyjny, drugi efekt
dochodowy, z lewej strony zapisana jest ogólna zmiana popytu z tytułu strukturalnej
zmiany popytu i zmiany realnego dochodu konsumenta.
Definicja 3.9. Jeżeli popyt rośnie wraz ze wzrostem dochodu tj.
0
m
x
i
to takie dobro nazywa się dobrem luksusowym (wyższego rzędu).
Wtedy według (3.10)
subst
j
i
j
i
p
x
p
x
co oznacza, że jeżeli popyt rośnie wraz ze wzrostem ceny, to on rośnie szybciej
jeżeli mamy kompensację i jeżeli popyt maleje wraz ze wzrostem ceny, to on maleje w
mniejszym stopniu jeżeli mamy kompensację. Może stać się, że
0
j
i
p
x
, i
subst
j
i
p
x
0
,
www.zadania-projekty.pl
13
co oznacza, że dobra i-te i j-te są wzajemnie zamienialne, natomiast bez
kompensacji są wzajemnie dopełniające się.
Rozpatrzymy równanie Słuckiego dla
j
i
.
i
i
subst
i
i
i
i
x
m
x
p
x
p
x
. (3.11)
Dla spełnionych dodatkowych założeń 1) – 3)
0
subst
i
i
p
x
Definicja 3.10. Jeżeli popyt rośnie wraz ze wzrostem ceny tj.
0
i
i
p
x
wtedy takie dobro nazywa się dobrem Giffena.
Definicja 3.11. Jeżeli popyt maleje wraz ze wzrostem dochodu tj.
0
m
x
i
,
wtedy takie dobro nazywa się. drugorzędnym dobrem (niższego rzędu).
Więc dobro Giffena jest zawsze drugorzędnym dobrem.
Dobra normalne
0
i
i
p
x
Dobra Giffena
0
i
i
p
x
Dobra luksusowe
0
m
x
i
Luksusowe samochody
Drugorzędne dobra
0
m
x
i
Jabłka.
Chleb, ziemniaki.
3.4. Elastyczność cenowa i dochodowa. Paradoksy Giffena i Veblena
Z matematycznego punktu widzenia, jeśli dana jest funkcja Y = f(X1, X2, ... , Xn),
to elastycznością zmiennej Y względem zmiennej Xj nazywamy wyrażenie:
)
,...,
,
(
)
,...,
,
(
2
1
2
1
n
j
j
n
X
X
X
X
f
X
X
X
X
X
f
E
j
. (3.12)
Główną zaletą badania popytu przy użyciu pojęcia elastyczności jest fakt, że
elastyczności są niezależne od jednostek, w jakich mierzy się poszczególne zmienne.
Istnieje zatem możliwość porównania wyników analizy popytu na dane dobro nawet w
różnych krajach (wartości pieniężne wyrażone w innych walutach) bądź też popytu na
różne dobra mierżono w odmiennych jednostkach fizycznych. Elastyczności popytu nie
zawsze są wielkościami stałymi względem zmian w poziomach ceny i dochodu. W pewnych
14
przypadkach rozsądnym wydaje się jednak przyjęcie założenia o stałości elastyczności, tzn.
uznanie, iż z każdego procenta przyrostu dochodów konsumenci przeznaczają pewną stałą
(w przybliżeniu) część na dodatkowy zakup określonego dobra bądź też, że każdy procent
wzrostu ceny. tego dobra powoduje jednakowy co do wartości spadek popytu na nie.
Pojęcie elastyczności odgrywa w analizie popytu podstawową rolę. Praktycznie rzecz
biorąc, elastyczność popytu na pewne dobro względem danej zmiennej jest to procentowy
przyrost (lub spadek) popytu wywołany przyrostem wartości tej zmiennej o 1%. Jest to
zatem pewna miara siły wpływu danej zmiennej na poziom popytu. Informacja o poziomie
elastyczności popytu na pewne dobro względem ceny tego dobra, czy dochodu
konsumentów może być więc bardzo cenna dla podejmowania konkretnych decyzji
gospodarczych.
Definicja 3.12..Wartość
i
i
i
i
c
i
x
p
p
x
nazywa się elastyczność popytu względem ceny (elastyczność cenowa)
Definicja 3.13.. Wartość
i
i
m
i
x
m
m
x
nazywa się elastyczność popytu względem dochodu (elastyczność dochodowa).
Zrozumiałe jest, że zwykle elastyczność dochodowa jest wielkością dodatnią (wzrost
dochodów wywołuje wzrost popytu), a cenowa - ujemną (wzrost ceny danego dobra
powoduje spadek popytu na dobro). Istnieją jednakże wyjątki od tej reguły znane w
literaturze pod nazwą paradoksów Giffena i Veblena. Pierwszy z nich mówi, że popyt na
takie dobra, jak chleb czy ziemniaki, może wzrastać ze zwiększeniem się cen tych dóbr, co
tłumaczy się tym, że ludność biedna reaguje na wyższą cenę, np. chleba, zmniejszeniem
wydatków na żywność wyższego rzędu (np. mięso) nabywając więcej chleba. Zjawisko to
zaobserwowano w Irlandii. Paradoks Veblena polega na tym, że w pewnych grupach
społecznych o wysokich dochodach wyższa cena na niektóre dobra powoduje (ze względów
snobistycznych) zwiększenie popytu na te dobra. Inną anomalią, już nie paradoksalną, jest
spadek popytu na niektóre dobra niższego rzędu (np. margarynę) w miarę wzrostu
dochodów. Popyt kieruje się po prostu do dóbr wyższego rzędu (np. masło).
Z tego co powiedzieliśmy o elastyczności wynika, że dobra można klasyfikować w
zależności od poziomu elastyczności dochodowej (oznaczmy ją przez Eq). i cenowej (Ep). I
tak: powiemy, że popyt na pewne dobro jest nieelastyczny względem dochodu, jeśli Eq
< 1, elastyczny, jeśli Eq > l. Podobnie: popyt uznamy za nieelastyczny względem
ceny, jeśli Ep > -1, elastyczny, jeśli Ep < -1. Z drugiej strony powiemy, że dobro jest
niższego rzędu, gdy Eq < 0, jest dobrem podstawowym, jeśli 0 < Eq < 1 oraz jest
dobrem luksusowym, jeśli Eq > 1.
Prócz elastyczności cenowej i dochodowej pewną rolę w badaniach popytu odgrywa
elastyczność mieszana popytu na pewne dobro względem ceny innego dobra. Jest to
zwykle wielkość dodatnia, gdy mamy do czynienia z dobrami substytucyjnymi i ujemna
— jeśli są to dobra komplementarne.
Sprawdzimy równanie Słuckiego dla naszego przykładu. Mamy:
2
1
1
1
2 p
m
p
x
,
1
1
2
1
p
m
x
,
0
1
2
p
x
,
2
1
subst
1
1
4 p
m
p
x
,
2
1
subst
1
2
4
p
p
m
p
x
.
www.zadania-projekty.pl
15
Więc dobro
1
x
jest dobro luksusowe, popyt na niego rośnie wraz ze wzrostem dochodu
konsumenta i maleje wraz ze wzrostem ceny
1
p
.
Podstawiając cząstkowe pochodne w (3.11) i (3.10) mamy:
2
1
1
1
2
1
2
1
2
1
2
2
1
4
2
p
p
m
p
p
m
p
m
;
0
2
2
1
4
0
1
2
2
1
p
m
p
p
p
m
.
Model Edgwortha
Rozpatrzymy najprostszy model równowagi rynkowej, gdy na rynku
X
obecny tylko
dwa konsumenta A i B każdy z których dysponuje tylko dwoma dobrami
1
x
i
2
x
.
Konsument A posiada
A
W
1
jednostek dobra pierwszego i
A
W
2
jednostek dobra drugiego.
Konsument B posiada
B
W
1
jednostek dobra pierwszego i
B
W
2
jednostek dobra drugiego.
Zakłada się, że konsumenci dąży do tego, żeby wymieniając dwoma dobrami
1
x
i
2
x
maksymalizować użyteczność dla swoich koszyków
A
A
x
x
2
1
,
i odpowiednio
B
B
x
x
2
1
,
:
A
A
A
X
x
x
x
x
U
A
A
2
1
,
,
max
2
1
, (5.1)
B
B
B
X
x
x
x
x
U
B
B
2
1
,
,
max
2
1
, (5.2)
gdzie
A
U
i
B
U
funkcji użyteczności konsumentów A i B odpowiednio.
Pokażemy geometrycznie proces wymiany dóbr konsumentów. W układzie
współrzędnych
A
A
x
x
2
1
,
narysujemy punkt
B
A
B
A
W
W
W
W
P
2
2
1
1
;
wspólnych zasobów
dóbr i punkt
A
A
W
W
A
2
1
,
początkowego zasobu konsumenta
A
:
Rys. 5.1
Łatwo zauważyć, że punkt
A
w układzie współrzędnych
A
A
x
x
2
1
,
pokazuje
początkowy zasób konsumenta
A
i jednocześnie w układzie współrzędnych
B
B
x
x
2
1
,
pokazuje początkowy zasób konsumenta
B
. Narysujemy krzywe obojętności
1
const
U
A
i
1
const
U
B
do których należy punkt
A
. Wspólna część dziedzin, które znajdują się
powyżej krzywych obojętności odnośnie swoich osi współrzędnych (niebieski kolor)
A
x
2
A
x
1
B
x
1
P
x
A
x
1
const
U
B
1
const
U
A
2
const
U
A
2
const
U
B
B
x
2
16
pokazuje leprze koszyki jednocześnie dla obydwu konsumentów. Przecięcie preferowanych
obszarów nazywa się obszarem handlu. Więc w tej dziedzinie szukamy koszyk, który
będzie rozwiązaniem. Dla tego obliczymy ile kosztowali początkowe koszyki konsumentów.
Przyjmujemy, że były ustalony ceny
1
p
na dobro
1
x
i
2
p
na dobro
2
x
(na przykład na
podstawie poprzedniego okresu handlu). Mamy:
A
A
A
W
p
W
p
m
2
2
1
1
, (5.3)
B
B
B
W
p
W
p
m
2
2
1
1
. (5.4)
www.zadania-projekty.pl
17
Linii budżetu zawierają punkt
A
. Nachylenie linii budżetu konsumenta
A
do osi
A
x
1
równa się
2
1
p
p
, nachylenie linii budżetu konsumenta
B
do osi
B
x
1
również równa się
2
1
p
p
. Ponieważ osi
A
x
1
i
A
x
2
są równoległe, linie budżetu konsumentów A i B nakładają
się. Wykorzystując uogólnioną funkcję popytu możemy obliczyć wybór początkowy
konsumentów
A
i
B
, to są punkty
)
,
(
2
1
A
A
A
x
x
X
i
)
,
(
2
1
B
B
B
x
x
X
. Ogólnie mówiąc
punkty
)
,
(
2
1
A
A
A
x
x
X
i
)
,
(
2
1
B
B
B
x
x
X
nie nakładają się. Więc jednego dobra zabraknie a
drugiego będzie za dużo. Na rys. 5.2 brakuje pierwszego dobra i za dużo drugiego.
Rys. 5.2
Możliwości zmiany wartości
A
m
i
B
m
nie ma, więc polepszenie koszyka może być
dokonane tylko przez zmianę stopy wymiany dóbr, tj. zmiany cen
2
1
, p
p
. Dokładniej
mówiąc
przez
zmianę
stosunku
2
1
p
p
ponieważ
B
A
B
A
w
w
x
x
1
1
1
1
i
B
A
B
A
w
w
x
x
2
2
2
2
(podaż dobra 1 jest mniejszy popytu, dla dobra 2 odwrotnie).
Powstaje pytanie: czy istnieją ceny
2
1
, p
p
(czy istnieje nachylenie linii budżetu)
przy których rynek okaże się zbilansowany?
Twierdzenie. Jeśli preferencje, reprezentowane przez funkcje
)
,
(
2
1
x
x
U
A
i
)
,
(
2
1
x
x
U
B
są monotoniczne, ciągłe i silnie wypukłe, to istnieje jedyny stosunek cen
2
1
p
p
,
przy którym
B
A
B
A
w
w
x
x
1
1
1
1
i
B
A
B
A
w
w
x
x
2
2
2
2
.
Ścisły dowód pominiemy, zauważmy tylko, że przy
0
2
1
p
p
linia budżetu dąży do
poziomej prostej, popyt na dobro
2
1
,
0 x
x
, przy
2
1
p
p
linia budżetu dąży do
poziomej pionowej, popyt na dobro
0
,
2
1
x
x
. Ponieważ preferencje są ciągłe, to
popyt na dobra
2
1
, x
x
przy zmianie cen zmienia się ciągłe. To znaczy istnieją ceny, przy
których popyt na dobro
1
x
jest równy podaży (wspólnemu zasobowi). Tak samo istnieją
ceny,
wyrównujące popyt i podaż dobra
2
x
. Jak widać z wykresu, równowaga dóbr
następuje jednocześnie. Monotoniczność i wypukłość preferencji gwarantują, że taki punkt
jest jedynym.
5.2. Optimum Pareta, krzywa kontraktów
Optimum Pareta
Mówimy, że sytuacja ekonomiczna jest efektywną w rozumieniu Pareta, jeżeli nie
ma sposobu poprawienia sytuacji jakiejkolwiek osobie bez skrzywdzenia kogokolwiek
innego.
Efektywność w rozumieniu Pareta jest stanem pożądanym – jeśli są sposoby
poprawienia sytuacji pewnych grup ludzi, dla czego by tego nie zrobić. Jednakże efektywność
ta nie jest jedynym celem polityki ekonomicznej, ponieważ nie ma ona nic wspólnego ze
sprawiedliwością.
A
x
2
A
x
1
B
x
1
P
x
A
x
1
const
U
B
1
const
U
A
3
const
U
A
2
const
U
B
B
x
2
B
X
A
X
18
Traktowanie na poprzednim przykładzie.
Definicja. Zbiór punktów,
A
A
x
f
x
1
2
,
lub
B
B
x
x
1
2
(5.5)
reprezentujących stany równoważne modelu Edgewortha przy wszystkich możliwych
podziałach zasobu początkowego nazywa się krzywą kontraktów.
Z drugiej strony, krzywa kontraktów, to zbiór punktów, efektywnych w rozumieniu
Pareta.
Z powyższego bezpośrednio wnioskujemy, że w przypadku dwu dóbr w ogólnej postaci
układ równań, rozwiązanie którego jest krzywa kontraktów może być zapisany w postaci:
1
2
1
2
1
1
1
1
2
1
2
2
2
2
1
1
1
1
1
1
1
1
,
,
,
,
,
,
lub
.
A
A
A
B
B
B
A
A
A
A
B
B
B
A
A
B
A
B
A
B
A
B
U
x
x
U
x
x
x
x
p
U
x
x
U
x
x
p
x
x
x
x
W
W
x
x
W
W
(5.6)