Pojecie stabilności

Pojęcie stabilności możemy określić jako zdolność układu do przywracania równowagi w
razie jej zakłócenia. Określenie stabilności jest jedną z najważniejszych czynności podczas
procesu syntezy. Stabilność charakteryzuje właściwości dynamiczne układu, które są
warunkiem jego prawidłowej pracy. Przykładem destabilizacji układu jest sprzężenie w
wzmacniaczach i układach nagłaśniających audio. Chodzi tu o chrakterystyczny pisk w
glośnikach wywołany zblizeniem mikrofonu do glośnika. W tym wypadku mała odległość
między mikrofonem a głośnikeim powoduje niestabilność systemu. Innym przykładem może
być utrata stabilnosci mostu w wyniku podmuchów wiatru. Silne podmuchy wiatru mogą
spowodować oscylacje mostu w wyniku, których jego konstrukcja może zostać naruszona.

Możemy rozróżnic nastepujace rodzaje stabilności:

- -

zwykła – gdy układ po wytraceniu ze stanu równowagi przyjmuje nowy stan

równowagi różny od stanu równowagi poprzedniej

- -

asymptotyczna – gdy układ po wytraceniu ze stanu równowagi powraca do stanu

równowagi poprzedniej

Warunki stabilnosci

Dla układów których transmitancja jest funkcja wymierna postaci

G s

( )

L s

( )

M s

( )

:=

Po przyrównaniu mianownika do zera otrzymujemy równanie charakterystyczne postaci:

a

n

* s

n

+ a

n-1

* s

n-1

+ .... + a

2

* s

2

+ a

1

* s + a

0

= 0

posiadające n pierwiastków s

1,2,...,n

Wówczas warunki stabilności możemy zdefiniować następująco:

Warunki stabilności asymptotycznej:

- -

wszystkie pierwiastki równania charakterystycznego ( bieguny transmitancji)

musza znajdować się w lewej półpłaszczyźnie zmiennej zespolonej, czyli wszystkie
pierwiastki rzeczywiste oraz wszystkie części rzeczywiste pierwiastków zespolonych
powinny być ujemne

Warunki stabilności zwykłej:

- -

pierwiastki równania charakterystycznego są rozmieszczone na płaszczyźnie

zespolonej tak, ze żaden z nich nie znajduje się w prawej półpłaszczyźnie, natomiast
na osi urojonej występują pierwiastki pojedyncze (co najwyżej jeden równy zero).

W praktyce wymaga się aby układ był stabilny asymptotycznie, bowiem z właściwości
stacjonarnych układów liniowych wynika, ze jeżeli są one stabilne asymptotycznie w stanie
swobodnym, to jest to stabilność globalna.

Kryteria oceny stabilnosci ukladow liniowych

1.

1.

Kryteria algebraiczne umożliwiają sprawdzenie czy układ jest asymptotycznie

stabilny na podstawie zależności miedzy współczynnikami równania charakterystycznego

M(s) = a

n

* s

n

+ a

n-1

* s

n-1

+ .... + a

2

* s

2

+ a

1

* s + a

0

gdzie wszystkie współczyniki a

i

dla i = 0...n

sa rzeczywiste.

Kryterium Hurwitza

Warunki:

- -

wszystkie współczynniki równania charakterystycznego a

i

dla i=0...n muszą mieć

ten sam znak

- -

wszystkie wyznacznik macierzy Hurwitza

∆

i

> 0, i=1,2,...,n.

Macierzą Hurwitza nazywamy macierz postaci:

H

a

n 1

−

a

n 3

−

a

n 5

−

....

0

a

n

a

n 2

−

a

n 4

−

.....

0

0

a

n 1

−

a

n 3

−

.....

0

0

a

n

a

n 2

−

.....

0

....

....

....

....

....

....

....

....

....

a

0

⎛⎜

⎜

⎜

⎜

⎜

⎜⎝

⎞
⎟

⎟

⎟

⎟
⎠

:=

∆

1

= a

n-1

∆

2

det

a

n 1

−

a

n 3

−

a

n

a

n 2

−

⎛

⎜

⎝

⎞
⎠

:=

∆

3

det

a

n 1

−

a

n 3

−

a

n 5

−

a

n

a

n 2

−

a

n 4

−

0

a

n 1

−

a

n 3

−

⎛⎜

⎜

⎜⎝

⎞
⎟
⎠

:=

.......

∆

n

= a

0 *

∆

n-1

= det H

1.Wyznaczamy transmitancje ukladu

2.Po przyrównaniu mianownika transmitancji do zera otrzymujemy rownanie
charakterystyczne stopnia n.
3.Sprawdzamy czy wspolczynniki a

i

dla i=0...n sa tego samego znaku, nastepnie

wyznaczamy kolejne wyznaczniki

∆ i sprawdzamy czy sa wieksze od zera, jeżeli

obydwa warunki sa spelnione uklad jest stabilny.

2. 2.

Kryteria częstotliwościowe umożliwiają ocenę stabilności układu na podstawie

przebiegu odpowiednich charakterystyk częstotliwościowych.

Kryterium Nyquista

Wykorzystywane do badania układów ze sprzężeniem zwrotnym ( układów zamkniętych).

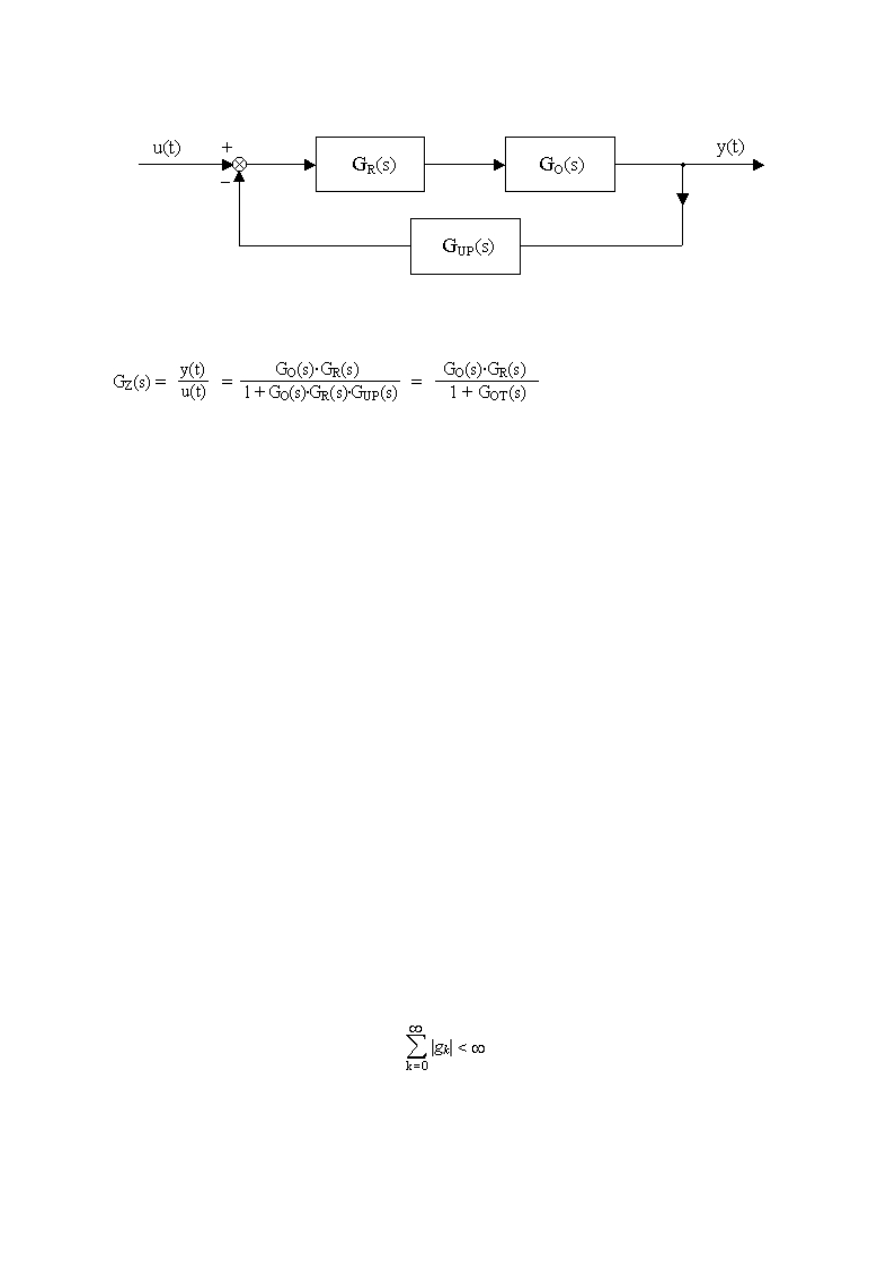
Transmitancja układu zamkniętego wyraża się wzorem

gdzie G

O

(s)-transmitancja obiektu

G

R

(s)- transmitancja regulatora

G

UP

(s)-transmitancja urządzenia pomiarowego

G

OT

(s)= G

O

(s)*G

R

(s)*G

UP

(s) –transmitancja układu otwartego

Wówczas kryterium Nyquista można przedstawić następująco:
1. Jeżeli układ otwarty jest stabilny asymptotycznie, to układ zamknięty jest stabilny
asymptotycznie wówczas, gdy wykres charakterystyki amplitudowo-fazowej G

o

(j

ω) przy

zmianach pulsacji

ω od zera do ∞ nie obejmuje punktu (-1,j0).

2. Jeżeli układ otwarty jest niestabilny i jego transmitancja ma l

0

biegunów w prawej

półpłaszczyźnie to układ zamknięty jest stabilny wówczas, gdy wykres charakterystyki
amplitudowo-fazowej G

o

(j

ω) przy zmianach pulsacji ω od zera do ∞ obejmuje punktu (-1,j0)

l

0

/2.

1.Wyznaczamy transmitancje G

o

(s) układu otwartego

2.Podstawiamy j

ω za s i otrzymujemy G

o

(j

ω) w postaci G

o

(jω) = Re + j Im

3.Wyznaczamy wartosc

ω dla ktorej Im G

o

(j

ω) =0, nastepnie sprawdzamy czy spelniony

jest warunek ReG

o

(j

ω) > -1, jeżeli warunek ten jest spelniony oznacza to ze uklad jest

stabilny. Oznacza to ze wykres charakterystyki czestotliwosciowej omija punkt (-1,j0)
od strony prawej

Układy dyskretne

Definicje określające stabilność układów ciągłych są prawdziwe także dla układów
dyskretnych.
Liniowy układ dyskretny jest stabilny, jeżeli dyskretne wartości składowych przejściowych
zmiennych stanu x[n] maleją do zera dla n dążącego do

∞.

( g

k

– odpowiedź układu dyskretnego dla kroku k )

Ponieważ transmitancja operatorowa układu dyskretnego jest funkcją operatora przesunięcia
z, a nie operatora różniczkowania s, wrunki stabilności mają jednak inną postać.

Dla układów, których transmitancją jest funkcja wymierna postaci

G z

( )

b

0

b

1

z

1

−

⋅

+

..

+

b

n

z

n

−

⋅

+

1

a

1

z

1

−

⋅

+

..

+

a

m

z

m

−

⋅

+

:=

warunek stabilności można wyrazić następująco

⎮z

i

⎮<1 dla i=1,2,...m

Czyli układ jest stabilny wówczas, gdy pierwiastki z

i

równania charakterystycznego znajdują

się na płaszczyźnie zmiennej zespolonej z wewnątrz okręgu o promieniu jednostkowym i
środku w początku układu współrzędnych.


Kryteria stabilności dla układów dyskretnych


Krytrium Jury’ego

M(z) = a

n

· z

n

+ a

n-1

· z

n-1

+ .... + a

2

· z

2

+ a

1

· z + a

0

Wszystkie pierwiastki wielomianu charakterystycznego M(z) zmiennej zespolonej z znajduja
się wewnątrz okręgu jednostkowego jeśli spełnione są wszystkie następujące warunki:

- -

M(1) > 0

- -

(-1)

n

· M(-1) > 0

- -

wyznaczniki macierzy ∆

+

, ∆

-

oraz wszystkich ich macierzy wewnętrznych są

dodatnie.

Macierze wewnętrzne macierzy ∆ (+ i - ) wyznacza się w nastepujący sposób:
Jeżeli macież ∆ jest nast. postaci:

∆

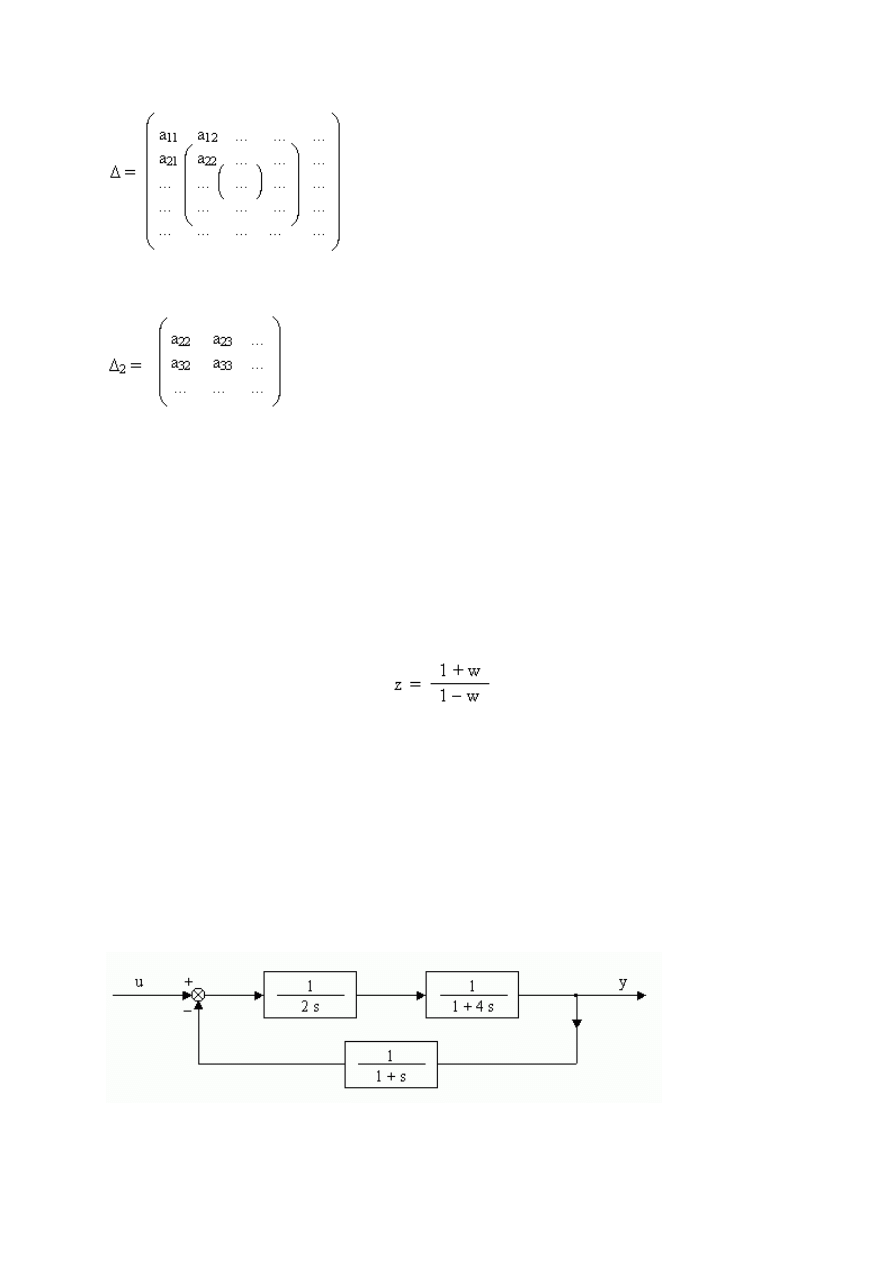
2

- Pierwsza macierz wewnetrzna macierzy ∆

∆

3

= a

33

Zastosowanie kryterium Hurwitza dla układów dyskretnych

Próbując określić położenie pierwiastków równania charakterystycznego, możemy
wykożystywać, po odpowiednich przekształceniach, kryteria stabilności dla układów
ciągłych. W tym celu należy przetransformować płaszczyzne zespoloną zmiannej z, tak aby
przekształcić koło jednostkowe - w lewą półpłaszczyznę.

G(z)

⇒ G(w)

Stosowane w takim przypadku podstawienie nazywane jest przekształceniem Oldenbourga i
Sartoriusa :

Otrzymujemy w ten sposób G(w), a więc także i równanie charakterystyczne M(w), dla
którego możemy zastosować kryteria stabilności dla układów ciągłych: przedstawione
wczesniej kryterium Hurwitza, lub inne np. kryterium Routha.

Przykład

Badanie stabilności następującego układu regulacji przy zastosowaniu kryterium Hurwitz’a i
Nyquista.

Przykład zastosowania kryterium Hurwitz’a.

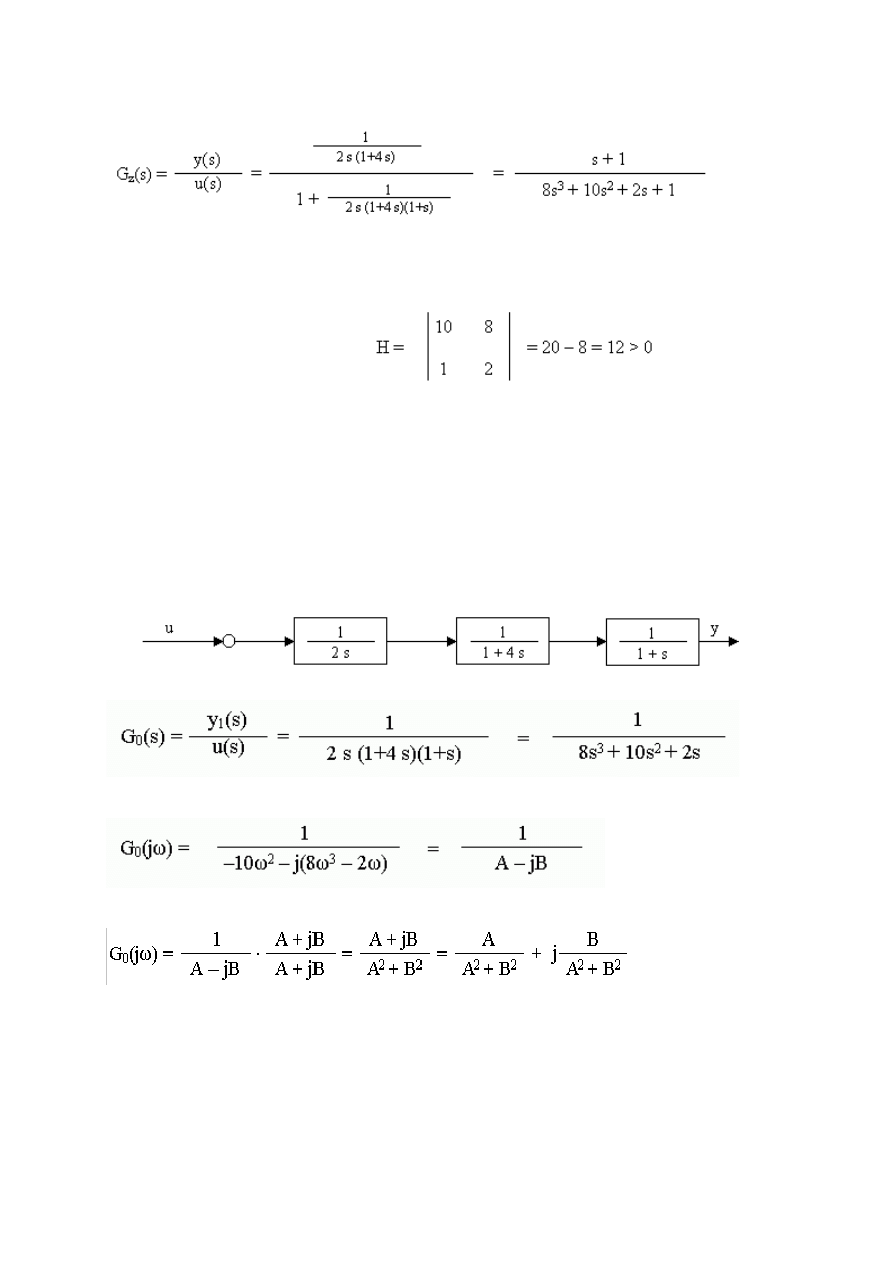
Transmitancja zamkniętego układu regulacji

Równanie charakterystyczne układu: 8s

3

+ 10s

2

+ 2s + 1 = 0

Warunek nałożony na współczynniki równania; a

i

> 0 jest spełniony.

Wyznacznik Hurwitz’a:

Podwyznacznik jest równy sprawdzonemu poprzednio współczynnikowi a

2

więc także jest

dodatni.
Ponieważ spełnione są obydwa warunki kryterium stabilnosci Hurwitz’a układ jest stabilny.



Przykład zastsowania kryterium Nyquist’a.

Badamy otwarty układ regulacji

Podstawiamy jω za s i otrzymujemy wtedy:

gdzie A = -10ω

2

, B = 8ω

3

- 2 ω

G

0

(jω) = Re + j Im

Im = 0 gdy B = 0
8ω

3

- 2ω = 0

⇔

ω1 = 0 , ω2 = 0,5 ;

Re(ω2 = 0,5) = -0,4 > -1

Wykres charakterystyki Nyquista przecina oś części rzeczywistej w punktach: (-0.4, 0) i (0,
0), nie obejmuje wiec punktu (-1, 0). Warunek spełniony.

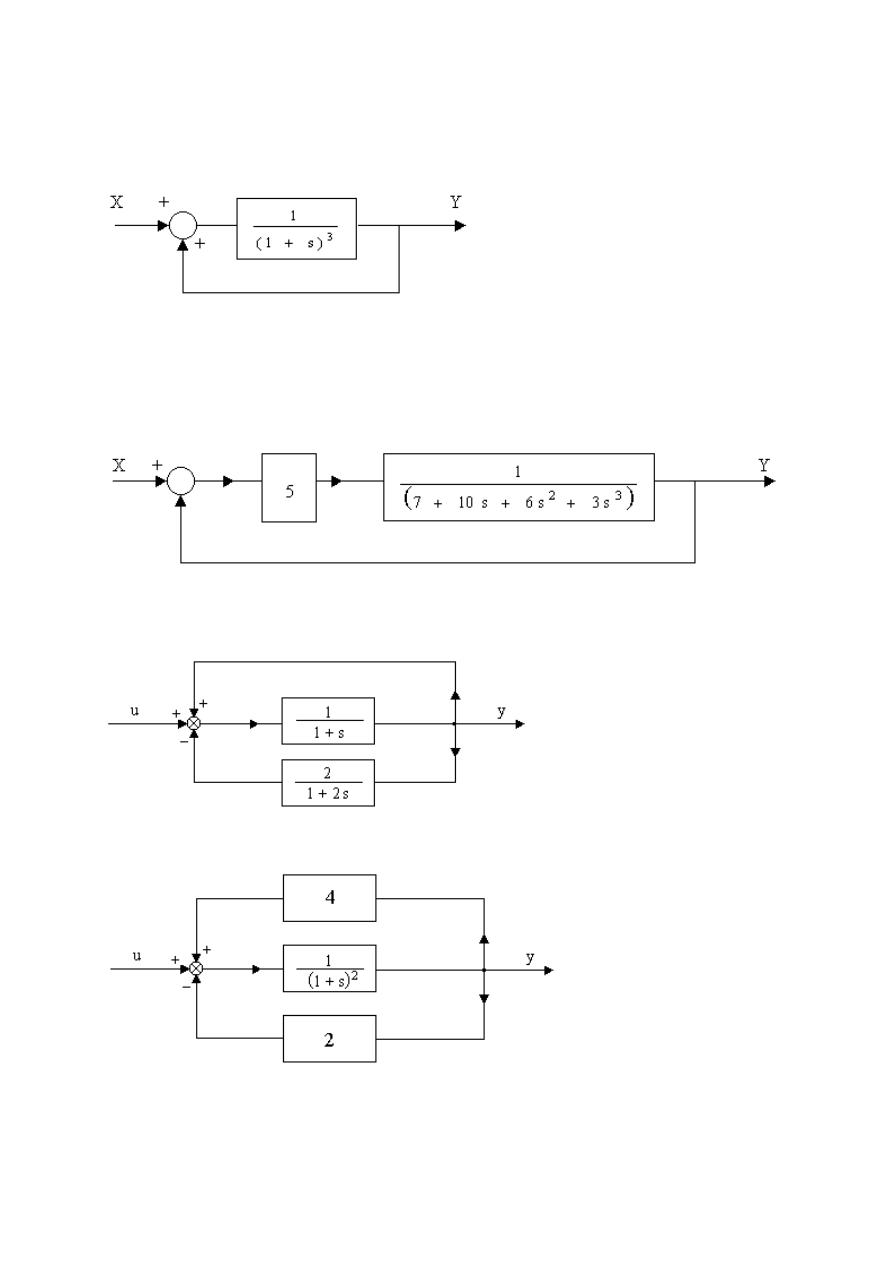
Zadania do samodzielnego rozwiązania:

zad. Udowodnić, że podany poniżej układ jest niestabilny.

zad. Sprawdzic stabilnosc podanego układu regulacji

a) a)

poprzez okreslenie pierwiastkow równania charakterystycznego

b) b)

stosujac kryterium Hurwitz`a

c) c)

stosujac kryterium Nyquist`a

zad. Zbadać czy układ o danym schemacie blokowym jest stabilny.

zad. Zbadać czy układ o danym schemacie blokowym jest stabilny.