
1
Wprowadzenie do Teorii Algorytmów
(Introduction to Algorithms Theory)
Prof. Dr hab. Alexander Prokopenya
Szkoła Główna Gospodarstwa Wiejskiego w Warszawie
Katedra Zastosowań Informatyki
Wykład 4-5.
Algorytmy „dziel i zwyciężaj”
Pry użyciu strategii „dziel i zwyciężaj” (angl. Divide and conquer) problem roz-
wiązuje się, postępując zgodnie z następującym schematem:
1. Dzielimy problem na podproblemy, z których każdy jest mniejszym egzempla-
rzem problemu tego samego typu.
2. Kolejno rozwiązujemy te podproblemy.
3. Lączymy odpowiednio uzyskane rozwiązania.
Zadanie jest realizowane stopniowo, na trzech różnych etapach: pierwszy polega na
dzieleniu problemów na podproblemy; drugi ma miejsce, gdy podproblemy są już tak m a-
łe, że ich rozwiązania są natychmiastowe i nie wymagają stosowania rekursji; natomiast
na samym końcu rozwiązania częściowe skleja się w calość. Wszystko to jest skoordyn o-
wane dzięki rekurencyjnej strukturze algorytmu.
Jako przykład wprowadzający zobaczymy, w jaki sposób, stosując tę technikę, uz y-
skamy nowy algorytm mnożenia liczb, który jest znacznie bardziej efektywny niż metoda
mnożenia, z jaką spotkaliśmy w skole.
1. Mnożenie
Pewnego razu matematyk Carl Friedrich Gauss (1777 – 1855) zauważył, że choć wydaje się, że
iloczyn dwóch liczb zespolonych
i
ad
bc
bd
ac
i
d
c
i
b
a
)
(
)
)(
(
wymaga czterych mnożeń liczb rzeczywistaych, w istocie można go otrzymać, wykonyjąc zale-
dwie trzy mnożenia: ac ,
bd
oraz
)
)(
(
d
c
b
a
, gdyż
bd
ac
d
c
b
a
ad
bc
)
)(
(
.
Rozpatrując to punktu widzenia notacji O, zdawać by się mogło, że zredukowanie liczby
mnożeń z czterech do trzech jest grą niewartą świeczki. Jednak to niewielkie ulepszenie staje się
znaczące, gdy jest stosowane rekurencyjnie.
Porzućmy liczby zespolone i zobaczmy, jak to może pomoc w zwykłym mnożeniu. Niech
x i y będą n-bitowami liczbami natutalnymi. Założmy też dla wygody, że n jest potęga dwójki
(ogólny przypadek jest bardzo podobny). Pierwszym krokiem w stronę wymnożenia x oraz y bę-
dzie rozbicie obu liczb na ich lewe i prawe połowy, z których każda ma
2
/
n
bitów:
R
L
n
x
x
x
2
/
2
,
R
L
n
y
y
y
2
/
2
.
Na przykład, jeśli
2
10110110
x
(indeks dolny 2 oznacza zapis dwójkowy), to
2
1011
L
x
,
2
0110
R
x
oraz
2
4
2
0110
2
1011
x
. Iloczyn x i y może być zatem zapisany jako
R
R
L
R
R
L
n
R
L
n
R
L
n
R
L
n
y
x
y
x
y
x
x
x
y
y
x
x
xy
)
(
2
2
)
2
)(
2
(
2
/
2
/
2
/
.

2
Obliczymy
xy
, korzystając z wyrażenia po prawej stronie. Czas wykonania dodawania
jest liniowy, podobnie jak mnożenie przez potęgi 2 (które jest po prostu przesunięciem w lewo).
Znaczącymi operacjami są cztery
2
/
n
-bitowe mnożenia:
L
L
y
x
,
R
L
y
x
,
L
R
y
x
oraz
R
R
y
x
, z któ-
rymi można sobie poradzić za pomocą czterych wywołań rekurencyjnych. Zatem nasza metoda
mnożenia n-bitowych liczb zaczyna się od wykonania wywołań rekurencyjnych w celu wymno-
żenia tych czterych par
2
/
n
-bitowych liczb (cztery podproblemy dla danych o połowę mniej-
szych), po czym następuje obliczenie wartości wyrażenia po prawej stronie równania w czasie
)
(n
O
. Oznaczając przez
)
(n
T
całkowity czas działania algorytmu na n-bitowych danych wej-
ściowych, dostajemy zależność rekurencyjną
)
(
)
2
/
(
4
)
(
n
O
n
T
n
T
.
Wkrótce zobaczymy, jak wyglądają ogólne metody rozwiązywania takich równań. Tym-
czasem rozwiązanie tego konkretnego równania okazuje się być rzędu
)
(
2
n
O
, czyli czas działa-
nia jest taki sam jak dla tradycyjnej , szkolnej techniki mnożenia. Mamy zatem zupełnie nowy
algorytm, ale nie osiągneliśmy żadnego postępu w efektywności. W jaki sposób możemy jeszcze
usprawnić tę metodę?
W tym momencie przychodzi nam na myśl sztuczka Gaussa. Chociaż obliczenie iloczynu
xy
zdaje się wymagać czterech
2
/
n
-bitowych mnożeń, tak jak już było pokazane wcześniej,
wystarczą zaledwie trzy:
L
L
y
x
,
R
R
y
x
oraz
)
)(
(
R
L
R
L
y
y
x
x
, gdyż
R
R
L
L
R
L
R
L
L
R
R
L
y
x
y
x
y
y
x
x
y
x
y
x
)
)(
(
.
Czas działania wynikającego stąd algorytmu, przedstawionego na rysunku poniżej, jest krótszy:
)
(
)
2
/
(
3
)
(
n
O
n
T
n
T
.
Rzecz w tym, że poprawę stałego czynnika z 4 na 3 wykożystuje się na każdym poziomie rekur-
sji, a zwielokrotnienie tego wynika prowadzi do znacznego zmniejszenia ograniczenia czasu
działania – aż do
)
(
)
(
59
.
1
3
log
n
O
n
O
.
funkcja multiply(x, y)
// wejście: dwie n-bitowe liczby naturalne x i y
// wyjście: ich iloczyn
if
1
n
then return
xy
L
x ,
R
x
lewe
2
/
n
, prawe
2
/
n
bitów x
L
y ,
R
y
lewe
2
/
n
, prawe
2
/
n
bitów y
P
1
= multiply(
L
x ,
L
y )
P
2
= multiply(
R
x ,
R
y )
P
3
= multiply(
R
L
x
x
,
R
L
y
y
)
return
2
2
/
2
1
3
1
2
)
(
2
P
P
P
P
P
n
n
Czas działania algorytmu można uzyskać po analize równania rekurencyjnego
cn
n
aT
n
T
)
2
/
(
)
(
.
Przy podstawianiu
k
n
2
otrzymamy
k
k
k
k
k
k
c
c
aT
a
c
aT
T
2
)
2
)
2
(
(
2
)
2
(
)
2
(
1
2
1
k
k
k
k
k
k
k
c
ac
c
aT
a
c
ac
T
a
2
2
)
2
)
2
(
(
2
2
)
2
(
1
2
3
2
1
2
2
k
k
k
k
c
ac
c
a
T
a
2
2
2
)
2
(
1
2
2
3
3

3
k
k
k
k
k
c
ac
c
a
c
a
T
a
2
2
2
2
)
2
(
1
2
2
1
1
0
a
a
c
a
a
a
a
a
c
a
a
k
k
k
k
k
k
/
2
1
)
/
2
(
1
2
)
)
/
2
(
...
)
/
2
(
/
2
1
(
2
1
1
2
1
2
2
2
2
1
2
2
2
2
2
1
2
2
2
log
a
cn
n
a
c
a
c
a
c
a
a
a
c
a
a
k
k
k
k
k
.
Dla szkolnej techniki mnożenia mamy
4
a
i wtedy
)
(
)
1
(
)
2
/
(
4
)
(
2
2
n
O
cn
n
c
cn
n
T
n
T
.
Zatem dla
3
a
)
(
2
)
2
1
(
)
2
/
(
3
)
(
3
log
3
log
n
O
cn
n
c
cn
n
T
n
T
,
w przybliżeniu jest równy
)
(
59
.
1
n
O
.
W algorytmach „dziel i zwyciężaj” liczba podproblemów odpowiada współczynnikowi
rozgałęzenia dzewa rekursji, niewielkie zmiany tego wspólczynnika mogą mieć wielki wpływ na
czas działania.
Uwaga praktyczna: w ogólnym przypadku nie ma potrzeby stosować rekursji aż do mo-
mentu osiągnięcia 1 bitu. Dla większości procesorów mnożenie 16- lub 32-bitowe jest pojedyn-
czą operacją, więc dopóki liczby nie wychodzą poza ten zakres, należy korzystać z wbudowa-
nych procedur.
Na koniec odwieczne pytanie: Czy możemy znaleźć lepsze zorwiązanie? Okazuje się, że
istnieje szybszy algorytm mnożenia liczb oparty na innym ważnym algorytmie typu „dziel i
zwyciężaj”: szybkiej transformacie Fouriera, o której pomówimy pózniej.
2. Zależności rekurencyjne
Algorytmy „dziel i zwyciężaj” często działają według ogólnego schematu: radzą sobie z proble-
mem o rozmiarze n poprzez rekurencyjne rozwiązywanie a podproblemów o rozmiarze
b
n /
każdy, a następnie łączenie tych rozwiązań w czasie
)
(
d
n
O
, dla pewnych
0
,
,
d
b
a
(w algo-
rytmie mnożenia
3
a
,
2
b
,
1
d
). Ich czas działania może być zatem wyrażony równaniem
)
(
)
/
(
)
(
d
n
O
b
n
aT
n
T
. Wyprowadzimy teraz zwarte rozwiązanie tej rekurencji, aby w przy-
szłości nie musieć rozwiązywać jej dla nowych danych.
Twerdzenie o rekurencji universalnej. Jeśli
)
(
)
/
(
)
(
d
n
O
b
n
aT
n
T
dla pewnych stałych
0
a
,
1
b
oraz
0
d
, to
a
d
gdy
n
O
a
d
gdy
n
n
O
a
d
gdy
n
O
n
T
b
a
b
d
b
d
b
log
)
(
log
)
log
(
log
),
(
)
(
log
To jedno twierdzenie mówi nam o czasach działania większości programów typu „dziel i
zwyciężaj”, z którymi się spotkamy.
Dowód. Aby udowodnić tezę, dla wygody zacznijmy od założenia, że n jest potęga b:
k
b
n
.
Nie wpłynie to w istotny sposób na ostateczny wynik – w końcu n różni się od pewnej potęgi b
co najwyżej o stały czynnik – pomoże nam to natomiast zignorować zaokrąglanie
b
n /
.
kd
d
k
k
kd
k
k
b
c
b
c
b
aT
a
b
c
b
aT
b
T
)
)
(
(
)
(
)
(
)
1
(
2
1
kd
d
k
d
k
k
kd
d
k
k
b
c
b
ac
b
c
b
aT
a
b
c
b
ac
b
T
a
)
1
(
)
2
(
3
2
)
1
(
2
2
)
)
(
(
)
(
kd
d
k
d
k
k
b
c
b
ac
b
c
a
b
T
a
)
1
(
)
2
(
2
3
3
)
(

4
kd
d
k
d
k
d
k
k
b
c
b
ac
b
c
a
b
c
a
b
T
a
)
1
(
2
2
1
0
)
(
1
)
1
(
2
)
2
(
2
2
1
1
)
1
(
k
d
k
k
d
k
d
d
d
k
k
a
b
a
b
a
b
a
b
b
c
a
T
a
.
Gdy
a
d
b
log
, otrzymujemy
a
b
b
a
d
b
log
, zatem
)
)
1
(
(
)
1
(
)
(
log
k
c
T
b
k
c
a
T
a
b
T
a
k
k
k
k
b
)
log
(
)
log
)
1
(
(
)
(
log
n
n
O
n
c
T
n
n
T
d
b
a
b
.
Gdy
a
d
b
log
i k zmierza się od 0 do
n
b
log
, wartoście w nawiasie tworzą ciąg geometryczny
o ilorazie
a
b
d
/ . Znaczenie sumy k wyrazów tego ciągu może być zapisane jako
a
b
a
b
d
k
kd
/
1
/
1
.
Zatem otrzymujemy
kd
d
d
d
d
k
d
k
kd
d
k
k
k
b
b
a
b
c
b
a
b
c
T
a
a
b
a
b
b
c
a
T
a
b
T
)
1
(
/
1
/
1
)
1
(
)
(
1
.
a
d
gdy
n
O
a
d
gdy
n
O
n
b
a
b
c
b
a
b
c
T
n
n
T
b
a
b
d
d
d
d
d
d
a
b
b
log
),
(
log
),
(
)
1
(
)
(
log
log
3. Mnożenie macierzy
Iloczynem dwóch macierzy
n
n
, X oraz Y, jest trzecia macierz
n
n
,
XY
Z
, której element o
współrzędnych
)
,
( j
i
jest dany wzorem
n
k
kj
ik
ij
Y
X
Z
1
.
Powyższy wzór implikuje algorytm mnożenia macierzy działający w czasie
)
(
3
n
O
; należy obli-
czyć wrtości
2
n elementów, a każde obliczenie zajmuje czas
)
(n
O
.
W 1969 roku niemieecki matematyk Volker Strassen ogłosił znacznie bardziej efektywny
algorytm, oparty na strategii „dziel i zwyciężaj”. Mnożenie macierzy bardzo łatwo można po-
dzielić na podproblemy, ponieważ może być wykonywane blokowo. Aby zobaczyć, co to ozna-
cza, podzielmy X na cztery bloki o rozmiarach
2
/
2
/
n
n
, to samo zróbmy dla Y:
D
C
B
A
X
,
H
G
F
E
Y
.
Wtedy ich iloczyn może być wyrażony za pomocą tych bloków, dokładnie tak, jakby te bloki
bały pojedynczymi elementami:
DH
CF
DG
CE
BH
AF
BG
AE
H
G
F
E
D
C
B
A
XY
.
Stosujemy teraz strategię „dziel i zwyciężaj”: aby obliczyć iloczyn macierzy XY o roz-
miarze n, rekurencyjnie obliczamy osiem iloczynów AE, BG, CE, DG, AF, H, CF, DH macierzy
o rozmiarze
2
/
n
każda, a następnie wykonujemy kilka dodawań w czasie
)
(
2
n
O
. Całkowity
czas działania jest opisany zależnością rekurencyjną:

5
)
(
)
2
/
(
8
)
(
2
n
O
n
T
n
T
.
To prowadzi do mało imponującego rozwiązania
)
(
3
n
O
, takiego samego wynik jak przy
zwykłym algorytmie. Jednak efektywność może zostać ulepszona i podobnie jak przy mnożeniu
liczb całkowitych, kluczowe będzie sprytne wykorzystanie algebry. Okazuje się, że iloczyn XY
można obliczyć przy użyciu zaledwie siedmiu podproblemów o rozmiarach
2
/
2
/
n
n
:
7
3
5
1
4
3
2
1
6
2
4
5
P
P
P
P
P
P
P
P
P
P
P
P
XY
,
gdzie
)
(
1
H
F
A
P
,
)
)(
(
5
H
E
D
A
P
,
H
B
A
P
)
(
2
,
)
)(
(
6
H
G
D
B
P
,
E
D
C
P
)
(
3
,
)
)(
(
7
F
E
C
A
P
,
)
(
4
E
G
D
P
.
Nowy czas działania wynosi
)
(
)
2
/
(
7
)
(
2
n
O
n
T
n
T
,
który na podstawie twierdzenia o rekurencji uniwersalnej okazuje się być równy
)
(
)
(
81
.
2
7
log
n
O
n
O
.
4. Sortowanie przez scalanie (merge sort)
Sortowanie to problem bardzo często rozwiązywany na komputerach. Jego popularność wiąże
się z faktem, że łatwiej jest korzystać ze zbiorów uporządkowanych niż nieuporządkowanych.
Sortowanie jest dobrym przykładem tego, że określone zadanie może być wykonane według
wielu różnych algorytmów. Każdy z algorytmów ma pewne zalety i wady, które trzeba przeana-
lizować dla konkretnego zastosowania.
Sortowaniem (ang. sorting) nazywamy proces ustawiania zbioru obiektów w określo-
nym porządku. Sortowanie stosuje się w celu ułatwienia późniejszego wyszukiwania elementów
sortowanego zbioru.
Niech U będzie zbiorem obiektów
n
a
a
a
,...,
,
2
1
Sortowanie polega na permutowaniu tych obiektów aż do chwili osiągnięcia uporządkowania
n
k
k
k
a
a
a
,...,
,
2
1
takiego, że dla zadanej funkcji porządkującej f zachodzi
)
(
...
)
(
)
(
2
1
n
k
k
k
a
f
a
f
a
f
.
Wartość funkcji f nazywa się kluczem obiektu i służy do identyfikacji obiektów.
Zauważmy, że w sformułowanym powyżej problemie sortowania nic nie wiemy o natu-
rze elementów z U. Na U mogą składać się zarówno liczby całkowite lub rzeczywiste, jak i U
może być zbiorem rekordów, które należy posortować według ich kluczy. Przyjmujemy, że ele-
menty ciągu
n
a
a
a
,...,
,
2
1
znajdują się w tablicy
]
..
1
[ n
a
. Jedynym sposobem ustalenia porządku w
tablicy a jest porównywanie jej elementów parami. Operacja porównania będzie operacją do-
minującą. Ponieważ będziemy chcieli ustalić wynik także w tablicy a, potrzebna nam jest jesz-
cze operacja zamiany dwóch elementów w tablicy. Operacją tą będzie operacja
)
,
( j
i
Swap
pole-
gająca na zamianie elementów w tablicy a z pozycji i oraz j,
n
j
i
,
1
.
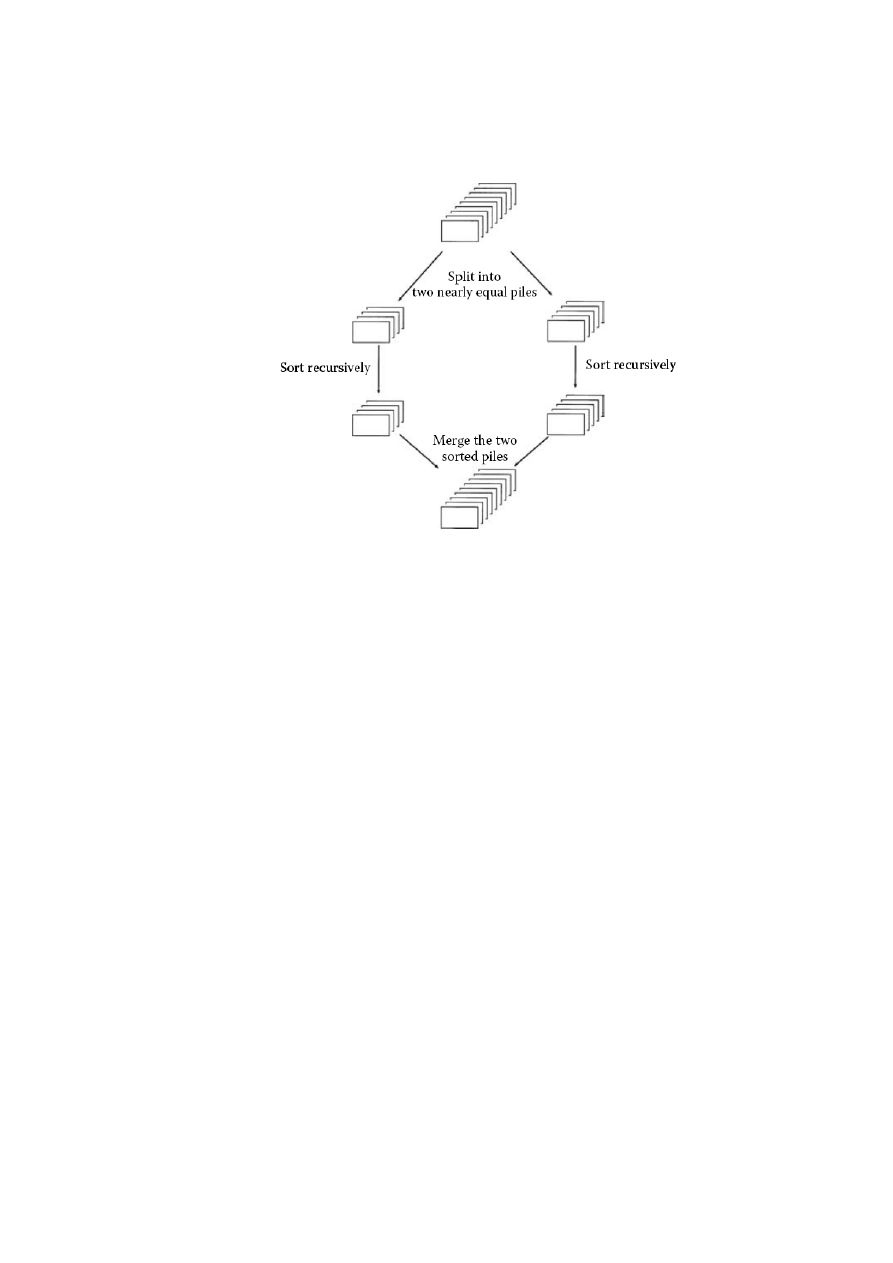
6
Problem posortowania listy liczb prowadzi bezpośrednio do zastosowania strategii „dziel
i zwyciężaj”: dzielimy listę na połowy, rekurencyjnie sortujemy każdą połowę, a następnie sca-
lamy (ang. merge) dwie posortowane podlisty (Rys. 1).
Rys. 1. Schemat sortowania przez scalanie
Przykład. Rozważmy ciąg 5,7,4,9,3,6,2,1. Potraktujmy, każdy z elementów tego ciągu jako jed-
noelementowy uporządkowany ciąg. Zastosujemy procedurę scalania do sąsiadujących ciągów,
otrzymując 4 dwuelementowe posortowane ciągi: {5,7}, {4,9}, {3,6}, {1,2}. Teraz ponownie
zastosujemy scalanie sąsiednich ciągów tworząc dwa czteroelementowe segmenty uporządko-
wane {4,5,7,9}, {1,2,3,6}. Wykonanie jeszcze jednego scalania pozwoli nam utworzyć ciąg upo-
rządkowany {1, 2, 3, 4, 5, 6, 7, 9}.
Niech a będzie ciągiem o długości n, a b ciągiem o długości m. W opisanym poniżej al-
gorytmie Merge, oba ciągi wejściowe a i b zostały rozszerzone o jeden element, oznaczony tu-
taj
. Zakładamy, że jest on większy od wszystkich innych elementów obu ciągów. Taki za-
bieg pozwoli nam uprościć nieco strukturę algorytmu. Zadbamy jednak o to, by ciąg e otrzyma-
ny w wyniku miał dokładnie n+m elementów.
Algorytm Merge(a[1..n], b[1..m])
if n=0 return b[1..m]
if m=0 return a[1..n]
a[n+1] :=
; b[m+1]:=
;
i := 1; j := 1; k :=1;
while (k
(n+m)) do
if (a[i]
b[j]) then
e[k] := a[i]; i := i+1
else
e[k] := b[j]; j := j+1
fi;
k := k+1
od;
return e

7
4.1. Poprawność algorytmu
Zauważmy, że elementy dodatkowe, dopisane do ciągów a i b, nie mogą się znaleźć w ciągu
wynikowym, gdyż pętla jest wykonywana tylko (n+m) razy. Gdyby, w którymś momencie
1
n
i
, tzn. a[i] =
, to przy porównywaniu tego elementu z b[j] dla
1
m
j
, wygra b[j] i
to b[j] zostanie zapisane w ciągu wynikowym. Analogicznie w przypadku, gdy
1
m
j
. Jeśli
zaś oba wskaźniki i, j wskazują element specjalny, to znaczy, że wszystkie poprzednie elementy
już zostały wpisane do tablicy wynikowej, a więc k musi być w tym momencie równe
1
m
n
.
Warunek pętli "while" nie będzie spełniony i zakończymy wykonywanie algorytmu.
Jest oczywiste, że algorytm zatrzymuje się dla dowolnych danych, gdyż zmienna kontro-
lująca pętlę zmienia się od 1 do n+m. Trzeba jeszcze pokazać, że otrzymany wynik jest ciągiem
uporządkowanym złożonym z elementów danych ciągów.
Przed pierwszym wejściem do pętli "while" jest trywialnie spełniony warunek e[1]
e[2]
...
e[k-1]. Załóżmy, że rozpoczynamy pewną iterację pętli "while" i spełnione są własno-
ści:
e[1]
e[2]
...
e[k-1], i
n+1, j
m+1, k = (i + j -1), k
(n+m+1), (*)
(ciąg e[1],...,e[k-1] jest permutacją ciągu a[1],...,a[i-1],b[1],...,b[j-1] ).
Formuły te mówią, że k-1 elementów w ciągu e tworzy ciąg uporządkowany, a ponadto i-1 ele-
mentów ciągu a oraz j-1 elementów ciągu b zostało już zapisanych na pozycjach od 1 do k-1
ciągu e.
Po wykonaniu instrukcji warunkowej "if (a[i]
b[j])..." , na miejscu k-tym w ciągu e po-
jawi się mniejszy z elementów a[i], b[j] oraz, albo i, albo j wzrośnie o jeden. Ponieważ ciągi a i
b są uporządkowane niemalejąco zatem wstawiony element e[k] jest niemniejszy od wszystkich
elementów, które znajdują się na wcześniejszych pozycjach w ciągu e. Mamy więc w tablicy e
aż k elementów uporządkowanych, oraz i+j-1 = k+1.
e[1]
...
e[k-1]
e[k], i
n+1, j
m+1, (k+1) = (i + j -1), k
(n+m+1),
(ciąg e[1],...,e[k] jest permutacją elementów ciągu a[1],...,a[i-1],b[1],...,b[j-1] ).
Po wykonaniu instrukcji przypisania "k:=k+1;" ponownie spełnione są własności (*). Wykazali-
śmy tym samym, że jest to niezmiennik pętli. Z twierdzenia o niezmienniku, ta sama formuła jest
spełniona w chwili wyjścia z pętli. Wtedy jednak k = n+m+1 i wszystkie elementy, zarówno cią-
gu a, jak i b, znalazły się już w ciągu e oraz e[1]
...
e[n+m]. Spełniony jest zatem warunek
końcowy specyfikacji.
Twierdzenie. Algorytm Merge jest całkowicie poprawnym rozwiązaniem problemu scalania za
względu na specyfikację,
wp = {a[1]
...
a[n], b[1]
...
b[m], n>0, m>0}
wk = {ciąg e[1],...,e[n+m] jest uporządkowaną niemalejąco permutacją elementów a[1],..., a[n],
b[1],...,b[m] }
w każdej strukturze danych z liniowym porządkiem
.
4.2. Koszt algorytmu
Ponieważ w pętli "while" wykonujemy w każdej iteracji tylko jedno porównanie, a liczba iteracji
wynosi dokładnie n+m, zatem koszt algorytmu jest liniowy w stosunku do długości ciągów sca-
lanych i wynosi
T(n) = O(n+m).
funkcja mergesort(a[1..n])
// wejście: tablica liczb a[1..n]

8
// wyjście: tablica wejściwa po posortowaniu
if
1
n
then
return merge(mergesort(
2
/
..
1
[
n
a
),mergesort(
n
n
a
..
1
2
/
[
))
else return a
Poprawność tego algorytmu jest oczywista, o ile tylko określona jest poprawna procedura
merge. Funkcja merge wykonuje taką samą pracę przy każdym wywolaniu rekurencyjnym, a
jej całkowity czas działania to
)
(n
O
. Zatem procedura scalania jest liniowa, a całkowity czas
potrzebny na wykonanie mergesort to
)
log
(
)
(
)
2
/
(
2
)
(
n
n
O
n
O
n
T
n
T
.
Spoglądając raz jeszcze na mergesort, możemy zauważyć, że cała właściwa praca po-
lega na scalaniu, które jednak nie może się zacząć, dopoki rekurcja nie zejdzie do tablic jednoe-
lementowych. Takie tablice jednoelementowe są scalane parami, co prowadzi do powstania ta-
blic dwuelementowych. Następnie pary takich tablic dwuelementowych są scalane, tworząc czte-
roelementowe itd.
Takie podejście wskazuje również, w jaki sposób mergesort może być wykonywany
iteracyjne. W każdym momencie dany jest zbiór „aktywnych” tablic – początkowo są to tablice
jednoelementowe – które scalane parami tworzą nowy zestaw aktywnych tablic. Tablice te mogą
być zorganizowane w kolejkę i przetwarzane przez sukcesywne usuwanie dwóch pierwszych
tablic, scalanie ich i umieszczenie otrzymanej tablicy na końcy kolejki.
5. Mediany
Medianą listy liczb nazywamy pięćdziesiąty percentyl listy: połowa liczb jest od niej większa, a
połowa mniejsza. Na przykład medianą
]
25
,
30
,
10
,
1
,
45
[
jest 25, poniewaz jest to środkowy ele-
ment uporządkowanej listy zlożonej z tych samych liczb. Jeśli lista ma parzystą długość, istnieją
dwie możliwe wartości dla elementu środkowego, wtedy, powiedzmy, wybieramy mniejszą z
nich.
Obliczenie mediany z n liczb jest proste: wystarczy je posortować. Wadą jest czas trwa-
nia algorytmu –
)
log
(
n
n
O
, podczas gdy zdecydowanie wolelibyśmy czas liniowy. Nie powinni-
śmy jednak tracić nadziei, ponieważ podczas sortowania wykonujemy znacznie więcej pracy niż
w rzeczywistości potrzebujemy – chcemy tylko znaleźć środkowy element i nie interesuje nas
właściwe uporządkowanie pozostalych.
Szukając rozwiązania rekurencyjnego, często paradoksalnie łatwiej jet pracować z ogól-
niejszą wersją problemu – z tego prostego powodu, że możemy się oprzeć na silniejszej rekursji.
W naszym przypadku rozważanym uogólnieniem będzie selekcja.
Selekcja.
Wejście: lista liczb S; liczba naturalna k,
Wyjście: k-ty najmniejszy element S.
Na przykład, jeśli
1
k
, szukane jest minimum S, natomiast jeśli
2
/
|
| S
k
, to szu-
kamy mediany.
5.1. Randomizowany algorytm „dziel i zwyciężaj” dla selekcji
Oto podejście „dziel i zwyciężaj” do problemu selekcji. Dla dowolnej liczby v wyobraźmy sobie
podzielenie listy S na trzy kategorie elementów: elementy mniejsze od v, równe v (elementy mo-
gą się powtarać) oraz większe od v. Nazwijmy je odpowiednio
L
S ,
v
S ,
R
S . Na przykład, jeśli
tablica
S :
2
36
5
21 8 13
11
20
5
4
1
jest podzielona dla
5
v
, trzy wygenerowane podtablice wyglądają następująco:

9
S
L
:
2
4
1
S
v
:
5
5 S
R
:
36
21
8
13
11
20
Przeszukiwanie może być natychmiast zawężone do jednej z tych podlist. Jeśli chcemy
znaleźć, powiedzmy, ósmy najmniejszy element S, wiemy, że będzie to trzeci najmniejszy ele-
ment
R
S , ponieważ
5
|
|
|
|
v
L
S
S
. Czyli selection(S,8) = selection(
R
S ,3). Ogólnie rzecz bio-
rąc, porównując k z rozmiarem podtablic, możemy szybko stwierdzić, która z nich zawiera po-
szukiwany element:
|
|
|
|
|)
|
|
|
,
(
|
|
|
|
|
|
|
|
)
,
(
)
,
(
v
L
v
L
R
v
L
L
L
L
S
S
k
gdy
S
S
k
S
selection
S
S
k
S
gdy
v
S
k
gdy
k
S
selection
k
S
selection
Trzy podlisty
L
S ,
v
S ,
R
S można uzyskać z S w czasie liniowym; w rzeczywistości takie
obliczenie może być nawet wykonane bez przydzielania dodatkowej pamięci. Następnie wyko-
nuje się obliczania rekurencyjnie na właściwej liście. Wynikiem podziału tablicy jest zatem
zmniejszenie liczby elementów z
|
| S do co najwyżej
|}
|
|,
max{|
R
L
S
S
.
Nasz algorytm „dziel i zwyciężaj” dla selekcji jest teraz w pełni opisany, z wyjątkiem
kluczowego szczegółu, jakim jest wybór v. Wartość v musi być wybrana szybko i powinna być
taka, by tablica została istotnie zmniejszona, sytuacja jest idealna dla
|
|
2
1
|
|
|,
|
S
S
S
R
L
. Gdyby-
śmy potrafili zawsze zagwarantować taką sytuację, dostalibyśmy czas działania
)
(
)
2
/
(
)
(
n
O
n
T
n
T
,
który zgodnie z naszym życzeniem jest liniowy. To jednak wymaga wybrania na v mediany, co
przecież jest naszym ostatecznym celem. Zamiast tego posłużymy się znacznie prostszym roz-
wiązaniem: wybieramy v z S losowo.
5.2. Analiza efektywności
Oczywiście czas działania naszego algorytmu zależy od losowych wyborów v. Może się zdarzyć,
że każdy wybór będzie pechowy i wartością v będzie największy (lub najmniejszy) element ta-
blicy, a zatem tableca będzie się zmniejszać w każdym kroku tylko o jeden element. We wcze-
śniejszym przykładzie mogliśmy najpierw wybrać
36
v
, następnie
21
v
itd. Ten czarny sce-
nariusz zmusiłby nasz algorytm selekcji do wykonania
)
(
2
...
)
2
(
)
1
(
2
n
n
n
n
n
operacji (podczas obliczania mediany), niemniej takie zdarzenie jest wyjątkowo mało prawdo-
podobne. Równie mało prawdopodobny jest najlepszy przypadek przedyskutowany wcześniej, w
którym każde losowo wybrane v okazuje się rozdzielać tablicę idealnie na pół, skutkując czasem
działania
)
(n
O
. Gdzie, w przedziale od
)
(n
O
do
)
(
2
n
, znajduje się średni czas działania? Na
szczęście znajduje się on bardzo blisko czasu działania w najlepszym przypadku.
Aby rozróżnic szczęsliwe wybory v od nieszczęśliwych, powiemy, że v jest dobre, jeśli
znajduje się pomiędzy 25 a 75 percentylem tablicy, z której jest wybierany. Takie wybory v się
nam podobają, ponieważ gwarantują, że podlisty
L
S oraz
R
S mają rozmiar równy co najwyżej
trzy czwarte S, a zatem tablica znacznie się zmniejsza. Na szczęście dobre wartości v są liczne:
połowa elementów dowolnej listy musi leżeć między 25 a 75 percentylem.
Zatem średnio po dwóch operacjach podziału tablica zmniejszy się do co najwyżej trzech
czwartych swego wyjściowego rozmiaru. Oznaczając przez
)
(n
T
oczekiwany czas działania dla
tablicy o rozmiarze n, dostajemy
)
(
)
4
/
3
(
)
(
n
O
n
T
n
T
.

10
Na podstawie tej rekurencji wnioskujemy, że
)
(
)
(
n
O
n
T
: dla dowolnych danych wejściowych
nasz algorytm zwraca poprawną odpowiedź po – średnio – liniowej liczbie kroków.
6. Szybka transformata Fouriera
Widzieliśmy do tej pory, w jaki sposób stosując strategię „dziel i zwyciężaj”, można uzyskać
szybkie algorytmy mnożenia liczb całkowitych i macierzy. Naszym kolejnym celem są wielo-
miany. Iloczynem dwóch wielomianów stopnia n jest wielomian stopnia 2n, na przykład
4
3
2
2
2
12
11
12
5
2
)
4
2
(
)
3
2
1
(
x
x
x
x
x
x
x
x
.
Ogólniej, jeśli
n
n
x
a
x
a
a
x
A
...
)
(
1
0
oraz
n
n
x
b
x
b
b
x
B
...
)
(
1
0
, to ich iloczyn
n
n
x
c
x
c
c
x
B
x
A
x
C
2
2
1
0
...
)
(
)
(
)
(
ma współczynniki
k
i
i
k
i
k
k
k
k
b
a
b
a
b
a
b
a
c
0
0
1
1
0
...
(dla
n
i
bierzemy
i
a oraz
i
b równe zero). Obliczenie
k
c na podstawie tego wzoru wymaga
)
(k
O
kroków, a znalezenie wszystkich
1
2
n
współczynników wydaje się wymagać czasu
)
(
2
n
. Czy możemy szybciej mnożyć wielomiany?
Rozwiązanie, którym będziemy się teraz zajmować, szybka transformata Fouriera, zre-
wolucjonizowalo – a właściwe stworzyło – dziedzinę przetwarzania sygnalów. Z uwagi na
ogromne znaczenie i bogactwo zastosowań w różnych dziedzinach badawczych, podejdziemy do
tego zagadnienia nieco dokładniejniż zazwyczaj.
6.1. Alternatywne reprezentacje wielomianów
Reprezentacja przez współczynniki wielomianu
n
j
j
j
x
a
x
A
0
)
(
stopnia n to wektor współczyn-
ników
)
,...,
,
(
1
0
n
a
a
a
a
. Reprezentacja za pomocą współczynników jest dogodna przy niektó-
rych operacjach na wielomianach. Na przykład operacja ewaluacji wielomianu
)
(x
A
w danym
punkcie
0
x polega na obliczeniu wartości
)
(
0
x
A
. Ewaluacje można wykonać w czasie
)
(n
,
korzystając t tzw. schematu Hornera:
))...))
(
(
...
(
(
)
(
0
1
0
2
0
1
0
0
0
n
n
a
x
a
x
a
x
a
x
a
x
A
.
Podobnie, dodawanie dwóch wielomianów reprezentowanych przez wektory współczynników
)
,...,
,
(
1
0
n
a
a
a
a
i
)
,...,
,
(
1
0
n
b
b
b
b
zajmuje czas
)
(n
: wynik stanowi wektor
)
,...,
,
(
1
0
n
c
c
c
c
,
gdzie
j
j
j
b
a
c
dla
n
j
,...,
1
,
0
.
Reprezentacja przez wartości w punktach wielomianu
)
(x
A
stopnia n to zbiór par
punkt-wartość
)}
,
(
...,
),
,
(
),
,
{(
1
1
0
0
n
n
y
x
y
x
y
x
taki, że wszystkie
k
x są parami różne oraz
)
(
k
k
x
A
y
dla
n
k
,...,
1
,
0
. Wielomian może mieć
wiele różnych reprezentacji przez wartości w punktach, ponieważ jako podstawy tej reprezenta-
cji można użyć dowolnego zbioru
1
n
różnych punktów
0
x ,
1
x , ...,
n
x .
Obliczanie omawianej reprezentacji dla wielomianu danego w reprezentacji przez współ-
czynniki jest proste, poniaważ wystarczy w tym celu wybrać
1
n
różnych punktów
0
x ,
1
x , ...,
n
x
, a następnie obliczyć
)
(
k
x
A
dla
n
k
,...,
1
,
0
. Korzystając z metody Hornera, można zrobić
to w czasie
)
(
2
n
. Jak się później przekonamy, odpowiednio dobierając
k
x
, możemy zreduko-
wać czas obliczeń do
)
log
(
n
n
.

11
Zadanie odwrotne do ewaluacji – wyznaczanie współczynników wielomianu na podsta-
wie reprezentacji przez wartości w punktach – nosi nazwę interpolacji.
Twierdzenie. Dla dowolnego zbioru
)}
,
(
...,
),
,
(
),
,
{(
1
1
0
0
n
n
y
x
y
x
y
x
złożonego z
1
n
par punkt-
wartość istnieje dokładnie jeden wielomian
)
(x
A
stopnia n taki, że
)
(
k
k
x
A
y
dla
n
k
,...,
1
,
0
.
Dowód. Dowód opiera się na istnieniu odwrotności pewnej macierzy. Równanie
)
(
k
k
x
A
y
jest
równoważnie z równaniem macierzowym
n
n
n
n
n
n
n
n
y
y
y
a
a
a
x
x
x
x
x
x
x
x
x
1
0
1
0
2
1
2
1
1
0
2
0
0
1
1
1
.
(1)
Macierz po lewej stronie oznaczamy jako
)
,...,
,
(
1
0
n
x
x
x
V
i nazywamy macierzą Vandermonde’a.
Wyznacznikiem tej macierzy jest
n
k
j
j
k
x
x
0
)
(
Zatem jeśli
k
x są różne, to jest ona odwracalna (to znaczy nieosobliwa). Współczynniki
j
a
można więc wyznaczyć jednoznacznie na podstawie reprezentacji przez wartości w punktach:
y
x
x
x
V
a
n
1
1
0
)
,...,
,
(
.
Dowód twierdzenia opisuje algorytm interpolacji polegający na rozwiązaniu układu (1)
równań liniowych. Korzystając z metody eleminacji Gaussa, ten układ możemy rozwiązać w
czasie
)
(
3
n
O
. Szybszy algorytm interpolacji w punktach opiera się na wzorze Lagrange’a:
n
k
k
j
j
k
k
j
j
k
x
x
x
x
y
x
A
0
)
(
)
(
)
(
.
(2)
Oczywiście prawa strona równania (2) jest wielomianem stopnia n, spełniającym równanie
k
k
y
x
A
)
(
dla każdego k.
Reprezentacje wielomianów za pomocą współczynników i wartości w punktach są w
pewnym sensie równoważne; to znaczy, wielomian representowany przez wartości w punktach
ma swój wyznaczony jednoznacznie odpowiednik w reprezentacji przez współczynniki. Tak
więc ewaluacja i interpolacja w
1
n
punktach są dobrze zdefiniowanymi, wzajemnie odwrot-
nymi operacjami, realizującymi przejście między reprezentacją wielomianu przez współczynniki
a reprezentacją przez wartości w punktach. Opisane powyżej algorytmy dla tych problemów
działają w czasie
)
(
2
n
.
Reprezentacja przez wartości w punktach jest dość wygodna do użycia przy wielu opera-
cjach na wielomianach. W dodawaniu, jeśli
)
(
)
(
)
(
x
B
x
A
x
C
, to
)
(
)
(
)
(
k
k
k
x
B
x
A
x
C
w
każdym punkcie
k
x
. Czas dodawania dwóch wielomianów stopnia n, zadanych przez wartości w
punktach, wynośi zatem
)
(n
.
Reprezentacja przez wartości w punktach jest równie dogodna do mnożenia wielomia-
nów. Jeśli
)
(
)
(
)
(
x
B
x
A
x
C
, to
)
(
)
(
)
(
k
k
k
x
B
x
A
x
C
w każdym punkcie
k
x
, więc w celu
otrzymania reprezentacji przez wartości w punktach wielomianu C możemy w każdym punkcie z
osobna przemnożyć wartość wielomianu A przez wartość wielomianu B. Ponieważ jednak sto-
pień wielomianu C jest równy 2n, do reprezentowania C potrzebujemy 2n par punkt-wartość.
12
Musimy zatem wyjść od „rozszerzonych” reprezentacji przez wartości w punktach dla A i B, z
których każda będzie się składać z 2n par punkt-wartość. Widać stąd, że dla dwóch wejściowych
wielomianów w rozszerzonej reprezentacji przez wartości w punktach czas potrzebny na obli-
czanie reprezentacji przez wartości w punktach ich iloczynu wynosi
)
(n
, a więc znacznie
mniej niż w przypadku reprezentacji przez wspołczynniki.
Rozważmy na koniec problem ewaluacji w nowym punkcie wielomianu zadanego przez
wartości w punktach. Nie widać tu żadnego prostszego sposobu niż przekształcenie wielomianu
do reprezentacji przez współczynniki, a następnie obliczenie jego wartości w nowym punkcie.
6.2. Szybkie mnożenie wielomianów reprezentowanych przez współczynniki
Czy możemy skorzystać a działającej w czasie liniowym metody mnożenia wielomianów repre-
zentowanych przez wartości w punktach, żeby przyspieszyć mnożenie wielomianów w reprezen-
tacji przez współczynniki? Odpowiedź na to pytanie zależy od tego, czy umiemy szybko wyko-
nywać przekształcenie wielomianu z reprezentacji przez współczynniki do reprezentacji przez
wartości w punktach (ewaluacja) i na odwrót (interpolacja).
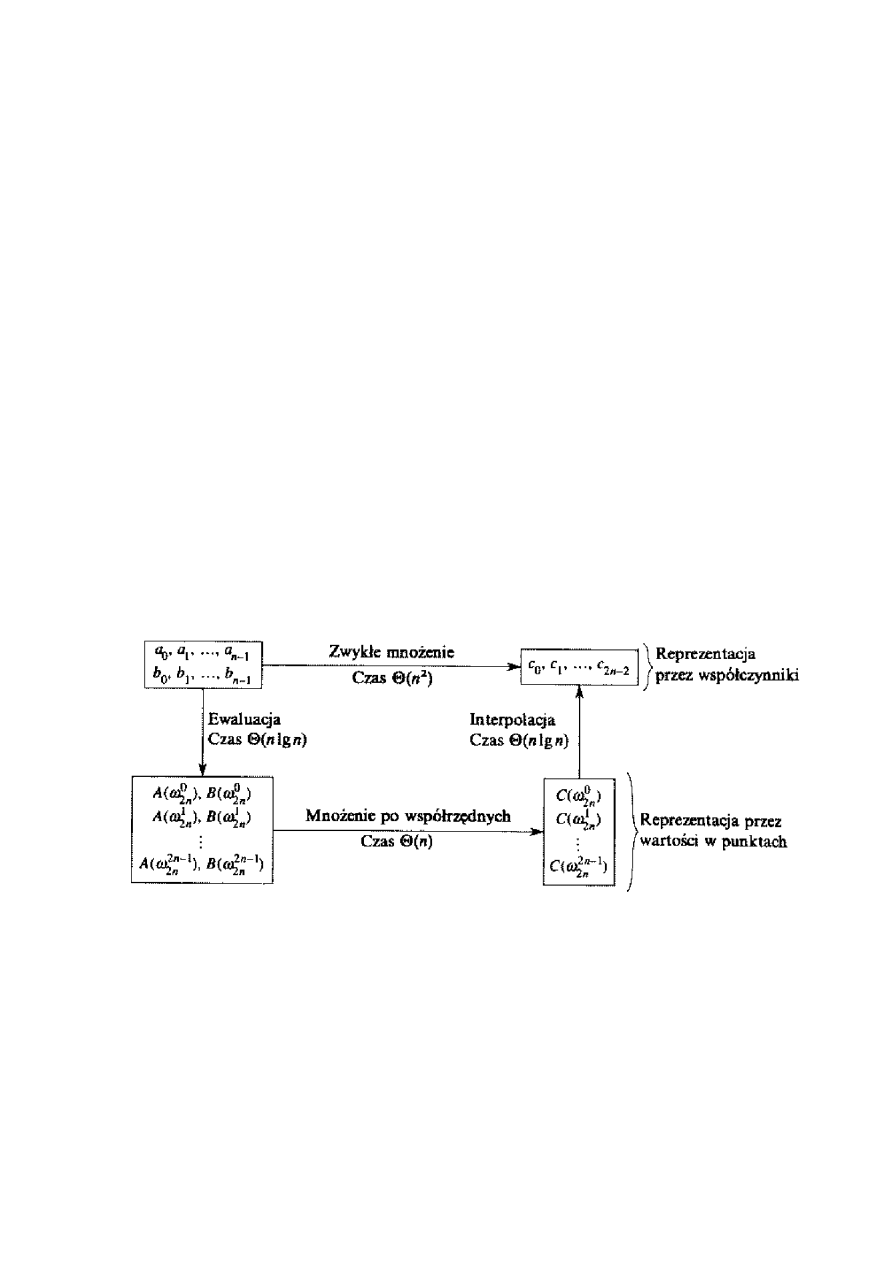
Do obliczania wartości możemy użyć zupełnie dowolnych punktów, ale jeśli wybierzemy
je odpowiednio, będziemy mogli dokonywać konwersji między obiema reprezentacjami w czasie
)
log
(
n
n
. Strategię tę ilustruje rysunek poniżej.
Należy jeszcze poruszyć drobną kwestię związaną z ograniczeniami stopni wielomianów.
Iloczyn dwóch wielomianów stopnia
1
n
jest wielomianem stopnia
)
1
(
2
n
. Przed zmianą re-
prezentacji wejściowych wielomianów A i B podwajamy zatem najpierw ich stopni do wartości
)
1
(
2
n
, dodając n zerowych współczynników przy najwyższych potęgach. Ponieważ wektory
mają po 2n elementów, korzystamy z „zespolonych pierwiastków stopnia 2n z jedności”, ozna-
czonych na rysunku symbolami
n
2
.
Poniższa, korzystająca z FFT procedura mnoży dwa wielomiany
)
(x
A
i
)
(x
B
stopnia n
w czasie
)
log
(
n
n
, przy czym wielomiany wejściowe i wyjściowy są reprezentowane przez
współczynniki. Zakładamy, że n jest potęga dwójki; warunku tego można zawsze dotrzymać,
dostawiając zerowe współczynniki przy najwyższych potęgach x.
1. Podwojenie stopnia wielomianów: Rozszerz reprezentacje przez współczynniki wielo-
mianów
)
(x
A
i
)
(x
B
do wartości stopnia 2n, dodając do każdej po n zerowych współczynników
przy najwyższych potęgach.
2. Ewaluacja: Oblicz reprezentacje przez wartości w punktach dla wielomianów
)
(x
A
i
)
(x
B
, stosując dwukrotnie FFT rzędu 2n. Reprezentacje te składają się z wartości wielomianów
dla pierwiastków stopnia 2n z jedności.
13
3. Mnożenie po współrzędnych: Oblicz reprezentację przez wartości w punktach wielo-
mianu
)
(
)
(
)
(
x
B
x
A
x
C
, wymnażając odpowiadające sobie wartości. Reprezentacja ta składa się
z wartości C(x) we wszystkich pierwiastkach stopnia 2n z jedności.
4. Interpolacja: Utwórz reprezentację przez współczynniki wielomianu C(x), stosując
jednokrotnie FFT do wektora 2n wartości w celu oblicznia odwrotnej DFT.
Kroki 1 i 3 realizuje się w czasie
)
(n
, a 2 i 4 w czasie
)
log
(
n
n
. Jeśli więc pokażemy,
jak wykonywać FFT, udowodnimy następujące twierdzenie.
Twierdzenie. Iloczyn dwóch wielomianów stopnia n można obliczyć w czasie
)
log
(
n
n
, przy
czym wielomiany wejściowe i wyjściowy są reprezentowane przez współczynniki.
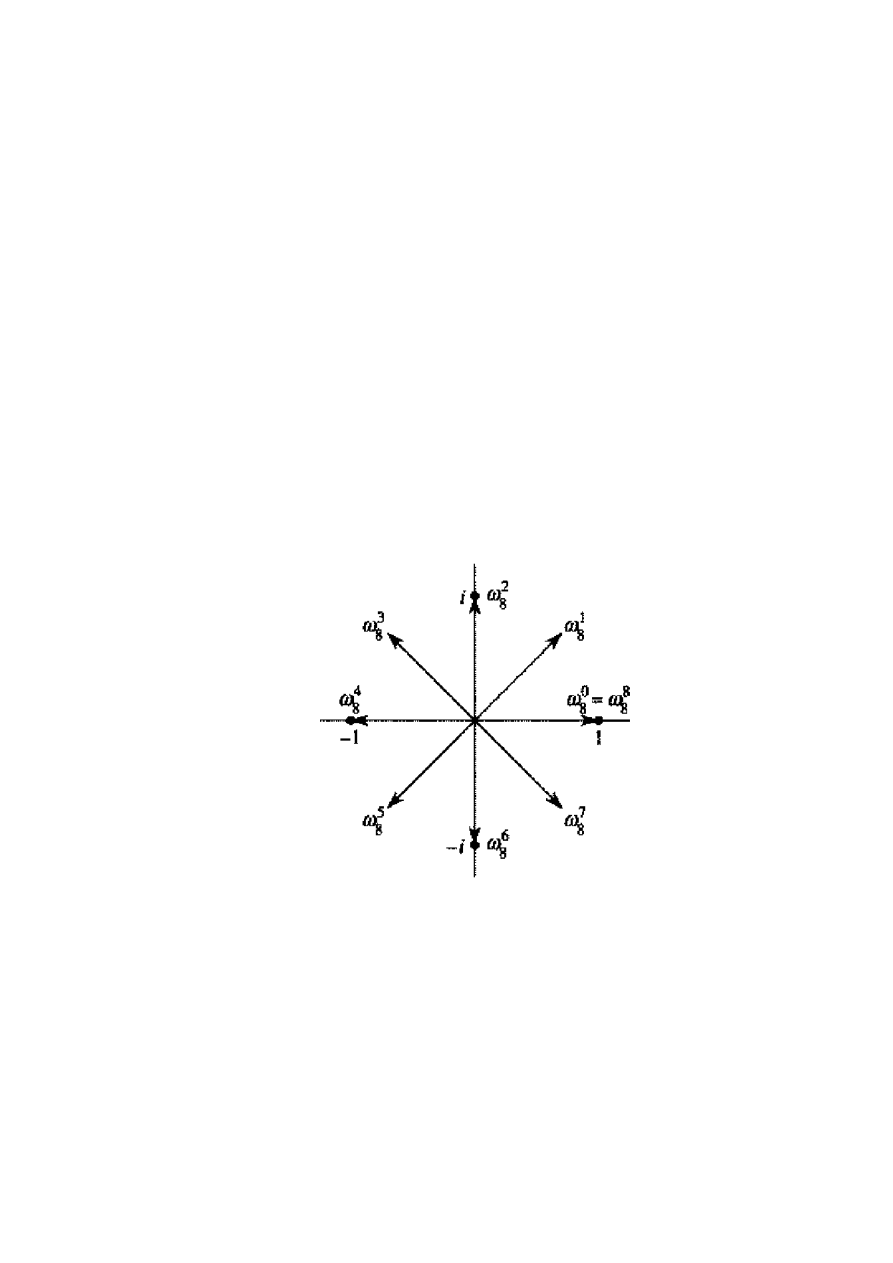
6.3. Zespolone pierwiastki z jedności
Zespolony pierwiastek n-tego stopnia z jedności to liczba zespolona
taka, że
1
n
. Istnieje
dokladnie n zespolonych pierwiastków n-tego stopnia z jedności; są to liczby
n
ki
e
/
2
dla
1
,...,
1
,
0
n
k
. Na rysunku poniżej widać, że n zespolonych pierwiastków z jedności jest roz-
mieszczonych w równych odstępach na okręgu o promieniu jednostkowym i środku w początku
układu współrzędnych na plaszczyznie zespolonej. Wartość
n
i
n
e
/
2
.
Nazywamy glównym pierwiastkiem n-tego stopnia z jedności; wszystkie pozostałe zespolone
pierwiastki n-tego stopnia z jedności są potęgami
n
.
Podstawowe własności zespolonych pierwiastków n-tego stopnia z jedności opisują po-
niższe lematy.
Lemat 1. (Lemat o skracaniu) Dla dowolnych liczb całkowitych
0
n
,
0
k
i
0
d
zachodzi
k
n
dk
dn
.
Lemat 2. (Lemat o redukcji) Jeśli
0
n
jest parzyste, to zbiór kwadratów n zespolonych pier-
wiastków n-tego stopnia z jedności to zarazem
2
/
n
zespolonych pierwiastków stopnia
2
/
n
z
jedności.
Lemat 3. (Lemat o sumowaniu) Dla dowolnej liczby całkowitej
1
n
i dowolnej nieujemnej
liczby całkowitej k niepodzielnej przez n zachodzi

14
0
)
(
1
0
n
j
j
k
n
.
6.4. Dyskretna transformata Fouriera (DFT)
Przypominamy, że chcemy dokonać ewaluacji wielomianu
1
0
)
(
n
j
j
j
x
a
x
A
stopnia n w punktach
0
n
,
1
n
,
2
n
, ...,
1
n
n
(to znaczy w n zespolonych pierwiastkach n-tego
stopnia z jedności). Bez straty ogólności możemy zalożyć, że n jest potęga 2, ponieważ dane
ograniczenie stopnia można zawsze powiększyć – zawsze możemy w miarę potrzeb dodawać
zerowe współczynniki przy najwyższych potęgach. Zakładamy, że wielomian A jest zadany
przez współczynniki:
)
,...,
,
(
1
1
0
n
a
a
a
a
. Zdefiniujmy wartości
k
y dla
1
,...,
1
,
0
n
k
wzorem
1
0
)
(
n
j
kj
n
j
k
n
k
a
A
y
.
Wektor
)
,...,
,
(
1
1
0
n
y
y
y
y
jest dyskretną transformatą Fouriera (DFT) wektora współczyn-
ników
)
,...,
,
(
1
1
0
n
a
a
a
a
. Piszemy także
)
(a
DFT
y
n
.
6.5. Szybkie przekształcenie Fouriera (FFT)
Stosując metodę znaną jako szybkie przekształcenie Fouriera, korzystającą ze szczególnych wła-
sności zespolonych pierwiastków z jedności, możemy obliczyć
)
(a
DFT
n
w czasie
)
log
(
n
n
,
chociaż zwykła metoda wymaga czasu
)
(
2
n
.
Metoda FFT opiera się na strategii „dziel i zwyciężaj”, wyodrębniając współczynniki o
parzystych i nieparzystych indeksach i definiując dwa nowe wielomiany stopnia
2
/
n
, oznaczane
jako
)
(x
A
e
i
)
(x
A
o
:
1
2
/
2
2
4
2
0
...
)
(
n
n
e
x
a
x
a
x
a
a
x
A
,
1
2
/
1
2
5
3
1
...
)
(
n
n
o
x
a
x
a
x
a
a
x
A
.
Wielomian
)
(x
A
e
zawiera wszystkie współczynniki o parzystych indeksach w A (binarna repre-
zentacja indeksu kończy się zerem), a wielomian
)
(x
A
o
zawiera wszystkie współczynniki o nie-
parzystych indeksach (binarna reprezentacja indeksu kończy się jedynką). Wynika stąd, że
)
(
)
(
)
(
2
2
x
xA
x
A
x
A
o
e
,
zatem problem ewaluacji A(x) w punktach
0
n
,
1
n
,
2
n
, ...,
1
n
n
sprowadza się do:
i) ewaluacji wielomianów
)
(x
A
e
i
)
(x
A
o
stopnia
2
/
n
w punktach
2
0
n
,
2
1
n
,
2
2
n
, ...,
2
1
n
n
,
a następnie
ii) połączenia wyników zgodnie ze wzorem
)
(
)
(
)
(
2
2
x
xA
x
A
x
A
o
e
.
Na mocy lematu o redukcji, lista
2
0
n
,
2
1
n
,
2
2
n
, ...,
2
1
n
n
sklada się nie z n róż-
nych wartości, ale tylko z
2
/
n
zespolonych pierwiastków stopnia
2
/
n
z jedności, z których
każdy występuje dokładnie dwa razy. Dokonujemy zatem rekurencyjnie ewaluacji wielomianów
)
(x
A
e
i
)
(x
A
o
stopnia
2
/
n
we wszystkich
2
/
n
zespolonych pierwiastkach stopnia
2
/
n
z jed-
ności. Obudwa podproblemy są dokładnie tej samej postaci co problem pierwotny, ale dwukrot-

15
nie mniejszego rozmiaru. Udało nam się podzielić obliczenie n-elementowego
n
DFT na dwa ob-
liczenia
2
/
n
-elementowego
2
/
n
DFT
. Podział ten jest podstawą poniższego rekurencyjnego al-
gorytmu FFT, obliczającego DFT dla n-elementowego wektora
)
,...,
,
(
1
1
0
n
a
a
a
a
, gdzie n jest
potęga dwójki.
RECURSIVE-FFT(a)
1
n := length(a) // n jest potęga 2
2
if n = 1
3
then return a
4
)
/
2
exp(
:
n
i
n
5
1
:
6
)
,...,
,
(
:
0
2
2
0
n
a
a
a
a
7
)
,...,
,
(
:
1
1
3
1
n
a
a
a
a
8
y0 := RECURSIVE-FFT(a0)
9
y1 := RECURSIVE-FFT(a1)
10
for k := 0 to
1
2
/
n
do
11
k
k
k
y
y
y
1
0
:
12
k
k
n
k
y
y
y
1
0
:
)
2
/
(
13
n
:
14
return y od // y jest wektorem kolumnowym
Procedura RECURSIVE-FFT działa następująco. Wiersze 2-3 odpowiadają największemu za-
głębieniu rekursji; wartość DFT pojedynczego elementu jest równa jemu samemu, bo wówczas
0
0
0
1
0
1
a
a
a
y
.
W wierszach 6-7 są definiowane wektory współczynników wielomianów
)
(x
A
e
i
)
(x
A
o
. Wier-
sze 4, 5 i 13 zapewniają poprawną aktualizację wartości
, dzięki czemu przy każdym wyko-
nywaniu instrukcji w wierszach 11-12 mamy
k
n
. (Aktualizacja wartości
zamiast obli-
czania
k
n
od początku w każdym przebiegu pętli for pozwala zaoszczędzić na czasie). W wier-
szach 8-9 obliczamy rekurencyjnie
2
/
n
DFT
, kładąc dla
1
2
/
,...,
1
,
0
n
k
)
(
0
2
/
k
n
e
k
A
y
,
)
(
1
2
/
k
n
o
k
A
y
lub
)
(
0
2k
n
e
k
A
y
,
)
(
1
2k
n
o
k
A
y
(ponieważ
k
n
k
n
2
2
/
na mocy lematu o skracaniu).
W wierszach 11-12 są lączone wyniki rekurencyjnych obliczeń
2
/
n
DFT
. Dla
0
y ,
1
y , ...,
1
2
/
n
y
w wierszu 11 obliczamy
)
(
)
(
)
(
1
0
2
2
k
n
k
n
o
k
n
k
n
e
k
k
n
k
k
A
A
A
y
y
y
,
gdzie ostatnia równość wynika ze wzoru
)
(
)
(
)
(
2
2
x
xA
x
A
x
A
o
e
. Dla
2
/
n
y
,
1
2
/
n
y
, ...,
1
n
y
,
przyjmując
1
2
/
,...,
1
,
0
n
k
, w wierszu 12 obliczmy
)
(
)
(
1
0
1
0
2
)
2
/
(
2
)
2
/
(
)
2
/
(
k
n
o
n
k
n
k
n
e
k
n
k
n
k
k
k
n
k
n
k
A
A
y
y
y
y
y

16
)
(
)
(
)
(
)
2
/
(
2
)
2
/
(
2
n
k
n
n
k
n
o
n
k
n
n
k
n
e
A
A
A
.
Druga równość wynika z pierwszej, ponieważ
k
n
n
k
n
)
2
/
(
. Czwarta równość wynika z trze-
ciej, bo z tego, że
1
n
n
, wynika, że
n
k
n
k
n
2
2
. Ostatnia równość wynika ze wzoru
)
(
)
(
)
(
2
2
x
xA
x
A
x
A
o
e
. Wektor y obliczany przez procedurę RECURSIVE-FFT jest zatem
rzeczywiście dyskretną transformatą Fouriera (DFR) wejściowego wektora a.
W celu oszacowania czasu działania procedury RECURSIVE-FFT zauważmy, że poza
wywołaniami rekurencyjnymi wykonanie procedury zajmuje czas
)
(n
, gdzie n jest długościa
wejściowego wektora. Równanie rekurencyjne na złożoność czasową wygląda następująco:
)
log
(
)
(
)
2
/
(
2
)
(
n
n
n
n
T
n
T
.
Korzystając z szybkiego przekształcenia Fouriera, możemy zatem dokonywać ewaluacji wielo-
mianu stopnia n w zespolonych pierwiastkach n-tego stopnia z jedności w czasie
)
log
(
n
n
.
6.6. Interpolacja w zespolonych pierwiastkach z jedności
Dla przejścia od reprezentacji wielomianu przez wartości w punktach z powrotem do reprezenta-
cji przez współczynniki musimy obliczyć interpolację w zespolonych pierwiastkach z jedności.
Wzór na interpolację wyprowadzamy zapisując DFT jako równanie macierzowe, a następnie
analizyjąc postać macierzy odwrotnej.
Obliczenie DFT możemy przedstawić jako mnożenie macierzy
a
V
y
n
, gdzie
n
V jest
macierzą Vandermonde’a zawierającą odpowiednie potęgi
n
;
1
3
2
1
0
)
1
)(
1
(
)
1
(
3
)
1
(
2
1
)
1
(
3
9
6
3
)
1
(
2
6
4
2
1
3
2
1
3
2
1
0
1
1
1
1
1
1
1
1
1
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
a
a
a
a
a
y
y
y
y
y
.
Element na pozycji
)
,
(
j
k
w macierzy
n
V to
kj
n
dla
1
,...,
1
,
0
,
n
k
j
, ich wykładniki tworzą
więc tabliczkę mnożenia.
Operację odwrotną, którą zapisujemy jako
)
(
1
y
DFT
a
n
, wykonujemy, mnożąć y przez
1
n
V
(macierz odwrotną do
n
V ).
Twierdzenie. Dla
1
,...,
1
,
0
,
n
k
j
elementem na pozycji
)
,
( k
j
w macierzy
1
n
V
jest
n
jk
n
.
Znając postać macierzy odwrotnej
1
n
V
, wiemy, że
)
(
1
y
DFT
n
zadane jest wzorem
1
0
1
0
2
exp
1
1
n
j
k
n
k
jk
n
k
j
jk
n
i
y
n
y
n
a
dla
1
,...,
1
,
0
n
j
. Widzimy, że transformatę odwrotną do DFT można obliczyć za pomocą
modyfikacji algorytmu FFT, polegającej na zamianie rolami wektorów a i y, zastępieniu
n
przez
1
n
i podzieleniu wartości każdej współrzędnej wyniku przez n. A więc
)
(
1
y
DFT
n
można
obliczyć również w czasie
)
log
(
n
n
.
Korzystając z FFT i odwrotnego przekształcenia FFT, możemy zatem dla danego wielo-
mianu stopnia n przechodzić od reprezentacji przez współczynniki do reprezentacji przez warto-

17
ści w punktach i z powrotem w czasie
)
log
(
n
n
. W kontekście mnożenia wielomianów udo-
wodniliśmy następujące twierdzenie:
Twierdzenie o splocie. Dla dowolnej pary wektorów a i b długości n, gdzie n jest potęgą
dwójki, mamy
)
(
)
(
2
2
1
2
b
DFT
a
DFT
DFT
b
a
n
n
n
,
gdzie wektory a i b są uzupełnone zerami do długości 2n, a „
” oznacza mnożenie po współrzęd-
nych dwóch 2n-elementowych wektorów.
6.7. Iteracyjna wersja algorytmu FFT
Przedstawimy teraz wersję iteracyjną algorytmu FFT, korzystającą z pomocniczej procedury
BIT-REVERSE-COPY(a, A) w celu skopiowania elementów wektora a do tablicy A w odpo-
wiednim porządku.
ITERATIVE-FFT(a)
1
BIT-REVERSE-COPY(a, A)
2
n := length(a) // n jest potęga 2
3
for s := 1 to log n do
4
s
m
^
2
:
5
)
/
2
exp(
:
m
i
m
6
1
:
7
for j := 0 to m/2-1 do
8
for k := j to n-1 step m do
9
]
2
/
[
:
m
k
A
t
10
]
[
:
k
A
u
11
t
u
k
A
:
]
[
12
t
u
m
k
A
:
]
2
/
[
od
13
m
:
od od
14
return A
BIT-REVERSE-COPY(a, A)
1
n := length(a)
2
for k := 0 to n - 1 do
3
k
a
k
rev
A
:
)]
(
[
W jaki sposób procedura BIT-REVERSE-COPY(a, A) wstawia elementy wejściowego wektora
a na właściwe miejsca w tablicy A? Funkcja
)
(k
rev
: dla binarnej reprezentacji liczby k oblicza
się odwrotna kolejność bitów i znajduje odpowiedną liczbę w systemu dziesiątnym.
Wyszukiwarka
Podobne podstrony:
Algorytmy wyklad 1 id 57804 Nieznany
Algorytmy wyklad 6 7 id 57806 Nieznany
LOGIKA wyklad 5 id 272234 Nieznany
ciagi liczbowe, wyklad id 11661 Nieznany
algorytmy sortujace id 57762 Nieznany
AF wyklad1 id 52504 Nieznany (2)
Neurologia wyklady id 317505 Nieznany
Algorytmy obliczen id 57749 Nieznany
ZP wyklad1 id 592604 Nieznany
CHEMIA SA,,DOWA WYKLAD 7 id 11 Nieznany
or wyklad 1 id 339025 Nieznany
II Wyklad id 210139 Nieznany
cwiczenia wyklad 1 id 124781 Nieznany
BP SSEP wyklad6 id 92513 Nieznany (2)
MiBM semestr 3 wyklad 2 id 2985 Nieznany
algebra 2006 wyklad id 57189 Nieznany (2)
olczyk wyklad 9 id 335029 Nieznany
Kinezyterapia Wyklad 2 id 23528 Nieznany
więcej podobnych podstron