WILiŚ - Budownictwo

- sem.1 -

dr Jolanta Dymkowska - 1

Granica funkcji

f : D → R,

D ⊂ R

x

0

∈ D

lub

∃

{x

n

}∈D

x

n

−→ x

0

Definicja

Niech f

będzie określona przynajmniej w sąsiedztwie punktu x

0

. Funkcja f

ma w

punkcie x

0

granicę g , co zapisujemy

lim

x→x

0

f (x) = g,

gdy dla dowolnego otoczenia U

punktu g istnieje sąsiedztwo S

punktu x

0

takie, że dla każdego

x ∈ S wartość f (x) należy do otoczenia U .

• Jeżeli x

0

∈ R i g ∈ R , to mamy:

lim

x→x

0

f (x) = g

⇐⇒

∀

ε>0

∃

δ>0

∀

x∈D

0 < | x − x

0

| < δ

⇒ | f (x) − g | < ε

( Definicja Cauchy’ego granicy właściwej w punkcie )

• Jeżeli x

0

= +∞ i g ∈ R , to mamy:

lim

x→+∞

f (x) = g

⇐⇒

∀

ε>0

∃

K>0

∀

x∈D

x > K

⇒ | f (x) − g | < ε

( Definicja Cauchy’ego granicy właściwej w plus nieskończoności )

• Napisz definicję Cauchy’ego granicy właściwej w minus nieskończoności.

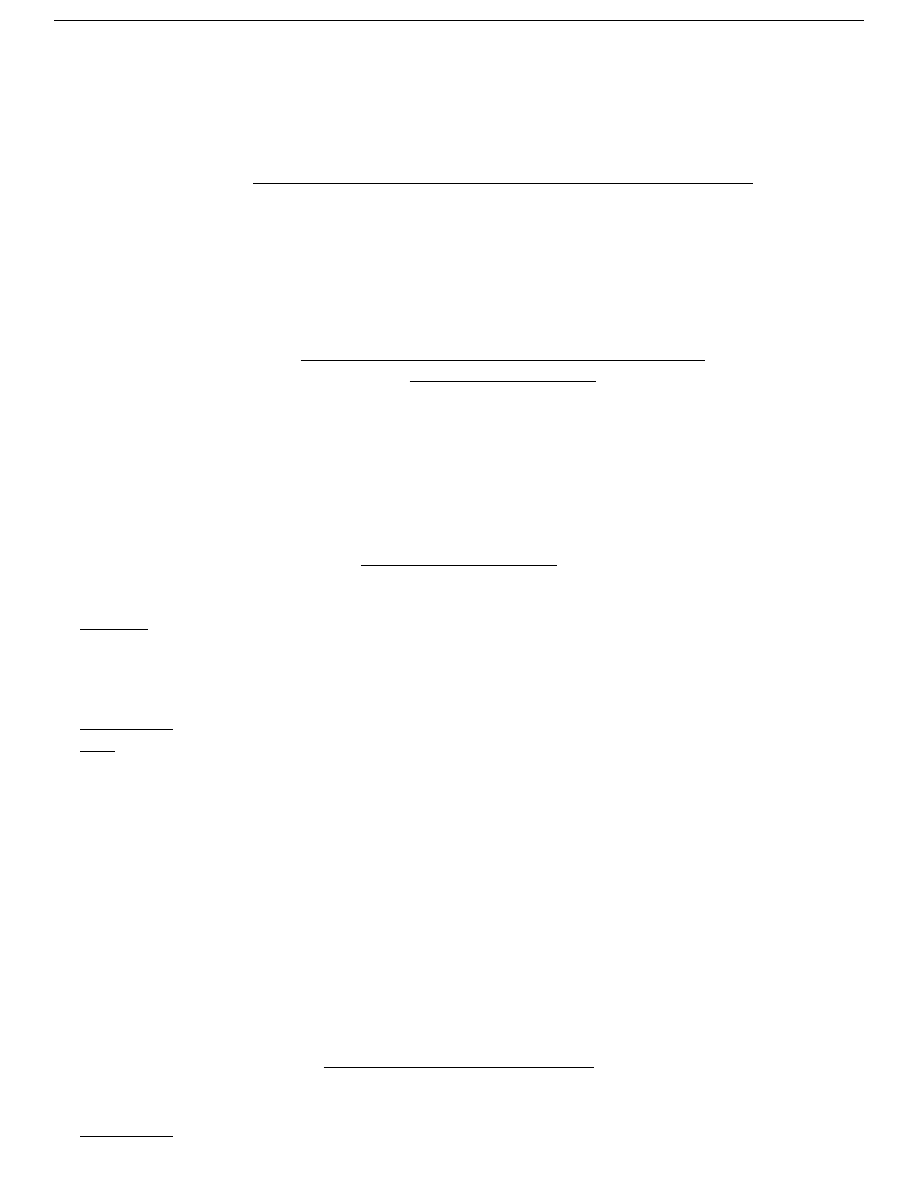
WILiŚ - Budownictwo

- sem.1 -

dr Jolanta Dymkowska - 2

• Jeżeli x

0

∈ R i g = −∞ , to mamy:

lim

x→x

0

f (x) = −∞

⇐⇒

∀

M <0

∃

δ>0

∀

x∈D

0 < | x − x

0

| < δ

⇒ f (x) < M

( Definicja Cauchy’ego granicy niewłaściwej (= −∞) w punkcie )

• Napisz definicję Cauchy’ego granicy niewłaściwej (= +∞) w punkcie.

• Jeżeli x

0

= +∞ i g = +∞ , to mamy:

lim

x→+∞

f (x) = +∞

⇐⇒

∀

M >0

∃

K>0

∀

x∈D

x > K

⇒ f (x) > M

( Definicja Cauchy’ego granicy niewłaściwej (= +∞)

w plus nieskończoności )

• Napisz definicję Cauchy’ego granicy niewłaściwej (= +∞) w minus nieskończoności.

• Napisz definicję Cauchy’ego granicy niewłaściwej (= −∞) w plus nieskończoności.

• Napisz definicję Cauchy’ego granicy niewłaściwej (= −∞) w minus nieskończoności.

Definicja Heinego granicy

Definicja

g ( g ∈ R lub g = ±∞ ) jest granicą funkcji f w x

0

( x

0

∈ R lub x

0

= ±∞ ) wtedy i

tylko wtedy, gdy dla dowolnego ciągu { x

n

} , takiego, że x

n

∈ S(x

0

) ⊂ D , zachodzi

lim

n→∞

x

n

= x

0

=⇒

lim

n→∞

f (x

n

) = g.

Twierdzenie

Definicje: Cauchy’ego i Heinego granicy funkcji są równoważne.

Fakt

Jeżeli istnieją ciągi { x

0
n

} i { x

00
n

} spełniające warunki:

•

lim

n→∞

x

0
n

= x

0

, przy czym x

0
n

6= x

0

dla n ∈ N oraz

lim

n→∞

f (x

0
n

) = g

0

,

•

lim

n→∞

x

00
n

= x

0

, przy czym x

00
n

6= x

0

dla n ∈ N oraz

lim

n→∞

f (x

00
n

) = g

00

,

• g

0

6= g

00

,

to granica lim

x→x

0

f (x) nie istnieje.

Wnioski z definicji Heinego granicy

Twierdzenie

(Arytmetyka granic funkcji)

Jeżeli funkcje f i g mają granice właściwe w x

0

, to

WILiŚ - Budownictwo

- sem.1 -

dr Jolanta Dymkowska - 3

•

lim

x→x

0

( f (x) ± g(x) ) = lim

x→x

0

f (x) ± lim

x→x

0

g(x) ,

•

lim

x→x

0

( c · f (x) ) = c · lim

x→x

0

f (x) ,

gdzie c ∈ R ,

•

lim

x→x

0

( f (x) · g(x) ) = lim

x→x

0

f (x) · lim

x→x

0

g(x) ,

•

lim

x→x

0

f (x)

g(x)

=

lim

x→x0

f (x)

lim

x→x0

g(x)

,

o ile lim

x→x

0

g(x) 6= 0 .

Twierdzenie

lim

x→x

0

f (x) = 0

⇐⇒

lim

x→x

0

| f (x) | = 0

Twierdzenie

Załóżmy, że funkcje f i g są określone w sąsiedztwie x

0

. Jeżeli granica funkcji f w

x

0

jest równa 0 , a funkcja g jest ograniczona, to

lim

x→x

0

f (x) · g(x) = 0.

Twierdzenie

Załóżmy, że funkcja f jest określona w sąsiedztwie x

0

. Wówczas

lim

x→x

0

f (x) = +∞ (−∞)

=⇒

lim

x→x

0

1 +

1

f (x)

!

f (x)

= e.

Twierdzenie

(O trzech funkcjach)

Jeżeli funkcje f, g i h , określone co najmniej w sąsiedztwie S(x

0

) punktu x

0

, spęłniają warunki:

• f (x) 6 g(x) 6 h(x) dla każdego x ∈ S(x

0

)

•

lim

x→x

0

f (x) = lim

x→x

0

h(x) = p ,

to lim

x→x

0

g(x) = p .

Granice jednostronne funkcji

Definicja Załóżmy, że funkcja f jest określona w pewnym prawostronnym (lewostronnym) sąsiedztwie

punktu x

0

∈ R . Funkcja f ma w punkcie x

0

granicę prawostronną (lewostronną) g , co zapisujemy

lim

x→x

+
0

f (x) = g

( lim

x→x

−
0

f (x) = g ),

gdy dla dowolnego otoczenia U punktu g istnieje sąsiedztwo prawostronne (lewostronne) S

+

( S

−

)

punktu x

0

takie, że dla każdego

x ∈ S

+

( x ∈ S

−

) wartość f (x) należy do otoczenia U .

• Definicja Cauchy’ego granic jednostronnych

lim

x→x

+
0

f (x) = g

⇐⇒

WILiŚ - Budownictwo

- sem.1 -

dr Jolanta Dymkowska - 4

∀

ε>0

∃

δ>0

∀

x∈D

x

0

< x < x

0

+ δ

⇒ | f (x) − g | < ε

lim

x→x

−
0

f (x) = g

⇐⇒

∀

ε>0

∃

δ>0

∀

x∈D

x

0

− δ < x < x

0

⇒ | f (x) − g | < ε

• Definicja Heinego granic jednostronnych

lim

x→x

+
0

f (x) = g

⇐⇒

∀

{x

n

}, x

n

>x

0

lim

n→∞

x

n

= x

0

⇒

lim

n→∞

f (x

n

) = g

lim

x→x

−
0

f (x) = g

⇐⇒

∀

{x

n

}, x

n

<x

0

lim

n→∞

x

n

= x

0

⇒

lim

n→∞

f (x

n

) = g

Ćwiczenie

Napisz definicje granic jednostronnych w przypadku, gdy g = +∞ lub g = −∞ .

Twierdzenie

(Warunek dostateczny istnienia granicy)

Dla istnienia granicy g funkcji f

w punkcie x

0

∈ R potrzeba i wystarcza, by istniały obie granice

jednostronne w punkcie x

0

i żeby były sobie równe. Ponadto wówczas

lim

x→x

0

f (x) = lim

x→x

+
0

f (x) =

lim

x→x

−
0

f (x).

Uwaga Twierdzenia sformułowane dla granic funkcji są również prawdziwe dla granic jednostronnych.