dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

5. Korelacja i regresja liniowa

5.1. Uwagi wstępne

•

Dotychczasowe rozważania dotyczyły analizy struktury zbiorowości
i opierały się na obserwacjach jednej cechy (zmiennej).

•

Bardzo często jednostki tworzące zbiorowość charakteryzowane są
za pomocą więcej niż jednej cechy i dlatego zachodzi potrzeba ich
łącznego badania.

◦

Zazwyczaj cechy te pozostają ze sobą w pewnym związku.

◦

Np. zdanie „rak płuc powiązany jest z paleniem papierosów"
mówi, że im więcej papierosów się pali, tym jest bardziej prawdo-
podobne, że zachoruje się na raka płuc (czyli im więcej jednego,
tym więcej drugiego).

1

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

•

Taka analiza ma na celu stwierdzenie, czy między badanymi zmien-
nymi zachodzą jakieś zależności, jaka jest ich siła, jaki jest ich
kształt i kierunek.

•

Dział statystyki zajmujący się badaniem związków między kilkoma
cechami (zmiennymi) nosi nazwę teorii współzależności.

•

Współzależność pomiędzy zmiennymi może być funkcyjna lub
stochastyczna (probabilistyczna).

•

Zależność funkcyjna polega na tym, że zmiana wartości jednej
zmiennej powoduje ściśle określoną (wg pewnego wzoru) zmianie
drugiej zmiennej, czyli każdej wartości jednej zmiennej niezależnej
(X) odpowiada tylko jedna, jednoznacznie określona wartość zmien-
nej zależnej (Y).

◦

Np. obwód kwadratu jest funkcją (liniową) jego boku Ob=4a,
a pole P = a

2

.

2

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

•

Zależność stochastyczna występuje wtedy, gdy wraz zmianą jednej
zmiennej zmienia się rozkład prawdopodobieństwa drugiej zmiennej.

•

Szczególnym przypadkiem zależności stochastycznej jest zależność
korelacyjna (statystyczna).

•

Zależność korelacyjna (statystyczna) polega na tym, że określo-
nym wartościom jednej zmiennej odpowiadają ściśle określone śred-
nie wartości drugiej zmiennej.

◦

Zależność ta mówi nam jak zmieni się (średnio) wartość zmiennej
zależnej (objaśnianej) Y w zależności od wartości zmiennej nieza-
leżnej (objaśniającej) X.

•

Jeśli pomiędzy badanymi zmiennymi nie ma związku stochastyczne-
go, to oczywiście nie ma również związku korelacyjnego.

◦

Twierdzenie odwrotne nie jest prawdziwe.

3

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

•

Na podstawie analizy merytorycznej należy oczywiście najpierw
uzasadnić logiczne występowanie związku, a dopiero potem przy-
stąpić do określenia siły i kierunku zależności.

◦

W literaturze znane są przykłady badania - nawet istotnej staty-
stycznie - zależności np. między liczbą zajętych gniazd bocianich a
liczbą urodzeń na danym obszarze, czy między liczbą zarejestro-
wanych odbiorników TV a liczbą chorych umysłowo.

•

Liczbowe stwierdzenie występowania współzależności nie zawsze
oznacza występowanie związku przyczynowo-skutkowego między
badanymi zmiennymi.

•

Współwystępowanie dwóch zjawisk może również wynikać z bezpo-
średniego oddziaływania na nie jeszcze innego, trzeciego zjawiska.

•

Prostym sposobem wykrywania związku korelacyjnego między ba-
danymi cechami jest obserwacja szeregów statystycznych, które
zawierają informacje o tych cechach.

4

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

•

Graficzny związek pomiędzy zmiennymi możemy zobaczyć na wy-
kresach rozrzutu.

•

Analizę zależności powinno się rozpoczynać od sporządzenia wy-
kresów rozrzutu.

•

Wzrokowa ocena umożliwia często określenie siły i rodzaju zależności.

•

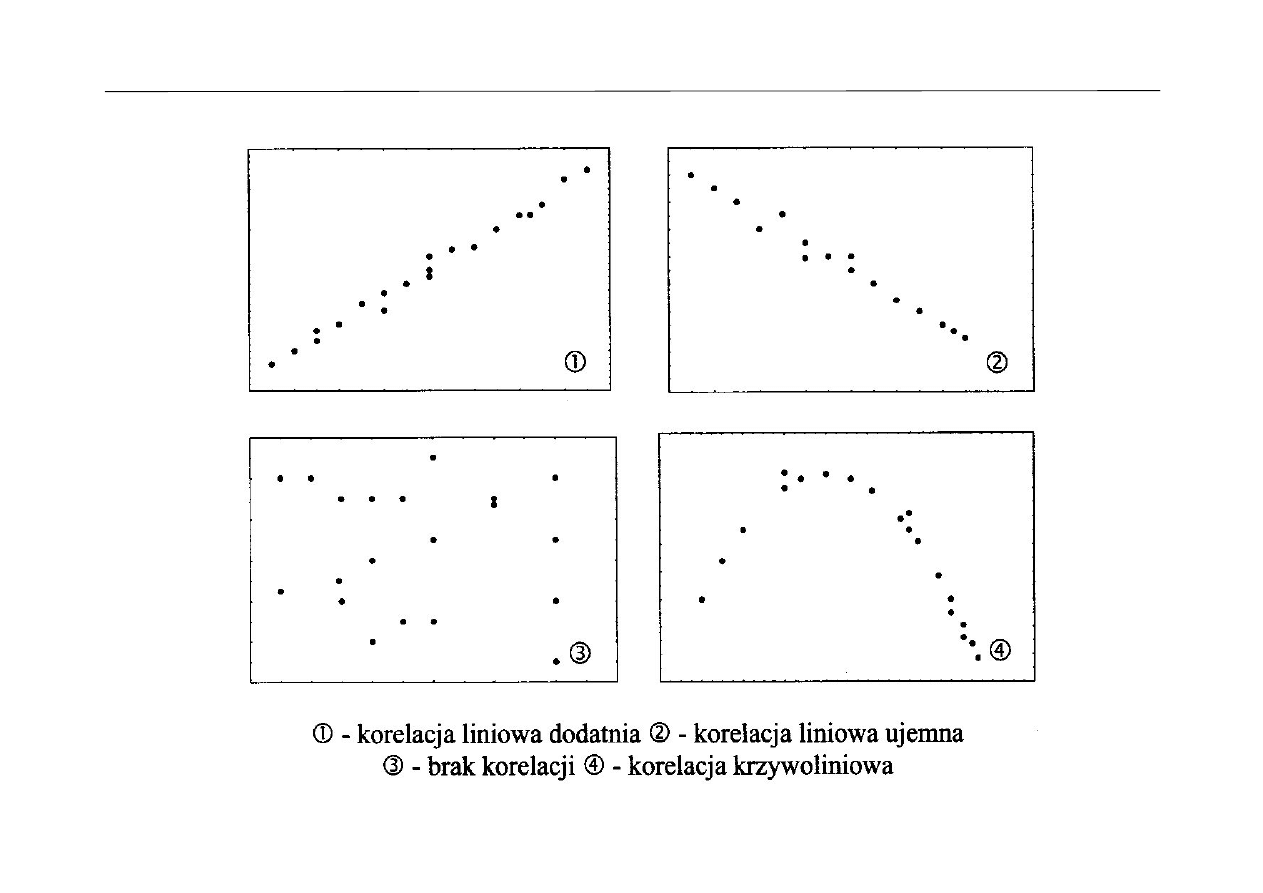
Ze względu na postać zależności możemy mówić o dwóch odmia-
nach:

◦

zależność liniowa (przypadek 1 i 2 na rysunku poniżej),

◦

zależność krzywoliniowa (przypadek 4).

5

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

Rysunek pochodzi z książki Andrzeja Stanisza „Przystępny kurs statystyki z zastosowaniem STATISTICA PL

na przykładach z medycyny. Tom 1. Statystyki podstawowe” StatSoft, Kraków 2006

6

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

5.2. Współczynnik korelacji liniowej Pearsona

•

Załóżmy, że zbiorowość jest badana ze względu na dwie zmienne
X i Y, a realizacje tych zmiennych w populacji lub próbie n-elemen-
towej zestawione są w postaci dwóch szeregów szczegółowych lub
rozdzielczych.

•

Punkty, odpowiadające poszczególnym wartościom cech, tworzą ko-
relacyjny wykres rozrzutu.

◦

W prostokątnym układzie współrzędnych:

▪

na osi odciętych zaznaczamy pierwszą zmienną,

▪

a na osi rzędnych wartości drugiej zmiennej.

•

Bardzo rzadko zdarza się, aby zaznaczone punkty leżały dokładnie
na linii prostej (wówczas jest pełna korelacja).

•

Częściej spotykana konfiguracja składa się z wielu zaznaczonych
punktów leżących mniej więcej wzdłuż konkretnej krzywej (najczę-
ściej linii prostej, przypadek 1 i 2 na wcześniejszym rysunku).

7

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

•

Gdy korelacja staje się coraz mniej wyraźna, wówczas punkty za-
czynają się rozpraszać i przesuwać, aż do kolistego tworu (brak ko-
relacji, przypadek 3).

•

Korelacja dodatnia występuje wtedy, gdy wzrostowi wartości jed-
nej cechy odpowiada wzrost średnich wartości drugiej cechy (przy-
padek 1).

•

Korelacja ujemna występuje wtedy, gdy wzrostowi wartości jednej ce-
chy odpowiada spadek średnich wartości drugiej cechy (przypadek 2).

•

Gdy obserwacje statystyczne dotyczące badanych zmiennych są bar-
dzo liczne, wówczas konstruuje się tablicę korelacyjną.

◦

Na skrzyżowaniu kolumn z wierszami wpisywane są liczebności
jednostek zbiorowości statystycznej, u których zaobserwowano
jednoczesne wystąpienie określonej wartości

x

i

i

y

j

(lub warto-

ści z odpowiednich przedziałów).

8

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

Przykładowa tablica korelacyjna

•

Natężenie (siłę) współzależności dwóch zmiennych można wyra-
zić liczbowo za pomocą wielu mierników.

•

Pierwszy syntetyczny opis zależności między zmiennymi to para-
metr zwany kowariancją.

9

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

•

Załóżmy, że rezultatem pewnego doświadczenia są pary liczb



x

i

, y

i



, gdzie

i=1, 2,... , n.

•

Określamy w ten sposób dwuwymiarową zmienną losową, którą
oznaczamy jako (X, Y).

•

Wówczas kowariancja dla danych z naszej próby określana jest na-
stępującym wzorem:

cov  x , y =

1
n

∑

i=1

n



x

i

−x y

i

−y=

1
n

∑

i=1

n

x

i

y

i

−x y

gdzie

x

i

y

oznaczają średnie obu zmiennych.

•

Dla danych pogrupowanych w tablicę korelacyjną (dwuwymiarowy
szereg rozdzielczy):

cov  x , y =

1
n

∑

i=1

k

∑

j=1

l



x

i

−x y

j

−yn

ij

=

1
n

∑

i=1

k

∑

j=1

l

x

i

y

j

n

ij

−x y

10

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

•

Kowariancja przekazuje następujące informacje o związku korela-
cyjnym:

◦

cov  x , y =0 – brak zależności korelacyjnej;

◦

cov  x , y 0 – ujemna zależność korelacyjna (inaczej nega-

tywna, przy wzroście X wartości Y na ogół maleją);

◦

cov  x , y 0 – dodatnia zależność korelacyjna (inaczej pozy-

tywna; przy wzroście wartości X, wartości Y na ogół także rosną).

•

Kowariancja charakteryzuje zatem we właściwy sposób powiązanie
pomiędzy zmiennymi X i Y.

•

Wadą kowariancji jest to, że jej wartość zależy od jednostek pomiaru cech.

•

Kowariancja nie może zatem określać siły zależności, ale może posłu-
żyć do budowy innego parametru oceniającego siłę powiązania X i Y,
czyli współczynnika korelacji liniowej Pearsona.

11

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

•

Dla kowariancji zachodzi następująca nierówność:

−

s

x

s

y



cov  x , ys

x

s

y

gdzie

s

x

i

s

y

są odchyleniami standardowymi otrzymanymi dla

danych wartości cechy X i cechy Y odpowiednio.

•

Jeżeli podzielimy kowariancję przez iloczyn odchyleń standardo-
wych, to otrzymamy bezwymiarową miarę intensywności powiąza-
nia o wartościach pomiędzy

−

1

a



1

– jest to najbardziej popu-

larny współczynnik korelacji, nazywany współczynnikiem korela-
cji liniowej Pearsona.

•

Współczynnik korelacji (liniowej) Pearsona oznaczamy symbolem

r

xy

=

cov  x , y 

s

x

s

y

=

∑

i=1

n



x

i

−x y

i

−y



∑

i=1

n



x

i

−x

2

∑

i=1

n



y

i

−y

2

•

Oczywiście

−

1r

xy



1

.

12

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

•

Współczynnik korelacji (liniowej) Pearsona jest miernikiem siły
związku prostoliniowego między dwiema cechami mierzalnymi.

•

Znak współczynnika korelacji informuje nas o kierunku korelacji,
natomiast jego bezwzględna wartość o sile związku.

•

Mamy oczywiście równość

r

xy

=

r

yx

.

•

Jeżeli

∣

r

xy

∣=

1

, to zależność korelacyjna przechodzi w zależność

funkcyjną (funkcja liniowa).

•

Jeżeli r

xy

=

0 , to mamy zupełny brak związku korelacyjnego mię-

dzy badanymi zmiennymi X i Y.

•

Założeniem stosowalności tego współczynnika jest liniowa zależ-
ność między analizowanymi zmiennymi.

13

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

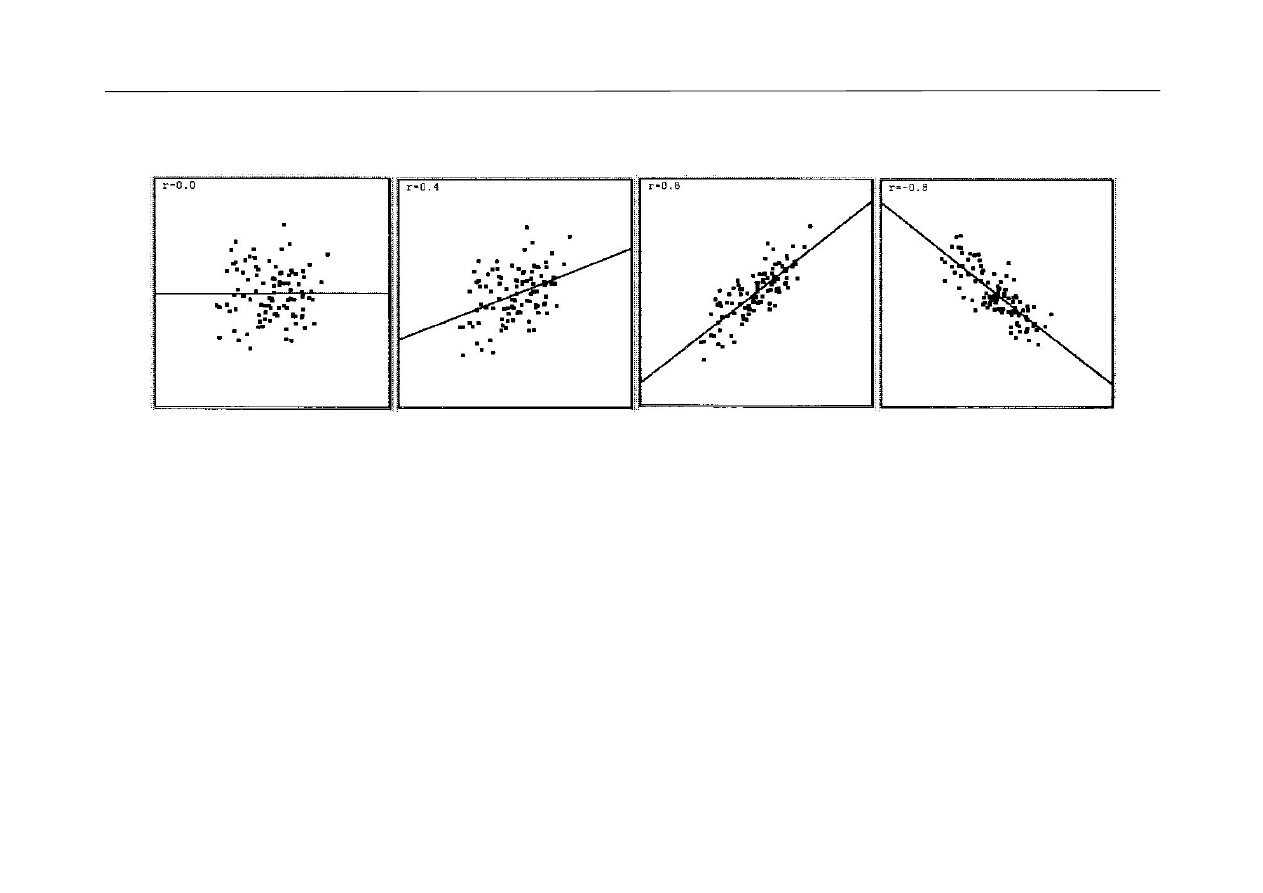
Powiązanie między współczynnikiem korelacji a układem punktów

Rysunek pochodzi z książki Andrzeja Stanisza „Przystępny kurs statystyki z zastosowaniem STATISTICA PL

na przykładach z medycyny. Tom 1. Statystyki podstawowe” StatSoft, Kraków 2006

•

W pierwszym przypadku nie występuje korelacja



r

xy

=

0.

Na wy-

kresie widzimy bezkształtną chmurę punktów (coś w rodzaju koła).

•

Na kolejnych dwóch wykresach wartości współczynników Pearsona
wzrastają r

xy

=

0,4 i r

xy

=

0,8. Zmienia się również położenie

punktów, które układają się coraz bliżej pewnej linii prostej.

•

W ostatnim przypadku współczynnik korelacji przyjmuje wartość
ujemną



r

xy

=−

0,8.

W takiej sytuacji punkty układają się wzdłuż

pewnej prostej skierowanej w dół.

14

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

•

Oglądając wykres rozrzutu, możemy sprawdzić założenie liniowości oraz
przewidzieć siłę korelacji pomiędzy zmiennymi. Im bliżej prostej położone
są punkty na wykresie tym większej korelacji możemy się spodziewać.

•

Wartość współczynnika korelacji bliska 0 nie zawsze oznacza brak zależ-
ności, a jedynie brak zależności liniowej.

•

Wielkość współczynnika korelacji podlega wpływom wartości skrajnych i odstających.

•

Do opisu i interpretacji korelacji możemy przyjąć następującą skalę okre-
ślającą siłę związku (stopień zależności dwóch cech):

◦

r

xy

=

0

– zmienne nie są skorelowane

◦

0∣r

xy

∣

0,1

– korelacja nikła

◦

0,1∣r

xy

∣

0,3

– korelacja słaba

◦

0,3∣r

xy

∣

0,5

– korelacja przeciętna

◦

0,5∣r

xy

∣

0,7

– korelacja wysoka

◦

0,7∣r

xy

∣

0,9

– korelacja bardzo wysoka

◦

0,9∣r

xy

∣

1

– korelacja prawie pełna

◦

∣

r

xy

∣=

1

– korelacja pełna.

15

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

•

Kwadrat współczynnika korelacji r

xy

nazywamy współczynnikiem

determinacji (określoności).

•

Współczynnik determinacji r

xy

2

informuje o tym, jaka część zmian

zmiennej objaśnianej (skutek) jest wyjaśniona przez zmiany zmien-
nej objaśniającej (przyczyna).

•

Np. jeśli zmienna X (zmienna objaśniająca) koreluje ze zmienną Y
(zmienna objaśniana) na poziomie r

xy

=

0,5 , to współczynnik de-

terminacji r

xy

2

=

0,25 oznacza, że tylko 25% zmian wartości zmien-

nej objaśnianej zostało wyjaśnione przez zmiany przyjętej zmiennej
objaśniającej. Można zatem stwierdzić, że na zmienną objaśnianą
oddziaływają jeszcze inne zmienne objaśniające (przyczyny).

16

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

Przykład 5.1.

Z populacji dzieci i młodzieży wybrano losowo próbę 15-osobową i okre-
ślono następujące dane:

x

i

- wiek w latach,

y

i

- wzrost w centymetrach.

Otrzymano następujące dane:

x

i

7

8

9

10

11 11,5 12

13

14

15

16

17 17,5 18

19

y

i

120 122 135 131 135 140 142 145 150 154 159 162 164 168 170

Wyznaczyć współczynnik korelacji liniowej Pearsona oraz współczyn-
nik determinacji.

r

xy

=

cov  x , y 

s

x

s

y

=

∑

i=1

n



x

i

−x y

i

−y



∑

i=1

n



x

i

−x

2

∑

i=1

n



y

i

−y

2

cov  x , y =

1
n

∑

i=1

n



x

i

−x y

i

−y=

1
n

∑

i=1

n

x

i

y

i

−x y

17

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

18

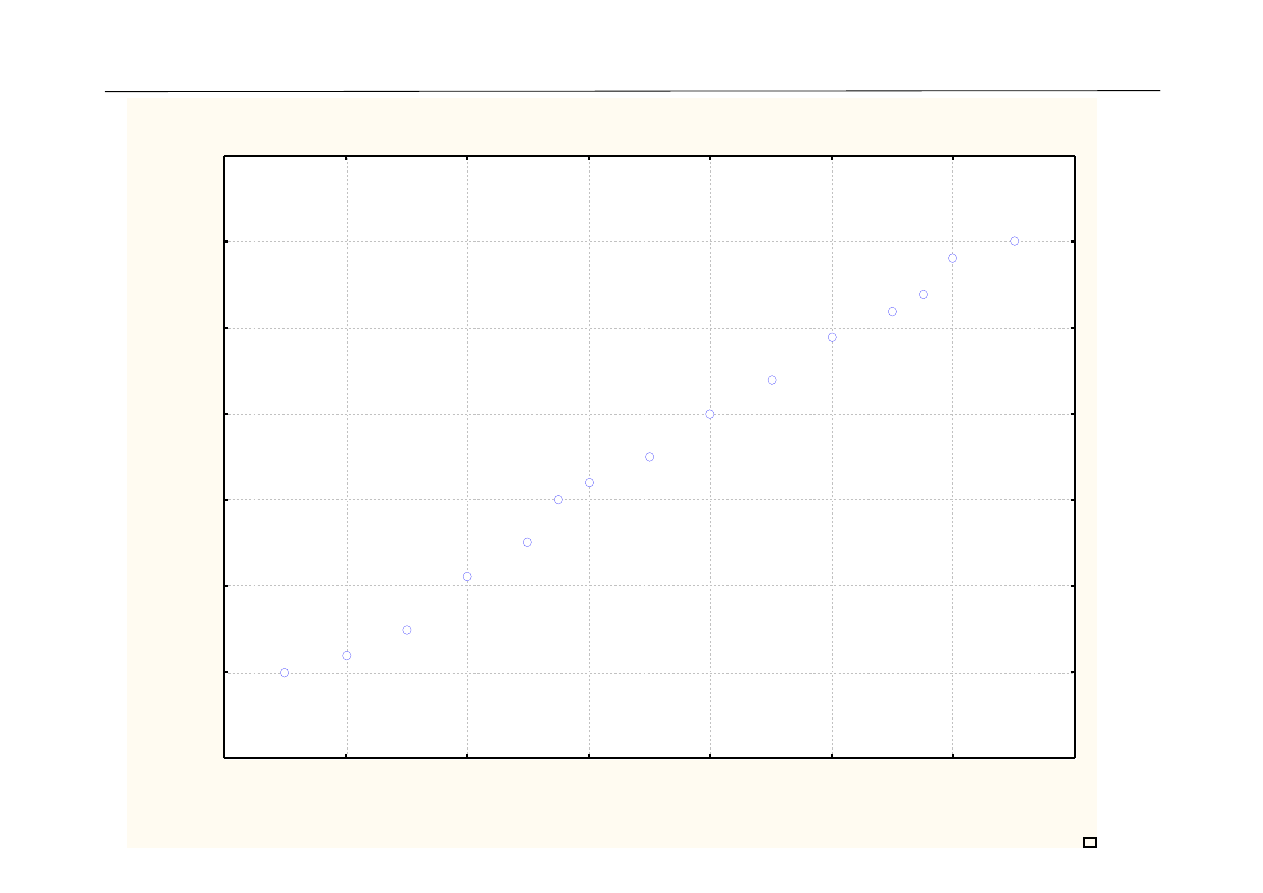
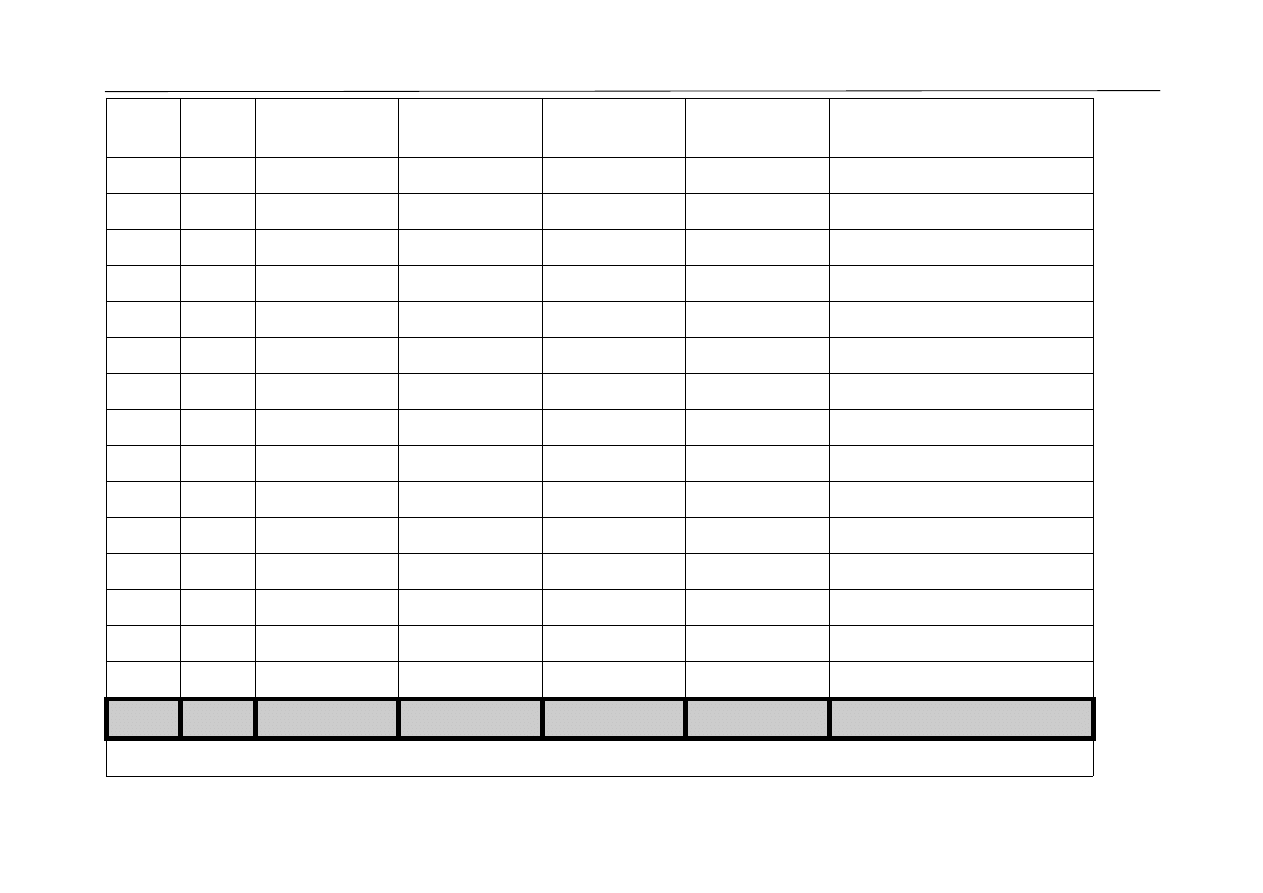
Wykes rozrzutu: Wiek (w latach) vs Wzrost (w centymetrach)

7; 120

8; 122

9; 125

10; 131

11; 135

11,5; 140

12; 142

13; 145

14; 150

15; 154

16; 159

17; 162

17,5; 164

18; 168

19; 170

6

8

10

12

14

16

18

20

Wiek (w latach)

110

120

130

140

150

160

170

180

W

zr

o

st

(

w

c

e

n

ty

m

e

tr

a

ch

)

7; 120

8; 122

9; 125

10; 131

11; 135

11,5; 140

12; 142

13; 145

14; 150

15; 154

16; 159

17; 162

17,5; 164

18; 168

19; 170

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

x

i

y

i

x

i

−x

y

i

−y



x

i

−x

2



y

i

−y 

2



x

i

−x⋅ y

i

−y

7

120

-6,2

-25,8

38,44

665,64

159,96

8

122

-5,2

-23,8

27,04

566,44

123,76

9

125

-4,2

-20,8

17,64

432,64

87,36

10

131

-3,2

-14,8

10,24

219,04

47,36

11

135

-2,2

-10,8

4,84

116,64

23,76

11,5

140

-1,7

-5,8

2,89

33,64

9,86

12

142

-1,2

-3,8

1,44

14,44

4,56

13

145

-0,2

-0,8

0,04

0,64

0,16

14

150

0,8

4,2

0,64

17,64

3,36

15

154

1,8

8,2

3,24

67,24

14,76

16

159

2,8

13,2

7,84

174,24

36,96

17

162

3,8

16,2

14,44

262,44

61,56

17,5

164

4,3

18,2

18,49

331,24

78,26

18

168

4,8

22,2

23,04

492,84

106,56

19

170

5,8

24,2

33,64

585,64

140,36

198 2187

-

-

203,90

3980,40

898,60

SUMA

19

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

x=

198

15

=

13,2

,

y=

2187

15

=

145,8

s

x

2

=

203,90

15

=

13,59

s

y

2

=

3980,40

15

=

265,36

s

x

=



13,59=3,69

s

y

=



265,36=16,29

cov  x , y =

1
n

∑

i=1

n



x

i

−x y

i

−y=

898,60

15

=

59,91

r

xy

=

cov  x , y 

s

x

s

y

=

59,91

3,69⋅16,29

=

0,997 lub

r

xy

=

∑

i=1

n



x

i

−x y

i

−y 



∑

i=1

n



x

i

−x

2

∑

i=1

n



y

i

−y

2

=

898,60



203,90⋅3980,40

=

898,60
900,89

=

0,997

r

xy

2

=

0,994=99,4 %

20

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

5.3. Korelacje cząstkowe

•

Jeśli na pewną zmienną oddziałuje więcej niż jedna zmienna, a nas
interesuje ścisły związek korelacyjny jedynie między dwoma zmien-
nymi, przy wyłączeniu wpływu pozostałych zmiennych, to powinni-
śmy wyliczyć współczynniki korelacji cząstkowej.

•

Załóżmy, że mamy trzy zmienne

X

1

,

X

2

oraz

X

3

. Zdefiniujemy

współczynniki korelacji liniowej, mierzące siłę powiązania między
dwiema zmiennymi przy wyłączeniu oddziaływania trzeciej zmiennej.

•

W przypadku trzech zmiennych współczynniki korelacji cząstkowej
oznaczamy następująco: r

12.3

, r

13.2

oraz r

23.1

.

•

Symbol r

12.3

oznacza korelację między zmiennymi

X

1

a X

2

przy wyłączeniu działania zmiennej

X

3

.

21

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

•

Współczynnik korelacji cząstkowej r

12.3

wyraża się następującym

wzorem:

r

12.3

=

r

12

−

r

13

r

23





1−r

13

2



1−r

23

2



gdzie r

ij

oznacza korelację między zmiennymi

X

i

a

X

j

.

•

Zdefiniowany współczynnik korelacji cząstkowej przyjmuje również
wartości z przedziału

<−1,1 >

. Interpretuje się go podobnie jak

współczynnik korelacji liniowej Pearsona.

•

Podobnie:

r

13.2

=

r

13

−

r

12

r

23





1−r

12

2



1−r

23

2



r

23.1

=

r

23

−

r

12

r

13





1−r

12

2



1−r

13

2



22

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

Przykład 5.2.

Załóżmy, że interesuje nas korelacja pomiędzy czasem pobytu

(w dniach) w szpitalu (X

1

) a poziomem fibrynogenu (X

2

) i cholesterolu

(X

3

) w dniu przyjęcia. Zebrane dane dla losowej próby 20 pacjentów za-

warte są w poniższej tabeli:

Wyznaczyć wszystkie współczynniki korelacji cząstkowej (w pierw-

szym etapie należy wyliczyć macierz korelacji).

23

Nr pacjenta

1

2

3

4

5

6

7

8

9 10 11 12 13 14 15 16 17 18 19 20

Dni

15 23 23 24 13 22 27 25 19 19 25 27 14 18 13 25 23 25 17 21

Cholesterol

5,8 4,8 4,6 4,2 5,6 4,8 3,9 4,4 5,3

5 4,5 3,7

6 5,6 6,3 4,4 4,8 4,2 5,8 5,1

Fibrynogen

3,9

5 5,9

6 3,5 5,1 6,3 5,6 4,4 5,1 6,2 6,1 4,3 4,2 2,9 6,1 5,5 6,2 4,4 5,1

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

Odpowiednie korelacje Pearsona są następujące:

r

12

=−

0,9579 , r

13

=

0,9474 , r

23

=−

0,9328 ,

Macierz korelacji: M =

[

1,0000

−

0,9579

0,9474

−

0,9579

1,0000

−

0,9328

0,9474

−

0,9328

1,0000

]

r

12.3

=

r

12

−

r

13

r

23





1−r

13

2



1−r

23

2



=−

0,6430

r

13.2

=

r

13

−

r

12

r

23





1−r

12

2



1−r

23

2



=

0,5206

r

23.1

=

r

23

−

r

12

r

13





1−r

12

2



1−r

13

2



=−

0,2752

24

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

5.4. Współczynnik korelacji rang Spearmana

•

Poprzednie miary (kowariancja i współczynnik korelacji Pearsona)
mogą być stosowane tylko dla zmiennych mierzalnych (liczbowych)
między którymi związek jest liniowy.

•

Nie można używać tych miar do analizy powiązań zmiennych mie-
rzonych na skali porządkowej – do tego służą inne miary, np. współ-
czynnik korelacji rang Spearmana lub nie omawiane tutaj inne kore-
lacje nieparametryczne, jak współczynniki Tau Kendalla i Gamma.

•

Współczynnik korelacji rang Spearmana

r

s

służy do opisu siły

korelacji dwóch cech, zwłaszcza wtedy, gdy mają one charakter ja-
kościowy i istnieje możliwość uporządkowania obserwacji empi-
rycznych w określonej kolejności.

◦

Miarę tę można stosować także do badania zależności między ce-
chami ilościowymi w przypadku niewielkich liczby obserwacji.

25

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

•

Ponieważ zmienne są mierzalne na skali porządkowej, więc możliwe
jest uporządkowanie zarówno wartości zmiennej X, jak i Y w ciąg
rosnący, a następnie przyporządkowanie każdemu pomiarowi odpo-
wiedniego numeru (rangi).

•

Najmniejszy pomiar otrzyma numer l, następny 2 itd.

•

Mówimy wówczas, że otrzymane wyniki zostały uporządkowane
w kolejności rang.

•

Numer każdego pomiaru nazywamy rangą.

•

Taka zamiana konkretnych wartości na odpowiadające im rangi ni-
weluje negatywny wpływ punktów odstających.

•

Mówiąc o powiązaniu zmiennych, myślimy teraz o korelacji rang.

•

Spotykane w literaturze współczynniki korelacji rang są więc miara-
mi współzależności, w których wartość zmiennych X i Y zastąpiono
rangami od l do n, przyporządkowanymi każdej ze zmiennych.

26

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

•

I tak jeśli we wzorze na współczynnik korelacji Pearsona zamiast
konkretnych wartości umieścimy rangi, to otrzymamy (po krótkim
przekształceniu) współczynnik korelacji rang, zwany właśnie współ-
czynnikiem korelacji rang Spearmana.

•

Współczynnik korelacji rang Spearmana obliczamy według wzoru:

r

s

=

1−6

∑

i=1

n

d

i

2

nn

2

−

1

gdzie

d

i

oznacza różnice między rangami odpowiadających sobie

wartości cech.

•

Współczynnik ten służy do opisu siły korelacji cech jakościowych,
które możemy uporządkować.

•

Podobnie jak współczynnik korelacji liniowej Pearsona, współczynnik
korelacji rang Spearmana

r

s

∈

<−1, 1 >

i ma podobną interpretację.

27

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

Przykład 5.3.

Ustalić współzależność między opiniami wydanymi przez dwóch leka-
rzy wydanymi o zdrowiu 10 pacjentów. Opinie te zostały ujęte
w punktach:

Pacjenci

A

B

C

D

E

F

G

H

I

J

Punkty

uzyskane od

I lekarza

42

27

36

33

24

47

39

52

43

37

II lekarza

39

24

35

29

26

47

44

51

39

32

Nadajemy rangi (n=10) :

Pacjenci

A

B

C

D

E

F

G

H

I

J

Rangi

uzyskane od

I lekarza

4

9

7

8

10

2

5

1

3

6

II lekarza

4,5

10

6

8

9

2

3

1

4,5

7

28

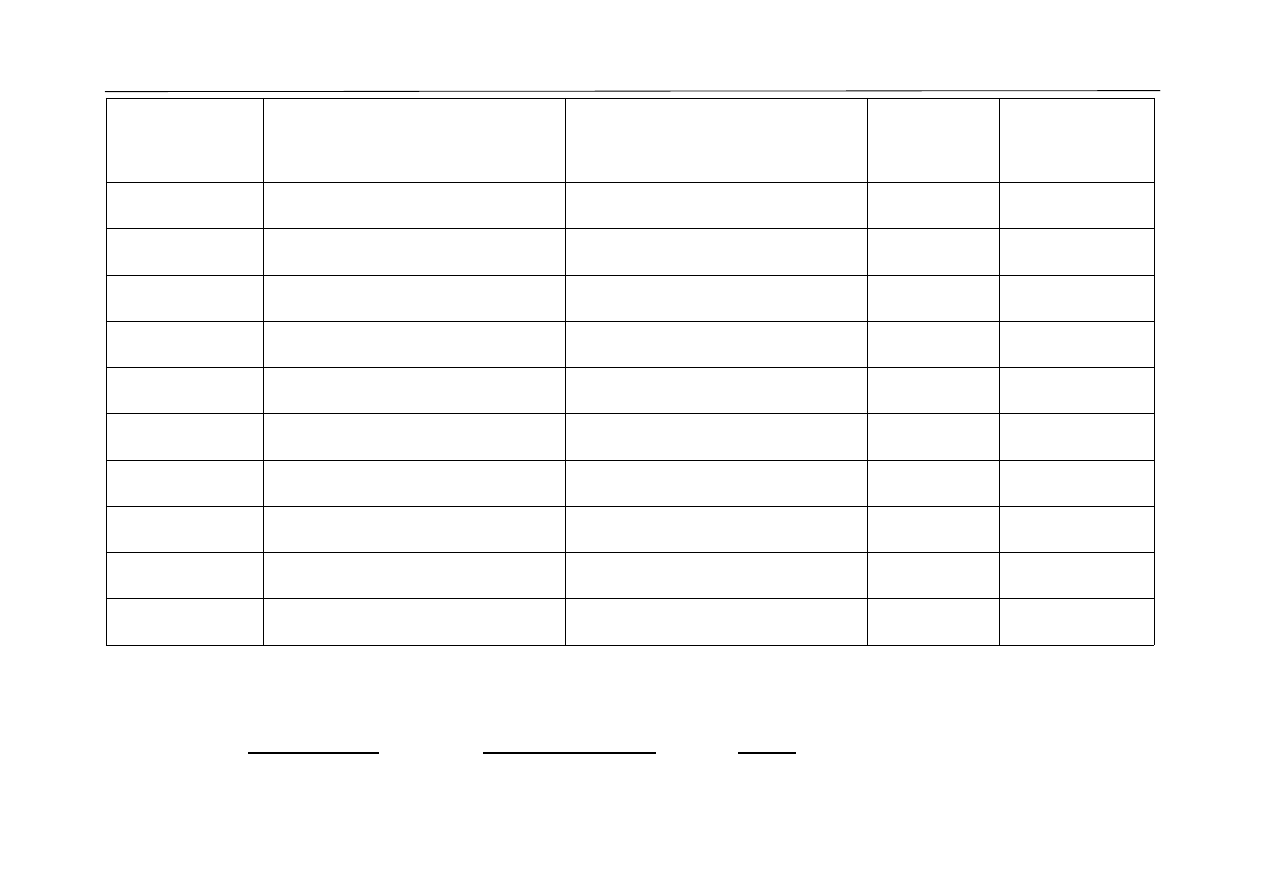
dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

Pacjenci

Miejsce w rankingu I

lekarza

Miejsce w rankingu II

lekarza

d

i

d

i

2

A

4

4,5

-0,5

0,25

B

9

10

-1

1

C

7

6

1

1

D

8

8

0

0

E

10

9

1

1

F

2

2

0

0

G

5

3

2

4

H

1

1

0

0

I

3

4,5

-1,5

2,25

J

6

7

-1

1

r

s

=

1−6

∑

i=1

n

d

i

2

nn

2

−

1

=

1−6

10,5

10⋅10

2

−

1

=

1−

63

990

=

0,9363

29

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

5.5. Funkcja regresji

•

Funkcja regresji służy do badania powiązań między zmiennymi.

•

Funkcja regresji to analityczny wyraz przyporządkowania średnich
wartości zmiennej objaśnianej (zależnej) konkretnym wartościom
zmiennej objaśniającej (niezależnej).

•

Funkcja regresji I rodzaju realizacjom zmiennej objaśniającej
przypisuje średnie warunkowe zmiennej objaśnianej.

•

Funkcją regresji I rodzaju zmiennej losowej Y względem zmiennej
losowej X nazywamy:

E Y | X = x

i

=

g

1



x

i



,i=1, 2, , k.

•

Podobnie, funkcją regresji I rodzaju zmiennej losowej X względem
zmiennej losowej Y nazywamy:

E  X | Y = y

j

=

g

2



y

j



, j=1, 2,, l.

30

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

•

Analityczne postaci funkcji g

1



x

i



oraz g

2



y

j



są zwykle niezna-

ne i dlatego na podstawie zaobserwowanych wyników w próbie
przedstawia się je graficznie w prostokątnym układzie współrzęd-
nych w formie tzw. empirycznych linii regresji.

•

Empiryczna linia regresji zmiennej Y względem zmiennej X jest linią
łamaną powstałą przez połączenie punktów o współrzędnych:



x

i

, y | x

i



dla i=1, 2, , k.

•

Natomiast empiryczna linia regresji zmiennej X względem zmiennej Y
jest linią łamaną powstałą przez połączenie punktów o współrzędnych:

x | y

j

, y

j

 dla j=1, 2,,l.

31

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

Przykład 5.4.
W celu zbadania zależności między wiekiem kobiet a liczbą posiada-
nych dzieci wylosowano w sposób niezależny 100 kobiet. Wyniki badań
przedstawia tabela:

Liczba dzieci (X)

Wiek kobiety w latach (Y)

15 – 25

25 – 35

35 – 45

45 – 55

0
1
2
3
4
5

2

10

8

–
–
–

1

12
19

–

–
–

–

15
10

5
–
–

–
–
5
4
3
6

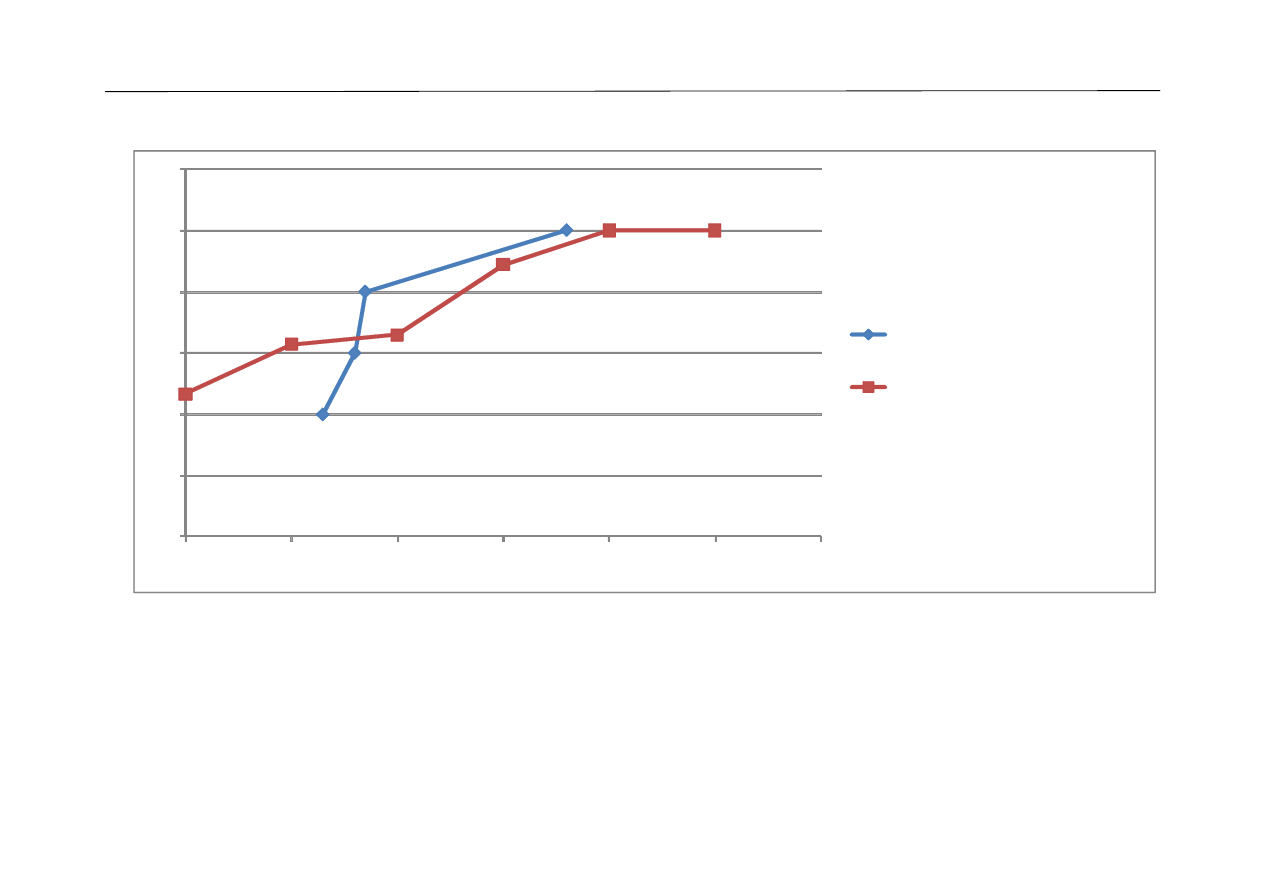
Na podstawie tych informacji sporządzić wykres empirycznych linii re-
gresji.

32

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

•

W celu określenia empirycznych linii regresji należy obliczyć śred-
nie warunkowe obydwu zmiennych.

•

Średnie warunkowe zmiennej X przy ustalonych wartościach zmien-
nej Y są równe:

x

1 | ˚y=20

=

0⋅21⋅102⋅8

20

=

1,3

x

2 | ˚y=30

=

0⋅11⋅122⋅19

32

=

1,6

x

3 | ˚y=40

=

1⋅152⋅103⋅5

30

=

1,7

x

4 | ˚y=50

=

2⋅53⋅44⋅35⋅6

18

=

3,6

•

Empiryczna linia regresji zmiennej X względem zmiennej Y jest linią
łamaną powstałą przez połączenie punktów o współrzędnych:



1,3 ;20 ,1,6 ; 30 ,1,7 ;40 ,3,6 ;50.

33

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

•

Średnie warunkowe zmiennej Y przy ustalonych wartościach zmien-
nej X są równe:

y

1| x=0

=

2⋅201⋅30

3

=

23,3

y

2 | x=1

=

10⋅2012⋅3015⋅40

37

=

31,4

y

3| x=2

=

8⋅2019⋅3010⋅405⋅50

42

=

32,9

y

4 | x=3

=

5⋅404⋅50

9

=

44,4

y

5| x=4

=

3⋅50

3

=

50,0

y

6 | x=5

=

6⋅50

6

=

50,0

•

Empiryczna linia regresji zmiennej Y względem zmiennej X jest linią
łamaną powstałą przez połączenie punktów o współrzędnych:



0 ;23,3 ,1 ;31,4 ,2 ;32,9 ,3 ;44,4 ,4 ;50,0 ,5, 50,0.

34

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

35

0

10

20

30

40

50

60

0

1

2

3

4

5

6

Empiryczna linia regresji zmiennej X
względem zmiennej Y

Empiryczna linia regresji zmiennej Y
względem zmiennej X

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

•

Wykres empirycznych linii regresji pozwala na postawienie hipotezy
dotyczącej postaci funkcji matematycznej (może to być np. funkcja
liniowa, kwadratowa, wykładnicza) opisującej sposób powiązania
między rozpatrywanymi zmiennymi.

•

Gdy określimy postać (typ) funkcji, to mówimy wówczas o funkcji
regresji II rodzaju.

•

Funkcja regresji II rodzaju jest więc przybliżeniem funkcji regresji I
rodzaju, która jak wiemy opisuje zależność korelacyjną zmiennych
w próbie losowej.

•

Wybór analitycznej postaci funkcji regresji II rodzaju (liniowa, nieli-
niowa) nie jest sprawą łatwą.

•

Decyzje należy podejmować na podstawie wstępnej analizy materia-
łu statystycznego, wykresu rozrzutu oraz na podstawie źródeł poza-
statystycznych dotyczących badanej dziedziny zjawiska.

36

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

5.6. Regresja liniowa

•

Najprostsze i najczęściej spotykane zależności między zmiennymi to
te, które mają postać liniową.

•

Krzywe regresji II rodzaju będące liniami prostymi nazywamy pro-
stymi regresji.

•

Mają one następującą postać:

◦



y=a

y

xb

y

– prosta regresji zmiennej Y względem X

◦



x=a

x

yb

x

– prosta regresji zmiennej X względem Y

•

Parametry równania prostej regresji szacuje się z próby klasyczną
metodą najmniejszych kwadratów.

37

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

•

Metoda najmniejszych kwadratów (MNK) polega na takim osza-
cowaniu parametrów powyższych funkcji, aby dla danych z próby
spełniony był warunek (dla funkcji



y=a

y

xb

y

):

◦

wyrażenie

W a

y

, b

y

=

∑

i=1

n



y

i

− 

y

i



2

=

∑

i=1

n



y

i

−

a

y

x

i

−

b

y



2

ma osiągnąć minimum, gdzie

y

i

oznaczają wartości empiryczne

zmiennej Y, a



y

i

, wartości „teoretyczne” wyznaczone na podsta-

wie równania



y=a

y

xb

y

 

y

i

=

a

y

x

i



b

y



.

•

Zatem mamy znaleźć minimum funkcji kwadratowej dwóch zmien-
nych a

y

i b

y

.

•

Warunkiem koniecznym istnienia ekstremum jest zerowanie się po-
chodnych cząstkowych.

38

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

•

Pochodne cząstkowe funkcji W a

y

, b

y

=

∑

i=1

n



y

i

−

a

y

x

i

−

b

y



2

:

◦

∂

W a

y

, b

y



∂

a

y

=

∑

i=1

n

2 y

i

−

a

y

x

i

−

b

y

−

x

i



◦

∂

W a

y

, b

y



∂

b

y

=

∑

i=1

n

2 y

i

−

a

y

x

i

−

b

y

−

1

•

Przyrównujemy te pochodne cząstkowe do zera i dokonujemy odpo-
wiednich elementarnych przekształceń i otrzymujemy równania:

◦

a

y

∑

i=1

n

x

i

2



b

y

∑

i=1

n

x

i

=

∑

i=1

n

x

i

y

i

◦

a

y

∑

i=1

n

x

i



n b

y

=

∑

i=1

n

y

i

39

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

•

Rozwiązując powyższy układ równań otrzymujemy:

a

y

=

n

∑

i=1

n

x

i

y

i

−

∑

i=1

n

x

i

∑

i=1

n

y

i

n

∑

i=1

n

x

i

2

−



∑

i=1

n

x

i



2

i b

y

=

∑

i=1

n

y

i

∑

i=1

n

x

i

2

−

∑

i=1

n

x

i

∑

i=1

n

x

i

y

i

n

∑

i=1

n

x

i

2

−



∑

i=1

n

x

i



2

•

Okazuje się dla tak wyznaczonych wartości zmiennych

a

y

i

b

y

funkcja

W a

y

, b

y

=

∑

i=1

n



y

i

−

a

y

x

i

−

b

y



2

przyjmuje wartość najmniejszą (spełniony jest również warunek do-
stateczny).

40

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

•

Współczynniki

a

y

i

b

y

możemy przedstawić w prostszej postaci:

a

y

=

∑

i=1

n



x

i

−x y

i

−y

∑

i=1

n



x

i

−x

2

=

cov  X ,Y 

s

x

2

=

r

xy

s

y

s

x

i

b

y

=y−a

y

x

•

Parametry

a

y

i

b

y

noszą nazwę parametrów prostej regresji.

•

Parametr

b

y

to wyraz wolny równania prostej regresji.

•

Współczynnik

a

y

określa o ile jednostek przeciętnie wzrośnie (lub

zmaleje, gdy

a

y



0

) wartość zmiennej zależnej, gdy wartość

zmiennej niezależnej wzrośnie o jedną jednostkę.

•

Ze względu na prostą i logiczną interpretację współczynnik

a

y

ma

duże znaczenie praktyczne.

41

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

•

Podobnie parametry (współczynniki a

x

i b

x

) równania prostej re-

gresji (zmiennej X względem Y)



x=a

x

yb

x

oszacowane metodą najmniejszych kwadratów mają postać:

a

x

=

∑

i=1

n



x

i

−x y

i

−y 

∑

i=1

n



y

i

−y

2

=

cov  X ,Y 

s

y

2

=

r

xy

s

x

s

y

b

x

=x−a

x

y

•

Zauważmy, że iloczyn współczynników regresji a

y

i a

x

jest kwa-

dratem współczynnika korelacji liniowej Pearsona:

a

y

⋅

a

x

=

r

xy

2

42

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

Przykład 5.5.

(kontynuacja przykładu 5.1.)

Z populacji dzieci i młodzieży wybrano losowo próbę 15-osobową i okre-
ślono następujące dane:

x

i

- wiek w latach,

y

i

- wzrost w centymetrach.

Otrzymano następujące dane:

x

i

7

8

9

10

11 11,5 12

13

14

15

16

17 17,5 18

19

y

i

120 122 135 131 135 140 142 145 150 154 159 162 164 168 170

Wyznaczyć odpowiednie proste regresji.

43

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

x

i

y

i

x

i

−x

y

i

−y



x

i

−x

2



y

i

−y 

2



x

i

−x⋅ y

i

−y

7

120

-6,2

-25,8

38,44

665,64

159,96

8

122

-5,2

-23,8

27,04

566,44

123,76

9

125

-4,2

-20,8

17,64

432,64

87,36

10

131

-3,2

-14,8

10,24

219,04

47,36

11

135

-2,2

-10,8

4,84

116,64

23,76

11,5

140

-1,7

-5,8

2,89

33,64

9,86

12

142

-1,2

-3,8

1,44

14,44

4,56

13

145

-0,2

-0,8

0,04

0,64

0,16

14

150

0,8

4,2

0,64

17,64

3,36

15

154

1,8

8,2

3,24

67,24

14,76

16

159

2,8

13,2

7,84

174,24

36,96

17

162

3,8

16,2

14,44

262,44

61,56

17,5

164

4,3

18,2

18,49

331,24

78,26

18

168

4,8

22,2

23,04

492,84

106,56

19

170

5,8

24,2

33,64

585,64

140,36

198 2187

-

-

203,90

3980,40

898,60

SUMA

44

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)



y=a

y

xb

y

x=

198

15

=

13,2

y=

2187

15

=

145,8

a

y

=

∑

i=1

n



x

i

−x y

i

−y

∑

i=1

n



x

i

−x

2

=

898,60

203,90

=

4,41

b

y

=y−a

y

x=145,8−4,41⋅13,2=87,59



y=4,41 x87,59

45

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

46

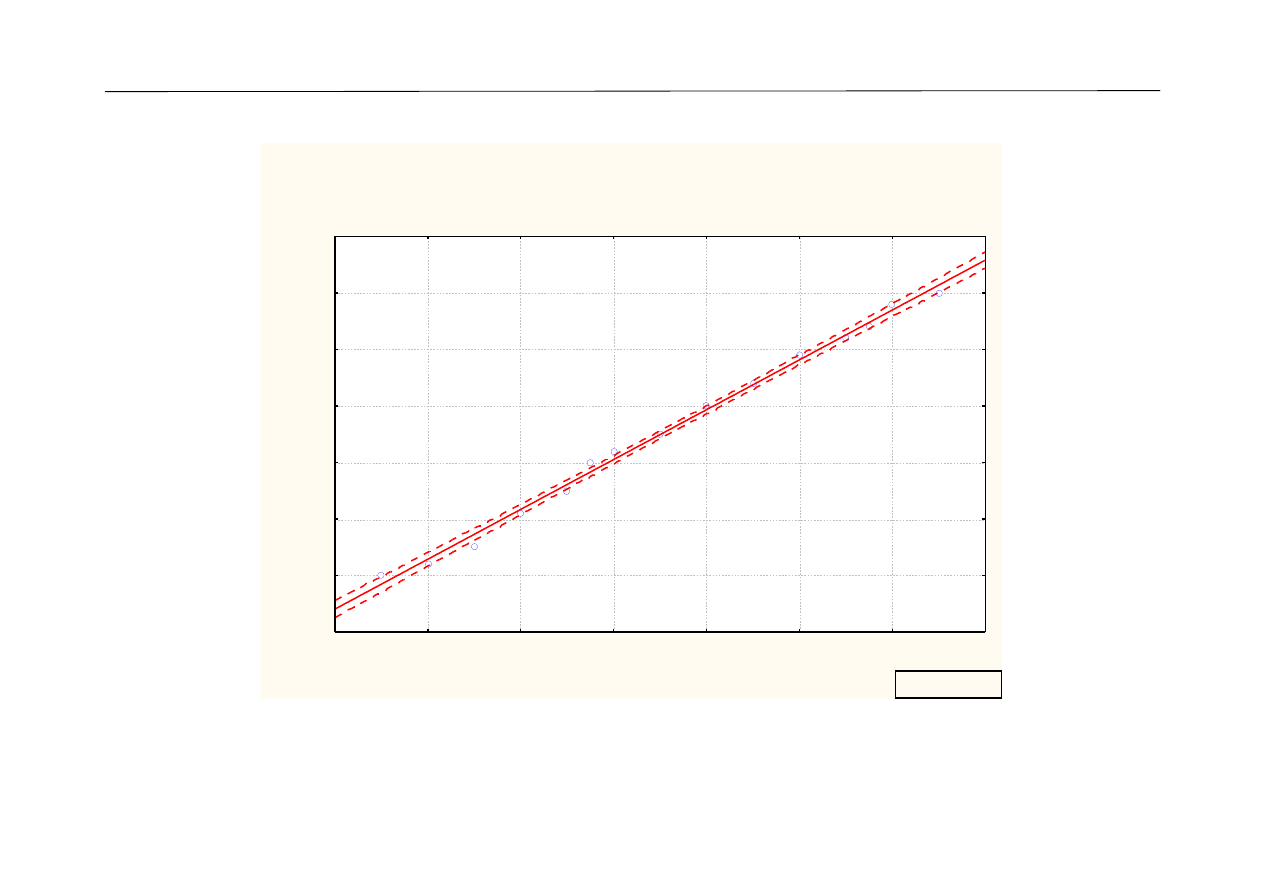
Wykres rozrzutu: Wiek (w latach) vs Wzrost (w centymetrach)

Wzrost (w centymetrach) = 87,63 + 4,41 * Wiek (w latach)

Korelacja: r = 0,997

6

8

10

12

14

16

18

20

Wiek (w latach)

110

120

130

140

150

160

170

180

W

zr

o

st

(

w

c

e

n

ty

m

e

tr

a

ch

)

0,95 Prz.Ufn.

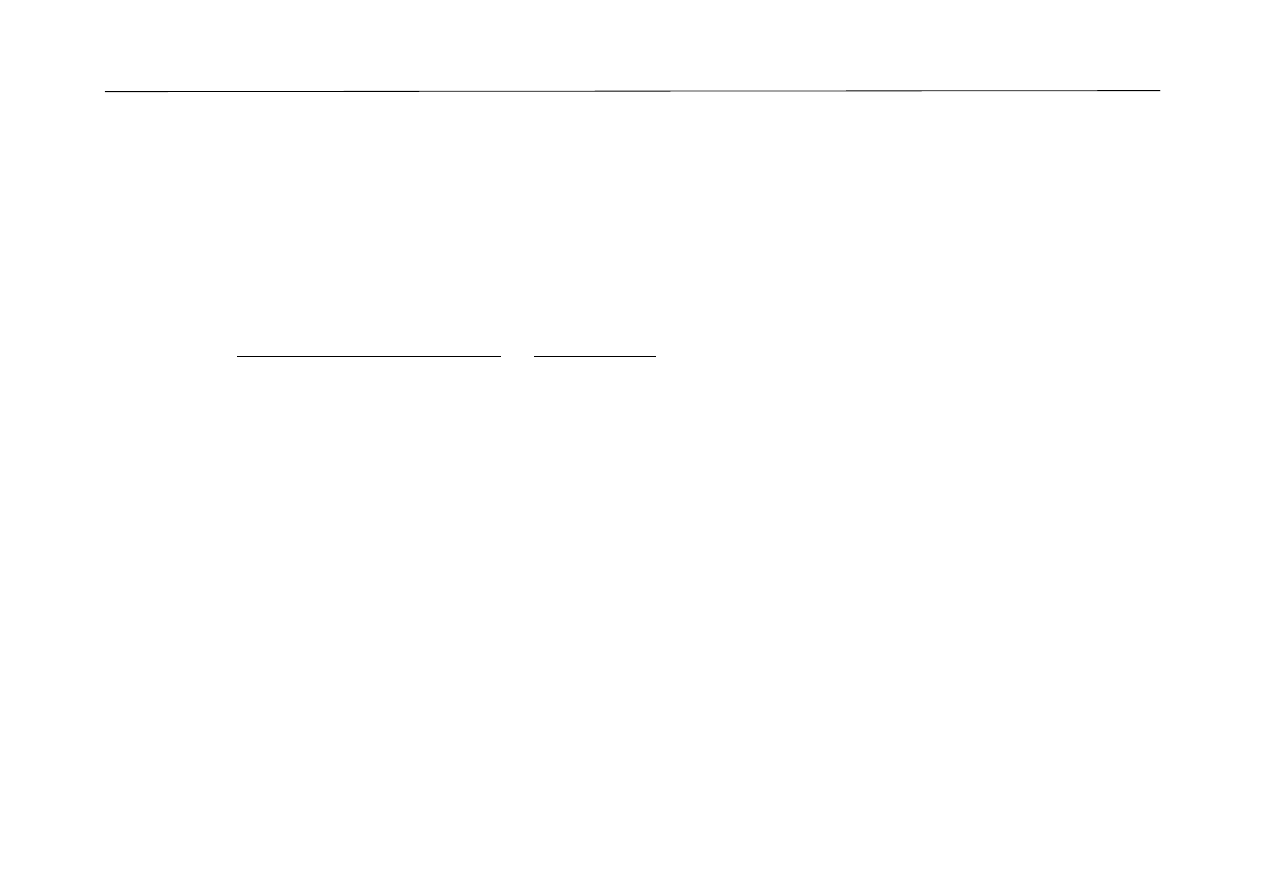
dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

Podobnie



x=a

x

yb

x

a

x

=

∑

i=1

n



x

i

−x y

i

−y 

∑

i=1

n



y

i

−y

2

=

898,60

3980,40

=

0,23

b

x

=x−a

x

y=13,2−0,23⋅145,8=−20,33



x=0,23 y−20,33

47

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

48

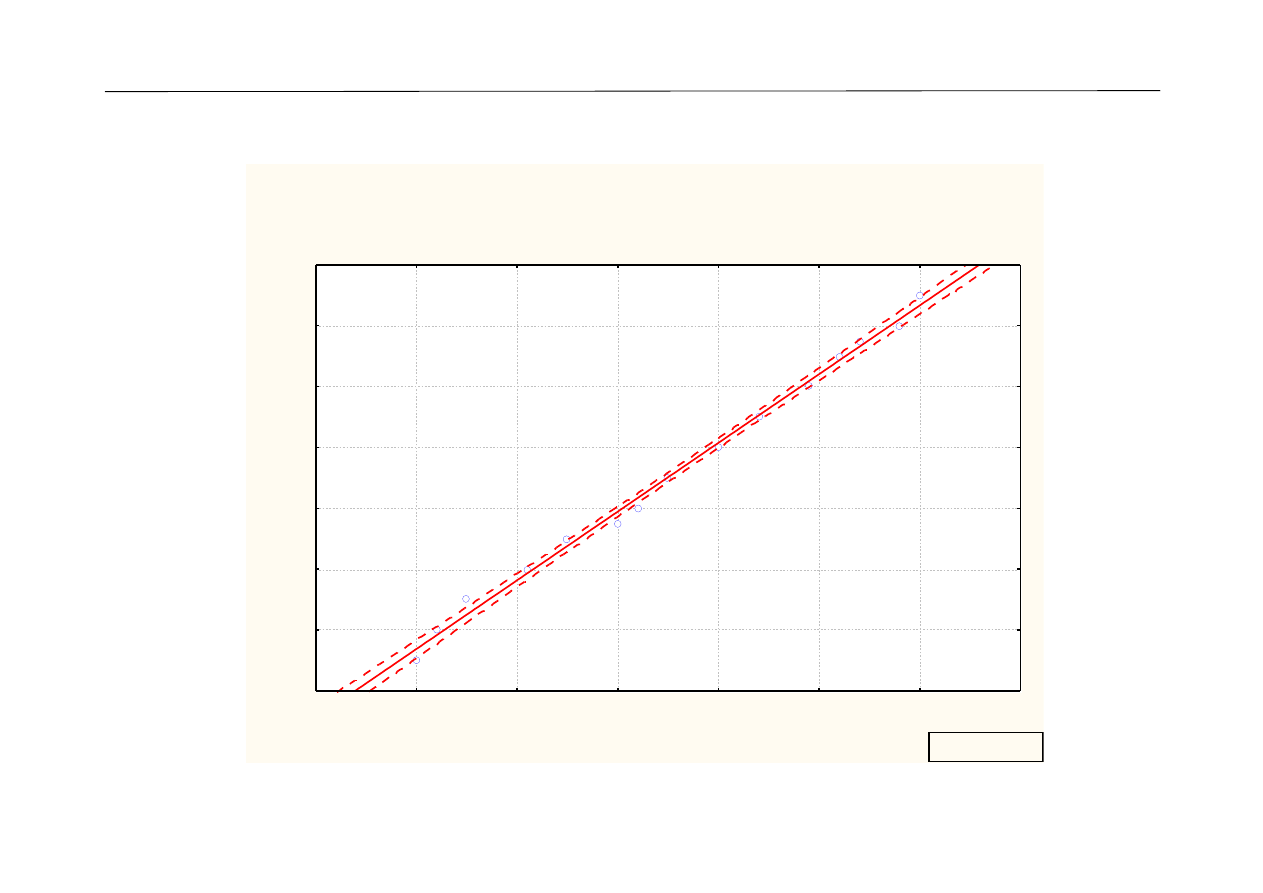
Wykres rozrzutu: Wzrost (w centymetrach) vs Wiek (w latach)

Wiek (w latach) = -19,72 + 0,23 * Wzrost (w centymetrach)

Korelacja: r = 0,997

110

120

130

140

150

160

170

180

Wzrost (w centymetrach)

6

8

10

12

14

16

18

20

W

ie

k

(w

la

ta

ch

)

0,95 Prz.Ufn.

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

5.7. Ocena dopasowania prostej regresji

•

Ocenimy teraz stopień zgodności przebiegu danych empirycznych

( y

i

i x

i

) i ( y

i

i x

i

) teoretycznych otrzymanych z oszacowa-

nia prostej regresji.

•

Podstawą do określenia tego dopasowania są różnice (zwane reszta-
mi) między wartościami empirycznymi a teoretycznymi (wynikają-
cymi z oszacowanej prostej regresji).

•

Dla prostej regresji Y względem X resztę definiujemy jako:

u

i

=

y

i

− 

y

i

,i=1, 2, , n.

•

Dla prostej regresji X względem Y resztę definiujemy jako:

v

i

=

x

i

− 

x

i

,i=1, 2, , n.

•

Wartości reszt powinny być relatywnie niskie w stosunku do warto-
ści przeciętnej zmiennej zależnej i dostatecznie często zmieniać
znak.

49

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

•

Wariancje resztowe dla obu równań prostej regresji wyznaczamy
w następujący sposób:

◦

s

2



u=

1

n−2

∑

i=1

n



y

i

− 

y

i



2

=

1

n−2

∑

i=1

n

u

i

2

◦

s

2



v =

1

n−2

∑

i=1

n



x

i

− 

x

i



2

=

1

n−2

∑

i=1

n

v

i

2

•

Odchylenia standardowe reszt otrzymujemy pierwiastkując warto-
ści wariancji resztowych:

◦

su=



s

2



u oraz sv=



s

2



v

•

W celu relatywnego spojrzenia na rolę reszt w obu prostych regresji
określamy wartość współczynnika zmienności losowej:

◦

V u=

su

y

⋅

100 % oraz V v=

sv 

x

⋅

100 %

50

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

•

W celu oceny stopnia dopasowania prostej regresji do punktów empirycz-
nych



x

i

, y

i



najczęściej stosuje się współczynnik zbieżności 

2

:



y

2

=

∑

i=1

n



y

i

− 

y

i



2

∑

i=1

n



y

i

−y

2

i 

x

2

=

∑

i=1

n



x

i

− 

x

i



2

∑

i=1

n



x

i

−x

2

•

Przy poprawnie i dokładnie wykonanych obliczeniach 

y

2

=

x

2

i dlate-

go też w praktyce używa się 

2

.

•

Współczynnik determinacji r

xy

2

można otrzymać następująco:

r

xy

2

=

1−

2

•

Zauważmy, że całkowity obszar zmienności zmiennej zależnej jest sumą
zmienności wyjaśnionej regresją



r

xy

2



i zmienności resztowej (niewy-

jaśnionej regresją), czyli:

r

xy

2



2

=

1

51

dr Tomasz Walczyński – Statystyka matematyczna (III Rok Matematyki z informatyką) - Wykład 5. (21.03.2012 r.)

•

Oba współczynniki r

xy

2

i 

2

przyjmują wartości z przedziału

[

0,1

]

.

•

Im wartość współczynnika zbieżności 

2

jest bliższa zeru, a tym sa-

mym wartość współczynnika determinacji r

xy

2

jest bliższa jedności, tym

dopasowanie prostych regresji do danych rzeczywistych jest lepsze.

•

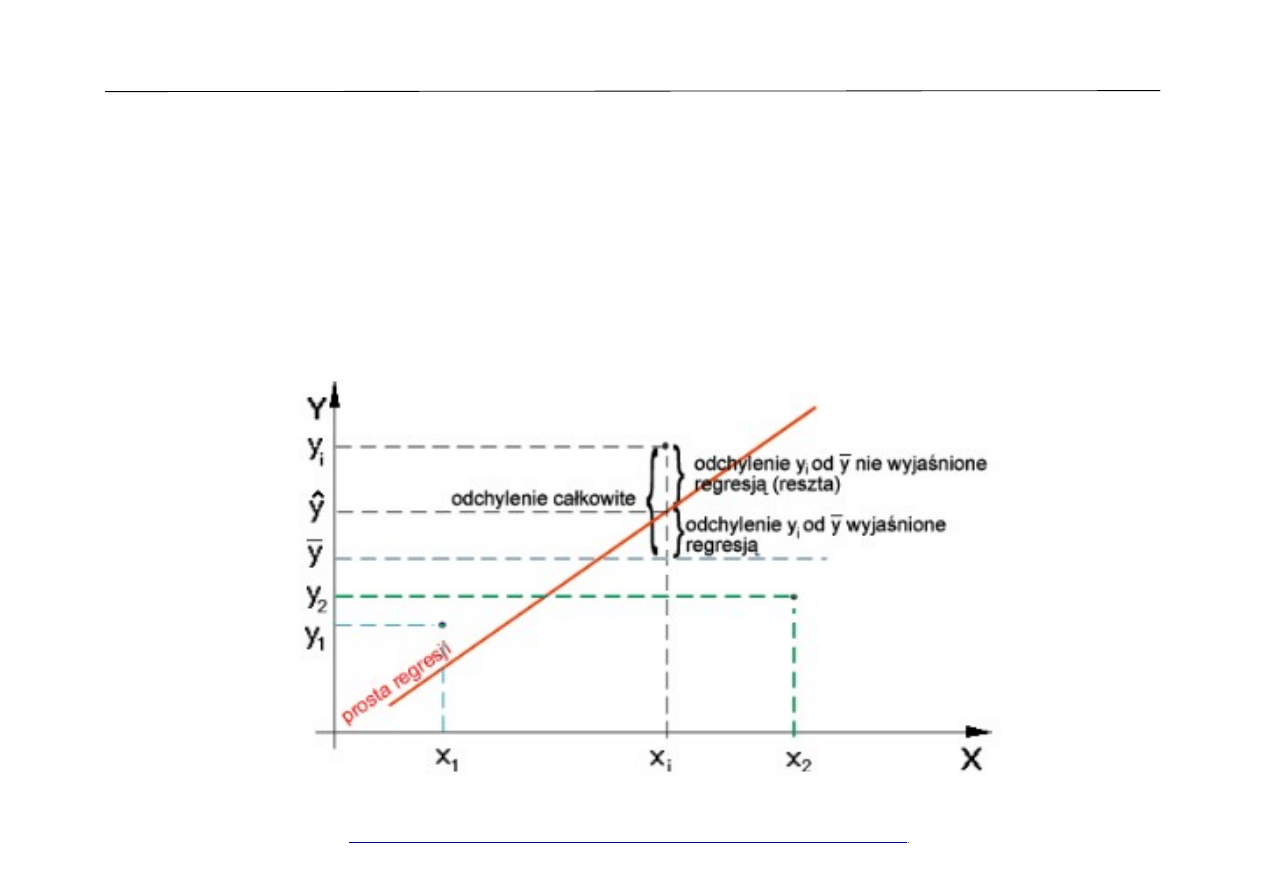
Interpretacja geometryczna:

Rysunek pochodzi ze strony:

http://home.agh.edu.pl/~bartus/index_druk.php?druk=y&action=statystyka&subaction=regresja_i_korelacja

52