
Egzamin dla Aktuariuszy z 17 stycznia 2005 r.
Matematyka Finansowa
Zadanie 1
ú
û
ù
ê
ë
é
+
+
+
+
=
+
+
=
+
+
=
...
08
,
1
1
,
1
6
1
,
1
5
1
,
1
4
1
,
1
3
1
,
1
1
...
3
2
...
2
3
3
2
2
3
3
2
2
2
1
R
v
v
R
v
v
R
Zauważmy, że:
4
4
4
4
3
4
4
4
4
2
1
4
4
4
4
4
3
4
4
4
4
4
2
1
5
1
,
1
1
2
5
2
5
2
5
2
4
2
3
2
2
2
....
08
,
1
1
,
1
7
08
,
1
1
,
1
6
1
,
1
5
1
,
1
4
1
,
1
3
1
,
1
2
1
,
1
1
B
A
OD
+
+
+
+
+
+
+
=
[
]
10%
stopie
przy
1
25
2
25
5
...
2
2
25
)
1
5
2
(
...
)
1
2
2
(
)
1
(
5
...
3
2
...
6
1
,
0
;
5
1
,
0
;
5
6
5
5
2
6
5
2
6
2
4
2
3
2
2
v
v
a
Ia
A
v
a
v
v
v
v
v
v
v
v
A
v
v
v
v
Av
A
−
−
−
=
−
−
+
+
+
=
−
−
⋅
+
+
−
⋅
+
=
−
+
+
+
+
=
=
[
]
0,08
stopie
...
1
5
2
25
...
...
7
6
2
24
...
)
1
8
2
(
)
1
7
2
(
6
)
1
(
...
7
6
...
7
6
3
2
2
3
2
2
3
2
2
2
2
2
2
przy
B
a
v
a
v
v
v
v
v
v
v
v
v
v
v
B
v
v
Bv
v
v
B
=
→
−
úû
ù
êë
é
−
−
+
=
=
−
−
−
+
+
+
=
+
−
⋅
+
−
⋅
+
=
−
+
+
=
+
+
=
∞
∞
bo:
∞
+
=
+
+
+
=
−
+
+
=
+
+
=
a
v
v
v
v
v
N
v
v
Nv
v
v
N
5
...
6
)
1
(
...
7
6
...
7
6
3
2
3
2
2
4000
15
,
1
1
≈
+
=
B
A
OD
Zadanie 2
300
var
60
)
90
;
30
(
~
1
50
1
=
=
−
=
X
EX
J
X
X
Y
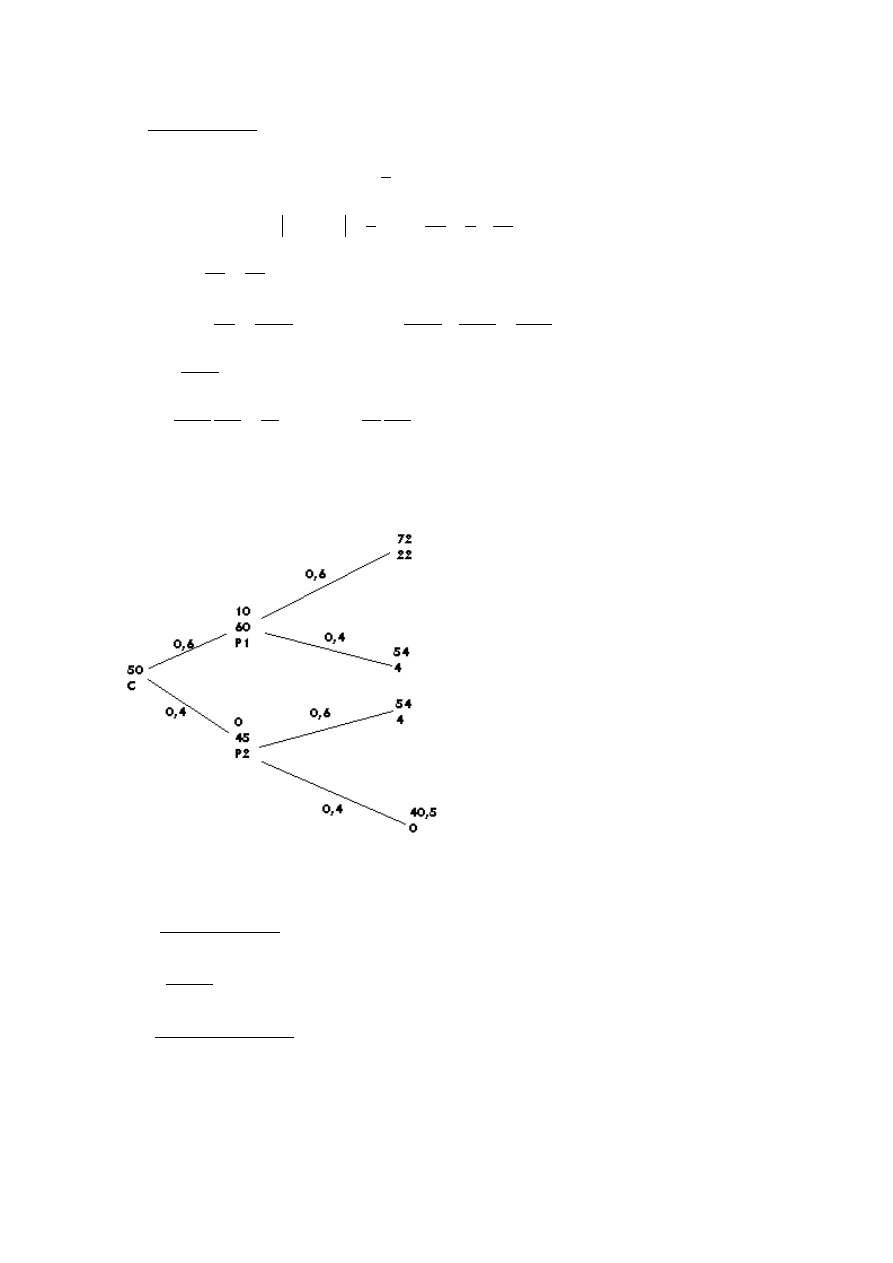
1
10
)
0
;
50
max(
2
−
−
=
X
Y
(
)
(
)
ò
+
+
=
+
=
>
=
≤
−
=
≤
=
=
−
t
t
t
X
P
X
P
X
P
50
50
60
3
1
60
1
3
1
0
t
dla
)
0
;
50
max(
3
1
)
50
(
0
)
0
;
50
max(
ò
ò
=
−
=
→
=
=
=
=
40
0
2
2
40
0
9
1600
9
1600
9
3200
var(max)
9
3200
60
(max)
3
40
60
(max)
x
E
X
E
5
,
14
12
100
9
16
9
16
100
1
9
1600
2
var
12
,
0
2500
300
)
1
var(
≈
=
→
=
=
=
=
ODP
Y
Y
Zadanie 3
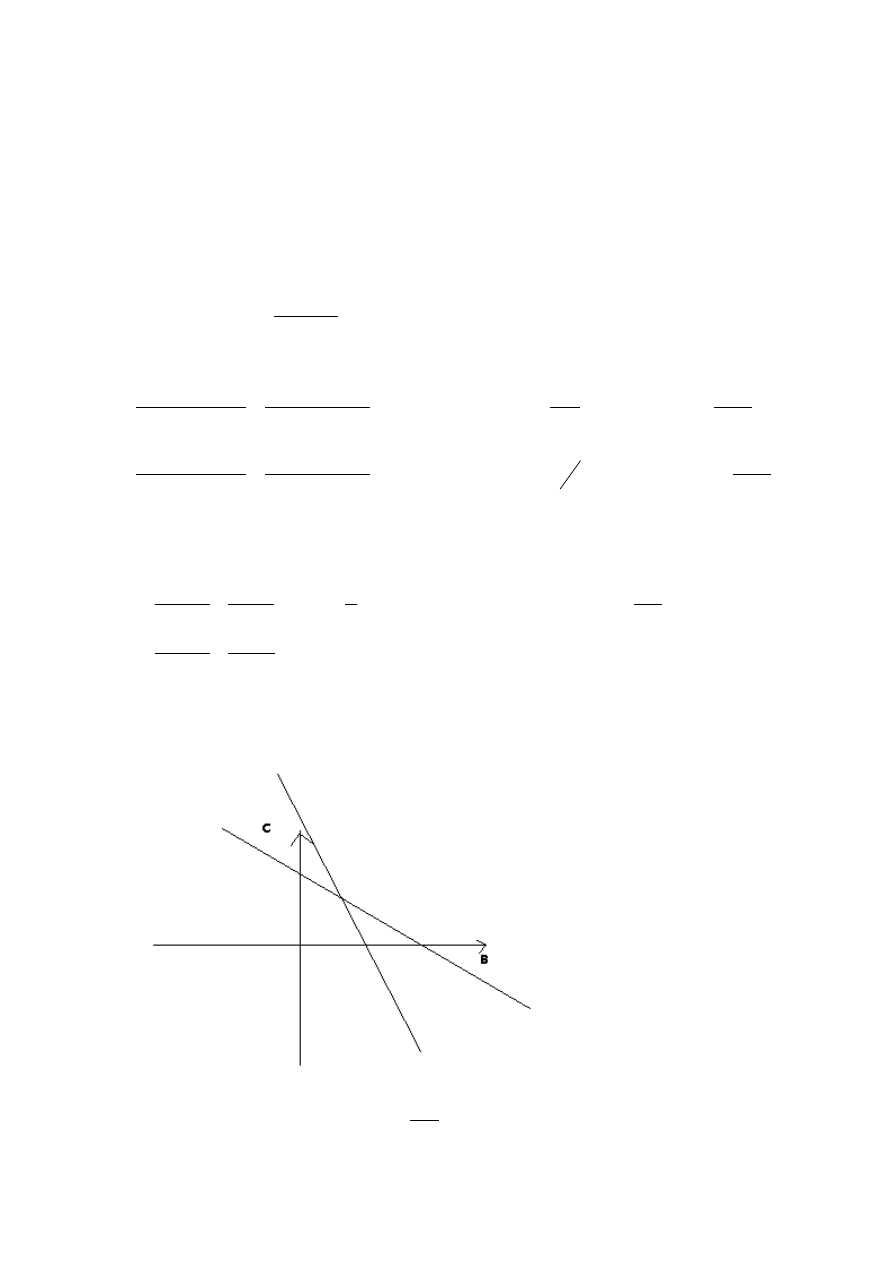
Dolna liczba oznacza warto
ść
opcji, górna dochód z wcze
ś
niejszego wykonania, obok warto
ść
jako max.
)
1
;
10
max(
)
1
(
1
,
1
4
4
,
0
22
6
,
0
1
P
W
P
=
⋅
+
⋅
=
)
2
;
0
max(
)
2
(
1
,
1
9
6
,
0
2
P
W
P
=
⋅
=
1
,
9
1
,
1
)
2
(
4
,
0
)
1
(
6
,
0
≈
+
=
W
W
C
Zadanie 4
A - depozyt
B - WWW
C - ZZZ
A+B+C=1000000
1. je
ś
li który
ś
indeks maleje 1,12A>=1000000
mo
ż
na przyj
ą
c,
ż
e
2
1
,
1
1000000
=
A
bo dla wy
ż
szych wzrostów bardziej zale
ż
y od indeksów
Zał.
ś
e B,C>=0 bo inaczej mo
ż
liwa nieograniczona strata
2.
)
2500
)
(
(
2000
)
2000
)
(
(
280
)
25000
)
(
(
40
2000
2000
)
(
25000
25000
)
(
−
+
−
≤
−
−
≤
−
z
ind
C
w
ind
B
z
ind
k
w
ind
z
ind
3.
)
25000
)
(
(
2000
)
2000
)
(
(
280
)
2000
)
(
(
500
2000
2000
)
(
25000
25000
)
(
−
+
−
≤
−
−
≥
−
z
ind
C
w
ind
B
w
ind
k
w
ind
z
ind
prawe strony s
ą
minimalne gdy wzrosty procentowe indeksów s
ą
równe, st
ą
d po podstawieniu
za w z odpowiednio:
2.
)
12
,
1
1
1
(
1000000
80000
7
4
80000
140000
−
+
−
=
+
−
≥
→
+
≤
B
C
i
k
B
C
C
B
k
3.
30000
140000
C
B
k
+
≤
je
ż
eli 2 spełniona to i 3 spełnione
wi
ę
c wystarczy:
musi le
ż
e
ć
na prostej
Szukamy maksymalnego k by istniały B i C tzn. takiego k by proste przecinały si
ę
w
(0;1000000(1-1/1,12), st
ą
d
32
,
1
80000
)
12
,
1
1
1
(
1000000
≈
→
=
−
k
k
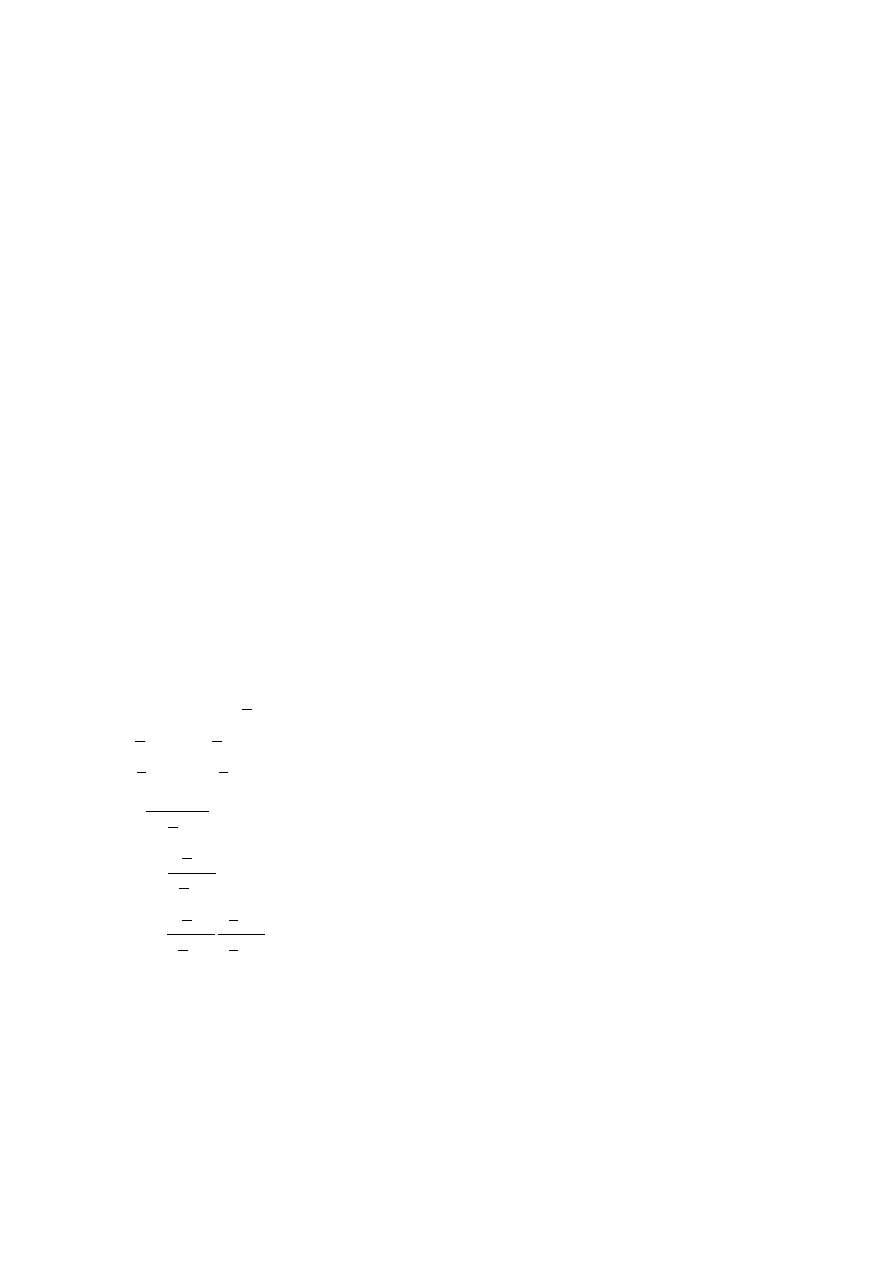
Zadanie 5
1) TAK:
)
;
max(
P
U
k
C
−
=
U - ilo
ść
akcji
k-kurs
mniejsza szansa,
ż
e P b
ę
dzie max
2) NIE:
Pytanie sprowadza si
ę
do pytania; czy gdy
ρ
ro
ś
nie czy z tego wynika,
ż
e P(X+Y>0) ro
ś
nie
Kontrprzykład: P(X+Y>0)>0 i zwi
ę
kszamy
ρ
do 1 tak,
ż
e X=-Y i wtedy P(X+Y>0)=0
3) TAK:
Z ogólnych własno
ś
ci - duration wła
ś
nie zabezpiecza w ten sposób
4) TAK
)
,
var(
))
,
var(min(
var
var
var
var
1
1
1
1
Y
X
Y
X
Y
Y
X
X
<
<
<
var cało
ś
ci wzrasta, z tego wynika,
ż
e je
ż
eli wariancja wzrasta to cena wzrasta (teoria)
Zadanie 6
06
,
0
;
10
3
08
,
0
;
10
2
08
,
0
;
30
2
1
,
0
;
20
1
1
,
0
;
30
1
1000000
:
a
R
a
R
a
R
a
R
a
R
X
=
=
=
06
,
0
;
10
08
,
0
;
10
08
,
0
;
20
1
,
0
;
20
1
3
08
,
0
;
20
1
,
0
;
20
1
2
1
,
0
;
30
1
1000000
a
a
a
a
R
R
a
a
R
R
a
R
=
=
=
?
5
10
5
:
3
2
1
=
+
+
R
R
R
X
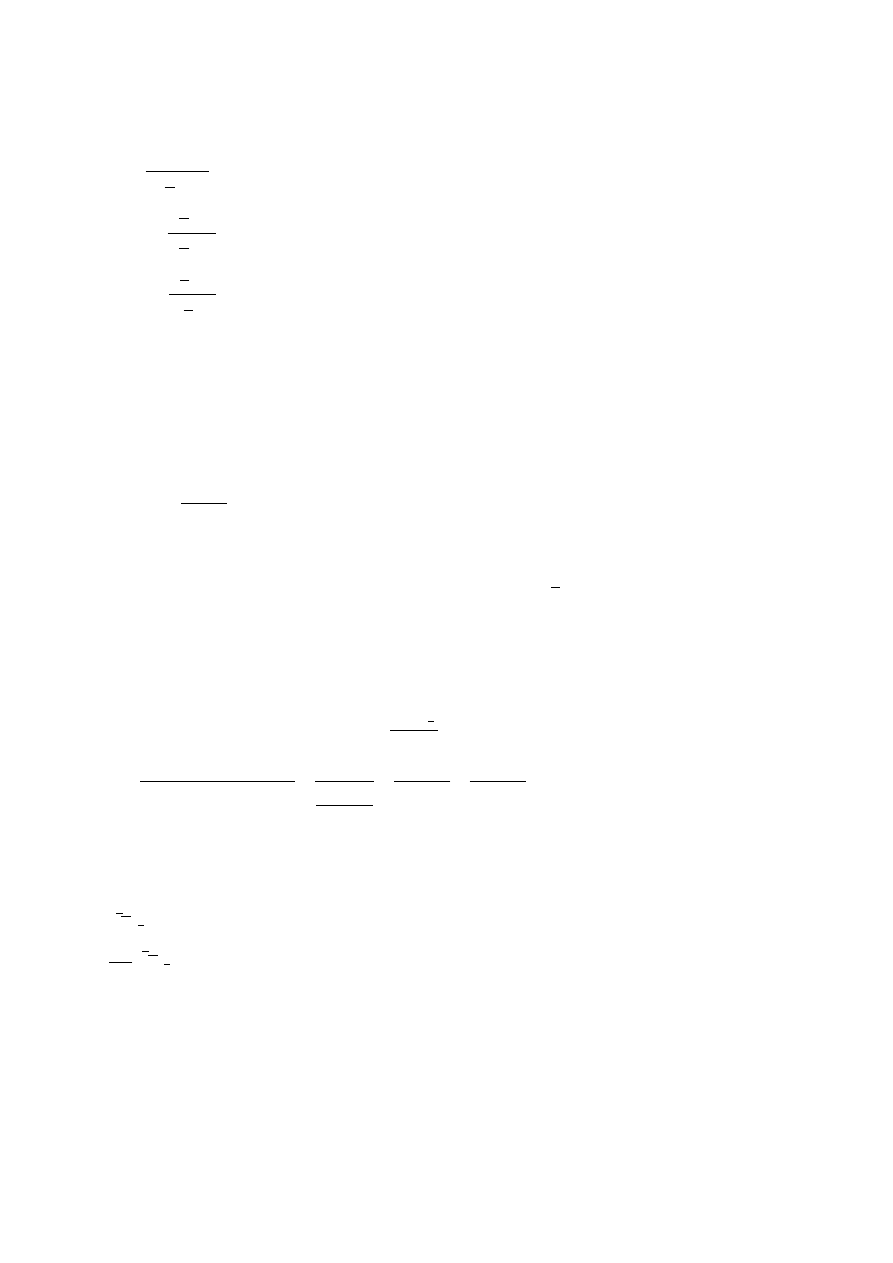
dla Y:
1
,
0
;
10
08
,
0
;
10
2
3
08
,
0
;
20
06
,
0
;
20
1
2
06
,
0
;
30
1
1000000
a
a
R
R
a
a
R
R
a
R
=
=
=
3
2
1
5
10
5
R
R
R
Y
+
+
=
19400
≈
−
≈
Y
X
ODP
Zadanie 7
Iteracyjnie startuj
ą
c z 0,06
)
(
)
(
1
k
k
k
k
i
f
i
f
i
i
′
−
=
+
wystarcz
ą
3,4 kroki
ż
eby zobaczy
ć
jak bliska jest stopa
125
1200
060369
,
0
8
,
4
)
1
(
)
1
(
)
1
(
)
(
;
15
7
8
9
≈
→
=
→
≈
→
−
+
+
+
+
+
=
R
Ra
i
i
i
i
i
f
i
k
Zadanie 8
(i)
TAK:
cakowitego
1
t
dla
)
1
(
)
1
(
)
1
(
2
2
)
1
(
...
)
1
(
...
)
1
(
1
...
)
2
(
)
1
(
1
1
1
2
≥
→
+
+
≥
+
=
+
>
+
+
−
+
+
+
−
+
=
−
−
=
+
+
−
+
−
+
=
−
−
−
n
n
t
t
n
n
t
n
n
t
v
v
n
n
v
v
t
t
P
v
a
n
v
v
n
v
n
n
I
n
t
n
n
(ii)
TAK
( )
( )
=
+
+
+
−
=
−
−
=
+
−
−
−
=
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
ò
1
2
2
3
3
2
1
2
0
3
3
2
1
2
2
2
2
2
2
2
2
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
n
n
n
n
n
n
n
n
n
n
n
t
e
n
ne
e
a
I
d
d
e
ne
a
I
e
ne
e
n
dt
e
t
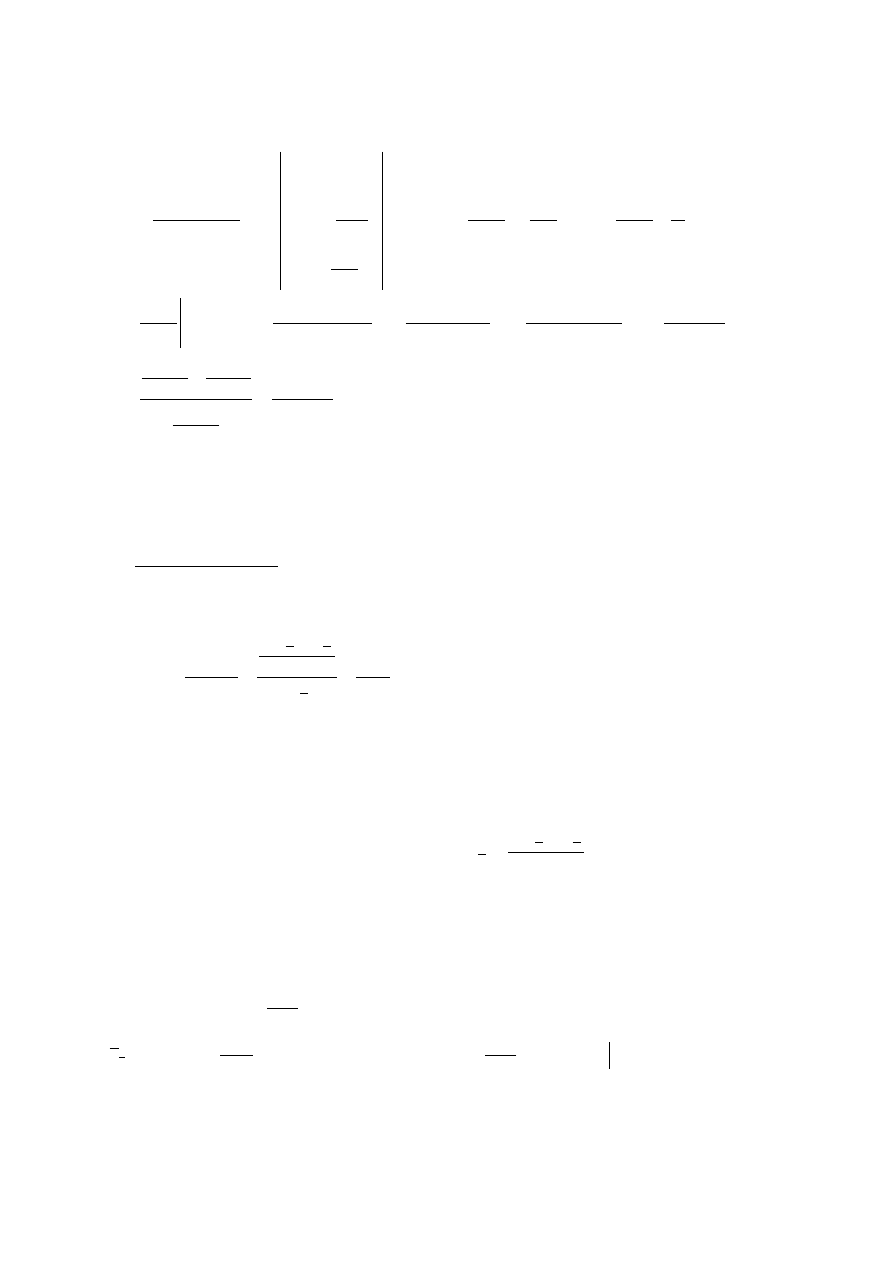
(iii)
TAK
÷÷
ø
ö
çç
è
æ
−
−
=
−
−
=
−
−
=
−
−
=
−
=
=
+
−
=
÷
ø
ö
ç
è
æ
−
−
=
−
=
−
=
=
+
=
−
+
=
+
−
−
−
−
−
−
−
ò
ò
ò
1
ln
)
1
(
)
(
ln
ln
ln
1
ln
1
1
1
1
1
1
ln
)
1
(
1
)
1
(
2
2
2
2
))
(
exp(
)
exp(
))
(
exp(
)
exp(
0
n
t
n
n
n
n
t
n
n
n
n
t
n
t
n
t
n
t
n
n
t
n
n
t
n
n
x
n
t
x
n
e
e
e
e
e
e
e
e
e
e
e
e
e
e
e
e
w
w
w
w
dw
w
w
dw
w
dx
w
n
x
w
i
dx
i
L
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
L
P
i
ln
tego
z
1
1
1
1
=
→
−
−
=
−
−
−
−
=
n
t
n
n
t
n
e
e
e
e
e
e
P
δ
δ
δ
δ
δ
δ
δ
δ
δ
Zadanie 9
}
{
å
å
−
+
−
+
=
Y
t
t
n
t
X
t
t
v
t
tv
n
v
t
v
t
n
2
1
3
2
)
1
(
)
1
(
lim
dzielimy licznik i mianownik przez n+1 i wtedy X i Y d
ążą
do zera.
Granica =
6
,
29
1
1
1
2
1
1
2
≈
−
+
=
−
−
=
∞
∞
∞
∞
=
∞
=
å
å
v
v
Ia
v
a
Ia
tv
v
t
t
t
t
t
Bo wyliczenia pomocnicze:
v
a
Ia
a
v
v
v
v
v
I
v
v
Iv
v
v
I
−
−
=
−
+
+
=
+
−
⋅
+
=
−
+
+
=
+
+
=
∞
∞
∞
1
2
...)
2
(
2
...
)
1
2
2
(
1
)
1
(
...
2
1
...
2
1
2
2
2
3
2
2
2
2
2
2
Zadanie 10
f jest odwzorowaniem liniowym (ci
ą
gła bo
t
δ
ci
ą
głe)
Z tego wynika:
f(0)=1, f(1)=2
t
t
+
=
→
1
1
δ
ò
ò
ò
ò
+
=
+
=
+
=
+
−
=
+
−
=
n
t
n
n
n
n
n
t
dt
t
dt
t
dt
ds
s
a
0
0
0
0
0
)
1
ln(
)
1
ln(
1
1
))
1
ln(
exp(
)
1
1
exp(
Wyszukiwarka
Podobne podstrony:
Egzamin 2005.01.17, rozwiazania zadań aktuarialnych matematyka finansowa
2003.01.25 matematyka finansowa
2005 10 10 matematyka finansowaid 25344
2007 01 08 matematyka finansowaid 25640
2008 03 17 matematyka finansowaid 26447
2003 05 17 matematyka finansowaid 21697
2007.01.08 matematyka finansowa
1 2000.01.15 matematyka finansowa
2005 05 16 matematyka finansowaid 25340
2005.10.10 matematyka finansowa
2005.01.17 prawdopodobie stwo i statystyka
2008.03.17 matematyka finansowa
1 2000 06 17 matematyka finansowaid 8918
2005.05.16 matematyka finansowa
2005 12 05 matematyka finansowaid 25347
2005 01 17 pra
2005 01 17 prawdopodobie stwo i statystykaid 25338
mat fiz 2005 01 17
więcej podobnych podstron