33

KOD ZDAJĄCEGO

MMA-P1A1P-021

EGZAMIN MATURALNY

Z MATEMATYKI

Arkusz I

Czas pracy 120 minut

Instrukcja dla zdającego

1. Proszę sprawdzić, czy arkusz egzaminacyjny zawiera 13 stron.

Ewentualny brak należy zgłosić przewodniczącemu zespołu
nadzorującego egzamin.

2. Rozwiązania i odpowiedzi należy zapisać czytelnie w miejscu

na to przeznaczonym przy każdym zadaniu.

3. Proszę pisać tylko w kolorze czarnym; nie pisać ołówkiem.
4. W rozwiązaniach zadań trzeba przedstawić tok rozumowania

prowadzący do ostatecznego wyniku.

5. Nie wolno używać korektora.
6. Błędne zapisy trzeba wyraźnie przekreślić.
7. Brudnopis nie będzie oceniany.
8. Obok każdego zadania podana jest maksymalna liczba punktów,

którą można uzyskać za jego poprawne rozwiązanie.

9. Podczas egzaminu można korzystać z załączonego zestawu

wzorów matematycznych, cyrkla i linijki oraz kalkulatora.
Nie można korzystać z kalkulatora graficznego.

10. Do ostatniej kartki arkusza dołączona jest karta odpowiedzi,

którą wypełnia egzaminator.

Życzymy powodzenia!

ARKUSZ I

MAJ

ROK 2005

Za rozwiązanie

wszystkich zadań

można otrzymać

łącznie 50 punktów

(Wpisuje zdający przed rozpoczęciem pracy)

PESEL ZDAJĄCEGO

Miejsce

na naklejkę

z kodem

(Wpisuje zdający przed

rozpoczęciem pracy)

34

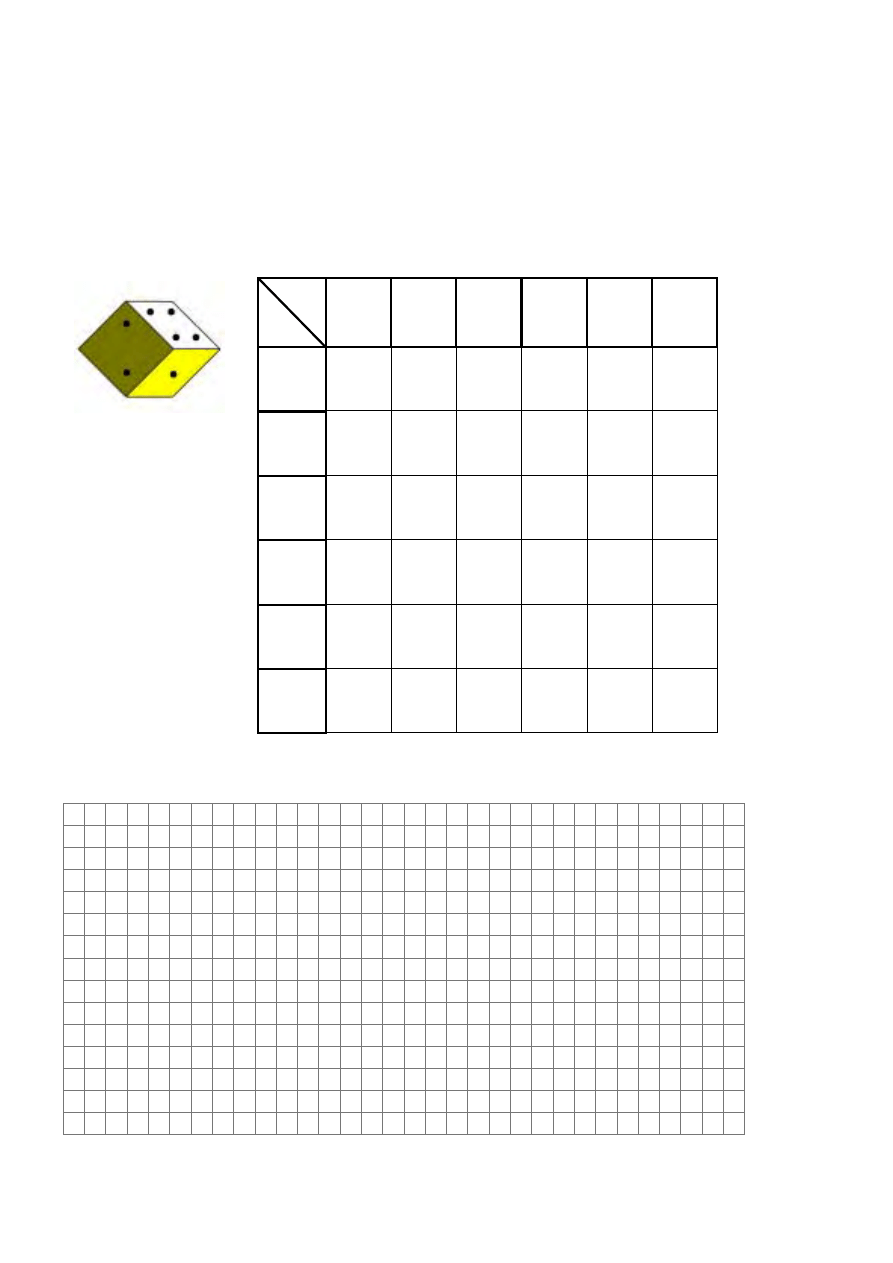
Zadanie 1. (3 pkt)

Gracz rzuca dwa razy symetryczną sześcienną kostką do gry i oblicza sumę wyrzuconych
oczek. Jeśli suma ta jest jedną z liczb: 6, 7 lub 8, to gracz wygrywa. W pozostałych
przypadkach przegrywa.
a) Uzupełnij tabelę, tak aby przedstawiała wszystkie możliwe wyniki tego doświadczenia

losowego.

SUMA WYRZUCONYCH OCZEK

b) Podaj liczbę wyników sprzyjających wygranej gracza i oblicz prawdopodobieństwo

wygranej.

I rzut

II
rzut

1

2

3

4

5

6

1

2

3

4

5

6

7

2

3

4

3

4

5

4

5

5

6

35

Zadanie 2. (3 pkt)

Średnia miesięczna płaca netto w pewnym zakładzie zatrudniającym 30 pracowników
wynosiła 2500 złotych. Po zatrudnieniu nowego, wysoko wykwalifikowanego pracownika
średnia miesięczna płaca netto w zakładzie wzrosła o 0,4%. Oblicz płacę netto nowego
pracownika.

36

Zadanie 3. (5 pkt)

Prawdą jest, że: „Jeżeli w czterocyfrowej liczbie naturalnej suma cyfr tysięcy i dziesiątek jest
równa sumie cyfr setek i jedności, to liczba ta jest podzielna przez jedenaście”.
Ponieważ

2

8

6

4

+

=

+

, to liczba 4862 jest podzielna przez 11.

a) Wykorzystując podaną cechę podzielności sprawdź, czy liczba 5764 jest podzielna

przez 11.

b) Podaj, jaką cyfrą można zastąpić

2, aby liczba 9528 była podzielna przez 11.

Uzasadnij stwierdzenie, że czterocyfrowa liczba, w której cyfry: tysięcy, setek i dziesiątek są
jednakowe, a cyfra jedności inna, nie jest podzielna przez 11.

37

Zadanie 4. (4 pkt)

Dane są liczby:

5
3
5
3

m

 

 

 

=

i

( )

5

2

1
6

2

0,5

64

n

−

−

⋅

=

.

a) Sprawdź, wykonując odpowiednie obliczenia, czy liczby m i n są całkowite.
b) Wyznacz liczbę k tak, by liczby

k

n

m ,

,

były odpowiednio pierwszym, drugim i trzecim

wyrazem ciągu geometrycznego.

38

Zadanie 5. (4 pkt)

Wiedząc, że 2

tgα = − i

(

)

0;

α

π

∈

oblicz, bez użycia tablic i kalkulatora, wartości

pozostałych funkcji trygonometrycznych kąta

α .

39

Zadanie 6. (5 pkt)

Wszystkie pary liczb naturalnych ( , )

x y spełniające równanie

7

4

=

− y

xy

można wyznaczyć

stosując następującą metodę:

•

zapisać lewą stronę równania w postaci iloczynu

(

)

4

7

x

y

−

= ;

•

stwierdzić, że zarówno

4

x

− jak i y muszą być liczbami naturalnymi;

•

zauważyć, że liczbę 7 daje się przedstawić w postaci iloczynu dwóch liczb naturalnych
tylko na jeden sposób, a korzystając z przemienności mnożenia mamy dwie
możliwości: 1

7

⋅ lub 7

1

⋅ ;

•

rozpatrzyć dwa przypadki







=

=

−

7

1

4

y

x

lub

4 7

1;

x

y

− =





=



•

wyznaczyć wszystkie pary liczb spełniające te warunki







=

=

7

5

y

x

lub

11

1 .

x

y

=



 =



Stosując przedstawioną wyżej metodę wyznacz wszystkie pary liczb naturalnych

( )

y

x,

spełniające równanie

4

=

− y

xy

.

40

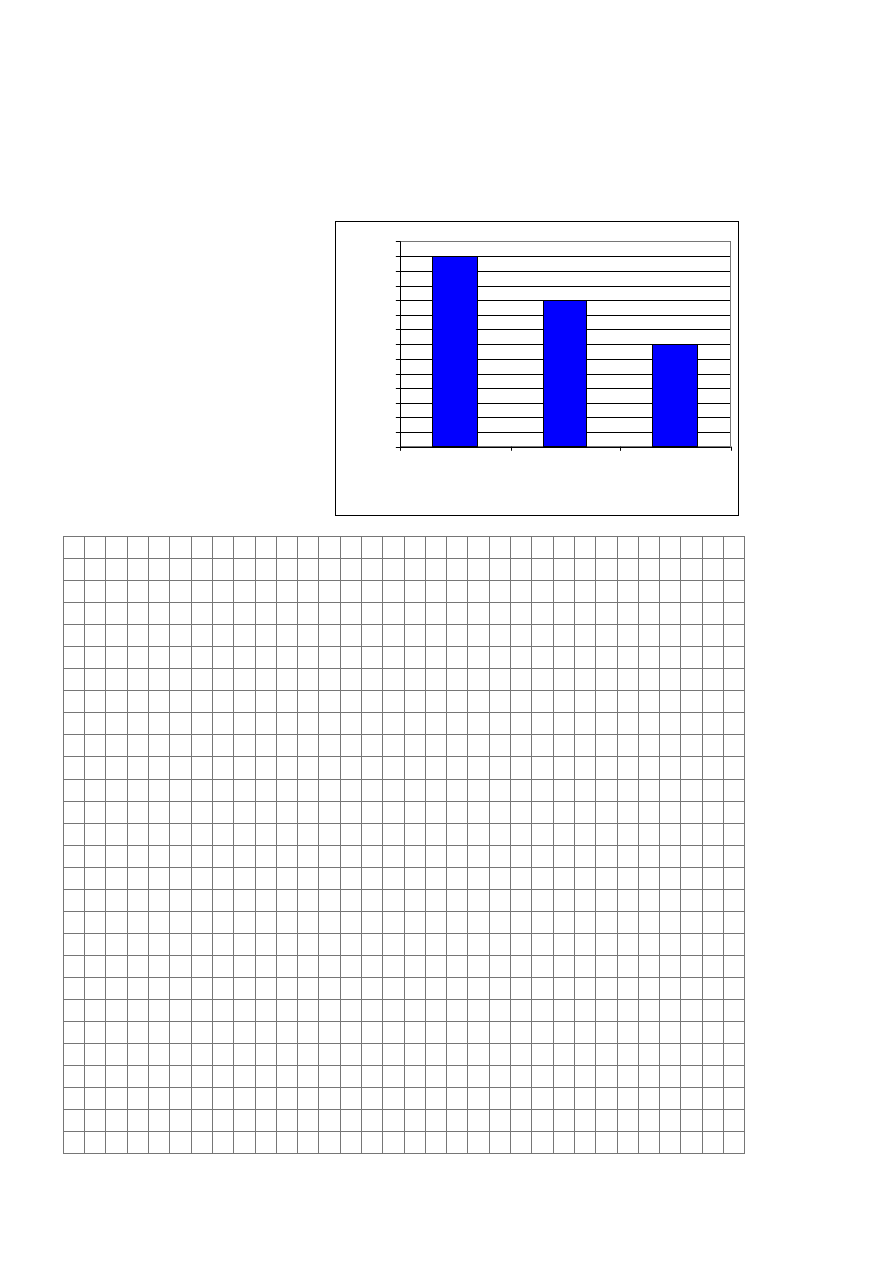
Zadanie 7. (4 pkt)

Na poniższym diagramie zestawiono wyniki ankiety dotyczącej czasu przeznaczanego dziennie
na uprawianie sportu.


a) Oblicz

średnią liczbę godzin

przeznaczoną dziennie na
uprawianie sportu w badanej
grupie.

b) Oblicz

wariancję i odchylenie

standardowe czasu
przeznaczanego dziennie na
uprawianie sportu.

Wynik podaj z dokładnością
do 0,01.

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

0

1

2

czas [godz.]

li

cz

b

a

os

ób

41

Zadanie 8. (4 pkt)

Funkcja f określona na zbiorze liczb całkowitych nieujemnych przyporządkowuje każdej
liczbie n resztę z dzielenia tej liczby przez 4.

a) Określ zbiór wartości funkcji f .
b) Podaj zbiór wszystkich miejsc zerowych funkcji f .
c) Narysuj wykres funkcji f dla

10

≤

n

.

42

Zadanie 9. (6 pkt)

Maszyna wycina z krążków kwadraty w ten sposób, że wykorzystuje materiał maksymalnie.
Gdyby promień danego krążka zwiększono o 1, to pole wyciętego kwadratu zwiększyło by się
czterokrotnie. Oblicz pole danego krążka.

43

Zadanie 10. (7 pkt)

Funkcja f jest określona wzorem:

( )

2

2

7

f x

x

x c

=

−

+ dla x R

∈ .

a) Wyznacz wszystkie wartości współczynnika ,

c dla których funkcja f ma dwa różne

miejsca zerowe.

b) Wyznacz wszystkie wartości współczynnika ,

c dla których miejscami zerowymi funkcji

f są liczby 1 i

2

1

2 .

c) Wyznacz wszystkie wartości współczynnika ,

c tak aby wierzchołek paraboli, która jest

wykresem funkcji f , należał do prostej o równaniu

x

y

= .

44

Zadanie 11. (5 pkt)

Objętość ostrosłupa prawidłowego trójkątnego, o długości krawędzi podstawy 6 cm , jest
równa

3

9 3 cm . Oblicz miarę kąta nachylenia ściany bocznej tego ostrosłupa do płaszczyzny

jego podstawy. Sporządź rysunek ostrosłupa i zaznacz na nim szukany kąt. Zapisz obliczenia.

47

MODEL ODPOWIEDZI I SCHEMAT OCENIANIA

ARKUSZA I

Numer

zadania

Etapy rozwiązania zadania

Liczba

punktów

Uzupełnienie tabeli (punkt przyznajemy również w przypadku
jednego błędu nieuwagi).

1

Podanie liczby wyników sprzyjających wygranej gracza: 16.

1

1

Obliczenie prawdopodobieństwa wygranej:

9

4

.

1

Obliczenie średniej płacy netto w zakładzie po przyjęciu nowego
pracownika: 2510 zł.

1

Zapisanie równania pozwalającego obliczyć płacę netto nowego

pracownika: np.

2510

31

2500

30

=

+

⋅

x

.

1

2

Obliczenie płacy netto nowego pracownika: 2810 zł. 1
Stwierdzenie, że liczba 5764 jest podzielna przez 11, ponieważ

4

7

6

5

+

=

+

.

1

Zapisanie warunku

+

9

2

8

5

+

=

i wyznaczenie

2

4

=

.

1

Zapisanie liczby czterocyfrowej w postaci np.

X

A

A

A

+

+

+

10

100

1000

, gdzie

{

}

9

,

8

,

7

,

6

,

5

,

4

,

3

,

2

,

1

∈

A

,

{

}

9

,

8

,

7

,

6

,

5

,

4

,

3

,

2

,

1

,

0

∈

X

.

1

Zapisanie powyższej liczby w postaci sumy składników, z których
jeden jest liczbą podzielną przez 11, np.

)

10

(

1100

X

A

A

+

+

.

1

3

Uzasadnienie, że suma pozostałych składników )

10

(

X

A

+

nie jest

liczbą podzielną przez 11, gdy

X

A

≠

i sformułowanie wniosku.

1

Obliczenie liczby m : 6

=

m

.

1

Obliczenie liczby n : 4

=

n

.

1

Zapisanie warunku na to by

k

n

m ,

,

były kolejnymi wyrazami

ciągu geometrycznego: np.

n

k

m

n = .

1

4

Obliczenie liczby k :

3

2

2

=

k

.

1

Obliczenie wartości cotangensa kąta

α :

1
2

ctg

α = − .

1

5

Zapisanie układu równań pozwalającego obliczyć sinus i cosinus
danego kąta.

1

48

Rozwiązanie układu równań:

2 5

sin

5

5

cos

5

α

α



= −







=



lub

2 5

sin

5

5

cos

5

α

α



=







= −



1

5

Wybranie odpowiedzi uwzględniającej założenia:

2 5

sin

5

5

cos

5

α

α



=







= −



1

Przekształcenie równania do postaci iloczynu: (

1)

4

x

y

−

= .

1

Rozpatrzenie wszystkich przypadków (za każdy przypadek

przyznajemy 1 p.):

1 4

1

x

y

− =





=



lub







=

=

−

4

1

1

y

x

lub

1 2

2

x

y

− =





=



3

6

Wyznaczenie rozwiązań otrzymanych układów równań:

5
1

x

y

=



 =



lub

2

4

x
y

=



 =



lub

3

2

x

y

=



 =



1

Obliczenie średniej liczby godzin: 0,8 .

1

Obliczenie wariancji (w tym 1 p. za metodę oraz 1 p. za
obliczenia): 0,63.

2

7

Obliczenie odchylenia standardowego: 0,79 .

1

Określenie zbioru wartości funkcji f :

{

}

0,1, 2,3 .

1

Podanie zbioru miejsc zerowych funkcji: np.

{

}

N

k

k

x

x

∈

∧

= 4

:

lub słownie np. „zbiór wielokrotności liczby 4” (za wymienienie
co najmniej trzech miejsc zerowych przyznajemy 1 punkt).

2

8

Narysowanie wykresu funkcji f dla

10

≤

n

.

1

Wykonanie rysunku wraz z oznaczeniami lub wprowadzenie
dokładnie opisanych oznaczeń.

1

Zapisanie pola mniejszego kwadratu w zależności od promienia
krążka, z którego jest wycięty:

2

1

2r

P

=

.

1

Zapisanie pola większego kwadratu w zależności od promienia
mniejszego krążka:

(

)

2

2

1

2

+

= r

P

.

1

Zapisanie związku pomiędzy polami mniejszego i większego
kwadratu:

(

)

2

2

1

4

+

= r

r

.

1

Rozwiązanie otrzymanego równania:

1

r

= lub

1
3

r

= − .

1

9

Wybór rozwiązania spełniającego warunek

+

∈ R

r

i obliczenie

pola danego krążka:

π

=

K

P

.

1

49

Zapisanie warunku na to, by funkcja f miała dwa różne miejsca
zerowe: 49 8

0

c

−

> .

1

Wyznaczenie zbioru wartości współczynników c , dla których

funkcja f ma dwa różne miejsca zerowe:

1

6

8

c

<

.

1

Zapisanie funkcji f w postaci iloczynowej:

( ) (

)











 −

−

=

2

1

2

1

2

x

x

x

f

.

1

Przekształcenie wzoru funkcji f do postaci ogólnej:

( )

5

7

2

2

+

−

=

x

x

x

f

.

1

Podanie wartości współczynnika c , dla której miejsca zerowe

funkcji f są równe 1 i

2

1

2 : 5

c

= .

1

Zapisanie warunku na to, by wierzchołek paraboli, która jest

wykresem funkcji f należał do prostej

x

y

= : np.

7

8

49

4

8

c

−

=

.

1

10

Obliczenie wartości współczynnika ,

c dla której wierzchołek

paraboli, która jest wykresem funkcji f należy do prostej

x

y

= :

7

7

8

c

=

.

1

Sporządzenie rysunku i zaznaczenie na nim szukanego kąta.

1

Obliczenie długości wysokości ostrosłupa:

3 cm

H

=

.

1

Obliczenie trzeciej części długości wysokości podstawy: 3 cm .

1

Obliczenie tangensa szukanego kąta: 3 .

1

11

Podanie miary kąta szukanego: 60

!

.

1

Za prawidłowe rozwiązanie każdego z zadań inną metodą od przedstawionej w schemacie
przyznajemy maksymalną liczbę punktów.