XVI Zbiory miary zero. Miara zewnętrzna Lebesgue'a w Rⁿ. Zbiory mierzalne w sensie Lebesgue'a. Mierzalność zbiorów borelowskich. Funkcje mierzalne i ich własności.

Definicja

Przedziałem domkniętym w p-ni
nazywamy zbior

.

Jeżeli
to P nazywamy przedziałem zdegenerowanym.

Definicja

Objętością przedziału P nazywamy liczbę
.

Definicja

Załóżmy, że X jest pewnym zbiorem,
jest
-ciałem. Funkcję
nazywamy miarą jeśli:

1)

2).
jest przeliczalnie addytywną funkcją zbioru.

Wówczas trójkę (
) nazywamy p-nią z miarą, elementy rodziny M zb. mierzalnymi.

Gdy
to A nazywamy zbiorem miary 0.

Gdy
to A nazywamy zbiorem miary skończonej.

Twierdzenie (własności miary)

Załóżmy, że (
) jest p-nia z miarą. Wówczas zachodzą następujące w-ki:

1).
jest addytywną funkcją zbioru tj, gdy

2).
jest niemalejącą funkcją zbioru tj, gdy

3). Gdy

4). Jeśli dla dowolnego

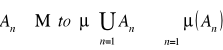
5). Gdy
to

6). Gdy
jest wstępującym ciągiem zbiorów mierzalnych to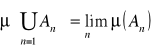

7). Gdy
jest zstępującym ciągiem zbiorów mierzalnych oraz
to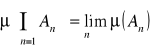
.

Twierdzenie (własności miary zero)

Załóżmy, że (
) jest p-nią z miarą. Wówczas

1). Dla dowolnego ciągu
zbiorów z M jeśli miara
dla dowolnego
, to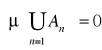
. (przeliczalna suma zbiorów miary zero jest zbiorem miary zero)

2). Dla dowolnego zbioru A mierzalnego i B mierzalnego jeśli miara
. ( mierzalny podzbiór zbioru miary 0 jest zbiorem miary 0)

3).dla dowolnych zbiorów A i B z rodziny M, jeśli
. (dodanie lub odjęcie od zbioru mierzalnego A zbioru miary 0 nie zmienia miary zbioru A).

Definicja

Miarę
nazywamy zupełną jeśli każdy podzbiór dowolnego zbioru miary zero jest mierzalny czyli :

.

Definicja ( miara zewnętrzna Caratheodory'ego)

Funkcję
określoną na rodzinie wszystkich podzbiorów zbioru X nazywamy miarą zewnętrzną C, jeśli spełnione są w-ki:

1).

2). Dla dowolnego zbioru
i dowolnego ciągu
podzbiorów zbioru X jeśli
.

Twierdzenie Caratheodory'ego

Załóżmy, że
jest miarą zewnętrzną. Niech
(C) w-k Caratheodory'ego

Wówczas M jest
-ciałem oraz gdy
│
, to
jest miarą zupełną, przy tym dla dowolnego
jeśli
.

MIARA LEBESGUE'A

Załóżmy, że
. Załóżmy, że
jest dowolnym zbiorem.

Definicja

Wielkość
zdefiniowaną wzorem

- ciąg podzbiorów domkniętych taki, że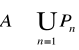
nazywamy k-wymiarową miarą zewnętrzną Lebesgue'a. Gdy
to mówimy, że rodzina
jest pokryciem zbioru A.

Z definicji miary Lebesgue'a i definicji kresu dolnego wynikają następujące własności:

a). dla dowolnego pokrycia zbioru A przedziałami domkniętymi zachodzi równość

b). dla dowolnego
istnieje ciąg
przedziałów domkniętych pokrywających A taki, że

.

Definicja

Elementy rodziny
nazywamy zbiorami mierzalnymi w sensie Lebesgue'a zaś funkcje
nazywamy k-wymiarową miarą Lebesgue'a.

Twierdzenie 1

Każdy przedział ograniczony
jest mierzalny w sensie Lebesgue'a oraz
.

Twierdzenie 2

Miara Lebesgue'a zbioru ograniczonego
jest liczbą skończoną. Każdy zbiór
da się przedstawić w postaci
gdzie
są zbiorami ograniczonymi.

Twierdzenie 3

Miara Lebesgue'a jest półskończona.

Definicja

Miara
jest półskończona, gdy istnieje ciąg zbiorów mierzalnych (A_i) taki, że

.

Twierdzenie 4

Każdy podzbiór borelowski p-ni
jest mierzalny (L). w szczególności jest mierzalny (L) każdy zbiór otwarty, domkniętyi wszystkie zbiory typu
.

Definicja

Zbiory postaci 1) i 2) należą do rodziny B(X) gdzie

1).

2).
są zbiorami domkniętymi dla dowolnego
.

Zbiory postaci 1) nazywamy zbiorami typu
, zaś 2) typu
.

Twierdzenie (o pełnej charakteryzacji zbiorów mierzalnych)

Załóżmy, że
. Następujące w-ki są równoważne:

1). A jest mierzalny w sensie Lebesgue'a (
)

2). Dla dowolnego
istnieje zbiór otwarty G taki, że
i

3). Istnieją zbiory B i C takie, że A=B\C, przy tym B jest typu
zaś C jest zbiorem miary 0

4). Dla dowolnego
istnieje zbiór domknięty F, taki, że
i

5). Istnieją zbiory D i E takie, że
, gdzie D jest zbiorem typu
zaś E jest zbiorem miary 0.

Definicja

Załóżmy, że M jest
-ciałem. Mówimy, że funkcja
jest mierzalna, jeżeli

1).

2)
.

Twierdzenie (w-ki równoważne mierzalności)

Załóżmy, że
oraz
. Następujące w-ki są równoważne:

1). F jest FM

2).

3).

4).
.

Twierdzenie (własności FM)

Załóżmy, że
jest FM. Wówczas zachodzą własności:

1).

2). Dla dowolnego przedziału

3).
.

Twierdzenie (o 2 FM)

Załóżmy, że
są FM. Wówczas następujące zbiory należą do rodziny M:

,
,
,
.

Twierdzenie (o iloczynie stałej FM)

Jeśli
jest FM oraz
jest FM.

Twierdzenie (o sumie i różnicy FM)

Jeśli
są FM oraz funkcja f+g jest poprawnie określona to f+g jest FM. Jeśli f-g jest określona poprawnie to f-g jest FM.

Twierdzenie (o iloczynie FM)

Załóżmy, że
. Wówczas fg jest FM.

Twierdzenie (o min i max FM)

Jeżeli funkcje
są mierzalne, to funkcja min{f, g} i max{f, g} też są mierzalne.