Do wykładu № 2

Zasady dynamiki Newtona. Pierwsza zasada dynamiki Newtona i inercjalne układy odniesienia. Siła, masa, pęd. Druga i trzecia zasada Newtona. Rodzaje sił w przyrodzie.

Wykłady realizowany są w ramach projektu pt. „Mechatronika kierunkiem przyszłości - dostosowanie oferty edukacyjnej Uniwersytetu Kazimierza Wielkiego do potrzeb rynku pracy”, Działanie 4.1.1, Programu Operacyjnego Kapitał Ludzki, współfinansowanego ze środków Europejskiego Funduszu Społecznego”.

• Resnik R., Holliday D. Fizyka. - Warszawa: WN PWN, 1998. W 2 t.

• Feynman R.P., Leighton R.B., Sands M. Feynmana wykłady z fizyki. - Warszawa: PWN, 1971. - W 5 t.

• Bobrowski C. Fizyka - krótki kurs. - Warszawa: WNT, 2007.

Układ odniesienia. Jednym z podstawowych spostrzeżeń przy badaniu ruchu ciała jest konstatacja jego względności. Oznacza to, że o ruchu ciała możemy mówić tylko, określając ciało odniesienia - ciało względem, którego analizujemy ruch.

Układem odniesienia nazywamy układ współrzędnych, który w jednoznaczny sposób związany z ciałem odniesienia, oraz zaopatrzony o sposób pomiaru czasu.

Ruchem nazywamy zmianę położenia ciała w przestrzeni względem wybranego układu odniesienia.

Rozróżniamy ruch postępowy i obrotowy.

Mówimy o ruchu postępowym jeśli wszystkie punkty ciała poruszają się po takich samych torach (geometrycznie podobnych).

W ruchu obrotowym tory poszczególnych punktów są okręgami współśrodkowymi.

Punktem materialnym nazywamy ciało obdarzone masą, rozmiaru którego można zaniedbać w pewnych zagadnieniach fizycznych.

Ruch prostoliniowy.

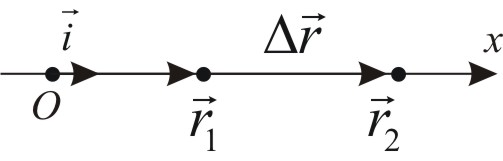
Ruchem prostoliniowym nazywamy ruch punktu materialnego po torze prostym. W tym przypadku możemy skorzystać z jednowymiarowego układu odniesienia. Ruch ciała opisuje zależność funkcyjna

,

gdzie
— czas.

Określimy prędkość średnią wzorem

,

gdzie
i
— wektory wodzący punktu materialnego w chwili czasu
i
, odpowiednio, oraz
— wektor przemieszczenia punktu materialnego i
.

Ponieważ, w danym przypadku prędkość średnia i wektor wodzący mogą być zapisane w postaci
i
, gdzie
i
— współrzędne, to również mamy

,
,

gdzie
i
— odległości od punktu
do punktu materialnego w chwili czasu
i
, odpowiednio, oraz
— długość wektora przemieszczenia
.

Z powyższych wzorów otrzymamy

:

lub z wykorzystaniem współrzędnej

:
.

Prędkością chwilową nazywamy granicę

lub
.

W przypadku ogólnym prędkość średnia zależę od wyboru chwil czasu
i
, a prędkość chwilowa od czasu
.

Jeśli prędkość ciała zależę od czasu, to ruch nazywamy zmiennym.

Przyspieszeniem średnim nazywamy iloraz różnicowy prędkości i czasu

,

gdzie
i
— prędkości punktu materialnego w chwili czasu
i
, odpowiednio, oraz
— zmiana prędkości w ciągu czasu
.

Przyspieszeniem chwilowym nazywamy granicę

.

Podobnie dla określonych wielkości zapisujemy z wykorzystaniem współrzędnej

oraz
.

Zaznaczmy, że

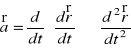
lub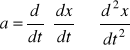
.

Z powyższych wzorów znajdziemy

lub z wykorzystaniem współrzędnej

.

Ruch jest prostoliniowym jednostajnym, jeśli za równe przedziały czasu
, odliczane od dowolnej chwili, punkt materialny dokonuje jednakowych przemieszczeń
. Wtedy
,
i jeżeli
:
;
:
, to droga
pokonana przez ciało będę

,

oraz położenie na osi

.

Graficzna ilustracja ruchu jednostajnego jest następująca.

Zaznaczmy, że

,

gdzie
jest kątem pokazanym na rysunku.

Ruch, w którym przyspieszenie jest stałe nazywamy ruchem jednostajnie zmiennym (przy
— jednostajnie przyspieszonym,
— jednostajnie opóźnionym). Oznaczając
, a także przyjmując
:
,
;
:
,
, z powyższych wzorów dla ruchu jednostajnego znajdziemy

:
;

:
.

Ponieważ w ruchu jednostajnym

,

to ostatecznie otrzymamy

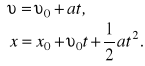
Eliminując czas otrzymamy korzystną w zastosowaniach zależność

.

Graficzna ilustracja ruchu prostoliniowego jednostajnie zmiennego jest następująca.

Ruch krzywoliniowy w przestrzeni trójwymiarowej.

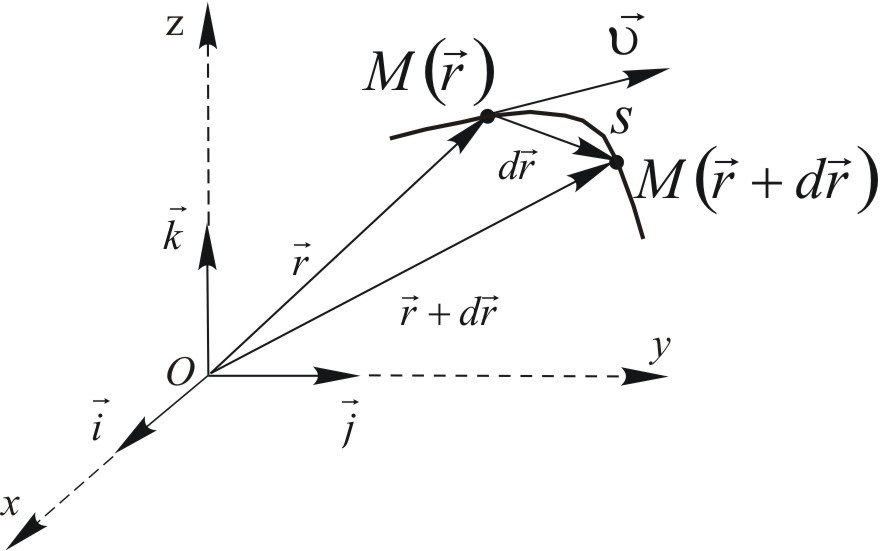
Jak i wcześniej, definicji prawa ruchu, prędkość i przyspieszenie są następujące

,

,

oraz
.

Zapis przez współrzędne jest następujący. Ponieważ

,
,
,

to prawo ruchu określają trzy skalarne zależności

;

dla składowych prędkości mamy

;

oraz dla składowych przyspieszenia

.

Rzut ukośny.

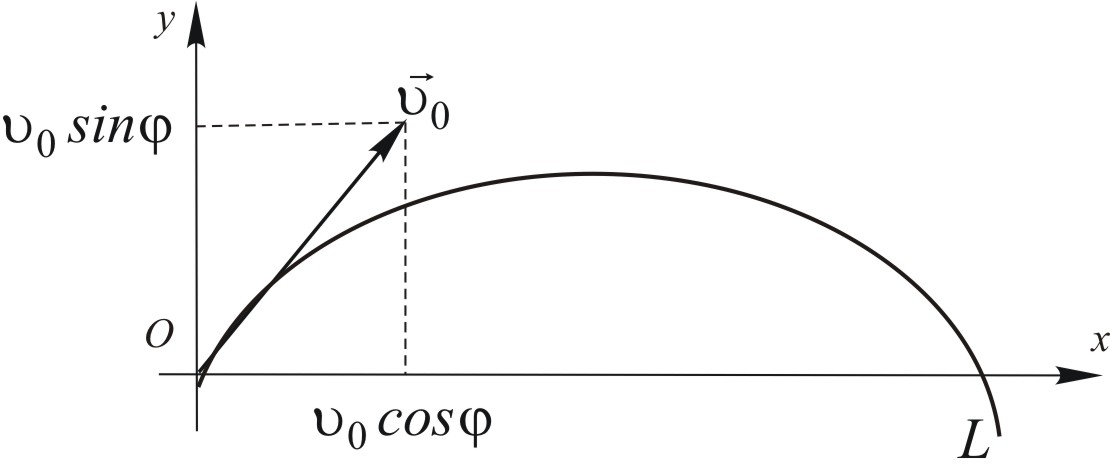
Ciało pozostało wyrzucone z prędkością
tworzącą kąt
z poziomem. Wybierzmy układ współrzędnych tak, jak pokazano na rysunku.

W kierunku osi
ciało porusza się ze stałą prędkością
, zaś w kierunku osi
dokonuje ruchu jednostajnie zmien­nego (jednostajnie opóźnionego) z wiadomym przyspieszeniem
i prędkością początkową
.

Więc współrzędne ciała w dowolnej chwili czasu będą

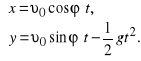
Dla znalezienia toru ruchu ciała eliminujemy czas. Z pierwszego równania

.

Podstawiamy w drugie równanie

.

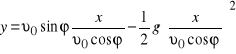
Po uproszczeniach otrzymamy

.

Jest to równanie paraboli

o parametrach

,
,
.

Punkt spadania na powierzchnie poziomą określa się z warunku

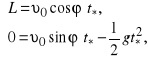
gdzie
— czas przelotu,
— odległość. Z pierwszego równania

.

Podstawiając w drugie

,

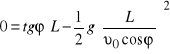
otrzymamy

.

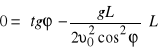
Skąd

i
.

Dalej

i

lub

i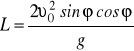

i ostatecznie

i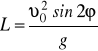
.

Pierwsze rozwiązanie
odpowiada punktu
. Drugie rozwiązanie daje możliwość znalezienia kąta
, przy którym odległość
będzie maksymalną. Notujemy

.

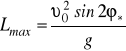
Funkcja
osiąga wartość maksymalną jeden przy
. Więc
.

Ruch po okręgu.

Ciało z prędkością
porusza się po okręgu o promieniu
. Zgodnie z definicją kąta w radianach

,

mamy

,

gdzie
i
— kąt i długość łuku zakreślonego w ciągu małego przedziału czasu
.

Dzielimy dwustronnie przez

i kierujemy przedział czasowy
do zera. Ponieważ
, to uwzględniając definicję

i
,

otrzymamy

,

gdzie
— prędkość kątowa.

Prędkość kątowa definiuje się jak wektor prostopadły do płaszczyzny okręgu tak, żeby z jego końca ruch po okręgu był przeciwny do ruchu strzałek zwykłego zegarka, a jego długość oznacza się powyższą granicą.

Okresem ruchu nazywamy czas pełnego obiegu
punktu materialnego po okręgu. Z definicji prędkości kątowej
, przy
, mamy
. Wówczas

.

Częstotliwością nazywamy wielkość fizyczną określoną ilorazem

.

Przyspieszenie kątowe określamy przez wzór

lub w postaci skalarnej

.

Połączymy otrzymane definicji. Ponieważ

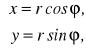
gdzie
i
. Różniczkując otrzymamy

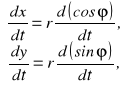
lub, ponieważ
i
, to

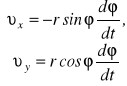
lub, ponieważ
, to

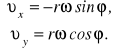
Różniczkując dalej otrzymane wyrażenia, zapisujemy

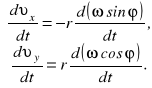
Korzystając z definicji przyspieszenia i rozpisując pochodne od iloczynu funkcji, mamy

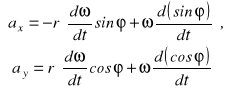
lub, ponieważ
, to

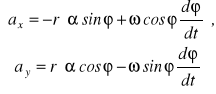
lub, uwzględniając, że
, zapisujemy

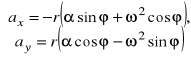
lub

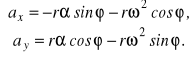
Korzystając z poprzednich wzorów dla składowych prędkości i współrzędnych punktu, mamy

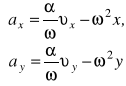
lub w postaci wektorowej

.

Pierwszy składnik

nazywamy przyspieszeniem stycznym, dla modułu którego mamy

.

Wówczas drugi składnik

nazywamy przyspieszeniem normalnym, dla modułu którego mamy

.

Prawa Newtona (1687 r.)

Pierwsze prawo:

• istnieją układy odniesienia, zwane inercjalnymi, względem których sprawiedliwe jest twierdzenie — punkt materialny zachowuje stan spoczynku lub prostoliniowego jednostajnego ruchu ze stałą prędkością, jeśli na niego nie działają inne ciała lub ich działanie wzajemnie jest zrównoważone;

• jeżeli istnieje chociażby jeden układ inercjalny, to ich istnieje nieskończenie wiele, i są to układu poruszające się wzajemnie ze stałą prędkością.

Drugie prawo

W wyniku oddziaływań punkt materialny zmienia swoją prędkość. Przyspieszenie wprost proporcjonalne działającej sile wypadkowej

,
.

Współczynnik proporcjonalności jest odwrotność masy punktu i drugie prawo Newton'a zapisuje się w postaci

.

Pęd punktu materialnego określamy wzorem

.

Drugie prawo Newton'a zapiszemy w postaci

i przyjmując
otrzymamy

lub

.

Jest to postać końcowa drugiego prawa dynamiki sformułowanego jeszcze przez Newton'a. W jakości wielkości zmiennych mogą występować masa
i prędkość
.

Trzecie prawo.

Wzajemne oddziaływania ciał wyglądają następująco

.

Siły w mechanice.

Ciężar

.

Siła sprężysta (prawo Hooke'a)

Tradycyjnie prawo Hooke'a zapisujemy w postaci

,

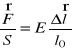
gdzie
— wydłużenie,
— stała Younga,
— pole przekroju pręta.

Stosując trzecią zasadę Newton'a

(akcja)
(reakcja)

i zmieniając układ odniesienia otrzymamy

,

gdzie
— współczynnik proporcjonalności,
— wektor wodzący punktu wychylenia od położenia równowagi.

Siła tarcia.

Siła tarcia zawsze jest skierowana przeciwko aktualnemu kierunku ruchu ciała, tzn. wektora prędkości
.

W przypadku ruchu ciała stałego po powierzchni innego ciała stałego (podstawy) mamy

,
,

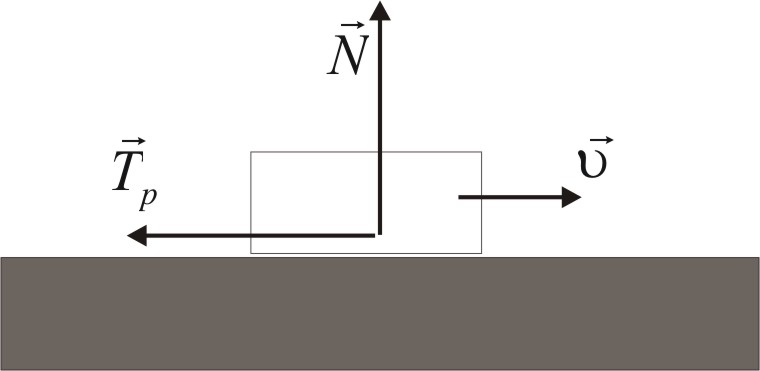
gdzie
— siła tarcia,
— reakcja podstawy (siła normalna do powierzchni kontaktu, działająca na ciało).

Jest to tarcie poślizgowe.

Siła oporu przy ruchu w powietrzu.

Fragmenty analizy wymiarowej. Z obserwacji ustalonego ruchu spadających ciał kulistych w atmosferze stwierdzono, że siła oporu ośrodka
jest zależna od jego gęstości
, pola powierzchni przekroju ciała
, a także prędkości
, tzn.
. Znaleźć postać niewiadomej zależności funkcyjnej.

Załóżmy, że

,

gdzie
,
i
są nieznanymi wykładnikami potęgi, strzałką podwójną
oznaczono proporcjonalność.

Przeanalizujmy teraz wymiar wielkości po obu stronach proporcjonalności. Ponieważ
,
,
i
, to warunek jednakowego wymiaru zależności fizycznych zapiszemy w postaci

,

lub

.

Skąd nieznani wykładniki potęgi powinni spełniać warunki

,

,

.

Rozwiązując ten układ równań znajdziemy

,
,
.

Więc dla siły oporu otrzymujemy

,

lub

,

gdzie
jest współczynnikiem proporcjonalności, który znajdujemy z wyników eksperymentu.

Siła dośrodkowa
i odśrodkowa
.

,

Siły bezwładności

,

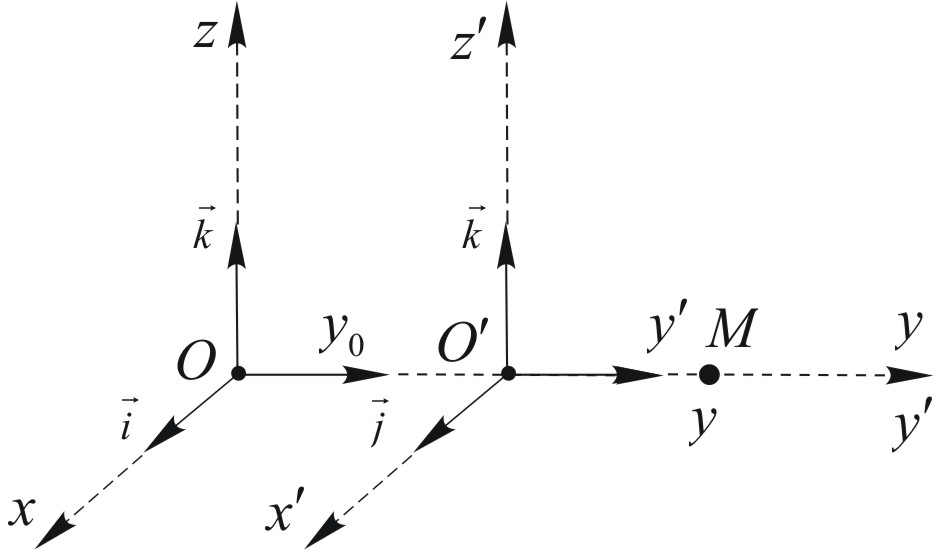
lub

.

Siła bezwładności (siła pozorna)

i ostatecznie

.

Siła Coriolisa

.

---