 | Pobierz cały dokument projekt.z.wytrzymalosci.ugiecie.belki.doc Rozmiar 420 KB |
ĆWICZENIE PROJEKTOWE Z WYTRZYMAŁOŚCI MATERIAŁÓW
Wyznaczyć linię ugięcia belki metodą Clebsch'a.
Przekrój poprzeczny pręta stanowi figura płaska na rys.1.
Obciążenia wywołujące przemieszczenie (rys.2), z wyłączeniem siły P, działają w płaszczyźnie przechodzącej przez oś ustroju oraz główną centralną oś bezwładności, względem której moment bezwładności jest minimalny.
Wyznaczyć oś zerowych naprężeń normalnych oraz obliczyć ich ekstremalne wartości uwzględniając siłę skupioną P przyłożoną w punkcie A i pochyloną względem głównych osi bezwładności pod kątami: α1=50° α2=60°
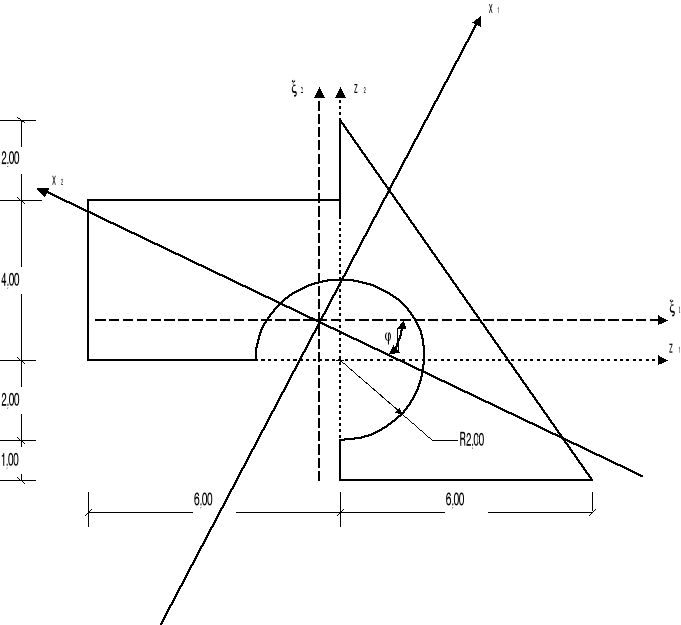

Rozłożenie siły P na składowe
![]()
![]()
![]()

Rozwiązujemy belkę z pominięciem siły P1
![]()
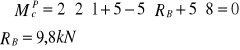
![]()
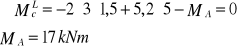
![]()
![]()
![]()
![]()
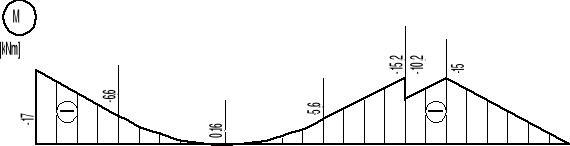
dla x=0 Mα1= -17 kNm
dla x=2 Mα1= -6,6 kNm
![]()
![]()
![]()
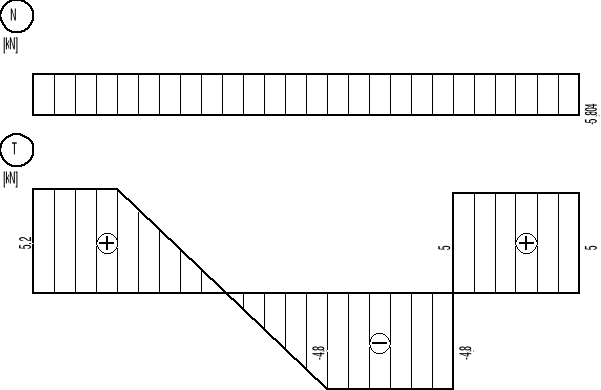
dla x=2 Tα2 = 5,2 kNm
dla x=5 Tα2 = -0,8 kNm
dla x=7 Tα2 = -4,8 kNm
![]()
dla x=2 Mα2= -6,6 kNm
dla x=5 Mα2= 0 kNm
dla x=7 Mα2= -5,6 kNm
![]()
![]()
![]()
![]()
dla x=7 Mα3= -5,6 kNm
dla x=9 Mα3= -15,2 kNm
![]()
![]()
![]()
![]()
dla x=9 Mα4= -10,2 kNm
dla x=10 Mα4= -15 kNm
![]()
![]()
![]()
![]()
dla x=10 Mα4= -15 kNm
dla x=13 Mα4= 0 kNm
Rozwiązujemy belkę obciążoną wyłącznie siłą P1

![]()
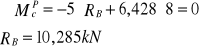
![]()
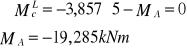
![]()
![]()
![]()
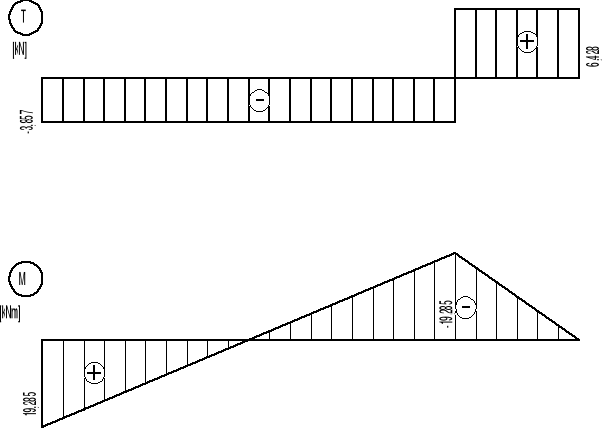
dla x=0 Mα1= 19,285 kNm
dla x=5 Mα1= 0 kNm
dla x=10 Mα1= -19,285 kNm
![]()
![]()
![]()
dla x=10 Mα2= -19,285 kNm
dla x=13 Mα2= 0 kNm
Obliczenie pola powierzchni.
![]()
Obliczenie momentów statycznych.
![]()
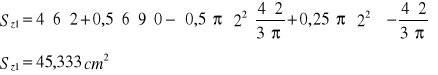
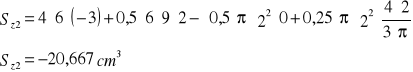
Obliczenie współrzędnych środka ciężkości.
![]()
![]()
Obliczenie momentów bezwładności ![]()
![]()
:
-obliczamy momenty bezwładności względem osi z1 z2 i na podstawie tych momentów obliczamy momenty bezwładności względem osi ξ1 ξ2.
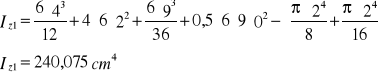
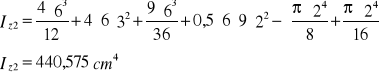
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
-bezpośrednie obliczenie momentów bezwładności względem osi ξ1 ξ2.
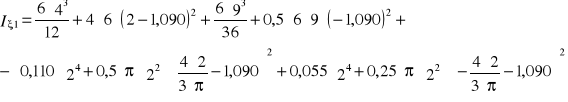
![]()
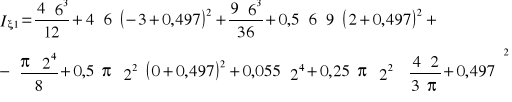
![]()
Obliczenie momentów dewiacji ![]()
.
-obliczamy momentu dewiacji względem osi z1 z2 i na podstawie tego momentu obliczamy moment dewiacji względem osi ξ1 ξ2.
 | Pobierz cały dokument projekt.z.wytrzymalosci.ugiecie.belki.doc rozmiar 420 KB |