1. Sprawdzenie współczynnika przenikania ciepła Uk (z rysunkami rozkładu temperatur).

Dane:

Ti=25°C

• pomieszczenie wewnętrzne- łazienka

Te= -16°C

• budynek zlokalizowany jest w Mielnie (I strefa klimatyczna)

od lewej

1. tynk cementowo - wapienny- d1=0,015 m, λ=0,82

2. cegła klinkierówka- d2=0,12 m, λ=1,05

3. styropian- d3=0,06 m, λ=0,045

4. cegła dziurawka- d4=0,25 m, λ=0,62

5. tynk cementowo - wapienny- d5=0,015 m, λ=0,82

• Całkowity współczynnik przenikania ciepła

gdzie:

Uo- współczynnik przenikania ciepła

ΔUo- człon korekcyjny współczynnika przenikania ciepła

ΔU- dodatek do współczynnika wyrażający wpływ mostków cieplnych

1. Współczynnik przenikania ciepła Uo

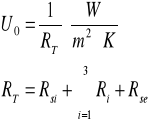
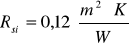
- opór przejmowania ciepła na wewnętrznej powierzchni

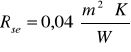
- opór przejmowania ciepła na zewnętrznej powierzchni

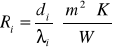
- opór cieplny jednorodnej warstwy materiału

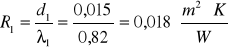
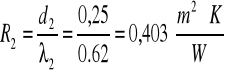
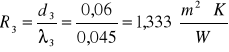
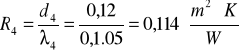
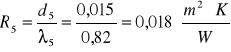
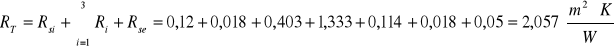
2. poprawki w odniesieniu do współczynnika przenikania ciepła ΔUo

ΔUo=ΔUg+ΔUf

gdzie:

ΔUg- poprawka z uwagi na nieszczelności,

ΔUo- poprawka z uwagi na łączniki mechaniczne.

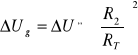
Mamy:

ΔU''=0,01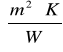
- 1 poziom poprawki

R3=1,333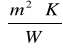
- opór cieplny warstwy zawierającej nieszczelności

RT=2,057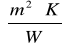
-całkowity opór komponentu

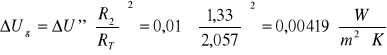
Mamy:

α=6
- współczynnik

- współczynnik przewodzenia ciepła łącznika

- liczba łączników na

- pole powierzchni przekroju łącznika (kotew ∅6)

C. Dodatek wyrażający wpływ mostków cieplnych

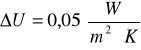
• Całkowity współczynnik przenikania ciepła

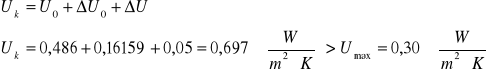
4. Rozkład temperatury na przegrodzie

gdzie:

- temperatura wewnętrznej powierzchni przegrody

- opór przejmowania ciepła na wewnętrznej powierzchni kolejnej przegrody

Mamy:

,

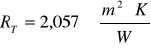
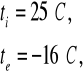
2. Sprawdzenie możliwości roszenia na powierzchni wewnętrznej przegrody

Dane:

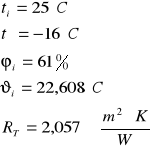
• Temperatura na powierzchni ściany od strony pomieszczenia:

- ciśnienie cząsteczkowe pary wodnej nasyconej przy temperaturze

Ciśnienie cząsteczkowe pary wodnej w pomieszczeniu

Dla wyznaczonego ciśnienia odczytano temperaturę punktu rosy:

• Sprawdzenie możliwości roszenia na powierzchni wewnętrznej przegrody

Ponieważ zachodzi warunek
, na powierzchni przegrody od strony pomieszczenia nie wystąpi kondensacja pary wodnej.

3. Sprawdzenie możliwości kondensacji pary wodnej wewnątrz przegrody (metoda Fokina)

Dane:

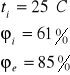
1. Sprawdzenie możliwości kondensacji pary wodnej w przegrodzie dla
   

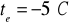
1. Wartość ciśnienia nasyconej pary wodnej
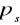
   dla temperatur obliczeniowych

stąd

Ciśnienie rzeczywiste w pomieszczeniu

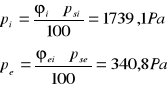
3.3Opory dyfuzyjne
poszczególnych warstw oraz opór dyfuzyjny całej przegrody

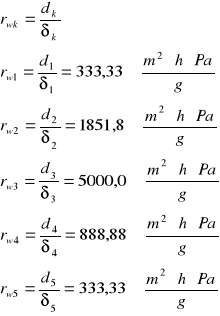
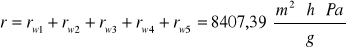
WNIOSEK:

Z wykresu ciśnienia pary wodnej nasyconej ps wynika, że w przegrodzie nie nastąpi kondensacja pary wodnej dla temperatury t_e= -5^oC. Zatem z rocznego średniego rozkładu temperatur dla I strefy klimatycznej dla okresu zimowego dla którego najniższa średnia temperatura wynosi (dla stycznia) -1.3^oC wynika że w przegrodzie nie wystąpi w przegrodzie kondensacja pary wodnej w okresie zimowym. Biorąc pod uwagę izolacyjność cieplną przegrody stwierdzam, że przy założeniu, iż dopuszczalna wartość współczynnika przenikania ciepła wynosi
[W/m²K] przegroda nie spełnia wymagań normowych (
[W/m²K]). Należy również podkreślić, iż stwierdzono, że na powierzchni przegrody od strony pomieszczenia nie wystąpi kondensacja pary wodnej.

---