ZAGADNIENIA NA EGZAMIN LICENCJACKI DLA KIERUNKU
INFORMATYKA I EKONOMETRIA
W WSIIE TWP W OLSZTYNIE
Rok Akademicki 2001/2002

MATEMATYKA

Pochodna i jej interpretacja. Elastyczność funkcji.

Pochodna funkcji w punkcie

Punktem wyjścia do określenia pochodnej funkcji jest pojęcie ilorazu różnicowego funkcji.

Jeśli funkcja f jest określona w przedziale (a;b) i x₀ , x₁
(a;b), to różnicę x₁ - x₀ nazywamy przyrostem argumentu od x₀ do x₁ ozancza się to przez h.

Ilorazem różnicowym funkcji f: (a;b)
R odpowiadającym przyrostowi argumentu x₀
(a;b) o liczbę ≠ 0 taką że x₀ +h
(a;b) nazywamy : f '( x₀ ) =

Y Iloraz różnicowy ma prostą interpretacje

B geometryczną. Punkty A i B należą do wykresu

A funkcji f. Prostą AB nazywamy sieczną wykresu

x₀ x₁ X funkcji f. Iloraz różnicowy
jest

równy tangensowi kąta
, jaki tworzy sieczna

AB z osią x .

Pochodna jako funkcja

Mając funkcję f : (a;b)
R oznaczamy przez A zbiór wszystkich argumentów x funkcji f takich że istnieje pochodna funkcji f w punkcie x. Wówczas funkcję, która każdej liczbie x
A przyporządkowuje liczbę f `(x)nazywamy pochodną funkcji f. Dziedziną funkcji f 'jest więc zbiór A

Pochodna i jej interpretacje. Elastyczność funkcji.

Pochodna funkcji jednej zmiennej y=f(x) jest nowa f-cja y` zmiennej x, równa przy każdej wartości x granicy stosunku przyrostu funkcji Δ y do odpowiadającego mu przyrostu zmiennej niezależnej Δ x, gdy Δ x dąży do zera F`(x)= lim f(x - Δ x) / Δ x = Δ y / Δ x

Obliczanie pochodnej nazywamy różniczkowaniem funkcji.

Interpretacja geometryczna:

Jeżeli wykresem funkcji y = f(x) jest pewna krzywa, to wartość pochodnej f`(x) w danym punkcie x równa jest tg α gdzie α jest kątem między osią OX a styczną do krzywej w danym jej punkcie.

Elastyczność f-cji możemy określić wzorem ε (y,x) = (Δ y / y) / (Δ x / x) = y` *x / y

Elastyczność funkcji informuje o ile procent zmieni się wartość y jeżeli zmienna niezależna wzrośnie o 1 procent.

Pochodne cząstkowe rzędu 1-go i 2-go oraz ich zastosowanie do badania ekstremów funkcji

Pochodną cząstkową f-cji wielu zmiennych u = f(x,y,z .. t) względem jednej z tych zmiennych, np. względem x określa wzór f `_x = lim f{( x+ Δ x,y,z, .. t) - f(x,y,z,..t)} / Δ x w tym przypadku przyrost otrzymuje tylko jedna ze zmiennych niezależnych. Pochodne cząstkowe oblicza się zgodnie
z zasadami różniczkowania f-cji jednej zmiennej, przy czym pozostałe zmienne niezależne uważa się w danym przypadku za stałe.

Pochodna cząstkowa rzędu drugiego f-cji u=f(x,y, .. t) to pochodna pochodnej rzędu pierwszego. Może być brana względem tej samej zmiennej co i pierwsza pochodna lub też względem innej zmiennej (pochodna mieszana rzędu drugiego), ciągłej w danym punkcie

Badanie ekstremów funkcji

F-cja u=f(x,y, .. t) osiąga ekstremum w punkcie P₀ (x₀ ,y₀, .. t₀ ) jeżeli można wskazać taką liczbę dodatnią ε, że obszar określony nierównościami x₀ - ε< x< x₀ + ε, .., t₀ - ε< t₀ + ε zawiera się
w obszarze oznaczoności danej funkcji i przy każdym p-cie (x,y,..,t) wewnątrz tego obszaru spełnione są warunki

F (x,y,..,t) < f (x₀ ,y₀, .. t₀ ) dla min

F (x,y,..,t) > f (x₀ ,y₀, .. t₀ ) dla max

Warunkiem koniecznym by funkcja n zmiennych f(x,y, .. t) miała ekstremum w punkcie (x,y, .. t) jest spełnienie w tym punkcie n następujących równań

F`(x)=0 , f `(y)=0 itd.

Dla ustalenia czy rozwiązany układ równań daje ekstremum należy badać funkcję w punktach bliskich punktowi, który jest rozwiązaniem.

Metoda najmniejszych kwadratów

Jest ona jedną z najczęściej stosowanych metod estymacji parametrów strukturalnych modelu ekonometrycznego. Polega ona na wyznaczeniu takich estymatorów stałych parametrów modelu, dla których suma kwadratów różnic pomiędzy wartościami empirycznymi a wyznaczonymi z modelu była jak najmniejsza. Funkcja osiąga ekstremum, jeżeli spełnione zostaną odpowiednie warunki.
W praktyce sprowadza się to do wyznaczenia pochodnych cząstkowych względem każdego stałego parametru modelu. Przyrównując je do zera (warunek konieczny istnienia ekstremum funkcji), uzyskuje się układ równań normalnych, z którego wylicza się konkretne wartości liczbowe parametrów modelu. Uzyskany w ten sposób model szczegółowy analizuje się jeszcze pod względem dokładności prezentowania pomiarów empirycznych za pomocą nieobciążonej oceny wariancji (błąd standardowy oceny).

Macierze i wyznaczniki (operacje na macierzach, rodzaje macierzy, odwracanie macierzy, własności wyznaczników, obliczanie wyznaczników).

Mamy dany zbiór {1,2,...,n}{1,2,...,m} par liczb naturalnych. Jeśli każdej spośród tych par przyporządkujemy np. liczbę rzeczywistą, to takie przyporządkowanie nazywa się macierzą
o elementach rzeczywistych. Liczbę przyporządkowaną parze (i,j) oznaczamy symbolem a_ij (i,j nazywamy wskaźnikami (lub indeksami) elementu a_ij).

A) Rodzaje macierzy :

1. macierz wierszowa (inaczej wektor wierszowy )

b) macierz kolumnowa (inaczej wektor kolumnowy), oznaczana małymi literami;

c) macierz prostokątna (o wymiarach 2·3);

d) macierz kwadratowa (o wymiarach 3·3);

e) macierz transponowana macierzy A powstaje z macierzy A przez utworzenie wierszy z kolumn

Powtórne transponowanie powoduje powrót macierzy do jej pierwotnej postaci tzn. (A^T)^T=A

f) macierz zerowa - macierz której wszystkie elementy są zerami ;

g) macierz symetryczna - macierz której nie zmienia transponowanie, tzn. A^T=A

8. macierz diagonalna - macierz kwadratowa której wszystkie elementy położone poza główną przekątną są zerami

9. macierz jednostkowa - macierz kwadratowa której wszystkie elementy położone na głównej przekątnej są jedynkami.

B) Odwracanie macierzy:

Tw.1. Macierz A nazywamy odwracalną wtedy i tylko wtedy, gdy istnieje macierz A^-1 taka że :

A·A^-1 = A^{-1 ·} A = I (I - macierz jednostkowa)

Macierz A^-1 nazywamy macierzą odwrotną macierzy A

Tw.2. Jeśli macierz A odwracalna , to det A^-1 = 1/det A
(det A - wyznacznik macierzy A)

Przy założeniu det ≠ 0 możemy określić macierz odwrotną macierzy A .

`

Macierz A^-1 = 1/det A · (adj A) ^T jest macierzą odwrotną macierzy A (adj A - macierz dołączona (adjoint of ) macierzy A)

3. Operacje na macierzach :

1. Dodawanie macierzy

Dwie macierze można dodać wtedy i tylko wtedy , gdy mają te same wymiary (dodajemy elementy na tych samych pozycjach)

Twierdzenie

• a) Dodawanie macierzy jest przemienne : A+B=B+A

b) Dodawanie macierzy jest łączne : (A+B)+C=A+(B+C)

c) Macierz zerowa jest elementem neutralnym dodawania macierzy : A+O=O+A=A

2. Mnożenie macierzy przez liczby ·

To działanie niema żadnych ograniczeń gdyż każdą liczbę można pomnożyć przez dowolną macierz; mnożymy wszystkie elementy macierzy przez daną liczbę.

Przykład :

Jeśli A =
to 3A = 3·
=
=

3. Mnożenie macierzy

działanie to jest uzależnione od spełnienia wymagania dotyczącego wymiaru czynników a, mianowicie liczba kolumn czynnika pierwszego jest równa liczbie wierszy czynnika drugiego

Przykład
. Obliczamy iloczyn macierzy A =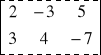
B =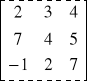

Pierwsza macierz jest wymiaru 2 3 a druga wymiaru 3 4, więc mnożenie A·B jest wykonalne. Natomiast iloczyn B·A nie istnieje gdyż pierwszy czynnik ma 3 kolumny a drugi czynnik ma 2 wiersze. Przy mnożeniu macierzy wygodnie jest stosować schemat Falka :

2 3 4

7 4 5

-1 2 7

2 -3 5 2·2+(-3)·7+5·(-1)= -22 2·3+(-3)·4+5·2= 4 2·4+(-3)·5+5·7= 28

3 4 -7 3·2+4·7+(-7)·(-1)= 41 3·3+4·4+(-7)·2=11 3·4+4·5+(-7)·7= -17

zatem A·B =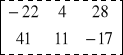

4. Własności wyznaczników :

1. transponowanie macierzy kwadratowej nie zmienia wyznacznika tej macierzy ( detA ^T = detA )

1. Zamiana dwu wierszy (kolumn) macierzy kwadratowej zmienia wartość wyznacznika tej macierzy na przeciwną.

2. Jeśli w macierzy dwa wiersze (dwie klumny) są identyczne , to wyznacznik tej macierzy jest zerem.

3. Jeżeli macierz B powstaje z macierzy A przez pomnożenie wszystkich elementów pewnego wiersza (kolumny) przez liczbę α, to detB = α·detA

4. Dodanie do wiersza (kolumny) macierzy kwadratowej wielokrotności innego wiersza (kolumny) nie zmienia wyznacznika tej macierzy.

5. Twierdzenie Couchy'ego - wyznacznik iloczynu dwu macierzy kwadratowych jest równy iloczynowi wyznaczników tych macierzy: det(A·B) = detA · detB

E) Obliczanie wyznaczników

1. Obliczanie wyznaczników macierzy 2. Stopnia.

Wyznacznikiem macierzy A =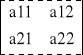
nazywamy liczbę

detA =
= a11·a22 - a12·a21

2. Obliczanie wyznaczników macierzy 3. Stopnia

• Wzór Laplace'a

det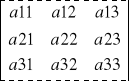
=
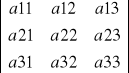
= a11
-a12
+a13

• Schemat Sarrusa
  = (a11·a22·a33+a12·a23·a31+a13·a21·a32)-

(a13·a22·a31+a12·a21·a33+a11·a23·a32)

• Reguła Chio
  =
  ·
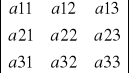
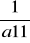
  , o ile a11 ≠ 0

Macierze i wyznaczniki(operacje na macierzach, rodzaje macierzy, odwracanie macierzy, własności wyznaczników, obliczanie wyznaczników)

MACIERZĄ nazywamy każdą funkcję określoną na takim zbiorze, którego elementami są pary liczb a_ij ⊂ R {1,2...n}*{1,2..m} .Elementami macierzy są poziome rzędy zwane wierszami i pionowe zwane kolumnami.

Rodzaje macierzy:

• diagonalna - macierz kwadratowa w której elementy stojące na głównej przekątnej są różne od zera, a pozostałe są zerami.

• Jednostkowa- macierz diagonalna , w której elementy na głównej przekątnej są równe jedności

• Zerowa - wszystkie elementy są zerami

• Kwadratowa- liczba kolumn=liczbie wierszy

• Prostokątna- o wymiarach np. 2x3

• Kolumnowa- inaczej wektor kolumnowy

• Wierszowa - inaczej wektor wierszowy

• Transponowana- powstaje z danej macierzy przez utworzenie wierszy z kolumn

Operacje na macierzach:

1. dodawanie- obie macierze muszą mieć te same wymiary i dodajemy wyrazy na tych samych pozycjach.

2. Mnożenie macierzy przez liczbę- nie ma żadnych ograniczeń, wszystkie elementy mnożymy przez tę samą liczbę

3. Mnożenie macierz przez macierz- mnożenie macierzy nie jest przemienne, ilość kolumn pierwszej musi być równa ilości wierszy drugiej (Schemat Falka)

4. Odejmowanie macierzy- do macierz A dodajemy macierz B pomnożoną przez (-1)

Odwracanie macierzy

Macierz kwadratowa jest odwracalna wtedy i tylko wtedy gdy jej postacią normalną jest macierz jednostkowa. Okazuje się, że jeśli na wierszach macierzy jednostkowej wykonamy te same operacje elementarne, które daną macierz A przeprowadzają do postaci normalnej i jest nią macierz jednostkowa, to uzyskamy macierz odwrotną macierz A.

Macierz A jest odwracalna wtedy i tylko wtedy, gdy jej wyznacznik jest różny od zera

Własności wyznaczników:

1. transponowanie macierzy kwadratowej nie zmienia wyznacznika tej macierzy

2. zamiana dwu wierszy(kolumn)macierzy kwadratowej zmienia wartość wyznacznika tej macierzy na przeciwną.

3. Jeśli w macierzy są dwa wiersze(kolumny) identyczne to wartość wyznacznika jest równa zero.

4. Dodawanie do wiersza(kolumny) macierzy kwadratowej wielokrotności innego wiersza(kolumny) nie zmienia wartości wyznacznika tej macierzy.

5. Jeśli macierz B powstała z macierz A przez pomnożenie wszystkich elementów pewnego wiersza(kolumny) przez liczbę k to wyznacznik macierzy B jest równy iloczynowi k*det A

6. Wyznacznik iloczynu dwu macierzy kwadratowych jest równy iloczynowi wyznaczników tych macierzy.

Obliczanie wyznaczników:

Wyznacznik macierzy 2 -go stopnia - jest to (a11*a22)-(a21*a12)

Wyznacznik macierzy 3-go stopnia- wzór Laplace'a -rozwinięcie wyznacznika wg pierwszego wiersza, sposób Sarrusa- polega na tym, że po prawej stronie wyznacznika dopisujemy pierwszą kolumnę, a potem drugą, poczym tworzymy sumę iloczynów wyrazów głównej przekątnej oraz dwu przekątnych do niej równoległych, a następnie od uzyskanej sumy odejmujemy sumę iloczynów wyrazów drugiej przekątnej oraz dwu przekątnych do niej równoległych.

Układy równań liniowych i sposoby ich rozwiązywania.

Równaniem liniowym o n zmiennych (niewiadomych) nazywamy równanie postaci

a₁x₁+ a₂x₂+...+ a_nx_n =b

Jeśli w postaci normalnej macierzy głównej układu występuje r jedynek wiodących, to zmienne, których współczynnikami są jedynki wiodące traktujemy jako zmienne bazowe, zaś pozostałe jako parametry (parametrów jest n-r). Następnie z równań układu odpowiadającego postaci normalnej macierzy rozszerzonej wyliczamy zmienne bazowe.

Metody rozwiązywania układów równań:

Metoda eliminacji Gaussa.

Metoda ta polega na stosowaniu następującego schematu:

Układ równań liniowych

↓

Macierz rozszerzona tego układu

↓

Postać normalna tej macierzy

↓

Układ równań liniowych

Metoda macierzy odwrotnych

Układy równań piszemy w postaci równania macierzowego

A ^. X = B

n^x n n^x 1 n^x 1

i jeśli spełniony jest warunek detA≠0, to mnożąc lewostronnie to równanie przez macierz A^-1,

otrzymamy

A^-1 AX= A^-1 B

a następnie

X= A^-1 B

Na równaniach układu wykonuje się następujące operacje elementarne:

- przestawienie równania i-tego z j-tym

- pomnożenie i-tego równania przez liczbę α=0

- pomnożenie i-tego równania przez liczbę α i dodanie do j-tego równania

Programowanie liniowe

Najbardziej znanym i najczęściej stosowanym działem programowania matematycznego jest programowanie liniowe. Metoda PL ma liczne zastosowania w praktyce gospodarskiej. Przydatna jest głównie w takich dziedzinach, w których procesy produkcyjne przebiegają w stałych, sztucznie stworzonych warunkach, np. w przemyśle, gdzie można ściśle określić parametry modelu. Problem programowania liniowego można określić jako problem minimalizacji lub maksymalizacji funkcji liniowej na zbiorze określonym przez układ warunków liniowych, tj. nierówności lub równań liniowych. Uniwersalną metodą rozwiązania tego problemu jest metoda simpleks, a proste przypadki zadań PL można rozwiązywać graficznie.

Modelowanie matematyczne można podzielić na następujące etapy:

1. Zdefiniowanie celu zadania i oceny rozwiązania;

2. Zebranie i uporządkowanie danych liczbowych;

3. Konstrukcja ogólnej struktury modelu matematycznego;

4. Budowa modelu szczegółowego;

5. Wyznaczenie rozwiązania modelu;

6. Kontrola prawidłowości wyników rozwiązania;

7. Analiza formalna i merytoryczna rozwiązania;

8. Korekta modelu szczegółowego pod względem łatwiejszego zastosowania w praktyce;

9. Uzyskanie rozwiązania suboptymalnego.

Warunkiem uzyskania poprawnego modelu matematycznego, a więc i wyników jego rozwiązania jest stosowanie odpowiednio trafnych danych wyjściowych oraz prawidłowa budowa modelu ogólnego. W przeciwnym bowiem przypadku uzyskuje się w wyniku programowania matematycznego plany produkcji mało realne lub nawet wręcz fałszywe.

Zagadnienie PL można zapisać w formie kanonicznej lub standardowej. Forma kanoniczna charakteryzuje się tym, że wszystkie warunki ograniczające podaje się w postaci nierówności jednego typu. Również nie żąda się by współczynniki były liczbami dodatnimi a warunki nieujemności nie muszą być pełne. Forma standardowa charakteryzuje się tym, że zasadnicze warunki ograniczające są dane w postaci równań, wyrazy wolne są liczbami nieujemnymi oraz warunki nieujemności są pełne. A więc zagadnienie PL w formie standardowej będzie: zmaksymalizować lub zminimalizować funkcję liniową przy danych warunkach ograniczających. Forma ta jest konieczna przy rozwiązywaniu zagadnień PL. Istnieje jeszcze trzecia forma najczęściej spotykana w praktyce, w której ograniczenia występują w postaci równań i nierówności, nazywa się formą mieszaną.

Prawdopodobieństwo i jego własności. Prawdopodobieństwo warunkowe.

Parę (Ω , P)gdzie Ω jest skończonym zbiorem zdarzeń elementarnych (Ω={ω₁, ω_{2 ,} ...., ω_n}(n є N)) i funkcja P określona wzorami : 1. p₁ ≥ 0, p₂ ≥ 0, .... , p_n ≥ 0 ; 2. p₁ + p₂ + ... + p_n = 1 ; 3. P(̣Ø) = 0. Nazywany przestrzenią probabilistyczną. Funkcję P nazywany wówczas prawdopodobieństwem.

Własności prawdopodobieństwa :

1. prawdopodobieństwo dowolnego zdarzenia jest liczbą nieujemną,

2. prawdopodobieństwo zdarzenia niemożliwego jest równe 0,

3. prawdopodobieństwo zdarzenia pewnego jest równe 1.

Prawdopodobieństwo warunkowe.

Jeśli para (Ω,P) będzie przestrzenią probabilistyczną, natomiast A i B dowolnymi podzbiorami zbioru Ω oraz P(A) > 0 to prawdopodobieństwem warunkowym zdarzenia B pod warunkiem zdarzenia A nazywamy liczbę

Dla uproszczenia zapisu liczbę
oznaczamy symbolem P(B/A).

Zatem P(B/A) =
Wzór ten zapisujemy często w postaci : P(B
A) = P(A)·P(B/A)

Prawdopodobieństwo i jego własności. Prawdopodobieństwo warunkowe.

Definicja prawdopodobieństwa

Niech Ω będzie przestrzenią zdarzeń elementarnych doświadczenia losowego D , Z - jego zbiorem zdarzeń losowych. Prawdopodobieństwem nazywamy funkcję P przyporządkowującą każdemu zdarzeniu A∈Z liczbę

P(a) zgodnie z następującymi warunkami:

1. P(A)≥0 dla każdego zdarzenia A∈Z,

2. P(Ω)=1,

3. Jeżeli A1,......An....jest dowolnym ciągiem parami rozłącznych zdarzeń ze zbioru Z, to

4. P(A1 ∪...∪An∪...)=P(A1)+....+P(An)+..

Wartość prawdopodobieństwa dla danego zdarzenia A∈Z, czyli liczbę P(A) nazywamy prawdopodobieństwem

Zdarzenia A.

Elementarne własności prawdopodobieństwa:

1. Prawdopodobieństwo zdarzenia niemożliwego równa się zeru

2. Jeżeli zdarzenie A pociąga zdarzenie B, i A⊂B, to P(A)≤ P(B)

3. Prawdopodobieństwo dowolnego zdarzenia jest nie większe od jedności. P(A)≤1

4. Jeżeli zdarzenie A pociąga zdarzenie B, A⊂B, to P(B\A)=P(B)-P(A)

5. Jeżeli zdarzenia A1...An, są rozłączne parami ,to P(A1..∪..∪An)=P(A1)+..P(An)

6. Suma prawdopodobieństw zdarzeń przeciwnych równa się jedności P(A) + P(A′) =1

7. Prawdopodobieństwo alternatywy dowolnych zdarzeń(czyli prawdopodobieństwo zajścia co najmniej jednego z tych zdarzeń) jest równe sumie prawdopodobieństw tych zdarzeń zmniejszonej o prawdopodobieństwo ich koniunkcji, P(A∪B)=P(A)+P(B)-P(AB)

8. Jeżeli przestrzeń zdarzeń elementarnych Ω jest co najwyżej przeliczalna i przy tym są określone prawdopodobieństwa p_i poszczególnych zdarzeń jednoelementowych {w_i},czyli p_i =P({w_i}), p_i≥0

p₁+..p_n=1, gdy przestrzeń Ω jest skończona

p₁+..+p_n+..=1, gdy przestrzeń Ω jest przeliczalna, to prawdopodobieństwo zdarzenia A, któremu sprzyjają zdarzenia elementarne w_i1,...w_ik,, jest dane równością: P(A)=p_i1+...p_ik.

9. Klasyczna definicja prawdopodobieństwa. Jeżeli:

1. przestrzeń Ω składa się z n zdarzeń elementarnych, czyli n(Ω)=n

2. zdarzenia jednoelementowe {w_i} są jednakowo prawdopodobne, a więc P({w₁})=P({w₂})=...P({w_n})=1/n, to prawdopodobieństwo dowolnego zdarzenia A składającego się z k zdarzeń elementarnych, n(A)=k, wyraża się równością

P(A) = n(A)/n(Ω) = k/n = liczba zdarzeń elementarnych sprzyjających zdarzeniu A/ liczba zdarzeń elementarnych sprzyjająca zdarzeniu Ω.

Prawdopodobieństwo warunkowe

Niech A i B będą dowolnymi zdarzeniami. Prawdopodobieństwo zdarzenia A obliczone przy założeniu że zaszło zdarzenie B nazywamy prawdopodobieństwem warunkowym zdarzenia A pod warunkiem B i oznaczamy symbolem P(A\B) . Równoważne określenie:

Niech ( Ω,Z,P) będzie przestrzenią probabilistyczną pewnego doświadczenia, zaś b dowolnym ustalonym zdarzeniem o dodatnim prawdopodobieństwie. Prawdopodobieństwem warunkowym pod warunkiem B dowolnego zdarzenia A∈Z nazywamy liczbę P(A\B) określoną następującą równością

P(A\B) = P(AB) \ P(B)

Zmienne losowe i ich rozkłady ( dwumianowy, wariancje, odchylenie standardowe).

Zmienna losowa- funkcja X odwzorowująca zbiór Ω wyników pewnego doświadczenia losowego w zbiór liczb rzeczywistych.

Wśród z.l. wyróżnia się:

• zmienną losową skokową

• zmienną losową ciągłą

Zmienna losowa skokowa (zmienna losowa dyskretna)- zmienna losowa X przyjmująca co najwyżej przeliczalną liczbę wartości x₁,x₂,...x_n.. odpowiednio z dodatnimi prawdopodobieństwami p₁,p₂,...p_n.. takimi że : _∞

∑p_i = 1

ⁱ⁼¹

Rozkład zmiennej losowej skokowej - jest to zbiór par mających postać(x_i,p_i) gdzie x_i dla

i =1,2,3... są wartościami jakie przyjmuje zmienna losowa, p_i zaś jest prawdopodobieństwem, z jakim ta zmienna losowa przyjmuje wartości x_i . Rozkład zmiennej losowej skokowej przedstawia się graficznie stosując różne konwencje. Wśród rozkładów z.l.s. najbardziej znane są rozkłady:

• dwumianowy (Bernoullego)

• Poissona

Wartość oczekiwana i wariancja zmiennej losowej X o rozkładzie dwumianowym wynoszą odpowiednio: EX=np, D²X = np(1-p)

Rozkład Poissona to rozkład z.l.s. X, która przyjmuje wszystkie wartości całkowite nieujemne przy czym

P(X=i)=( λⁱ/λ^!) e ^-2

Wartość oczekiwana EX=λ wariancja D²X=λ

Zmienna losowa ciągła - zmienna losowa X dla której istnieje funkcja nieujemna f , taka że, dystrybuanta E tej zmiennej wyraża się całką Lebesgue'a F(x)=P(X ≤ x)=∫ f (t)dt

^-∞

Najbardziej znanymi rozkładami z.l.c. są rozkład normalny i rozkład normalny standaryzowany. 1 _{- (x-m)}²

Rozkład normalny(rozkład Gaussa) jest to rozkład określony wzorem ^_____ e 2δ²

δ√2π

Rozkład normalny jest określony przez dwa parametry m i δ . Jeśli X: N(m,δ) to wartość oczekiwana i wariancja zmiennej losowej X wynoszą odpowiednio EX=m D²X=δ² (czyli δ jest odchyleniem standardowym zmiennej X)

Rozkład normalny standaryzowany jest to rozkład normalny o parametrach m=0 , δ=1

Jeżeli X jest dowolną zmienną losową o rozkładzie normalnym o parametrach m i δ to nowa zmienna losowa Y=(x-m)/δ ma rozkład normalny standaryzowany

WSTĘP DO INFORMATYKI

1. Pojęcie algorytmu.

Algorytm - „przepis” rozwiązania postawionego zadania, bez potrzeby odwoływania się do konkretnego języka programowania. Algorytm można wyrazić językiem mówionym lub za pomocą schematów blokowych.

Algorytmy dzielimy na moduły, które stanowią opis wyróżnionego, dobrze określonego działania na równie dobrze określonych obiektach. Z tych zadań zbudujemy ogólny plan (algorytm) całego problemu. Problemy dzielimy na podproblemy - procedury lub podprogramy.

Obiekty (dane)

Problem Analiza Algorytm Program Wyniki

Moduły Procedury

Akcje (instrukcje)

Pojęcie algorytmu - jest to opis danych wejściowych, potrzebny do rozwiązania problemu, łącznie z jednoznacznie zrozumiałym opisem operacji, czyli instrukcji, zleceń, pozwalających na podstawie wartości danych wejściowych otrzymać oczekiwane wyniki - dane wyjściowe jako rezultat działania algorytmu.

Pojęcie algorytmu często używamy w kontekście języków programowania. Pozwalają one zapisać algorytm w postaci programu, inaczej mówiąc programowanie jest umiejętnością prawidłowego układania i właściwego zapisywania algorytmów. Umiejętność ta dobrze opanowana pozwala zaoszczędzić nakład pracy, czasu i wykorzystać optymalne możliwości komputera. Liczba operacji algorytmu powinna być skończona.

Składnia a semantyka języków programowania.

Podstawą każdego języka jest słownik. Elementy słownika są zazwyczaj nazywane słowami - symbolami. Cechą charakterystyczną języków jest to , że pewne ciągi słów są rozpoznawane jako poprawne, dobrze zbudowane zdania języka a inne nie. O tym, które zdania są poprawne a, które nie decyduje gramatyka - składnia języka. Składnią nazywamy zbiór reguł lub formuł , określający zbiór poprawnych zdań. Taki zbiór reguł nie tylko pozwala decydować czy dany ciąg słów jest zdaniem, ale także dla tego konkretnego zdania określa jego strukturę, pomocną w rozpoznaniu znaczenia zdania. Więc składnia i semantyka czyli znaczenie są blisko powiązane.

Znaczenie - semantyka

Składnia - struktura

Typy danych: proste typy danych a złożone typy danych (tablice, rekordy, pliki)

Wszystkiego typu informacje przechowuje się informatycznie w postaci danych różnego typu ( data, charakter, numeryczne). Aby z nich skorzystać wyciąga się je pod postacią zmiennych i operuje się nimi.

Dane te (zmienne ) są fundamentalnym aspektem języka komputerowego i w ogóle informatyki. Jest to obszar pamięci komputera zarezerwowany dla określonego typu danych i posiadający nazwę. Zmienne - dane są używane w taki sposób, że to samo miejsce w pamięci może przechowywać różne wartości w różnym czasie, mogą być one proste i złożone.

Proste typy danych (zmiennych) mogą przechowywać jedną informację, jedna dane - jeden typ danej, a tablice kilka informacji tego samego typu.

Natomiast typ danych: struktura, plik, układ różnych tablic, rekordów może przechowywać dane różnego typu. Składają się one z wielu elementów danych, które nie muszą być tego samego typu , zgrupowanych razem w celu dalszego działania na nich.

Architektura komputera, zasady działania najważniejszych elementów sprzętowych : procesor, pamięć wewnętrzna, podstawowe magistrale, pamięci i urządzenia zewnętrzne.

RAM pamięci - Dane z dysku przenoszone są i przechowywane w pamięci RAM do czasu aż oprogramowanie zleci procesorowi przetworzenie tych danych.

Oprogramowanie wysyła impuls elektryczny wzdłuż linii adresowej (w RAM). W miejscu gdzie można przechować dane, impuls włącza tranzystor podłączony do linii danych. Oprogramowanie wysyła impulsy el.. Każdy impuls to jeden bit - 1 lub 0 (elementarną jednostkę informacji).

Mikroprocesor - zawiera specyficzne zestawy instrukcji do zarządzania pamięcią.

Pobiera dane i instrukcje z pamięci, przechowuje je tam, gdzie inne jednostki mogą łatwo do nich sięgać, wykonuje instrukcje i dostarcza wyniki z powrotem do pamięci RAM.

Dysk twardy - talerze, na których zapisane są dane, wirują. Każde odwołanie do dysku, by zapisać lub odczytać, wywołuje ruchy, które muszą być wykonane przez głowice odczytu/zapisu.

Języki wewnętrzne komputerów, realizacja języków wyższego poziomu,

pojęcie interpretacji i kompilacji.

Komputer bez oprogramowania może wykonywać jedynie instrukcje w języku maszynowym
( wewnętrznym), jedynie taki jest dla niego zrozumiały. Oznacza to, że programy napisane w innych (źródłowych) językach muszą być przed ich uruchomieniem przetłumaczone na język maszynowy, zrozumiały dla danego typu komputera. Tłumaczenie tekstów programów z języka programowania na język maszynowy nazywa się translacją, która jest wykonywana przez komputer automatycznie za pomocą specjalnego programu zwanego translatorem. Translator dokonuje nie tylko tłumaczenia tekstu programu źródłowego, lecz także kontroluje prawidłowość jego napisania z punktu widzenia składni wybranego języka programowania.

Istnieją dwa zasadnicze typy translacji: kompilowanie i interpretowanie. W zależności od typu translacji translator może być nazywany kompilatorem lub interpretatorem.

Kompilator tłumaczy cały program na język maszynowy i dopiero taka wersja programu może być wykonywana.

Interpreter tłumaczy i wykonuje poszczególne operacje po kolei w miarę odczytywania ich z programu źródłowego.

Rozróżniamy translatory języków wysokiego poziomu, tzn. takie, w których jednej operacji języka programowania odpowiada wiele operacji maszynowych, oraz translatory języków symbolicznych- np. translator języka Asembler.

Wśród języków wysokiego poziomu najczęściej są wykorzystywane: Basic, Pascal, Fortran, C.

Miejsce oprogramowania systemowego, narzędziowego i użytkowego.

Oprogramowanie systemowe - najważniejszym składnikiem tego oprogramowania są systemy operacyjne. System operacyjny to zespół programów, którego podstawowymi zadaniami są:

• zarządzanie zasobami komputera w celu zapewnienia możliwie optymalnego wykorzystania sprzętu,

• tworzenie środowiska pracy dla użytkownika oraz wspomaganie go w procesie opracowywania, uruchamiania oraz eksploatacji programów użytkowych.

Po uruchomieniu komputera, system operacyjny musi być załadowany do pamięci operacyjnej przed rozpoczęciem jakichkolwiek działań na komputerze.

W zależności od przeznaczenia komputera, jego mocy obliczeniowej może na nim być zainstalowany jeden z wielu stosowanych obecnie systemów operacyjnych. Pewne systemy operacyjne pozwalają na wykorzystywanie jednego komputera przez wielu użytkowników jednocześnie( wielodostęp). Nowoczesne oprogramowanie pozwala łączyć komputery w tak zwane sieci. Za pomocą łączności telefonicznej lub satelitarnej potrzebne programy, dane i wyniki mogą być przesyłane od jednego komputera do drugiego na nieograniczoną odległość. W ten sposób rozbudowany system operacyjny nazywamy sieciowym. Jest on zwykle zainstalowany na tzw. komputerze - serwerze, do którego może być podłączona pewna liczba innych komputerów

Jednostanowiskowe systemy operacyjne: MS DOS, MS Windows 95, MS Windows 98.

Wielostanowiskowe (sieciowe) : MS Windows NT, Novell Net Ware, Unix, Linux.

Oprogramowanie użytkowe - stanowi warstwę, która jest najbliżej użytkownika. Są to pakiety programów narzędziowych potrzebne do konstruowania innych programów ( translatory, asemblery, biblioteki programów), programy składające tekst (Word), edytory grafiki komputerowej, arkusze kalkulacyjne (Excel ) systemy baz danych ( FoxBase, Clipper, Access), gry komputerowe, systemy finansowe, systemy wspomagające programowanie, programy nauczania i kontroli wiedzy

TEORIA PROGNOZ I SYMULACJI KOMPUTEROWYCH

Pojęcie prognozy i symulacji.

Prognozowanie to racjonalne, naukowe przewidywanie przyszłości.

Prognozy- potrzebne do podejmowania racjonalnych decyzji, niezbędna umiejętność przewidywania zjawisk.

PROGNOZOWANIE- przewidywanie procesów rozwojowych zjawisk.

Prognozowanie - to oparte na naukowych podstawach przewidywanie kształtowania się zjawisk i procesów w przyszłości

Prognoza - sąd o przyszłych stanach zjawisk i zdarzeń sformułowany w trakcie procesu prognozowania

Prognozowanie to racjonalne, naukowe przewidywanie przyszłych zdarzeń.

Przez prognozę rozumiemy sąd o zajściu określonego zdarzenia.

Głównym celem prognoz jest wspomaganie procesów decyzyjnych.

Rodzaje prognoz:

1.ze względu na horyzont czasowy

-długoterminowe

-średnioterminowe

-krótkoterminowe

-perspektywiczne

-ponad perspektywiczne

-operacyjne

-strategiczne

prognozy krótkoterminowe nie przekraczają 1 roku

prognozy średnioterminowe dotyczą od 2 do 5 lat

prognozy długoterminowe ponad 5 lat

Symulacje.

Model jest uproszczoną reprezentacją systemu, w czasie i przestrzeni, stworzoną w zamiarze zrozumienia zachowania systemu rzeczywistego.

    Symulacja jest to manipulowanie modelem w taki sposób że działa on w zmienionej skali w czasie
i / lub w przestrzeni, umożliwiając nam uchwycenie oddziaływań i zachowań, które w innym przypadku byłyby nieuchwytne z tytułu ich oddalenia w czasie i przestrzeni.

1. Pojęcia prognozy i symulacji.

Prognoza - przewidywanie przyszłościowe zjawisk na podstawie danych historycznych i dostępnych dotyczących zdarzenia.

Symulacja - opisywanie w sposób sformalizowany modelu i badanie jak model będzie się zachowywał w różnych warunkach. Symulacja stosowana jest, gdy bezpośrednie zaobserwowanie zachowania się obiektu jest niemożliwe lub trudne.

Prognozowanie może służyć symulacji i odwrotnie

Prognozowanie na podstawie szeregów czasowych.

Oprogramowanie do prognoz na podstawie szeregów czasowych:

1. MS EXCEL- (średnia ruchoma, wygładzanie szeregów czasowych, wygładzanie wykładnicze, regresja liniowa - modele trendu, tendencja rozwojowa)

2. STATISTICA firmy StatSoft.

Przyczyny użycia w prognozowaniu modeli szeregów czasowych:

• Zbytnia złożoność zjawisk, aby zrozumieć je i opisać bez użycia modeli;

• Zadaniem prognozowania jest przewidzieć co się wydarzy a nie dlaczego się wydarzy;

• Koszt zdobycia wiedzy o przyczynach zjawisk może być zbyt wysoki w stosunku do prognozy opartej o szereg czasowy.

Wyróżniamy następujące modele:

• Naiwne;

• Średniej ruchomej;

• Wygładzania wykładniczego;

• Tendencji rozwojowej;

• Składowej periodycznej.

Metody naiwne

Stosowane są do prognozowania krótkookresowego, na jeden okres naprzód (t=n+1, n - liczba obserwacji zmiennej prognozowanej).

Opierają się na założeniu, że w dotychczasowym sposobie oddziaływania czynników określających wartość zmiennej prognozowanej nie nastąpią zmiany. W efekcie np. sprzedaż w okresie prognozowanym wzrośnie w tym samym stopniu co w poprzednim miesiącu, zysk będzie kształtował się na tym samym poziomie co w poprzednim kwartale.

W niektórych przypadkach prognozę na moment lub okres t konstruuje się na poziomie wartości zmiennej prognozowanej w momencie lub okresie t-1.

Y_t^* = Y_t-1

Gdy w szeregu czasowym występuje tendencja rozwojowa, to konstruując prognozę na moment lub okres t możemy ją utworzyć powiększając wartość zmiennej prognozowanej z okresu lub momentu t-1 o wartość przyrostu tej zmiennej w okresie t-1 i t-2.

Y_t^* = Y_t-1 + (Y_t-1 - Y_t-2 )

Koszty w okresie t-2 = 120.000 zł

Koszty w okresie t-1 = 122.300 zł

Koszty w okresie prognozowanym t =

K = 122.300 zł + (122.300 zł - 120.000) = 122.300 zł + 2.300 zł = 124.600 zł

Gdy prognozowana zmienna wykazuje tendencję do wzrostu lub spadku wówczas do prognozowania można zastosować metodę polegającą na założeniu, że wartość zmiennej prognozowanej
w momencie lub okresie t wzrośnie (spadnie) o określony procent w porównaniu do wartości tej zmiennej w momencie lub okresie t-1.

Y_t^* = (1+c) Y_t-1

Jeżeli np. koszty w przedsiębiorstwie mają tendencję wzrostową o 2% co miesiąc to prognozę można wyznaczyć następująco:

Koszty w okresie t-1 = 122.300 zł.

Koszty w okresie prognozowanym t

K = (1+ 2%) * 122.300 zł = 1,02 *122.300 zł = 124746

Prognoza może także być sporządzona na podstawie założenia, że wartość zmiennej prognozowanej w momencie lub okresie t będzie równa wartości zmiennej prognozowanej w momencie lub okresie t-1 powiększonej (zmniejszonej) o pewną stałą c. Wartość stałej można wyznaczyć np. na podstawie obserwowanych zmian lub według opinii ekspertów.

Y_t^* = Y_t-1 + c

Ponadto prognozę można wyznaczyć na podstawie założenia, że wielkość zmiennej prognozowanej
w momencie lub okresie t będzie równa wartości zmiennej w momencie lub okresie t-1 powiększonej
o średni przyrost wartości tej zmiennej w dostępnym materiale statystycznym.

t-2

Y_t^* = Y_t-1 +(1/(t-2)) * Σ (Y_I+1 - Y_i )

I=1

Przykład:

Koszty w firmie XYZ w miesiącach 10.99 do 03.2000 kształtowały się następująco:

Miesiąc	Koszty	Przyrost kosztów
10.1999	108.300 zł	-
11.1999	110.100 zł	1.800 zł
12.1999	114.000 zł	3.900 zł
01.2000	117.100 zł	3.100 zł
02.2000	120.000 zł	2.900 zł
03.2000	122.300 zł	2.300 zł

Ustal prognozę na miesiąc kwiecień 2000.

T=7, średni przyrost = 14.000 zł /5 = 2.800 zł

Koszty w okresie prognozowanym t

K = 122.300 zł + 2.800 zł = 125.100 zł

Metoda średniej ruchomej

Wykorzystywane są do wygładzania i prognozowania szeregu czasowego.

Polega ona na zastępowaniu wartości zmiennej prognozowanej jej średnimi arytmetycznymi.

Yt=(1/k) Σ yi

K - stała wygładzania

Jeśli dużo elementów - silniej wygładza szereg ale wolniej reaguje na zmiany poziomu zmiennej prognozowanej.

Mało elementów (wyrazów) - szybciej reaguje na zmiany zachodzące w wartościach zmiennej prognozowanej ale większy wpływ wywierają na nią wahania przypadkowe (mniejszy efekt wygładzania szeregu).

Wskazówka praktyczna - 3 do 5 wyrazów dla danych miesięcznych.

Do oceny wykorzystuje się średni kwadratowy błąd prognozy. Do prognozowania wybiera się tą wielkość dla której s jest najmniejszy.

1 T

S^* = Σ (Y_t - Y_t^*)²

n-k t=k+1

Zastosowania:

• Do prognozowania, gdy w rozpatrywanym okresie poziom wartości jest prawie stały
  (z niewielkimi odchyleniami losowymi)

• Nie występuje tendencja rozwojowa, wahania sezonowe i wahania cykliczne.

Postulat postarzania informacji (nowsze dane zawierają bardziej aktualne informacje więc powinno im się nadawać relatywnie większą wagę niż informacjom starszym).

Model średniej ruchomej ważonej

Yt = Σ yi * w _i-t+k+1

0<w1<w2<w3<w4< .... <wk<=1

Σ wi = 1

Wygładzanie wykładnicze

Zastosowanie:

W przypadku występowania w szeregu czasowym prawie stałego poziomu zmiennej prognozowanej oraz wahań przypadkowych.

Y_t^* = Y_t-1^* + αq_t-1

Gdzie:

α - parametr wygładzania ( 0<α < 1)

q_{t-1 -} błąd prognozy ex post.

Modele tendencji rozwojowej

Funkcja liniowa

Yt = α + β t

Funkcja wykładnicza:

Yt = αβ^t

Gdzie:

β > 1

Funkcja potęgowa:

Yt = αtβ

Szacowanie parametrów modeli liniowych

B= (Σ(t-tsr)*Yt)/ Σ(t-tsr)^2

A=ysr -b*tsr

Założenia prognozowania:

• Stabilność relacji strukturalnych w czasie (postać modelu i oceny parametrów nie ulegną zmianie)

• Stabilność rozkładu składnika losowgo

Składowe szeregów czasowych

Tendencja rozwojowa ( trend) - jest długookresową skłonnością do jednokierunkowych zmian (wzrostu lub spadku) wartości badanej zmiennej. Jest rozpatrywana jako konsekwencja działania stałego zestawu czynników (np.: sprzedaż - liczba potencjalnych klientów, ich dochody lub preferencje zakupu). Może być wyznaczana, gdy dysponuje się długim ciągiem obserwacji.

Stały (przeciętny) poziom prognozowanej zmiennej występuje wówczas, gdy w szeregu czasowym nie ma tendencji rozwojowej, a wartości prognozowanej zmiennej oscylują wokół pewnego, stałego poziomu.

Wahania cykliczne wyrażają się w postaci długookresowych, rytmicznych wahań wartości zmiennej wokół tendencji rozwojowej lub stałego (przeciętnego) poziomu tej zmiennej (np. cykl koniunkturalny).

Wahania sezonowe są wahaniami wartości obserwowanej zmiennej wokół tendencji rozwojowej lub stałego (przeciętnego) poziomu tej zmiennej (np. wpływ pogody).

Podstawowe rodzaje szeregów:

Jednowymiarowy szereg czasowy - ciąg zaobserwowanych stanów zmiennej Y, uporządkowanych według wartości zmiennej czasowej t, t=1, ...., n.

Produkcja miedzi elektrolitycznej w latach 1994 - 1998

Wyszczególnienie	Lata
		1994	1995	1996	1997	1998
Produkcja (w tys. Ton)	405	412	427	423	439

Temperatura w Sopocie w 1999 r o godz. 21.00

Wyszczególnienie	Data
		01.01	02.01	03.01	04.01	05.01
Temperatura (°C)	-2,7	-3,4	-2,9	-4,8	-5,7

Wielowymiarowy szereg czasowy - jest utworzony przez szeregi czasowe zmiennych Y₁, ..., Y_z, opisujących określony obiekt.

Linie kolejowe i drogi publiczne w km na 100 km² w Polsce w dn. 31.12.

Wyszczególnienie	Lata
		1990	1991	1992	1993	1994
Linie kolejowe Drogi publiczne	7,7 69,9	7,6 72,2	7,5 73,3	7,5 74,1	7,3 75

Jednowymiarowy szereg przekrojowy - ciąg zaobserwowanych stanów zmiennej Y, odnoszący się do tego samego okresu lub momentu do k-tego obiektu przestrzennego.

Samochody osobowe w wybranych krajach na 1000 mieszkańców w 1993 r.

Wyszczególnienie	Austria	Belgia	Czechy	Holandia	Polska
Samochody (szt/1000 mieszk.)	422	409	261	375	176

Wielowymiarowy szereg przekrojowy - jest utworzony przez szeregi przekrojowe zmiennych Y₁, ..., Y_z, rozpatrywane w jednym momencie lub okresie.

Prognozowanie na podstawie szeregów czasowych.

W szeregach czasowych wyróżnia się dwie składowe: Składową systematyczną, będącą efektem oddziaływania stałego zestawu czynników na zmienną prognozowaną, oraz składową przypadkową zwaną często składnikiem losowym lub wahaniami przypadkowymi. Składowa systematyczna może wystąpić w postaci tendencji rozwojowej (trendu), stałego (przeciętnego) poziomu zmiennej prognozowanej, składowej okresowej. Składowa okresowa występuje w postaci wahań cyklicznych lub okresowych.

Tendencja rozwojowa (trend) jest długo okresową skłonnością do jednokierunkowych zmian (wzrostu lub spadku) wartości badanej zmiennej. Jest rozpatrywana jako konsekwencja działania stałego zestawu czynników. Może być wyznaczona gdy dysponuje się długim ciągiem obserwacji.

Stały (przeciętny) poziom prognozowanej zmiennej występuje wówczas gdy w szeregu czasowym nie ma tendencji rozwojowej, wartości zaś prognozowanej zmiennej oscylują wokół pewnego poziomu.

Wahania cykliczne wyrażają się w postaci długo okresowych, rytmicznych wahań wartości zmiennej wokół tendencji rozwojowej lub stałego poziomu tej zmiennej.

Wahania sezonowe są wahaniami wartości obserwowanej zmiennej wokół tendencji rozwojowej lub stałego poziomu tej zmiennej. Wahania mają skłonność do powtarzania się w określonym czasie, nie przekraczającym jednego roku.

Proces wyodrębniania poszczególnych składowych danego szeregu czasowego określa się mianem dekompozycji szeregu. Identyfikacje poszczególnych składowych szeregu czasowego konkretnej zmiennej umożliwia w wielu przypadkach ocena wzrokowa sporządzonego wykresu. Dla wielu szeregów czasowych wystarczająco adekwatne mogą okazać się modele ujmujące tylko niektóre składowe szeregu czasowego. Wykres szeregu czasowego umożliwia ponadto wykrycie obserwacji nietypowych oraz punktów zwrotnych. Wizualny przegląd danych może w niektórych przypadkach nasunąć wątpliwości co do sezonowości pewnych obserwacji. Występowanie w szeregu czasowym obserwacji nietypowych może w poważnym stopniu wpłynąć na rezultat procesu konstrukcji prognozy.

Ma to duże znaczenie w szeregach złożonych z niedużej liczby obserwacji, w których efekt wyrównania obserwacji nietypowych przez typowe jest mniejszy konieczne może być wówczas wyeliminowanie tego rodzaju obserwacji z szeregu czasowego. Gdy występują w szeregu czasowym tzw. punkty zwrotne następuje w nich zmiana kierunku tempa wzrostu lub spadku wartości zmiennej. Występowanie punktów zwrotnych wpływa w istotny sposób na przebieg procesu prognozowania, może wymagać użycia określonych metod prognozowania, np. analogowych, heurystycznych bądź opartych na funkcjach segmentowych, a nie na funkcjach analitycznych tendencji rozwojowej (w skrajnych przypadkach może nawet udaremnić prognozowanie). Na proces przewidywania składają się: przetworzenie informacji o przeszłości oraz przejście do informacji przetworzonej do prognozy.
W przypadku prognozowania na podstawie szeregu czasowego przetworzenie informacji o przyszłości następuje przez budowę odpowiedniego modelu formalnego, przejście zaś od informacji przetworzonej do prognozy przez wybór reguły prognozowania. Jeżeli w szeregu czasowym prognozowanej zmiennej występuje tylko jedna postać składowej systematycznej, to dość łatwo jest zbudować prognozę tej zmiennej. W procesie dekompozycji szeregu czasowego może by określony wpływ każdej ze składowych szeregu na zmienną prognozowaną. Konstrukcja prognozy polega na ogół na ekstrapolacji funkcji trendu, a nie na jej korekcie uwzględniającej oddziaływanie wahań okresowych na prognozowaną zmienną. Używanie w prognozowaniu modeli szeregów czasowych jest spowodowane trzema głównymi przyczynami. Po pierwsze, zjawisko jest zbyt złożone, by można je opisać i zrozumieć bez zużycia modeli. Po drugie, głównym zadaniem prognosty jest przewidzenie tego, co się zdarzy, a nie wyjaśnienie, dlaczego to się zdarzy. Po trzecie zaś, koszty zdobycia wiedzy o przyczynach wystąpienia przewidywanych zjawisk mogą być niewspółmiernie wysokie w porównaniu z konstrukcją prognozy opartą na modelu szeregu czasowego. W zależności od zmiennych objaśniających danego modelu oraz jego postaci można wyróżnić modele: naiwne, średniej ruchomej, wygładzania wykładniczego, tendencji rozwojowej, składowej periodycznej, autoregresyjnej itd.

Modele symulacyjne i ich budowa.

Prosty model symulacyjny, w pełni jednak użyteczny dla przedsiębiorstwa, można opracować w zwykłym arkuszu kalkulacyjnym, np. Excela lub Lotusa.

Model to przedstawienie obiektywnie istniejącego zjawiska, procesu czy rzeczy (oryginału) za pomocą odpowiednich środków odtwarzających. Zadaniem modelu jest imitowanie oryginału.

Symulacja jest to manipulowanie modelem w taki sposób że działa on w zmienionej skali w czasie i / lub w przestrzeni, umożliwiając nam uchwycenie oddziaływań i zachowań, które w innym przypadku byłyby nieuchwytne z tytułu ich oddalenia w czasie i przestrzeni.

Modele symulacyjne w analizach wariantów zmian.

Dynamiczny rozwój symulacji komputerowej zapoczątkowany w latach sześćdziesiątych, doprowadził do powstawania głównie dwóch typów modeli:

1. ukierunkowanych na zastosowania cząstkowe (zasoby oraz produkcja, marketing, finanse),

2. całościowe modele organizacji gospodarczych.

 

Coraz bardziej realna staje się obecnie możliwość formułowania rozleglejszych modeli (c) oddziaływań między różnymi podmiotami gospodarczymi.

Wydaje, że wszystkie trzy wymienione klasy modeli mogą mieć istotne znaczenie w analizach różnych wariantów funkcjonowania organizacji.

 

a) Modele ukierunkowane na zastosowania cząstkowe (zasoby oraz produkcja, marketing, finanse),

 

Pierwsza grupa modeli wspomaga specyficzne potrzeby organizacji oraz często jest włączana w bardziej rozległe narzędzia informatyczne. Dla przykładu , dalej przedstawione, szeroko rozpowszechnione narzędzia symulacyjne włączane do systemów wspomagają cech reinżynierię biznesu można zaliczyć do tej klasy modeli.

 

Również norma American Production and Inventory Control Society dla standardu MRPII uwzględnia funkcję symulacji umożliwiającą ocenę wpływu wprowadzanych zmian do planu produkcji i sprzedaży, harmonogramów oraz wszystkich innych elementów MRPII na plany finansowe, potrzeb materiałowych i zdolności wykonawczych.

Użytkownicy końcowi przy użyciu specjalnie przygotowanego oprogramowania bardzo często samodzielnie wykonują oraz z powodzeniem posługują się prostymi modelami. Szereg organizacji np. du Pont donosi o utworzeniu przez pracowników tych organizacji setek prostych systemów ekspertowych na bazie specjalnie przygotowanych systemów szkieletowych. Czas realizacji takich systemów szacuje się na około 6 miesięcy przy koszcie sięgającym około 50000 dolarów. Analizując (Stanek, 1995 str 30-31) kierunki rozwoju systemów ekspertowych zauważyliśmy, że systemy takie mogą być w organizacji agregowane w kierunku systemów o wysokiej kompleksowości wiedzy oraz poprzez zaangażowanie kompleksowej technologii mogą doprowadzić do powstania w organizacji systemu o oddziaływaniu strategicznym. Analizując takie możliwości w warunkach krajowych w ramach Grantu KBN na początku lat 90-tych podjęliśmy próbę zaadaptowania systemu ekspertowego do oceny ryzyka kredytowego wykonanego w jednej z wyróżniających się prac magisterskich. Nieznacznie zmodyfikowany prototyp skierowaliśmy do oddziału dużego banku z prośbą o dokonanie weryfikacji. Odpowiedź niestety była negatywna. Jednak niespełna miesiąc wystarczył aby rozwinąć ogólny prototyp zgodnie z uwagami ekspertów banku (por. Stanek, J. Palonka, P. Palonka, 1994, P. Palonka 1995).

 

b) Całościowe modele organizacji gospodarczych.

Druga grupa modeli wspomaga zwykle zarządzanie strategiczne np. systemy modeli cząstkowych opisane w klasycznym podręczniku Naylora (1979). Również w warunkach krajowych w przypadku systemu scentralizowanego, parametrycznego oraz rynkowego podejmowane były próby tworzenia systemów modeli cząstkowych w organizacjach gospodarczych (por. np. Sroka, Stanek 1986a, 1986b, 1989, 1996).

Z kolei w szeregu pracach kryzys planowania strategicznego jaki odnotowano w latach osiemdziesiątych, jak ocenia obecnie wielu autorów był związany z niepowodzeniami w dążeniu do bezkrytycznego stosowania prostych reguł tzw. reguł kciuka w tej złożonej problematyce. Niestety posługiwanie się tymi regułami w zestawieniu z bardzo niedoskonałymi jeszcze w tym czasie arkuszami elektronicznymi powodowało zbyt wielkie uproszczenia. Coraz bardziej obecnie rozpowszechnione podejścia wielowymiarowe (np. SAS MOTORE, ORACLE OLAP) postrzega się jako możliwość przezwyciężenia zaistniałego kryzysu.

W komputerowym modelowaniu symulacyjnym generalne postulaty prostoty nie tylko nigdy nie były tak radykalne jak bywały w grach, ale obserwować można było raczej przeciwne tendencje. Jak się wydaje akceptowalną złożoność ograniczały tu głównie aktualne możliwości budowy sprawnego oprogramowania, wielkość komputerów (pamięć, szybkość), trudności projektowania oraz stosunki z odbiorcami i rozporządzalne fundusze [Rzońca 1983]. Jednak zawsze używano też - co najmniej w dydaktyce - skrajnie prostych modeli. Forrester, na przykład [1972: (2 - 4) - (2 - 10)], używa bardzo prostego modelu magazynu jako przewodniego przykładu modelu w konwencji dynamiki systemów (SD) oraz jako przykładu równie prosto modelowo ujmowanych zjawisk i ich badania. Jednym z ulubionych w dydaktyce oryginałów takich najprostszych modeli bywała spłuczka klozetowa [Forrester 1972: 22 - 26; Łukaszewicz 1975: 103 - 104]. Można wskazać wiele przykładów podobnie prostych modeli w licznych podręcznikach czy to symulacji (np. Cafee cooling - wykładniczy spadek [Roberts et al 1983: 267 - 281]), czy to do nauczania za pomocą symulacji o systemach (np. Infekt - infekcja w populacji [Bossel 1985: 53 - 58]), czy też do nauczania symulacji w określonej dziedzinie (np. regulator procesu produkcyjnego - w ekonomii [Wąsik 1983: 71-74]).

Modele symulacyjne i ich budowa.

Symulację należy stosować gdy inne sposoby rozwiązania problemu odrzucono, a proces modelowania jest nie możliwy. Korzyści jakie zyskujemy przy stosowaniu symulacji to:

• zachowanie systemu można modelować w warunkach rzeczywistych i hipotetycznych

• można zbadać rozwiązania bez budowy prototypów

• każdy eksperyment symulacyjny można przeprowadzić dokładnie w tych samych warunkach

• uzyskuje się duży przedział wartości czasu symulowanego do rzeczywistego

Etapy tworzenia modeli symulacyjnych:

• określenie symulowanego systemu

• sformułowanie modelu

• przygotowanie danych

• zaprogramowanie modelu

• ocena adekwatności modelu

• planowanie eksperymentów symulacyjnych

• wprowadzenie eksperymentów

• interpretacja uzyskanych wyników

• dokumentowanie

Dokumentacja:

• krótka charakterystyka symulowanego systemu. System z wyszczególnieniem obiektów i zależności.

• Projekt systemu symulacyjnego

• Plan eksperymentów

• Wykaz danych wejściowych

• Zestawienie wyników

• Analiza wyników

• Wnioski

Błędy symulacji:

• złe określenie celu symulacji

• nieodpowiednia szczegółowość

• nieodpowiedni wybór języków symulacji.

Projektowanie eksperymentów symulacyjnych.

W ostatnich latach nastąpił szczególny rozwój metodyki badań doświadczalnych, zwanej teorią eksperymentu. Złożoność obiektów zmusza do przeprowadzania doświadczeń obejmujących coraz to większą liczbę badanych wielkości. Występują przy tym trzy istotne fakty, które spowodowały powstanie teorii eksperymentu:

- po pierwsze: liczba kombinacji wartości czynników badanych przekracza praktycznie możliwości realizacji doświadczeń;

- po drugie: nie wszystkie czynniki mogą być badane oddzielnie, gdyż wpływ jednego czynnika na wynik badania zależy często od wartości innego czynnika dotychczas z różnych przy-czyn nie uwzględnianego w realizowanym doświadczeniu;

- po trzecie: istnieją czynniki, których wartości nie można ustalić na stałym poziomie, a nawet są czynniki w ogóle niemierzalne lub po prostu nie znane, które jednak wpływają na wynik doświadczenia.

W ten sposób niemożliwe stało się zachowanie w doświadczalnictwie klasycznej koncepcji determinizmu, które należało poszerzyć o metody statystyki matematycznej oraz włączyć w proces badania nowoczesnych technik informatycznych. Dało to początek teorii eksperymentu (TE) obejmującej następującą problematykę:

- modelowanie analityczne obiektów badań (MA);

- programowanie badań doświadczalnych (PBD);

- analizę wyników badania (A).

Jak wynika z rys. 7.1 przedstawione problemy są zespolone w jedną całość i występują w różnych etapach realizacji eksperymentu. Teoria eksperymentu powstała pod presją dążeń do po-

                   

Rys.7.1 Schemat struktury teorii eksperymentu.

prawy efektywności badań naukowych, rozumianej jako stosunek ilości i jakości informacji naukowej do poniesionych kosztów i czasu badań. Ponieważ badanie złożonych obiektów wymaga uwzględnienia wielu czynników „n” wpływających na wynik końcowy „z”, to niezbędne jest wyznaczenie z badań funkcji wielu zmiennych w postaci:

(7.1)

Liczba pomiarów określana jest więc z zależności:

(7.2)

Można łatwo obliczyć, że dla i=10, ni = 10, stąd n =
skąd wynika, że gdyby jeden po-miar trwał 1 godzinę, to czas badań kompletnych można oszacować na około 1 mln lat.

Teoria eksperymentu umożliwia na początku określenie celu i metod analizy wyników pomiarów, a potem dopiero przyjęcie odpowiedniego planu doświadczenia i realizacje pomiarów. Plan doświadczenia musi równocześnie uwzględniać postulat, aby liczba pomiarów wymaganych według tego planu była możliwie mała.

W naukach empirycznych tworzenie wartościowych informacji poznawczych jest zawsze uzależnione od sposobu przeprowadzenia badań empirycznych, mających na celu zebranie odpowiednich wyników pomiarów lub weryfikację sformułowanych hipotez i założeń badawczych[4, 7]. Wśród badań empirycznych rozróżnia się (rys.7.2) :

- obserwacje;

- doświadczenia;

- eksperymenty.

Obserwacje mają miejsce wtedy, gdy badacz B lub system badający B może tylko odbierać sygnały pochodzące z systemu badanego S i nie wywiera na ten system żadnego wpływu. Zrozumienie odbieranych sygnałów przez badającego B dostarcza mu informacji o źródle owych sygnałów. Na rys.7.2 A). przedstawiono najprostszy schemat badania empirycznego. Badany system S posiada wartościowe dla badającego B informacje zawarte w zbiorach Is1 oraz Is2. Na skutek niedoskonałości aparatury pomiarowej, ułomności badającego lub innych losowo-uzależnionych przyczyn, co ilustruje filtr F1, system B otrzymuje tylko pewien podzbiór Is2 wartościowych informacji. Korzystając z wiedzy badacza WB pobiera on IWB informacji, które wykorzystuje do przetworzenia informacji Is2. Jeżeli system B nie wy-korzysta wszystkich wartościowych informacji, tracąc informacje zbioru IB1-co ilustruje filtr F2, to wyprowadza na zewnątrz ich część IB2 jako końcowy zbiór informacji Ik. Informacje te są także gromadzone przez badającego B, zwiększając jego wiedzę WB.

 

           

 

Rys. 7.2 Specyfika badań empirycznych: obserwacja (A), doświadczenie (B) oraz  eksperyment (C).

 

Schemat badania empirycznego polegającego na przeprowadzaniu doświadczeń pokazano na rys. 7.2 B), w którym występuje dodatkowo blok wiedzy badacza o modelu matematycznym lub fizycznym M(S). W celu uproszczenia opisu i schematu nie zaznaczono już w tym i następnym schemacie filtrów F1 i F2, mimo iż istnieją one również i odgrywają identyczną rolę co poprzednio. Badający system B korzystając ze swej wiedzy WB opracowuje przy pomocy zbioru wartościowych informacji IWB1 model badanego systemu, optymalizujący przebieg badania. Wartość informacji IB2 wytworzonych przez system B jest zdecydowanie większa niż w poprzednim przypadku.

Eksperyment, którego schemat badania pokazano na rys.7.2 C) w porównaniu
z doświadczeniem różni się dodatkowym wprowadzeniem następujących urządzeń:

- informatycznych systemów pomiarowych ISP, przekazujących bezpośrednio informacje
do komputera;

- komputera o konfiguracji wynikającej z celu badania;

- banku informacji w zewnętrznej pamięci komputera;

- systemem sterowania stanami badanego systemu S za pomocą sygnałów Ir.

Ten schemat badania systemu S pozwala na uzyskiwanie informacji o jeszcze większej wartości niż poprzednio. Z banku informacji na każde żądanie możliwe jest uzyskiwanie dodatkowych informacji
o badanym systemie S.

Przebieg procesu tworzenia wartościowych informacji poznawczych przez system badający B na systemie empirycznym S ilustruje schemat pokazany na rys.7.3. System badający B składa się zawsze ze zbioru ludzi oraz aparatury pomiarowej. System ten posiada wiedzę o badanym obiekcie S w postaci zbioru Ip. Podczas badań system B otrzymuje o systemie

       

Rys.7.3 Schemat procesu wytwarzania nowych informacji wartościowych.

 

S informacje Is, które przetwarza metodami M i algorytmami A. Rezultatem tych działań są wytworzone informacje poznawcze I o badanym systemie S.

W badaniach diagnostycznych podczas planowania i realizacji pomiarów dla potrzeb oceny stanu maszyny znajduje zastosowanie najczęściej eksperyment, w formie czynnej, biernej i bierno-czynnej, których charakterystyka została dalej omówiona.

Planowanie eksperymentów  

Planowanie eksperymentów prowadzi się dla potrzeb wyznaczenia (lub weryfikacji) podanego opisu matematycznego modelu obiektu, weryfikacji hipotez badawczych, obserwacji nowych faktów oraz ułatwienia obliczeń w fazie opracowywania wyników.

                

- programy statyczne stosowane w eksperymentach czynnych i bierno-czynnych;

- programy dynamiczne (sekwencyjne) - stosowane w eksperymentach biernych.

Główną cechą programów statycznych jest to, że wszystkie układy wartości czynników badanych Xi (cech stanu), dla których będą przeprowadzane pomiary wartości symptomów Sj zostają określone jednocześnie przed rozpoczęciem badań. Uzyskiwane kolejne wyniki pomiarów nie mają wpływu na program badań. Zaliczenie tych programów do grupy eksperymentów czynnych i bierno-czynnych wynika z faktu, że zgodnie z rys. 7.5 na każdym kroku badania znany jest wektor cech stanu X, przy zadanym i znanym Z,E = const oraz N-przypadkowym.

Cechą podstawową programów dynamicznych jest to, że przed rozpoczęciem badań określa się tylko jeden wybrany układ wartości czynników badanych (cech stanu) Xi, od którego rozpoczyna się pomiary oraz ustala się procedurę dla wyznaczenia kolejnego układu czynników badanych, uwzględniających wynik poprzednich pomiarów. W tym przypadku w zastosowaniu badań diagnostycznych są to eksperymenty bierne, gdyż Z,E=const, N-przypadkowe, X-szukane.

Programy statyczne pozwalają na określenie rodzaju, liczby i warunków pomiaru przed rozpoczęciem badań, co znakomicie ułatwia ich przygotowanie techniczno-organizacyjne. Natomiast programy dynamiczne to sekwencje, z których każda uwzględnia wyniki po-przednich pomiarów, co z kolei utrudnia techniczno-organizacyjną stronę realizacji badań. Należy od razu podkreślić, że między tymi programami istnieje silne powiązanie: pewne programy o zbliżonych zasadach mogą być traktowane jako statyczne, albo przy pewnych niewielkich zmianach stają się programami dynamicznymi.

Teoretycznie najlepszą drogą do rozwiązywania problemów badań doświadczalnych jest właściwie zaprojektowana procedura eksperymentu. Planowanie to może mieć różny przebieg, zależnie od przedmiotu badań, celów poznawczych, charakteru żądanych informacji,

wreszcie od procedur i technik badawczych jakie są dostępne w badaniach. Istnieją jednak pewne ogólne reguły postępowania w procesie planowania, ważne dla wszelkiego rodzaju problemów i procedur, przestrzeganie których wprowadza porządek do procesu planowania i chroni badacza przed zaniedbaniami niekorzystnymi dla rezultatów badań.

Istota przydatności teorii eksperymentu w planowaniu badań polega na tym, że właściwie dobrany program badań zapewnia:

- wyznaczenie funkcji stanowiącej matematyczny opis obiektu badań (model OB) i to funkcji o z góry przyjętej postaci;

- ograniczenie ogólnej liczby pomiarów do rozsądnych, raczej małych wartości.

Realizacja tak formułowanych zadań jest możliwa za pomocą odpowiednio dobranych do celów badania gotowych lub opracowanych planów. I tak:

- jeżeli celem badań jest wyznaczenie funkcji obiektu badań, to należy poszukiwać planu w grupie planów zdeterminowanych (uwarunkowanych);

- jeżeli celem badań jest weryfikacja istotności wpływu wielkości wejściowych, to należy po-szukiwać planu w grupie planów statycznych randomizowanych (losowych);

- jeżeli celem badań jest wyznaczenie ekstremum obiektu badań, to właściwe plany znajdują się w grupie planów optymalizacyjnych.

Planowanie badań doświadczalnych obejmuje następujące etapy badań:

1. charakterystyka obiektu badań, opracowując ją należy:

- ustalić stan wiedzy w zakresie tematu, a tym samym określić zagadnienia wymagające rozwiązania na drodze doświadczalnej;

- określić zbiory wielkości charakteryzujących obiekt badań (wielkości wejściowe, wyjściowe, stałe i zakłócające);

- określić relacje między wielkościami, które należy rozpoznać w wyniku badań doświadczalnych;

2. cel badań doświadczalnych dobrze określony stanowi podstawę powodzenia i najczęściej dotyczy jednej z możliwości:

- wyznaczenia funkcji (modelu) obiektu badań, gdzie celem jest ustalenie związków między wszystkimi wielkościami wejściowymi a wielkością wyjściową;

- wyznaczenia stanu granicznego symptomów lub granic dla klasyfikacji zdatności i niezdatności badanych obiektów;

- weryfikacja istotności wpływu wybranych wielkości wejściowych na wielkości wyjściowe na tle zakłóceń losowych;

3. metoda badań doświadczalnych dotyczy:

- wyboru właściwego planu doświadczenia;

- określenia sposobu jego realizacji i liczby powtórzeń pomiarów;

- określenia metod i środków pomiarowych (stanowisko badawcze);

4. realizacja badań doświadczalnych na przygotowanym stanowisku badawczym zgodnie z zasadami punktu 3;

5. analiza wyników i wnioskowanie prowadzone w zależności od realizowanego celu badania, dostępnymi metodami wnioskowania i narzędziami wizualizacji wyników;

6. wnioski z badań formułuje się w postaci:

- wniosków poznawczych;

- wniosków utylitarnych (praktycznych);

- rozwojowych, określających kierunki dalszych badań.

Ogólne zasady eksperymentowania

Realizacja badań eksperymentalnych wymaga wykonania kilku kompleksowo zgrupowanych zespołów czynności, takich jak:

- sformułowanie celów i programu badań;

- przygotowanie stanowiska badawczego;

- prowadzenia badań według przyjętego planu;

- opracowanie wyników pomiarów.

           

Rys.7.9 Organizacja prac eksperymentalnych.

Organizację czynności podczas przebiegu eksperymentu można schematycznie przed-stawić jak na rys.7.9, wyróżniając:

- warstwę bezpośredniego sterowania eksperymentem, polegającego na uzmiennianiu wielkości wejściowych i wykonywaniu pomiarów zgodnie z planem badań;

- warstwę przetwarzania wstępnego i dokładnego danych pomiarowych, badania modelowe i porównywanie ich z danymi pomiarowymi;

- warstwę decyzji, w której eksperymentator na podstawie otrzymanych wyników częściowych dokonuje korekt dalszego przebiegu eksperymentu, zmian w modelu i obiekcie.

Wymienione czynności są pracochłonne, ich realizacja natomiast kosztowna z powodu złożoności i wysokich kosztów eksploatacji współczesnych stanowisk badawczych. Prowadzenie badań jest więc coraz częściej przedmiotem automatyzacji i wspomagane jest nowoczesnymi technologiami informatycznymi.

Schemat podstawowych czynności eksperymentatora, wynikający z zakresu ogółu prac eksperymentalnych pokazano na rys. 7.10.

 

       

 

Poprawne zrealizowanie eksperymentu obejmuje zatem elementy badania naukowego w postaci niżej podanych zagadnień :

- postawienie problemu i hipotez roboczych,

- określenie materiału dowodowego weryfikującego przyjęte hipotezy,

- wskazanie aspektów uogólniających sformułowanego problemu,

- przyjęcie zakresu prowadzonych badań,

- zaplanowanie kolejnych etapów badań,

- rozważenie potrzebnych środków technicznych, finansowych i liczebności personelu.

Analizując elementy główne każdego eksperymentu uwzględniające obiekty badań (w losowo różnym stanie), opis generowanych sygnałów jak i sposoby ich przetwarzania można stwierdzić, że wszelkie własności diagnostyczne wyrażane są w kategoriach losowych. Te losowe własności powodują, że wszystkie stwierdzenia w diagnostyce są wyrażane w kategoriach prawdopodobieństw z określonym poziomem ufności. Warunkuje to potrzebę stosowania nowoczesnych metod i technik badawczych dla uzyskania maksimum prawdopodobieństwa wypracowywanych decyzji.

Wydaje się mało prawdopodobne, by sformułowanie pełnego i zarazem dostatecznie ogólnego wykazu zasad praktycznych realizacji badań było możliwe. Niemniej jednak, poniżej podano zestawienie pewnej liczby pytań, które istotnie wpływają na wyniki eksperymentów:

- czy problem badawczy został właściwie sformułowany ?

- czy cel badań jest precyzyjnie określony ?

- czy przyjęto właściwy plan badań ?

- czy umiejętności zespołu odpowiadają wymogom planu badań ?

- jak wygląda bilans potrzeb wynikających z planu badań w zakresie czasu pracy, środków rzeczowych i finansowych ?

- czy narzędzia i metody badawcze zostały sprawdzone pod względem rzetelności i skuteczności;

- jakich trudności i zakłóceń można oczekiwać w toku realizacji badań ?

- jakie przedsięwzięto środki dla zauważenia istniejącego rozwiązania problemu lub jego braku ?

- czy w planie badań uwzględniono ewentualną konieczność formułowania i rozwiązywania zadań pomocniczych i pobocznych ?

- jakie ustalono zasady analizy wyników częściowych ?

- czy ustalono zasady zmiany planu badań warunkowane przez wyniki częściowe ?

- jaki przyjęto sposób opisu materiału badawczego?

Przy formułowaniu wyników zrealizowanego eksperymentu należy podać rzetelne odpowiedzi na następujące pytania:

- czy i w jakim zakresie rozwiązano problem badawczy ?

- w jakich dziedzinach nauki i praktyki znajdzie zastosowanie uzyskane rozwiązanie ?

- jakie nowe problemy wyłaniają się w związku z wynikami badań ?

- jak przebiegała realizacja planu badań ?

- jak należy ocenić zastosowane metody i narzędzia badawcze ?

- jakie wystąpiły zakłócenia w trakcie badań (czasowe, merytoryczne, sprzętowe) ?

- co wynika z pozyskania nowej wiedzy w zakresie sformułowanego problemu badawczego ?

  Komputerowe wspomaganie eksperymentu

 

Wykorzystanie komputerów podczas badań eksploatacyjnych preferuje różne formy eksperymentów, gdzie istnieje możliwość automatycznej akwizycji danych, przetwarzania i wnioskowania maszynowego. Także w eksperymentach tych istnieje możliwość programowanej ingerencji w zmiany stanu (zachowań) badanych obiektów, co znacznie ułatwia rozwiązywanie problemów modelowania i symulacji.

Podstawowe funkcje realizowane przez system obsługi eksperymentu, budowany w oparciu o nowoczesne technologie informatyczne pokazano na rys.7.11.

Rys. 7.11 Struktura systemu obsługi eksperymentu (SOE).

 

Różnorodność obiektów technicznych i realizowanych zadań powoduje różnorodność potrzeb w zakresie metod i środków badawczych, w tym także metod i form komputeryzacji. Całościowe opracowanie przedstawionych problemów tworzy podstawy oczekiwanych systemów komputerowego wspomagania eksperymentów.

Warto zaznaczyć, że profesjonalne oprogramowanie planowania eksperymentu jest bardziej rozwinięte od oprogramowania realizacji i opracowania wyników samego eksperymentu, od których oczekuje się:

- większej odporności na przetwarzanie danych zawierających grube błędy;

- zwiększonej odporności na niedokładności w specyfikacji modelu;

- stosowania nieliniowych algorytmów przetwarzania danych;

- przetwarzania on-line związanego z szybkimi urządzeniami wprowadzania i wyprowadzania danych pomiarowych;

- poszerzenia możliwości i niezawodności algorytmów identyfikacji zjawisk opisywanych równaniami różniczkowymi i różnicowymi.

Wydaje się, że mimo znacznego postępu podstawowe problemy użytkowników komputerowych systemów eksperymentalnych skupiają się dalej wokół zagadnień sprzęgania komputera z obiektem oraz z potrzebą wizualizacji danych wielowymiarowych wraz z możliwościami animowanej eksploracji w dowolnie zadanych kierunkach. Postęp w dziedzinie technologii cyfrowej oraz w informatyce nie jest jednak w stanie zastąpić opóźnień w za-kresie metodologii eksperymentu i tworzenia modeli o charakterze poznawczym. Nowym wyzwaniem dla metodologii eksperymentu są dokonane na przestrzeni kilkunastu ostatnich lat odkrycia w zakresie dynamiki procesów znajdujących się daleko od punktów równowagi i wykazujących zachowania chaotyczne.

Odpowiedzialność człowieka za poprawne działanie najczęściej zautomatyzowanych systemów technicznych, mimo wsparcia nowoczesnymi technologiami informatycznymi, wcale się nie zmniejszyła. Skomputeryzowane systemy badania i sterowania są najbardziej podatne na błędy popełniane przez operatora w rozumowaniu, kojarzeniu i wnioskowaniu, które są niebezpieczne przede wszystkim dlatego, że ujawniają się zwykle dopiero swoimi skutkami gdy jest już za późno na odwrócenie działań.

Istotnym zagrożeniem są również błędy w procedurach pracy i niedopatrzenia nadzoru, czyli błędy w zarządzaniu eksploatacją systemu technicznego. Z tego powodu poszukuje się intensywnie metod wykrywania źródeł błędów człowieka i takich rozwiązań konstrukcyjnych i organizacyjnych, które zredukują wpływ błędów ludzkich na bezpieczeństwo systemu.

Niedoskonałości człowieka w badaniach eksperymentalnych powodują podobne skutki, wprowadzając ograniczenia co do poprawności ich rezultatów.

Rolę człowieka w badaniach doświadczalnych można omówić w dwóch aspektach : jako twórcy i jako użytkownika.

Twórca badań uznaje potrzebę ich podjęcia a następnie po przeprowadzeniu analizy celowości i możliwości podjęcia badań, precyzuje cele badań. Z celem badania łączy się opracowanie zadań, których wykonanie ma umożliwić realizację celów badań. Po tym należy:

- dokonać krytycznej analizy stanu zagadnienia w literaturze,

- zorganizować zespół badawczy,

- ustalić założenia badawcze i formy pracy zespołu.

Treści merytoryczne w pracy zespołu (jak i pojedynczego badacza) obejmują :

- opracowanie modeli matematycznych i hipotez wyjaśniających stan obiektu diagnostyki,

- opracowanie programu badań,

- przeprowadzenie pomiarów,

- opracowanie i interpretacja uzyskanych wyników,

- ocenę stopnia potwierdzenia hipotez wyjaśniających,

- sformułowanie wniosków oraz przedstawienie zaleceń,

- opracowanie sprawozdania z badań.

Efektywność działania i wykorzystania możliwości obiektu zależy od współdziałania ba-daczy z tym obiektem. Krótkie cykle robocze z wieloma rozruchami i zatrzymaniami na tle zmiennych stanów otoczenia, ciągłe zmiany czynności, natężenie hałasu, toksyczność spalin, ograniczona widoczność i oświetlenie miejsca pracy, obserwacja urządzeń sygnalizacyjnych itp. powodują szybkie zmęczenie i wyczerpywanie się zdolności do prawidłowych zachowań badającego.

Prawidłowe współdziałanie człowieka z obiektem, traktowanym jako system antropotechniczny, stawia określone wymogi dla jego stanu psychofizycznego, wśród których do najbardziej ogólnych zalicza się :

- indywidualne cechy badacza,

- stopień wykształcenia,

- zgodność wymagań techniki z cechami badacza,

- motywacje działania,

- organizacja pracy,

- stan zdrowia,

- stan obiektu technicznego,

- stan otoczenia.

Przedstawione uwagi mają decydujący wpływ na wyniki prowadzonych eksperymentów diagnostycznych, przy czym zagadnienie roli człowieka w systemach antropotechnicznych jest dopiero postrzegane w aspekcie wzajemnego oddziaływania obiektu i człowieka.

BADANIA OPERACYJNE

Budowa i zastosowanie liniowych modeli optymalizacji

W wielu różnych sytuacjach podejmujemy decyzje. Sytuacje te nazywamy sytuacjami decyzyjnymi, a osobę podejmującą decyzję - decydentem. Warunki, w jakich działa decydent, nie pozwalają na wybór dowolnej decyzji. Decyzję zgodną z warunkami ograniczającymi nazywamy decyzją dopuszczalną.

Nie każda decyzja dopuszczalna jest równie dobra. W świetle celów, jakie sobie stawia decydent, jedne decyzje mogą być lepsze, inne gorsze. Stąd wynika problem wyboru decyzji najlepszej, zwanej decyzją optymalną. Wybór decyzji optymalnej wymaga przyjęcia określonego kryterium, według którego oceniamy decyzje jako lepsze lub gorsze. Kryterium to nazywamy kryterium wyboru (oceny).

Opis określonej sytuacji decyzyjnej nazywamy problemem (zagadnieniem) decyzyjnym w którym warunki ograniczające, kryterium wyboru i decyzje dają się opisać
w języku matematycznym.

Warunki ograniczające najczęściej opisywane są za pomocą układów równań lub nierówności. W równaniach tych(lub nierównościach) występować będą pewne wielkości dane, zwane parametrami, oraz wielkości, które należy ustalić, zwane zmiennymi decyzyjnymi.

Oprócz warunków ograniczających w zadaniu decyzyjnym mogą także występować warunki dotyczące znaku zmiennych (np. warunek nieujemności) lub typu zmiennych (np. warunek ich ciągłości, całkowitoliczbowości lub binarności).

Decyzję dopuszczalne utożsamiać będziemy z takim układem wartości zmiennych (układem liczb), które spełniają wszystkie warunki opisujące badaną sytuację. Rolę kryterium wyboru będzie pełnić pewna funkcja zmiennych decyzyjnych mierząca cel, który chce osiągnąć decydent. Funkcją tę nazywa się funkcja celu.

Wybór decyzji optymalnej polega na ustaleniu takiej decyzji dopuszczalnej, przy której funkcja celu osiąga wartość najkorzystniejszą, tzn. w zależności od badanej sytuacji wartości minimalną lub maksymalną.

Opisanie sytuacji decyzyjnej w języku matematycznym ma na celu sprowadzenie problemu wyboru najlepszego decyzji do rozwiązania pewnego jednoznacznie określonego zadania matematycznego. Aby rozwiązanie takiego zadania rzeczywiście umożliwiło wybór najlepszej decyzji, trzeba je tak sformułować, by dokładnie opisywało ono daną sytuację decyzyjną. Należy zatem ustalić:

1. jakie wielkości mają być wyznaczone i odpowiednio je oznaczyć (tzn. należy podać zmienne decyzyjne),

2. jakie wielkości są dane ( określić parametry zadania),

3. jakie warunki ograniczające musi spełnić dopuszczalne decyzje i sformułować je w postaci równania lub nierówności wiążących zmienne decyzyjne (zapisać warunki ograniczające),

4. cel, jaki chce osiągnąć decydent oraz sformułować funkcję zmiennych decyzyjnych określającą stopień osiągnięcia celu (podać funkcję celu).

Jeżeli w zadaniu decyzyjnym funkcja celu oraz warunki ograniczające są liniowe, to zadanie takie nazywamy liniowym modelem optymalizacji.

Budowa i zastosowanie liniowych modeli optymalizacji.

Modele optymalizacji liniowej stanowią najliczniejszą i najbardziej rozpo­wszechnioną grupę modeli matematycznych dotyczących wyboru decyzji optymal­nej, tj. takiej, która przy istniejących ograniczeniach zapewnia, ze względu na przy­jęte kryterium, najlepszą realizację określonego zamierzenia - celu. Proces budowy modelu umożliwiającego wyznaczanie decyzji optymalnej składa się z czterech etapów:

(1) zdefiniowania pojęcia decyzji,

(2) ustalenia warunków wyznaczających zbiór decyzji dopuszczalnych D,

(3) przyjęcia miernika oceny stopnia (poziomu) realizacji założonego celu przez każdą z decyzji dopuszczalnych,

(4) określenia pojęcia decyzji optymalnej przy przyjętym mierniku oceny.

Otrzymany w takim postępowaniu model wyboru decyzji optymalnej jest zada­niem optymalizacji liniowej, gdy:

• Sformułowany problem decyzyjny pozwala na ilościowe ujęcie rezultatów każdego z wymienionych etapów budowy modelu.

• Jego zapis formalny ma niżej wymienione własności:

(a) Dowolną decyzję można wyrazić za pomocą nieujemnych wartości licz­bowych k zmiennych - zmiennych decyzyjnych, tzn. dowolną decyzję można zapisać jako wektor x = [x_l x₂ ... x_k], w którym x_j≥ 0 (j = 1, 2, ..., k) oznacza określoną wartość j-tej zmiennej decyzyjnej, a liczba k ­liczbę zmiennych decyzyjnych, wynikającą z treści modelowanego pro­blemu.

(b) Ograniczenia dotyczące swobody wyboru decyzji (definiujące zbiór D można zapisać w postaci układu nierówności lub równań liniowych, jakie muszą spełniać wartości zmiennych decyzyjnych x_l, x₂, ..., x_k, tzn. zapis formalny ograniczenia można przedstawić za pomocą nierówności:

a₁x₁+a₂x₂+...+a_kx_k ≤ b lub a₁x₁+a₂x₂+...+a_kx_k ≥ b

albo równania:

a₁x₁+a₂x₂+...+a_kx_k = b

(c) Ocenę stopnia osiągnięcia celu przez decyzję dopuszczalną x wyraża war­tość pewnej funkcji liniowej f (funkcji celu), określonej na zbiorze D.

Miernikiem oceny jest więc funkcja:

f (x) = c₁x₁ + c₂x₂ + ... + c_kx_k.

(d) Ustalenie, czy decyzja optymalna x° ma być tą spośród decyzji dopusz­czalnych, która zapewnia, że f (x°) jest największą (maksymalną) czy też jest najmniejszą (minimalną) wartością funkcji celu f osiąganą na zbio­rze D.

Wiele praktycznych zagadnień w ekonomii, badaniach operacyjnych, teorii decyzji i technice, nauce czy przemyśle może być sformułowanych jako modele LP. Na przykład przepływy gotówkowe, planowanie kadr osobowych, planowanie lotów personelu lotniczego, dostawy za pomocą ciężarówek czy statków, planowanie obciążenia maszyn, przepływ wody, ropy czy gazu w sieci rurociągów.

Metoda simpleks.

Uniwersalną metodą rozwiązywania programów liniowych jest algorytm simpleks. Istota algorytmu polega na badaniu kolejnych rozwiązań bazowych (dopuszczalnych) w taki sposób że:

1. znajdujemy (dowolne) rozwiązanie bazowe programu;

2. b) sprawdzamy czy jest ono optymalne;

3. c) jeżeli dane rozwiązanie bazowe nie jest optymalne konstruujemy następne (lepsze).

Postępowanie kończymy w momencie osiągnięcia optymalnego rozwiązania bazowego.

Zapis modelu w postaci macierzowej:

cx -> max

Ax <= b

x>=0

gdzie : | x₁ |

| a₁₁ a₁₂ ...... a _n| | x₂ | | b₁|

A = | a_m1 a_{m2 ..........}a_mn| x = |x ₃| b = |b_n| c = | c₁, c_n|

| x_n|

Przed przystąpieniem do budowy pierwszej tablicy simpleks zmieniamy wszystkie nierówności na równania przez wprowadzenie nowych zmiennych(swobodnych), które stanowią początkowe rozwiązanie bazowe. W przypadku nierówności typu >= od lewej strony odejmujemy zmienne swobodne i dodajemy zmienne sztuczne. Zmienne sztuczne wchodzą do pierwszej bazy. Do definicji celu zmienne swobodne wchodzą ze współczynnikami = 0 a zmienne sztuczne ze współczynnikami M ( M-> ∞ )

Metoda simpleks.

3.1. Wyprowadzenie zrewidowanej metody sympleks

Rozważmy zagadnienie LP w standardowej postaci (1.1) - (1.3) i załóżmy, że macierz A jest rzędu m. Jeśli B jest dowolną nieosobliwą podmacierzą stopnia m macierzy A, a N jest pozostałą podmacierzą A, to (1.2) możemy zapisać w postaci

(1.4)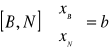

gdzie x_B i x_N, mają odpowiednio, m i n - m składowych. Wygodnie jest założyć, że B składa się z pierwszych m kolumn macierzy A.

Jeśli x_N = 0, to rozwiązanie (1.4) nazywa się rozwiązaniem bazowym x_B = B ^-1b, a nieosobliwą macierz B nazywa się bazą. Jeśli ponadto x ≥ 0, to mówimy, że x jest bazowym rozwiązaniem dopuszczalnym.

Następujące twierdzenie określa ważną rolę bazowych rozwiązań dopuszczalnych:

Twierdzenie 1.1. Jeśli istnieje rozwiązanie dopuszczalne (spełniające (1.2) - (1.3), to istnieje bazowe rozwiązanie dopuszczalne. Co więcej, jeśli istnieje rozwiązanie opty­malne minimalizujące z, to istnieje optymalne rozwiązanie bazowe.

To podstawowe twierdzenie stanowi klucz do algorytmu sympleks, najpotężniejszej metody rozwiązywania programów liniowych. Istnieje kilka różnych wersji tej metody i wiele implementacji numerycznych. Poniżej opiszę prymalną metodę sympleks w wersji zrewidowanej, która jest najpopularniejszą metodą rozwiązywania LP.

Zauważmy najpierw, że dzieląc wektor kosztów c na dwa zbiory elementów związa­nych z x_B i x_N , możemy wyrazić funkcję celu x następująco:

Po podstawieniu

(1.5.) x_B = B^-1b - B^-1 N_xN

otrzymamy

(1.6)

gdzie

(1.7)

(1.8)

Wartość funkcji celu z można polepszyć w następnej iteracji, jeśli znajdziemy ujemną składową w p i wprowadzimy odpowiadającą jej niebazową zmienną do bazy. Wektor p może być wygodnie obliczony w dwóch krokach:

B^Tλ = c_B oraz p^T = c^T_N - λ^TN,

gdzie λ nazywa się wektorem mnożników sympleksowych, a p - wektorem względnych, kosztów. Jeżeli

p_k = c_Nk - λ^Ta_k ≤ 0

dla pewnego m+1 ≤ k ≤ n, to a_k jest niebazową kolumną macierzy A, która może wejść do bazy B w następnej iteracji, a wartość funkcji celu zostanie zmniejszona. Pozostaje znaleźć kolumnę macierzy B, którą należy usunąć z bazy. Oznaczając bieżące bazowe rozwiązanie dopuszczalne przez x₀, żądamy by:

(1.9) x_B = x_o - B^-1 a_kx_Nk ≥ 0,

czyli by

x_B = x₀ - yx_Nk ≥ 0,

gdzie y otrzymuje się jako rozwiązanie układu By = a_k. Nierówność (1.9) musi być spełniona, aby zachować dopuszczalność następnego rozwiązania x_B. Kolumnę opuszczającą bazę można znaleźć, rozpatrując x_oi / y_i dla y_i > 0, i = 1, 2, ..., m. Jeśli

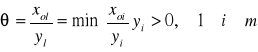
to zmienna x_Bl staje się zerem i jest przesuwana do zbioru niebazowego. Odpowiednio, kolumna a_i przechodzi do macierzy niebazowej N.

Programowanie liniowe całkowitoliczbowe, algorytm podziału i ograniczeń

W wielu sytuacjach praktycznych pożądane jest wyznaczenie rozwiązania zadania optymalizacyjnego w liczbach całkowitych. Może to być, na przykład, żądanie ażeby wielkość produkcji wyrobów występujących w planie optymalnym podawać w liczbach całkowitych. W zadaniu może występować problem wykorzystania dużych niepodzielnych obiektów - turbin, samolotów, okrętów itp. Również w zadaniach optymalizacji transportu towarów niepodzielnych konieczne jest uzyskanie rozwiązania w liczbach całkowitych. Problem matematyczny, jaki stąd wynika, polega na znalezieniu najkrótszej drogi do wyznaczenia optymalnego rozwiązania w liczbach całkowitych - bez uciekania się do rozpatrzenia wszystkich możliwych kombinacji.

Niekiedy rozwiązanie zadania optymalizacyjnego w liczbach całkowitych można uzyskać w sposób najprostszy, choć zarazem trywialny - tzn. drogą zaokrąglenia ułamków (występujących w rozwiązaniu) do liczb całkowitych. Najczęściej jednak postępowanie takie jest nie możliwe i musimy posłużyć się jedną ze specjalnie opracowanych metod. Większość tych metod przewiduje dwa etapy wyznaczenia optymalnego rozwiązania:

• w etapie pierwszym wyznacza się rozwiązanie w liczbach ułamkowych

• w etapie drugim sprowadza się rozwiązanie w liczbach ułamkowych do rozwiązania w liczbach całkowitych

Metoda Landa-Doiga opracowana ponad 30 lat temu przewiduje takie właśnie, dwuetapowe postępowanie optymalizacyjne. Warunki uboczne układu oraz warunki brzegowe wyznaczają obszar rozwiązań dopuszczalnych dla szukanych danych. Na obszarze tym należy wyznaczyć minimum (maksimum) funkcji. W tym etapie wyznaczyliśmy wierzchołek optymalny (rozwiązanie optymalne). Punkt ten leży na prostej będącej zbiorem punków, z których każdy wyznacza jednakową (minimalną - maksymalną) wartość funkcji.

Niestety, ani wierzchołek optymalny, ani inne punkty leżące na prostej nie spełniają wszystkich równocześnie wszystkich warunków ubocznych i brzegowych. Należy więc przejść do etapu drugiego.

W etapie drugim przechodzi się od wierzchołka optymalnego równolegle do prostej wartość funkcji, do punktu który wyznacza nowe rozwiązanie zadania - tym razem rozwiązania w liczbach całkowitych.

Metoda Gomory'ego przewiduje również dwuetapowe postępowanie optymalizacyjne:

• za pomocą jednej z metod programowania liniowego wyznacza się wierzchołek optymalny, któremu odpowiadają zmienne wyrażone (najczęściej) w liczbach ułamkowych.

• Następnie do układu warunków ubocznych zadania dodaje się pewien nowy warunek (i pewną dodatkową zmienną), w wyniku czego obszar rozwiązań zostaje zmniejszony tak aby nowe rozwiązanie było w liczbach całkowitych.

. Programowanie liniowe całkowitoliczbowe, algorytm podziału i ograniczeń.

W większości rozpatrywanych zadań programowania liniowego zmienne decyzyjne mogły przyjmować dowolne wartości nieujemne. W zapisie formalnym wyrażały to warunki nieujemności x_j≥0 (j=1, 2, ...,n). Jednak w wielu zagadnieniach praktycznych potrzeba ograniczenia wartości zmiennych decyzyjnych do nieujemnych liczb całkowitych jest warunkiem koniecznym, aby możliwe było dokonanie sensownej interpretacji uzyskanego rozwiązania. Matematyczny model problemu wyboru decyzji optymalnej, którą muszą wyrażać liczby całkowite, nazywamy całkowitoliczbowym zadanie optymalizacyjnym.

Niech D_C oznacza zbiór rozwiązań dopuszczalnych zadania programowania liniowego z żądaniem, aby wartości zmiennych decyzyjnych (niekoniecznie wszystkie przyjmowały wartości całkowite. Przez D oznaczymy zbiór rozwiązań dopuszczalnych osłabionej wersji tego zadania.

Z zależności D_C ⊂ D wynikają inne ważne numerycznie własności.

Własność 1.

f ^M = max f(x) ≤ max f(x) = f ^O

x∈ D_C x∈ D

f ^m = min f(x) ≥ min f(x) = f ^O

x∈ D_C x∈ D

tzn. Optymalna wartość funkcji celu zadania całkowitoliczbowego jest zawsze ograniczona przez optymalną wartość funkcji celu z wersji osłabionej tego zadania: od góry - przy kryterium maksymalizacji; od dołu - przy kryterium minimalizacji.

Własność 2.

(x^o ∈ D^opt ∧ x^o ∈ D_C) ⇒ x^o∈ D^opt_C

tzn. Jeśli x^o jest decyzją optymalną osłabionej wersji zadania całkowitoliczbowego I jednocześnie spełnia warunek całkowitoliczbowości, to x^o jest decyzją optymalną zadania całkowitoliczbowego, z którego utworzono wersję osłabioną.

Rozwiązując zadanie optymalizacji liniowej w liczbach całkowitych za pomocą Solvera, stosuje się metodę podziału i ograniczeń. Polega ona na rozwiązaniu serii odpowiednio budowanych zwykłych zadań optymalizacji liniowej. Termin podział

w nazwie metody pochodzi stąd, że zbiory decyzji dopuszczalnych rozwiązywanych zadań otrzymuje się z podziału zbioru D początkowej wersji osłabionej zadania na mniejsze podzbiory. Optymalne wartości tej samej funkcji celu są ograniczane, zgodnie z własnością 1, odpowiednio przez jej wartość optymalną osiąganą przed przeprowadzonym podziałem. Specyficzny podział zbioru D na mniejsze fragmenty i stosowanie określonych reguł przy obliczeniach spowoduje, że decyzja optymalna ze zbioru D_C stanie się w pewnym momencie wierzchołkiem i jednocześnie decyzją optymalną reprezentowaną przez wierzchołek jednego z utworzonych podzbiorów.

Zagadnienie transportowe

ZT jest specyficznym problemem z zakresu zastosowań programowania liniowego. ZT wykorzystuje się najczęściej do optymalnego planowania transportu towarów, przy minimalizacji kosztów, lub czasu wykonania zadania. Można również przy jej pomocy rozwiązać zadania optymalnego rozdziału czynników produkcji, w celu maksymalizacji wartości produkcji, zysku, lub dochodu rolniczego. Stosuje się oryginalną metodę budowy modelu matematycznego oraz technikę jego optymalnego rozwiązywania. Przyjmując m punktów wytwarzania pewnego dobra oraz n punktów odbioru tegoż produktu, uzyskuje się macierz połączeń pomiędzy nimi w postaci tabeli o wymiarach m*n, gdzie każdy element przedstawia określoną ilość jednostek masy towaru przesłany od punktu wytwarzania i do punktu odbioru j. wprowadzając dodatkowe oznaczenia kosztu transportu jednej jednostki dobra zbudować można model matematyczny odwzorowujący problem transportowy.

Zagadnienie można rozwiązywać metodą simpleks, jednak jest ona w tym przypadku mało efektywna. Najczęściej stosuje się metodę potencjałów oraz najprostszą metodę - kąta północno-zachodniego. Służy ona do znalezienia pierwszego wewnętrznie zgodnego rozwiązania bazowego.

Zagadnienie transportowe

Istnieje duża grupa wyspecjalizowanych zagadnień programowania liniowego, które ­są sformułowane jako zagadnienia sieciowe. Należą do nich takie zagadnienia, jak zagad­nienie transportowe i jego uogólnienia, zagadnienie przydziału, zagadnienie sieci kom­puterowych, zagadnienie lokalizacji i zagadnienie przepływu wielotowarowego. Zagadnie­nia tego typu opisują szerokie spektrum zastosowań w nauce i przemyśle; na przykład, przepływy gotówkowe, planowanie przewozów lotniczych i okrętowych, optymalna go­spodarka wodna, planowanie kadr osobowych, planowanie obciążenia maszyn i teleko­munikacja. W teorii modele te mogą być rozwiązywane za pomocą ogólnych algorytmów linio­wych, ale często wymagałoby to nadmiernie długich czasów obliczeń i znacznie więcej pamięci niż potrzebują specjalne metody liniowe i sieciowe.

W tym paragrafie rozpatrujemy następujące zagadnienie transportowe:

znaleźć minimum

(1.21)

przy warunkach

(1.22)
i = 1, 2, ..., m,

(1.23)
j = 1, 2, ..., n,

x_ij ≥ 0, i = 1, 2, ..., m; j = 1, 2, ..., n.

Zagadnienie transportowe ma prostą interpretację sieciową. Przypuśćmy, że mamy sieć skierowaną (zwaną także diagramem ważonym), określoną za pomocą zbioru wierzchoł­ków V i zbioru łuków (tj. skierowanych łuków) E. W zagadnieniu transportowym sieć jest dwudzielna i pełna, tzn. wszystkie jej wierzchołki można podzielić na dwie grupy, na węzły dostawy ponumerowane i = 1, 2, . . . , m i węzły odbioru ponumerowane j = 1, 2, . . . , n, a każdy wierzchołek dostawy ma n łuków wychodzących z niego do wszystkich wierzchołków odbioru (zob. rys. 1.2). Dla każdego łuku jest określony jednostkowy koszt c_ij transportowanego dobra.

Zagadnienie polega na wyznaczeniu takich wielkości przewozu x_ij, które minimalizują całkowity koszt transportu z. Pierwszych m nierówności odnosi się do wierzchołków dostawy, następne n nierówności odnosi się do wierzchołków odbioru. Zagadnienie transportowe ma rozwiązanie dopuszczalne, gdy

a ograniczenia odbioru stają się równościami dla rozwiązania optymalnego, tj.

dla wszystkich j .Ponadto, jeśli

to każde rozwiązanie dopuszczalne spełnia wszystkie nierówności jako równości.

Bez utraty ogólności można przyjąć, że (1.22) i (1.23) są równościami, ponieważ zawsze możemy wprowadzić fikcyjny wierzchołek odbioru n +1 z odbiorem

Rys. 1.2. Graficzne przedstawienie sieci transportowej

i kosztami c_{i, n+l} = 0, i = 1, 2, . . . , m.

Zagadnienie transportowe jest szczególnym przypadkiem zagadnienia LP i może być rozwiązywane za pomocą specjalnej prymalnej metody sympleks. Istnieje inne podejście, znane jako metoda prymalno-dualna, oparte na iteracyjnym użyciu algorytmu najwięk­szego przepływu. Metoda ta wykorzystuje konieczne i wystarczające warunki na to, by program liniowy był optymalny.

Sieciowe problemy optymalizacji

Wiele problemów zarządzania przedsiębiorstwem, na przykład planowania produkcji, problemy transportu wewnątrzzakładowego, problemy sterowania procesami aparaturowymi (w przemyśle chemicznym) można sprowadzić do zadania maksymalizacji lub minimalizacji przepływu przez sieć. Metody rozwiązujące dla tego typu zadań nazywane są metodami sieciowymi lub metodami programowania sieciowego.

Rozważać będziemy przedsięwzięcie jako wyodrębniony zbiór czynności powiązanych ze sobą technologią, tj. sposobem wykonania.

Def:

Sieć czynności to graf spójny antycykliczny, który ma jeden wierzchołek początkowy i jeden wierzchołek końcowy. Łuki sieci reprezentują czynności, wierzchołki zaś zdarzenia.

Do wykreślenia sieci czynności dla dowolnego projektu niezbędnego są informacje dotyczące czynności wchodzących w skład przedsięwzięcia oraz ustalenie kolejności ich występowania. Ponadto w trakcie wykreślania sieci powinny być przestrzegane następujące zasady:

1. zdarzenie początkowe nie ma czynności poprzedzających,

2. zdarzenie końcowe nie ma czynności następujących,

3. dwa kolejne zdarzenia mogą być połączone tylko jedną czynnością,

4. wszystkie zdarzenia w sieci, z wyjątkiem początkowego lub końcowego, powinny być początkiem i końcem co najmniej jednej czynności.

Wyróżniamy następujące etapy konstruowania sieci:

1. ustalenie listy czynności,

2. ustalenie zdarzenia początkowego i końcowego przedsięwzięcia,

3. określenie kolejności wykonywania czynności,

4. numerowanie wierzchołków.

Sieciowe problemy optymalizacji.

Duża liczba systemów transportowych, dystrybucyjnych i komunikacyjnych jest pro­jektowana i badana za pomocą modeli sieciowych. Przykładami mogą być tutaj sieci dróg, trasy komunikacji miejskiej, sieci telefoniczne, sieci gazowe, sieci rozdziału energii elektrycznej i sieci komputerowe. Pojawiające się w tych problemach grafy są tak duże, że analiza, bez pomocy komputera, jest praktycznie niemożliwa. Nasze możliwości roz­wiązywania problemów rzeczywistych technikami sieciowymi są więc takie jak możliwości analizy dużych sieci za pomocą komputera. Efektywne algorytmy rozwiązywania problemów sieciowych mają zatem duże znaczenie praktyczne. Najczęściej spotykane problemy optymalizacyj­ne na sieciach to:

• problem najkrótszych dróg

• problem najkrótszego drzewa rozpinającego

• problem maksymalnego przepływu w sieci {opracowano jako przykład niżej}

• problem najtańszego przepływu

• problem komiwojażera

• problemy transportowe

Graf nieskierowany G = (V, E) składa się ze skończonego zbioru wierzchołków V= {v_l, v₂, ..., v_n} i skończonego zbioru krawędzi E = {e₁, e₂, . . ., e_n} (zob. rys. 1). komputerowych implementacjach algorytmów grafowych przyjmujemy najczęściej V= {1, 2, . . . , n}. Każdej krawędzi e odpowiada nieuporządkowana para różnych wierzch­ołków (u, v), o których mówimy, że są incydentne z e. Graf nazywamy skierowanym lub w skrócie digrafem (zob. rys. 2), jeśli para wierzchołków (u, v) incydentnych z krawędzią e (nazywaną w tym przypadku łukiem) jest parą uporządkowaną. Mówimy wtedy, łuk e jest skierowany z wierzchołka u do wierzchołka v, a kierunek ten jest zazna­my na rysunku grotem strzałki. Siecią nazywamy graf skierowany (lub nieskierowany), w którym każdemu łukowi (lub krawędzi) jest przyporządkowana liczba, zwana najczęści­ej wagą. W sieci o praktycznym znaczeniu, waga może reprezentować długość drogi, koszt jej budowy, czas przejazdu, niezawodność połączenia, prawdopodobieństwo przejści­a, przepustowość lub jakąkolwiek inną podobną cechę ilościową przyporządkowaną łukowi (lub krawędzi).

Rys. 1. Graf nieskierowany z 5 wierzchołkami i 6 krawędziami

Dla przykładu jeden z sieciowych problemów omawiam bliżej

Maksymalny przepływ w sieci

Rozważmy sieć N = (V, E), w której dwa wierzchołki są wyróżnione jako źródło s i odpływ t. Każdemu łukowi sieci przyporządkowana jest nieujemna liczba całkowita k_ij, zwana przepustowością luku.

Przepływem w sieci N nazywamy przyporządkowanie każdemu łukowi takiej liczby rzeczywistej x_ij (zwanej przepływem łukowym), że:

1. 0 ≤ x_ij ≤ k_ij dla wszystkich łuków (i, j) ∈ E.

2. W każdym wierzchołku j, różnym od s i t, spełnione jest równanie zachowania przepływu

gdzie i odnosi się do zbioru łuków wchodzących do wierzchołka j, a l - do zbioru. łuków wychodzących z wierzchołka j.

Wartość (wielkość) przepływu f (t) określa się jako sumę przepływów łukowych wpły­wających do wierzchołka odpływu.

Zagadnienie największego przepływu polega na znalezieniu dla wszystkich łuków takich wartości x_ij, by f(t) było maksymalne. Aby znaleźć największy przepływ, można wykorzystać technikę ścieżki powiększającej. Ścieżka powiększająca jest ciągiem łuków, z których dowolne dwa kolejne są sąsiednie, prowadzącym z s do t i umożliwiającym powiększenie wartości przepływu. Jeśli skierowanie łuku (i, j) jest zgodne z kierunkiem ścieżki, to, w celu powiększenia przepływu, x_ij musi być mniejsze od k_ij. Jeśli zaś łuk (i, j) jest niezgodnie skierowany, to aby powiększyć wartość przepływu, trzeba zmniejszyć przepływ łukowy, czyli wymaga się, aby x_ij > 0.

Dynamiczne modele optymalizacji

Idea programowania dynamicznego polega na tym, że zadanie optymalizacyjne
z n zmiennymi rozkładamy na n zadań z jedną zmienną, poszukując dla takich maksimum lub minimum funkcji jednej zmiennej. W zadaniach takich nie ma znaczenia postać analityczna funkcji systemu, lecz struktura rozwiązywania problemu. Programowanie dynamiczne ma zastosowanie przy rozwiązywaniu wielu problemów z dziedziny zarządzania, jak alokacja kapitału, sterowanie zapasami, wymiana urządzeń itp.

U podstaw procedur programowania dynamicznego leżą dwie własności, które umożliwiają podejmowanie decyzji w procesie n-etapowym:

1. wartość funkcji celu w zadaniu n-etapowym jest sumą wartości uzyskanych
   w poszczególnych etapach, a wartość uzyskana w j-tym etapie zależy od stanu
   w etapie poprzednim oraz od decyzji podjętej w j-tym etapie. Nie zależy natomiast od tego, jaką drogą system doszedł do stanu j-1 (własność ta nosi nazwą własności Markowa).

2. Aby ciąg decyzji (x₁*, x₂*, ... ,x_N*) był optymalną strategią w procesie
   n-etapowym, potrzeba, by ciąg decyzji (x₂*, x₃*, ... ,x_N*) był optymalną strategią w procesie (n-1)-etapowym wynikającym z podjęcia w pierwszym etapie decyzji x₁*.

Dla matematycznego opisu i badania wielostadialnych procesów decyzyjnych stosuje się metody programowania dynamicznego rozumianego dwojako:

1. szeroko - jako programowanie matematyczne oparte na stosowaniu modeli opisujących wielostadialne procesy decyzyjne; w tym sensie takie metody matematyczne jak: algebra macierzowa, rachunek różniczkowy, programowanie liniowe i nieliniowe, programowanie dyskretne, mogą być uważane za metody programowania dynamicznego, jeżeli tylko stosuje się je do opisu i badania problemów zarządzania aproksymowanych (przybliżonych) modelami dynamicznymi, tzn. modelami, w których wartości zmiennych są funkcjami czasu;

2. wąsko - jako metoda Bellmana opisu i badania procesów wielostadialnych za pomocą zbioru zależności rekursywnych, kiedy każda następna decyzja „etapowa” zależy od wyników decyzji poprzednich. Pojęcie „etap” nie musi się przy tym wiązać tylko z upływem czasu, ale np. ze zmianą położenia geograficznego (rozpatrywanie wariantów lokalizacji n domków jednorodzinnych na m działkach).

PROGRAMOWANIE KOMPUTEROWE

1. Stałe i zmienne i ich deklarowanie.

Stała - jest to pewna wartość przypisana znakowi/wyrazowi której nie można zmienić np.: stałej PI jest przyporządkowana liczba 3.1415...

Zmienna - Jak sama nazwa wskazuje zmienna jest to wyraz, któremu jest przypisana pewna wartość, która w czasie działania programu możemy swobodnie zmieniać w zakresie danego typu.

Deklaracja Stałych (const)

Stałe deklaruje się jeszcze przed głównym programem słowem kluczowym "Const", w programie przykładowo wygląda to tak:

Const

abc=500;

l3='tu jest tekst';

sprawdz=TRUE;

begin

end.

Zastosowano wcięcia dzięki temu widzimy, które linie są liniami ze stałymi a które nie. Zadeklarowałem tutaj trzy stale: "abc" - przypisana została do niej liczba 500, teraz jeżeli dalej w programie użyjemy stałej "abc" będzie ona postrzegana przez kompilator jako liczba 500, można ja dodawać, odejmować, wyświetlać itd. Stala "l3" jest ciągiem znaków 'tu jest tekst', a "sprawdz" jest postrzegane jako stała logiczna "PRAWDA"

Deklaracja Zmiennych (var)

Zmienne deklaruje się podobnie jak stałe jeszcze przed głównym programem, słowem kluczowym "Var", w programie przykładowo wygląda to tak:

Var

abc:byte;

l3,linia,t:string; {1}

sprawdz:boolean;

begin

end.

Teraz zmienne zostały przypisane do danego typu , i ich wartość będzie można dowolnie zmieniać w zakresie tego typu. Zwróć uwagę że pomiędzy nazwa zmiennej a jej rodzajem, został użyty dwukropek zamiast znaku równości jak to miało miejsce przy stałych. Możliwe jest definiowanie wielu zmiennych tego samego typu w jednej linii, wystarczy je wtedy rozdzielić przecinkami {1}. KAŻDA ZMIENNA PRZED UŻYCIEM W PROGRAMIE MUSI BYĆ WCZEŚNIEJ ZADEKLAROWANA.

1. Stałe i zmienne i ich deklarowanie

Podstawowymi obiektami występującymi w programie są stałe i zmienne. Znaczenie ich jest takie same jak w matematyce. Stałe i zmienne muszą posiadać nazwę i mogą mieć przypisaną wartość. Nazwa jest ciągiem znaków, z których pierwszy musi być literą.

Stałe deklaruje się w części deklaracyjnej programu rozpoczynającej się od słowa kluczowego const

Np.: program Stałe;

Const

Pi = 3,1214

Begin ........End

Zmienne deklaruje się w części deklaracyjnej programu rozpoczynającej się od słowa kluczowego VAR. Podaje się listę zmiennych oddzielonych przecinkami i następnie po dwukropku nazwę typu zmiennych

Np.: program zmienne;

Var

i,j: integer;

begin ... end

Stałe i zmienne i ich deklarowanie

Deklarowanie zmiennych wg schematu:

Var (variable - zmienna)

Nazwa zmiennej : typ zmiennej;

var

A :integer;

S :string[20];

Q :real;

B :boolean;

Deklarowanie stałych wg schematu:

Const (constans - stała)

Nazwa stałej = wartość;

Const

A = 10;

S = `tekst'

Q = 2 div 3;

prawda = true;

fałsz = false;

Podstawowe instrukcje: przypisanie, złożenie, instrukcja warunkowa, pętla while.

Instrukcja przypisania składa się z trzech części i ma następującą postać: zmienna := wyrażenie;

zmienna to nazwa zmiennej lub nazwa funkcji.

Symbol := oznacza przypisanie wartości.

wyrażenie wartość arytmetyczna lub logiczna.

(oblicz wartość wyrażenia i podstaw w miejsce zmiennej)

Zazwyczaj typ zmiennej umieszczony z lewej strony symbolu := powinien być taki sam jak typ wyrażenia z jego prawej strony.

Wartość wyrażenia przypisana z prawej strony symbolu przypisania := może być obliczona tylko wtedy, gdy komputer będzie znał wartości wszystkich składowych tego wyrażenia.

Instrukcja przypisania, służy do nadawania zmiennym wartości, wygląda ona tak: ":=" i przykładowo jeżeli zmiennej ABC typu WORD ( liczba przypisywana MUSI znajdować się w zakresie typu tej zmiennej ) chcemy nadać wartość 456 to piszemy: "ABC:=456;". Niektórych może zaintrygować dlaczego instrukcję przypisania zapisuje się tak ":=" zamiast zwykłego znaku równości "=" ? Zobacz na przykładzie: operacja "kolejna:=kolejna+1" z punktu widzenia matematyki może wydawać się błędna i to wygląda jak np. "4=4+1" co jest absolutną bzdurą, to my wykonujemy tu jednak nie równanie matematyczne, a nadanie zmiennej nowej wartości, aby to wyjaśnić zobacz jak taką linię postrzega komputer: najpierw sumowane jest to co znajduje się po prawej stronie, a dopiero potem podstawiane jest do zmiennej po lewej np. zmienna "kolejna" ma wartość 2, wykonujemy prawą stronę "2+1" komputer zapamiętuje sobie tam gdzieś u siebie w pamięci "3" ( wynik równania ) i dopiero potem wykonuje lewą stronę "kolejna:=liczba z pamięci".

Instrukcja złożenia składa się z ciągu instrukcji ujętych w nawiasy BEGIN (początek), END (koniec). Instrukcja złożona tworzy z ciągu instrukcji jedną i jest używana w przypadku, gdy składnia języka wymaga użycia jednej instrukcji, a niezbędne jest wykonanie wielu.

Begin

Instr 1;

Instr 2;

.…..

end.

Instrukcje warunkowe. Do nich zalicza się instrukcja IF i CASE.

Instrukcja warunkowa IF służy do podejmowania decyzji w Pascalu i ma postać:

IF warunek THEN instrukcja1 ELSE instrukcja2;

Jeśli warunek przed THEN jest spełniony, następuje wykonanie instrukcji umieszczonej za THEN, zaś w przypadku przeciwnym wykonywana jest instrukcja znajdująca się za słowem ELSE. Po wykonaniu wybranej listy instrukcji program przechodzi do wykonywania instrukcji znajdującej się bezpośrednio za instrukcją IF.

Instrukcja IF służy do dokonywania wyboru między dwiema możliwościami.

Pętla WHILE. Instrukcje wykonuje się dopóty, dopóki wyrażenie logiczne jest spełnione:

WHILE wyrażenie_logiczne DO instrukcja; (dopóki wyrażenie wykonuj instrukcje)

Sprawdzana jest wartość wyrażenia logicznego przed wykonaniem instrukcji. Jeżeli wartość tego wyrażenia jest TRUE (prawda - warunek został spełniony), zaczyna się wykonywanie listy instrukcji. Jeżeli wartością wyrażenia logicznego jest FALSE (fałsz), to wykonana zostanie kolejna instrukcja znajdująca się bezpośrednio po instrukcji WHILE.

2. Podstawowe instrukcje: przypisanie, złożenie, instrukcja warunkowa, pętla while

1. Przypisanie.

A:=B - A staje się B (zawartość zmiennej B zostaje przypisana do zmiennej B)

A:=2 - do zmiennej A zostaje przypisana wartość 2

2. instrukcja warynkowa

if ... then ...else

if A <> B then instrukcja1;

jeśli A jest różne od B to wykonaj ....

if A > 0 then

begin

instrukcja1;

instrukcja2;

end

else

begin

instrukcja3;

instrukcja4;

end;

jeśli A jest większe od 0 to wykonaj instrukcja1, instrukcja2 - w przeciwnym razie (jeśli A jest mniejsze lub równe 0) wykonaj instrukcja 3, instrukcja4;

c) pętla while

while A <> B do A := A + 1;

dopóki A jest różne od B wykonuj instrukcję A:=A+1;

while I > 0 do

begin

instrukcja1;

instrukcja2;

I:=I+1; // zwiększamy licznik pętli;

end;

Typy skalarne i okrojone i ich wykorzystanie.

Funkcje "skalarne"

Funkcje elementarne

Funkcje trygonometryczne

Funkcje specjalne

Typ okrojony

   Typ okrojony służy do ograniczania zakresu wartości dowolnego z typów porządkowych.

Definicja typu okrojonego :
    type identyfikator_typu = stała .. stała;

gdzie stała oznacza liczbę całkowitą, literał znakowy, literał logiczny, nazwę literału, identyfikator ze zbioru wartości typu wyliczeniowego lub wyrażenie stałe. Pierwsza z nich podaje ograniczenie dolne i nie może być większa od drugiej - ograniczenia górnego.

Przykład :

type	Dni tygodnia = (pon, wt, sr, czw, pi, so, nie);
	Dni_robocze = pon..pi;
	Wiek_dwudziesty = 1901..2000;
	Totto_Lotek = 1..49;
	Alfabet = 'A'..'Z';
var	Praca : Dni robocze ;
	Liczba : Totto_Lotek ;
	Rok : Wiek dwudziesty ;
	Litera : Alfabet ;

Typy skalarne i okrojone i ich wykorzystanie.

Typy wyliczeniowe i okrojone są typem danych, które mogą zostać zdefiniowane przez programistę.

Typ wyliczeniowy jest definiowany następująco:

type nazwa = (s₁, ..., s_k)

gdzie nazwą jest nazwa typu a s_i są identyfikatorami stałych, których wartości może przyjmować zmienna danego typu.

Np.

type

Meble = (stol, krzeslo, szafa);

var

m1,m2: meble;

( typ wyliczeniowy meble oraz zmienne m1, m2 typu wyliczeń)

Wartości typu wyliczeniowego nie można wczytać ani drukować w normalny sposób. Można je wykorzystywać w relacjach, funkcjach i instrukcjach przypisania.

Typ okrojony jest to podzbiór wartości typu całkowitego, znakowego, logicznego lub wyliczeniowego. Typ ten deklarujemy następująco:

type nazwa = min......max

gdzie nazwa- jest nazwą typu, min jest dolnym a max górnym ograniczeniem wartości, jakie może przyjmować zmienna typu okrojonego.

Np.

type

litera = `a'..'z'

tydzien = (pon,wt,sr,cz,pt,s,n);

robocze = pon..pt;

var l1,l2: litera; -----

dni: robocze; ------ zmienne typu okrojonego

z1,z2 : zakres ------

Typy te są typami porządkowymi. Można dla jednej zmiennej podać wartość poprzednią i następną.

Pojęcie tablic na przykładzie wybranego języka programowania.

PASCAL

Tablica jest to zbiór ustalonej liczby elementów tego samego typu. Niech np. tablica zawiera 20 elementów typu string. Deklarujemy ją normalnie, po słówku var:

var moja_tablica : array [1..20] of string;

Każdy element tablicy ma swój numer porządkowy. Są to numery 1-20, ale mogłyby być również 30-50  ( [30..50] ) albo w postaci liter ( ['A'..'Z'] ). Do poszczególnych elementów tablicy odwołujemy się przez ich numer porządkowy: nazwa_tablicy[nr]. I tak zamiast pisać dwadzieścia razy:

...

readln (car1);

readln (car2);

readln (car3);

readln (car4);

...

...i tak dalej, możemy szybciutko to załatwić w jakiejś pętelce. Np.:

...

for i:=1 to 20 do

readln (moja_tablica[i]);

...

W ten oto sposób możemy 20 zmiennych wpakować do 1.

Jest to tablica jednowymiarowa.

Można w Pascalu deklarować tablice dwu- i więcej wymiarowe.

Wyobraź sobie, że chcesz napisać grę w statki lub szachy. Szachownica ma 64 pola.

Nie trzeba deklarować 64 zmiennych.

Nie trzeba deklarować 8 tablic, każda po 8 elementów.

Wystarczy do tego jedna tablica! Robi się to w ten sposób:

var szachownica : array [1..8,1..8] of byte;

W nawiasach kwadratowych, oddzielając przecinkami, określamy ilość elementów każdego "wymiaru". Teraz gdy zechcę wypisać na ekranie zawartość komórki o współrzędnych [2,5] w naszej tablicy, wystarczy że napiszę:

write (szachownica[2,5]);

. Pojęcie tablicy na przykładzie wybranego języka

Deklarowanie tablicy

Tablica jednowymiarowa:

Tab :array [1..10] of integer;

Indeks	Wartość
1	...
2	...
3	...
4	...
...	...
...	...

Zadeklarowano tablice jednowymiarową o indeksie od 1 do 10. Tablica jest typu integer. Oznacza to że możemy do niej wpisać liczy całkowite mieszczące się w typie integer;

Przypisanie do tablicy

Tab[3]:=5;

Do tablicy Tab w pole o indeksie 3 wpisaliśmy liczbę 5

Odczytywanie wartości z tablicy

A:=Tab[3];

Do zmiennej A wpisaliśmy wartość z tablicy o indeksie 3;

Tablica wielowymiarowa

Tab :array [0..10,0..15] of real;

Zadeklarowano tablice dwuwymiarową o indeksie od 0 do 10 - pierwszy wymiar i od 0 do 15 - drugi wymiar

	0	1	2	3	4	5	...	15
0	...	...	...
1	...	...
2	...
3
4
...
10

Odwoływanie się do tablicy

A:=Tab[3,4];

Przypisanie do zmiennej A wartości z tablicy o indeksie w3, k4 (wiersz 3, kolumna 4);

Tablica może mieć także więcej wymiarów

Np. Tab 4 wymiarowa

Tab :array [0..10,0..10,0..10,0..10] of byte;

Pojęcie rekordów na przykładzie wybranego języka programowania.

PASCAL

Rekord to złożona struktura, którą dzielimy na części zwane polami. Każde pole może być zupełnie dowolnego typu, dzięki czemu np. każdy samochód możemy opisać na kilka sposobów:

var car : record

marka : string;

rocznik : integer;

kolor : string;

end;

Sytuacja jest podobna jak przy tablicach, jeśli chcemy np. wypisać rok produkcji na ekranie to piszemy: write (car.rocznik). Bardzo przydatna przy obsługiwaniu rekordów jest tzw. instrukcja wiążąca with. Spójrz:

...

car.marka:='Chevrolet Corvette';

car.rocznik:=1969;

kolor:='czerwony';

...

Wszystko jasne, a teraz:

...

with car do begin

marka:='Chevrolet Corvette'; {nawet prawdziwy Bill Gates}

rocznik:=1969; {chciałby mieć taką}

kolor:='czerwony'

end;

...

Oba przykłady robią dokładnie to samo, jednak wyobraź sobie gdybyśmy opisywali nasz samochód za pomocą 50 pól, a nie 3 (moc, pojemność, max. moment obrotowy itd

Definicja typu rekordowego zaczyna się identyfikatorem RECORD i kończy słowem END. Pomiędzy nimi podaje się listę składowych, nazywanych polami rekordu. Dla każdej składowej określa się jej identyfikator i typ.

Dostęp do zawartości poszczególnych składowych rekordu następuje poprzez podanie nazwy zmiennej rekordowej, kropki i nazwy składowej (pola).

Pojęcie plików na przykładzie wybranego języka programowania.

PASCAL

Kiedy napiszesz np. bazę danych wypadałoby, aby cała jej zawartość była zapisane gdzieś na dysku. Można by było odczytywać poszczególne elementy, dopisywać nowe... Bez tego nie można byłoby nazwać tego programu bazą. Aby utworzyć plik w Pascalu, musisz się zdecydować, jaka będzie jego zawartość. Może to być zwykły plik tekstowy, składający się z samych elementów typu word lub np. rekordów. Istnieje jeszcze typ niezdefiniowany czyli taki, który może naraz zawierać wiele elementów różnego typu (np. BMP). Taka definicja pliku jest niezbędna, gdyż komputer musi wiedzieć, jak interpretować zawartość takiego pliku. Rolę pośrednika między nami, a plikiem pełni pewna zmienna typu odpowiedniego dla danego pliku, np:

var plik1 :text; {plik tekstowy}

plik2 :file of byte; {plik z elementami typu byte}

plik3 :file of array [1..100] of word;

plik4 :file; {plik niezdefiniowany}

Można tutaj wymyślać naprawdę różne twory. Sama jednak zmienna jest nic nie warta. Musimy ją skojarzyć z odpowiednim zbiorem na dysku. Może to być również plik nieistniejący, jeśli zamierzamy dopiero go utworzyć. Do przypisania zmiennej konkretnego pliku służy procedura assign:

...

assign (plik1,'c:\autoexec.bat');

...

Od tej pory wszystkie operacje wykonywane na zmiennej plik1, będą wykonywane na pliku autoexec.bat. Oznacza to, że jeśli chcesz coś zrobić z plikiem, to używasz nazwy zmiennej, a nie nazwy pliku. Ponieważ nasz plik jest tekstowy, więc akurat pasuje do zmiennej plik1. Zanim jednak zaczniemy cokolwiek z nim wyrabiać trzeba ten plik otworzyć. I tutaj sposobów jest kilka. Jeśli, tak jak w naszym przypadku, plik jest tekstowy, to w zależności od potrzeb możesz użyć:

rewrite (zmienna) | zostanie utworzony nowiutki, pusty plik

reset (zmienna) | otwarcie już istniejącego pliku

append (zmienna} | jw. z tą tylko różnicą, że po otwarciu pliku

kursor zostanie ustawiony na jego końcu,

co umożliwia bezpośrednie dopisywanie tekstu

na jego końcu

read(P1,L)

write(P1,L) |zapisanie do pliku P1 zmiennych, których nazwy są wymienione na liście L

seek(P1,n) |wyszukiwanie składowej o numerze porządkowym równym n

close(zmienna) |zamknięcie pliku

Jeżeli mamy plik inny niż tekstowy, to stosujemy te same procedury poza append, która dotyczy tylko i wyłącznie plików tekstowych. Jeżeli chodzi o dwie pierwsze instrukcje, to możemy opcjonalnie dodać im drugi parametr, który określa rozmiar tworzonych zapisów. Jest to ważne szczególnie przy plikach niezdefiniowanych, gdyż wtedy domyślnie ustawiana jest wartość 128, co oznacza, że każdy zapis miałby długość 128 bajtów (byłoby to bardzo niepożądane). Do zapisu i odczytu stosujemy standardowe procedury read i write (w przypadku plików tekstowych również readln i writeln), spróbujmy zatem rozgryźć naszego autoexeca:

program showfile;

var plik : text;

linijka : string;

begin

assign (plik,'c:\autoexec.bat');

reset (plik);

repeat

readln (plik,linijka);

writeln (linijka)

until eof(plik);

close (plik)

end.

Widać jak na dłoni, że aby odczytać z pliku jakąś wartość to jako pierwszy parametr procedury read (tutaj readln) podajemy zmienną charakteryzującą plik.

Funkcja eof (end of file) sprawdza czy kursor jest na końcu pliku i jeśli, to zwraca wartość true. Na końcu programu zawsze powinno się zamykać pliki. Służy do tego procedura close (ostatni wiersz). Ten programik odczytywał poszczególne linijki pliku, ale można też (mowa cały czas o plikach wyłącznie tekstowych) odczytywać po kawałku, np. literami:

...

var litera : char;

...

read (plik,litera);

...

lub kilkuliterowymi porcjami:

...

var porcja : string[8];

...

read (plik,porcja);

...

Jednak nasze rozwiązanie wydaje się najrozsądniejsze, gdyż nie trzeba dodatkowo sprawdzać, czy kursor jest na końcu linijki i czy trzeba przejść do następnego wiersza. Problem ten nie występuje w plikach nietekstowych gdyż nie wyróżniamy w nich linijek (wszystko jest zapisane jakby w jednej), dlatego też nie możemy stosować readln'ów i writeln'ów. Oprócz znaków z plików tekstowych można również wyciągnąć liczby. Załóżmy, że w pierwszej linijce mamy jakąś liczbę z przedziału 0-65535:

var liczba : word;

plik : text;

begin

assign (plik,'bla.txt');

reset (plik);

read (plik,liczba);

close (plik)

end.

Na pewno zadziała. Jeśli byłoby nawet kilka liczb w tej samej linijce (pooddzielanych spacjami) to moglibyśmy je odczytywać do bólu i też by działało. A jak ma się sprawa z plikami innych typów (w końcu tekstowe odstawiamy na bok)? Też jest banalna. Załóżmy przykładową książkę telefoniczną:

program telefony_write;

type osoba = record {definiujemy własny typ}

nazwisko,

imie : string[20];

telefon : longint;

end;

var plik : file of osoba;

kto : osoba;

begin

assign (plik,'tel.dat');

rewrite (plik);

kto.nazwisko:='Jaworski';

kto.imie:='Bartosz';

kto.telefon:=2582408;

write (plik,kto);

kto.nazwisko:='Święty';

kto.imie:='Mikołaj';

kto.telefon:=0700123456;

write (plik,kto);

close (plik)

end.

Plik tel.dat zawiera teraz dwa rekordy z danymi. Teraz je odczytamy:

program telefony_read;

type osoba = record

nazwisko,

imie : string[20];

telefon : longint;

end;

var plik : file of osoba;

kto : osoba;

begin

assign (plik,'tel.dat');

read (plik,kto);

writeln (kto.nazwisko,' ',kto.imie,' - ',kto.telefon);

read (plik,kto);

writeln (kto.nazwisko,' ',kto.imie,' - ',kto.telefon);

close (plik)

end.

Chyba jasne. Jeżeli byśmy chcieli odczytać od razu drugi rekord to posłużylibyśmy się instrukcją seek:

...

seek (plik,1);

read (kto,plik);

writeln (kto.nazwisko,' ',kto.imie,' - ',kto.telefon);

...

Drugi parametr to numer elementu w pliku przy czym elementy są numerowane od zera. A jak dopisać do bazy jeszcze jedną osobę? Append odpada. Wystarczy jednak znać funkcję filesize, która zwraca rozmiar pliku (czyli ilość jego elementów). Dzięki temu możemy zastosować taki chwyt:

...

seek (plik,filesize(plik));

...

I już! To może zastąpić nam append.. Najgorzej jest z plikami niezdefiniowanymi (po prostu file). Tutaj  do zapisu i odczytu stosuje się procedury blockread i blockwrite, a przy otwieraniu takich plików trzeba też pamiętać aby do procedury np. reset dodać drugi parametr, o którym wspominałem na początku (na razie wystarczy jak podamy 1). Wtedy: blockread (plik,x,size) do zmiennej x wczyta taką porcję danych określiliśmy parametrem size (zazwyczaj jest to rozmiar zmiennej x). Blockwrite podlega tym samym zasadom. Bardziej szczegółowo przyjrzymy się tym instrukcjom przy innej okazji. Na koniec wspomnę jeszcze tylko o kliku instrukcjach, które się przydają:

filepos (zmienna) | zwraca pozycję kursora w pliku

eoln (zmienna) lub eoln | czy osiągneliśmy koniec linijki?

truncate (zmienna) | usuwa wszystkie elementy od aktualnej pozycji

kursora do końca pliku

erase (zmienna) | kasuje plik

Procedury i funkcje.

Głównymi przyczynami powszechnego stosowania procedur i funkcji są:

1. oszczędzenie czasu poświęconego na programowanie oraz otrzymywanie krótszych programów w przypadku gdy wyodrębniona w postaci funkcji lub procedury część programu powtarza się kilkakrotnie w różnych miejscach danego programu lub jest na tyle typowa, że warto ją umieścić w bibliotece funkcji 
   i procedur w celu wielokrotnego ich wykorzystania w innych programach;

2. zwiększenie czytelności i przejrzystości złożonych programów poprzez
   ich dekompozycię na mniejsze logiczne spójne części programu ;

3. efektywniejsze wykorzystanie pamięci wewnętrznej spowodowane dynamicznym przydziałem pamięci, polegającej na tym, że zmiennym lokalnym (tzn. zmiennym zadeklarowanym w bloku funkcji lub procedury) pamięć jest przydzielona
   w chwili wywołania funkcji lub procedury i zwalniana po ich wywołaniu. 

Procedura - jest to w skrócie pewien wyraz, który po wstawieniu do programu, coś nam wykona np. wyczyści ekran, narysuje linię (sformatuje dysk :) itd.

Funkcja - jest to podobnie jak procedura, pewien wyraz, który nie dość że coś wykona to również zwróci nam rezultat tego co zrobił, przykładowymi funkcjami są: pierwiastkowanie, sinus, cosinus. Zwracaną wartością niekoniecznie musi być liczba może to być również inny rodzaj zmiennych.

Różnica między procedurą, a funkcją jest taka, że funkcja potrafi zwrócić jakąś wartość.

W Pascalu istnieją dwa typy podprogramów: funkcje i procedury. Funkcje różnią się od procedur tym, że można je traktować jako wartość określonego typu (inaczej określa się to że funkcje zwracają wartość) - oznacza to że mogą występować w wyrażeniach. Przykładem znanych nam funkcji są funkcje SIN, COS, ORD itp.
Procedury traktowane są jako nowa instrukcja języka - nie mogą być używane w wyrażeniach.

Funkcje i procedury mogą mieć lub nie mieć parametrów. Ewentualne parametry przekazuje się w wywołaniu podprogramu w nawiasach okrągłych (np. x:= SIN(2*y)).

Deklaracja
Funkcje i procedury przed ich użyciem należy zadeklarować. Deklaruje się je w części deklaracyjnej programu (czyli pomiędzy słowem program a słowem begin) podobnie jak typy, zmienne i stałe. Deklaracja zaczyna się odpowiednio słowem kluczowym FUNCTION lub PROCEDURE. Podprogram ma strukturę analogiczną do programu - występuje w nim część deklaracyjna i część robocza (BEGIN...END;). W części deklaracyjnej podprogramu mogą być zadeklarowane te same elementy co w programie głównym, a więc w szczególności kolejne podprogramy!

Składnia deklaracji podprogramów:

PROCEDURE nazwa (parametr1:typ; parametr2 : typ;...);
część deklaracyjna
BEGIN
  instrukcje procedury
END;

Składnia deklaracji funkcji:

FUNCTION nazwa (parametr1:typ;parametr2:typ;...):typfunkcji;
część deklaracyjna
BEGIN
  instrukcje funkcji
END

Parametry funkcji i procedur przekazywane przez wartość
Kluczowym pojęciem w podprogramie są parametry podprogramu. W Pascalu można deklarować funkcje i procedury z parametrami jak i bezparametrowe. Deklaracje podprogramów bezparametrowych nie zawierają nawiasu z opisem parametrów.

Parametry definiuje analogicznie jak zmienne się poprzez podanie nazwy parametru (lub parametrów oddzielone przecinkami), a następnie po dwukropku określeniu typu parametrów. Definicje kolejnych parametrów separuje się średnikami.
Istotoną różnicą w stosunku do deklaracji zmiennych jest to, że w deklaracji parametrów formalnych podprogramów można używać tylko typów wcześniej zadeklarowanych (tzn. typów standardowych takich jak integer, real itp. lub zdefiniowanych samodzielnie deklaracja TYPE). Oznacza to, że nie można w parametrach procedury umieścić następującej deklaracji:

PROCEDURE COSTAM(X:ARRAY [1..3] OF REAL);

Aby zadeklarować taka procedurę należy zapisać następujące deklaracje:

TYPE
  TABLICA=ARRAY[1..3] OF REAL;

PROCEDURE COSTAM(X TTABLICA);

Parametry podprogramów zadeklarowane w ten sposób traktowane są jako zmienne lokalne (widoczne tylko w obrębie deklaracji podprogramu), których wartość początkowa określana jest w chwili wywołania podprogramu. Mogą one być swobodnie modyfikowane przez podprogram i nie wpływa to w żaden sposób na program główny. Parametry takie nazywa się „parametrami przekazywanymi przez wartość”.

Parametry przekazywane przez wskazanie
Jeśli w deklaracji parametrów podprogramu umieścimy słowo VAR to uzyskamy podprogram, który może wpływa na wartości zmiennych z programu głównego. Parametry przekazywane przez wskazanie tak naprawdę nie deklarują w podprogramie nowej zmiennej tylko pozwalają podprogramowi odwoływać się do zmiennych, które są aktualnymi parametrami wywołania podprogramu. Zastosowanie tego typu parametrów jest sposobem umożliwiającym podprogramowi zwracanie wartości do programu głównego!

Przykład deklaracji:

PROCEDURE UpStr(VARSTRING);
{ procedura zamienia wszystkie litery w zmiennej x na duże }
VAR
  i :INTEGER;
BEGIN
  FOR i := 1 TO LENGTH(i) DO
    x[i] := UpCase(x[i]);
END;

Wartości zwracane przez funkcję
Funkcja w odróżnieniu od procedury może być traktowana jak wartość typu określonego przy deklaracji funkcji. Aby funkcja zwracała wartość w jej ciele musi znaleźć się instrukcja przypisania nadająca zmiennej o takiej samej nazwie jak funkcja odpowiednią wartość. Nazwa funkcji jest specjalną zmienną (w ciele funkcji), którą można tylko zapisywać - użycie nazwy funkcji w wyrażeniu (np. po prawej stronie instrukcji przypisania) powoduje kolejne wywołanie funkcji, a nie odczytanie wartości tej zmiennej!

Przykład:

FUNCTION PotegaN(x:REAL; n:INTEGER):real;
{ funkcja wyznacza N-tą potęgę liczby x}
VAR
  i :INTEGER;
  wynik: REAL;

BEGIN
  wynik := 1.0;
  FOR i := 1 TO n DO
    wynik := wynik*x;
  PotegaN := wynik;
END;

. Procedury i funkcje.

Ogólna postać procedury jest następująca:

procedure nazwa (lista parametrów fubkcyjnych);

| {deklaracja stałych , typów i zmiennych}

begin

| {treść procedury}

end.

Po nazwie procedury lista parametrów formalnych może wystąpić lub nie. Wywołanie procedury polega na podaniu nazwy procedury wraz z listą parametrów aktualnych.

Parametry są łącznikiem między procedurą a programem głównym. Te parametry które są wyspecyfikowane w deklaracji procedury tzn. występują w nawiasach po słowie procedure nazywają się formalnymi. W momencie wywołania procedury parametry występujące w nawiasach po tej nazwie nazywają się aktualnymi.

Parametry mogą być przekazywane przez wartości lub adres. Przed parametrem przekazywanym przez adres musi być umieszczone słowo var . Przekazanie przez wartość polega na przekazaniu w momencie wywołania procedury wartości danego parametru, natomiast przekazanie przez adres polega na przekazaniu adresu danego parametru.

Różnice między tymi sposobami przekazywania parametrów polega na tym, że można zmienić i przekazać na zewnątrz wartości parametru przekazywanego przez adres. np.:

procedure suma (t : tablice; m,n: integer; var sum : integer);

var i,j : integer;

begin

sum:= 0

for i := 1 to m do

for j := 1 to n do

sum := sum + t [ i, j];

end.

Ogólna postać funkcji jest następująca:

function nazwa (lista parametrów formalnych); typ wyniku;

| {deklaracje stałych, zmiennych i typów}

begin

|treść funkcji

end.

W treści funkcji musi być umieszczone przypisanie

nazwa := wynik

gdzie wynik jest zmienną lub stałą określającą zwracaną wartość. Ponadto

nagłówek funkcji musi zawierać typ wyniku. Wywołanie funkcji ma postać:

zmienna := nazwa (lista parametrów aktualnych)

gdzie zmienna jest dowolną zmienną a nazwa nazwą funkcji. Np.:

fonction suma (t : teblice; m : integer; n: integer);

var

i, j, sum : integer;

begin

sum:= 0

for i:= 1 to m do

for j:=1 to n do

sum:= sum + t[i, j];

suma := sum;

end.

PROJEKTOWANIE SYSTEMÓW KOMPUTEROWYCH

Pojęcie systemu informacyjnego, system informacyjny a system informatyczny.

System informacyjny integruje działanie obiektu gospodarczego, obejmuje swoim zasięgiem całą jego działalność. Składa się z dwóch podsystemów: wytwarzania i zarządzania. Podstawowymi komponentami są: zbiór nadawców informacji, zbiór stosowanych metod i środków, zbiór informacji, zbiór odbiorców.

Podstawowym celem systemu jest: zbieranie, gromadzenie, przetwarzanie przechowywanie i przekazywanie decydentom informacji, służących podejmowanie przez nich racjonalnych decyzji i pomocy w sprawnym zarządzaniu.

W systemie informacyjnym procesy przetwarzania danych i procesy komunikacyjne mogą być realizowane ręcznie i automatycznie.

System informacyjny, w którym procesy przetwarzania danych i procesy komunikacyjne realizowane są technikami tradycyjnymi nazywamy tradycyjnym systemem informacyjnym, o systemie z zastosowaniem technik komputerowych mówimy, że jest to system informatyczny.

ADMINISTROWANIE SYSTEMAMI KOMPUTEROWYMI

Architektura systemów komputerowych.

Windows NT ma dwie podstawowe wersje: workstation ( ograniczone funkcje dostępne)i serwer (pełne funkcje) obie wersje mają to samo oprogramowanie lecz inną konfigurację.

Wersja serwer podzielona jest na dwie części:

sekcję systemową i użytkową ( jest to budowa modułowa)

Sekcja systemowa odwołuje się do sprzętu poprzez abstrakcyjne sterowniki.

W każdym serwerze najważniejszą częścią architektury jest podsystem dysków

Architektura systemów komputerowych

System operacyjny tworzy środowisko, w którym są wykonywane inne programy. Pod względem organizacji wewnętrznej systemy bardzo różnią się od siebie. Systemy operacyjne można oceniać pod względem:

• świadczonych przez system usług

• udostępnianemu interfejsowi dla użytkownika i programisty

• wzajemne połączenia systemów.

Zarządzanie procesami

Za proces można uważać program, który jest wykonywany. Aby wypełnić swoje zadanie proces musi korzystać z pewnych zasobów, takich jak: czas jednostki centralnej, pamięć, pliki, urządzenia wejścia-wyjścia. Wykonanie procesu musi przebiegać w sposób sekwencyjny. Jednostka centralna wykonuje instrukcje procesu jedna po drudiej, aż do jej zakończenia. Ponadto w dowolnej chwili na zamówienie procesu jest wykonywana najwyżej jedna instrukcja. Chociaż z jednym i tym samym programem mogą być związane dwa procesy, zawsze będzie się je uważać jako dwa oddzielne ciągi instrukcji. Proces jest jednostką pracy w systemie. W takim ujęciu system składa się ze zbioru procesów, z których część to procesy systemu operacyjnego. W odniesieniu do zarządzania procesami system operacyjny odpowiada za następujące czynności:

• tworzenie i usuwanie procesów użytkowników, jak i systemowych

• wstrzymanie i wznawianie procesów

• dostarczanie mechanizmów synchronizacji procesów

• dostarczanie mechanizmów komunikacji procesów

• dostarczanie mechanizmów obsługi zakleszczeń

Zarządzanie pamięcią operacyjną

Aby program mógł być wykonany, musi byś zaadresowany za pomocą adresów bezwzględnych oraz załadowany do pamięci. Podczas wykonywania programu rozkazy i dane są pobierane z pamięci za pomocą tych właśnie adresów bezwzględnych. Jeżeli chcemy uzyskać zarówno lepsze wykorzystanie jednostki centralnej jak i szybszą reakcję komputera na polecenia jego użytkownika, to musimy przechowywać kilka programów w pamięci operacyjnej. W odniesieniu do zarządzania pamięcią system operacyjny odpowiada za :

• utrzymywanie ewidencji aktualnie zajętych części pamięci wraz z informacją w czyim są władaniu

• decydowanie o tym, które procesy mają być załadowane do zwolnionych obszarów pamięci.

• Przydzielanie i zwalnianie obszarów pamięci stosownie do potrzeb.

Zarządzanie plikami

Zarządzanie plikami jest jedną z najbardziej widocznych części składowych systemu operacyjnego. Plik jest zbiorem powiązanych ze sobą informacji zdefiniowanych przez jego twórcę. W plikach przechowuje się programy ( zarówno w postaci źródłowej jak i wynikowej ) oraz dane. System operacyjny realizuje abstrakcyjny model plików przez zarządzanie nośnikami pamięci masowych, takich jak dyski, taśmy. Pliki są zazwyczaj zorganizowane w katalogi, co ułatwia ich użytkowanie. Poza tym. Jeżeli wielu użytkowników ma dostęp do plików, to może być pożądane sprawowanie pieczy nad tym, kto i w jaki sposób korzysta z tego dostępu.

W odniesieniu do zarządzania plikami system operacyjny odpowiada za :

• tworzenie i usuwanie plików

• tworzenie i usuwanie katakogów

• dostarczanie elementarnych operacji do manipulowania plikami i katalogami

• odwzorowanie plików na obszary pamięci pomocniczej

• składowanie plików na trwałych nośnikach pamięci.

Zarządzanie systemem wejścia-wyjścia

Jednym z celów systemu operacyjnego jest ukrywanie przed użytkownikiem szczegółów dotyczących urządzeń sprzętowych. Na przykład w systemie UNIX osobliwości urządzeń wejścia-wyjścia są ukrywane przed większością samego systemu operacyjnego przez tzw. Podsystem wejścia-wyjścia.

Zarządzanie pamięcią pomocniczą

Podstawowym zadaniem systemu komputerowego jest wykonanie programów. Podczas wykonywania programy oraz używane przez nie dane muszą znajdować się p pamięci operacyjnej. Ponieważ pamięć operacyjna jest za mała, aby pomieścić dane i programy system komputerowy musi mieć pamięć pomocmiczą będącą zapleczem pomięci operacyjnej. Większość systemów (współczesnych) posługuje się pamięcią dyskową.

W odniesieniu do zarządzania dyskami system operacyjny odpowiada za:

• zarządzanie obszarami wolnymi

• przydzielanie pamięci

• planowanie przydziału odszarów pamięci dyskowej

Praca sieciowa

System rozproszony jest zbiorem procesów, które nie dzielą pamięci, urządzeń zewnętrznych ani zegara. Procesory w systemie rozproszonym są zróżnicowane pod względem wielkości i funkcji. Są one ze sobą połączone za pomocą sieci komunikacyjnej, która może być skonfigurowana na wiele różnych sposobów. System rozproszony gromadzi fizycznie oddzielnie bądź w sposób spójny, umożliwiając użytkownikowi dostęp, różnorakie zasoby. Dostęp do zasobów dzielonych pozwala na przyśpieszenie obliczeń, zwiększenie osiągalności danych i podnoszenie niezawodności. W systemach operacyjnych dostęp sieciowy jest na ogół uogólniany pod postacią dostępu do plików.

System ochrony

Jeżeli system komputerowy ma wielu użytkowników i umożliwia współbieżne wykonywanie wielu procesów, to poszczególne procesy należy chronić przed wzajemnym oddziaływaniem. Muszą istnieć mechanizmy gwarantujące, że pliki, segmenty pamięci, procesor i inne zasoby będą użytkowane tylko przez te procesy, które zostały przez system odpowiednio ustawione. Ochrona jest mechanizmem nadzorowania dostępu programów, procesów lub użytkowników do zasobów zdefiniowanych przez system komputerowy. Mechanizm ten musi zawierać sposoby określania, co i jakiej ma podlegać ochronie, jak również środki wymuszenia zaprowadzonych ustaleń. Za pomocą działań ochronnych polegających na poszukiwaniu błędów ukrytych w interfejsach między składowymi podsystemami można polepszać niezawodność systemu.

System interpretacji poleceń

Jednym z najważniejszych programów w systemie operacyjnym jest interpreter poleceń będący interfejsem pomiędzy użytkownikiem a systemem operacyjnym. Niektóre systemy zawierają interpreter poleceń w swoim jądrze. W innych systemach (MS-DOS, UNIX) interpreter jest specjalnym programem, wykonywanym przy rozpoczynaniu zadania lub wtedy, gdy użytkownik rejestruje się w systemie (z podziałem czasu).

Polecenia rozpoznawane przez interpreter dotyczą : tworzenia procesów i zarządzania nimi, obsługi wejścia-wyjścia, administrowania pamięcią pomocniczą i operacyjną, dostępu do plików, ochrony i pracy sieciowej.

Usługi systemu operacyjnego

• wykonanie programu: System powinien móc załadować program do pamięci i rozpocząć jego wykonywanie. Program powinien móc zakończyć swoją pracę w sposób normalny lub z przyczyn wyjątkowych (sygnalizując błąd).

• Operacje wejścia-wyjścia: Wykonywany program może potrzebować operacji wejścia-wyjścia odnoszących się do pliku lub jakiegoś urządzenia. Poszczególne urządzenia mogą wymagać specyficznych funkcji. Ze względu na wydajność użytkownicy za zwyczaj nie mogą bezpośrednio nadzorować operacji wejścia-wyjścia, środki do realizacji tych czynności musi zapewnić system operacyjny.

• Manipulowanie systemem plików : System plików ma znaczenie szczególne. Nie podlega wątpliwości, że programy muszą zapisywać i odczytywać pliki. Jest również potrzebna możliwość tworzenia i usuwania zbiorów przy użyciu ich nazw.

• Komunikacja : Istnieje wiele sytuacji, w których procesy wymagają wzajemnego kontaktu i wymiany informacji. Są dwie podstawowe metody organizowania takiej komunikacji. Pierwszą stosuje się w przypadku procesów działających na tym samym komputerze; drugą - przy komunikowaniu się procesów w różnych systemach komputerowych, powiązanych ze sobą w sieci. Komunikacji może przebiegać za pomocą `pamięci dzielonej' lub przy użyciu techniki `przekazywania komunikatów', w której pakiety z informacjami są przemieszczane między sobą za pośrednictwem systemu operacyjnego

• Wykrywanie błędów: System operacyjny powinien być nieustannie powiadamiany o występowaniu błędów. Błędy mogą się pojawiać w działaniu jednostki centralnej i pamięci (sprzętowa wada lub awaria zasilania), w urządzeniach wejścia-wyjścia (błą parzystości na taśmie, awaria połączenia, brak papieru w drukarce) lub programie użytkownika (nadmiar arytmetyczny, próba sięgnięcia poza obszar pamięci programu). Na wszystkie rodzaje błędów system operacyjny powinien odpowiednio reagować, gwarantując poprawność i spójność obliczeń.

• Przydzielenie zasobów : jeżeli wiele użytkowników i wiele zadań pracuje w tym samym czasie, to każdemu z nich muszą być przydzielane zasoby. System operacyjny zarządza różnego rodzaju zasobami. Na przykład do określenia najlepszego wykorzystania z jednostki centralnej służą systemowi operacyjnemu procedury planowania podziału jednostki centralnej w zależności od szybkości procesora, zadań czekających na wykonywanie, liczby dostępnych rejestrów i innych czynników.

• Rozliczanie : Przechowywanie danych o tym, którzy użytkownicy i w jakim stopniu korzystają z poszczególnych zasobów komputera, jest kolejnym zadaniem systemu operacyjnego. Przechowywanie takich danych może służyć do rozliczania (aby można użytkownikom wystawić rachunki) lub po prostu dla gromadzenia informacji w celach statystycznych.

• Ochrona : Właściciele informacji przechowywanej w systemie skupiającym wielu użytkowników mogą chcieć kontrolować jej wykorzystanie. Gdy kilka oddzielnych procesów jest wykonywane współbieżnie, wówczas żaden proces nie powinien zaburzać pracy innych procesów lub samego systemu operacyjnego. Do zadań ochrony należy gwarantowanie nadzoru nad wszystkimi dostępami do zasobów systemu. Nie mniej ważne jest zabezpieczenie systemu przed niepożądanymi czynnikami zewnętrznymi. Zabezpieczenia tego rodzaju polegają przede wszystkim na tym, że każdy użytkownik, aby uzyskać dostęp do zasobów, musi uwierzytelnić w systemie swoją tożsamość, na ogół za pomocą hasła. Dalszym rozszerzeniem zabezpieczeń jest ochrona zewnętrznie zlokalizowanych urządzeń wejścia-wyjścia, w tym modemów, adapterów sieciowych.

Infrastruktura sprzętowa i programowa sieci komputerowych.

Infrastruktura sprzętowa (sieć fizyczna) jest tym co po prostu widać i co można wziąć do ręki: sprzęt. Są to komputery, zainstalowane w nich karty sieciowe, okablowanie, koncentratory, przełączniki itd.

Komputery i inne urządzenie sieciowe najczęściej są łączone w sieci parą skręconych przewodów nie ekranowanych lub kablami współosiowymi, podobnymi do tych używanych w telewizjach kablowych. Przewody lub kable dochodzą do gniazd na kartach sieciowych w komputerach, które to karty odpowiadają za wszelką komunikacje między danymi komputerami a resztą sieci.

W sieć mogą być łączone różne urządzenie komputerowe np. stacje robocze, serwery, drukarki sieciowe. Oprócz tych urządzeń występują też urządzenia specyficzne tylko dla sieci komputerowych: koncentratory, routery i mosty, okablowanie.

Sieci komputerowa nie może istnieć bez oprogramowania. Pierwszym i podstawowym programem ożywiającym sieć komputerową jest system operacyjny.

Z jednej strony to zbiór procedur umożliwiających komunikację ze sprzętem, zaś z drugiej - interfejs użytkownika. Systemy operacyjne należą do jednej z dwóch kategorii określających liczbę zadań, które komputer może wykonywać w danej chwili:

• systemy jednozadaniowe,

• systemy wielozadaniowe,

oraz do jednej z dwóch kategorii określających liczbę użytkowników, którzy mogą równocześnie pracować na danych komputerze:

• systemy jednoużytkownikowe,

• systemy z wielodostępem.

Rodzaje topologii sieci komputerowych :

a) magistrala: urządzenia sieciowe są podłączone szeregowo do liniowego systemu kablowego. Jeżeli odłączymy jeden komputer to cała sieć przestanie funkcjonować:

b) gwiazda: urządzenia sieciowe są podłączone do centralnych urządzeń, rozdzielających sygnały (np.: HUB, SWITCH). Mimo odłączenia jakiegokolwiek komputera sieć nadal będzie pracować:

c) pierścień: zbudowana jest w ten sposób, że wszystkie komputery połączone są kolejno ze sobą jednym przewodem, tworząc obwód zamknięty:

d) drzewo: pakiet wysyłany przez dowolną stację sieciową dociera, za pośrednictwem medium, do wszystkich stacji sieciowych, są tu możliwe gałęzie z wieloma węzłami.

Zarządzanie pamięcią, pamięć wewnętrzna, pamięć zewnętrzna, pamięć wirtualna.

Jednym z głównych zadań zarządzania pamięcią jest składowanie danych na dysku twardym -i w razie potrzeby- ponowne ich załadownie do pamięci. Część pamięci zostaje już zajęta zaraz po starcie.

Każdy komputer dysponuje ograniczoną pamięcią wirtualną, każdy użytkownik otrzymuje pewną część pamięci. Pamięć wewnętrzna jest stronicowana. Jeżeli w pamięci wewnętrznej brakuje jakiej strony to istniejąca strona usuwana jest na dysk, a potrzebna strona pobierana jest do pamięci wewnętrznej (symulacja pamięci wyższej niż jest dostępna).

Każdy proces otrzymuje 4GB pamięci wirtualnej z czego:

• 2 GB na potrzeby systemu,

• 2 GB na potrzeby użytkownika

Do pamięci wewnętrznej zaliczamy:

• ROM - pamięć stała - odczytywana w czasie startu komputera,

• RAM - pamięć operacyjna komputera pozwalająca nie tylko na odczytywanie z niej danych, ale na ich zmianę czyli zapisywanie. Wyłączenie zasilania powoduje bezpowrotną utratę całej zawartości pamięci RAM.

Do pamięci zewnętrznej zaliczamy: dyski twarde, dyskietki

Pamięć zewnętrzna jest pamięcią trwałą, informacje raz w niej zapisane mogą być wielokrotnie odczytywane. Dopuszczalny jest oczywiście ponowny zapis.

Systemy plików, metody dostępu do plików:

System plików to sposób organizacji twardego dysku. Zróżnicowane są one w zależności od systemu operacyjnego na jakim pracują.

Windows NT

Systemy operacyjny Windows NT może obsługiwać poniższe trzy systemy plików:

• File Allocation Table (FAT) - system plików tradycyjnie używany w systemie operacyjnym MS-DOS i w środowisku Windows 95/98. Nazwy plików są tu ograniczone do 8 znaków, kropki i 3 znaków tzw. rozszerzenia po kropce.

• High Prformance File System (HPFS) - system plików z długimi nazwami, stosowany macierzyście w systemie operacyjnym OS/2 firmy IBM i uwzględniony w wersji Windows NT 3.5. W wersji Windows NT 4.0 obsługi HPFS po cichu zaniechano.

• NT File System (NTFS) - własny system plików Microsoft'u, który miał za zadanie okazać się lepszy od HPFS. Oczywiście obsługiwane są długie nazwy plików (do 254 znaków). Istnieje możliwość wpółpracy z Windows 95/98, OS/2, systemem NFS z Uniksów, oraz AppleShare dla Macintoshy. Czyli system operacyjny NT prkatycznie współpracuje
  z dowolnymi plikami.

Unix

System pików Unix-a wygląda podobnie do systemu plików systemu DOS (właściwie to autorzy systemu DOS wzorowali się na Unix-ie, a nie na odwrót). Istnieje jedna zasadnicza różnica: każda partycja w systemie DOS jest oznaczona osobną literą, podczas gdy w systemie Unix wszystko jest jedną partycją. Innymi słowy w systemach Unix-owych istnieje tylko jeden wirtualny dysk logiczny zorganizowany w strukturę drzewiastą, a jego katalog główny jest oznaczony / . Wszystko jest tu podrzędne w stosunku do katalogu głównego, podczas gdy
w systemie DOS może być kilka niezależnych katalogów głównych poszczególnych dysków logicznych C:\, D:\, E:\ itd.

Organizacja dysków w Unix-ach jest w dużej mierze znormalizowana. Uporządkowana struktura katalogów ma także znormalizowane zestawy praw dostępu.

Sieciowe systemy operacyjne.

Sieciowy system operacyjny, patrząc z pozycji administratorów jest czynnikiem decydującym o wyborze oprogramowania zarządzającego sieciami i systemami, dlatego też poświęca mu się najwięcej uwagi. Systemy takie wykonują 3 główne operacje:

- przyjmowanie ostrzeżeń i alarmów wysyłanych przez obiekty w czasie rzeczywistym,

- transmisje poleceń do obiektów,

- cykliczne monitowanie urządzeń sieciowych.

Rynek sieciowych systemów operacyjnych dzieli się na dwie duże rodziny:

a) Oprogramowanie typu klient/serwer, jak Windows NT, Unix oraz Novell (obsługujące sieci złożone z kilkudziesięciu lub kilkuset stacji) - dalej można odwołać się do odpowiedzi na pytania: 51, 52 i 53, ponieważ są one kontynuacją tego zagadnienia.

b) oprogramowanie typu stacja do stacji (peer-to-peer, bez dedykowanego serwera) dla niewielkich konfiguracji sieciowych. Typowym przedstawicielem tej grupy jest LANtastic firmy Artisoft, ale Windows 95, 98 został również wyposażony w pewne, tego rodzaju funkcje i nieco neutralizuje różnice między dwiema grupami.

Sieciowe systemy operacyjne

Każda, nawet najlepiej zaprojektowana i wykonana sieć nie

będzie działała bez zastosowania jednego z wielu dostępnych obecnie

sieciowych systemów operacyjnych, które stanowią podstawę działania

serwerów.

Do zadań sieciowych systemów operacyjnych należy udostępnianie

w sieci plików i katalogów, wspólnych drukarek, modemów, zmieniaczy

płyt CD-ROM, aplikacji oraz baz danych. Korzystanie z poszczególnych

zasobów jest zwykle regulowane przez nadanie użytkownikom i stacjom

roboczym odpowiednich praw dostępu. Ponadto system sieciowy powinien

zapewniać możliwość porozumiewania się użytkowników ze sobą oraz

pozwalać na korzystanie z usług internetowych, przy zapewnieniu

bezpieczeństwa zasobów lokalnych.

Zadania te są wypełniane przez różne systemy w różny sposób

i na rozmaitym poziomie. Dobór najbardziej odpowiedniego zależy od

charakteru zastosowań, którym będzie służyła dana sieć lokalna, a

także od jej wielkości, mierzonej liczbą serwerów i stacji roboczych.

Do najbardziej znanych należą: NetWare firmy Novell, Windows NT Server

Microsoftu oraz Linux należący do rodziny systemów UNIX-owych.

Charakterystyka systemu Windows NT

Microsoft Windows NT (ang. Windows New Technology) to sieciowy system operacyjny firmy Microsoft, produkowany z myślą o wydajnych komputerach i zastosowaniach w przemyśle. W systemie Windows NT (wersja 4.0 oraz wersja 5.0) postawiono przede wszystkim na niezawodność systemu i bezpieczeństwo, oferując sprawdzony i bardzo wygodny interfejs użytkownika pochodzący ze środowiska Microsoft Windows 95 oraz pełną 32-bitowość. Wadą systemu jest słaba obsługa urządzeń i zaawansowany system plików NTFS niekompatybilny z urządzeniami używającymi Windows 95/98. Problematyczna jest również instalacja systemu, należy z góry wiedzieć jakim urządzeniom przysługują określone przerwania gdyś system nie wykryje tego automatycznie tak jak to ma miejsce w systemie Windows.

System Windows NT w wielu dziedzinach przewyższa inne systemy operacyjne (z rodziny Windows ).

Najważniejsze korzyści w tym systemie to:

1. Stabilność - można na nią narzekać (istnieje wiele systemów stabilniejszych od NT), ale prawda jest jedna: NT jest najstabilniejszym systemem z rodziny Windows. Jeżeli sprzęt jest sprawny, system (po zastosowaniu wszystkich środków bezpieczeństwa, poczynając od najnowszego Service Packa a kończąc na najświeższych hot fixach) nie ma prawa (teoretycznie) zawiesić się. Jeżeli nawet padnie jakaś aplikacja, jej zgon nie będzie miał wpływu na wszystkie inne pracujące w tym momencie - nawet na chwilę nie zatrzymają się. Taki poziom "niezawieszalności" nieznany jest użytkownikom innych wersji systemu Windows.
2. Przenośność - choć w tej chwili poważnie ograniczona (z dotychczas obsługiwanych platform Intela, Alphy, MIPSa i PowerPC zapowiadana jest obsługa jedynie Intela i Alphy), pozwala na pracę z tym samym środowiskiem graficznym na komputerach o różnej architekturze, a czasem nawet na uruchamianie tych samych aplikacji (często bez konieczności rekompilacji - poprzez emulację procesora Intela).
3. Skalowalność - system Windows NT robi znacznie lepszy użytek z porządnego sprzętu, niż jego mniejsi bracia. Jest jedynym systemem w rodzinie Windows obsługującym ponad jeden procesor. Dzięki dość skomplikowanemu systemowi zarządzania pamięcią potrafi przyspieszać nawet przy rozszerzaniu pamięci ponad 256MB.
4. Wielozadaniowość - o ile uruchamianie wielu aplikacji pod kontrolą Windows 95 to dopraszanie się kłopotów, to taka działalność w Windows NT jest normalną praktyką. NT bezbłędnie obsługuje setki wątków jednocześnie, rozdzielając je między wszystkie dostępne w systemie procesory. Jedyna niemiła cecha to zawieszanie wielozadaniowości przy każdym odwołaniu do pliku wymiany; problem ten można zredukować stosując dyski SCSI i usunąć instalując więcej pamięci operacyjnej.
5. Bezpieczeństwo - aczkolwiek NT w praktyce nie jest aż tak bezpiecznym systemem, to jednak kontrola dostępu do plików, audyty, zabezpieczenia przed atakami z sieci i stabilność jądra systemu czynią NT znacznie trudniejszym do "złamania" systemem niż pozostałe wersje Windows. Często jednak niestety bezpieczeństwo systemu poprawiają jego błędy - gdy superstabilne serwery stoją już otworem dla hackerów, serwer pracujący pod NT ciągle się opiera... ponieważ zawiesił się ;-)

6. Wydajność - chociaż jedynie w bardzo poważnych zastosowaniach, to jednak NT potrafi być szybszy od swych młodszych braci. W pełni 32-bitowa architektura systemu i system plików NTFS potrafią zapewnić oprócz większego bezpieczeństwa również znacznie szybszą pracę. Niestety, wiele prostych aplikacji nie może skorzystać z tych możliwości.
7. Pełna implementacja Win32 API - Windows NT 3.1 był pierwszą implementacją interfejsu programisty Win32 API i dlatego Windows NT cały czas wyprzedza Windows 95/98 w jakości tej implementacji. W przeciwieństwie do Windows 95/98 i dość już podstarzałego Windows NT 3.1, NT 4.0 zawiera wszystkie udokumentowane funkcje Win32 API, zarówno w wersji Multibyte, jak i UniCode (Windows 95 i 98 obsługują jedynie kilkanaście funkcji w wersji UniCode). Daje mu to przewagę w zastosowaniach wymagających obsługi wielu języków, grafiki trójwymiarowej i kontroli bezpieczeństwa.

Problemy najczęściej występujące to:

1. Wymagania sprzętowe - Minimum to komputer klasy PR-166 i co najmniej 48MB pamięci RAM.
2. Wydajność - nawet, na superwydajnym komputerze, w większości przypadków Windows NT będzie pracował tak samo szybko lub wolniej, niż Windows 98. Niestety, jest on znacznie bardziej skomplikowany i proste jednowątkowe aplikacje nie zajmujące wiele pamięci będą wolniejsze. Dopiero skomplikowane, wielowątkowe aplikacje korzystające z olbrzymich przestrzeni pamięci operacyjnej będą działały szybciej pod kontrolą NT (a dodatkowo będą mogły skorzystać z zainstalowanych dodatkowych procesorów).
3. Sterowniki - czysty komputer (bez drukarki, skanera, dużego monitora czy karty dźwiękowej) nie będzie miał żadnych problemów z obsłużeniem Windows NT. Problemy pojawią się dopiero w momencie dodawania urządzeń. Karta dźwiękowa powinna być zgodna z Sound Blasterem 16, drukarka z produktami firm Hewlett Packard lub Epson (i na pewno nie GDI), skaner najlepiej jeśli korzysta z szyny SCSI i jest znanego producenta.
4. Kompatybilność - wiele programów i gier przeznaczonych dla starszych wersji systemu Windows może nie działać w systemie Windows NT. Szczególne problemy sprawiają programy bezpośrednio odwołujące się do sprzętu - edytory dyskowe, gry, aplikacje korzystające z modemów, skanerów, portów i specyficznych kart rozszerzeń.
5. Brak możliwości aktualizacji Windows 95 - program instalacyjny Windows NT nie przewiduje możliwości aktualizacji systemów Windows 95 i 98. Jeżeli chcemy przesiąść się na NT, trzeba zainstalować od nowa wszystkie aplikacje. Ponadto, Windows NT nie obsługuje systemu plików FAT32, więc zarówno partycja zawierająca system, jak i partycja typu primary z której rozpoczynać się będzie ładowanie systemu muszą korzystać z systemu plików FAT16 lub NTFS.
6. Brak obsługi Advanced Power Management - w przypadku komputerów stacjonarnych to żadna strata, ale w przypadku notebooków uniemożliwia praktycznie wykorzystanie systemu Windows NT. APM nie będzie też obsługiwany przez przyszłe wersje NT - korzystać będą one jedynie z nowszego systemu ACPI.

7cena.

Charakterystyka systemu Windows NT Server.

Windows NT Server gwarantuje bezproblemową integrację na jednej platformie serwera poczty elektronicznej, serwera plików, baz danych i komunikacji. Działa z istniejącymi systemami, takimi jak NetWare, UNIX i komputery IBM typu mainframe. Jest też zgodny ze wszystkimi obecnymi protokołami sieciowymi, w tym TCP/IP, IPX/SPX, NetBEUI, AppleTalk, DLC, HTTP, SNA, PPP i PPTP. Jeśli chodzi o zgodność z oprogramowaniem klientów, jest najbardziej elastycznym z dostępnych systemów operacyjnych - pracuje z rozmaitymi systemami klientów, takimi jak: Windows 3.x, Windows 95, Windows NT Workstation, IBM OS/2 i Macintosh.

Usługa katalogowa Windows NT Directory Service (NTDS) może obejmować ponad
25 000 użytkowników w domenie i setki tysięcy użytkowników w firmie. Niezależnie od tego jak scentralizowana czy zdecentralizowana jest organizacja, usługa NTDS pozwala skonfigurować katalog adresowy dokładnie odpowiadający wymaganiom i zapewniający pełne zarządzanie zasobami, usługami i aplikacjami.

Windows NT Server jest sieciowym systemem operacyjnym z wbudowanym serwerem WWW. Za pomocą serwera IIS 2.0 można zdalnie administrować miejscami sieci WWW
z dowolnego komputera z zainstalowaną przeglądarką sieci.

Microsoft Windows NT

Microsoft Windows NT (ang. Windows New Technology) to sieciowy

system operacyjny firmy Microsoft, produkowany z myślą o wydajnych

komputerach i zastosowaniach w przemyśle. Występuje w dwóch

podstawowych wersjach: Workstation i Server. Wersja Workstation

przeznaczona jest dla stacji roboczych natomiast wersja Server dla

serwerów sieciowych. W systemie Windows NT postawiono przede wszystkim

na niezawodność systemu i bezpieczeństwo, oferując sprawdzony i bardzo

wygodny interfejs użytkownika pochodzący ze środowiska Microsoft

Windows 95 oraz pełną 32-bitowość.

Windows NT Server umożliwia dostęp do systemu operacyjnego i

usług aplikacyjnych na podstawie pojedynczej rejestracji (ang. login)

użytkownika. Zapewnia wysoki stopień bezpieczeństwa, realizowany

według tego samego modelu dla wszystkich usług sieciowych. Z punktu

widzenia administratora, zarządzanie użytkownikami, zasobami

sieciowymi (prawami dostępu), a także samym systemem i całą siecią

odbywa się w sposób wysoce zintegrowany, z jednej konsoli, za pomocą

interfejsu graficznego.

System sieciowy Microsoftu może także służyć jako serwer

aplikacji - większość używanych na świecie programów komercyjnych,

pracujących wcześniej pod innymi systemami, zostało przeniesionych na

platformę NT. Ponadto udostępnia on usługi routingowe oraz DNS -

serwer nazw domenowych, zapewniając przekład internetowych adresów

komputerowych ze "słownych" na "liczbowe" i odwrotnie,

na przykład: www.micros.com na 169.123.102.41. Serwer NT umożliwia

również zdalne startowanie bezdyskowych stacji roboczych, podobnie

jak w Novell NetWare. Windows NT daje się zintegrować z siecią

Novell NetWare oraz UNIX-ową, współpracuje też z systemami

Apple Macintosh. Wśród administratorów systemów zdania na temat

systemu Microsoftu są jednak podzielone. Niektórzy mówią o szybkim

spadaniu wydajności serwera, gdy liczba obsługiwanych przezeń stacji

wzrasta powyżej kilkunastu, innym nie podoba się duża "samodzielność"

systemu, który sam rozpoznaje sprzęt czy otoczenie sieciowe i stara

się skonfigurować wszystko automatycznie, nie zawsze z powodzeniem.

Niewątpliwą zaletą Windows NT jest jego spójność i kompatybilność z

szeroką gamą działającego wcześniej oprogramowania.

Charakterystyka systemu Unix

Ostatnimi czasy zaobserwować można coraz większy wzrost popularności darmowych sieciowych systemów operacyjnych rodziny UNIX (między innymi Linuxa). Systemy te ze względu na coraz większą ilość przeznaczonych dla nich aplikacji oraz możliwość darmowej eksploatacji stają się coraz poważniejszą konkurencją dla komercyjnych systemów sieciowych takich jak Microsoft Windows NT czy też Novell Netware.

Ponadto UNIX jako pierwszy z systemów na komputery PC zapewniał pracę za pośrednictwem sieci jak
i połączeń modemowych. W systemie zaszyta jest warstwa umożliwiająca komunikację z użytkownikami odległymi, którzy nawet nie zdają sobie z tego sprawy. Protokół komunikacyjny TCP/IP jest standardem, w wypadku sieci opartych o serwery UNIX'owe. Cała sieć Internet opiera się właśnie na tym protokole,
a najczęściej spotykanymi węzłami tej sieci są serwery UNIX'owe.

Zalety UNIX'a.

Najważniejszymi zaletami UNIX'a jest wielozadaniowość i wieloużytkowość. Wielozadaniowość oznacza, że użytkownik może wykonywać wiele zadań równocześnie, a co za tym idzie pracować bardziej efektywnie. Druga cecha: wieloużytkowość daje możliwość korzystania z zasobów komputera więcej niż jednej osobie, co wspomaga pracę grupową bez ponoszenia dużych kosztów zakupu pojedynczych komputerów.

Ale dlaczego UNIX jest takim ważnym systemem? Ponieważ można go uruchomić na prawie każdym komputerze (w przeciwieństwie do Windows NT). Istnieje wiele wersji systemu UNIX dla różnych typów komputera: począwszy od komputerów osobistych (IBM PC i Macintosh) poprzez komputery średniej wielkości (VAX firmy DEC) aż do superkomputerów firmy Cray. W praktyce są tylko dwa komputery,
na których niemożliwe jest uruchomienie tego systemu: starsze modele PC (np. PC XT) i systemy komputerowe do zadań specjalnych (np. AS/400).

Chyba najważniejszą jego zaletą jest przede wszystkim darmowy dostęp do samego systemu operacyjnego jak i dużej liczby przeznaczonych dla niego aplikacji. Dostępność darmowego oprogramowania serwerów WWW, FTP i poczty elektronicznej sprawia że możliwe jest stworzenie serwera internetowego przy wydatkach jedynie na sprzęt oraz połączenie z Internetem. Przy tym możliwość o wiele elastyczniejszej konfiguracji niż w przypadku systemów np. firmy Microsoft sprawia że taki system ma o wiele mniejsze wymagania sprzętowe niż równoważna instalacja oparta np. na Windows NT. Kolejną zaletą takich rozwiązań jest ich duża stabilność: wiele instalacji wykorzystujących te systemy może działać w sposób nie wymagający interwencji użytkownika latami, a nawet dość poważne zmiany konfiguracji systemu nie wymagają jego restartowania - nie wprowadzając tym samym zakłóceń w codziennej pracy, podczas gdy niewiele systemów działających w oparciu o Windows NT może się poszczycić nieprzerwaną pracą dłuższą niż 1 rok a nawet najmniejsza zmiana w konfiguracji systemu wymaga jego restartu tym samym zaburzając pracę wszystkich użytkowników korzystających z sieci.

Serwer sieci lokalnej

Wcale nie trzeba mieć połączenia z siecią Internet żeby w pełni wykorzystać zalety z posiadania darmowego systemu operacyjnego. Zarówno Linux jak i FreeBSD posiadają pakiety umożliwiające emulację podstawowych funkcji zarówno Windows NT jak i Novell Netware (m. in. udostępnianie plików oraz drukarek), co daje nie tylko możliwość stworzenia darmowego wariantu komercyjnego serwera sieciowego ale również pozwala połączyć w jednym serwerze funkcje zarówno Windows NT jak i Novell Netware przez co stacje robocze bez względu na to z jakiego protokołu korzystają mogą mieć dostęp do tych samych zasobów.

Hasła i zabezpieczenia,

System SCO UNIX spełnia wymagania bezpieczeństwa normy C2, ale dotyczy to tylko serwera pracującego samodzielnie, bez przyłączenia do sieci. W momencie zainstalowania karty sieciowej i włączenia serwera do jakiejkolwiek sieci, system staje się dostępny dla wszelkiego rodzaju operacji dokonywanych przez nie zawsze uczciwych ludzi.

Dlatego proces logowania jest bardzo restrykcyjny, gdyż nie wiemy czy podaliśmy źle nazwę użytkownika czy hasło, a jedynym stałym użytkownikiem jest root, czyli administrator. Przechwycenie jego hasła daje pełny dostęp do zasobów systemu, a co za tym idzie do plików użytkowników, jak również umożliwia manipulowanie ustawieniami systemu. Nie ma się co czarować, że ktoś kto zna hasło root'a nie skorzysta z okazji, aby się pobawić.

Następnym elementem bezpieczeństwa są hasła. Przy serwerze samodzielnym wystarczy je zmieniać co 30 dni, ale przy sieciowym zalecane jest raz w tygodniu. Hasło nie może zawierać imion i nazw własnych, różnego rodzaju dat, itp. Ale należy też wypracować własny system zmiany hasła i jego zapamiętywania. W niektórych systemach, administrator sam zmienia hasła użytkowników, dając im wykaz haseł np. na cały miesiąc. W tym przypadku administrator chroni własny system w przypadku obecności użytkowników, którzy używają jakiegoś programu, a w związku z tym nie mają dostępu do linii poleceń systemu.

Niektórych użytkowników może zdziwić fakt, że nie mogą korzystać z dyskietek lub innych nośników danych. To jest następny element systemu bezpieczeństwa. Użytkownik może dane przesyłać na swoje konto na serwerze wyłącznie z wykorzystaniem protokołu FTP. Związane jest to z tym, że napędy urządzeń zewnętrznych niosą potencjalne zagrożenie dla systemu związanie np. z odtwarzaniem danych przy ścieżkach bezwzględnych. Dlatego dostęp do tych urządzeń ma tylko administrator i/lub osoba odpowiedzialna za wykonywanie kopii bezpieczeństwa. Właściwie to administrator rzadko korzysta z napędów urządzeń zewnętrznych, gdyż większą część swojej pracy wykonuje ze stanowiska zdalnego.

Bodajże najważniejszym elementem bezpieczeństwa systemu jest sam system i jego odporność na różnego rodzaju działania użytkowników. Nawet jeżeli jakiś domorosły majsterkowicz złapie konto użytkownika, to ze względu na przydzielone prawa (a raczej ich brak) nie za wiele może zdziałać.

Wady.

Wady omawianych tu systemów to przede wszystkim brak jednolitej metody instalacji i konfiguracji systemu. Nawet w przypadku dystrybucji które zostały zaopatrzone w przyjazne użytkownikowi programy do instalacji i konfiguracji systemu nie da się za pomocą tych programów wykorzystać w pełni potencjalnych możliwości systemu. Oznacza to że do wykonania stabilnej i poprawnie działającej instalacji wymagana jest osoba posiadająca pewną wiedzę związaną z tymi systemami.

Charakterystyka systemu UNIX.

System operacyjny mający strukturę warstwową.

• użytkownicy

• programy użytkowe

• funkcje systemowe (open, exit, itd.)

• jądro systemu UNIX (zarządzanie pamięcią, procesorami, urządzeniami, system plików)

• sprzęt (procesory, pamięć dyski, terminale)

Cechy:

• wielodostępność - liczba użytkowników zależy głównie od mocy obliczeniowej sprzętu

• wieloprocesowość (wielozadaniowość) - jednostkami aktywnymi w systemie są procesy pracujące współbieżnie, przy wykorzystaniu różnych mechanizmów synchronizacji i komunikacji

• hierarchiczny system plików, z jednolitym potraktowaniem plików zwykłych, katalogów i plików opisujących urządzenia zewnętrzne

• wykonywanie operacji wejścia/wyjścia niezależnie od typu urządzeń zewnętrznych

• duża liczba programów narzędziowych (Basic, C, Pascal)

• duża liczba programów usługowych

• przenoszenie oprogramowania systemowego dzięki zapisowi w języku C.

UNIX

Jest to system najstarszy i najtrudniejszy do opanowania, a jednocześnie oferujący ogromne możliwości konfiguracyjne, bardzo wysoki poziom zabezpieczeń przed nieautoryzowanym dostępem do zasobów sieci oraz niespotykaną w innych systemach stabilność pracy. Jest powszechnie stosowany na serwerach internetowych. Pracuje on w trybie znakowym czyli tak jak znany chyba wszystkim Microsoft DOS. Jest przeznaczony wyłącznie dla sieci Client-Server.

UNIX zaprojektowany jest pod kątem obsługi dużych serwerów.

Ma wbudowane mechanizmy do pracy w sieci, jest wielozadaniowy (wykonuje wiele programów jednocześnie) i wielodostępny (wielu użytkowników na raz). W instalacjach sieciowych bazujących na

platformie UNIX-owej realizuje się współdzielenie zasobów dyskowych i urządzeń peryferyjnych, obsługę wielu zaawansowanych aplikacji o architekturze klient-serwer.

System może być wyposażony w narzędzia bezpieczeństwa - od haseł użytkowników i sterowanych praw dostępu do zasobów, po szyfrowane kanały komunikacyjne, w których przesyłane przez łącza

sieciowe dane są kodowane przed wysłaniem przez jeden z komputerów i dekodowane po odebraniu przez drugi, co zapobiega "podsłuchiwaniu" przez hackerów.

UNIX sprzedawany jest zazwyczaj wraz z komputerami, często w ramach całościowej instalacji sieciowej "pod klucz". Służy wówczas do obsługi sieci i aplikacji typu bazy danych. Najbardziej znane

oprogramowanie obsługujące bazy danych w architekturze klient-serwer, jak na przykład produkty firm Oracle czy Informix, posiada implementację na wszystkie platformy UNIX-owe. Pod kontrolą UNIX-a

pracują zwykłe pecety oraz najpotężniejsze na świecie, wieloprocesorowe superkomputery.

UNIX jest standardowo wyposażony w narzędzia komunikacyjne, a jego włączenie do sieci jest stosunkowo proste, przy czym nie ma znaczenia czy jest to sieć lokalna, czy Internet. Administrator UNIX-a musi posiąść sporą porcję wiedzy o systemie. Specyfika poszczególnych odmian UNIX-a, zwłaszcza na poziomie zaawansowanych narzędzi do zarządzania powoduje, że niemal każdej odmiany systemu trzeba się osobno nauczyć.

Sieci oparte na serwerach UNIX-owych stosowane są w dużych, bogatych firmach i instytucjach. W wersjach komercyjnych są to rozwiązania kosztowne. Jednak UNIX potrafi efektywnie wykorzystać moc i szybkość przetwarzania silnych maszyn, zaś serwery oferują wysoką stabilność i niezawodność pracy, co ma istotne znaczenie w niektórych zastosowaniach.

Charakterystyka systemu Novell

System operacyjny NetWare/intranetWare firmy Novell jest przeznaczony dla serwerów sieciowych sieci LAN/WAN czy Internet/Intranet. Może być wykorzystywany jako serwer dostępowy do sieci Internet, jako serwer plików i drukowania. Cechuje go ogromna stabilność i możliwości. Jest to system bardzo prosty w instalacji i administrowaniu. Po stronie stacji roboczej Novell wyposażył swój system w wiele potężnych narzędzi do administrowania całą siecią z jednego miejsca. Również po stronie serwera jest wiele doskonałych narzędzi do zarządzania serwerem jak i cała siecią.

Novell daje administratorowi możliwość zdalnej administracji systemu (to znaczy gdy nie mamy fizycznego dostępu do serwera. Serwer znajduje się np. w innym budynku czy pomieszczeniu ) a mamy tylko jeden monitor. Wprawdzie większość czynności administracyjnych wykonujemy przy pomocy programu NetWare Administrator na stacji roboczej ale są pewne rzeczy wymagające dostępu i bardziej bezpośredniego kontaktu z serwerem. Można to wykonywać przez tak zwaną Remote Console. Jest to nic innego jak przechwycenie ekranu i klawiatury odległego serwera. Pozwala to nam na wykonywanie wszystkich tych czynności które możemy robić siedząc bezpośrednio przy serwerze. Konfigurowanie zdalnego dostępu jest bardzo proste.

Poza tym Novell jak, przystało na sieciowy system operacyjny jest systemem wielozadaniowym i wieloużytkowym, ponadto oferuje dobrą stabilność oraz bezpieczeństwo systemu. A wymagania sprzętowe dla serwera są niewielkie, system może pracować już przy takiej konfiguracji serwera:

Procesor: 486DX

100 MHz

Pamięć: min. 20 MB
Dysk: min. 120 MB - 150 MB na partycję DOS'ową i 100 MB na NetWare'owy volumen sys. To oczywiście tylko minimalna ilość miejsca wymagana przez system operacyjny, jak ma się zamiar coś przechowywać na dysku serwera to musi on być odpowiednio duży.
Karta sieciowa: zgodna ze standardem NE2000, czyli jakaś najtańsza, w serwerze powinna być jednak karta o nieco lepszych parametrach.
Karta graficzna: VGA 1 MB
Stacja dyskietek: 3,5" 1,44 MB
CD-ROM: zgodny z IDE.

Charakterystyka systemu Novell.

Sieciowy system operacyjny - można go użyć do budowy dużej jak i małej sieci komputerowej. Może być trochę skomplikowany podczas instalacji i przygotowania do pracy, ale jest obecnie najpopularniejszym sieciowym systemem informacyjnym. NetWare sam jest sieciowym systemem operacyjnym dla serwera plików.

Buforowanie danych - przechowywanie w pamięci komputera właśnie czytanych danych z dysku, w nadziei że będą one potrzebne powtórnie. Jeśli się tak stanie nie trzeba odwoływać się do dysku tylko do pamięci.

Haszowanie („oznaczanie”)katalogów - jest skutecznym sposobem odszukiwania katalogów na dysku.

Przeszukiwanie taśmowe - sposób na poprawienie dostępu do dysku twardego w serwerze.

System tolerancji błędów (SFT) - pozwala na pracę w sieci nawet przy awariach sprzętowych.

Novell NetWare

Produkt firmy Novell Incorporated. Oferuje wysoki poziom stabilności pracy i bezpieczeństwa. System Novell NetWare jest obecnie najpopularniejszym systemem sieciowym dla małych, średnich i dużych przedsiębiorstw. Oferuje bardzo duże możliwości zarządzania zasobami sieci powiązane z rewelacyjną wydajnością. Obsługuje systemy wieloprocesorowe co pozwala administratorom na budowę centralnych baz danych bez poświęcania wydajności sieci na rzecz łatwego dostępu do danych.

Pracujący na dedykowanym serwerze Novell NetWare (w wersji od 4.11) oferuje, oprócz tradycyjnych usług w rodzaju współdzielenia plików czy drukarek, także inne, jak routing (dostarczanie danych przez sieć do miejsca przeznaczenia po najlepszej drodze), zarządzanie siecią, zintegrowaną obsługę TCP/IP oraz publikowanie w Internecie (udostępnianie informacji w postaci stron WWW). Zapewnia przy tym ochronę bezpieczeństwa pracy i zasobów użytkowników na wysokim poziomie. Mechanizmy NDS (Novell Directory Services) ułatwiają bezpośredni, szybki dostęp do zasobów sieci bez względu na ich lokalizację. Natomiast rozbudowane mechanizmy zabezpieczeń i kontroli pozwalają na zachowanie poufności danych, szczegółowe regulowanie praw dostępu do zasobów sieciowych, monitorowanie użytkowników itp. Serwer NetWare umożliwia także podłączenie bezdyskowych stacji końcowych, które czytają programy startowe bezpośrednio z serwera. Przeznaczony jest wyłącznie dla sieci Client-Server zarówno LAN jak i MAN oraz WAN.

3

---