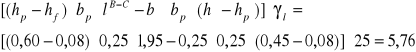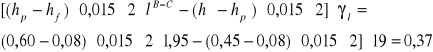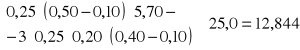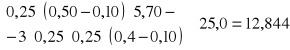Politechnika Koszalińska

Wydział Budownictwa i Inżynierii Środowiska

KATEDRA KONSTRUKCJI BETONOWYCH

ĆWICZENIE:

Budynek wielopiętrowy
o konstrukcji półszkieletowej

w wersji monolitycznej

SPRAWDZIŁ:

Dr inż. W. Borjaniec

WYKONAŁA:

Agnieszka Pająk B4Z

KOSZALIN, 2011R.

1. PŁYTA

DANE PROJEKTOWE :

- Długość L = 26,00 m

- Szerokość S = 16,85 m

- Ilość kondygnacji n = 2

- Obciążenia użytkowe q = 6,0 kN/m²

- Wysokość kondygnacji H = 4,2 m

- Podłoże gruntowe G

- Śnieg I strefa

Beton klasy C20/25:

fck=20,0MPa	fctk=1,5MPa	fctm=2,2MPa
fcd=13,3MPa	fctd=1,0MPa	Ecm=30*10^3MPa

Zbrojenie płyty stropu - stal klasy A-0 (St0S-b):

fyk=220MPa

fyd=190MPa

ftk=300MPa

ξeff,lim=0,63

Es=200*10^3MPa

Obliczenia płyty

1. przyjęcie przekroju żebra

przyjmuję h = 45cm

;
przyjmuję b =25cm

2. grubość płyty h_f = 8cm

3. rozpiętość w świetle

- przęsło skrajne

- przęsło środkowe

ZESTAWIENIE OBCIĄŻEŃ

Rodzaj obciążenia	Obciążenia charakterystyczne kN/m
OBCIĄŻENIA STAŁE
LASTRYKO	0,44
SZLICHTA CEMENTOWA	1,26
PŁYTA ŻELBETOWA	2,00
TYNK	0,285
II. OBCIĄŻENIA ZMIENNE

Przyjmuję wzór 6,10b

Obciążenia stałe obliczeniowe

Obciążenia zmienne obliczeniowe

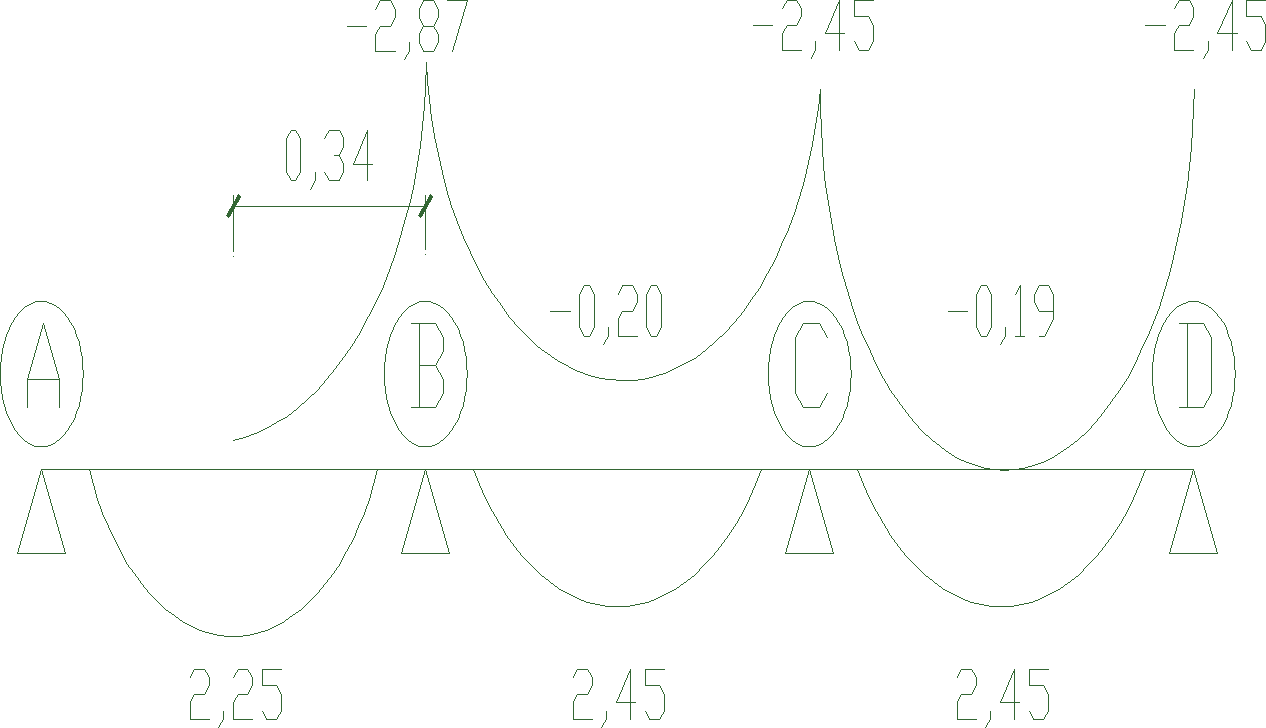
WYZNACZENIE SIŁ WEWNĘTRZNYCH W PŁYCIE (METODA PLASTYCZNEGO WYRÓWNANIA MOMENTÓW).

1. momenty przęsłowe i podporowe

2. moment minimalny w przęśle B-C

Obciążenie zastępcze:

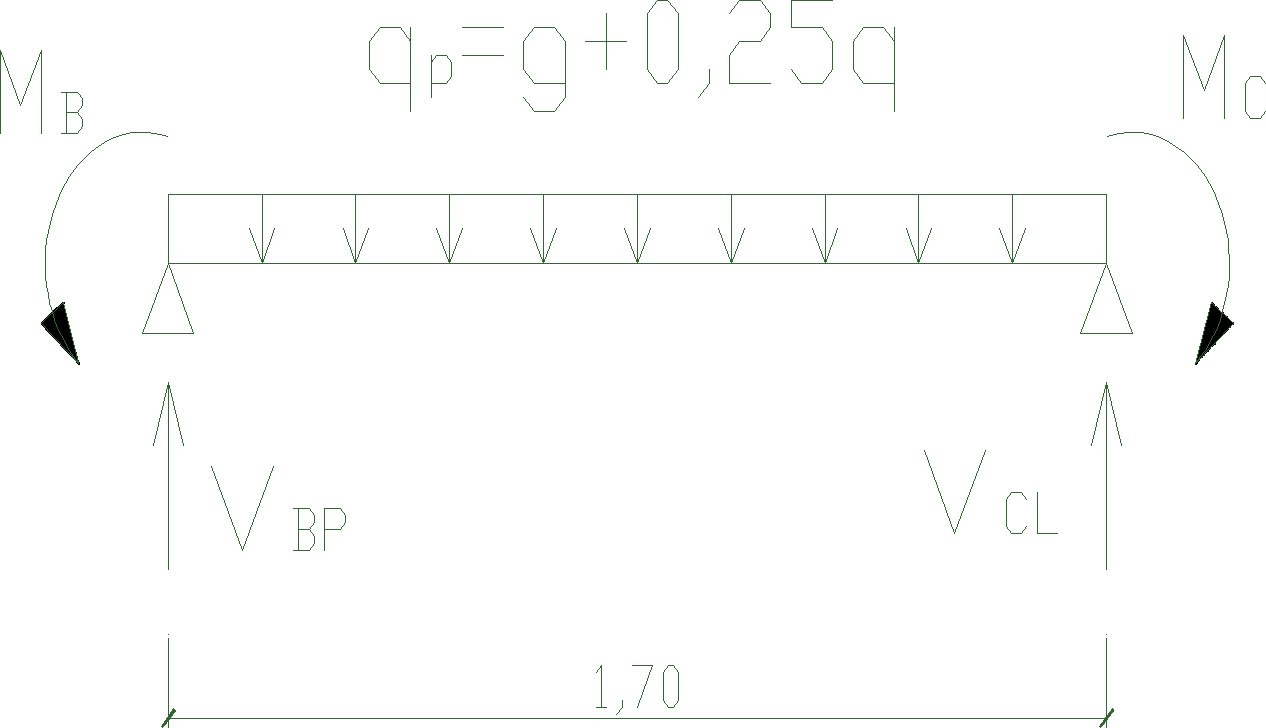
zasięg α_AB:

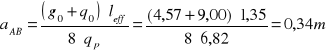
Wyznaczenie reakcji podporowych

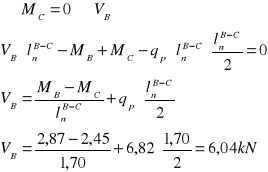
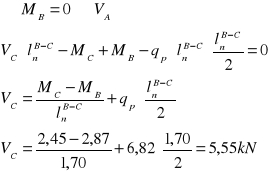
Równanie sił tnących i momentów zginających

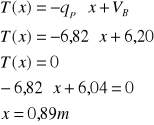
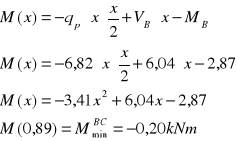
Wyznaczenie reakcji podporowych

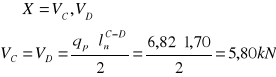
Równanie sił tnących i momentów zginających

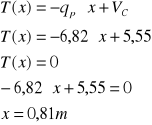
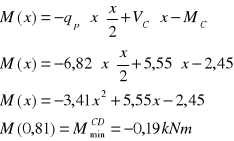
3. siły poprzeczne

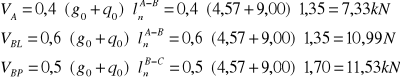
WYMIAROWANIE Z UWAGI NA ZGINANIE

a)Otulenie

Założenie

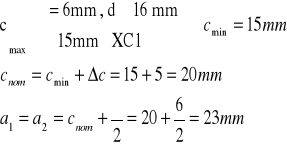
b) Wysokość użyteczna

c) Zbrojenie minimalne

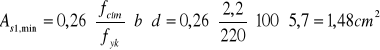
Zbrojenie przęsłowe

PRZĘSŁO A-B

M = 2,25kNm

PRZĘSŁO B-C M = 2,45kNm

Zbrojenie podporowe

PODPORA B M = 2,87 kNm

PODPORA C

M = 2,45kNm

Zbrojenie przęsłowe dla momentów minimalnych

PRZĘSŁO B-C

M = 0,20kNm

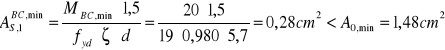
Przyjęte zbrojenie płyty:

Przęsło AB ø4,5/6 co 9 cm →

Przęsło BC ø4,5/6 co 9 cm →

Podpora B ø6 co 9 cm →

Podpora C ø4,5/6 co 9 cm →

Z uwagi na momenty minimalne:

Przęsło BC ø6 co 18 cm →

Przęsło CD ø6 co 18 cm →

WYMIAROWANIE Z UWAGI NA ŚCINANIE

PODPORA A

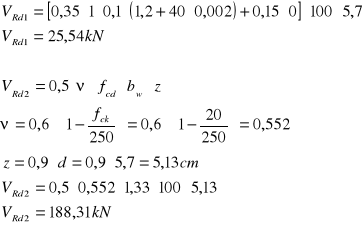
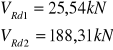
Zbrojenie przęsłowe doprowadzone do podpory należy przedłużyć poza jej krawędź o 10Ø=10x4,5/6=45/60mm, lecz nie mniej niż 100mm.

PODPORA B

>

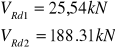
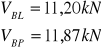
Zbrojenie przęsłowe doprowadzone do podpory należy przedłużyć poza jej krawędź o 10Ø=10x4,5/6=45/60mm, lecz nie mniej niż 100mm.

RYSY PROSTOPADŁE

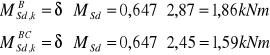
Maksymalna średnica zbrojenia płyty, przy której nie zostanie przekroczona wartość w_lim:

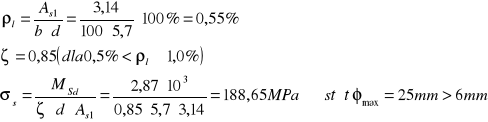
UGIĘCIE METODA UPROSZCZONA.

- przęsło skrajne

dla ρ_l ≤ 0,5%

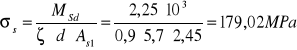
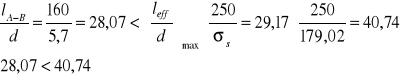
- przęsła środkowe

dla ρ_l ≤ 0,5%

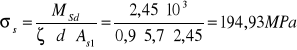
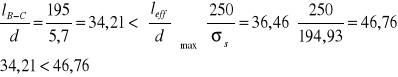
Stosunek rozpiętości l_eff do wysokości użytecznej d nie przekracza wartości dopuszczalnych, więc nie ma konieczności sprawdzania ugięć metodą dokładną.

2. ŻEBRO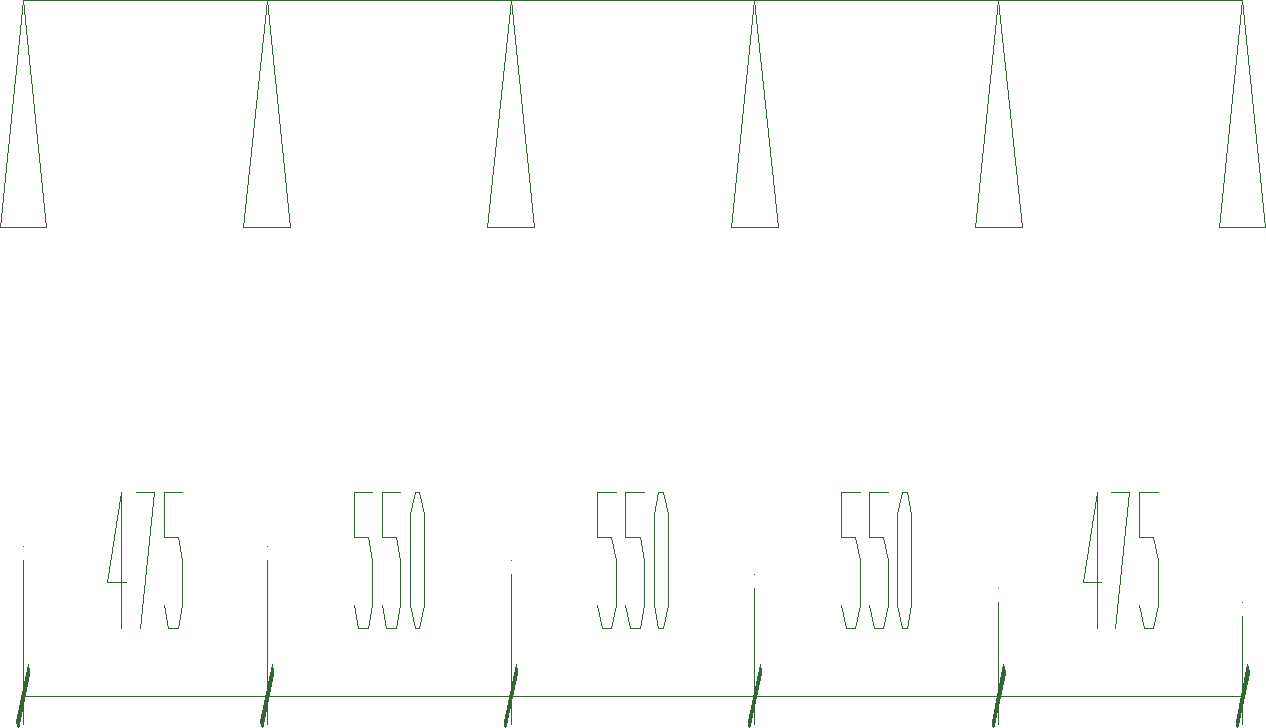
Beton klasy C20/25:

fck=20,0MPa	fctk=1,5MPa	fctm=2,2MPa
fcd=13,3MPa	fctd=1,0MPa	Ecm=30*10^3MPa

Strzemiona - stal klasy A-0 (St0S-b):

fyk=220MPa

fyd=190MPa

ftk=300MPa

ξeff,lim=0,63

Es=200*10^3MPa

Zbrojenie podłużne - stal klasy A-III (34GS):

fyk=410MPa

fyd=350MPa

ftk=550MPa

ξeff,lim=0,53

Es=200*10^3MPa

Wstępne określenie wymiarów podciągu:

Przyjmuję h =60cm

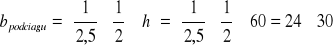
Przyjmuję b =25cm

Przęsło skrajne

Przęsła środkowe

ZESTAWIENIE OBCIĄŻEŃ DZIAŁAJĄCYCH NA ŻEBRO

Rodzaj obciążenia	Obciążenia charakterystyczne kN/m
I Obciążenia stałe
1) OBCIĄŻENIA Z PŁYTY	7,771
CIĘŻAR ŻEBRA	2,313
3) CIĘŻAR TYNKU NA ŻEBRZE	0,282
II Obciążenia zmienne

Obciążenia stałe obliczeniowe

Obciążenia zmienne obliczeniowe

WYZNACZENIE SIŁ WEWNĘTRZNYCH WG TABLIC WINKLERA

WYMIAROWANIE Z UWAGI NA ZGINANIE

Otulenie

- Dołem

Założenie

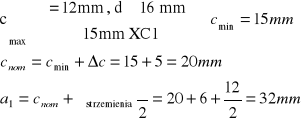
- Górą

Założenie

Wysokość użyteczna

ZBROJENIE PRZĘSŁA AB

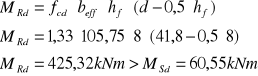
Przekrój pozornie teowy

ZBROJENIE PRZĘSŁA BC

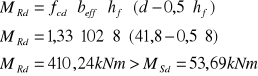
Przekrój pozornie teowy

ZBROJENIE PRZĘSŁA CD

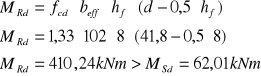
Przekrój pozornie teowy

ZBROJENIE PODPORY B

- dla momentu w osi podpory

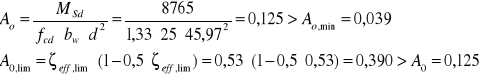
- dla momentu krawędziowego d = 41,8cm

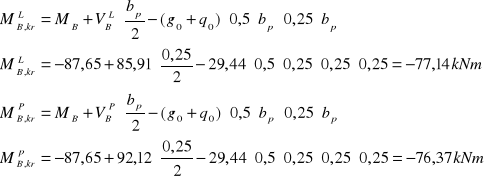
dla momentu

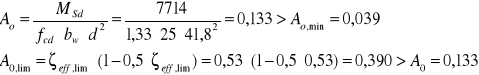
ZBROJENIE MINIMALNE W PRZĘŚLE BC

ZBROJENIE PODPORY C

- dla momentu w osi podpory

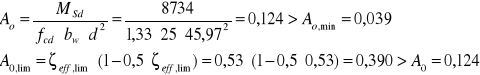
- dla momentu krawędziowego d = 41,8cm

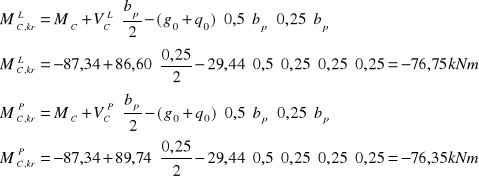
dla momentu

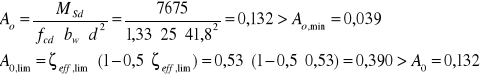
ZBROJENIE MINIMALNE W PRZĘŚLE CD

Przyjęto następujące zbrojenie: 1 x ø12mm = 1,13cm²

Przęsło A-B 4,22cm² dołem A_S = 4 x ø12mm = 4,52cm²

górą A_S = 2 x ø12mm = 2,26cm²

Przęsło B-C 3,74cm² dołem A_S = 4 x ø12mm = 4,52cm²

Zbrojenie min B-C 1,32cm² górą A_S = 2 x ø12mm = 2,26cm²

Przęsło C-D 4,33cm² dołem A_S = 4 x ø12mm = 4,52cm²

Zbrojenie min C-D 0,46cm² górą A_S = 2 x ø12mm = 2,26cm²

Podpora B 5,84cm² górą A_S = 6 x ø12mm = 6,79cm²

Podpora C 5,82cm² górą A_S = 6 x ø12mm = 6,79cm²

WYMIAROWANIE Z UWAGI NA ŚCINANIE.

PODPORA A

Wymiarowanie zbrojenia

- belka zginana bez udziału siły podłużnej,

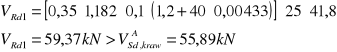
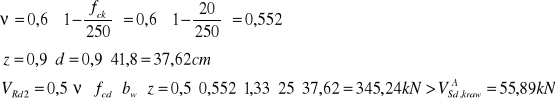
Rozstaw strzemion na odcinku pierwszego rodzaju

Przyjęto s₁=30cm

Sprawdzenie nośności zbrojenia podłużnego na krawędzi podpory

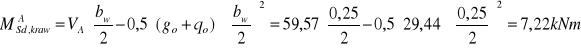
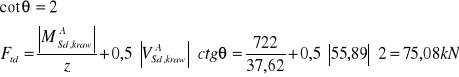
Nośność jest zachowana.

Długość zakotwienia

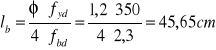
Obliczeniowa długość zakotwienia

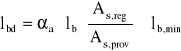
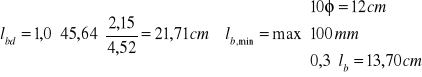
Pręty zbrojenia przęsłowego wprowadzono poza krawędź podpory A na głębokość 22cm

Sprawdzenie nośności zbrojenia podłużnego w osi teoretycznego punktu podparcia

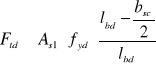
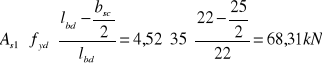
PODPORA B Z LEWEJ STRONY

Wymiarowanie zbrojenia.

- belka zginana bez udziału siły podłużnej

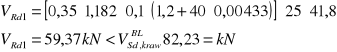
Element należy podzielić na odcinki drugiego rodzaju

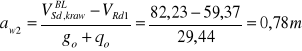
strzemiona dwucięte ø 6mm A_Sw1 = 0,56cm²

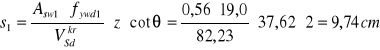
Przyjęto n = 10 w rozstawie

Sprawdzenie warunków normowych odnośnie stopnia zbrojenia strzemionami na odcinku drugiego rodzaju

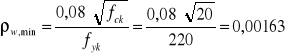
Sprawdzenie szerokości rozwarcia rys ukośnych

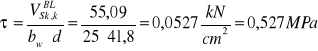
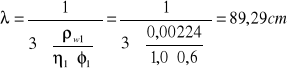
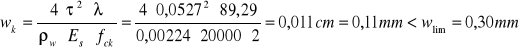
Szerokość rozwarcia rys ukośnych nie przekracza wartości granicznej

PODPORA B Z PRAWEJ STRONY

Wymiarowanie zbrojenia.

- belka zginana bez udziału siły podłużnej

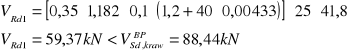
Element należy podzielić na odcinki drugiego rodzaju

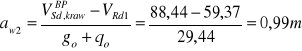
strzemiona dwucięte ø 6mm A_Sw1 = 0,56cm²

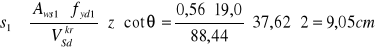
Przyjęto n = 12 w rozstawie

Sprawdzenie warunków normowych odnośnie stopnia zbrojenia strzemionami na odcinku drugiego rodzaju

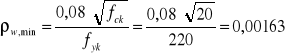
Sprawdzenie szerokości rozwarcia rys ukośnych

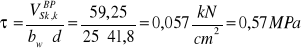
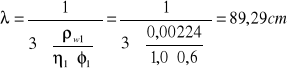
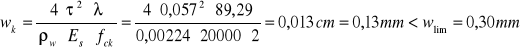
Szerokość rozwarcia rys ukośnych nie przekracza wartości granicznej

SPRAWDZENIE SZEROKOŚCI ROZWARCIA RYS PROSTOPADŁYCH

Moment rysujący

Momenty przęsłowe i podporowe od obciążeń charakterystycznych

Przekrój pracuje jako zarysowany

PRZĘSŁO A-B A_S = 4 x ø12mm = 4,52cm²

Maksymalna średnica prętów, to ø12mm

PRZĘSŁO B-C A_S = 4 x ø12mm = 4,52cm²

Maksymalna średnica prętów, to ø16 mm

PODPORA B A_S = 6 x ø12mm = 6,79cm²

Maksymalna średnica prętów, to ø18 mm

STAN GRANICZNY UGIĘCIA

PRZĘSŁO A-B

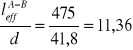
Wniosek: ugięć można nie sprawdzać metodą dokładną

PRZĘSŁO B-C

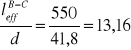
Wniosek: ugięć można nie sprawdzać metodą dokładną

3. TRÓJPRZĘSŁOWY PODCIĄG

SCHEMAT STATYCZNY ORAZ ZESTAWIENIE OBCIĄŻEŃ

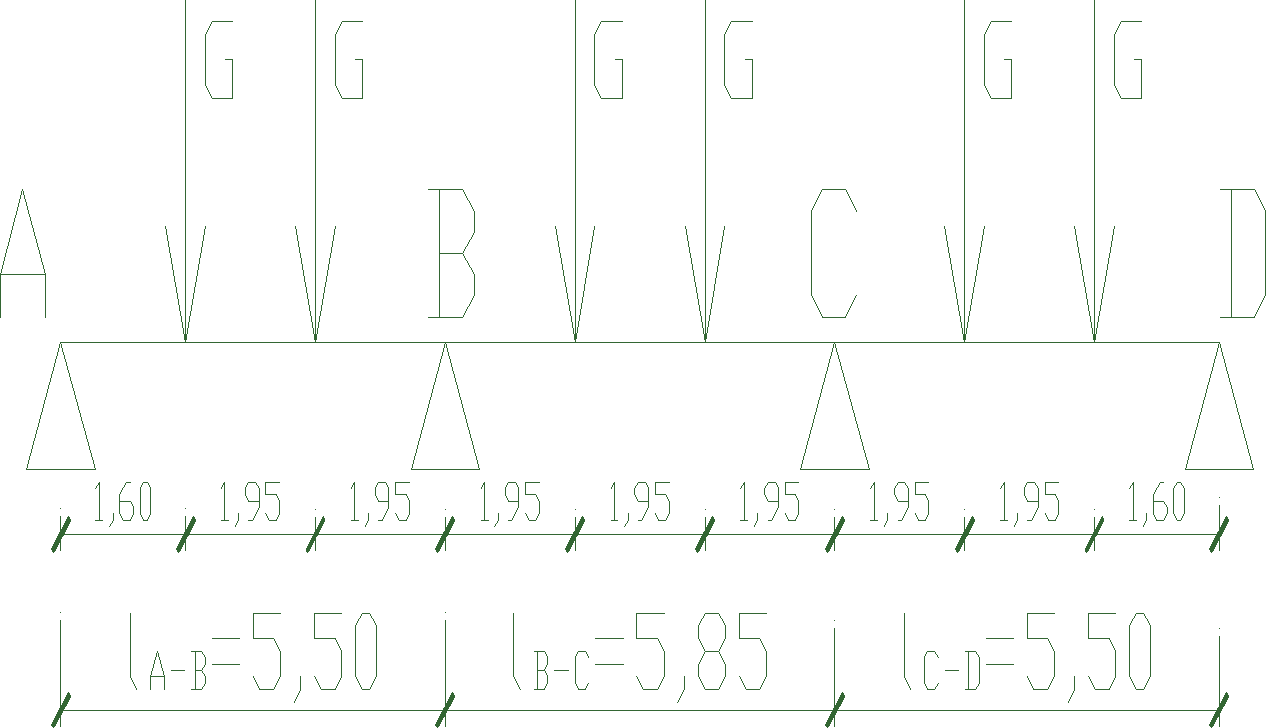
Rodzaj obciążenia	Obciążenia charakterystyczne [kN]	Współ. obciążenia	Obciążenia obliczeniowe [kN]
I OBCIĄŻENIA STAŁE Obciążenia z pozycji 2.0	53,13	-	60,94
CIĘŻAR WŁASNY PODCIĄGU	5,76	1,15	6,61
CIĘŻAR TYNKU NA PODCIĄGU	0,37	1,15	0,42
Σ obciążeń stałych	Gk=59,26	-	G0=67,97
II OBCIĄŻENIA ZMIENNE	Qk=59,96	-	Q0=89,94
Σ obciążeń stałych i zmiennych	Σ(Gk+Qk) = 119,22		Σ(G0+Q0) = 157,91

Wstępne określenie wymiarów słupów:

Rozpiętości przęseł podciągu w świetle podpór:

Skrajne przęsła:

Środkowe przęsła:

WYZNACZENIE SIŁ WEWNĘTRZNYCH W PODCIĄGU (WG TABLIC WINKLERA)

Wyznaczenie momentów zginających na podporze B

Wyznaczenie sił poprzecznych na podporze A

Wyznaczenie sił poprzecznych na podporze B z lewej strony

Wyznaczenie sił poprzecznych na podporze B z prawej strony

Wyznaczenie momentów zginających pod siłą skupioną, schemat nr1

Wyznaczenie momentów zginających pod siłą skupioną, schemat nr2

Wyznaczenie momentów zginających pod siłą skupioną, schemat nr3

Wyznaczenie momentów zginających pod siłą skupioną, schemat nr4

Nr schematu	M1 [kNm]	M2 [kNm]	MB [kNm]	M3 [kNm]
I	79,71	44,32	-102,99	29,55
II	118,29	87,07	- 90,85	- 51,91
III	-19,14	-42,46	- 67,88	107,50
IV	6,34	14,06	22,46	- 16,48
MAX	198,00	131,39	-80,53	137,05
MIN	60,57	1,86	-193,84	- 22,36

Nr schematu	VA [kN]	VB^L[kN]	VB^P[kN]
I	49,82	86,12	67,97
II	73,93	105,95	19,97
III	-11,96	11,96	89,94
IV	3,96	- 3,96	-19,97
MAX	123,75	192,07	157,91
MIN	37,86	82,16	48,00

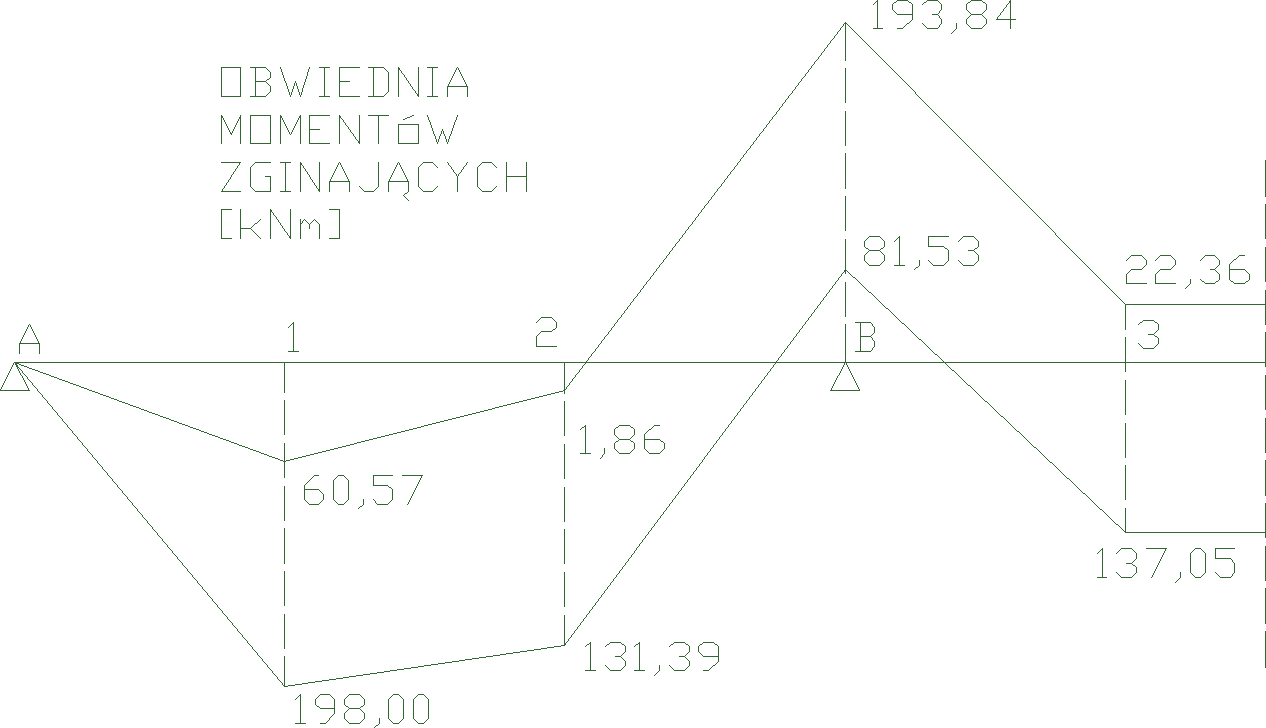
WYMIAROWANIE PODCIĄGU

Beton klasy C20/25:

fck=20,0MPa	fctk=1,5MPa	fctm=2,2MPa
fcd=13,3MPa	fctd=1,0MPa	Ecm=30*10^3MPa

Strzemiona - stal klasy A-I (St3SX-b):

fyk=240MPa

fyd=210MPa

ftk=320MPa

ξeff,lim=0,62

Es=205*10^3MPa

Zbrojenie podłużne - stal klasy A-IIIN (B500SP):

fyk=500MPa

fyd=420MPa

ftk=575MPa

ξeff,lim=0,50

Es=205*10^3MPa

ZBROJENIE PODCIĄGU Z UWAGI NA ZGINANIE

Otulenie

- Dołem

Założenie

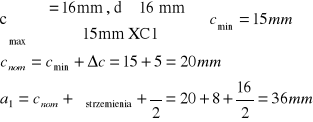
Przyjmuję a₁= 46mm

- Górą

Założenie

Wysokość użyteczna

Zbrojenie minimalne

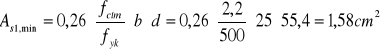
ZBROJENIE W PRZĘŚLE A-B Z UWAGI NA MOMENT MAKSYMALNY

- przekrój pozornie teowy

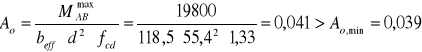
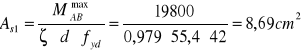
ZBROJENIE W PRZĘŚLE B-C Z UWAGI NA MOMENT MAKSYMALNY:

- przekrój pozornie teowy

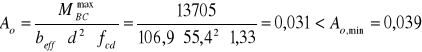
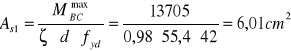
ZBROJENIE W PRZĘŚLE B-C Z UWAGI NA MOMENT MINIMALNY:

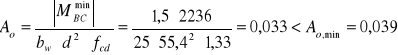
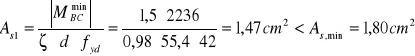
WYMIAROWANIE ZBROJENIA NAD PODPORĄ B:

Momenty zginające na krawędziach podpory:

Przekrój zbrojenia w osi podpory (z uwzględnieniem ukrytego skosu):

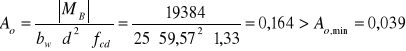
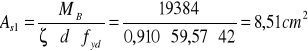
Przekrój zbrojenia krawędzi podpory:

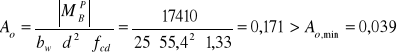
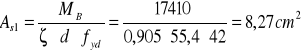
Przyjęto następujące zbrojenie: 1 x ø16mm = 2,01cm²

Przęsło A-B 8,69cm² dołem A_S = 5 x ø16mm = 10,05cm²

górą A_S = 2 x ø16mm = 4,02cm²

Przęsło B-C 6,01cm² dołem A_S = 3 x ø16mm = 6,03cm²

Zbrojenie min B-C 1,80cm² górą A_S = 2 x ø16mm = 4,02cm²

Podpora B 8,51cm² górą A_S = 5 x ø16mm = 10,05cm²

ZBROJENIE PODCIĄGU Z UWAGI NA ŚCINANIE

PODPORA „A”:

Siła poprzeczna na krawędzi podpory:

Do podpory doprowadzono trzy pręty, natomiast pozostałe dwa odgięto

- belka zginana bez udziału siły podłużnej

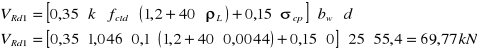
Wystąpi odcinek drugiego rodzaju

Odcinek drugiego rodzaju jest równy wartości odległości od krawędzi podpory do krawędzi pierwszego żebra a_w2=135cm

Przyjęto:
strzemiona dwucięte ø 8mm A_Sw1 = 1,01cm²
pręty odgięte ø 16mm A_Sw2 = 2,01cm²

Strzemiona pionowe powinny przenieść co najmniej 50% wartości siły poprzecznej stąd:

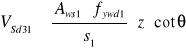
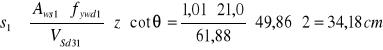
Przyjęto

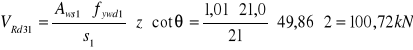
Wartość siły poprzecznej do przeniesienia przez pręty odgięte

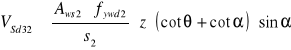
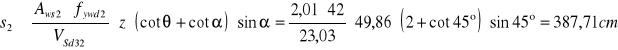
Przyjęto

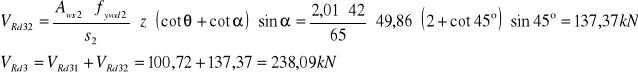
Stopień zbrojenia

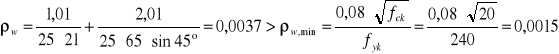
Sprawdzenie warunku normowego rozstawu strzemion na kierunku podłużnym

Sprawdzenie nośności krzyżulców betonowych

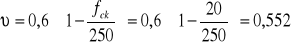
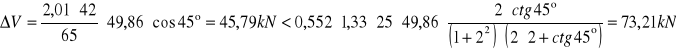
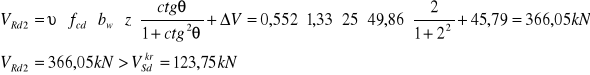
Sprawdzenie nośności zbrojenia podłużnego na krawędzi podpory

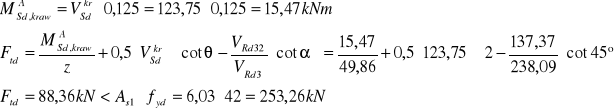
Długość zakotwienia

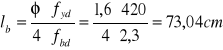
Obliczeniowa długość zakotwienia

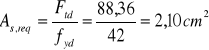
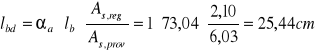
Minimalna długość zakotwienia dla prętów rozciąganych

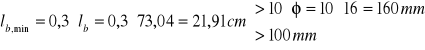
Pręty zbrojenia przęsłowego wprowadzono poza krawędź podpory A na głębokość 22cm

Sprawdzenie nośności zbrojenia podłużnego w teoretycznym punkcie podparcia

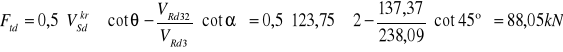
Sprawdzenie szerokości rozwarcia rys ukośnych

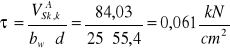
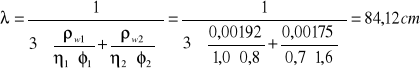
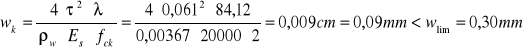
Szerokość rozwarcia rys ukośnych nie przekracza wartości granicznej

PODPORA „B” - Z LEWEJ STRONY:

Do podpory doprowadzono trzy pręty, natomiast pozostałe dwa odgięto (dodano jedną wkładkę ze względu na ścinanie)

- belka zginana bez udziału siły podłużnej

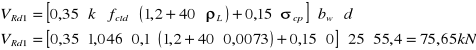
Wystąpi odcinek drugiego rodzaju

Odcinek drugiego rodzaju jest równy wartości odległości od krawędzi podpory do krawędzi pierwszego żebra a_w2=170cm

Przyjęto:
strzemiona dwucięte ø 8mm A_Sw1 = 1,01cm²
pręty odgięte ø 16mm A_Sw2 = 2,01cm²

Strzemiona pionowe powinny przenieść co najmniej 50% wartości siły poprzecznej stąd

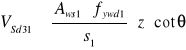
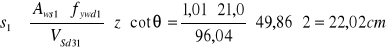
Przyjęto

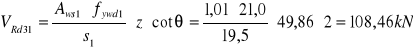
Wartość siły poprzecznej do przeniesienia przez pręty odgięte

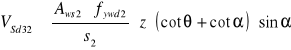
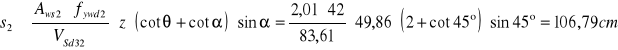
Przyjęto

Stopień zbrojenia

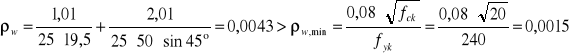
Sprawdzenie warunku normowego rozstawu strzemion na kierunku podłużnym

Sprawdzenie nośności krzyżulców betonowych

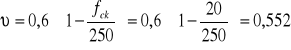
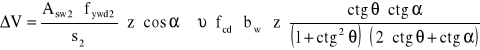
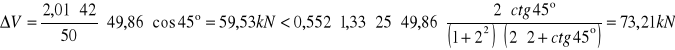
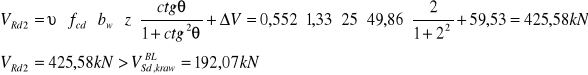
Sprawdzenie szerokości rozwarcia rys ukośnych

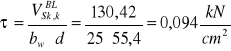
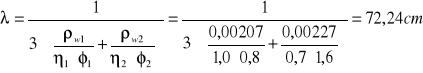
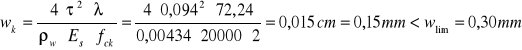
Szerokość rozwarcia rys ukośnych nie przekracza wartości granicznej

PODPORA „B” - Z PRAWEJ STRONY:

Do podpory doprowadzono trzy pręty (dodano trzy wkładki ze względu na ścinanie)

- belka zginana bez udziału siły podłużnej

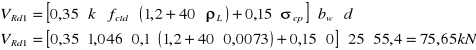
Wystąpi odcinek drugiego rodzaju

Odcinek drugiego rodzaju jest równy wartości odległości od krawędzi podpory do krawędzi pierwszego żebra a_w2=170cm

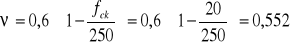
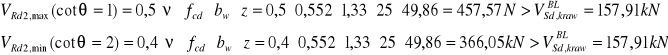
Przyjęto:
strzemiona dwucięte ø 8mm A_Sw1 = 1,01cm²
pręty odgięte ø 16mm A_Sw2 = 2,01cm²

Strzemiona pionowe powinny przenieść co najmniej 50% wartości siły poprzecznej stąd

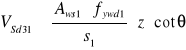
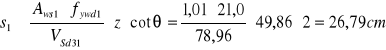
Przyjęto

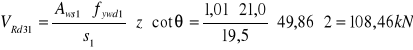
Wartość siły poprzecznej do przeniesienia przez pręty odgięte

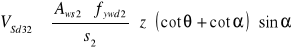
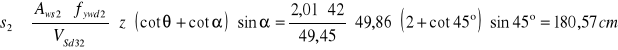
Przyjęto

Stopień zbrojenia

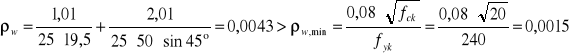
Sprawdzenie warunku normowego rozstawu strzemion na kierunku podłużnym

Sprawdzenie nośności krzyżulców betonowych

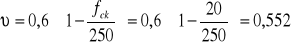
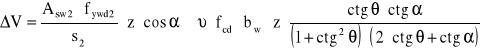
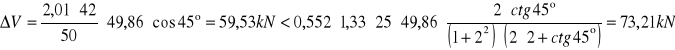
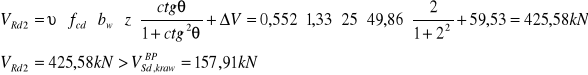
Sprawdzenie szerokości rozwarcia rys ukośnych

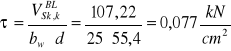
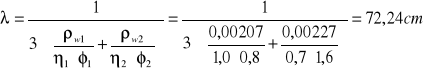
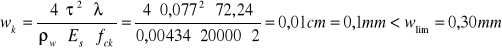
Szerokość rozwarcia rys ukośnych nie przekracza wartości granicznej

ŚCINANIE MIĘDZY PÓŁKĄ A ŚRODNIKIEM PODCIĄGU

PRZĘSŁO A-B

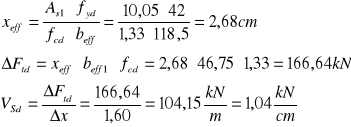
Przyjęto
ø 6mm A_sf = 0,28cm²

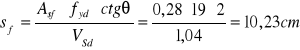
Przyjęto

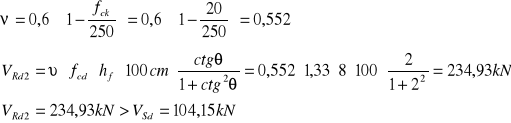
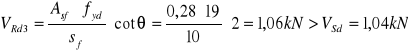
PRZĘSŁO B-C

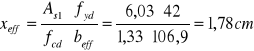
Przyjęto
ø 6mm A_sf = 0,28cm²

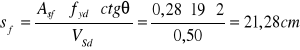
Przyjęto

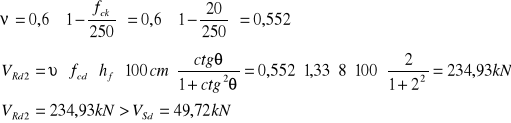
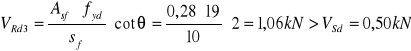
RYSY PROSTOPADŁE

PRZĘSŁO A-B

Pole przekroju środnika ze współpracującą częścią płyty A_c

Moment statyczny S_c

Wysokość strefy ściskanej przekroju niezarysowanego x₁

moment bezwładności przekroju podciągu przed pojawieniem się rys (faza I)

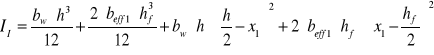
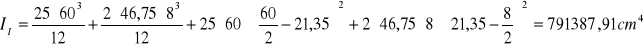
Wskaźnik wytrzymałości przekroju niezarysowanego na zginanie

Moment rysujący

Przekrój ulegnie zarysowaniu (faza II)

Przekrój sprowadzony

B25 t₀=28dni RH=50%

Końcowa wartość współczynnika pełzania

Efektywny moduł sprężystości betonu

Współczynnik α_e,t:

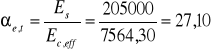
Wysokość strefy ściskanej przekroju sprowadzonego przy x_II<h_f

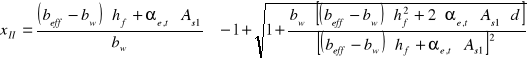
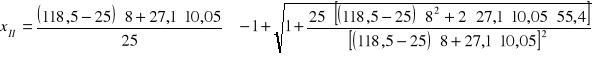
- przekrój teowy

Moment bezwładności przekroju sprowadzonego w fazie II

Naprężenia w zbrojeniu rozciąganym (faza II) wywołane momentem M_Sd

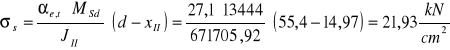
Efektywne pole przekroju strefy rozciąganej

Do dalszych obliczeń przyjęto: A_ct,eff = 287,5cm²

Efektywny stopień przekroju zbrojenia rozciąganego

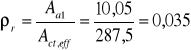
Średni rozstaw rys w fazie ustabilizowanego zarysowania

Średnie odkształcenia zbrojenia rozciąganego

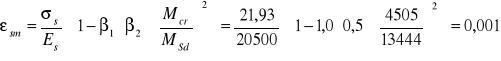
Obliczeniowa szerokość rozwarcia rys prostopadłych

PRZĘSŁO B-C

Pole przekroju środnika ze współpracującą częścią płyty A_c

Moment statyczny S_c

Wysokość strefy ściskanej przekroju niezarysowanego x₁

moment bezwładności przekroju podciągu przed pojawieniem się rys (faza I)

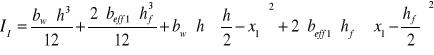
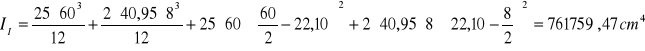
Wskaźnik wytrzymałości przekroju niezarysowanego na zginanie

Moment rysujący

Przekrój ulegnie zarysowaniu (faza II)

Przekrój sprowadzony

B25 t₀=28dni RH=50%

Końcowa wartość współczynnika pełzania

Efektywny moduł sprężystości betonu

Współczynnik α_e,t:

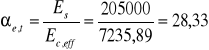
Wysokość strefy ściskanej przekroju sprowadzonego przy x_II<h_f

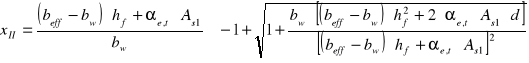
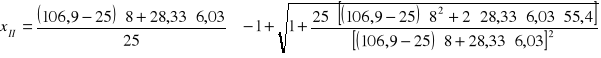
- przekrój teowy

Moment bezwładności przekroju sprowadzonego w fazie II

Naprężenia w zbrojeniu rozciąganym (faza II) wywołane momentem M_Sd

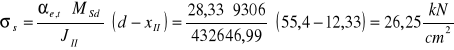
Efektywne pole przekroju strefy rozciąganej

Do dalszych obliczeń przyjęto: A_ct,eff = 287,5cm²

Efektywny stopień przekroju zbrojenia rozciąganego

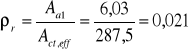
Średni rozstaw rys w fazie ustabilizowanego zarysowania

Średnie odkształcenia zbrojenia rozciąganego

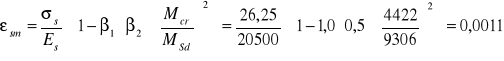
Obliczeniowa szerokość rozwarcia rys prostopadłych

PODPORA B

Wskaźnik wytrzymałości przekroju niezarysowanego na zginanie

Moment rysujący

Przekrój ulegnie zarysowaniu (faza II)

Przekrój sprowadzony

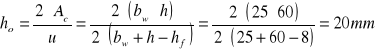
B25 t₀=28dni RH=50%

Końcowa wartość współczynnika pełzania

Efektywny moduł sprężystości betonu

Współczynnik α_e,t:

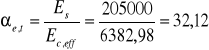
Położenie osi obojętnej

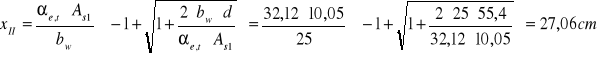
Naprężenia w zbrojeniu rozciąganym (faza II) wywołane momentem M_Sd

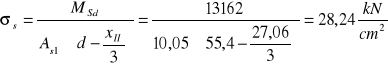
Efektywne pole przekroju strefy rozciąganej

Do dalszych obliczeń przyjęto: A_ct,eff = 274,5cm²

Efektywny stopień przekroju zbrojenia rozciąganego

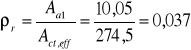
Średni rozstaw rys w fazie ustabilizowanego zarysowania

Średnie odkształcenia zbrojenia rozciąganego

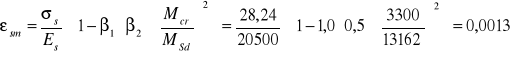
Obliczeniowa szerokość rozwarcia rys prostopadłych

SPRAWDZENIE UGIĘCIA PODCIĄGU

PRZĘSŁO A-B

Położenie osi obojętnej w przekroju w fazie I

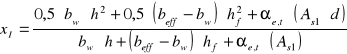
Moment bezwładności przekroju na zginanie w fazie I (niezarysowanej)

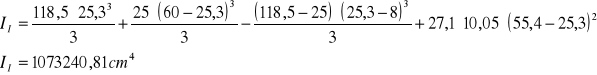
- przekrój teowy

Sztywność przekroju zarysowanego

Ugięcie wywołane ciężarem długotrwałym

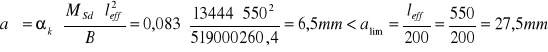
PRZĘSŁO B-C

Położenie osi obojętnej w przekroju w fazie I

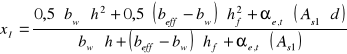
Moment bezwładności przekroju na zginanie w fazie I (niezarysowanej)

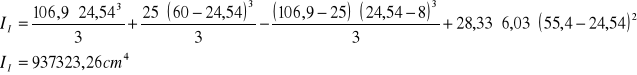
- przekrój teowy

Sztywność przekroju zarysowanego

Ugięcie wywołane ciężarem długotrwałym

4. 
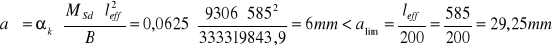
   SŁUPY

ZESTAWIENIE OBCIĄŻEŃ NA SŁUP II KONDYGNACJI

Rodzaje obciążeń	wartość obc. stałych gk [kN]	współcz.	wartość obliczeniowa obc. stałych [kN]
1* papa asfaltowa oraz papa termozgrzewalna	3,45	1,15	3,96
szlichta cementowa gr. 3cm z zalewką złączy płyt korytkowych	18,748	1,15	21,56
prefabrykowane zamknięte płyty korytkowe DKZ/60 * 300 (masa płyty 160kg)	26,4	1,15	30,36
ocieplenie z wełny mineralnej gr. 18cm oraz folia paroizolacyjna	11,2	1,15	12,88
ścianki ażurowe z cegły dziurawki gr. 12cm	11,2	1,15	12,88
sufit podwieszany oraz instalacje (25kg)	7,41	1,15	8,52
ΣN1	75,16	1,15	86,46
płyta	74,1	1,15	85,215
żebra	29,25	1,15	33,64
podciąg	12,844	1,15	14,77
tynk	12,15	1,15	13,98
Σ N2	128,344	1,15	147,60
Σ N1 + N2	203,504	1,5	234,03
słup	5,545	1,15	6,379
tynk cem.-wap. na słupie	1,012	1,15	1,164
Σ NSd1,It	210,063	1,15	241,573
obciążenie śniegiem (II strefa) - współcz. kształtu dachu C=0,8 (dla α<15^o)	21,341	1,5	32,012
OBCIĄŻENIE CAŁKOWITE Σ NSd1	231.404		273,585

ZESTAWIENIE OBCIĄŻEŃ NA SŁUP I KONDYGNACJI

Rodzaje obciążeń	wartość obciążeń stałych [kN]	współcz.	wartość obliczeniowa obc. stałych [kN]
siła normalna od obciążeń długotrwałych przekazywana przez słup II kondygnacji oraz ciężar własny tego słupa	231,404	-	273,585
podłoga - lastryko	13,042	1,15	15,00
płyta	74,1	1,15	85,215
żebra	29,25	1,15	33,64
podciąg	12,844	1,15	14,77
tynk	12,15	1,15	13,98
Σ N1 + N2	372,79		436,19
słup	6,17	1,15	7,1
tynk cem.-wap. na słupie	1,012	1,15	1,16
Σ NSd2,It	379,97		444,45
obciążenie śniegiem (I strefa) - współcz. kształtu dachu C=0,8 (dla α<15^o)	21,34	1,5	32,01
obciążenie zmienne stropów (Ψ=0,80) - strop II kondygnacji	183,77	1,5	275,65
OBCIĄŻENIE CAŁKOWITE Σ NSd2	585,08		752,11

Założenia materiałowe i konstrukcyjne

• beton klasy B25:

fck=20,0MPa	fctk=1,5MPa	fctm=2,2MPa
fcd=13,3MPa	fctd=1,0MPa	Ecm=30*10^3MPa

- strzemiona - stal klasy A-I (St3Sx):

fyk=240MPa

fyd=210MPa

Es=200*10^3MPa

ξeff,lim=0,63

• zbrojenie podłużne - stal klasy A-III (20G2VY-b):

fyk=490MPa

fyd=420MPa

Es=200*10^3MPa

ξeff,lim=0,5

4.2. WYMIAROWANIE SŁUPA

4.2.1. SŁUP PARTERU

schemat statyczny słupa:



















długość:





4,25 = 2,98m










Wymagany przekrój zbrojenia obliczono ze wzoru:




Współczynnik ϕ₁ podstawiono według tablicy 9.4. skryptu wydanego przez Politechnikę Koszalińską dla wartości:







Stąd: ϕ₁ = 0,86







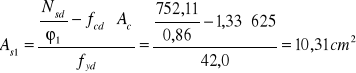
minimalny stopień zbrojenia prętami:







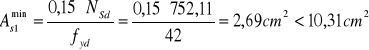
Przyjęto 8 φ 16 o


strzemiona:

Średnica prętów powinna spełniać następujące wymagania:


i


Przyjmuję strzemiona φ6mm.

Rozstaw strzemion uzależniony jest od stopnia zbrojenia słupa, który wynosi:




Stąd rozstaw strzemion nie powinien być większy niż
zbrojenia podłużnego.

Przyjęto strzemiona dwucięte φ6mm w rozstawie co 20cm

w strefie łączenia zbrojenia podłużnego strzemiona zagęszczono do 10cm

1. SŁUP DRUGIEJ KONDYGNACJI.

długość:





3,75 = 2,7m










Wymagany przekrój zbrojenia obliczono ze wzoru:




Współczynnik ϕ₁ podstawiono według tablicy 9.4. skryptu wydanego przez Politechnikę Koszalińską dla wartości:







Stąd:








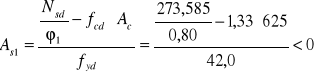
minimalny stopień zbrojenia prętami:







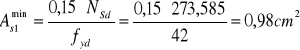
Przyjęto 4 φ 12 o


strzemiona:

Średnica prętów powinna spełniać następujące wymagania:


i


Przyjmuję strzemiona φ6mm.

Rozstaw strzemion uzależniony jest od stopnia zbrojenia słupa, który wynosi:




Stąd rozstaw strzemion nie powinien być większy niż
zbrojenia podłużnego.

Przyjęto strzemiona dwucięte φ6mm w rozstawie co 18cmw strefie łączenia zbrojenia podłużnego strzemiona zagęszczono do 9cm

5.0. STOPA FUNDAMENTOWA.

5.1. PARAMETRY GEOTECHNICZNE GRUNTU ORAZ ZESTAWIENIE OBCIĄŻEŃ.

W poziomie posadowienia zalegają grunty nośne, tj. piaski średnie w stanie średnio zagęszczonym (I_D = 0,6) o następujących parametrach geotechnicznych:

ρ = 1,85 t/m³ ; ρ^(r) = 0,9 ⋅ 1,85 = 1,67 t/m³

Φ = 33,5⁰ ; Φ^{(r )} = 0,9 ⋅ 33,5⁰ = 30,15⁰


=0


głębokość posadowienia przyjęto równą D_min = 0,90 m.

obciążenie przekazywane przez słup na stopę fundamentową:




obciążenie przekazywane przez stopę na podłoże gruntowe:

Średnią wartość ciężaru objętościowego gruntu oraz betonu zbrojonego przyjęto w wielkości


.

Obliczeniowy ciężar własny stopy wraz z gruntem na niej spoczywającym:







obliczeniowy opór jednostkowy podłoża gruntowego wg normy PN-81/B-03020:

Przyjęto stopę o podstawie kwadratu - stąd
.







1. OKREŚLENIE WYMIARÓW STOPY.













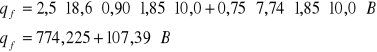
Przyjęto stopę o wymiarach B=L=1,20m,

Dla przyjętych wymiarów powyższa nierówność przyjmuje postać:




określenie wysokości stopy:








,







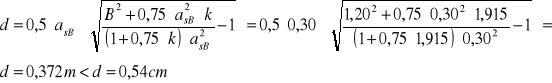
Otulinę zbrojenia stopy przyjęto w wielkości a=0,060m oraz d=54cm.

Wymagana długość zakotwienia zbrojenia słupa (φ16mm) ze stali A-III (20G2VY-b):







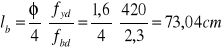
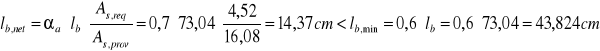
Przyjęto l_b,net=50cm

Przyjęto stopę o wysokości h=0,60m

Stopa nie wymaga sprawdzenia zbrojenia na przebicie.

sprawdzenie dokładności przyjętego do obliczeń ciężaru stopy wraz z gruntem:

ciężar własny stopy:




warstwa gruntu nad stopą:







WYMIAROWANIE STOPY.

Moment zginający od obliczeniowego odporu gruntu (z pominięciem ciężaru własnego stopy) określono według metody wsporników trapezowych:











Na obu kierunkach przyjęto φ12mm co 11cm

35










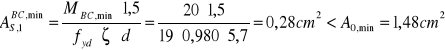
l_o = l_{col *} 0,7

l_o