Politechnika Śląska Wydział Elektryczny Laboratorium Automatyki i Sterowania	Studia Dzienne Magisterskie 2006 / 2007 rok Semestr: VI
Temat ćwiczenia: Regulacja nadążna
Studenci: Chropacz Paweł Motyka Ryszard Sawczuk Grzegorz	Data wykonania: 04,04,2005r, Grupa: KSS 2/mgr godz, 9^45 Sekcja: 2 Prowadzący: mgr inż, Wiesław Domański

1. Cel ćwiczenia

Celem naszego ćwiczenia było zapoznanie się z zasadą działania, realizacji, wykonana i zastosowania regulacji nadążnej, Dodatkowo zapoznaliśmy się ze sposobami wyznaczania podstawowych właściwości i parametrów elementów układu do których zaliczamy: silnik, przekładnie, prądnice tachometryczną układ mostkowy i wzmacniacz operacyjny, Dysponując podstawową wiedzą przystąpiliśmy do realizacji procesu regulacji, poprzez odpowiedni dobór nastaw elementów aby na wyjściu układu uzyskać charakterystyczne przebiegi odpowiedzi skokowej układu: oscylacje niegasnące, gasnące, przebiegi aperiodyczne o różnym czasie narastania,

II, Wprowadzenie Teoretyczne

Układy automatycznej regulacji klasyfikuje się ze względu na założenia dotyczące charakteru zmienności czasowej wartości zadanej, Wyróżnia się następujące grupy:

• Układy regulacji stałowartościowej (automatycznej stabilizacji), w których wartości zadane wielkości regulowanej są stałe, Układ realizuje dwa zadania:

• doprowadzić do równości wartości ustalonej na wyjściu i wartości zadanej,

• korygować zmiany wielkości regulowanej wywołanych zakłóceniami, które powstają zarówno w samym układzie (np, wpływ temperatury na parametry elementów), jak i poza nim (np, wpływ zewnętrznych czynników na wielkość regulowaną),

• Układy regulacji programowej, w których układ realizuje zadania podobne do podanych wyżej, jednakże wartości zadane nie są stałe, lecz zmieniają się według zadanych funkcji czasu,

• Układy regulacji nadążnej (śledzące), w których wartości zadane wielkości regulowanej również są zmienne, lecz zmienność ta ma charakter stochastyczny,
  tzn, niemożliwy do wcześniejszego przewidzenia i opisania równaniem funkcyjnym,

Od układów regulacji programowej i nadążnej wymaga się odwzorowania na wyjściu przebiegu czasowego wartości zadanej, tak aby błąd (uchyb) regulacji nie przekroczył założonych wartości dopuszczalnych, Ponieważ jednak wielkości te nie osiągają wartości ustalonych, lecz są zmienne w czasie, to wspomniane założenia dotyczące błędu regulacji muszą uwzględniać jego dynamiczny charakter, Dla określenia wartości dopuszczalnych błędu regulacji stosuje się więc różne funkcjonały stanowiące tzw, miary błędu dynamicznego,

Miary te charakteryzują jednocześnie jakość regulacji nadążnej - są pewnego rodzaju wskaźnikami jakości regulacji, Najczęściej stosowane miary dynamicznego błędu regulacji definiowane są następująco:

• wartość maksymalna,

• wartość średnia,

• wartość średnia modułu,

• wartość średniokwadratowa,

Układy regulacji nadążnej

Schemat ogólny

Układy regulacji nadążnej mają podstawową strukturę typową dla wszystkich zamkniętych układów regulacji z głównymi blokami:

• węzeł sumacyjny (1),

• regulator (2),

• element wykonawczy (3),

• sterowany obiekt (4)

• oraz układ pomiarowy wielkości wyjściowej (5) w torze ujemnego sprzężenia zwrotnego,
  Często stosowaną modyfikacją podstawowej struktury, szczególnie w układach mechanicznych, jest wprowadzenie pokazanego na rysunku dodatkowego sprzężenia zwrotnego (elementy 1a, 2a i 5a) od pewnej wielkości pomocniczej y_n występującej w obiekcie, przez co uzyskuje się tzw, układ regulacji kaskadowej, Rozwiązanie takie pozwala na znaczne polepszenie jakości regulacji, szczególnie w przypadkach, gdy elementy wykonawcze lub obiekt wykazują znaczną nieliniowość, niejednoznaczność (histerezę) lub opóźnienie, Wprowadzenie dodatkowego sprzężenia daje dobre rezultaty, gdy w regulowanym procesie można wyróżnić wielkość pomocniczą y_n(t), nie podlegającą (lub podlegającą w mniejszym stopniu) wymienionym przekształceniom nieliniowym,
  

Przykład układu regulacji nadążnej

Typowym przykładem układu regulacji nadążnej jest tzw, serwomechanizm, tj, elektromechaniczny układ regulacji położenia, Schemat ideowy serwomechanizmu stosowanego w rejestratorze autokompensacyjnym,

W układzie zastosowano następujące elementy:

• silnik S napędzający karetkę z pisakiem (poprzez zespół przekładni mechanicznych)

• prądnicę tachometryczną P sprzężoną mechanicznie z silnikiem i karetką, Napięcie na zaciskach prądnicy jest proporcjonalne do prędkości obrotowej jej wału, a dzięki mechanicznemu sprzężeniu z karetką również do liniowej prędkości ruchu karetki,

• wzmacniacz napięciowy W, którego napięcie wyjściowe zasila silnik,

• potencjometr, którego suwak jest mechanicznie sprzężony z karetką, Potencjometr włączony
  jest w układ mostka czteroramiennego, Przesunięcie suwaka potencjometru powoduje powstanie napięcia U_a proporcjonalnego do przesunięcia karetki,

Omawiany układ jest kaskadowym układem regulacji ze względu na zastosowanie podwójnego sprzężenia zwrotnego: od wielkości regulowanej α(napięcie u_α jest proporcjonalne do położenia) oraz od wielkości pomocniczej, którą jest prędkość ruchu karetki (napięcie u_v jest proporcjonalne do tej prędkości),

Zadaniem układu jest regulacja położenia αkaretki w ślad za zmianami napięcia wejściowego U_x, Napięcie to jest sumowane (z uwzględnieniem znaku) z napięciami sprzężeń zwrotnych U_α od wielkości regulowanej i U_v od wielkości pomocniczej, Napięcie wynikowe U₁ reprezentujące uchyb regulacji, podawane jest na wejście wzmacniacza W, którego napięcie wyjściowe U₂ zasila silnik S, Dopóki karetka nie osiągnie położenia odpowiadającego aktualnej wartości napięcia wejściowego U_x i jednocześnie zerowej prędkości, napięcie U₁ jest różne od zera, co powoduje, że silnik przesuwa karetkę, W stanie równowagi karetka osiąga położenie odpowiadające podanemu napięciu wejściowemu, spełnione są warunki: U_α=U_X i U_V=0 i silnik nie zmienia położenia karetki,

Transmitancja zastępcza układu:

K(s)=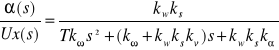


Wzmocnienie statyczne:


Pulsacja drgań własnych nietłumionych:



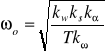
Współczynnik tłumienia:

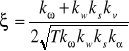
III, Przebieg ćwiczenia

Ćwiczenie nr 1:

Badanie elementów układu

Schemat pomiarowy:

1, Wyznaczenie parametrów silnika:

• zasilamy silnik napięciem u_s zmienianym skokowo przez podanie na wejście układu napięcia zmiennego skokowo przy wyłączonych sprzężeniach zwrotnych,

• rejestrujemy odpowiedź skokową układu otwartego - przebieg wychylenia α(t),

• wyznaczamy parametry silnika i przekładni,

• pomiary wykonujemy dla różnych wartości napięcia zasilającego silnik,
  
  Przebieg napięcia zasilania dla U_s=±5,5V
  Na podstawie przebiegu U_s= f(t) odczytujemy ΔU_s= 5,2V-(-5,5V)=10,7V

Odpowiedź skokowa układu regulacji dla U_s=±5,5V

Na podstawie przebiegu U_a= f(t) odczytujemy:

T=110ms

ΔU_α=3V

Δt= 100ms

Wyliczmy zależność dla silnika ze wzoru:

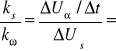
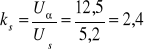
=0,86

Przebieg napięcia zasilania dla U_s=±11,5V

Na podstawie przebiegu U_s= f(t) odczytujemy ΔU_s= 11V-(11,3V)=22,3V

Odpowiedź skokowa układu regulacji dla U_s=±11,5V

Na podstawie przebiegu U_a= f(t) odczytujemy:

T= 80ms ΔU_α= 6,3 V
Δt= 100ms

= 2,82


=0,39

2, Wyznaczenie współczynnika wzmocnienia statycznego prądnicy tachometrycznej

• w trakcie rejestracji odpowiedzi skokowej silnika i przekładni mierzyliśmy wartość ustaloną napięcia u_vust na wyjściu prądnicy,

• wyznaczamy wzmocnienie prądnicy wg zależności:

k_vmax=

Na podstawie przebiegu U_a= f(t) odczytujemy wartości:

ΔUα= 9,5V
Δt= 500ms

Z powyższego przebiegu odczytujemy wartość napięcia ustalonego na wyjściu prądnicy:
U_vust=1,2V

Współczynnik wzmocnienia prądnicy: k_vmax=
=

Na podstawie przebiegu U_a= f(t) odczytujemy wartości:

Δα= 12,5V
Δt=250ms

Z powyższego przebiegu odczytujemy wartość napięcia ustalonego na wyjściu prądnicy:
U_vust=4,8V

Współczynnik wzmocnienia prądnicy:
k_vmax=
=

3, Wyznaczenie wzmocnienia układu mostkowego:

• odłączamy napięcie wejściowe, aby uzyskać u_s=0,

• mierzymy napięcia u_α1 i u_α2 na wyjściu układu odpowiadające dowolnym znanym położeniom karetki α₁ i α₂ uzyskanym przez ręczne przesuwanie karetki,

• wyznaczamy wzmocnienie wg zależności:

k_αmax=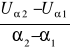

• pomiary powtarzamy dla różnych położeń karetki,

Zmiana położenia karetki l	Napięcie na wyjściu układu mostkowego U1	Zmiana położenia karetki Δl	Zmiana napięcie na wyjściu układu mostkowego ΔU1	Współczynnik wzmocnienie układu mostkowego kum
[cm]	[V]	[cm]	[V]	[V/cm]
1	-12,5	1	0,6	0,6
2	-11,0	1	0,9	0,9
3	-10,8	1	1	1
4	-9,8	1	1,1	1,1
5	-8,7	1	0,9	0,9
6	-7,8	1	1,1	1,1
7	-7,0	1	1,1	1,1
8	-5,9	1	1	1
9	-4,5	1	1	1
10	-3,5	1	1	1
11	-2,6	1	1	1
12	-1,9	1	1	1
13	-0,8	1	1	1
14	0,2	1	1,1	1,1
15	2	1	1	1
16	3,1	1	1	1
17	4,2	1	1	1
18	5,1	1	1	1
19	7,0	1	1	1
20	8,3	1	1	1
21	8,3	1	1,1	1,1
22	9,4	1	0,9	0,9
23	10,0	1	2,1	2,1
24	11,1	1	1,1	1,1
25	11,4	-	-	-

Wartość współczynnika wzmocnienia układu mostkowego:

Wyliczona przy pomocy programu EXELL:

k=1,0302

Wartość obliczona jako średnia arytmetyczna ze wszystkich wyników pomiarowych:

k=1,0417

4, Wyznaczenie wzmocnienia wzmacniacza:

• wyłączamy sprzężenia zwrotne i potencjometr na wejściu wzmacniacza ustawiamy w położeniu 1,

• doprowadzamy do wejścia układu napięcie o znanej amplitudzie i mierzymy odpowiadającą mu amplitudę sygnału wyjściowego,

• wyznaczamy wzmocnienie k_wmax jako stosunek wartości napięcia wyjściowego do

wejściowego,

• pomiary powtarzamy dla różnych wartości napięcia wejściowego,

Wartość współczynnika wzmocnienia układu mostkowego:
Wyliczona przy pomocy programu EXELL:

k= 1,9363*10=19,363

Wartość obliczona jako średnia arytmetyczna ze wszystkich wyników pomiarowych:

k= 1,9394*10=19,394

Wartość współczynnika wzmocnienia układu mostkowego:

Wyliczona przy pomocy programu EXELL:

k= 12,1469*5=60,7345

wartość obliczona jako średnia arytmetyczna ze wszystkich wyników pomiarowych:

k= 12,1801*5=60,9005

5, Badanie procesu regulacji

Badanie procesu regulacji nadążnej należy polega na doprowadzenie do wejścia układu napięcia o znanym przebiegu czasowym (skokowym, trójkątnym i sinusoidalnym) i obserwacji przebiegu położenia karetki,

W trakcie badań musimy tak dobrać parametry układu, aby uzyskać charakterystyczne przebiegi odpowiedzi skokowej układu (oscylacje niegasnące i gasnące, przebieg aperiodyczny o różnym czasie narastania), a następnie obserwować przebieg odpowiedzi układu dla zadanych przebiegów, W ćwiczeniu stosowany jest rejestrator autokompensacyjny wyposażony w dwa serwomechanizmy przesuwające karetkę z pisakiem w dwóch prostopadłych kierunkach (x i y), Do wejścia toru x doprowadzone jest napięcie narastające liniowo, powodujące liniowe przesuwanie karetki w kierunku x, co tworzy mechanizm podstawy czasu (analogicznie jak w oscyloskopach), Pozwala to uzyskać wykres przebiegu czasowego ruchu karetki w kierunku y, Układ w torze y został zmodyfikowany tak, aby możliwe było nastawianie wartości niektórych parametrów, Współczynniki k_w, k_v i k_a mogą być zmieniane za pomocą potencjometrów w zakresie (O,,,l)k_imax, gdzie k_imm oznacza wartość maksymalną odpowiedniego współczynnika,

Nastawy odpowiednich wzmocnień:

kv	kw	Kα
0	0,5	0

Nastawy odpowiednich wzmocnień:

kv	kw	kα
0,6	0,5	0,75

Nastawy odpowiednich wzmocnień:

kv	kw	kα
0,2	0,1	0,75

Nastawy odpowiednich wzmocnień:

kv	kw	kα
0,4	0,1	1,25

Nastawy odpowiednich wzmocnień:

kv	kw	kα
0	0,2	1

Nastawy odpowiednich wzmocnień:

kv	kw	kα
0	0,2	0,75

Nastawy odpowiednich wzmocnień:

kv	kw	kα
0	1	1,25

Nastawy odpowiednich wzmocnień:

kv	kw	kα
0	0,7	1,25

Warunki dopasowania:

Nastawy odpowiednich wzmocnień:

kv	kw	kα
0,3	0,4	0,9

Warunki niedopasowania parametrycznego:

Nastawy odpowiednich wzmocnień:

kv	kw	kα
0,15	0,1	0,87

IV, Wnioski

Pierwszym naszym badanym układem był silnik, Z przebiegu odpowiedzi skokowej na wymuszenie możemy stwierdzić, że jest to układ inercyjny pierwszego rzędu, Przy wzroście wartości skoku widzimy, że wzrost napięcia (dwukrotnie) powoduje zmniejszenie wartości współczynników wzmocnienia silnika i przekładni-karetki dwukrotnie,

Ponieważ układ mostka z góry jest założony jako proporcjonalny nie analizujemy więc odpowiedzi skokowej lecz poszczególne wartości wielkości mierzonych, Wartość współczynnika kierunkowego funkcji regresji reprezentuje wartość współczynnika wzmocnienia układu mostkowego i wynosi ona k=1,0302, co prawda odbiega ona od wartości współczynnika wzmocnienia obliczonego ze średniej arytmetycznej wszystkich wyników pomiarowych k=1,0417, Ta nie znaczna różnica między wynikami pomiarowymi wynosząca Δk=0,0115 może wynikać z błędnej aproksymacji liniowej,

Badany układ wzmacniacza podobnie jak układ mostkowy jest układem proporcjonalnym, Na podstawie przeprowadzonych obliczeń widzimy, że niezależnie od stosowanego sposobu obliczeń współczynniki wzmocnienia wartościowo są do siebie zbliżone, a niewielka ich rozbieżność wynika podobnie jak w układzie mostkowym tylko ze sposobu aproksymacji,

Proces regulacji nadążnej, przeprowadzony wstępnie przy stałej wartości wzmocnienia wzmacniacza k_w=0,5 był przeprowadzany dla układu otwartej pętli, Z przebiegu wyjściowego wynika, że jest on opóźniony, wzmocniony a dla ruchu karetki miało to przełożenie w postaci gwałtownych ruchów i obijania jej o ścianki boczne, Zamknięcie obwodu regulacji i wzrost współczynników k_v i k_α powoduje obniżenie amplitudy odpowiedzi skokowej powodując jednocześnie wzrost opóźnienia ( wzmocnienie k_v) co miało przełożenie w ograniczeniu ruchu karetki, Przy małych wartościach k_w i dużych k_α amplituda sygnału wyjściowego jest stłumiona względem sygnału wejściowego, Powodowało to maksymalne ograniczenie ruchu karetki, Przy małych (zerowych) ustawieniach k_v, ale dużych ustawieniach k_α obserwujemy oscylacje gasnące, które pojawiają się przy skrajnych położeniach karetki, Im mniejsza wartość k_α, tym więcej pojawia się oscylacji, Zerowe wartości k_v i maksymalne k_α i k_w powodują uzyskanie oscylacji o charakterze niegasnącym w badanym przez nas zakresie, Przełożenie to miało wpływ na karetkę w ten sposób, że drgania karetki nie były widoczne lecz można było zauważyć drgania linki do której była przymocowana karetka,
Zgodnie z definicją regulacji nadążnej odpowiednie dobranie współczynników wzmocnień umożliwia uzyskanie sygnału wyjściowego, który jest realnym odzwierciedleniem wartości zadanej zarówno co do wartości amplitudy jak i fazy,

W naszym przypadku odpowiednie nastawy wynosiły:

k_v= 0,3 k_w=0,4 k_α= 0,9

Zmiana parametrów na wartości:

k_v= 0,15 k_w=0,1 k_α= 0,87

uwidacznia brak równości amplitud i przesunięcie fazowe sygnału odpowiedzi skokowej względem wymuszenia,

Regulacja nadążna Strona 14 z 27

Politechnika Śląska w Gliwicach

---