 | Pobierz cały dokument statystyka.1.rzutnik.statystyka.egzamin.u.doc Rozmiar 521 KB |
Przedział ufności dla wskaźnika struktury
Często badanie statystyczne a raczej jej badana cecha ma charakter niemierzalny, jakościowy i wtedy zamiast wartości liczbowej badanej cechy z badania próbnego uzyskujemy jedynie informacje o tym, czy dany element populacji generalnej ma badaną, wyróżnioną cechę jakościową czy też jej nie ma.
Elementy populacji generalnej dzielą się wówczas na dwie klasy:
elementy wyróżnione,
elementy niewyróżnione.
Frakcja (wskaźnik struktury populacji) - podstawowy parametr populacji szacowany w przypadku badań statystycznych ze względu na mierzalną cechę elementów wyróżnionych w populacji. Wskaźnik ten jest oznaczany symbolem p.
Przedział ufności dla wskaźnika struktury p , otrzymujemy jak zwykle z odpowiedniego rozkładu estymatora tego parametru. Takim estymatorem jest wskaźnik struktury z próby m/n, gdzie m oznacza liczbę elementów wyróżnionych znalezionych w losowej próbie o liczebności n.
Budowę przedziału ufności dla p w zależności od wielkości próby można oprzeć na dokładnym rozkładzie estymatora m/n lub też na jego rozkładzie granicznym (w przypadku dużej próby).
Najczęściej frakcje p elementów wyróżnionych w populacji szacujemy w oparciu o wyniki dużej próby (n>100). Wówczas można wyznaczyć przybliżony przedział ufności dla parametru p.
Model
Generalna populacja ma rozkład dwupunktowy z parametrem p, tzn. elementy populacji są podzielone na dwie klasy, przy czym frakcja elementów wyróżnionych w populacji wynosi p, które nie jest małym ułamkiem (p>0,05). Z populacji tej wylosowano niezależnie dużą liczbę n elementów do próby (n>100). Wtedy przedział ufności dla wskaźnika struktury p populacji generalnej jest określony przybliżonym wzorem:
(1.0) 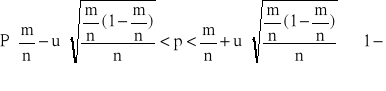
gdzie m jest liczbą elementów wyróżnionych znalezionych w próbie, a uα jest odczytaną z tablicy rozkładu normalnego N(0,1) wartością zmiennej normalnej standaryzowanej U, w taki sposób, by spełniona była relacja P{- uα <U< uα }=1-α dla ustalonego z góry współczynnika ufności 1-α.
Przykład
Chcemy oszacować, jaki procent pracujących mieszkańców Warszawy jada obiady w stołówkach pracowniczych. Pobrano w tym celu n=900 osób wylosowanych niezależnie do próby i znaleziono w tej próbie m=300 osób, które jedzą obiady w stołówkach. Przyjmując współczynnik ufności 1-α=0,95 zbudować przedział ufności dla procentu badanej kategorii pracujących w Warszawie.
Rozwiązanie
Przedział ufności dla szacowanej frakcji p pracowników można wyznaczyć według wzoru (1.0). Dokonujemy niezbędnych obliczeń:
![]()
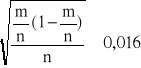
 | Pobierz cały dokument statystyka.1.rzutnik.statystyka.egzamin.u.doc rozmiar 521 KB |