wykład 1. wstęp do metrologii

1.1. Wprowadzenie

Nie jest przesadą stwierdzenie, że człowiekowi w ciągu całego jego życia towarzyszą pomiary. Już noworodka czekają pomiary: ważenie, mierzenie wzrostu i temperatury. Człowiek dorosły styka się z pomiarami codziennie w domu i poza domem: w sklepie, w zakładzie pracy, u lekarza, w samochodzie; a tok życia człowieka jest regulowany przez wskazania najpopularniejszego przyrządu pomiarowego * zegarka. Po śmierci zaś, na Sądzie Ostatecznym, czeka jeszcze człowieka ważenie jego grzechów i dobrych uczynków.

Człowiek zaczął mierzyć już we wczesnym stadium rozwoju intelektualnego i cywilizacyjnego. Zanim jednak do tego doszło, człowiek nauczył się liczyć. Wyrobienie umiejętności liczenia i mierzenia zostało spowodowane potrzebą rozwiązywania problemów związanych z codziennym życiem człowieka.

Liczenie to doświadczenie, którego celem jest wyznaczenie liczby naturalnej określającej liczność czyli moc zbioru przedmiotów. Liczenie polega na porównywaniu liczności zbioru z licznością innych zbiorów o znanych licznościach. Zbiory o znanej liczności były początkowo tworzone z palców rąk, a po odkryciu liczby ze zbiorami tworzonymi z kolejnych liczb.

Pomiar to doświadczenie, którego celem jest wyznaczenie pewnej liczby, zwanej wartością liczbową wielkości albo miarą wielkości. Liczność jest abstrakcyjną cechą zbioru; wielkość jest abstrakcyjną cechą obiektów określonej kategorii, np. długość jest cechą odcinków, masa jest cechą przedmiotów materialnych. Wartość liczbowa wielkości odnoszącej się do wybranego obiektu jest liczbą równą stosunkowi tej wielkości do wielkości przyjętej jako jednostka miary. Pomiar polega na porównywaniu pod względem mierzonej wielkości badanego obiektu z obiektami o znanych wartościach tej wielkości, czyli wzorcami, tak jak przy pomiarze długości linijką lub ważeniu za pomocą wagi dźwigniowej i odważników. Liczność jest cechą daną w sposób naturalny. Wielkość musi być najpierw zdefiniowana, a mierzyć ją można dopiero po przyjęciu jednostki miary.

Metrologia rozpoczęła się pierwszym pomiarem wykonanym świadomie przez człowieka. Historycznie pierwsze były pomiary czasu, pomiary długości i odległości, pomiary objętości ciał sypkich i płynów, pomiary masy oraz pomiary pola powierzchni. Mierzył już człowiek pierwotny, ale wyraźny rozwój miernictwa jest związany z wczesnymi cywilizacjami Starożytności: Mezopotamii, Egiptu, Chin, Indii.

Długość przedmiotów człowiek mierzył porównując je z elementami swojego ciała, prowadziło to do wykształcenia się jednostek długości takich jak: cal (szerokość dużego palca ręki), piędź (długość odcinka między czubkami kciuka i małego palca przy rozpostartych palcach), stopa, łokieć, sążeń (długość odcinka między czubkami palców rozpostartych ramion). Odległości, czyli większe długości, były mierzone takimi jednostkami jak: odległość rzutu kamieniem lub oszczepem, odległość strzału z łuku, godzina lub dzień drogi, krok, podwójny krok, tyczka lub pręt, staje (grecki stadion, dystans, który można przebiec z maksymalną prędkością bez odpoczynku), mila (rzymska równa tysiącowi podwójnych kroków, stąd nazwa).

Początkowo jednostki długości i odległości były jednostkami naturalnymi i subiektywnymi, a nośnikiem ich "wzorców" był mierzący. Z czasem następowała obiektywizacja jednostek. Stopa czy łokieć jako jednostki długości przestawały być długościami stopy czy łokcia określonego człowieka, a stawały się abstraktami - średnią długością stopy lub łokcia pewnej zbiorowości ludzkiej, długością stopy czy łokcia ideału człowieka, pewnymi arbitralnie wybranymi długościami, przyjętymi jako jednostki w obrębie miasta, regionu, plemienia. Wzorce długości były zwykle wzorcami sztucznymi i miały postać prętów, lasek, odcinków zaznaczanych na płytach kamiennych i metalowych.

W Anglii do dziś stosuje się jeszcze, obok systemu metrycznego, tzw. angielski system miar długości

Mila mile	staje furlong, fur	pręt rod	jard yard, yd	metry		jard yard, yd	stopa foot, ft	cal inch, in, "	centymetry
1	8 1	320 40 1	1760 220 5,5	4609,34 201,17 5,0292		1	3 1	36 12 1	91,440 30,4800 2,540000

W Królestwie Kongresowym w latach 1818-1839 stosowano tzw. nowopolskie miary długości

Sznur	pręt	sążeń	łokieć	metry		łokieć	stopa	cal	linia	centymetry
1	10 1	25 2,5 1	75 7,5 3	43,2 4,320 1,728		1	2 1	24 12 1	288 144 12 1	57,60 28,80 2,400 0,2000

Większe jednostki długości używane w Królestwie Kongresowym: 1 mila = 8 staji = 8 534 m, 1 staje = 1 067 m

Wprowadzona pod koniec XVIII w. nowa jednostka długości - metr - była zdefiniowana początkowo jako 1/10 000 000 część długości ćwiartki południka ziemskiego, oparto więc ją na wzorcu naturalnym. W 1889 r. powrócono jednak do wzorca sztucznego definiując metr jako odległość między osiami dwóch głównych kres na wzorcu uznanym przez I Generalną Konferencję Miar (1889 r.) za międzynarodowy prototyp metra przechowywany w Międzynarodowym Biurze Miar (BIPM) w Sèvres pod Paryżem. Prototyp międzynarodowy metra jest wykonany ze stopu platyny (90%) z irydem (10%). Zdefiniowany w ten sposób metr jest o około 0,23 mm krótszy od 1/10 000 000 ćwiartki południka. W 1960 r. XI Gen. Konf. Miar wróciła do wzorca naturalnego definiując metr jako długość równą 1 650 763,73 długości fali w próżni promieniowania odpowiadającego przejściu między poziomami 2p i 5d atomu kryptonu 86. W 1983 r. XVII Gen. Konf. Miar zmieniła definicję metra określając go jako długość drogi przebytej w próżni przez światło w czasie 1/299 792 458 sekundy.

Masę, a ściślej ciężar, przedmiotów początkowo porównywano unosząc je kolejno tą samą ręką lub unosząc je równocześnie, każdy przedmiot inną ręką. Takie porównywanie pozwalało wskazać przedmiot cięższy lub stwierdzić, że obydwa przedmioty są jednakowo ciężkie. Stąd już był tylko krok do pierwszego w historii ludzkości narzędzia pomiarowego - wagi dźwigniowej wynalezionej jeszcze w czasach prehistorycznych. Następny krok to przyjęcie jednostek miary ciężaru czyli wag i ich wzorców czyli odważników i już można było ważyć metodą bezpośredniego porównania. Ten sposób ważenia do dziś jest stosowany.

Pierwszymi wzorcami masy były ziarna roślinne, co ma odbicie w nazwach dawnych jednostek masy: babilońskie sze, greckie κερατιον (keration) czyli ziarno chleba świętojańskiego, stąd karat, obecnie stosowany w jubilerstwie, średniowieczne gran (z łac. granum - ziarno, nasienie i stąd angielskie grain). W Babilonii ukształtował się sześćdziesiątkowy system wag: talent - mina - szekel. System babiloński został przyjęty przez wszystkie ludy basenu Morza Śródziemnego, także przez Greków, którzy wzbogacili go swoimi jednostkami: drachmą, obolem, karatem. Rzymowi zawdzięczamy funt (łac. libra lub as), przejęty przez Średniowiecze, używany jeszcze w czasach nowożytnych, a wyparty dopiero w XX w., i to nie wszędzie, przez kilogram.

W Średniowieczu ukształtowały się dwa rodzaje "funtów": funt handlowy i aptekarski:

Funt handlowy							Funt aptekarski
funt	uncja	łut	drachma	skrupuł	gran		funt	uncja	drachma	skrupuł	gran
1	16 1	32 2 1	128 8 4 1	384 24 12 3 1	9216 576 288 72 24		1	12 1	96 8 1	288 24 3 1	5760 480 60 20

W różnych ośrodkach różna była waga funta handlowego; funt paryski ważył 489,5 g, wiedeński * 560,06 g, pruski * 467,711 g, krakowski * 405,23 g, warszawski * 477 g, nowopolski (używany w Królestwie Kongresowym) * 405,06 g, rosyjski * 409,5124 g. Funt aptekarski miał również różne wagi; w systemie norymberskim ważył 358,5024 g, funt aptekarski wiedeński ważył 420,05 g. Anglicy do dziś używają funta handlowego (ang. pound avoirdupois) wynoszącego dokładnie 453,592 37 g i funta aptekarskiego (ang. apothecaries' pound) oraz troy pound (do ważenia złota i srebra) równych po 373,24 g.

Avoirdupois Weight					Apothecaries' Weight						Troy Weight
pound lb av	ounce oz av	dram dr av	grain gr		pound lb ap	ounce oz ap	drachm dr ap	scruple sc	grain gr		pound lb t	ounce oz t	penny weight dwt	grain gr
1	16 1	256 16 1	7000		1	12 1	96 8 1	288 24 3 1	5760 480 60 20		1	12 1	240 20 1	5760 480 24

Jednostką większą od funta był kamień. Nowopolski kamień liczył 25 funtów, angielski stone * 14 funtów, wiedeński Stein * 20 funtów, Rosjanie używali jednostki pud (пуд) liczącej 40 funtów.

Obecnie stosowaną jednostką masy jest kilogram, wprowadzony pod koniec XVIII w. we Francji i zdefiniowany jako masa jednego decymetra sześciennego czystej wody w temperaturze, w której gęstość wody ma wartość maksymalną (około 4 C). W 1889 r. I Generalna Konferencja Miar zdefiniowała kilogram jako masę międzynarodowego wzorca tej jednostki przechowywanego w Międzynarodowym Biurze Miar w Sèvres pod Paryżem, wykonanego w kształcie walca ze stopu platyny (90%) z irydem (10%).

Czas był początkowo traktowany przez człowieka relatywistycznie, a jego istnienie wynikało z obserwowalnej zmienności: pogody, klimatu, zjawisk astronomicznych, zjawisk biologicznych w świecie otaczającym człowieka i w nim samym, wszelkich wreszcie innych zjawisk. Mierzenie czasu wymagało przyjęcia zegara, czyli ciągu powtarzających się zjawisk. Czas między sąsiednimi zjawiskami stanowi jednostkę lub podwielokrotność jednostki czasu, a pomiar czasu polega na policzeniu zjawisk zegarowych mieszczących się w mierzonym okresie. Trzeba odróżniać pomiar okresu czasu i pomiar czasu w sensie kalendarzowym, czyli ustalanie daty. Pierwszy wymaga tylko ustalenia jednostki czasu, drugi wymaga ustalenia jednostki (takiej samej jak jednostka do pomiaru okresu czasu) oraz zera czyli początku epoki.

Wiele zjawisk astronomicznych, klimatycznych i biologicznych tworzy naturalne zegary i wyznacza naturalne jednostki czasu. Obrót Ziemi dookoła własnej osi wyznacza dobę, obrót Księżyca wokół Ziemi wyznacza miesiąc, obrót Ziemi dookoła Słońca wyznacza rok. Kłopot polega jednak na tym, że główne jednostki czasu: doba, miesiąc i rok, określające rytm życia ludzkiego, są dane w sposób naturalny, a stosunki między nimi nie tylko nie są liczbami całkowitymi, ale ulegają nieznacznym zmianom w czasie. Obecnie wiadomo, że tzw. rok zwrotnikowy, czyli odstęp czasu między dwoma kolejnymi przejściami Słońca przez punkt równonocy wiosennej, wynosił w 1900 r. 365,242 1988 dni i ulega skróceniu o 0,614×10-7 dnia (0,53 sekundy) na stulecie, miesiąc synodyczny, czyli okres miedzy dwoma pełniami Księżyca, zmienia się w granicach od 29,25 dni do 29,83 dni, średnio wynosi 29,530 589 dni, co daje 12-miesięczny rok księżycowy liczący 354,367 dni. Te "nieeleganckie" związki komplikowały kalendarz, czyli rachubę dni i dłuższych okresów czasu. Tradycyjnie przyjmowany system rachuby czasu określa datę trójką: numer dnia w miesiącu, numer miesiąca w roku i numer roku. Odmienny system datowania, zwany long count lub ciągła rachuba czasu, użyty po raz pierwszy przez Majów, polega na podawaniu tylko kolejnego numeru dnia liczonego od pewnej daty zerowej. System ten nie znalazł zastosowania w życiu codziennym i związanej z nią działalności, gdyż człowiek w dacie pragnie znaleźć także informację o porze roku.

Jako podstawową jednostkę czasu już w XVII w. przyjmowano sekundę definiując ją jako 1/86 400 część doby słonecznej. Ruch Ziemi nie jest jednak tak regularny jak tego chcielibyśmy przy ustalaniu skali czasu. W 1832 r. Gauss definiował sekundę jako 1/86 400 część średniej doby słonecznej. W 1954 r. X Generalna Konferencja Miar zdefiniowała sekundę jako 1/31 556 925,9747 część roku zwrotnikowego 1900. Skala pomiarowa czasu określona przez taką sekundę wyznacza czas astronomiczny nazywany także czasem uniwersalnym (UT). W 1967 r. XIII Gen. Konf. Miar zrezygnowała z zegara astronomicznego na rzecz atomowego i zdefiniowała sekundę jako czas trwania 9 192 631 770 okresów promieniowania, odpowiadającego przejściu między dwoma nadsubtelnymi poziomami stanu podstawowego atomu cezu 133Cs. Powstała w ten sposób atomowa skala czasu wyznacza czas atomowy (AT), jej początek ustalono na północ 1 stycznia 1958 r. Okazało się, że skale te różnią się nieznacznie między sobą, różnica jest rzędu sekundy na rok. Dla celów dokładnego wyznaczania i przekazywania czasu zorganizowano służbę czasu.

1.2. Jednostka miary. Międzynarodowy System Jednostek Miar (SI)

Wielkość fizyczna - cecha zjawiska, ciała lub substancji, którą można wyróżnić jakościowo i wyznaczyć ilościowo.

1. Zjawisko, ciało lub substancję, dla których jest określana wielkość, będziemy nazywali obiektem fizycznym.

2. Termin wielkość może mieć znaczenie ogólne, w sensie rodzaju cechy wszystkich obiektów mających daną cechę (np. długość jako cecha odcinków) i znaczenie szczegółowe w sensie cechy, jaką ma dany obiekt (np. długość określonego odcinka). Wielkość w znaczeniu szczegółowym, będziemy nazywali przejawem wielkości.

3. Wyróżnienie jakościowe polega na tym, że można różne obiekty porównywać pod względem cechy tworzącej wielkość, stwierdzając, że dwa obiekty są albo identyczne pod względem danej cechy, tzn. mają jednakowe przejawy wielkości, albo jeden z nich ma daną cechę w stopniu większym niż drugi, tzn. jego przejaw wielkości jest większy.

4. Wyznaczanie ilościowe wielkości fizycznych polega na przyporządkowaniu przejawom wielkości liczb zwanych wartościami liczbowymi, w taki sposób, że jednakowym przejawom przyporządkowuje się liczby większe, przejawom większy - liczby większe. Sposób przyporządkowania wartości liczbowych przejawom wielkości nazywa się skalą pomiarową. Stosowane wielkości fizyczne mają prawie zawsze skale pomiarowe ilorazowe. Dla wielkości o skali ilorazowej sens fizyczny mają działania dodawania i zwielokrotniania przejawów wielkości (np. łączenie odcinków i punktów materialnych oznaczające dodawanie długości i mas) odwzorowywane przez dodawanie wartości liczbowych i mnożenie wartości liczbowych przez liczby rzeczywiste.

5. Obiekty, dla których definiuje się wielkości są obiektami idealizowanymi, np. długość definiuje się dla odcinków, masę - dla punktów materialnych.

Jednostka miary wielkości - zdefiniowany przejaw wielkości, któremu przyporządkowuje się umownie wartość liczbową równą 1.

1. Jednostka miary określa jednoznacznie skalę pomiarowa ilorazową. Wartość liczbowa przejawu wielkości o skali ilorazowej (tj. wielkości mierzalnej według skali ilorazowej) jest krotnością tego przejawu względem przejawu obranego za jednostkę miary .

2. Jednostka miary danej wielkości ma swoją nazwę i symbol (oznaczenie), np. jednostką miary długości jest metr oznaczany symbolem m.

3. Wartości wielkości nadaje się często postać wartości mianowanej, tj. formalnego iloczynu wartości liczbowej i symbolu jednostki. Wartością mianowaną jednostki miary jest

e = 1×e = 1·e = e (1.1)

gdzie e - symbol jednostki miary,

wartością mianowaną przejawu wielkości o wartości liczbowej x jest

x = x×e = x·e = x e (1.2)

Norma ISO 31-0 zaleca zapis wartości mianowanej w postaci

w = {w} [w]

gdzie: w - wartość mianowana, {w} - wartość liczbowa, [w] - jednostka miary wielkości.

4. Wartości mianowane można dodawać, dodając wartości liczbowe, i mnożyć przez liczby rzeczywiste, mnożąc wartość liczbową przez liczbę-mnożnik. Mnożenie wartości mianowanych nie ma sensu w obrębie wielkości.

5. Wartość mianowaną zwykle nazywa się krótko wartością.

System wielkości fizycznych - kompletny zbiór wielkości fizycznych używany do modelowania obiektów fizycznych i zachodzących w nich zjawisk

1. Wielkości tworzące podsystem wystarczający do modelowania obiektów i zjawisk określonej natury fizycznej są nazywane wielkościami tej natury, np. wielkościami mechanicznymi, elektrycznymi, świetlnymi.

2. System wielkości fizycznych obejmuje wielkości podstawowe i wielkości pochodne oraz zależności definiujące wielkości pochodne.

3. System wielkości fizycznych jest zdefiniowany dla obiektów fizycznych idealizowanych, powiązanych uproszczonymi zależnościami, wielkości takiego systemu są używane do modelowania (tj. opisu) obiektów fizycznych realnie istniejących, opis taki, jak każdy model, jest zawsze opisem przybliżonym.

Wielkość podstawowa -jedna z wielkości, które w danym systemie wielkości są umownie uznane jako niezależne od siebie

1. Wielkościami podstawowymi systemu wielkości fizycznych, na których opiera się Międzynarodowy System Jednostek Miar są: długość, czas, masa, natężenie prądu elektrycznego, temperatura, liczność materii i światłość. Pozostałe wielkości podstawowe są zdefiniowane poprzez związki z długością, czasem i masą. Natężenie prądu jest zdefiniowane przez siłę (a ta przez masę, długość i czas) oddziaływania przewodów z prądem elektrycznym, temperatura przez energię w odwracalnym obiegu Carnota, liczność materii przez liczbę cząsteczek, światłość przez energię i długość fali promieniowania świetlnego.

2. Tylko długość i czas są wielkościami prawdziwie niezależnymi, nawet masa jest definiowana przez odwołanie się do długości. Masę bowiem definiuje się jako tę cechę przedmiotów materialnych, pod względem której można je porównywać na wadze dźwigniowej równoramiennej, pojęcie wagi dźwigniowej wymaga uprzedniego zdefiniowania długości i przesunięcia.

Wielkość pochodna - wielkość zdefiniowana w systemie wielkości jako funkcja wielkości podstawowych systemu.

1. Definicja wielkości pochodnej przez inne wielkości (podstawowe lub pochodne uprzednio zdefiniowane) o ustalonych jednostkach, oznaczonych symbolami e1,..., eM opiera się na przyjętej zależności między wartością liczbową y wielkości definiowanej a wartościami liczbowymi x1,..., xM wielkości definiujacych. Zależność ta ma zwykle postać iloczynu potęg

(1.3)

gdzie: 1,..., M * wykładniki potęg, liczby całkowite dodatnie lub ujemne,

K * współczynnik proporcjonalności zależny od jednostki wielkości definiowanej.

2. Zależność (1.3), określoną na wartościach liczbowych, rozszerza się formalnie na wartości mianowane nadając jej postać także iloczynu potęg

(1.4)

gdzie: x1 = x1e1,..., xM = xMeM, y = y ey ,*  wartości mianowane wielkości,

ey * symbol jednostki wielkości definiowanej.

Zmienne x1,..., xM, y  utworzone przez wartości mianowane wielkości, nazywa się wprost wielkościami. Przyjmuje się, że do iloczynu potęg wielkości stosują się formalnie reguły działań na potęgach, co pozwala sprowadzić równanie (1.4) definicyjne do postaci

(1.5)

Jednostkę wielkości pochodnej wybiera się tak, aby było K = 1. Wielkość y spełniającą powyższy warunek nazywa się wielkością koherentną (czyli spójną) z wielkościami. x1,..., xM. Jednostka pochodnej wielkości koherentnej jest równa iloczynowi potęg jednostek wielkości ją definiujących

(1.6)

Zależność powyższa ma charakter formalny i definiuje symbol jednostki ey w języku potęg jednostek e1,..., eM wielkości już zdefiniowanych.

3. Wielkość bezwymiarowa jest wielkością, której jednostka określona zależnością (1.6) jest równa 1.

System (układ) jednostek miar - zbiór jednostek miar wielkości tworzących system wielkości.

Jednostka podstawowa - jednostka miary wielkości podstawowej w systemie wielkości, na którym opiera się system jednostek.

Jednostka pochodna - jednostka miary wielkości pochodnej w systemie wielkości, na którym opiera się system jednostek.

Międzynarodowy System (Układ) Jednostek Miar (SI)- system jednostek, przyjęty i zalecany przez Generalną Konferencję Miar.

1. Jednostki Międzynarodowego Systemu Jednostek Miar są nazywane jednostkami SI.

2. Międzynarodowy System Jednostek Miar (SI) opiera się na systemie wielkości obejmującym: siedem wielkości podstawowych: długość, masa, czas, natężenie prądu elektrycznego, temperatura termodynamiczna, liczność materii i światłość oraz wielkości pochodne, koherentne do wielkości podstawowych.

3. Jednostkami podstawowymi Międzynarodowego Systemu Jednostek Miar są:

(1) jednostka długości metr (symbol m) zdefiniowany jako:

długość drogi przebytej w próżni przez światło w czasie 1/299 792 458 sekundy

(2) jednostka masy kilogram (kg) zdefiniowany jako

masa międzynarodowego wzorca jednostki masy przechowywanego w Międzynarodowym Biurze Miar w Sèvres.

(3) jednostka czasu sekunda (s) zdefiniowana jako

czas równy 9 192 631 770 okresów promieniowania, odpowiadającego przejściu między dwoma nadsubtelnymi poziomami stanu podstawowego atomu cezu 133Cs

(4) jednostka natężenia prądu elektrycznego amper (A) zdefiniowany jako

natężenie prądu elektrycznego nie zmieniającego się, który płynąc w dwóch równoległych prostoliniowych, nieskończenie długich przewodach o przekroju kołowym znikomo małym, umieszczonych w próżni w odległości 1 m (metra) od siebie - wywołałaby między tymi przewodami siłę 2×10-7 N (niutona) na każdy metr długości

(5) jednostka temperatury termodynamicznej kelwin (K) zdefiniowana jako

1/273,16 temperatury termodynamicznej potrójnego punktu wody

(6) jednostka liczności materii mol (mol) zdefiniowany jako

liczność materii występująca, gdy liczba cząstek jest równa liczbie atomów zawartych w masie 0,012 kg 12C (węgla 12).

(7) jednostka światłości kandela (cd) zdefiniowana jako

światłość, jaką ma w kierunku prostopadłym powierzchnia (1/600 000) m2 (metra kwadratowego) promiennika zupełnego w temperaturze krzepnięcia platyny pod ciśnieniem 101 375 Pa (paskali).

4. Niektóre jednostki pochodne SI mają swoje nazwy i symbole

Tablica 1.1. Niektóre jednostki pochodne SI

	Wielkość	Jednostka miary		Zależności między
		nazwa	symbol	jednostkami
	Częstotliwość	herc	Hz	1/s
	Siła	niuton	N	kg⋅m/ s2
	Ciśnienie	paskal	Pa	N/m2
	Energia	dżul	J	N⋅m
	Moc	wat	W	J/s
	Ładunek elektryczny	kulomb	C	A⋅s
	Napięcie elektryczne	wolt	V	W/A
	Rezystancja	om	Ω	V/A
	Pojemność	farad	F	s/Ω
	Indukcyjność	henr	H	Ω⋅s
	Indukcja magnetyczna	tesla	T	V⋅s/m2
	Strumień magnetyczny	weber	Wb	V⋅s
	Strumień świetlny	lumen	lm	cd⋅sr
	Natężenie oświetlenia	luks	lx	lm/m

Nazwy i symbole innych jednostek pochodnych tworzy się korzystając z równania (1.6)

5. Jako wielokrotności i podwielokrotności jednostek SI używa się ich wielokrotności i podwielokrotności dziesiętnych. Nazwy i symbole wielokrotności i podwielokrotności jednostek SI tworzy się przez dodanie do nazwy i symbolu jednostki odpowiedniego przedrostka (Tabl. 1.2). Wyjątek stanowi masa, dla której jednostką jest kilogram (kg), ale nazwy wielokrotności i podwielokrotności jednostki tworzy się w oparciu o gram (g) równy 103 kg.

Tablica 1.2. Wielokrotności i podwielokrotności jednostek SI

	Krotność	Przedrostek		Krotność	Przedrostek
		nazwa	symbol		nazwa	symbol
	1024	yotta	Y	1024	yokto	y
	1021	zetta	Z	1021	zepto	z
	1018	eksa	E	1018	atto	a
	1015	peta	P	1015	femto	f
	1012	tera	T	1012	piko	p
	109	giga	G	109	nano	n
	106	mega	M	106	mikro	μ
	103	kilo	k	103	mili	m
	102	hekto	h	102	centy	c
	101	deka	da	101	decy	d

1.3. Pojęcia podstawowe metrologii

Metrologia jest nauką o pomiarach. Nazwa metrologia pochodzi od greckich słów μετρον * miara i λογος * słowo, nauka. Zamiast metrologia używa się także nazwy miernictwo, od czasownika mierzyć czyli wykonywać pomiary.

Pomiar jest zbiorem operacji mających na celu wyznaczenie wartości wielkości.

Nieodłączną cechą pomiaru jest jego niedokładność, co oznacza, że wartość zmierzona
(otrzymana w wyniku pomiaru) różni się na ogół od wartości prawdziwej wielkości mierzonej. Miarą niedokładności pomiaru są błędy pomiaru: prawdziwy błąd pomiaru i graniczny błąd pomiaru oraz niepewność standardowa pomiaru i niepewność rozszerzona pomiaru. Niedokładności pomiaru będzie poświęcony następny wykład.

Pomiary wykonuje się za pomocą narzędzi. Narzędzia charakterystyczne dla pomiarów nazywają się narzędziami pomiarowymi. Do narzędzi pomiarowych należą: wzorce miar, przyrządy pomiarowe i przetworniki pomiarowe.

Wzorzec miary jest narzędziem, substancją lub zjawiskiem fizycznym odtwarzającym, w granicach określonej niedokładności, przejaw wielkości o określonej wartości. O wzorcu miary (wielkości) mówi się, że odtwarza określoną wartość wielkości. Wzorzec jest wzorcem jednomiarowym, jeżeli odtwarza jedną tylko wartość wielkości i wzorcem wielomiarowym, jeżeli odtwarza wiele wartości wielkości. Deklarowana wartość wielkości, którą odtwarza wzorzec nazywa się wartością nominalną wzorca lub wskazaniem wzorca.

Przykład 1.1

1. Międzynarodowy prototyp metra przechowywany w Międzynarodowym Biurze Miar (BIPM) w Sèvres pod Paryżem i wyskalowana linijka są wzorcami miar długości.

2. Międzynarodowy prototyp kilograma przechowywany w Międzynarodowym Biurze Miar (BIPM) w Sèvres pod Paryżem i odważniki są wzorcami miary masy.

3. Opornik wzorcowy, kondensator wzorcowy, ogniwo wzorcowe są wzorcami miar wielkości elektrycznych.

4. Stałe punkty termometryczne Międzynarodowej Praktycznej Skali Temperatur są wzorcami temperatury.

Przyrząd pomiarowy jest narzędziem pomiarowym przeznaczonym do wykonywania pomiarów, samodzielnie lub w połączeniu z innymi urządzeniami, z udziałem lub bez udziału człowieka, tworzącym zamkniętą całość konstrukcyjną. Najpopularniejszy przyrząd pomiarowy to przyrząd pomiarowy wskazujący czyli miernik, tj. przyrząd formujący sygnał przenoszący odczytywalną przez człowieka informację o wartości wielkości mierzonej. Sygnał formowany przez miernik nazywa się wskazaniem miernika, a część miernika formująca wskazanie * urządzeniem wskazującym. Nazwy mierników tworzy się przez dodanie końcówki -omierz do nazwy wielkości mierzonej (np. długościomierz, częstościomierz) lub do nazwy jednostki mierzonej wielkości (np. amperomierz, woltomierz, sekundomierz).

Wskazanie miernika jest analogowe, jeżeli ma postać przesunięcia wskazówki wzdłuż skali pomiarowej, przesunięcie wskazówki mierzy się porównując je ze wskazami (kreskami) tworzącymi skalę, tak jak przy pomiarze długości wyskalowaną linijką, z tym, że linijka jest wyskalowana w jednostkach długości, skala miernika zaś w jednostkach wielkości mierzonej. Wskazanie jest cyfrowe, jeżeli ma postać ciągu wyświetlanych cyfr, reprezentujących wartość liczbową wielkości mierzonej. Miernik o wskazaniu analogowym nazywa się miernikiem analogowym, miernik o wskazaniu cyfrowym * miernikiem cyfrowym. Na rys. 1.1 schematycznie pokazano widok woltomierza analogowego i woltomierza cyfrowego. Istnieje jeszcze specyficzny rodzaj wskazań analogowych, zwanych analogowo-dyskretnymi, takich że wskazówka może przesuwać się skokowo jak w zegarku.

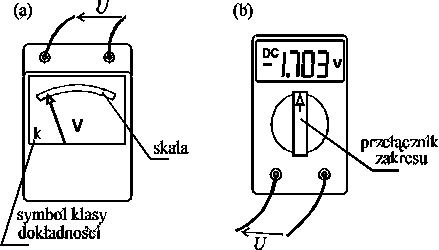
Rys. 1.1. Woltomierz analogowy (a) i cyfrowy (b)

Miernik analogowy może mieć wskazanie analogowo-ciągłe, tzn. jego wskazówka, przy ciągłych zmianach wielkości mierzonej, porusza się ruchem ciągłym, lub analogowo-dykretne, tzn. jego wskazówka, przy ciągłych zmianach wielkości mierzonej, porusza się ruchem skokowym.

Przykład 1. 2

1. Amperomierz magnetoelektryczny, termometr rtęciowy (wskazówką termometru rtęciowego jest koniec słupa rtęci) i waga sprężynowa są miernikami analogowymi.

2. Woltomierz cyfrowy i częstościomierz cyfrowy są miernikami cyfrowymi.

Miernik wielkości x wskazuje wartość
tej wielkości (jest to wartość zmierzona lub wskazanie miernika). Charakterystycznym dla miernika jest jego zakres pomiarowy [Xmin, Xmax], tzn. przedział, wewnątrz którego mieści się wskazanie
miernika. Różnica górnej granicy Xmax i dolnej granicy Xmin zakresu pomiarowego

(1.7)

nazywa się długością zakresu pomiarowego i jest ważnym parametrem miernika. Zwykle zakres pomiarowy zaczyna się od zera [0, Xmax], długość takiego zakresu pomiarowego, równa górnej granicy zakresu pomiarowego Xmm  Xmax, jest nazywana wprost zakresem pomiarowym, a zakres miernika określa się podając tylko Xmax.

Miernik cyfrowy ma wskazanie w postaci wyświetlanych cyfr i kropki (przecinka) między nimi. Pomijając znaczenie przecinka, cyfry tworzą liczbę całkowitą N w zapisie dziesiętnym (wskazanie cyfrowe). Wartość wielkości mierzonej wskazana przez miernik cyfrowy wynosi

(1.8)

gdzie q czyli wartość jednostki ostatniego rzędu (zwana także wartością cyfry, wprost cyfrą, kwantem, czułością lub LSD od ang. least significant digit - najmniej znacząca cyfra) jest prawie zawsze dziesiętną wielokrotnością lub podwielokrotnością jednostki wielkości mierzonej. Wskazanie
odczytuje się uwzględniając położenie wyświetlonej kropki (przecinka). Zakres wskazań cyfrowych [0, Nmax] i zakres wskazań wielkości mierzonej [0, Xmax] miernika cyfrowego zaczyna się zwykle od zera, podaje się go najczęściej jako Xmax, przy czym mierniki cyfrowe są z reguły wielozakresowe. Zmiana zakresu zmienia wartość q jednostki ostatniego rzędu i odpowiednio przesuwa wyświetloną kropkę (przecinek). Charakterystycznym parametrem miernika cyfrowego jest jego liczba cyfr i największa możliwa do wskazania cyfra najbardziej znacząca. Pozostałe cyfry wskazania mogą przyjmować wartości od 0 do 9. Przyjęły się nazwy:

• miernik M cyfrowy czyli miernik o M cyfrach mogących przyjmować wartości 0,1,...,9 każda, dla takiego miernika Nmax  10M - 1, ale jego zakres podaje się jako 10M q, i tak np. woltomierz czterocyfrowy o zakresie Xmax  10 V ma największe wskazanie 9.999 V (tj. Nmax  9999);

• miernik M i 
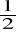
   cyfrowy czyli miernik o M cyfrach mogących przyjmować wartości 0,1,...,9 każda, i pierwszej mogącej przyjmować wartości 0 lub 1, (dla takiego miernika Nmax  2×10M - 1), lub miernik, dla którego największe wskazanie Nmax  2×10M, zakres miernika M i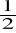 
   cyfrowego wynosi 2×10M q;

• miernik M i 
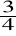
   cyfrowy czyli miernik o M cyfrach mogących przyjmować wartości 0,1,...,9 każda, i pierwszej mogącej przyjmować wartości 0,1,...,K, gdzie K  2,...8, (dla takiego miernika Nmax  K×10M - 1), lub miernik, dla którego największe wskazanie Nmax  K×10M, zakres miernika M i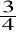 
   cyfrowego wynosi K×10M q.

Każdy miernik z natury jest niedokładny, wskazanie miernika
różni się od wartości prawdziwej wielkości mierzonej.

1.4. Typowe elektryczne przyrządy pomiarowe

Typowymi przyrządami do pomiarów w obwodach prądu stałego są:

• amperomierz czyli przyrząd do pomiaru natężenia prądu (zwykle zamiast nazwy natężenie prądu używa się nazwy skróconej * prąd),

• woltomierz czyli przyrząd do pomiaru napięcia,

• omomierz czyli przyrząd do pomiaru rezystancji.

Typowymi przyrządami do pomiarów w obwodach prądu okresowo zmiennego są:

• amperomierz czyli przyrząd do pomiaru prądu, prawie wyłącznie stosowane są amperomierze mierzące wartość skuteczną prądu,

• woltomierz czyli przyrząd do pomiaru napięcia, prawie wyłącznie stosowane są woltomierze mierzące wartość skuteczną napięcia,

• watomierz czyli przyrząd do pomiaru mocy czynnej, a ściślej wartości średniej okresowej iloczynu napięcia i prądu,

• częstościomierz czyli przyrząd do pomiaru częstotliwości napięcia okresowo zmiennego.

Oprócz wyżej wymienionych jako typowy przyrząd pomiarowy elektryczny można uznać

• oscyloskop zwany także oscylografem czyli przyrząd odwzorowujący rozkład czasowy napięcia krzywą narysowaną na ekranie.

Do niedawna każdy z wymienionych ośmiu przyrządów był w zasadzie budowany jako oddzielny przyrząd, obecnie przeważnie buduje się tzw.

• multimetry czyli przyrządy łączące wiele funkcji, zawsze amperomierza i woltomierza prądu stałego i zmiennego, omomierza i częstościomierza.

Amperomierz, jako przyrząd mierzący prąd, włącza się szeregowo w obwód badany "przepuszczając" przez amperomierz mierzony prąd i (rys. 1.2a). Amperomierz prądu stałego mierzy wartość chwilową (stałą w czasie) prądu i (zwykle oznacza się ją symbolem I). Większość amperomierzy prądu okresowo zmiennego mierzy wartość skuteczną prądu Irms (zwykle oznacza się ją także symbolem I, skrót "rms" pochodzi z ang. root mean square value * pierwiastek z wartości średnio kwadratowej)

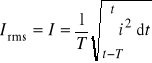
(1.9)

gdzie T * okres zmienności prądu.

Amperomierz jest dwójnikiem pasywnym, dla prądu stałego opisuje się go rezystancją RA, dla prądu zmiennego impedancją ZA (posiadającą zresztą zwykle przeważającą składową rezystancyjną). Włączenie amperomierza do obwodu badanego zmienia wartość mierzonego prądu i, stąd też od amperomierza wymaga się bardzo małej rezystancji (impedancji).

Rys. 1.2. Włączanie mierników: (a) amperomierza, (b) woltomierza, (c) omomierza.

Woltomierz, jako przyrząd mierzący napięcie, włącza się równolegle do badanego dwójnika "przykładając" do woltomierza mierzone napięcie u (rys. 1.2b). Woltomierz prądu stałego mierzy wartość chwilową (stałą w czasie) napięcia u (zwykle oznacza się ją symbolem U). Większość woltomierzy prądu okresowo zmiennego mierzy wartość skuteczną napięcia Urms (zwykle oznacza się ją także symbolem U)

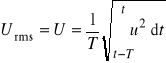
(1.10)

gdzie T * okres zmienności napięcia.

Woltomierz jest dwójnikiem pasywnym, dla prądu stałego opisuje się go rezystancją RV, dla prądu zmiennego impedancją ZV (zwykle modeluje się ją równolegle połączoną rezystancją RV i pojemnością CV). Włączenie woltomierza do obwodu badanego zmienia wartość mierzonego napięcia u, stąd też od woltomierza wymaga się bardzo dużej rezystancji i małej pojemności.

Amperomierze i woltomierze analogowe prądu stałego wymagają zwykle odpowiedniej polaryzacji włączanego prądu i napięcia. Amperomierze i woltomierze cyfrowe prądu stałego wskazują wartość wielkości mierzonej i jej polaryzację. Dla amperomierzy i woltomierzy prądu zmiennego kierunek włączonego prądu i napięcia nie wpływa na wskazanie miernika.

Omomierz, w odróżnieniu od amperomierza i woltomierza, jest dwójnikiem aktywnym. Sposób przyłączania omomierza pokazano na rys. 1.2c.

Watomierz, w odróżnieniu od amperomierza i woltomierza, jest czwórnikiem, ma dwa obwody wejściowe: napięciowy i prądowy. Watomierz mierzy wartość średnią okresową iloczynu napięcia uWU obwodu napięciowego watomierza i prądu iWI obwodu prądowego

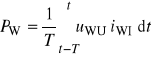
(1.11)

gdzie: PW * wskazanie watomierza,

T * okres napięcia i prądu.

Aby watomierz mierzył moc czynną wydzielaną w dwójniku o napięciu u i prądzie i, włącza się go obwodem napięciowym równolegle i obwodem prądowym szeregowo do badanego dwójnika (rys. 1.3). Możliwe są dwa układy połączeń: układ, w którym prądy watomierza i odbiornika są równe (rys. 1.3a) i układ, w którym napięcia watomierza i odbiornika są równe (rys. 1.3b). Zaniedbując nierówność napięć w układzie równoprądowym i nierówność prądów w układzie równonapięciowym mamy

Rys. 1.3. Dwa sposoby włączania watomierza przy pomiarze mocy odbiornika:

(a) równoprądowy, (b) równonapięciowy.

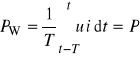
(1.12)

a w szczególnym przypadku prądu harmonicznego

(1.13)

gdzie  * przesunięcie fazowe między napięciem i prądem.

Przy  
 wskazanie watomierza będzie zerowe przy niezerowym napięciu i prądzie; stąd też, jeżeli obwody watomierza nie mają zabezpieczenia przed przeciążeniem, wskazane jest włączanie do obwodu pomiarowego watomierza także woltomierza i amperomierza, jak na rys 1.5. Przy   *
 i  >
 wskazanie watomierza będzie ujemne (wskazówka watomierza analogowego odchyla się w przeciwną stronę względem skali), w takim przypadku należy zmienić kierunek prądu iWI obwodu prądowego watomierza albo kierunek napięcia uWU obwodu napięciowego i wskazanie watomierza przyjmować jako ujemne. Watomierz ma wyróżniony zacisk (kropka na rys. 1.5) w obwodzie prądowym i napięciowym, jeżeli przesunięcie fazowe między prądem wpływającym do wyróżnionego zacisku i napięciem skierowanym do wyróżnionego zacisku spełnia ϕ≤ 
, to wskazanie watomierza jest dodatnie.

Częstościomierz włącza się do obwodu tak jak woltomierz.

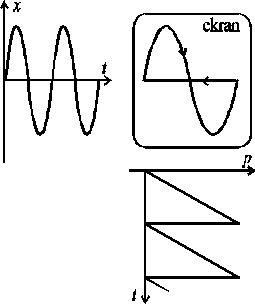
Oscyloskop, zwany także oscylografem, w swojej pierwotnej wersji był przyrządem do obserwacji krzywej wykresu funkcji x(t) opisującej rozkład czasowy wielkości x okresowo zmiennej. Urządzeniem wskazującym oscyloskopu jest ekran z ruchomą plamką świetlną.

Ruch plamki ma dwa stopnie swobody w dwóch osiach prostokątnego układu współrzędnych. Ruch w osi pionowej jest sterowany wielkością x, ruch w osi poziomej * specjalnie uformowaną wielkością okresową p o piłozębnym rozkładzie czasowym (rys. 1.4), zwaną podstawą czasu. Jeżeli okres podstawy czasu jest K-wielokrotnością okresu wielkości obserwowanej, to na ekranie, wskutek nakładania się ruchu plamki świetlnej, powstaje obraz K okresów krzywej x(t). Okres podstawy czasu jest dobierany przez mierzącego, proces tego doboru nazywa się synchronizacją. Tak właśnie działa oscyloskop katodowy, zwany także oscyloskopem analogowym. Odmienny zasadą działania jest coraz częściej używany oscyloskop cyfrowy, ale o nim będziemy mówili w dalszych wykładach.

Rys. 1.4. Powstawanie obrazu krzywej x(t) na ekranie oscyloskopu (x okresowo zmienne).

Oscyloskop włącza się do badanego obwodu tak jak woltomierz.

W dalszych wykładach będziemy bardziej szczegółowo omawiali właściwości tych i innych jeszcze elektrycznych przyrządów pomiarowych, sposoby ich wykorzystania do pomiaru różnych wielkości w różnych sytuacjach. Stosunkowo mało miejsca będziemy poświęcali budowie przyrządów pomiarowych, ograniczając się do krótkiego wyjaśnienia zasady działania wybranych przyrządów.

Literatura

BENTLEY, J,P.: Principles of Measurement Systems. J.Wiley, New York, 1988.

Calibration: Philosophy in Practice. FLUKE CORPORATION, 1994.

DOEBELIN, E.O.: Measurement systems. McGraw-Hill, New York, 1983.

DUDZIEWICZ, J. (red): Etalony i precyzyjne pomiary wielkości elektrycznych. WKŁ, Warszawa, 1982.

Guide to the Expression of Uncertainty in Measurement. ISO 1993, 1995. Tłumaczenie polskie: Wyrażanie niepewności pomiaru. Przewodnik. GUM 1999.

HAGEL, R., ZAKRZEWSKI, J.: Miernictwo dynamiczne. WNT, Warszawa, 1984.

HAGUE, B., FORD, T.R.: Alternating Current Bridge Methods. Pitman, London, 1971

JAWORSKI, J.: Matematyczne podstawy metrologii. WNT, Warszawa, 1979.

JAWORSKI, J.M., MORAWSKI, R.Z., OLĘDZKI, J. S.: Wstęp do metrologii i techniki eksperymentu. WNT. Warszawa, 1992.

JELLONEK, A., GĄSZCZAK, J., ORZESZKOWSKI, Z., RYMASZEWSKI, R.: Podstawy metrologii elektrycznej i elektronicznej. PWN, Warszawa, 1980.

KORN, G.A., KORN, T.M.: Matematyka dla pracowników naukowych i inżynierów. PWN, Warszawa, 1983.

KWIATKOWSKI, W.: Miernictwo elektryczne. Analogowa technika pomiarowa. Oficyna Wydawnicza Politechniki Warszawskiej. Warszawa 1999.

LEBSON, S.: Elektryczne przyrządy pomiarowe. WNT, Warszawa, 1965.

LEBSON, S., SZCZEPANIAK, C.: Kompensatory prądu stałego. WNT, Warszawa, 1965.

MARCYNIUK, A., PASECKI, E., PLUCIŃSKI, M., SZADKOWSKI, B.: Podstawy metrologii elektrycznej. WNT, Warszawa, 1984.

STABROWSKI, M.: Miernictwo elektryczne. Cyfrowa technika pomiarowa. Oficyna Wydawnicza Politechniki Warszawskiej. Warszawa 1999.

SYDENHAM, P.H., ed.: Handbook of Measurement Science. Vol.1. Theoretical Fundamentals. J.Wiley, Chichester, 1982. Tłum. pol.: Podręcznik metrologii. T.1. Podstawy teoretyczne. WKŁ, Warszawa 1988. Vol.2. Practical Fundamentals. J.Wiley, Chichester, 1983. Tłum. pol.: Podręcznik metrologii. T.2. Podstawy praktyczne. WKŁ, Warszawa, 1990.

SYDENHAM, P.H., THORN, R. (ed.): Handbook of Measurement Science. Vol 3. Elements of Change. J.Wiley, Chichester, 1992.

WINIECKI, W.: Organizacja cyfrowych systemów pomiarowych. Oficyna Wydawnicza Politechniki Warszawskiej. Warszawa 1997.

Lilipuci rewidujący Guliwera (Swift, J.: Podróże Guliwera) znajdują w jego kieszeni nieznany im przedmiot i tak o nim piszą w sprawozdaniu: "Człowiek - góra nazwał ten przedmiot zegarkiem, zdaje się wszakże, iż jest to jakieś zwierzę albo Bóg jego, gdyż sam przyznał, że przed każdą czynnością zwykle radzi się swego zegarka."

Liczenie na palcach obu rąk spowodowało wykształcenie się dziesiętnego systemu numeracji, tak jak u wiekszości ludów świata. Można jednak liczyć na palcach rąk i nóg, co prowadzi do systemu dwudziestkowego, tak jak u amerykańskich Majów. Można także liczyć na palcach jednej ręki, pozostałości systemu piątkowego widać wyraźnie w numeracji u Rzymian.

Te i większość dalej podanych wiadomości o kalendarzach i zegarach zaczerpnięto z książki: Zajdler, L.: Dzieje zegara. Wiedza Powszechna, Warszawa 1977.

System ciągłej rachuby dni jest stosowany w astronomii i służbie czasu. Pierwowzór tego systemu to System Dni Juliańskich (JD) opracowany w 1582 r. przez Josepha Scaligera, w systemie tym dniem zerowym jest dzień zaczynający się w południe 1 stycznia 4713 r. przed Chr. (według kalendarza juliańskiego). Obecnie stosuje się System Zmodyfikowanych Dni Juliańskich (MJD) z dniem zerowym rozpoczynającym się o północy 17 listopada 1858 r., dzień ten, poczynając od południa ma datę 2 400 000 J.D. Dzień 1 stycznia 2000 r. to 51 844 MJD.

Janusz M. Jaworski

METROLOGIA ELEKTRYCZNA

Wykład 1

Str. 15

---