Przekształcenia całkowe

1⁰. Wiadomości ogólne: Przekształceniem całkowym będziemy nazywać taką operację, która funkcjom rzeczywistym przyporządkowuje funkcje zespolone za pomocą wzoru:

f(s)=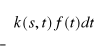

lub piszemy

f(s)= T

przy czym k(s,t) jest jądrem przekształcenia całkowego T, a s=
+ jw {
,

R).

Zbiór funkcji rzeczywistych f(t), gdzie t
(-
;
) ,dla których całka

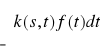
istnieje, oznaczać będziemy przez A i nazywać zbiorem oryginałów lub zbiorem funkcji

T - transformowalnych. Przez B oznaczać będziemy zbiór wszystkich funkcji zespolonych określonych wzorem: F(s)= T
i nazywać go będziemy zbiorem T-transformat.

Przykłady:

1. Jeżeli przyjmujemy za jądro

k(s,t) =

to takie przekształcenie całkowe nazywamy przekształceniem Laplace'a -piszemy wówczas :

[f(t)] =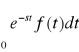
, s =
+ jw.

2. Jeżeli jądro przekształcenia wyraża się wzorem

k(s,t)=

to jest to przekształcenie Laplace'a - Carsona

C[f(t)] = s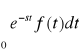
s
Z, s =
+ jw.

3. Jeżeli jądro k(s,t) =
, gdzie
Z , s = jw (
= 0 ), to:

F[f(t)] =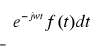

nazywamy przekształceniem Fouriera.

4. Jeżeli jądro przekształcenia k(s,t) =

, s
Z ,

to otrzymujemy przekształcenie Mellina postaci

M[f(t)] =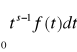
.

Jeżeli A - zbiór funkcji T - transformowanych jest zbiorem liniowym,
dla
,
i zachodzi
tzn. że T jest operatorem liniowym w zbiorze A funkcji transformowanych.

Jeżeli istnieje przekształcenie odwrotne
,

to

F(s) = T[f(t)]=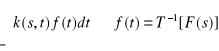

i wtedy

[T[f(t)]] = f(t).

Przekształcenia całkowe stosuje się do rozwiązywania niektórych zagadnień równań:

1. różniczkowych zwyczajnych,

2. różniczkowych cząstkowych,

3. całkowych typu splotowego.

Metoda bezpośrednia

Problem równania problemu - - - - - - - - - - - - - - - - - - - - rozwiązanie -

T równanie problemu

równanie przekształcone rozwiązanie równań przekształconych

2⁰. Przekształcenia Laplace'a

Podstawą rolę w tym przekształceniu odgrywa funkcja

(x) =

(x) - funkcja skoku jednostajnego funkcji Heaviside'a

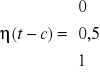
f(t) = t

Twierdzenie1: Jeżeli funkcja f (t) jest całkowalna w pewnym przedziale to funkcja
jest w tym przedziale również całkowalna i ponadto wartości całek są równe

.

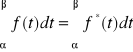
Definicja: (przekształcenia Laplace'a). Przekształceniem Laplace'a funkcji rzeczywistej f(t) zmiennej rzeczywistej t nazywamy funkcje F(s) zmiennej zespolonej s określonej następująco:

,

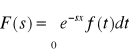
jeżeli ta całka istnieje to funkcja F(s) nazywa się transformacją Laplace'a funkcji f(t) i zapisujemy:

[f(t)]=F(s)

Twierdzenie2: Każda funkcja f(t) oryginalna ma transformację tzn. dla każdej funkcji wziętej z klasy oryginałów istnieje całka niewłaściwa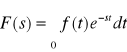
.

Dowód:

Zauważmy, że

.

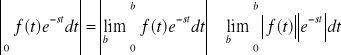
Ponieważ

i

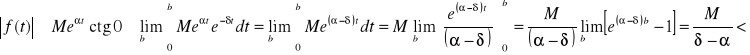
to całka powyższa jest bezwzględnie zbieżna dla
.

Dowiedliśmy, że całka niewłaściwa jest zbieżna bezwzględnie tzn. całka taka istnieje i jest określona dla
takiego że
.

UWAGA! Przekształcenie Laplace'a jako przekształcenie całkowe jest liniowe.

Twierdzenie 3: (o podobieństwie) Jeżeli
[f(t)] = F(s) to dla a>0 zachodzi

Dowód:

.

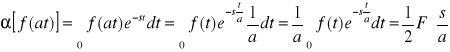
Twierdzenie 4: (o tłumienności) Jeżeli
to dla dowolnego stałego a mamy:

.

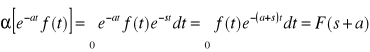
Twierdzenie o przesunięciu rzeczywistym:

,
.

Twierdzenie o przesunięciu zespolonym:

Jeżeli
i
są funkcjami oryginalnymi, to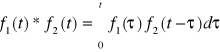

będziemy nazywać splotem funkcji
i
.

Z definicji wynika, że splot posiada następujące własności:

1.
- przemienność

2.

- jednorodność

3.
- łączność

4.
- przemienność szyku dodawania

5.
, t > 0 - (Twierdzenie Titschmarsha)

Twierdzenie Borela: Transformata splotu dwóch funkcji oryginalnych jest równa iloczynowi ich transformat:

Można dowieść, że jeżeli F(s) jest transformatą Laplace'a funkcji oryginalnej f(t) tzn.

, to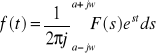
(*) gdzie a jest dodatnią liczbą rzeczywistą tak dobraną, że funkcja F(s) jest holomorficzna na prawo od x = a, przy czym całkę należy rozumieć następująco:

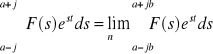
Wzór (*) pozwala obliczyć oryginał z równości:

,

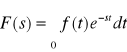
co można zapisać skrótowo w następujący sposób:

(**).

Funkcja f(t) jest więc rozwiązaniem równania całkowego (**) i określona jest wzorem (*).

Łatwo zauważyć, że przekształcenie odwrotne jest przekształceniem liniowym na wzór (*) tzn.

.

Twierdzenie: Jeżeli liczby
są biegunami funkcji F(s), która jest transformatą funkcji oryginalnej f(t), to f(t) wyraża się wzorem:

,

pod warunkiem, że funkcja F(s) nie ma poza tymi biegunami innych punktów osobliwych.

UWAGA 1: Jeżeli funkcja F(s) ma nieskończenie wiele biegunów izolowanych , czyli takich, że w otoczeniu każdego bieguna nie ma innych biegunów oraz funkcja f(t) nie ma punktów istotnie osobliwych to mamy:

,

przy czym można wykazać, że określony szereg jest zbieżny.

UWAGA 2: Jeżeli funkcja F(s) jest funkcja wymierną o współczynnikach rzeczywistych i liczba zespolona s_k jest biegunem funkcji F(s), to liczba sprzężona
jest biegunem tej funkcji oraz zachodzi wzór:

.

Twierdzenie o rozkładzie: Jeżeli F(s) jest funkcją wymierną właściwą
postaci
i jeżeli wielomian Q(s) ma tylko pojedyncze pierwiastki
, to transformata odwrotna (funkcja oryginalna) wyraża się wzorem:

.

Wniosek: Jeżeli wśród biegunów pojedynczych funkcji wymiernej F(s) będzie s₀ = 0 to funkcje F(s) można przedstawić w postaci:

, Q(s)
0, k=1,2,3.....,n.

Ponieważ
, więc

.

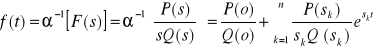
Wniosek: Jeżeli F(s) jest funkcją wymiernie właściwą w rzeczywistych współczynnikach

,

to na mocy uwagi 2:

.

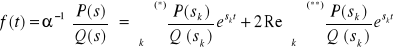
gdzie
jest rozciągnięte na wszystkie bieguny rzeczywiste, a
jest rozciągnięta na bieguny urojone sprzężone.

UWAGA 3: Jeżeli
oznaczymy biegunem funkcji wymiernej
, a ich krotność przez
to:

.

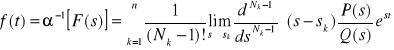
UWAGA 4: Jeżeli istnieje transformata odwrotna Laplace'a to twierdzenie Borela ma postać:

,

można zapisać:

.

Zestawienie ważniejszych własności przekształceń Laplace'a:

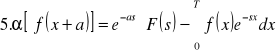
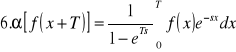
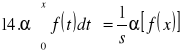
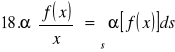
TABLICE TRANSFORMACJI LAPLACE'A:

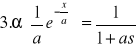
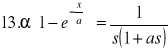
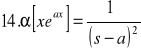
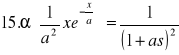
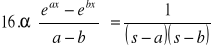
3⁰. Całka Fouriera (wzór całkowy Fouriera)

Twierdzenie Fouriera: Jeżeli funkcja f jest bezwzględnie całkowalna w przedziale
spełniająca w dowolnym przedziale skończonym [a;b] warunki Dirichleta

to można ją przedstawić za pomocą wzoru całkowego Fouriera:

(1)
.

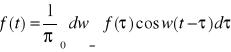
Po dokonaniu przekształcenia

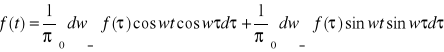
mamy tzw. całkę Fouriera

(2)
,

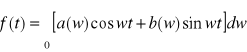
gdzie

(3)
,

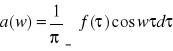
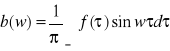
Wzór (2) będący analogią (podobieństwem) szeregu Fouriera dla funkcji f w przedziale ograniczonym orzeka, że funkcje f w nieograniczonym przedziale można rozłożyć na drganie harmoniczne o częstotliwości zmieniającej się od 0 do
. Funkcja a(w) i b(w) nazywa się współczynnikami widma ciągłego funkcji.

Własności:

a(-w) = a(w) - funkcja parzysta

-b(-w) = b(w) - funkcja nieparzysta

Funkcja, której wartość w każdym punkcie jest równa wartości jej całki Fouriera nazywamy rozwijalną na całkę Fouriera. Dla takiej funkcji zachodzi równość będąca analogią równości Parsevala:

(4)
,

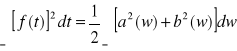
jeżeli funkcja f, na mocy wzoru(3) jest parzysta to b(w)=0 i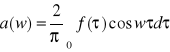
, wówczas otrzymujemy tzw. cosinusowy wzór Fouriera:

.

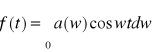
Jeżeli funkcja f jest nieparzysta, to a(w)=0 i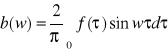
i wtedy mamy sinusowy wzór całkowy Fouriera:

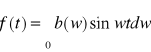
4⁰.Przekształcenia Fouriera.

Jeżeli każdy skończony przedział [a;b] można podzielić na skończoną liczbę przedziałów otwartych, w których funkcja f jest monotoniczna oraz w każdym punkcie [a;b] zachodzi

przy czym f jest bezwzględnie całkowalna w (-
;
) to funkcję:

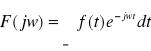
nazywamy transformatą Fouriera funkcji f i oznaczymy:
.

Funkcję F(jw) nazywamy też widmem funkcji f(t) i można ją przedstawić korzystając ze wzoru (2) następująco:

(5)
,

gdzie a(w) i b(w) są współczynnikami funkcji określonej wzorem (3).

Odwrotne przekształcenie Fouriera jest określone:

i przyporządkowuje ona funkcji
funkcję rzeczywistą.

Jeżeli f(t) spełnia założenie Fouriera ,to zachodzi:

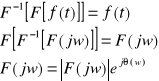
F(jw) - charakterystyka widmowa, gęstość widma, widmo;

- charakterystyka amplitudowa, widmo amplitudowe;

(w) - charakterystyka fazowa i widmo fazowe.

Ze wzoru (5) mamy
, ponieważ

Z drugiej strony

.

gdzie

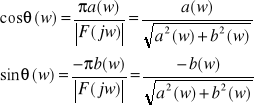
Jeżeli f(t) jest funkcją rzeczywistą to
jest funkcją parzystą ,
(w) jest funkcją nieparzystą zmiennej w.

Jeżeli f(t) jest parzysta to jej widmo jest rzeczywiste. Jeżeli f(t) jest nieparzysta to jej widmo jest urojone.

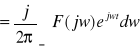
Można dowieść własności przekształceń Fouriera:

1⁰ Liniowość

2⁰ Pochodne transformaty

k=1....n

3⁰ Przesuniecie w transformacie

4⁰ mnożenie f(t) przez

5⁰ F - transformata pochodnej

przez założenie

UWAGA: Przekształcenie Fouriera postaci odwrotnej bywa również określone wzorem

a)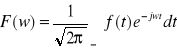


,

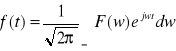
b)
,

Przekształcenie Fouriera stosujemy wówczas gdy poszukiwana funkcja (lub jej pochodne) dąży do nieskończoności dostatecznie szybko, tak aby istniały odpowiednie całki.

Jeżeli f(t) jest F - transformatą równą 0 dla t<0, to z porównania odpowiednich wzorów otrzymamy związek między transformatą Fouriera i Laplace'a:

=
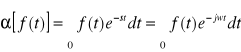
przy f(t)=0 dla t<0 i s=jw.

5⁰. Inne przekształcenia całkowe

Związek między przekształceniem Carsona i przekształceniem Laplace'a jest następujący:

=
.

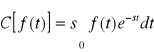
Stąd

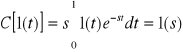
, s - liczba zespolona, podczas, gdy

Związek miedzy przekształceniem Carsona i Fouriera czyli

, f(t)=0 dla t<0 i s=jw.

Przypomnijmy przekształcenie Mellina

,

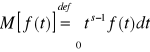
gdzie : f(t) - funkcja rzeczywista

M[f(t)] - transformata Melina.

Podstawiamy za
i otrzymujemy

Mamy więc: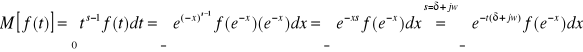
.

Licząc dalej otrzymujemy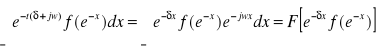

.

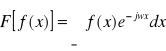
Poprawki i ulepszenia: Jakub Kozikowski i Krzysztof Klejdysz

C

---