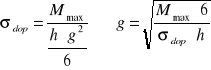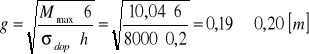OBLICZENIE ŚWIATŁA JAZU:

a - wysokość warstwy przelewowej [m]

h - dopuszczalne piętrzenie wody miarodajnej [m]

k - wysokość prędkości [m]

μ₁ - współczynnik wydatku =0,83 (dla jazu stałego i ruchomego)

μ₂ - współczynnik wydatku =0,67 (dla jazu stałego) =0,62 (dla jazu ruchomego)

I.) Stałego:

rys. 3. Schemat to obliczenia światła jazu stałego

h - dopuszczalne piętrzenie wody miarodajnej

232,15 - rzędna dna

234,90 - rzędna piętrzenia miarodajnego

235,39 - rzędna Q_3%

k=(α⋅v_m²)/(2⋅g)=(1⋅1,826²)/(2⋅9,81)=0,17

α - współczynnik Sant-Venanta

II.) Ruchomego:

rys. 4. Schemat to obliczenia światła jazu ruchomego

OBLICZENIE WSPÓŁCZYNNIKA DŁAWIENIA BOCZNEGO

Warunek:

1.)	Brz>(bu+df)⋅n 12,20<(3,06+1,0)⋅2=8,12
2.)	hz/H0≤0,85÷0,90 hz=a=2,74 H0=hz+h+k=2,74+0,50+0,17=3,41 2,74/3,41=0,80<0,85

Ponieważ obydwa warunki zostały spełnione współczynnik liczymy ze wzoru:

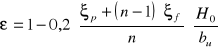
n=2 - ilość sekcji przelewowych

d_f =1,0 - szerokość filara

ξp - współczynnik odpływu przyczółka	ξf - współczynnik odpływu filara
ξp=0,70	ξf=0,51
Przyjęte z „Jazy zasady projektowania”, cz I Prof. T. Bednarczyk.

- przyjmuję b_uε=3,55 m

OBLICZENIE WYSOKOŚCI PODNIESIENIA ZASUWY

rys. 5. Schemat to obliczenia wysokości podniesienia zasuwy

ε' - współczynnik dławienia pionowego (odczytany z tabeli w zależności e/T)

Przyjmuję:

e=0,50 [m]

T=234,90-232,65-0,5⋅e=2,25-0,5⋅0,50=2,00

E/T=0,50/2,00=0,25 → ε'=0,622

OBLICZENIE PIERWSZEJ I DRUGIEJ GŁĘBOKOŚCI SPRZĘŻONEJ

rys. 6. Schemat to obliczenia pierwszej i drugiej głębokości sprężonej

h_s>h₂ - odskok zatopiony

h_s<h₂ - odskok nie zatopiony

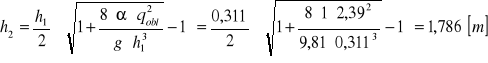
• odskok nie zatopiony, dlatego należy zaprojektować nieckę wypadową

rys. 7. Schemat to obliczenia głębokości niecki wypadowej

Warunek:

Przyjmuję d_n=0,35 [m]

zakładam h₁=0,342 [m]

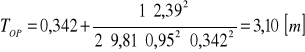
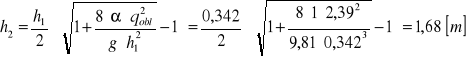
OBLICZENIE DŁUGOŚCI NIECKI WYPADOWEJ

rys. 8. Schemat to obliczenia długości niecki wypadowej

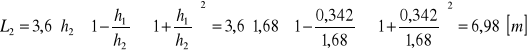
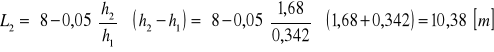
OBLICZENIE DŁUGOŚCI DORGI FILTRACJI POD BUDOWLĄ

rys. 9. Schemat to obliczenia długości drogi filtracji pod budowlą

1.) Metoda Bligh'a:

C_B - współczynnik ustalony przez autora, zależny od rodzaju gruntu (dla żwirów 5Ⴘ9)

- warunek spełniony

2.) Metoda Lena:

C_L - współczynnik ustalony przez autora, zależny od rodzaju gruntu (dla żwiru grubego 3)

- warunek spełniony

OBLICZENIE WNĘK REMONTOWYCH

rys. 10. Schemat to obliczenia wnęk remontowych

SPRAWDZENIE GRUBOŚCI NIESKI WYPADOWEJ

rys. 11. Schemat to sprawdzenia grubości niecki wypadowej

k_w -współczynnik na wypłynięcie dla IV klasy budowli =1,05

Ponieważ minimalna grubość płyty może być 0,30 [m] dlatego przyjmuję tą wartość.

ZESTAWIENIE CIĘŻARÓW

rys. 15. Zestawienie ciężarów

Ciężar doku	GD=2950,8 [kN]
Ciężar filara	GF=467,3 [kN]
Ciężar zasuw	GZ=32,2 [kN]
Ciężar urządzenia wyciągowego	GW=24,0 [kN]
Ciężar kładki	GK=8,4 [kN]
Ciężar wody górnej	GWG=403,6 [kN]
Ciężar wody dolnej	GWD=1422,6 [kN]

Parcie wody górnej	H1=541,0 [kN]
Parcie wody dolnej	H1=192,9 [kN]
Parcie filtracyjne	PF=849,9 [kN]
Siła wyporu	PW=806,1 [kN]

Sprawdzenie warunku na przesunięcie:

μ - współczynnik tarcia na styku fundamentu z podłożem; =0,55 wg PN 83/B - 03010 tab. 3

dla gruntów niespoistych, żwiry i pospółki, i betonu chropowatego.

G= G_D+ G_F+ G_Z+ G_W+ G_K+ G_WG+ G_WD

G =2950,8+467,3+32,2+24,0+8,4+403,6+1422,6=5308,9 [kN]

U= P_F+ P_W=849,9+806,1=1656,0 [kN]

W_x=H₁-H₂=541,0-192,9=348,1 [kN]

Sprawdzenie warunku na obrót:

Tabela 1. Zestawienie momentów utrzymujących

Lp.	Siła [kN]	Ramie siły [m]	Moment [kNm]
1	GD=2950,8 [kN]	6,62	19534,3
2	GF=467,3 [kN]	10,74	5018,8
3	GZ=32,2 [kN]	11,00	354,2
4	GW=24,0 [kN]	11,00	264,0
5	GK=8,4 [kN]	10,10	84,8
6	GWG=403,6 [kN]	12,20	493,9
7	GWD=1422,6 [kN]	5,42	7710,5
8	H1=192,9 [kN]	0,68	131,2
			33591,7

Tabela 1. Zestawienie momentów obracających

Lp.	Siła [kN]	Ramie siły [m]	Moment [kNm]
1	H1=541,0 [kN]	1,12	6911,3
2	PF=849,9 [kN]	8,64	7343,1
3	PW=806,1 [kN]	6,62	5336,4
			19590,8

OBLICZENIE DŁUGOŚCI DROGI FILTRACJI WOKÓŁ PRZYCZÓŁKA

rys. 16. Filtracja wokół przyczółka

α - współczynnik zmniejszający zależny od klasy budowli (dla klasy IV α=0,6)

C_L - współczynnik ustalony przez autora, zależny od rodzaju gruntu (dla żwiru grubego 4)

warunek spełniony

UBEZPIECZENIE OD STRONY DOLNEJ I GÓRNEJ WODY

rys. 17. Ubezpieczenie od strony dolnej i górnej wody

od strony górnej wody

ponieważ

przyjmuję długość materaca faszynowego równą 4,0 m

Podział płyt w dnie:

długość płyty

przyjęto wymiary płyt - długość 3,75 m

- szerokość 2,025 m

Ogółem będzie 8 płyt

Podział płyt na skarpach:

przyjęto wymiary płyt - długość 7,66 m

- szerokość 2,00 m

- grubość 0,30 m

od strony dolnej wody

L≤20 m dlatego przyjmuję tę wartość

L=20 m

Długość materaca faszynowego wynosi 10 m, z długości L

Podział płyt w dnie:

długość płyty

przyjęto wymiary płyt - długość 5,00 m

- szerokość 2,025 m

Ogółem będzie 8 płyt

Podział płyt na skarpach:

przyjęto wymiary płyt - długość 3,39 m

- szerokość 2,50 m

- grubość 0,30 m

Grubości płyt i materacy faszynowych w dnie rzeki:

	Powyżej jazu [cm]	Poniżej jazu [cm]
Grubość płyty	30	40
Grubość materaca faszynowego	60	100

232,15

234,90

PN

P=2,75

a=0,49

h=0,50

235,39

235,89

k=0,17

k=0,17

235,89

235,39

h=0,50

a=2,74

P=0,50

PN

234,90

232,15

45^o

d_f

h₁

PN

h₂

e

T

e

PN

234,90

232,65

T=2,0

e=0,50

PN

234,90

232,65

h_s=1,38

h_s1,38

h₁

h₂

t=2,75

p_d=0,85

PN

234,90

232,15

V≈0

d_n

T_OL

T_OP

SNW

P=0,50

d_n=0,35

SNW

L₁

h₁=0,342

h₂=1,68

H₀=2,25

e=0,50

PN

234,90

232,65

SNW

L_n

L₂

233,53

234,90

PN

d_n=0,35

SNW

0,30

H=1,37

0

1

2

3

234,90

PN

H=2,75

h=0,2

F

b_uε

W

W

l=3,93

g

q

g

x

g

g

Q

1 m

1 m

Q'

x

---