BELKA STROPOWA
1. Obciążenia przypadające na żebro.
Zakładam rozstaw belek stropowych co 2,0m (7 belek)
Odsunięcie od słupa: 0,3m.
qk qd
Opis [kN/mb] γf [kN/mb]
I Obciążenia stałe
-płyta żelbetowa: 0,1*2,0*25 5,00 1,35 6,75
-wykończenie: 2,0*0,6 1,20 1,35 1,62
-Obciążenia użytkowe 2,0*3,5 7,00 1,5 10,50
Σ: 13,2 18,87
Ciężar własny żebra gbelki = 9,81m/s2 * 57,1 kg/m * 1,35 = 0,76 kN/m wobec czego Qd=19,63 kN/m.
2. Schemat statyczny i obciążenia.
Schemat statyczny żebra to belka obustronnie podparta.
Schemat statyczny:
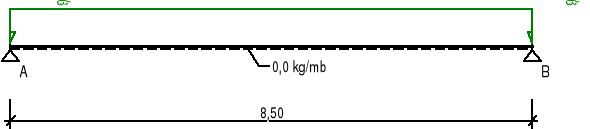
Momenty zginające [kNm]:

Siły poprzeczne [kN]:
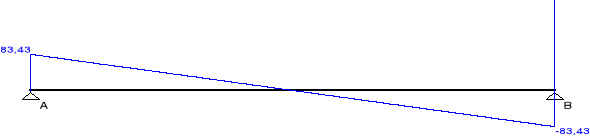
Maksymalny na środku przęsła:
![]()
Reakcje podporowe:
![]()
3. Wymiarowanie belki stropowej.
Wymiary: L=12,6 m B=8,5 m
Gatunek stali: S275 fy= 275 Mpa E=210000 MPa
γM0=1,0 γM1=1,0
Przyjmuję kształtownik IPE 360
Wymiary: h=360 mm
b=170 mm
tf=12,7 mm
tw=8 mm
r= 18,0 mm
A=72,7 cm2
Iy,ch= 16270 cm4 Iz,ch=1040 cm4
Wel,y=904 cm3
Masa belki: 57,1 kg/m
3.1. Sprawdzenie stanu granicznego nośności belki stropowej z dwuteownika walcowanego, zabezpieczonej przed zwichrzeniem.
3.1.1. Klasa przekroju.
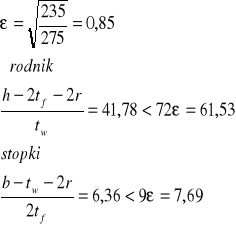
Cały przekrój klasy 1
3.1.2. Nośność obliczeniowa przekroju przy zginaniu.
Wpl,y = Wel,y x 1,13 = 1021,52cm3
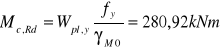
Rozkład momentu zginającego i siły tnącej jest taki, że można nie brać pod uwagę wpływu siły poprzecznej na nośność przekroju przy zginaniu.
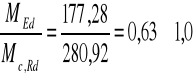
warunek jest spełniony.
3.1.3. Stan graniczny nośności przy ścinaniu na podporze
przyjęto η =1,2
![]()
środnik nie jest wrażliwy na utratę stateczności przy ścinaniu
Pole przekroju czynnego
![]()
![]()
lecz nie mniej niż
![]()
Obliczeniowa nośność przekroju przy ścinaniu
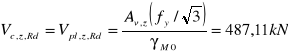
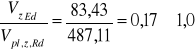
warunek jest spełniony
3.2 Sprawdzenie stanu granicznego użytkowalności.
Kombinacja obciążeń (charakterystyczne):
Gk+Qk=13,68 kN/m

wartość ugięcia nie powinna przekraczać wartości granicznej
![]()
warunek jest spełniony
PODCIĄG - BLACHOWNICA
4. Obliczenia statyczne podciągu.
4.1. Założenie wymiarów blachownicy.
h=1160 mm
b=250 mm
tf=20 mm
tw=10 mm
hw= 1160 mm
A=0,001696m3
ρ=7850 kg/m3
γ=13,3 kg/mb
4.2. Schemat statyczny i obciążenia.
Schemat statyczny (ciężar belki uwzględniony automatycznie):
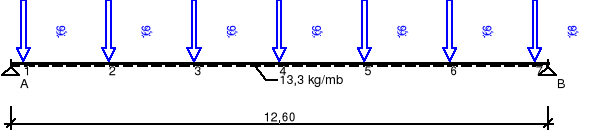
Momenty zginające [kNm]:

Maksymalny moment na środku przęsła:
![]()
Siły poprzeczne [kN]:
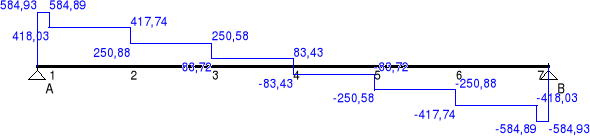
Maksymalna siła poprzeczna:
![]()
5. Wymiarowanie podciągu.
5.1. Sprawdzenie stanu granicznego nośności podciągu spawanego, stężonego bocznie punktowo, w przekroju przęsłowym i podporowym.
5.1.1. Klasa przekroju przy zginaniu.
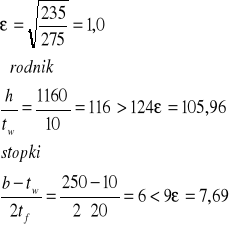
Ponieważ środnik jest klasy 4, to cały przekrój jest klasy 4.
5.1.2. Nośność obliczeniowa przekroju klasy 4 przy zginaniu.
Stateczność miejscowa środnika
Parametr niestateczności zginanej ścianki usztywnionej przy wspólczynniku rozkładu naprężeń Ψ=-1.
stąd kδ= 23,9
Smukłość płytowa ścianki:
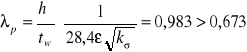
Współczynnik redukcyjny:
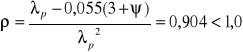
Szerokość strefy ściskanej i rozciąganej środnika
![]()
Szerokość współpracująca
![]()
Szerokość części przylegających do pasa ściskanego be1 i do osi obojętnej be2
![]()
![]()
Przesunięcie położenia osi obojętnej do pasa ściskanego przekroju współpracującego
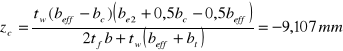
![]()
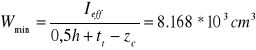
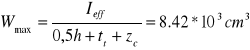
Nośność obliczeniowa przekroju klasy 4 przy zginaniu względem osi y-y:
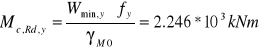
5.1.3. Uproszczona ocena zwichrzenia w budynkach.
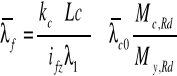
Rozkład momentu zginającego w przęśle między stężeniami jest bliski stałemu, tym samym można przyjąć:
kc=1
Lc= 2m
Iz=52180000mm4
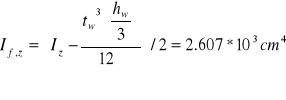
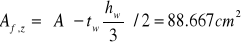
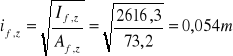
![]()
Obliczenie warunku na zwichrzenie miejscowe
![]()
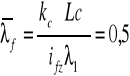
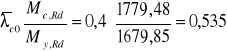
![]()
warunek jest spełniony
5.1.4. Sprawdzenie nośności podciągu przy zginaniu w przęśle.
![]()
![]()
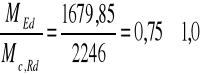
warunek jest spełniony
5.1.5. Sprawdzenie nośności podciągu przy ścinaniu na podporze.
Maksymalna wartość siły tnącej występuje w przekroju przypodporowym.
V = 584,93kN
przyjęto η =1,2
![]()
obliczeniowa nośność przekroju przy ścinaniu
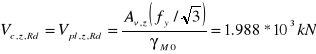
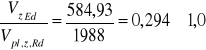
warunek jest spełniony
5.2. Sprawdzenie stanu granicznego użytkowalności.
Kombinacja obciążeń(charakterystyczne):
Gk+Qk= 68,81 kN/m
Iy= 4782080000mm4
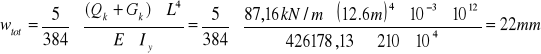
![]()
![]()
![]()
wartość ugięcia nie powinna przekraczać wartości granicznej
![]()
warunek jest spełniony
5.3. Sprawdzenie nośności spoin pachwinowych łączących pas ze środnikiem w strefie przypodporowej.
Spoina łącząca musi spełniać następujący warunek:
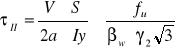
warunek spełniony dla a=5mm
Stal S275
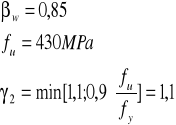
Jako maksymalną siłę tnącą przyjmuję siłę w podporze V = 584,93kN.
Obliczam moment statyczny przekroju pasa względem osi obojętnej, dla przekroju przypodporowego:
![]()
Ix= 4782080000mm4
Po przekształceniu
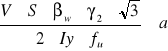
stąd
![]()
Ostatecznie przyjęto połączenie pasa ze środnikiem spoiną pachwinową ciągłą o grubości 5mm.
5.4. Dobór przekroju żebra w miejscu połączenia belek stropowych z podciągiem.
W miejscu połączenia belek stropowych z podciągiem, nad słupem stosuję żebra pełne o wymiarach:
hż1=1160mm
bż1=120mm
tż1=tw=10mm
W pozostałych miejscach stosuję żebra skrócone od dołu o wymiarach:
hż1=1140mm
bż1=120mm
tż1=tw=10mm
6. Wymiarowanie połączenia belki stropowej z podciągiem
Płaszczyzna ścinania przechodzi przez gwintowaną część śruby więc
αv=0,5
Zakładam 3 śruby leżące na jednej osi pionowej szeregu
Śruby klasy A, kat. 6.8,M16
A=As=161 mm2
d=16 mm
d0=17 mm
fub=600 MPa
Obliczeniowa nośność śrub na ścinanie
![]()
Obliczeniowa nośność na docisk
-odległość od osi skrajnej do krawędzi czołowej w poziomie - e1=60 mm
-rozstaw śrub w pionie - p2=100 mm
-odległość od śruby skrajnej do krawędzi bocznej w pionie - e2=80 mm
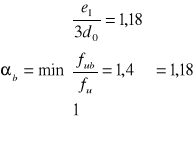
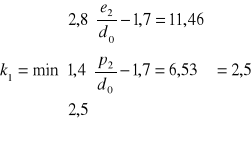
nośność obliczeniowa pojedynczej śruby na docisk: ![]()
obliczeniowa nośnośc grupy śrub na docisk: ![]()
Warunek nośności połączenia
Nj,Rd= min (Fv,Rd,Fb,Rd)=115,92kN
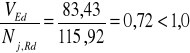
warunek jest spełniony
9
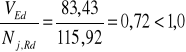
Wyszukiwarka
Podobne podstrony:
projekt 2 Karol, Studia, Sem 4, Semestr IV, Stal, Projekt 2
DoZadania5, Studia, Sem 4, Semestr IV, Mechanika gruntów, Projekt
Pytania 21-25, Studia, Sem 4, Semestr IV, Żelbet, Egzamin, Nowy folder
Skan Projektu od dr Kamela, studia, Budownctwo, Semestr IV, KB, projekty
obliczenia, STUDIA, Polibuda - semestr IV, Konstrukcje Betonowe, Projekt, PŁYTA, sem v
projekt budownictwo strop, Studia, Sem 3, III, III Semestr, Budownictwo ogólne I, bud ogólne
strona tytułowa-projekt, STUDIA, Polibuda - semestr IV, Instalacje Budowlane
Konstrukcje betonowe projekt, STUDIA, Polibuda - semestr IV, Konstrukcje Betonowe, Projekt, PŁYTA
grunty sprawko, Studia, Sem 4, Semestr 4 RŁ, gleba, sprawka i inne
PWiK - Opis techniczny, Budownictwo S1, Semestr IV, PWiK, Projekt, Projekt 4
plan szkolenia, WSPiA Poznań (2009 - 2012), ROK 2, semestr IV letni, Projekt edukacyjny w pracy dora
AI test1, Studia, ZiIP, SEMESTR IV, semestr IV zaoczny, Metody szt. int
Zad -rozliczenie niedoborów i szkód, Studia, ZiIP, SEMESTR IV, Finanse i Rachunkowość
Podstawy woiągów i kanalizacji 15.11.2007, STUDIA, Polibuda - semestr IV, Podstawy Woiągów i Kanaliz
PYTANIA skoczek, STUDIA, Polibuda - semestr IV, Organizacja Produkcji Budowlanej, obp zaliczenie
fiz1, Studia, Sem 2, SEMESTR II, SEMESTR I, fizyka, haksy, Fiza
więcej podobnych podstron