1.Cel ćwiczenia

Zapoznanie się z podstawami teoretycznymi na skręcanie oraz ze sposobami pomiaru kąta skręcania dla obliczenia modułu sprężystości postaciowej G i liczby Poissona ν.

2. Podstawowe definicje

Moduł sprężystości postaciowej G, w przypadku odkształceń sprężystych i proporcjonalnych, definiuje się jako

a w przypadku odkształceń sprężystych i nieproporcjonalnych oraz dla praktycznych pomiarów G definiuje się jako

Teoretycznie
ale ponieważ
jest pochodną funkcji
stąd można te funkcje interpretować jako styczną do krzywej

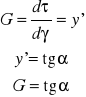
3. wyprowadzenie zależności między G i E

wydłużenie

wydłużenie

z trójkąta A'OD'

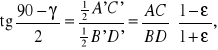
ponieważ AC = BD, to

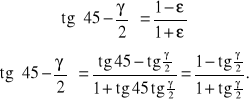
Korzystając z przybliżenia
otrzymujemy

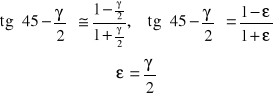
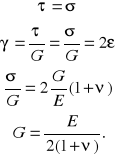
4. Schemat aparatu lusterkowego Martensa do pomiaru kąta skręcenia

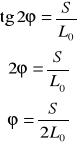
5. Schemat urządzenia do próby skręcania

6. Tabela pomiarów

Próbka poddana skręcaniu miała średnicę d₀ = 8 mm. Wykonała ona 6 obrotów i uległa ukręceniu.

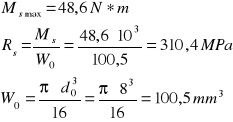
Ms	Ms	n	Φ	Rs
[kgN]	[Nm]	1	[rad]	[MPa]
220	22	2	6,28	-
270	27	3	12,54	-
280	28	4	18,84	-
290	29	5	25,12	-
300	30	6	31,4	-
308	30,8	7	37,68	-
310	31	8	43,86	-
312	31,2	9	48,6	310,4

8. Przykłady obliczeń

Dane:

1. M_s dla F = 1 daN

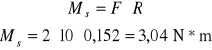
2. ϕ₁ dla F = 1 daN

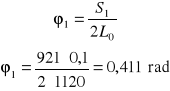
3. dla F = 1 daN

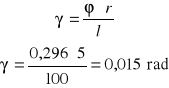
4. τ dla F = 1 daN

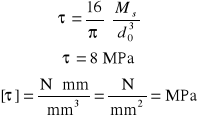
5. σ dla F = 1 daN

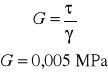
9. Wykresy

1. wykres histerezy sprężystej przy skręcaniu
   

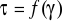
2. wykres skręcania
   

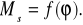
1

1

γ

τ