Definicja funkcji odwrotnej

Niech
będzie funkcją wzajemnie jednoznaczną. Wówczas zbiór
jest funkcją wzajemnie jednoznaczną odwzorowującą zbiór
na zbiór
. Nazywamy go funkcją odwrotną do funkcji
i oznaczamy jako
.

Definicja granicy funkcji

Niech x₀ ∈ (Df)^d (x₀ ∈ (Df)^d-, x₀ ∈ (Df)^d+ ). Mówimy, że g ∈ R jest granicą (granicą lewostronną, prawostronną) funkcji f w punkcie x₀, gdy

(
,
).

Fakt, że g jest granicą (granicą lewostronną, prawostronną) zapisujemy symbolicznie

(
,
).

Definicja szeregu

Niech
będzie ciągiem liczbowym. Szeregiem liczbowym nazywamy ciąg
gdzie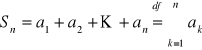
. Taki szereg liczbowy oznaczamy symbolem
. Liczbę
nazywamy n-tym wyrazem, a liczbę
- n-tą sumą tego szeregu.

Definicja szeregu zbieżnego, rozbieżnego i sumy szeregu

Mówimy, że szereg
jest zbieżny jeśli ciąg
jest zbieżny do granicy skończonej zwanej w tym przypadku sumą szeregu i oznaczanej symbolem identycznym z symbolem szeregu.

Mówimy, że szereg
jest rozbieżny gdy nie jest zbieżny.

Kryterium Cauchy'ego

Jeśli
to
jest zbieżny gdy
i rozbieżny gdy
.

Kryterium d'Alemberta

Jeśli
oraz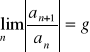
to szereg
jest zbieżny gdy
i rozbieżny gdy
.

Kryterium Leibniza

Jeśli
jest ciągiem nierosnącym zbieżnym do 0, to szereg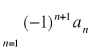
zwany szeregiem naprzemiennym jest zbieżny.

Twierdzenie Cauchy'ego (szeregi)

Jeśli szeregi
i
są bezwzględnie zbieżne, to szereg
jest zbieżny przy czym suma tego szeregu wynosi
gdzie
oznacza sumę szeregu
, a
sumę szeregu
.

Definicja pochodnej .

Pochodną (pochodną lewostronną, prawostronną) funkcji
w punkcie
nazywamy granicę
(
,
) o ile ona istnieje. Oznaczamy ją wtedy jako
(
,
).

Definicja różniczkowalności funkcji.

Mówimy, że funkcja
jest różniczkowalna (różniczkowalna lewostronnie, prawostronnie) w punkcie
jeśli ma w tym punkcie skończoną pochodną (pochodną lewostronną, prawostronną).

Mówimy, że funkcja
jest różniczkowalna w przedziale otwartym, jeśli jest różniczkowalna w każdym punkcie tego przedziału.

Mówimy, że funkcja
jest różniczkowalna w przedziale domkniętym, jeśli jest różniczkowalna w każdym punkcie wewnętrznym tego przedziału, oraz prawostronnie różniczkowalna w lewym krańcu i lewostronnie różniczkowalna w prawym krańcu.

Twierdzenie (o pochodnej funkcji złożonej).

Jeśli funkcja
jest różniczkowalna w punkcie
, zaś funkcja
jest różniczkowalna w punkcie
to funkcja
jest różniczkowalna w punkcie
przy czym [Author ID0: at Tue Aug 14 13:19:00 2001 ][Author ID0: at Tue Aug 14 13:19:00 2001 ]
[Author ID0: at Tue Aug 14 13:19:00 2001 ].

Twierdzenie (o pochodnej funkcji odwrotnej)

Niech
. Jeśli
jest ciągłą i różnowartościową funkcją różniczkowalną w punkcie
, taką, że
, to funkcja odwrotna
jest różniczkowalna w punkcie
i
.

Definicja różniczki .

Niech funkcja f będzie różniczkowalna w punkcie
. Różniczką funkcji f w punkcie
nazywamy funkcję liniową, która dowolnej liczbie rzeczywistej
przypisuje liczbę
. Różniczkę funkcji f w punkcie
będziemy oznaczać jako
.

Twierdzenie (CAUCHE'EGO ) (calki)

Jeżeli funkcje
i
są ciągłe w przedziale [Author ID0: at Tue Aug 14 14:56:00 2001 ][Author ID0: at Tue Aug 14 14:56:00 2001 ]
[Author ID0: at Tue Aug 14 14:56:00 2001 ], różniczkowalne w przedziale [Author ID0: at Tue Aug 14 14:57:00 2001 ][Author ID0: at Tue Aug 14 14:57:00 2001 ]
[Author ID0: at Tue Aug 14 14:57:00 2001 ] to istnieje przynajmniej jeden punkt [Author ID0: at Tue Aug 14 14:59:00 2001 ][Author ID0: at Tue Aug 14 14:59:00 2001 ]
[Author ID0: at Tue Aug 14 14:59:00 2001 ] taki, że
.

Twierdzenie (LAGRANGEA).

Jeżeli funkcja f jest ciągła w przedziale [Author ID0: at Tue Aug 14 14:56:00 2001 ][Author ID0: at Tue Aug 14 14:56:00 2001 ]
[Author ID0: at Tue Aug 14 14:56:00 2001 ]i różniczkowalna w przedziale [Author ID0: at Tue Aug 14 14:57:00 2001 ][Author ID0: at Tue Aug 14 14:57:00 2001 ]
[Author ID0: at Tue Aug 14 14:57:00 2001 ], to istnieje punkt [Author ID0: at Tue Aug 14 14:59:00 2001 ][Author ID0: at Tue Aug 14 14:59:00 2001 ]
[Author ID0: at Tue Aug 14 14:59:00 2001 ] taki, że
.

Twierdzenie. (REGUŁA DE L'HOSPITALA)

Niech
i
będą funkcjami różniczkowalnymi w pewnym sąsiedztwie
punktu
oraz
. Jeżeli
, oraz istnieje granica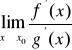
(właściwa lub nie), to istnieje również granica
przy czym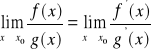
.

Uwaga: twierdzenie odwrotne nie jest prawdziwe.

Twierdzenie (WZÓR TAYLORA)

Jeśli funkcja f ma ciągłą pochodną rzędu
w przedziale
oraz pochodną rzędu
w przedziale
, to istnieje punkt
taki, że
. Ostatni składnik sumy występującej w powyższym wzorze oznaczać będziemy jako
i nazywać resztą w postaci Lagrange'a. Tak więc

Twierdzenie. ( I warunek wystarczający istnienia ekstremum lokalnego .

Załóżmy, że
. Przyjmijmy, że
jest ciągła na
i różniczkowalna na
. Jeśli
to
ma w punkcie
minimum właściwe. Jeśli
to
ma w punkcie
maksimum właściwe.

Twierdzenie. (II warunek wystarczający).

Jeżeli funkcja f ma pochodną rzędu
w pewnym otoczeniu punktu
, ciągłą w punkcie
, oraz
,
, to w przypadku gdy n jest liczbą parzystą, funkcja f ma ekstremum lokalne w punkcie
. Jest to maksimum właściwe, gdy
, zaś minimum właściwe, gdy
. Jeśli n jest liczbą nieparzystą, to f nie ma ekstremum lokalnego w punkcie
.

Twierdzenie (o całkowaniu przez części)

Jeżeli funkcje f i g mają ciągłe pochodne, to

Twierdzenie (o całkowaniu przez podstawienie)

Jeżeli :

1) funkcja f: I→R jest ciągła na przedziale I

2) funkcja
ma ciągłą pochodną na przedziale
,

to
+c , gdzie F jest dowolną funkcją pierwotną funkcji f oraz cR.