Pole napręŻeń w liniowo spręŻystym ośrodku ze szczelinĄ

dwuwymiarowe zagadnienia teorii sprężystości

- funkcja naprężeń Airy'ego

Westergaard wprowadził funkcję naprężeń :

- funkcja analit. zm. zespolonej.

zastosowanie funkcji naprężeń Westergaarda do analizy stanu naprężenia i przemieszczeń w pobliżu wierzchołka szczeliny

Szczelina I typu w paśmie nieskończonym.

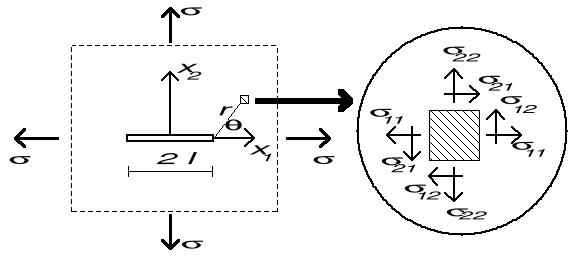
Szczelina w nieograniczonym paśmie rozciąganym w nieskończoności.

Warunki "brzegowe":

1.

2.

3.

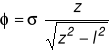
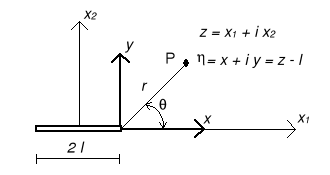
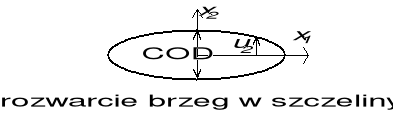
Transformacja układu współrzędnych do wierzchołka szczeliny.

"Lokalna" (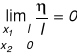
) funkcja naprężeń

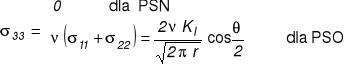
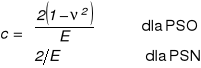
FUNKCJE NAPRĘŻEŃ I WIN DLA RÓŻNYCH PRZYPADKÓW SZCZELIN I TYPU

współczynnik intensywności naprężeń (WIN)

Irwin: tym co uwzględnia geometrię ciała ze szczeliną, jej długość oraz rodzaj i sposób przyłożenia obciążenia jest wsp. KI - tzw. współczynnik intensywności naprężeń.

Nieskończone pasmo z nieskończonym szeregiem szczelin kolinearnych, obciążone równomiernym obciążeniem o wartości

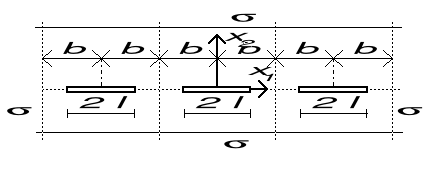
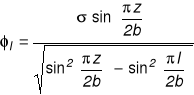
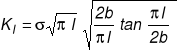
Nieskończone pasmo ze szczeliną, której powierzchnia jest obciążona obciążeniem ciągłym przyłożonym na odcinkach b x1 l; x2=0

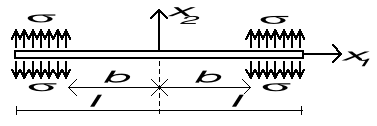
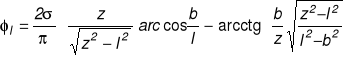
Nieskończone pasmo ze szczeliną, której powierzchnia jest obciążona siłami skupionymi P przyłożonymi w odległości b od wierzchołka

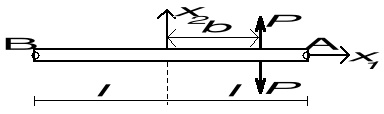
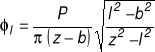
dla b = 0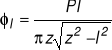

(WIN maleje ze wzrostem długości szczeliny ! )

Wpływ skończonych wymiarów ciała na wartości WIN

Szczelina centralna w paśmie rozciąganym

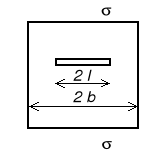
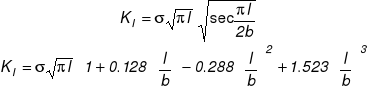
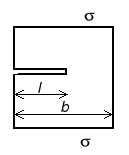
Szczelina krawędziowa w paśmie rozciąganym

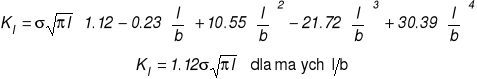
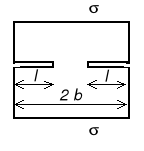
Dwie szczeliny krawędziowe w paśmie rozciąganym

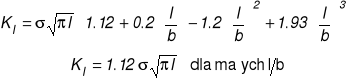
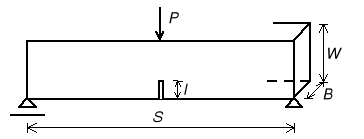
Belka trójpunktowo zginana siłą skupioną P [N] ze szczeliną krawędziową

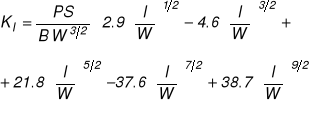
Wykorzystanie zasady superpozycji do wyznaczania WIN

Szczelina wychodząca z brzegu małego otworu kołowego (np. połączenie śrubowe lub nitowane)

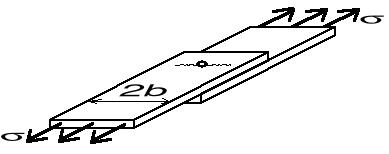
Założenia: promień otworu jest mały w stosunku do długości szczeliny

długość szczeliny jest mała w stosunku do szerokości 2b łączonego elementu

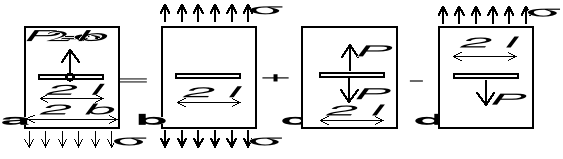
(konfiguracje "a" i "d" są identyczne)

PRZYKŁAD 1

Przeanalizować szczelinę o długości 2l, która tworzy kąt z kierunkiem x2 znajdującą się w nieograniczonym paśmie, poddanym działaniu obciążenia oraz k odpowiednio wzdłuż kierunku x2 i x1. Wyprowadzić wzory na WIN.

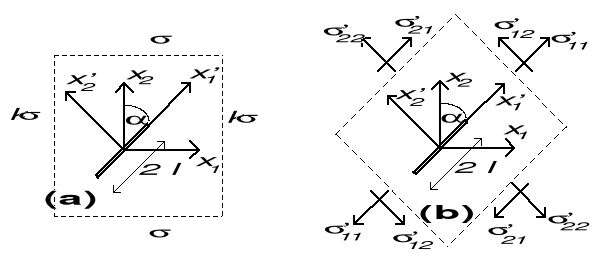
transformacja naprężeń σ₁₁=k , σ₂₂= ,do układu ( x₁' , x₂' ) :

superpozycja obciążeń (+ równoważne układy obciążeń)

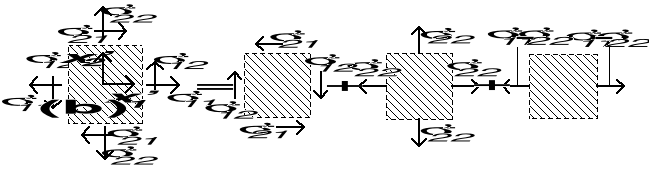
obciążenie szczeliny:

a) dwuosiowe rozciąganie σ'₂₂ [otwarcie szczeliny (I typ )]

b) jednoosiowe rozciąganie (σ'₁₁ -σ'₂₂) wzdłuż osi x'₁ [nie wywołuje osobliwego pola naprężeń, ale musi być uwzględnione w ostatecznej postaci naprężenia σ*₁₁ wzdłuż osi x'₁]

c) obciążeniu ścinającemu σ'₁₂ [poprzeczne ścinanie szczeliny (II typ)]

PRZYKŁAD 2

Cylindryczny zbiornik ciśnieniowy (powłoka walcowa z zamkniętymi końcami) o promieniu R i grubości t posiada skośną szczelinę o długości 2l zorientowaną pod kątem do kierunku obwodowego. Określić współczynniki intensywności naprężeń w wierzchołku szczeliny przy obciążeniu zbiornika ciśnieniem wewnętrznym p

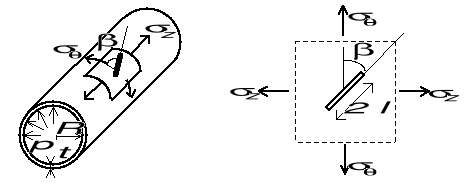
Rozwiązanie :

Naprężenie obwodowe σ_θ i podłużne σ_z w zbiorniku otrzymujemy z warunków równowagi sił

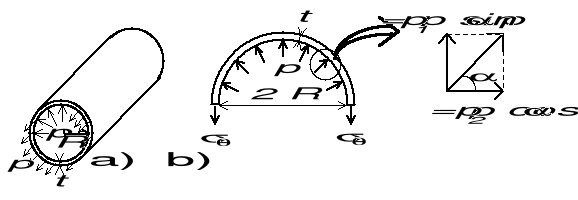
Równowaga sił na kierunku: a) południkowym, b) równoleżnikowym (obwodowym)

Równowaga sił wzdłuż osi zbiornika (kierunek południkowy) - rys. a :

Równowaga sił obwodowych (kierunek równoleżnikowy) - rys. b (równowaga sił pionowych):

;

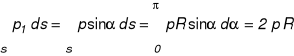
Oznaczenia:

PRZYKŁAD 3

Obliczyć dopuszczalną długość szczeliny l umieszczonej centralnie w paśmie o szerokości 30 cm, równomiernie rozciąganym obciążeniem o wartości 140 MPa. Krytyczna wartość WIN wynosi 55 MPa m1/2, wytrzymałość doraźna ma wartość 350 MPa.

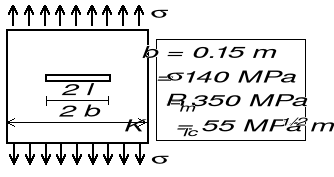
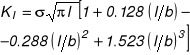
Dopuszczalną długość szczeliny wyznaczamy z warunku:

Dla pasma o nieograniczonych wymiarach

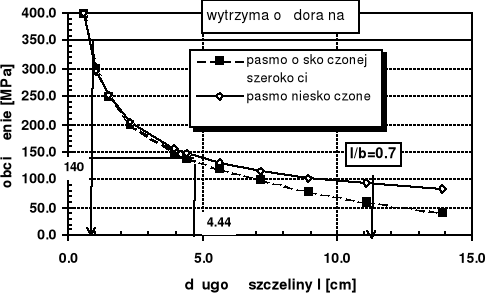
1. Dla obciążenia 140 MPa dopuszczalna wartość długości szczeliny wynosi 2l = 8.88 cm.

2. Czym większe obciążenie tym mniejsza jest długość dopuszczalna szczeliny

3. Dla szczelin bardzo krótkich ( 2l 1.6 cm) obciążenie niszczące wynikające z mechaniki pękania jest większe niż wytrzymałość doraźna. Szczelina nie powoduje w tym wypadku zmniejszenia nośności pasma.

4. Dla szczelin o długości 2l przekraczającej 21 cm uzyskane rozwiązanie jest wątpliwe, gdyż wykorzystany w rozwiązaniu współczynnik intensywności naprężeń obowiązuje w zasadzie dla stosunku l/b nie przekraczającego wartości 0.7.

5. Ze wzrostem długości szczeliny coraz silniejszy jest wpływ skończonej szerokości pasma

PRZYKŁAD 5

Obliczyć dopuszczalną długość centralnej szczeliny l1, jaką można wprowadzić do rozciąganego pasma o szerokości 2b osłabionego dwiema szczelinami krawędziowymi o długości l każda, nie zmniejszając nośności pasma.

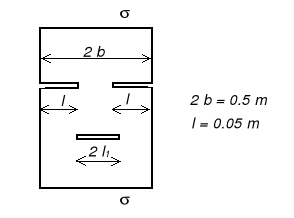
Rozwiązanie:

Zadanie rozwiążemy przy założeniu, że szczelina centralna znajduje się dostatecznie daleko od szczelin krawędziowych, można więc zaniedbać interakcję szczelin.

WIN dla pasma ze szczelinami krawędziowymi

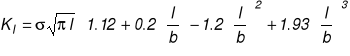
Obc.krytyczne wynikające z warunku KI =KIc

WIN dla szczeliny centralnej

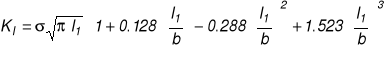
Wprowadzenie szczeliny centralnej nie zmniejszy nośności jeżeli:

2 l1 < 11.88 cm

PRZYKŁAD 5

Porównać nośność rozciąganego pasma o szerokości 2b w trzech przypadkach :1) ze szczeliną centralną 2l, 2) z jedną szczeliną krawędziową l , 3) z dwiema szczelinami krawędziowymi o długości l każda.

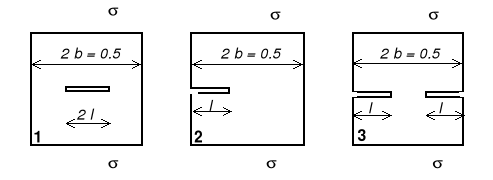
Rozwiązanie:

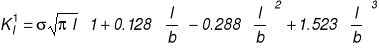
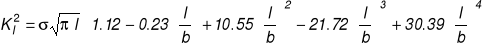
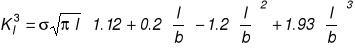
Obciążenie krytyczne KI =KIc.

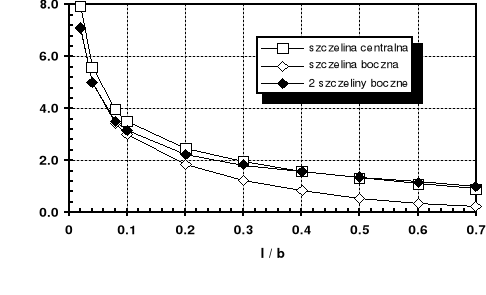
Obciążenie krytyczne kr / KIc w funkcji bezwymiarowej długości szczeliny l / b.

Wniosek : dla ustalonej długości szczeliny najmniejszą nośność ma zawsze pasmo z jedną szczeliną krawędziową, mimo że nominalna powierzchnia przekroju (tzn. pow. całkowita pomniejszona o pow. szczeliny) w płaszczyźnie szczeliny jest w tym przypadku największa. Uogólniając tę obserwację można powiedzieć, że niesymetryczne konfiguracje ciało-szczelina-obciążenie są szczególnie niebezpieczne, gdyż najbardziej obniżają nośność elementu konstrukcyjnego.

PRZYKŁAD 6

Porównać nośność rozciąganego pasma o szerokości 2b ze szczeliną centralną 2l stosując met. mechaniki pękania oraz met. naprężeń nominalnych.

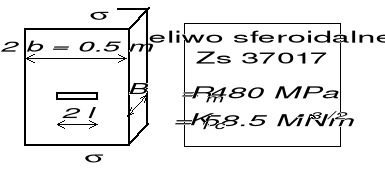
Rozwiązanie:
; A = 2 b B

Warunek równowagi sił :

Warunek wytrzymałościowy σ_nom<R_m:

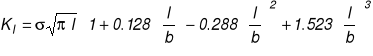
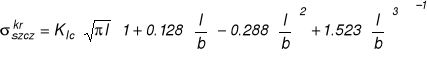
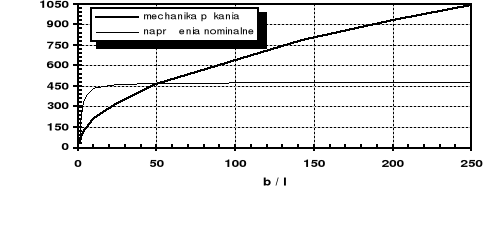
Nośność rozciąganego pasma ze szczeliną centralną.

Wniosek : O nośności elementu może decydować zarówno kryterium naprężeń nominalnych, jak i kryterium mechaniki pękania - zależnie od stosunku dług. szczeliny i szerokości pasma. W tym zadaniu taką wartością graniczną tego stosunku jest l /b 0.02. Oznacza to, że dla szczelin o dług. całkowitej 2l mniejszej od ok. 1 cm odpowiednie jest kryterium napr. nominalnych (daje ono mniejszą nośność elementu), a dla szczelin dłuższych od 1 cm należy posługiwać się metodami mechaniki pękania.

MECHANIKA PÊKANIA.

Pole naprężeń w liniowo-sprężystym ośrodku ze szczeliną 7

32

---