Sprawozdanie

Ćwiczenie nr 1-Obiekt dynamiczny liniowy

Na ćwiczeniach laboratoryjnych badaliśmy odpowiedzi na wymuszenie skokowe członów dynamicznych liniowych:

-proporcjonalnego

-całkującego

-inercyjnego

-różniczkującego rzeczywistego

-dwuinercyjnego

-proporcjonalno całkującego

-oscylacyjnego

Układ dynamiczny to układ którego zachowanie w czasie można opisać modelem matematycznym, to że układ jest liniowy oznacza że odpowiedź wypadkowa jest sumą odpowiedzi cząstkowych poszczególnych wymuszeń(sygnałów wejściowych oraz zakłócających).

Opis dynamiki układu można przeprowadzić za pomocą metody zmiennych stanu, metoda ta opisuje nie tylko wejścia i wyjścia układu ale także przebiegi zjawisk wewnątrz obiektu, umożliwia to stwierdzenie czy obiekt jest sterowalny i obserwowalny. Układy dynamiczne liniowe dają się opisać za pomocą liniowych równań różniczkowych, równania układu dla metody zmiennych stanu mają postać:

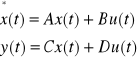
Gdzie:

u(t)-wektor sygnałów sterujących

y(t)-wektor sygnałów wyjściowych

x(t)-wektor stanu

A-macierz stanu

B-maciech wejść

C-macierz wyjść

D- macierz oddziaływania wejścia na wyjście

Stabilność układu jest to zdolność powrotu do stanu równowagi po ustaniu wymuszenia które wytrąciło układ z równowagi.

Układ jest sterowalny jeśli istnieje ograniczone ,przedziałami ciągłe sterowanie u(t) za pomocą którego można przeprowadzić układ z dowolnego stanu początkowego x(t0) do dowolnego stanu końcowego x(tk) w skończonym przedziale czasu w skończonym przedziale czasu.

Układ jest obserwowalny jeżeli przy dowolnym sterowaniu u(t) istnieje chwila tk po której na podstawie znajomości sygnałów wyjściowych y(t) i wejściowych u(t) w przedziale czasu od t0 do tk, można wyznaczyć stan układu x(t0) w dowolnej chwili t0.

Po zapoznaniu się ze stanowiskiem laboratoryjnym przystąpiliśmy do określenia macierzy A,B,C,D kolejnych członów a następnie badaliśmy ich odpowiedzi na wymuszenie skokowe:

Człon proporcjonalny

Transmitancja operatorowa : G(s)=k

y(s)=k*u(s) y(t)=k*u(t)

Transformata wymuszenia skokowego 1(t)=>

Odpowiedź jednostkowa obiektu:
=>

Macierze obiektu uzyskane na podstawie równania y(t)=k*u(t):

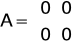
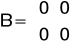
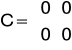
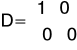
Odpowiedzi układu o takich wartościach macierzy uzyskane na laboratorium przy dwóch wartościach
przy czym
są następujące:

Odpowiedzi te potwierdzają proporcjonalność sygnału wyjściowego do wejściowego.

Człon całkujący:

Dla tego członu sygnał wyjściowy jest proporcjonalny do całki sygnał wejściowego co opisuje równanie różniczkowe:

Transmitancja operatorowa

Odpowiedź jednostkowa
=>

Równania potrzebne do wyznaczenia macierzy układu otrzymuje się w następujący sposób:

=>

Stosując podstawienie

Otrzymujemy układ równań różniczkowych opisujących układ:

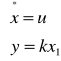
A następnie macierze układu:

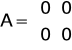
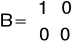
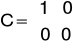
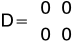
Wykresy odpowiedzi jednostkowych uzyskanych po wprowadzeniu macierzy potwierdza całkujący charakter tego członu :

Człon inercyjny

Odpowiedź jednostkowa

po wykonaniu transformacji Laplacea

Otrzymanie układu równań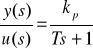

Podstawiając
otrzymuje się:

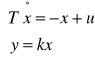
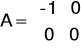
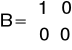
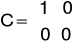
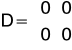
Po wprowadzeniu macierzy otrzymaliśmy następujące odpowiedzi:

Człon różniczkujący rzeczywisty:

Transmitancja operatorowa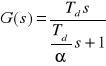

Upisujący układ równań różniczkowych rzędu pierwszego:

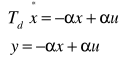
Macierze utworzone na podstawie układu równań

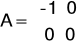
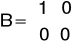
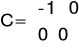
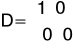
Ze względu na to że do macierzy D układu laboratoryjnego można wprowadzić tylko wartości ujemne, macierze C i D wyglądają następująco:

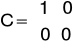
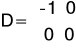
A podawane przez nas wymuszenie zmieniło znak na przeciwny

Wykresy odpowiedzi jednostkowej uzyskane na laboratorium:

Dobrze widoczna jest na nich inercja w działaniu różniczkującym, co przejawia się nie „natychmiastowym” zróżniczkowaniem wartości stałej wymuszenia do zera.

Człon Proporcjonalno-Całkujący:

Transmitancja operatorowa:

Układ równań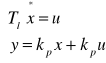

Macierze opisujące układ

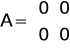
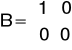
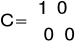
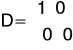
Z powodu występowania dodatniej wartości w macierzy D, macierze C i D przybrały następującą postać, a wymuszenie było ujemne.

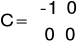
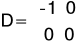
Odpowiedzi uzyskane na stanowisku laboratoryjnym:

Układ dwuinercyjny:

Transmitancja operatorowa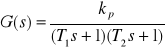

Układ równań: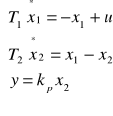

Macierze układu:

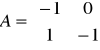
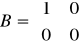
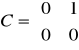
Odpowiedzi jednostkowe uzyskane na zajęciach:

Zejście odpowiedzi poniżej zera jest jedynie błędem urządzenia nie zaś wynikiem określonych właściwości badanego członu.

Człon oscylacyjny:

Transmitancja operatorowa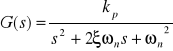

Układ równań różniczkowych pierwszego rzędu opisujących układ uzyskuje się następująco

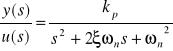
Przechodząc do dziedziny czasu:

Równanie to można zastąpic równaniami pierwszego stopnia przez podstawienie:

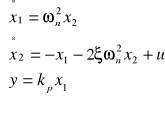
Macierze układu:

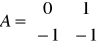
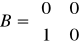
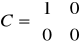
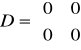
Odpowiedzi jednostkowe:

Człon oscylacyjny badaliśmy szczegółowo zmieniając poszczególne wartości macierzy A:

1)
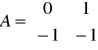
Z układu równań można zapisać

2)

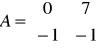
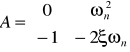
3)

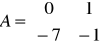
4)

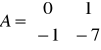
5)

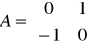
Odpowiedzi jednostkowe są następujące:

Możemy z nich wywnioskować dla przypadków:

1. układ jest taki jak badany wcześniej,widoczne są drgania tłumione

2. zwiększając wartośc
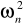
   do 7 uzyskaliśmy zwiększenie częstotliwości i amplitudy oscylacji

3. w wyniku zwiększenia wartości 2,1 macierzy zanikło przesunięcie wykresu odpowiedzi w górę(nie jest widoczny skok), drgania zostały bardzo szybko wytłumione.

4. W wyniku znacznego zwiększenia wartości
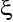
   tłumienie wzrosło do tego stopnia że w układzie nie występuje oscylacja, a układ zmienia się z układu oscylacyjnego w układ dwuinercyjny.

5. W tym przypadku tłumienie wynosi 0(element 2.2 macierzy) przez co wykres przedstawia oscylacje niegasnące.

W następnym punkcie ćwiczenia należało sprawdzić warunki sterowalności obserwowalności i stabilności układu jak na rysunku:

Aby wyznaczyć transmitancję układu należy napisać układ równań ,wprowadzając oznaczenie sygnałów u, t, a oraz transmitancję toru głównego Gr :

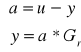
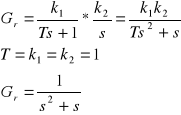
Podstawiając a =u-y do równania drugiego:

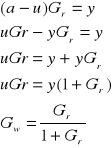
A więc

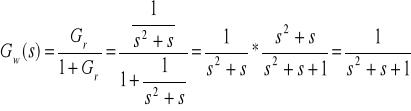
Aby wyznaczyć macierze tego układu należy przejść do dziedziny czasu tworząc równanie różniczkowe układu:

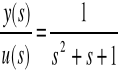
Przechodząc do dziedziny czasu:

Podstawiając:

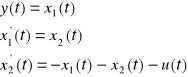
Otrzymane zostały równania różniczkowe pierwszego rzędu, na podstawie których można napisać macierze układu:

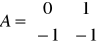
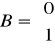
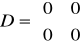
Porównując macierze opisujące ten układ z macierzami opisującymi człon oscylacyjny ,doszliśmy do wniosku że są to te same układy.

Stabilność układu można zbadać metodą Hurwitza, warunkiem koniecznym stabilności jest aby wszystkie współczynniki
równania charakterystycznego były wieksze od zera,a warunkiem koniecznym dodatnia wartość wyznacznika tablic n- tego rzędu, odpowiadającego rzędowi równania charakterystycznego,równanie charakterystyczne rozpatrywanego układu:

W naszym układzie

Tablica Hurwitza dla równania drugiego stopnia:

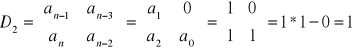
Oba wyznaczniki są większe od zera układ jest więc układem stabilnym

Zbadanie sterowalności układu, polega na sprawdzeniu warunku koniecznego i wystarczającego tj aby:

Dla naszego układu:

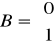
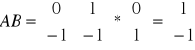
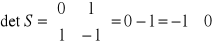
Układ jest więc układem sterowalnym

Sprawdzenie obserwowalności układu polega na sprawdzeniu warunku koniecznego i wystarczającego tj aby:

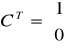
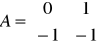
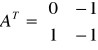
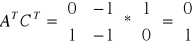
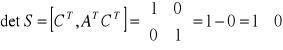
Obiekt jest więc obiektem obserwowalnym.

Wnioski

Badanie dynamicznych obiektów liniowych pokazało zgodność z odpowiedziami jednostkowymi teoretycznymi ,dobrze widoczne na wykresach są działania poszczególnych członów. Opis za pomocą zmiennych stanu pozwala dokładnie opisac parametry obiektu i zbadać jego obserwowalność sterowalność i stabilność. Badanie członu oscylacyjnego przy zmianach parametrów jego macierzy stanu pokazało że za każdym z elementów macierzy kryje za sobą określoną wartość danej zmiennej stanu którego zmiana może całkowicie zmienić charakter obiektu(na przykład znaczne zwiększenie tłumienia przekształca człon oscylacyjny w dwuinercyjny),dojście do tych wniosków nie było by możliwe gdybyśmy nie znali stanu obiektu od „środka” dzieki metodzie zmiennych stanu,a jedynie za pomocą obserwacji wejścia i wyjścia obiektu. Dla obiektu regulacji mimo że nie badaliśmy zmian uchybu w czasie, można wywnioskować że uchyb w stanie ustalonym będzie dążył do zera gdyż w mianowniku transmitancji obiektu występuje pierwiastek zerowy(obecność członu całkującego w torze głównym).

---